Atomically detailed folding simulation of the B domain of staphylococcal protein A from random structures

Abstract

The conformational space of the 10–55 fragment of the B-domain of staphylococcal protein A has been investigated by using the electrostatically driven Monte Carlo (EDMC) method. The ECEPP/3 (empirical conformational energy program for peptides) force-field plus two different continuum solvation models, namely SRFOPT (Solvent Radii Fixed with atomic solvation parameters OPTimized) and OONS (Ooi, Oobatake, Némethy, and Scheraga solvation model), were used to describe the conformational energy of the chain. After an exhaustive search, starting from two different random conformations, three of four runs led to native-like conformations. Boltzmann-averaged root-mean-square deviations (RMSD) for all of the backbone heavy atoms with respect to the native structure of 3.35 Å and 4.54 Å were obtained with SRFOPT and OONS, respectively. These results show that the protein-folding problem can be solved at the atomic detail level by an ab initio procedure, starting from random conformations, with no knowledge except the amino acid sequence. To our knowledge, the results reported here correspond to the largest protein ever folded from a random conformation by an initial-value formulation with a full atomic potential, without resort to knowledge-based information.

For many years, methods have been developed to compute the 3D structures of polypeptides, based on empirical atomic-based potential energy functions and global optimization of such functions. Because of limitations in computer power, these methods have been confined to small molecules such as the pentapeptide enkephalin (1–15), the decapeptide gramicidin S (16–21), and linear fibrous proteins such as collagen-like repeating polytripeptides (22–24). Inclusion of explicit or implicit hydration in the potential function only exacerbated the global optimization problem. However, with the recent availability of cost-effective alternatives to large supercomputers, such as Beowulf class cluster computers (25), it is now possible to extend the application of such ab initio physics-based methods to larger molecules.

In this article, we report the results of the global optimization of the all-atom force field ECEPP/3 (empirical conformational energy program for peptides) (26–29) plus two implicit hydration models [SRFOPT (Solvent Radii Fixed with atomic solvation parameters OPTimized; ref. 30) and OONS (Ooi, Oobatake, Némethy, and Scheraga solvation model; ref. 31)], using the electrostatically driven Monte Carlo (EDMC) method (32, 33) to explore the conformational space of the 10–55 fragment of the B-domain of the staphylococcal protein A molecule, efficiently. The structure of this fragment of the B-domain of the protein A molecule is known from x-ray (34) and NMR (35) investigations, and from minimalist and all-atom simulations (36–46). However, such initial-value-formulated simulations (except for ref. 46, which is a boundary-value formulation) were not started from a random conformation. Therefore, in this work, we attempted to provide an extensive exploration of the conformational space by starting from two different randomly chosen conformations, using a Beowulf class cluster.

Methods

Evaluation of the Conformational Energy. The conformations were generated with the EDMC method (32, 33). An all-atom representation of the chain was used with the ECEPP/3 force field (26–29). Two alternative forms of the potential energy function were used to evaluate the total energy, E(r_p), as a function of the coordinates r_p, namely,

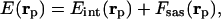[1]

where E_int(r_p) is the internal conformational energy of the molecule in the absence of solvent, assumed to correspond to the ECEPP/3 energy of the neutral molecule and F_sas(r_p) represents the solvation free energy as defined by Vila et al. (30). Two different solvation models were used during the simulations, namely, SRFOPT (30) and OONS (31).

The Starting Point: Generation of the Random Conformation. The N and C termini of the 10–55 fragment of the B-domain of the staphylococcal protein A molecule were blocked by amino-COCH₃ and carboxyl-NH₂ groups, respectively. The simulations were started from two different initial random conformations, i.e., namely rnd_1 and rnd_2. For each of these random conformations, all backbone and side-chain dihedral angles were chosen randomly between 180.0° and –180.0°, with the exception of the dihedral angles ω of the peptide group, which were always chosen in the trans (180.0°) conformation. All backbone and side-chain dihedral angles (including ω's) were allowed to vary freely during the simulations, with the exception of proline residues. In the ECEPP/3 fixed geometry approximation, both up (U) and down (D) puckering conformations of the pyrrolidine ring (which pertain to the following: φ = –53.0° and χ¹ = –28.1° and φ = –68.8° and χ¹ = 27.4° positions, respectively, of the C^γ atom of the proline residue) are considered. At the beginning of a simulation, the puckering of the proline residues is chosen randomly. However, up and down puckering and cis ↔ trans isomerization of the peptide group preceding proline residues were allowed to permute during the course of the simulations. During the EDMC search, if a proline residue is selected for a change, an attempt is made to change the puckering state with a probability of 1/2. In addition, the probability of changing the dihedral angles ω preceding proline from trans to cis is 1/3, and the values of ω were allowed to vary around the trans and cis conformations.

The Conformational Search. For each rnd_1 and rnd_2 initial conformation, an ensemble of conformations was generated by using the EDMC method, as shown in Table 1 for runs 1–4. During each of these runs, the energies of the initially generated and subsequent conformations were minimized by using the secant unconstrained minimization solver (SUMSL) algorithm (47) in combination with ECEPP/3 plus a surface accesible solvation model, either SRFOPT or OONS. Only a small set of low-energy conformations was retained. This set corresponded to the accepted conformations from the Monte Carlo path followed by the EDMC method in each of these runs. It should be noted that the acceptance rate (see Table 1) is low for all of the runs in our simulations. However, as was noted previously (48, 49), this acceptance rate is characteristic of the EDMC procedure.

Table 1.

Summary of the EDMC runs^*

Run	Solvent model	No. of energy-minimized conformations†	No. of accepted conformations‡	Lowest energy, kcal/mol	Total computational time, hr§
1¶	SRFOPT	2,168,453	14,654	-715.5	262
2∥	SRFOPT	2,199,341	14,539	-720.7	191
3**	OONS	815,002	6,546	-651.4	80
4††	OONS	431,214	3,045	-652.9	50
5‡‡	SRFOPT	247,471	1,840	-702.5	47
6§§	OONS	402,627	3,075	-654.3	47

^*Using an average of 60 processors for each run.

^†Number of generated conformations, using the procedure described in Methods.

^‡According to the Metropolis criterion.

^§Differences in computational time reflect different starting conformations and different judgments as to when the runs coverged.

^¶Run 1 was started from random conformation rnd_1.

^∥Run 2 was started from random conformation rnd_2. The lowest-energy identified with this solvation model is indicated in boldface type and belongs to a native-like structure.

^**Run 3 was started from random conformation rnd_1.

^††Run 4 was started from random conformation rnd_2, which led to a mirror image of the native fold. The energy of the mirror-image conformation is indicated in italics.

^‡‡Crosscheck test. Run 5 was started from the lowest energy conformation described in ** and run subsequently with the SRFOPT solvation model. Energy of the mirror-image conformation is indicated in italics.

^§§Crosscheck test. Run 6 was started from the lowest-energy conformation described in ¶ and run subsequently with the OONS solvation model. The lowest-energy identified with this solvation model is indicated in boldface type and belongs to a native-like structure.

Evaluation of the Results: Computation of the Root-Mean-Square Deviation (RMSD). We chose to compare the results of our simulations with the minimized-averaged structure of the 10–55 fragment of the B-domain of the staphylococcal protein A molecule free in solution determined from NMR at 30°C by Gouda et al. (35), and not with the three-dimensional structure of the 10–55 fragment of the B-domain of the staphylococcal protein A molecule bound to the Fc fragment of human polyclonal IgG, determined by x-ray crystallographic analysis by Deisenhofer (34). The reason for this decision was that the B-domain of the staphylococcal protein A molecule forms contacts with the Fc fragment in the crystal, and this could be the main source of the structural differences observed between the NMR and x-ray structures, i.e., the fragment¶ Ser-42–Ala-55 constitutes helix III of the NMR structure whereas, in the crystallographic structure, there is no structural information available for the segment Ala-49–Lys-59, and the portion of the polypeptide chain from Ser-42–Glu-48 is in an extended conformation.

Because all of the NMR constraints used to determine the most probable conformation in solution represent population-weighted-averaged measurements, we computed the Boltzmann-averaged values for the RMSD from the minimized-averaged structure obtained from the NMR experiment (35), using the separate ensembles of conformations generated from each of two different starting random conformations.

Results

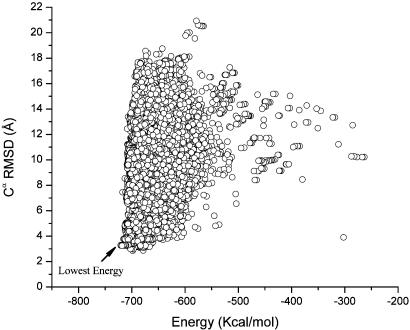
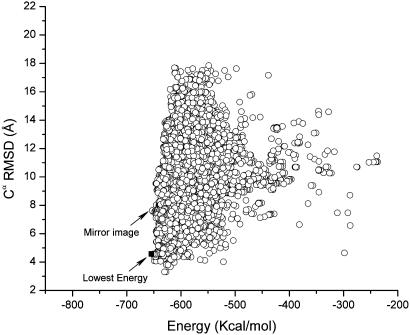
Figs. 1 and 2 show a scatter plot of the C^α RMSDs from the native structure for all the accepted conformations listed in Table 1 for the runs with the SRFOPT and OONS surface area model, respectively. Table 2 shows the Boltzmann-averaged RMSDs from the native fold obtained with these solvation models for all the accepted conformations obtained for each of the simulations starting from rnd_1 and rnd_2. The plots in Figs. 1 and 2 pertain to the C^α (rather than the backbone heavy atoms or all of the heavy atoms) RMSDs from the native structure because there are very good correlations between these quantities and the C^α RMSDs, with a correlation coefficient of R = 0.997 and 0.980, respectively. In other words, plots of the RMSDs of the backbone heavy atoms or all of the heavy atoms, instead of the C^α rms deviations from the native structure, do not add any new information.

Fig. 1.

C^α RMSD vs. the total energy, computed by Eq. 1 using the SRFOPT solvation model, for each of the accepted conformations obtained during runs 1 and 2. The scatter plot does not include those conformations obtained after the crosscheck (run 5). The lowest-energy identified in the figure belongs to the lowest-energy structure (–720.7 kcal/mol) identified in all the runs carried out with the SRFOPT model, namely, runs 1, 2, and 5.

Fig. 2.

C^α RMSD vs. the total energy, computed by Eq. 1 using the OONS solvation model, for each of the accepted conformations obtained during runs 3 and 4. The scatter plot does not include those conformations obtained after the crosscheck (run 6). The mirror image (–652.9 kcal/mol) of the native fold identified in the figure belongs to the lowest-energy found in runs 3 and 4. However, this conformation is higher in energy than those obtained after the crosschecking test in run 6 (–654.3 kcal/mol); the conformation in run 6 belongs to the native-like fold and is indicated by a filled square in the figure and represents the lowest-energy conformation identified in all the runs carried out with the OONS solvation model, namely, runs 3, 4, and 6.

Table 2.

Boltzmann-averaged RMSD^* between native and generated conformations

Solvent model	Cα atoms, Å	Backbone heavy atoms, Å	All heavy atoms, Å
SRFOPT†	3.96 (2.85)	4.05 (2.92)	5.29 (4.21)
SRFOPT‡	3.30 (3.24)	3.35 (3.30)	4.69 (4.62)
OONS§	4.09 (3.31)	4.54 (3.42)	5.46 (4.61)
OONS¶	7.59 (4.35)	7.59 (4.42)	8.91 (5.42)

^*Computed at 30°C by using separate ensembles of conformations generated in runs 1 to 4, listed in Table I. Values within parentheses belong to the lowest RMSD computed for a single conformation, i.e., they do not represent Boltzmann-averaged values.

^†Results from run 1, Table 1.

^‡Results from run 2, Table 1.

^§Results from run 3, Table 1.

^¶Results from run 4, Table 1, which led to a mirror image of the native fold.

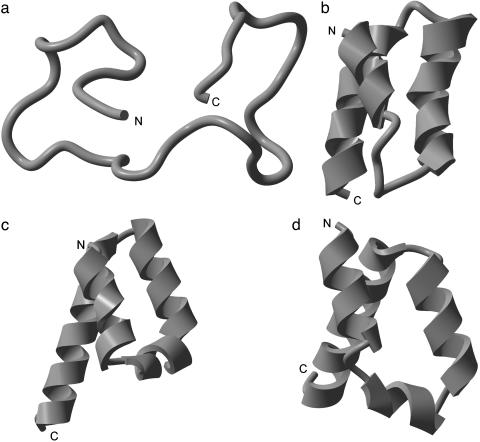
The NMR-determined structure of the 10–55 fragment of the B-domain of the staphylococcal protein A molecule is composed of a bundle of three α-helices as shown in Fig. 3b, i.e., helix I (Gln-10–His-19), helix II (Glu-25–Asp-37), and helix III (Ser-42–Ala-55). The lowest energy conformation found with SRFOPT (–720.7 kcal/mol) exhibits a similar distribution of helices, i.e., helix I (Gln-11–His-19), helix II (Arg-28–Asp-37), and helix III (Pro-39–Asp-54). Helices II and III are antiparallel to each other in both the NMR-derived native fold and in the lowest-energy conformation found with either SRFOPT or OONS, as shown in Fig. 3 c and d.

Fig. 3.

(a) Ribbon diagram of the starting conformation rnd_1. (b) Ribbon diagram of the native fold obtained by NMR. (c) Ribbon diagram of the lowest-energy (–720.7 kcal/mol) structure identified in this work by using the SRFOPT solvation model. (d) Ribbon diagram of the lowest-energy (–654.3 kcal/mol) structure identified in this work by using the OONS solvation model.

Independent of the starting conformation, the SRFOPT solvation model always led to a native-like structure. Both of the lowest-energy conformations identified in these runs (–715.5 and –720.7 kcal/mol, respectively) have native-like folds. Analysis of the runs from Table 1 shows that the potential function with the OONS solvation parameters led to two broad basins with similar energies. One of the basins contains the native-like structure (–651.4 kcal/mol) and the second one contains conformations that represent mirror images of the native-like structure (RMSD vs. Energy is indicated in Fig. 2).

To investigate the depth of the basins containing the native- and mirror-like conformations, we carried out additional crosschecking runs. The lowest-energy conformation obtained with SRFOPT in run 2 (–720.7 kcal/mol) was used as the starting conformation with the OONS solvation model and, vice versa, the lowest-energy conformation, i.e., the mirror image, obtained with OONS in run 4 (–652.9 kcal/mol) was used as the starting conformation with the SRFOPT solvation model. The resulting total energy shown in Table 1 for the mirror image (in italics) indicates that, for both solvation models, the mirror image is higher in energy than those belonging to the native-like conformation, after the crosschecking. It should be noted that no constraints were used to restrict the search during these runs.

It was found that the potential energy with OONS seems to distinguish the native-like structure (–654.3 kcal/mol) from the mirror image (–652.9 kcal/mol); however, the energy difference between these two basins is quite small. The potential energy with SRFOPT, on the other hand, shows a bigger difference between both structures, namely, –720.7 kcal/mol for the native-like vs. –702.5 kcal/mol for the mirror image structure, indicating that this solvation model can detect the correct fold. A summary of these crosschecking runs is shown in Table 1, runs 5 and 6.

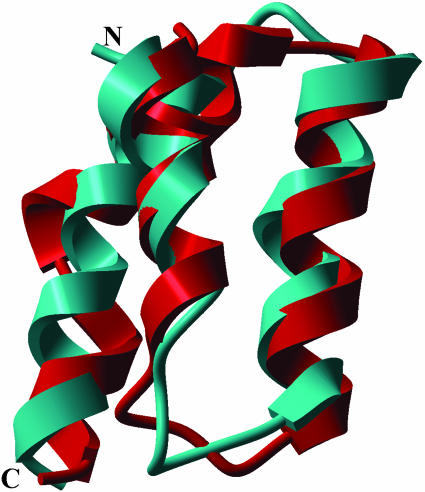
The scatter plots shown in Figs. 1 and 2 indicate that the differences in energy among the few conformations close to the lowest one are small whereas they display a broad dispersion in RMSD. This result represents one of the main difficulties in identifying the native-like structure. On the other hand, this result means that the total energy, as a scoring function, must be extremely precise to distinguish the correct folded structure from wrong ones. This requirement constitutes a challenge for improving existing force fields or for developing new potential functions. In addition, the small energy gap between basins containing quite different folds represents a great challenge for search methods. Regarding this observation, it can be seen from Table 2 that the EDMC method did find a conformation that is quite close to the native structure (with an RMSD for the C^α atoms of 2.85 Å). However, this conformation with the lowest RMSD (–698.3 kcal/mol) is higher in energy than the lowest energy minimum (–720.7 kcal/mol) found for this solvation model by >20 kcal/mol. Fig. 4 shows the superposition of this structure with the native-NMR fold. It should be pointed out, for comparative purposes only, that the C^α RMSD of the fragment containing helix I, helix II, and part of helix III, i.e., residues∥ 128–162 of the x-ray (35) and equivalent residues 10–44 of the NMR (36) structures, is 2.0 Å.

Fig. 4.

Ribbon diagram of the superposition of the native fold (cyan) and the conformation (red) with the lowest C^α RMSD (2.85 Å) from the native fold, obtained with the SRFOPT solvation model. The energy of this conformation is >20 kcal/mol above that of the lowest-energy conformation identified with this solvation model in runs 1, 2, and 5.

Discussion and Conclusions

There is an ongoing interest about how to represent the unfolded state of a protein. According to some authors (50), the denatured states are quite sensitive to their environment and hence they can span a continuum of conformational states, ranging from structured intermediates to statistical coils. In other words, it seems that the residual structure depends on the sequence and the environment. Correct characterization of the unfolded states represents a more complex problem than the protein-folding problem by itself because the unfolded state may not correspond to a well-defined structure such as that characterizing the native fold of a protein. For this reason, and also to avoid any bias in the conformational search, we started from random initial conformations with no knowledge other than the amino acid sequence, i.e., an ab initio search. Our results show that folding of a small protein, such as the 10–55 fragment of the B-domain of the staphylococcal protein A molecule can be accomplished with an all-atom potential with a reasonable degree of accuracy, as shown in Table 2. It is worth noting that other contributions to the total energy, such as coupling of the conformation with the state of ionization of the individual amino acids (proton-binding equilibrium) (51) or an estimation of the conformational entropy (52), were not taken into account in these simulations. Conceivably, incorporation of these components as well as a new parameterization of the existing all-atom force-field (53) should improve the accuracy of the predictions.

We wrote in 1994 (54), “With the recent development of various efficient approaches to overcome the multiple-minima problem, the problem has been in some sense solved for small oligopeptides, as well as for regular-repeating structures and assemblies of fibrous proteins. It can reasonably be expected that the current extension of these to globular proteins will result in efficient searches of their conformational space in the near future. Advances in computer hardware and software, especially the wider use of parallelism, will speed up computations, making practical the application to larger molecules. The point may have been reached where wider applicability of these techniques is becoming limited by the accuracy of the potential energy functions used to describe the energetic of polypeptide and protein structure.” Results of this work, in some sense, support this assertion. The 46-residue fragment of protein A is larger than the 36-residue α-helical protein from the villin headpiece, for which all-atom simulations starting from an extended structure were previously carried out (55, 56). It is worth noting that simulations on the villin headpiece were carried out with explicit solvent (55), which increases the computing time considerably compared with the time required for the implicit solvent models used in our simulations. However, despite the large progress in computer technology, we still cannot extend the all-atom approach to the prediction of the folding of globular proteins containing 100–200 residues. For this reason, the use of simpler models based on physical grounds, such as the hierarchical approach starting with the united-residue (UNRES) force field and finishing with an all-atom search (57), is necessary. Also, procedures that combine knowledge-based information with energy minimization (58–60) have achieved some measure of success in recent CASP (critical assessment of techniques for protein structure prediction) blind tests. Hopefully, further improvements will extend the applicability of all-atom ab initio procedures.