A Semianalytical Model to Study the Effect of Cortical Tension on Cell Rolling

Abstract

Cell rolling on the vascular endothelium plays an important role in trafficking of leukocytes, stem cells, and cancer cells. We describe a semianalytical model of cell rolling that focuses on the microvillus as the unit of cell-substrate interaction and integrates microvillus mechanics, receptor clustering, force-dependent receptor-ligand kinetics, and cortical tension that enables incorporation of cell body deformation. Using parameters obtained from independent experiments, the model showed excellent agreement with experimental studies of neutrophil rolling on P-selectin and predicted different regimes of cell rolling, including spreading of the cells on the substrate under high shear. The cortical tension affected the cell-surface contact area and influenced the rolling velocity, and modulated the dependence of rolling velocity on microvillus stiffness. Moreover, at the same shear stress, microvilli of cells with higher cortical tension carried a greater load compared to those with lower cortical tension. We also used the model to obtain a scaling dependence of the contact radius and cell rolling velocity under different conditions of shear stress, cortical tension, and ligand density. This model advances theoretical understanding of cell rolling by incorporating cortical tension and microvillus extension into a versatile, semianalytical framework.

Introduction

Cell rolling is the first step of the neutrophil inflammatory response, which facilitates cytokine activation, firm adhesion, and extravasation of the neutrophils by promoting close interaction between the neutrophils and the vascular endothelium (1,2). This process involves continuous formation and dissociation of adhesive bonds between leukocytes and the vascular endothelium under shear flow, mediated by glycoprotein receptors known as selectins (3–5). Cell rolling has also been implicated in the trafficking of lymphocytes, platelets, hematopoietic and mesenchymal stem and progenitor cells, and metastatic cancer cells (4,6,7). Cell rolling also holds promise as a method for separation of cells with therapeutic and diagnostic applications (8–10).

Cell rolling has been studied in vivo and in vitro (1,11,12), and has been mimicked using ligand-coated microspheres (13–16). It is now established that cell rolling involves transient formation and dissociation of cell-surface adhesive interactions involving interplay of different mechanisms from the molecular to the cellular levels (17). The fast association kinetics of selectins enables rapid formation of bonds, whereas the force-dependent dissociation prevents firm adhesion of the cell to the surface (18–21). The ligands that participate in cell rolling are distributed in clusters at the tips of cell membrane extensions known as microvilli (22). Interplay between the nonlinear mechanical properties of the microvilli (23,24) and the nonuniform ligand distribution dictates the rate at which microvilli detach from the surface and the resulting forces exerted on the cell. Furthermore, deformability of the body of the cell affects the cell-surface contact and influences rolling (25,26). Due to this complexity, modeling of cell rolling has emerged as an important tool that complements experimental studies to understand cell rolling.

Earliest models of cell rolling included the membrane-peeling model by Dembo et al. (27) and the stochastic models by Cozen-Roberts (28,29) and Zhao et al. (30). In the semianalytical model of cell rolling developed by Tozeren and Ley (31), bonds were assumed to have constant dissociation rates, and in that by Krasik and Hammer (32), the cell was modeled as a rigid sphere with elastic bonds. Among the computational models, adhesive dynamics incorporating microvilli, receptor clustering, and force-dependent bond dissociation into a stochastic model of cell rolling could recreate the transient nature of cell rolling and was used to study the sensitivity of rolling to bond kinetics (18,33) and effects of microvillus mechanics (34). Korn and Schwarz (35,36) combined adhesive dynamics with Langevin dynamics allowing spatial-temporal resolution of individual receptors on the cell surface. Modeling the cell as a rigid sphere, the authors studied the efficiency of initial tethering of cells on receptor-coated substrates (35) and also identified different dynamic states of cell rolling based on translational as well as rotational velocities of the cell (36). The effect of cell deformability was captured by the three-dimensional computational model by Konstantopoulos and co-workers (37,38), which described the cell as an elastic membrane with receptors clustered at focal adhesion points on microvilli. This model could explain the transient rolling motion of the cell and the effects of cell body and microvillus deformation on rolling. Adhesive dynamics simulations have so far not accounted for cell body deformation, but the simulation by Konstantopoulos and co-workers addressed it by modeling the membrane as an elastic plate. However, experiments to probe leukocyte mechanics have shown that the Newtonian drop model that describes the cell as a viscous liquid drop surrounded by a membrane with a cortical tension (∼20 μN/m) can explain their mechanical behavior (39). So far, these computational models have not incorporated cortical tension to describe cell body deformation during rolling. Although computational models enable detailed three-dimensional simulations, the range of parameters that can be explored is often limited by computational cost. Semianalytical models are more suitable for parametric studies because of their simplicity and flexibility, which lends itself more easily to an intuitive understanding of cell rolling and exploring of scaling relationships. However, previous semianalytical models have not included microvillus mechanics, receptor clustering, or cell body deformation.

In this work, we present a semianalytical model of cell rolling that integrates force-dependent kinetics, microvillus mechanics, and receptor clustering with cortical tension to describe cell-body deformation. Focusing on the microvillus as the unit of adhesion, the deterministic kinetics of bond formation and dissociation are incorporated into a probabilistic framework governing the transport of surface-tethered microvilli, thus overcoming some of the limitations of earlier deterministic models. This approach enables explicit modeling of the discrete nature of cell-surface adhesions and clustering of receptors on the microvillus tip and takes into account cell body deformation, microvillus mechanics, and force-dependent receptor-ligand kinetics. The model improves over prior treatments of microvillus mechanics by incorporating a microvillus dynamics description that shows good agreement with reported microvillus force-extension characteristics. Using values of parameters obtained from independent experiments, we compare the predictions of the model with experimental studies of neutrophil rolling reported in the literature. We use the model to define the state space of rolling and explore the effects of cortical tension and microvillus stiffness on the cell rolling behavior.

Model Description

We consider a cell rolling at a steady horizontal velocity V_x ($\overrightarrow{V}=-V_x\widehat{i}$) and rotational speed ω_z ($\overrightarrow{\Omega }={\omega }_z\widehat{k}$) on a plane receptor-coated surface under a fluid flow with shear rate γ (Fig. 1). For steady rolling we restrict the rotational speed by the relation ω_z= V_x/R. The cell has flexible microvilli with adhesion molecules on their tips (3,22). Cell deformation results in increased contact with the surface where bond formation takes place. As the cell rolls, microvilli extend and exert a tensile force on the receptor-ligand bonds and on the cell. This tensile force is distributed equally among the receptor-ligand bonds on the microvillus tip, which governs bond dissociation and hence the time span for which the microvillus remains attached to the substrate. At any given instant of time, the sum of forces and torques exerted on the cell by all the microvilli and the reaction force from the contact area balances the force and torque due to the fluid, enabling the cell to roll with a steady velocity.

Figure 1.

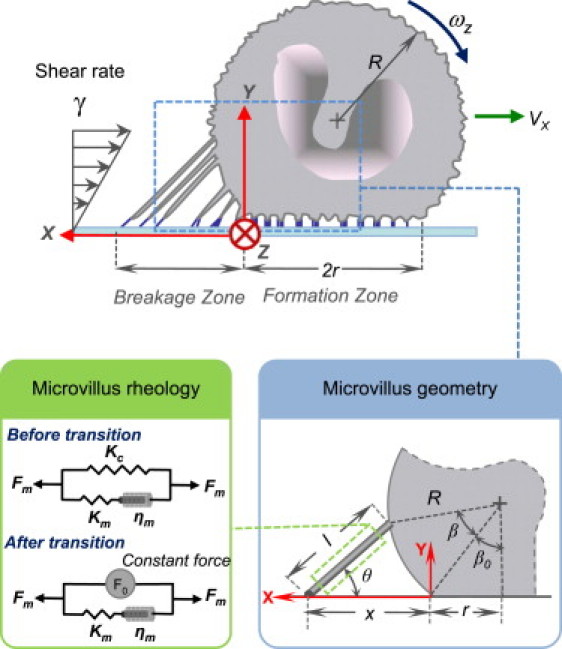
Schematic diagram of a cell rolling under shear flow. Adhesive bond formation takes place in the formation zone, whereas bond breakage occurs in the breakage zone. Microvilli with receptors on their tips extend in the process (inset) and detach after all bonds at the tip dissociate. A three-element viscoelastic model (inset) describes microvillus rheology, where one of the springs changes its state at a threshold force enabling transition from a viscoelastic to a viscous behavior.

Model of the cell

A schematic diagram of the cell geometry is shown in Fig. 1. We model the cell as a deformed sphere of radius R forming a circular contact area of radius r with the substrate. Extensible microvilli with a tip area of A_m are present on the cell surface at a density of N_m. Adhesive receptors are expressed on the cell surface at a nominal density of ${\overline{N}}_R$, but ∼80% are clustered on the tips of the microvillus (3), leading to a higher local density, given by $N_R=0.8{\overline{N}}_R/\left(N_m{A}_m\right)$.

Cell deformation

During cell rolling, the receptor-ligand bonds exert forces in both x and y-direction on the cell. The vertical component of the bond forces (y-direction) is balanced by a reaction force resulting from a uniform contact stress at the cell-substrate interface, which leads to cell deformation (40). Following the work of Lomakina et al. (41), and neglecting gravitational and dynamic effects, the contact radius is given by

$$r=\sqrt{\frac{F_y^{reac}R}{2\pi T_C}},$$ (1)

where $F_y^{reac}$is the reaction force from the substrate on the cell and T_c is the cortical tension of the cell. In all the simulations, r was restricted to be less than the cell radius R. In addition, to maintain constant cell volume, R is related to the contact radius r and the undeformed cell radius R₀ by the equation

$${\left(\frac{R}{R_0}\right)}^3\left[2+\sqrt{1-\frac{r}{R}}\left\{2+{\left(\frac{r}{R}\right)}^2\right\}\right]-4=0.$$ (2)

Microvillus mechanics

Microvilli serve a critical role in cell rolling by acting as mechanical linkages between the adhesive bonds and the body of the cell, being elastic at low tensile force and viscous at larger forces (23,42). Since earlier microvillus extension models (32,34) are valid only for static forces, we used a new three-element model consisting of spring (stiffness K_m) and damper (viscosity η_m) in series, which are both in parallel to another spring (stiffness K_c) (Fig. 1). Transmembrane proteins such as PSGL-1 and L-selectin are anchored to the cytoskeleton (43), and a force applied to the molecule is transmitted both to the cytoskeleton and the membrane. The elastic nature of the cytoskeletal extension is represented by the spring K_c, whereas the viscoelastic membrane is represented by the spring K_m and damper η_m in series. The transition from elastic- to viscous-dominated regime beyond a critical tensile force (23,44) is believed to be caused by uprooting of the PSGL-1 molecule from the cytoskeleton (44). Therefore, the force in the cytoskeletal spring (K_c) was clipped at a critical value of F₀ (Fig. 1), yielding viscous dominated behavior at high forces or long extensions, in agreement with experimental observations (23,42,44,45). The microvillus constitutive relations in the case of a steady rolling velocity are then given by

$$\{\begin{array}{l}{V}_x\frac{d{F}_m}{dx}+\frac{K_m}{{\eta }_m}{F}_m=\frac{K_m{K}_c}{{\eta }_m}l+\left(K_m+K_c\right)V_x\frac{dl}{dx}\text{for}{K}_{c}l\le F_0\\ V_x\frac{d{F}_m}{dx}+\frac{K_m}{{\eta }_m}\left(F_m-F_0\right)=K_m{V}_x\frac{dl}{dx}\text{for}{K}_{c}l>F_0,\end{array}$$ (3)

where l is the microvillus extension, F_m is the force exerted on the microvillus, and F₀ is the transition force. Numerical values for the cytoskeletal spring K_c (43 pN/μm) and the membrane damper η_m (11 pN-s/μm) were obtained by comparison to the experiments of Shao et al. (23). K_m (200 pN/μm) was determined by comparison with experimental data for viscoelastic relaxation of a microvillus by Xu et al. (45) (Fig. S1 in the Supporting Material). Although Xu et al. (45) proposed a different three-element model, the model described here was used because its elements correlated with the physical system and it showed good agreement with published data in the elastic as well as viscous regimes.

Kinetics of bond formation

Bond formation and breakage occurs at intrinsic (unstressed) rates in the contact area or formation zone where the microvilli are stress-free, i.e., k_f = k_f⁰ and k_b = k_b⁰. Microvilli are stressed in the breakage zone where only bond dissociation occurs and the formation rate is k_f = 0 (Fig. 1). The bond dissociation rate, k_b, in the breakage zone depends on the force on the bond as given by the model of Bell (18), $k_b=k_b^0\text{exp}\left(r_c{f}_b/k_{\text{B}}T\right)$, where k_b⁰ is the intrinsic breakage rate, r_c is the reactive compliance corresponding to the range of the receptor-ligand interaction, f_b is the force on a single bond and k_BT is the thermal energy. Since all bonds share the tensile force (F_m) on the microvillus, $f_b=F_m/(N\times A_m)$, where NA_m is the number of bonds on the microvillus tip. At steady state, the kinetic equation governing bond formation is expressed as

$$V_x\frac{dN}{dx}=k_f\left(N_R-N\right)\left(N_L-N\right)-k_{b}N,$$ (4)

where N is the bond density on the tip of a microvillus positioned at x, N_R is the actual receptor density on the microvillus tip, and N_L is the ligand density on the surface. The initial condition for the above equation is N = 0 at x = −2r.

Kinematic relations

We assume that the microvilli are unstressed up to the trailing edge (x ≤ 0) and start extending as they move away from the trailing edge (x ≥ 0). We define a microvillus by two parameters, that defining location of tethering to the substrate (x) and that of attachment to the cell surface (β) (Fig. 1, inset). The apparent surface area of leukocytes changes in response to external loads while maintaining a cortical tension (46); therefore, we allow the base of the microvilli to displace laterally to attain mechanical equilibrium. This assumption is in agreement with the concept of cortical tension and is supported by other experimental studies on cell rolling (24,47). To incorporate this effect, we assume a linear mapping for microvillus displacement on cell surface such that lateral displacement of each microvillus on the cell surface is linearly proportional to its distance from the trailing edge. Thus, β = (1 − α)x/R, where α is the linear mapping parameter with a maximum value of 1. The choice of a linear mapping is somewhat arbitrary, but it satisfies two important criteria: 1), no two microvilli can be tethered at the same location; and 2), the force and torque equilibrium must be satisfied. We note that this kinematic assumption does not allow for additional deformation of the cell body near the contact area. Based on the above definitions the microvillus extension, l, and the angle between the microvillus and the surface, θ (Fig. 1), can be expressed as

$$\begin{array}{l}l=\sqrt{{\left(x+r-R\sin \left(\beta +{\beta }_0\right)\right)}^2+{\left(R\cos {\beta }_0-R\cos \left(\beta +{\beta }_0\right)\right)}^2}\\ \theta ={\tan }^{-1}\left(\frac{R\cos {\beta }_0-R\cos \left(\beta +{\beta }_0\right)}{x+r-R\sin \left(\beta +{\beta }_0\right)}\right),\end{array}$$ (5)

where β₀ = sin⁻¹(r/R).

Kinetic relations

Since bond formation only occurs inside the contact region, a microvillus starts with a certain number of bonds at x = 0 and gradually loses bonds as it moves further into the breakage zone (x>0). The probability of a receptor-ligand bond that existed at x = 0 still existing at x = X is given by p_i = N/N₀, where N₀ is the initial bond density on the microvillus tip (at x = 0) and N is the bond density at x = X. Since the total initial number of bonds at the microvillus tip is given by z = N₀A_m, the probability that the microvillus is attached to the substrate at x = X, ϕ(x = X), becomes

$$\varphi =1-{\left(1-p_i\right)}^z$$ (6)

This equation assumes that microvillus detachment occurs only when all bonds at its tip have dissociated. The net forces and torques acting on the cell in different directions due to extended microvilli are obtained by integrating the forces and torques due to individual microvilli as

$$\begin{array}{l}\frac{d{F}_x^{bond}}{dx}=\varphi F_m{N}_m\left(2r\right)\cos \theta \\ \frac{d{F}_y^{bond}}{dx}=\varphi F_m{N}_m\left(2r\right)\sin \theta \\ \frac{d{T}_z^{bond}}{dx}=\varphi F_m{N}_m\left(2r\right)R\cos \left(\theta +{\beta }_0+\beta \right)\\ {\overrightarrow{F}}^{bond}=F_x^{bond}\widehat{i}-F_y^{bond}\widehat{j}\text{and}{\overrightarrow{T}}^{bond}=-T_z^{bond}\widehat{k}.\end{array}$$ (7)

Defining $\varphi \left(x\right)$ and using it as a weighing function allows us to compute parameters like local microvillus density and average microvillus extension and improve over earlier deterministic models that required arbitrary definitions of the extent of breakage regions (26,32). To find the force and torque on the cell due to the fluid flow, we model the cell as a sphere flowing close to the wall in a low Reynolds number flow. Following the methodology outlined by Goldman et al. (49,50), with ω_z = V_x/R, the expression for the net force and torque becomes

$$\begin{array}{c}\frac{F_x^{fluid}}{6\pi \mu R{V}_x}=\left[F_{tran}^{\ast }+F_{rot}^{\ast }+\frac{R\gamma }{V_x}{F}_{shear}^{\ast }\right]\\ \frac{T_z^{fluid}}{8\pi \mu R^2{V}_x}=\left[T_{tran}^{\ast }+T_{rot}^{\ast }+\frac{R\gamma }{2V_x}{T}_{shear}^{\ast }\right]\\ {\overrightarrow{F}}^{fluid}=-F_x^{fluid}\widehat{i}\text{and}{\overrightarrow{T}}^{fluid}=T_z^{fluid}\widehat{k}.\end{array}$$ (8)

The value of the coefficients used in this simulation as calculated by Goldman are $F_{tran}^{\ast }=-4.0223$, $F_{rot}^{\ast }=0.5132$, $T_{tran}^{\ast }=0.3894$, and $T_{rot}^{\ast }=-2.6790$ for a separation distance of 12.8 nm between the sphere and the wall and $F_{shear}^{\ast }=1.7005$ and $T_{shear}^{\ast }=0.9439$ for a sphere touching the wall. Although the above coefficients are, in general, a function of the separation distance between the sphere and the wall, the dominant terms $F_{shear}^{\ast }$ and $T_{shear}^{\ast }$ (since V_x is small compared to γR) are asymptotic at small separation distances, resulting in Eq. 8 being insensitive to separation distance. Increasing the separation distance from 12.8 nm to 500 nm changes the shear stress estimates by <5%, indicating that the somewhat arbitrary choice of the separation distance did not result in significant error.

Finally, since the cell is in mechanical equilibrium, the summation of all external forces and torques should be zero, which gives the equations

$$F_x^{bond}=F_x^{fluid},F_y^{bond}=F_y^{reac},\text{and}{T}_z^{bond}=T_z^{fluid}.$$ (9)

Numerical scheme

A computationally inexpensive iterative scheme was used to solve the coupled ordinary differential and nonlinear equations in the above formulation. For a given rolling velocity V_x and contact radius r, a value of α was assumed and Eqs. 2−7 were solved in succession to yield the forces and torques acting on the cell. These values were used to calculate the fluid shear stress from the force balance (Eqs. 8 and 9), and the shear stress was in turn used to calculate the torque due to the fluid (Eq. 8). Finally, the torque balance equation (Eq. 9) was used to calculate the mismatch (error) resulting from the torque due to the fluid and that due to the microvilli. Using a constrained error minimization scheme, a value of α was found at which the torque balance was satisfied. Using the above procedure, a lookup table for reaction force, $F_y^{reac}$, shear stress, radius, etc., was obtained for different values of V_x and r. Finally, a built-in optimization algorithm was used to find the values of V_x and r for which Eq. 1 was satisfied, which yielded the solution. All the ordinary differential equations were solved using a variable order solver in MATLAB with error tolerance of 10⁻⁴ and maximum step size of 10⁻² whereas the minimization schemes had an error tolerance of <10⁻³. Convergence for a given value of V_x and r on a PC (Dual processor at 1.6 GHz, 2 GB RAM) required only 20–40 s.

Results and Discussion

We used our model to study the rolling of neutrophils on P-selectin-coated surfaces mediated through the PSGL-1 present on the neutrophil surface (51). Numerical values for the parameters used in the simulations (Table 1) were taken directly from experimental studies published in the literature, except for the microvillus model parameters obtained by fitting to microvillus extension data reported in the literature.

Table 1.

Numerical values of parameters

Symbol	Definition	Value	Source
R0	Cell radius	4 μm	(34)
Tc	Cortical tension	24 pN/ μm	(41)
Kc	Microvillus spring constant representing cytoskeletal stiffness	43 pN/μm	Comparison with (23)
Km	Microvillus spring constant representing membrane stiffness	200 pN/μm	Fitting with data of (45)
F0	Transition force	45 pN	(23)
ηm	Membrane viscosity	11 pN-s/μm	Comparison with (23,42)
kf0	Intrinsic bond formation rate	0.1 μm2/s	(32)
kb0	Intrinsic bond breakage rate	1 s−1	(54)
rc	Reactive compliance of bond	0.5 Å	(54)
T	Temperature	37°C
$\overline{N}$ R	Average PSGL-1 density on cell	100 μm−2 (20,000/cell)	(3,55)
NL	Ligand density on substrate	50 μm−2
Nm	Microvillus density on cell	1.25 μm−2	(3,56)
Am	Area of microvillus tip	0.02 μm2	(3,34)
μ	Viscosity of water	0.673 × 10−3 N-s/m2

The values given are those used in the simulation unless otherwise specified.

We compared the variation of neutrophil rolling velocities with shear stress and ligand density predicted by the model with the experimental data of Puri et al. (19) (Fig. 2). At higher ligand densities, the model predicted an initial increase in rolling velocity followed by a plateau; the increase in velocity was rapid at lower ligand densities. The model quantitatively captured the experimental trends, including stabilization of rolling velocity at high shear stresses (>4 dyn/cm²). The predicted rolling velocities matched well at a ligand density of 50–60 sites/μm², which, although lower than the reported value of 90 sites/μm², is in good agreement given the possibility that site accessibility and molecular orientation can reduce the number of sites available for binding. Thus, the model was able to correctly predict the variation of cell rolling velocities with shear stress and showed good agreement with experimental data.

Figure 2.

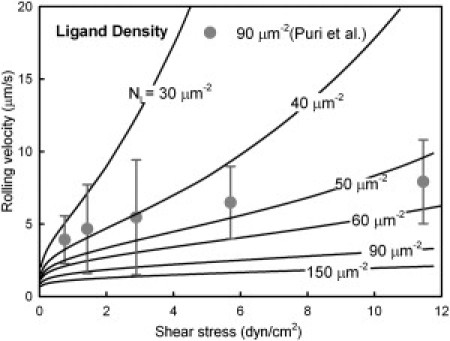
Variation of the cell rolling velocity with shear stress for different values of the P-selectin density. Experimental data from Puri et al. (19) regarding neutrophil rolling on P-selectin (N_L = 90 sites/μm²) are shown for comparison.

State space for cell rolling

One of the important objectives for modeling cell rolling is to elucidate conditions that support either rolling, slow rolling/firm adhesion, or transient rolling. An additional consideration is defining regimes in which the cells flatten or spread under the action of fluid shear. Previously, the state space representation has been used to elucidate the effects of different molecular properties such as on and off rates; however, cellular properties including deformation and microvillus extension were not included (32,33,35,36). We used our model to explore the state space for neutrophil rolling for different shear stresses and ligand densities. To better illustrate cell rolling, a nondimensional velocity was defined as V^∗ = V_x/V_HD, where V_HD is the hydrodynamic velocity of a free-flowing cell (at a wall separation distance of 12.8 nm) as derived by Goldman et al. (50). A cell was considered to be rolling if its velocity was in the range 0.01 ≤ V^∗ ≤ 0.1 and firmly adhered or slow-rolling if its velocity was in the range V^∗ ≤ 0.01, whereas any cell with velocity V^∗ ≥ 0.1 was considered fast-rolling. A similar approach has been used previously (32,33,36) to delineate different rolling regimes in the state space.

We consider the state space for neutrophil rolling on a P-selectin-coated substrate at different P-selectin ligand densities and shear stresses (Fig. 3). At high ligand densities (N_L > 50 sites/μm²), the cell rolls at moderate velocity (rolling regime) at low shear stress but switches to slow rolling with increasing shear stress, i.e., the cell rolling velocity does not increase in proportion to the shear stress. The slow-rolling regime is governed by shear-induced cell deformation leading to increased bond formation and hence low rolling velocity. For large shear stresses, the cell deforms and eventually the diameter of the contact area approaches the cell diameter. This regime (r > 0.9R) denotes spreading of the cell. Cell spreading and complex microvillus structure formation have been observed experimentally at similar shear stress and ligand densities (24), and it therefore denotes transition to a regime that cannot be captured with the model presented here. At low ligand densities (N_L < 50 sites/μm²), the rolling velocity is more sensitive to ligand density. With decreasing ligand density at a given shear stress, cells progressively transition from steady rolling to fast rolling and finally to transient tethering. This regime of transient tethering corresponds to conditions for which torque balance could not be satisfied, indicating that the assumption of steady rolling (ω_z = V_x/R) was invalid (see Korn and Schwarz (36).). The state space of rolling for different formation and dissociation rates of the receptor-ligand bonds also exhibited these rolling regimes (Fig. S2). The results are qualitatively similar to the state space of cell rolling with varying receptor-ligand association and dissociation rates where the cell was modeled as a hard sphere (36).

Figure 3.

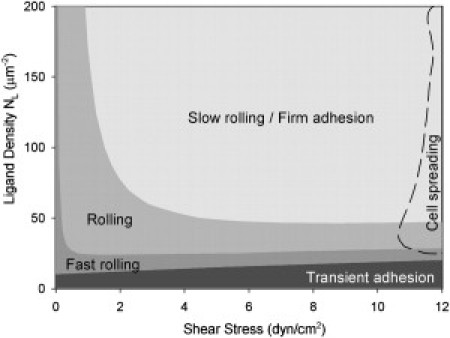
State diagram for rolling of neutrophils at different values of shear stress and ligand density (T_c = 24 pN/μm).

Effect of cortical tension on rolling velocity

Next, we investigated the effect of cortical tension on the rolling response to shear stress and found that the cortical tension indeed had a significant effect on the cell rolling behavior (Fig. 4 a). Highly deformable cells (T_c < 10 pN/μm) rolled with very low velocities that did not change significantly with shear stress. These cells exhibited a high degree of deformation and spreading (r > 0.9R) at relatively low shear stress (∼3–7 dyn/cm²). Such highly deformed cells can either adhere firmly or continue slow rolling through formation of complex microvillus structures (24). Sheikh et al. (47) reported that cytotoxic drugs such as cytochalasins can induce rolling cells to become adherent. Cytochalasin D treatment has been reported to decrease the neutrophil cortical tension by up to 66% to ∼10 pN/μm (52). Thus, the effect of cytochalasin treatment can be explained as a transition to the spreading regime induced by the decrease in the cortical tension. On the other extreme, cells with low deformability (T_c >100 pN/μm) are highly sensitive to shear stress and show stable rolling only at low values of shear stress, switching to transient adhesion at higher shear. This behavior is consistent with the higher rolling velocities of receptor density-matched microspheres compared to cells (17) and with their failure to roll at high shear stresses (14). Similar increase in rolling velocity has also been observed with fixed cells (17), although contrary results have also been reported (53). Cells with intermediate values of cortical tension (20–100 pN/μm) exhibited robust rolling with increasing velocity over a wide range of shear stress. The state diagram of rolling also exhibited major shifts in the regimes of rolling with variation of the cortical tension (Fig. S3).

Figure 4.

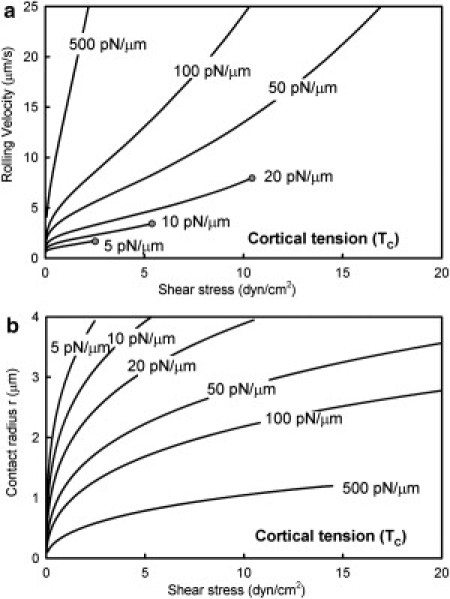
Effect of cortical tension on neutrophil rolling velocity. (a) Variation of the rolling velocity with shear stress for different values of the cortical tension. Lines that terminate in a sphere indicate transition to the cell spreading regime (r > 0.9R). (b) Modulation of the contact radius with shear stress for different values of the cortical tension. Termination of the line for T_c = 500 pN/μm corresponds to transition to the tethering regime. Ligand density N_L = 50 μm⁻².

The cell-surface-contact radius exhibited an initial steep increase with shear stress followed by a much slower increase at larger shear stresses (Fig. 4 b). This behavior is very similar to the experimental observations of the contact area of rolling HL60 cells reported by Dong et al. (25). Based on these results, one can arrive at a possible explanation for the differences in rolling behavior at different values of the cortical tension. Increase in cell deformability may be expected to aid rolling primarily by increasing the contact area or by decreasing the inclination angle of the microvilli (see Fig. 1). Deformable cells (low T_c) can balance an increase in shear by both of these mechanisms and hence exhibit stable rolling velocities against a wide range of shear stress. On the other hand, stiffer cells (high T_c) that lack these deformability-induced mechanisms to balance shear stress have to increase their rolling velocity. These mechanisms become clearer when we examine the microvillus behavior in the next section.

Effect of microvillus mechanics on rolling

Rolling cells form adhesive contacts with the substrate through receptors clustered on the tips of extensible microvilli. Microvilli are thus the force-transduction components of the cell, and the microvillus structure and rheology may be expected to influence cell rolling. We therefore used our model to study the effect of cell deformability and shear stress on the forces exerted by the microvilli and the role of microvillus stiffness in stabilizing cell rolling. We also used a schematic diagram of the actual cell shape with the microvilli scaled to their local density to illustrate the effect of cell-body deformation on the number, orientation, and extension of the microvilli (Fig. 5).

Figure 5.

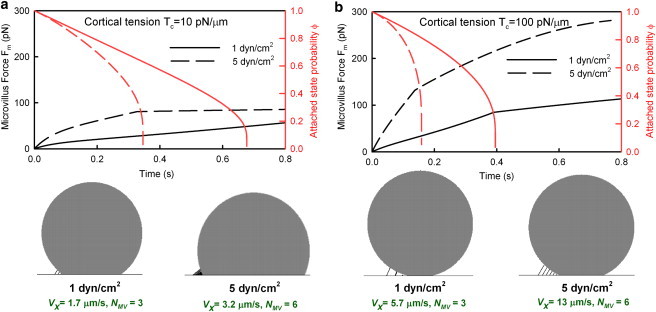
Time history of the force experienced by a microvillus (left y axis, black lines) and probability of being attached to the substrate (right y axis, red lines) as it moves past the trailing edge during cell rolling. Cells with different cortical tensions of 10 pN/μm (a) and 100 pN/μm (b) are shown side by side for two different shear stresses. Snapshots of cell rolling under these conditions are depicted to scale, with microvillus densities proportional to the density obtained from the model. Rolling velocity (V_x) and total number of extended microvilli (N_MV) at a given instant are also specified.

For a low cortical tension of 10 pN/μm, Fig. 5 a shows the force history that a microvillus experiences at low and high shear stress overlaid with the probability, ϕ, that the microvillus is attached to the substrate. The area under the force-time curve is the net impulse provided by each microvillus (direction of force and attachment probability needs to be taken into account), whereas the rate at which microvilli dissociate is proportional to the cell-surface contact area and the velocity. The product of these two quantities yields the net force exerted on the cell by microvilli, which balances the fluid force. At low shear stress, the microvillus exhibits a linear elastic behavior carrying lower forces, and at higher shear stresses, the viscoelastic rheology is evident by the nonlinear nature of the curves. The net force carried by the microvillus is also approximately doubled at the higher shear stress, but it leads to faster bond dissociation and shorter duration for which the microvillus carries load, maintaining a similar impulse. For a deformable cell (low T_c), the increased shear is balanced primarily by 1), an increase in the rate of formation of load-bearing microvilli due to cell deformation and a modest increase in velocity (from 1.7 to 3.2 μm/s); and 2), a change of the microvillus orientation (see schematic diagram (Fig. 5 a, lower), which further helps to balance the shear.

Conversely, for stiff cells (high T_c) (Fig. 5 b), the microvilli similarly bear increased force with increasing shear, but for shorter duration, approximately maintaining the area under the force-time curve. In this case, the increase in shear stress is balanced by an increase in the rate of formation of load-bearing microvilli originating primarily from the increased rolling velocity (from 5.7 to 13 μm/s), with little change in the microvillus orientation. Thus, stiffer cells exhibit higher rolling velocities.

We also examined the effect of microvillus stiffness on cell rolling for different values of the cortical tension. Although adhesive dynamics simulations of microvillus-coated rigid spheres (34) indicated a minimum in the rolling velocity with varying microvillus stiffness (treated as a spring), simulations by Pawar et al. (38) that modeled the cell as an elastic membrane showed little effect of microvillus stiffness except at high ligand densities and shear stresses. In our model, we varied the microvillus stiffness by scaling all microvillus parameters (F₀, η_m, K_m, and K_c) by a factor ξ. In the case of high cortical tension, the rolling velocity was sensitive to microvillus stiffness, exhibiting a minimum, as previously reported for rigid microvillus-coated spheres using adhesive dynamics (34) (Fig. 6). It is interesting to note that as the cortical tension decreased, cell rolling became insensitive to the microvillus stiffness until a high value of stiffness was reached. These results show that cell rolling is more sensitive to microvillus mechanics when the cortical tension is high, i.e., when the cell is not very deformable, as compared to the more deformable case.

Figure 6.

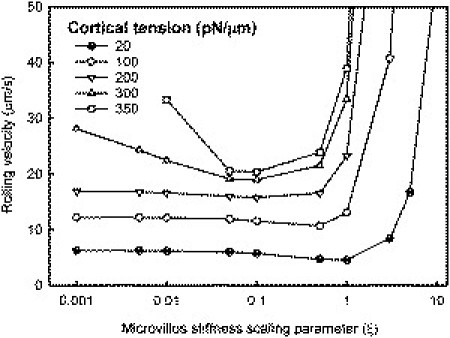
Variation of cell rolling velocity with microvillus stiffness for different values of the cortical tension (τ = 5 dyn/cm², N_L = 50 sites/μm²). ξ is a scaling factor such that the resulting microvillus parameters are ξF₀, ξη_m, ξK_m, and ξK_c, with the base values of the parameters given in Table 1.

Scaling of rolling behavior with cortical tension and shear stress

The model enables exploration of the effect of different parameters including shear stress and cortical tension on cell rolling. We therefore used our model to test scaling relationships that may be useful for predicting the cell-surface contact area and the rolling velocity. To obtain a scaling relationship for the contact radius, we note that the reaction force is given by 2πr²T_c/R₀ (from Eq. 1). Assuming that the reaction force scales with the shear force (τR₀²) acting on the cell, we get the relationship r ∼ (τR₀³/T_c)^1/2. Indeed, we found that the contact radius expressed as a function of τR₀³/T_c collapses onto a single curve for different values of shear stress and cortical tension (Fig. 7 a). A more remarkable finding was that the scaling relationship remains valid even at different values of the ligand density. We also examined whether a scaling relationship can be obtained for the cell rolling velocity. The force exerted by the microvilli on the cell is the product of the rate of breakage of the microvilli (N_mrV_x) and the impulse provided by each microvillus, which may be expected to scale with the shear force, τR₀². The impulse corresponding to each microvillus is in turn the product of the microvillus force (F_m) and lifetime (t_m). F_m ∼ K_cl, where K_c is the microvillus stiffness and l is the extension. In turn, l ∼ t_mvV_x. Assuming that t_mv scales with the off rate (t_mv ∼ 1/k_b⁰) gives a scaling factor K_cV_x/(k_b⁰)² for the microvillus impulse. Incorporating the scaling for r, we obtain the scaling relationship V_x⁴ ∼ τR₀(k_b⁰)⁴T_c/(K_c²N_m²). For a given N_m, K_c, and k_b⁰, we therefore expect the velocity to scale as V_x ∼ (τT_c)^1/4. This scaling relationship may be expected to hold in regimes where the microvillus detachment rate is not affected largely by force on the bonds. An interesting observation was that for different values of cortical tension and shear stresses, the velocity does scale with (τT_c)^1/4 (Fig. 7 b). For higher values of (τT_c)^1/4, the relationship deviates from linearity. Overall, the collapsed curves are exponential in nature, and their deviation from linearity corresponds to the regimes where microvillus detachment is accelerated by the force carried by the microvillus.

Figure 7.

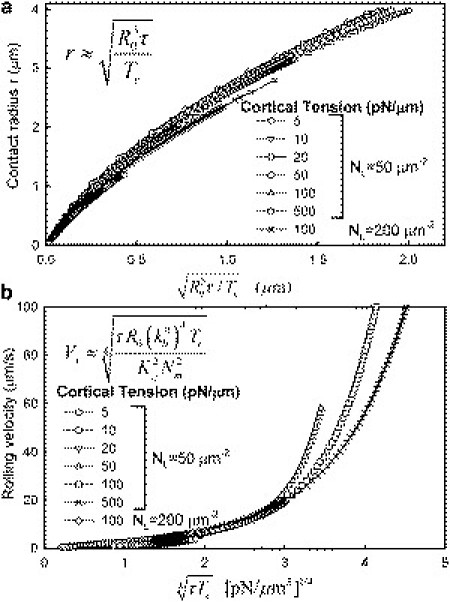
Scaling relationships for cell-surface contact radius and rolling velocity. Contact radius (a) and cell rolling velocity (b) scale with the indicated scaling parameters for different values of shear stress, cortical tension, and ligand density.

Conclusions

In summary, we developed a semianalytical model of cell rolling that focused on the microvillus as the unit of cell-surface adhesive interactions and incorporated cortical tension to describe cell-body deformation. The model was used to study the cell rolling behavior of neutrophils on P-selectin, and it showed good agreement with experimental data. The model enabled creation of a state-space diagram for neutrophil rolling, including the regimes of fast rolling, transient rolling, slow rolling/firm adhesion, and cell spreading on the substrate under high shear. Increasing the cortical tension resulted in increased cell-surface contact area and decrease of the rolling velocity. In a similar way, the cortical tension affected the force history experienced by the microvilli. Higher cortical tension resulted in greater dependence of cell rolling on microvillus stiffness, whereas this dependence almost vanished for smaller values of the cortical tension and moderate microvillus stiffness. Finally, the model allowed us to validate scaling relationships to predict the cell-surface contact area and cell rolling velocity for different values of shear stress and cortical tension. This model forms a versatile framework to study cell rolling in a variety of systems.