Hydraulic trade-offs and space filling enable better predictions of vascular structure and function in plants

Abstract

Plant vascular networks are central to botanical form, function, and diversity. Here, we develop a theory for plant network scaling that is based on optimal space filling by the vascular system along with trade-offs between hydraulic safety and efficiency. Including these evolutionary drivers leads to predictions for sap flow, the taper of the radii of xylem conduits from trunk to terminal twig, and how the frequency of xylem conduits varies with conduit radius. To test our predictions, we use comprehensive empirical measurements of maple, oak, and pine trees and complementary literature data that we obtained for a wide range of tree species. This robust intra- and interspecific assessment of our botanical network model indicates that the central tendency of observed scaling properties supports our predictions much better than the West, Brown, and Enquist (WBE) or pipe models. Consequently, our model is a more accurate description of vascular architecture than what is given by existing network models and should be used as a baseline to understand and to predict the scaling of individual plants to whole forests. In addition, our model is flexible enough to allow the quantification of species variation around rules for network design. These results suggest that the evolutionary drivers that we propose have been fundamental in determining how physiological processes scale within and across plant species.

Understanding the coevolution of plant internal vascular networks and external branching networks is essential to predict botanical form and function (1–4). Seminal studies have attempted to unite these internal and external networks (3, 5, 6). A decade ago West, Brown, and Enquist (3) proposed a model (WBE) that focuses on the primacy of vascular networks, predicts myriad aspects of plant form and function (3, 7), and has subsequently been tested by the collection of new data for vascular networks (8, 9) and analyses of fluxes through plants (10, 11), forests, and ecosystems (12, 13). Since the publication of the WBE model, several criticisms have been published that question its basic framework, assumptions, and generality (14–16). Indeed, focusing on plant models, several studies have: (i) highlighted how hydraulic safety and efficiency may have shaped the evolution of vascular networks (2, 17), (ii) questioned whether vascular safety and efficiency are adequately described by the WBE model (8, 18, 19), and (iii) revealed empirical patterns that contradict parts of the WBE model (9, 20–23). For example, building on earlier work (24, 25), Sperry and colleagues (2) compiled data for the xylem conduits that transport water in plants, and they documented a general principle termed the “packing rule”—the frequency of xylem conduits varies approximately inversely with the square of conduit radius. This packing rule contradicts the WBE model's assumption that conduit frequency remains unchanged as conduit radii taper, decreasing in size from trunk to terminal twig. Safety and efficiency considerations have been proposed to underlie the packing rule (2), suggesting new theory is needed to accurately describe vascular architecture (2, 19, 26, 27).

Here, we construct a plant network model that allows for a flexible and realistic representation of xylem vascular networks. We show how the internal vascular and external branching networks are coupled and jointly optimized by general evolutionary principles (2, 3, 22, 27–29). We argue that the evolution of plant networks is primarily guided by (i) space-filling geometries to maximize carbon uptake by leaves and sap flow through conduits; (ii) increasing hydraulic conductance and resource supply to leaves; (iii) protection against embolism and associated decreases in vascular conductance; (iv) enforcement of biomechanical constraints uniformly across a plant; and (v) independence of terminal twig size, flow rate, and internal architecture with plant size. Principles ii and iii are more central in our model than in the WBE model (3, 5). Furthermore, we apply space filling not only to the external network (like WBE) but also to the internal network, allowing us to relate conduit radius to conduit frequency. These principles together enable us to predict and incorporate the packing rule and other vital plant properties that better match real plant networks and empirical data.

Theoretical Framework

Geometric Model for Internal and External Networks in Plants.

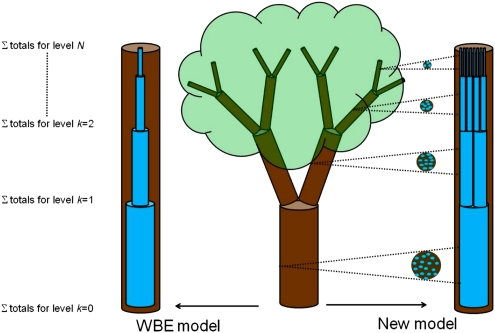
Plants are characterized as a symmetric, hierarchical branching network within our model (Fig. 1). Each branching junction is considered to be symmetric because the daughter branches have identical properties to each other for both the external branch and the internal conduits (30). The overall network is hierarchical because each branch segment can be labeled as being within level k, according to the number of branching points from the trunk to that branch segment (Fig. 1). We place the external and internal networks on the same footing by using three parallel scaling ratios that describe the changes in the radius, length, and number throughout the plant network. Letting N_•,k be the number of xylem conduits (branches) at level k, where _• represents either _int or _ext, we define the ratios

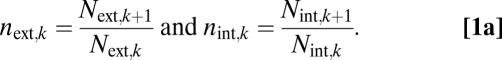Fig. 1.

Branching structures depicting the difference in internal network structure for our model compared with the WBE model. Trees are labeled from the base (level k = 0) to the terminal twigs (level k = N). The left and right columns represent simplified versions of the models. Both models predict conduit taper, but our model also allows the number of conduits to increase and potentially fill a constant fraction of available wood area (shown to the right).

The ratios for radii, r_•,k, and lengths, l_•,k, across branching levels are

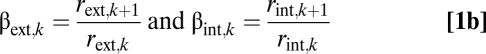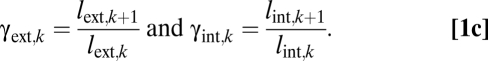The WBE model uses a_k instead of r_int,k for xylem conduit radius. Because the WBE model does not include the internal branching ratio, n_int,k, or length ratio, γ_int,k, it tacitly assumes that n_int,k = 1, preventing conduit number from increasing as conduits taper. In our model, because n_int,k differs from 1, we can assess how selection for increased conductance and protection against embolism through redundancy can shape the internal xylem network. We assume that the interconduit pits contribute a constant fraction to branch resistance (31), so within a branch, conduits connected end-to-end by pits have a resistance that scales like a single conduit that is the length of the external branch (i.e., l_int,k = l_ext,k and γ_int,k = γ_ext,k), as in the WBE model. The conduit radius, r_int,k, represents the average over all conduits within a level k, and we assume that a constant fraction of xylem cross-sectional area is actively conducting.

Biomechanical Trade-Offs, Space Filling, and Scaling in External Branching Networks of Plants.

Eqs. 1a–1c can describe a variety of networks and diverse plant types because the scaling ratios can differ at each level k. However, many networks in nature are self-similar: n_•,k = n_•, β_•,k = β_•, and γ_•,k = γ_•, where _• represents either _int or _ext. Our principles i–v predict self-similarity for both the internal and the external networks. Principle i gives

where constant b indicates self-similarity and b = 1/3 is space filling (3). Principle iv yields

because summing across levels predicts that plant path length, l_TOT, scales with trunk radius as l_TOT ∝ 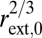for large plants. This relationship is observed for large plants and results in biomechanical stability with constant safety margins from Euler buckling—the deformation or buckling of a column (plant stem or tree trunk) under its own weight (32, 33). Combining Eqs. 2 and 3 predicts da Vinci's rule of area preservation (21, 34, 35),

where constant a indicates self-similarity and a = 1 is area preservation. Eqs. 2–4 are equally prioritized optimality constraints with any two implying the third.

Hydraulic Trade-Offs, Space Filling, and Scaling in Internal Vascular Structure of Plants.

Our characterization of the internal network differs from WBE's because we invoke the full generality of biomechanical stability, space filling, and hydraulic safety while also allowing the number of conduits to vary across branching levels. Our model's flexibility allows the full incorporation of principles i–v that together imply an optimal vascular network should (a) have sufficient nonconducting tissue in each branch to provide biomechanical strength, (b) pack as many conduits as possible into the remaining wood tissue area to increase conductance and buffer against embolism, (c) taper conduit radii to increase conductance and the number of parallel hydraulic pathways, and (d) minimize conduit taper, subject to the previous constraints, to decrease chances of embolism. We show how selection “drivers” a–d are constrained by the external network (Eqs. 2–4) and have shaped form and function within and across plants.

Joint Optimization of Internal Vascular and External Branching Networks As Guided by Core Evolutionary Principles.

First, a constant fraction of the total wood area does not conduct water because it is required to maintain mechanical strength by driver a. The remainder of wood area is potentially available for conducting water (Fig. 1), and by driver b, the total water-conducting area in each branch, 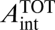= N_int,k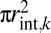, must fill this entire remainder portion of wood area to maximize conductance. Because total wood area is constant across levels (Eq. 4), the total branch conducting area, which is a constant fraction of the total, must also be constant across branching levels. Rearranging the expression for the water-conducting area gives the packing rule

Second, we derive the maximum conductance (driver c). This conductance calculation explicitly couples the internal geometry, via each conduit's resistance, and the external geometry, via number of terminal twigs, 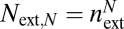, where N is the number of levels. Together, this coupling determines the total number of conduits at level k, 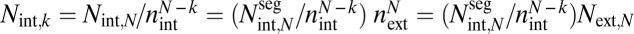, where is the number of conduits in a single terminal twig. Further, we define p to be the unique exponent such that 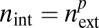. Using these relationships, the whole-plant conductance is

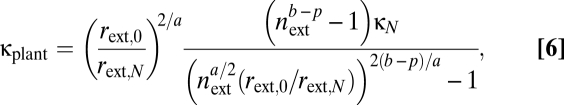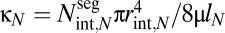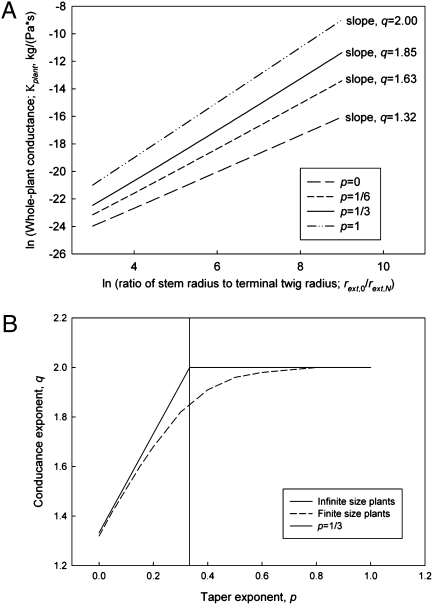
where is the conductance for laminar flow through all conduits in a terminal twig, invariant by principle v, and μ is the viscosity. As plants increase in size (r_ext,0/r_ext,N) >> 1, there are two possibilities dictated by the difference in the scaling exponent, b, for branch length ratios and the exponent, p, related to the taper of radii of xylem conduits: (i) If b − p ≥ 0, conductance scales with stem radius, r_ext,0, to an effective exponent, q, that is <2/a; or (ii) if b − p < 0, conductance scales maximally with plant size as 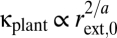. The latter result is approached asymptotically and holds only for plants of infinite size (SI Text) (36). For realistic size ranges, conductance always scales less than the maximal value (q < 2/a; Fig. 2).

Fig. 2.

(A) Plots of the logarithm of conductance [kg/(Pa·s)] vs. the logarithm of the ratio of base radius to terminal twig radius. We chose taper exponents of p = 0, 1/6 (WBE model), 1/3 (our model), and 1. We used n_ext = 2, r_ext,N = 0.5 mm, l_ext,N = 5 mm, μ = 10⁻⁶ kg/(mm·s), ρ = 1 g/cm³, r_int,N = 0.01 mm, 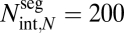, and a size range of r_ext,0 = 1 cm to r_ext,0 = 4 m for our parameters. The corresponding effective conductance exponent, q, is given beside each line. (B) Plot of the conductance exponent, q, vs. the taper exponent p. For plants of infinite size, the asymptotic relation is q = 4/3 + 2p for p ≤ 1/3 and q = 2 for p ≥ 1/3. For a realistic size range of r_ext,0 = 1 cm to r_ext,0 = 4 m (finite-size plants), q varies continuously with p. Nevertheless, the point of maximum curvature (i.e., the magnitude of the second derivative) occurs at p = 1/3, seemingly always an important transition point in the scaling of whole-plant conductance.

To complete our optimization calculation, we assume that the probability of embolism within the xylem increases with conduit radius (31). Because terminal twig size is assumed to be independent of plant size, increased tapering leads to larger conduit radii in the base. Thus, by driver d selection to maximize hydraulic safety will minimize taper relative to other constraints. Using Eqs. 5 and 6, the taper of xylem conduit radii is

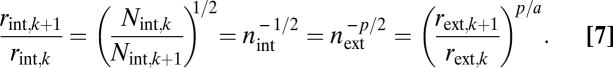Eqs. 6 and 7 reveal a trade-off between safety and conductance (Fig. 2). Specifically, as the taper exponent, p, increases, the scaling exponent of plant conductance with trunk radius, q, saturates to its maximum of 2 when a = 1 (Fig. 2). For extremely large trees, the scaling of conductance is maximized when b − p ≤ 0 or p ≥ b = 1/3 (SI Text; Fig. S1). Relative to this constraint, xylem taper is minimized when the tapering exponent p = 1/3, predicting that the ratio of radii across levels and thus the degree of taper follows r_int,k+1/r_int,k = 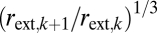when a = 1. For realistic size ranges of plants, the scaling of conductance, q, varies with the scaling of taper, p, more continuously (Fig. 2B). Nevertheless, irrespective of plant size, the taper exponent p = 1/3 still represents an important transition in the trade-off curve between conductance and safety. The maximum curvature in the q vs. p plot (Fig. 2B) occurs at p = 1/3, consistent with a break-even point in the diminishing gain for the scaling of conductance, q, as the exponent for taper, p, increases beyond 1/3. Thus, selection to maximize rates of return for conductance while tapering less for safety leads to p being close to 1/3. Elucidating the mechanisms underlying this trade-off between taper and safety (31) is necessary for species- and habitat-specific predictions and rigorous evaluation and extensions of our model.

Results

Tests of Predictions for Internal Vascular Structure and Hydraulic Function Within Plants.

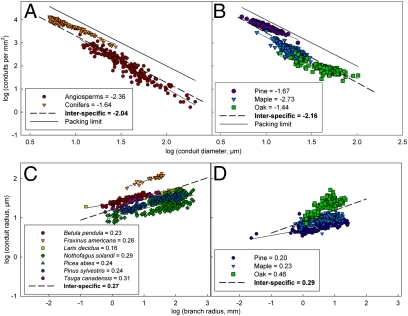
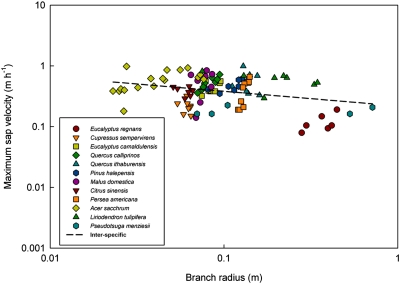
We use the central predictions of our model—the packing rule and taper scaling exponent p—to determine a suite of branch, stem, and whole-plant scaling relationships (Table 1 and Table S1). We test model predictions that differ substantially from the WBE and pipe models by compiling intra- and interspecific data from the literature (SI Text; Table S2) and our own detailed measurements of trees with diverse vascular anatomy: oak (Quercus gambelii), maple (Acer grandidentatum), and pine (Pinus edulis). In Table 1 and Fig. 3, scaling exponents were calculated separately for each species using standardized major axis (SMA) regression. These intraspecific exponents were then used to calculate cross-species (interspecific) weighted averages of exponents and 95% confidence intervals (CI) (Methods). Fig. 3 A and B shows conduit frequency changes with conduit radius with an average cross-species exponent of −2.04 (−2.74, −1.34) for literature data and −2.16 (−3.35, −0.97) for our measurements (Table 1). These average cross-species exponents agree well with our prediction of −2 for the packing rule and have 95% CIs that easily exclude the WBE model prediction of 0. Fig. 3 C and D displays that conduit taper, both across level k (axial) and within levels of k (radial) (SI Text), has cross-species average scaling exponents of 0.27 (0.20, 0.34) for literature data and 0.29 (0.08, 0.50) across measured trees (Table 1). These 95% CIs include our model prediction (p = 1/3 ≈ 0.33) and exclude the WBE model's prediction (p = 1/6) for literature data. We also predict 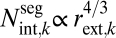for the scaling of conduit number with branch radius. Fits to empirical data for this relationship yield a scaling exponent of 1.19 (0.86, 1.52) (Table 1), again with 95% CIs that include our prediction of 4/3 and exclude the WBE model's prediction of 2. Moreover, in our model the total cross-sectional area of conducting tissue and fluid flow rate are conserved across levels, so the sap velocity is approximately constant within and across trees. Conversely, the WBE model predicts that velocity increases toward the terminal twigs (Fig. 1). We find no clear interspecific trend that maximum velocity changes with plant size or external branch radius (Fig. 4) or that conducting-to-nonconducting ratio changes with branch radius (Table 1). These results show that our model better matches available data, both within and across species, than the WBE or pipe models (3, 5).

Table 1.

Predicted scaling exponents for physiological and anatomical variables of plant internal networks as a function of branch radius (r_ext,k) for our model and the WBE model

Internal network property	WBE model exponent for rext,k	Our model exponent for rext,k	Observed average cross-species exponent from the literature for rext,k	Observed average cross-species exponent for all measured trees for rext,k (radial and axial data combined)	Observed average cross-species exponent for all measured trees for rext,k (axial data only)
Packing (conduit frequency vs. conduit radius, rint,k, not branch radius)	n.s.	−2	−2.04 (−2.74, −1.34)	−2.16 (−3.35, −0.97)	−1.86 (−2.91, −0.81)
Conduit radius taper (rint,k)	1/6 ≈ 0.17	1/3 ≈ 0.33	0.27 (0.20, 0.34)	0.29 (0.08, 0.50)	0.34 (0.04, 0.64)
Conduits in branch segment (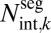)	2	4/3 ≈ 1.33	n.d.	1.19 (0.86, 1.52)	1.03 (0.11, 1.95)
Fluid velocity (uk)	−1/3	0 or n.s.	n.s.	n.m.	n.m.
Conducting-to-nonconducting ratio	1/3	0 or n.s.	n.d.	0.00 (−0.88, 0.88)	0.13 (−0.66, 0.92)
Network conductance (κk)	2	1.84 (finite)	1.44 (ref. 12)	n.m.	n.m.
		2 (infinite)
Branch segment conductivity (Kk)	8/3 ≈ 2.67	8/3 ≈ 2.67	2.78 (ref. 12)	n.m.	n.m.
Leaf-specific conductivity (Kk/Nleaves)	2/3 ≈ 0.67	2/3 ≈ 0.67	2.12 (−1.38, 5.62)	n.m.	n.m.
Volume flow rate (Qk)	2	2	1.77 (1.38, 2.16)	n.m.	n.m.
Pressure gradient along branch segment (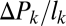)	−2/3	−2/3	n.d.	n.m.	n.m.
Branch segment conductance (Zk/Nint,k)	2	2	n.d.	n.m.	n.m.

Observed values for average cross-species scaling exponents [mean, 95% confidence intervals using standardized major axis (SMA) regression] are shown for literature data and our measurements for oak, maple, and pine. n.d., no data found; n.m., not measured; n.s., nonsignificant.

Fig. 3.

Plots of the packing rule and the conduit taper. For the packing rule A is reproduced from ref. 2, and B shows our measurements. For the taper C shows literature data (SI Text; Table S2) and D shows our measurements. Each colored symbol represents a different species. The packing limits in both plots (upper lines) represent wood tissue composed entirely of closest-packed conduits (i.e., the closest packing of both square-shaped conduits in conifers and circular-shaped conduits in angiosperms).

Fig. 4.

Plot of maximum sap velocity (m·h⁻¹) as a function of branch radius (m). Data were compiled from the literature (SI Text; Table S2) and each colored symbol represents a different species. The interspecific trend is nonsignificant (n.s.), matching the predictions of our model and contradicting the WBE model prediction. Intraspecific trends were nonsignificant (n.s. for eight species), significant but measured over a small radius range [much less than a factor of 2 (three species)], or significant for one species, Acer saccharum. Thus, these intraspecific trends support the predictions of our model.

Predictions for Allometric Scaling with Plant Mass.

Much of the field of allometric scaling, as applied to animals and plants, focuses on how physiological and anatomical properties scale with whole-body or whole-plant mass (3, 6, 37, 38). To facilitate comparisons across allometric scaling studies and promote future tests of our model, we list the predictions for both the WBE model and our new model in the SI Text (Table S1). For whole-plant properties, the WBE model and our model agree (by default) for those parameters defined by the external network. For properties of the basal stem (level k = 0), the models again share predictions of the external network but differ for many properties tied to the internal network, such as area of conductive tissue, number of conduits, conduit radius, and fluid velocity. These differences are measurable and provide an ideal test for empirically distinguishing between our model, the WBE model, and other models.

The predicted scaling exponents in Table S1 ignore finite-size effects that result from restricting the size range of plants to what is observed in nature (30). These finite-size effects are typically small but nonnegligible and can occur in a variety of ways (30). As an example, stem radius scales with plant mass as r_ext,0 ∝ M^3/8 (Table S1). Therefore, plant conductance scales with plant mass as 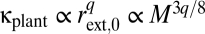. For optimal plants with a taper exponent of p = 1/3, Fig. 2 shows that q ≈ 1.85 for a realistic range (finite size) of tree sizes. Thus, if the pressure difference driving water transport is independent of tree size, we predict that conductance scales with plant mass as κ_plant ∝ M^0.69 for finite-sized trees, as opposed to the prediction of κ_plant ∝ M^3/4 for infinite-size trees. Although the WBE value of 3/4 is a useful reference point, there is scope within our theory for species- and environment-specific variation that corresponds well with empirical data from this and prior studies (22, 23).

Discussion

Our predictions are for a snapshot of an allometrically ideal plant (Table S1). However, plant architecture varies, likely reflecting phenotypic plasticity, the relative strength of differing selection pressures, phylogenetic histories, and differing size ranges (Fig. 2) (35). For example, if biomechanical constraints are not uniformly adhered to, the ratio of water-conducting area to total wood area may vary across branching levels, changing the space available to be filled by xylem conduits and allowing plant architecture to explore more of phenotypic space. We expect measured exponents for plants to cluster around the predicted exponents in Table 1.

In the SI Text (Table S3), we show that scaling exponents cluster around our predictions while exhibiting significant variation among species. Species-level variation may be due to differences in xylem anatomy that correspond to differences in functional types (e.g., ring porous, diffuse porous, or coniferous) (39) or differing growth environments (e.g., light and soil moisture). On the basis of size range of plants in Fig. 2 and measured tapering exponents for pine, maple, and oak [p = 0.20, 0.23, and 0.46 (Table S3)], we use Fig. 2B to obtain species-specific predictions for the conductance exponent of q = 1.66, 1.70, and 1.92, respectively. These values are in reasonable agreement with previously reported values for pine and maple (17) and bracket our interspecific prediction of 1.84 (Table 1; Fig. 2). Our model predicts that whole-plant hydraulic conductance scales with plant mass to the exponent 3q/8 for large plants, yielding species-specific predictions of 0.62, 0.64, and 0.72 for pine, maple, and oak. Because hydraulic conductance can limit rates of photosynthesis, the scaling of metabolic rate with plant mass is likely influenced by these values of the scaling exponent for conductance, q, potentially leading to scaling exponents lower than the WBE value of 0.75 for large plants. This argument is in contrast to studies that focus on carbon, rather than water use, and find metabolic scaling exponents for saplings that are >3/4 (40, 41). More intra- and interspecific data are needed to further test our model, evaluate species differences, and understand environmental and selective pressures.

Our model predictions are well matched by the cross-species average and interspecific trends across maple, oak, and pine as well as across our compiled literature data. However, closer analysis of our detailed empirical data (Table S3) for maple, oak, and pine reveals significant differences among these three species (39). The largest deviations away from our model are observed for oak. These deviations among different scaling exponents appear to be systematically interrelated in a way that characterizes hydraulic trade-offs specific to oak architecture. Specifically, the scaling exponent for the packing rule is significantly shallower than −2, and the scaling exponent for taper is significantly steeper than 1/3 (Table S3) (18, 42). Moreover, oak is the only tree for which the conducting-to-nonconducting ratio shows a significant trend with external branch radius. As discussed above, changes in the conducting-to-nonconducting ratio are reflected in the packing rule. When the fraction of conducting tissue increases toward the base, as for oak, more space is available for packing conduits. This additional space within the branch increases the total area packed by xylem conduits with larger radii and effectively flattens the relationships for the packing rule, as indicated by the exponent for oak of −1.44. This exponent for the packing rule influences the calculation for maximizing conductivity and thus the taper of conduit radii, with flatter packing rules leading to steeper taper, again as observed for oak (18). Consequently, our model predictions can be used as a baseline comparison for species differences among tree architectures and internal networks. Extensions of our model will help further illuminate the interconnections among these deviations in scaling exponents (23, 42).

We constructed a plant network model for the evolution of form and function within the xylem network of Tracheophytes. We tested our predictions using intra- and interspecific data compiled from the literature and our own detailed measurements from maple, oak, and pine. These data match our predictions better than those of the WBE or pipe models. Our model does not consider how differences in leaf form and function influence scaling relationships. Thus, further improvements of our theoretical framework may arise from an emerging literature on venation patterns and allometric scaling in leaves (27, 43, 44). Also, apart from the xylem tissue that delivers water, future work may add more realism to models by including the other transport tissue, phloem, that vascular plants use to deliver sucrose and other organic nutrients to cells.

Hydraulic architecture regulates the flow of water and resources to leaves and ultimately influences the fate of carbon in the canopy. Recent findings and models indicate relationships among xylem hydraulics, canopy conductance, sapwood-to-leaf area ratio, and canopy height (45). Elaboration of our model to include hydraulic limitation arising from finite-size effects may help to explain some of these relationships. To make realistic predictions for whole forests and land–atmosphere interactions, researchers need models that account for across-species differences and can translate across the water hydraulics–carbon metabolism gap, yet are simple enough to include in large-scale simulations (13, 35, 38, 45–47). Our model represents an important step in this direction.

Our model allows xylem conduit frequency to vary across levels, includes additional principles for protection from embolism, and more generally applies the principle of space filling than prior models. Indeed, the packing rule arises because the total cross-sectional area of conduits fills the space of a constant fraction of wood area. Thus, the principle of space filling now spans from conduits (2, 25) to branches (3) to canopies to forests (46), suggesting that space-filling geometries for the capture and delivery of resources may be one of the most pervasive principles in plant biology.

Methods

Empirical Measurements.

Study species.

A. grandidentatum Nutt. (bigtooth maple) and Q. gambelii Nutt. (Gambel oak) were chosen as representatives of diffuse- and ring-porous trees, respectively. Three mature trees from each species were obtained from Red Butte Canyon Natural Research Area [1,640 m above sea level (m.a.s.l.), 40° 46′ N, 111° 48′ W] in Salt Lake County, Utah. A. grandidentatum trees ranged from 72 to 90 y old and had an average height of 5.0 m (range: 4.7–5.2 m) and an average root-collar diameter of 11.8 cm (range: 11.1–12.5 cm). Q. gambelii trees ranged from 26 to 30 y old and had an average height of 5.8 m (range: 5.0–6.8 m) and an average root-collar diameter of 10.3 cm (range: 9.2–11.1 cm). P. edulis Engelm. (piñon pine) was used as a representative of tracheid-bearing species. Three reproductively mature trees were obtained from a ranch near Ojitos Frios, NM (35.5177° N, 105.3337° W, 2,050 m.a.s.l.). P. edulis trees ranged from 20 to 25 y old and had an average height of 1.7 m (range: 1.3–2.4 m tall) and an average root-collar diameter of 6.5 cm (range: 3.5–11 cm).

Xylem anatomy.

A subset of segments representing a wide distribution of diameters was selected from throughout each of the trees for xylem measurements (n = 36 for maple, n = 35 for oak, n = 25 for pine). Anatomical measurements were made to ensure data characterized xylem properties both axially (from the base to the tip of the tree) and radially (from the center pith to the outer bark). For the maple and oak, each stem segment was cut transversely and photographed using a digital camera (SPOT RT KE; Diagnostic Instruments) mounted to a stereo microscope (SZH; Olympus). Segments of pine were also cut transversely and photographed using a digital camera (Optronics Microfire) mounted to a stereo microscope (SZH; Olympus). From all photographs, stem, cambium, and pith areas were measured with image analysis software (Image-Pro Plus; Media Cybernetics) and converted to equivalent diameter.

To determine individual conduit size and number, transverse sections were made from multiple locations around each cross-sectional stem segment [using a razor blade for maple and oak and a sliding microtome (Spencer Lens Co.) for pine]. For maple and oak, in all young stems (<ca. 15 y) and some older stems, all rings were examined, whereas in other, older stems only the six most recent rings followed by every fifth ring were examined. For each examined growth ring, at least three areas of interest (AOI) were selected that occupied the entire thickness of the ring. For pine, all rings in each stem segment were examined, but only one AOI was measured within each ring. In maple and oak, AOIs were photographed at 40, 100, or 200× magnification using a digital camera (SPOT RT KE; Diagnostic Instruments) mounted to a light microscope (Eclipse E600W; Nikon). In pine, AOIs were photographed at 40, 100, or 200× magnification using a digital camera (Optronics Microfire) mounted to a light microscope (BX-51; Olympus). Using Image-Pro Plus, ring thickness and all conduit lumen areas were measured within each AOI. Lumen areas were converted to equivalent diameter and ring thicknesses were averaged within each ring. These data were used to calculate growth ring area, conduit density, and mean area-weighted lumen diameter for each ring. Using these calculations, we evaluated the number of conduits per branch segment across all trees (n = 3 trees/species). Because of questionable image quality for a single pine tree, data were excluded from calculations that required lumen area. Therefore, the packing rule, conduit taper, and conducting-to-nonconducting area were evaluated using n = 3 trees for maple and oak and n = 2 trees for pine. These differences in the number of trees and number of data points per tree were accounted for using our weighted cross-species averages and 95% confidence intervals, as explained below.

Literature Data Summary.

To test the predictions of our model, intra- and interspecific data were gathered from the available literature. This compilation results in an impressively large number of data points for plants that span a wide range of masses and represent diverse taxa. Table S2 lists the references and taxa used to evaluate each scaling relationship.

Statistical Analyses.

Bivariate scaling relationships between branch radius and internal network properties from both empirical and literature data were analyzed by fitting standardized major axis (SMA) regression to log-scaled variables. This technique is recommended for fitting allometric relationships because it yields an unbiased estimate of the scaling exponent (48). Using the statistical program (S)MATR (http://www.bio.mq.edu.au/ecology/SMATR/), SMA regression was used to estimate species-level slopes for intraspecific relationships. To obtain cross-species measures, we calculated a weighted average of the intraspecific slopes with weights (w_i = n_i/N) determined by the sample size, n_i, for each species, i, relative to the total number of data points across all species, N. To determine the 95% CIs, we summed the total intraspecific and interspecific variance to give the total variance, took the square root of this total variance to yield the SD, and multiplied by 1.96, corresponding to the number of SDs that contain 95% of the data. The total weighted intraspecific variance is the sum of the products of the weight and the variance for each species, with the latter calculated for the residuals of the data around the fitted SMA regression line. For the interspecific variance, we computed the difference between the weighted cross-species average slope and each intraspecific slope, squared this difference, multiplied by the weight for each species, and summed these values.