Kikuchi ultrafast nanodiffraction in four-dimensional electron microscopy

Abstract

Coherent atomic motions in materials can be revealed using time-resolved X-ray and electron Bragg diffraction. Because of the size of the beam used, typically on the micron scale, the detection of nanoscale propagating waves in extended structures hitherto has not been reported. For elastic waves of complex motions, Bragg intensities contain all polarizations and they are not straightforward to disentangle. Here, we introduce Kikuchi diffraction dynamics, using convergent-beam geometry in an ultrafast electron microscope, to selectively probe propagating transverse elastic waves with nanoscale resolution. It is shown that Kikuchi band shifts, which are sensitive only to the tilting of atomic planes, reveal the resonance oscillations, unit cell angular amplitudes, and the polarization directions. For silicon, the observed wave packet temporal envelope (resonance frequency of 33 GHz), the out-of-phase temporal behavior of Kikuchi’s edges, and the magnitude of angular amplitude (0.3 mrad) and polarization 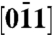elucidate the nature of the motion: one that preserves the mass density (i.e., no compression or expansion) but leads to sliding of planes in the antisymmetric shear eigenmode of the elastic waveguide. As such, the method of Kikuchi diffraction dynamics, which is unique to electron imaging, can be used to characterize the atomic motions of propagating waves and their interactions with interfaces, defects, and grain boundaries at the nanoscale.

With parallel-beam X-ray or electron illumination, the atomic structure of a material can be determined from measurement of the position and intensity of Bragg spots. When diffraction is time resolved, both for X-rays (1–5) and electrons (6–10), it is possible to track the motions of certain elastic excitations, such as breathing modes and optical phonons. These excitations create uniform structural distortions in the lateral directions (i.e., parallel to specimen’s surface) and, hence, they are ideal for detection with micron-size beams. On the other hand, for laterally propagating elastic waves originating from a localized source on the extended structure (see Fig. 1), the unit cell modulations vary with the wavelength on the nanoscale. Accordingly, such group waves are not amenable to probes with sizes larger than their spatial cycle (11). Moreover, these waves may exhibit complex unit cell distortions due to the pure and quasi-polarizations involved, similar to Rayleigh or “earthquake” waves.

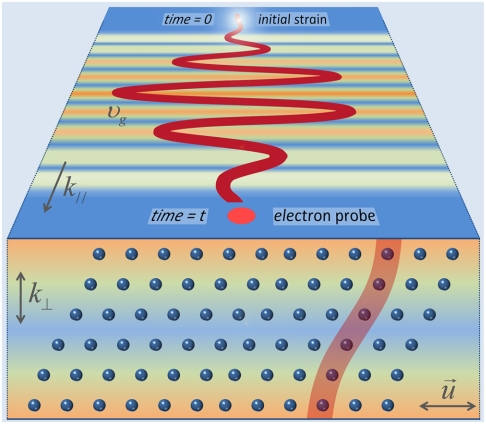
Fig. 1.

Schematic of coherent atomic motions leading to transverse waves in a nanostructure. A transverse elastic wave packet is created at time zero and detected later in space by using ultrafast electron packets. The initial strain originated at a distant point travels in the acoustic waveguide with a group velocity υ_g and wave vector k_// and crosses the “observation point,” i.e., the nanoscale electron probe, which enables us to measure the spatiotemporal characteristic of the transient shear strain. For the first antisymmetric shear-horizontal eigenmode of the waveguide, the atoms at the top and bottom halves of the slab slide in opposite directions (here emphasized with the red ribbon) and characterized by the polarization vector 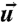. Along the surface normal, the standing wave condition results in a wave vector k_⊥. The transverse motion is color coded with increasing strain from blue to orange. The cross-sectional view is at the peak of the transient. The dimensions are not to scale.

Longitudinal elastic polarization is driven by linear forces that compress (or expand) the unit cell and such modes have successfully been studied with time-resolved Bragg diffraction. Transverse polarization, on the other hand, is impelled by torsional forces that buckle the unit cell and their direct imaging is not straightforward, as mentioned above, and especially when multiple electron scattering is involved (12,13). For bulk, thick materials, it is possible to identify the different elastic waves, longitudinal and transverse, by creating them using lasers and detecting them as they travel over macroscopic distances at very low temperatures (14, 15). However, such measurements cannot provide the microscopic spatial or temporal nature of atomic motions.

Ultrafast Kikuchi Nanodiffraction

With convergent-beam electron optics, which allows for the observation of nanodiffraction, the Kikuchi bands present in electron imaging (12, 13) exhibit unique atomic-scale interferences. When time resolved, they should, in principle, enable determination of laterally propagating transverse elastic waves with their polarization directions and amplitudes revealed, even in the presence of other excitations, such as breathing modes, and regardless of the extend of multiple scatterings. This unique probing is particularly significant because the dynamics is mapped in their band positions and not intensities. In general, Kikuchi bands appear as a result of multiple scattering (12, 13); first, the highly directional incident electrons scatter from the atoms and diffuse into a large-angle-cone (primary scattering), and then they undergo Bragg reflections (secondary scattering) from a specific crystalline plane, appearing as lines (or “bands”) on a CCD. This picture is well-known for studies of static images, i.e., with no time resolution, and the time resolution provided here is appropriate, as is in other X-ray and electron studies (10,16, 17,18), for making movies of the nuclear motions involved.

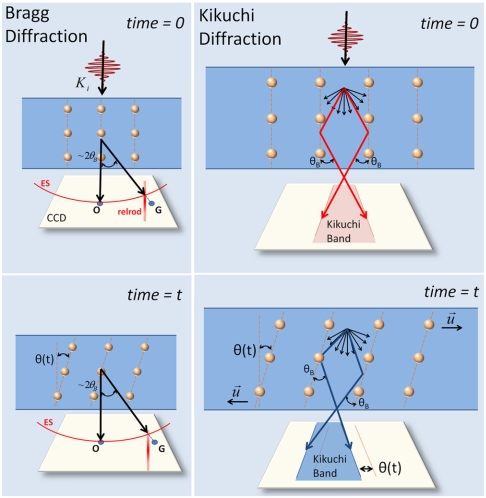
The concept introduced here for dynamic Kikuchi nanodiffraction is illustrated in Fig. 2. When the planes are experiencing shear (tilting) motion, the diffraction spot in conventional Bragg probing (Fig. 2 Left) could change its intensity (due to modulation in the “relrod”) but not its position. On the other hand, for Kikuchi band probing, because the cone after the primary scattering is large with sufficient span of scattering wave vectors, lines always appear at the exact Bragg condition regardless of the specimen thickness (or length of the relrods). In other words, there will be a new set of Ewald spheres corresponding to every scattered electron direction that will intersect the relrods at their center. Hence, Kikuchi lines are “attached” to the atomic planes (18), and any shear motion polarized perpendicular to the incident electron beam will shift their position in the diffraction pattern (Fig. 2). It follows that the amplitude and polarization of the motion can be directly measured.*

Fig. 2.

Kikuchi and Bragg diffraction dynamics. Specifically shown is the effect of transverse elastic waves on Bragg (Left) and Kikuchi (Right) diffractions. The Bragg spot G in the zero-order-Laue-zone, corresponding to the planes parallel to the incident electron beam, is defined by intersection of the Ewald sphere (ES) and the relrod in the reciprocal space. The tilt θ(t) of atomic planes at a time t causes this intersection point to move along the relrod, resulting in an intensity change but with no change in position on the CCD.* On the other hand, Kikuchi diffraction (Right) is a result of diffusely scattered electrons (black arrows) undergoing a second scattering from the atomic planes with a Bragg angle θ_B. Because the span of angles after the diffuse scattering is large, there are always electrons that will exactly satisfy the Bragg condition (shown with red and dark-blue arrows at time = 0 and time = t, respectively). Hence, Kikuchi lines will shift on the CCD by an amount proportional to atomic plane tilts θ(t), which enables us to directly measure the polarization amplitude and direction of the shear deformations. This schematic depiction is simplified in several ways: (i) The result of the diffuse scattering is actually a cone in three dimensions and the Bragg condition is satisfied along lines (or parabolas) that appear as Kikuchi lines on the CCD, in contrast to the left-panel case where the Bragg condition is satisfied along one direction only (and hence only one spot on the CCD). (ii) The space between the Kikuchi lines is filled and they appear as bands for thick enough samples. (iii) The objective lens that actually forms the diffraction pattern on the CCD is omitted for simplicity.

Besides the above-mentioned characteristics, one should be able to observe the transit of the resonance wave packet, provided that the spatial length scale (resolution) is shorter than the wavelength of the waves involved and the time resolution is shorter than their periods. Because electrons can be focused as single-electron packets and they have a high-interaction cross-section with the atoms involved in the motion, these requirements can be met to probe the wave group propagating in the nanostructure (Fig. 1) and obtain resonance and coherence times. We note that, although Kikuchi bands should, in principle, be visible in parallel electron-beam illumination, specimen imperfections in the large probed areas usually obscure them. Thus nanoscale electron beams are required to probe the homogeneous and local part of the crystal, which is the case in this study with convergent-beam ultrafast electron microscope (UEM).

Resonance Oscillations of Kikuchi Edges

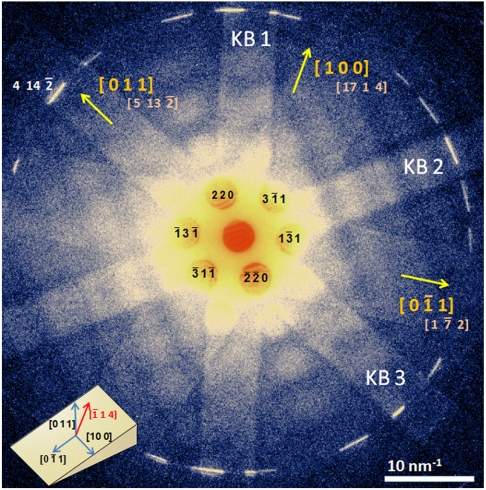
Fig. 3 depicts the observed convergent-beam ultrafast electron diffraction frame taken at a negative time (i.e., before the arrival of the clocking pulse) and with an electron-beam convergence angle of 9 mrad. Because the beam is convergent, the diffraction in the back-focal plane of the microscope’s objective lens is now made of discs, rings, and Kikuchi bands (19, 20). The strong second-order-Laue-zone ring (the white ring), which is solely due to Bragg diffraction, and zero-order-Laue-zone discs (labeled with Miller indices in black numbers), whose diameter gives the convergence angle, are visible in our patterns. The Kikuchi bands, which are the results of secondary scatterings, are labeled as KB1, KB2, and KB3. Projections of the three orthogonal crystallographic orientations (specimen coordinates) are also shown with yellow arrows. From this zone-axis diffraction, polarization of the displacement fields (linear or torsional waves) can be projected into the crystallographic coordinate system of the slab (Fig. 3) to provide an intuitive physical picture of the specimen’s atomic motions, as we shall show below.

Fig. 3.

Kikuchi diffraction in convergent-beam pattern. Shown is a frame taken along the 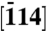zone axis, displaying the zero-order-Laue-zone discs (labeled with black Bragg indices), the second-order-Laue-zone ring (the white ring), and the Kikuchi bands labeled as KB1, KB2, and KB3. Yellow arrows indicate the relevant specimen axes and their projections with the acquired Miller indices underneath them. The 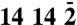HOLZ reflection, which is used to establish time zero, is also indicated. (Inset) Relevant specimen [100], [011], 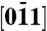and observation 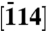directions: [011] is normal to the slab surface, whereas 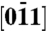is normal to the wedge.

The projection direction of a polarization vector 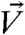in the reciprocal space defined in Fig. 3 by the 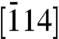zone axis can simply be written as,

[1]

where the × denotes the vector cross-product. For the specimen coordinate system shown in the inset of Fig. 3, the three crystallographic directions of are [100], [011], and . The projections of these three directions (the yellow vectors in Fig. 3 with the acquired Miller indices) can be used readily for conversion from the observed diffraction plane to the lateral plane of the specimen. For instance, movement along the 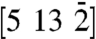direction is associated with real-space dynamics polarized along normal-to-surface direction (i.e., [011]) of the specimen. We note that 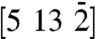has a component perpendicular to KB2, and a distinction can be made between the linear and angular changes of the planes, because both Bragg reflections and Kikuchi bands coexists in the diffraction pattern. Interatomic planar displacements, such as compressional strain, are reflected in the movements of the Bragg ring [in the high-order-Laue-zone (HOLZ) circle shown in Fig. 3]. These conclusions can be generalized irrespective of the zone axis used.

It is also possible to map polarization directions and determine the amplitude of shear strain. The KB1 band in Fig. 3, for instance, results from Bragg scatterings from the 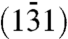atomic planes. Any shear polarization that is perpendicular to these planes (i.e., along the plane normal of 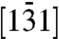) will result in a shift in the position of KB1 band. Similarly, a polarization along the [220] direction will shift KB2, and one along 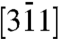will shift KB3. By measuring the movement of these three bands, one can uniquely map the lateral polarization direction. Note that any polarization perpendicular to the sample wedge (i.e., along 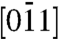) will shift KB1 the most, because the projection of the polarization vector (i.e., 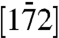) is almost perpendicular to KB1.

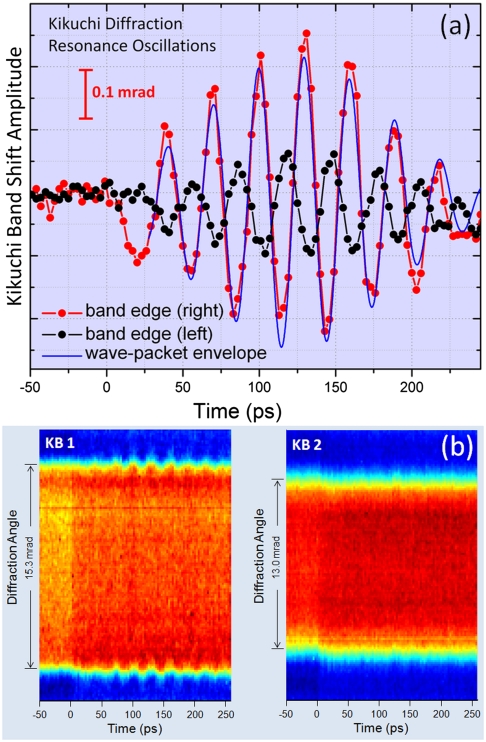
Fig. 4 displays the transient intensity behavior observed at the two edges of the Kikuchi band (KB1). Strong resonance oscillations are visible with a period of 30 ps. This temporal behavior obtained with the convergent electron beam displays two important features. First, the diffraction intensity rises at a delayed time from the measured t = 0 and then falls, giving a Gaussian-like wave packet envelope (see the fit in Fig. 4A); it is centered at 125 ps and has a full width at half-maximum of 143 ps. The time zero is determined in the same diffraction frames from the intensity drop of the HOLZ ring, more specifically the 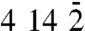reflection; this drop is due to the induced heating (Debye–Waller effect) which we studied previously in silicon (16).

Fig. 4.

Ultrafast spatiotemporal behavior of Kikuchi diffraction. (A) Shown is the observed resonance oscillations of intensity at the two edges of the KB1 band. The resonance at 33 GHz with a wave-packet-like envelope clearly displays the out-of-phase characteristic of the transverse motion for the atoms at the top and bottom surfaces of the acoustic waveguide. Time zero was determined by the intensity drop of a HOLZ reflection (see text). The red amplitude scale corresponds to the band edge (Right) curve. The difference in amplitudes between the two edges is due to dynamical scattering that is present at the low scattering angles and where this edge was measured. The apparent shape is also reminiscent of the superposition of group of vibrational modes (30), but because the time zero was established, the rise of both transients with the same value at t = 0 excludes such proposition. (B) Temporal behavior of two Kikuchi bands displaying the presence (KB1) and absence (KB2) of the oscillatory resonance. The bands’ cross-sections were taken close to the Laue-zone ring for better contrast. From the left image, the amplitude of the shifting oscillation can be measured directly.

The second observation is striking: an out-of-phase resonance oscillation of the two edges, which indicates that the KB1 band is shifting as a result of out-of-phase transverse motion of the atoms at the top and bottom surfaces of the slab. The atomic planes that are parallel to the surface shift with respect to each other, but in opposite directions at the top and bottom half of the specimen. This motion tilts the planes perpendicular to the surface and results in the observed Kikuchi dynamics. The amplitude is obtained to be 0.3 mrad (Fig. 4 A and B). It is interesting that if such motions had the same expansion coefficient for isotropic silicon (2.6 × 10^-6 K^-1), then the 0.3-mrad amplitude would correspond to a temperature rise of 100 K, nearly the same as that determined from the Debye–Waller effect of HOLZ intensity^† (16).

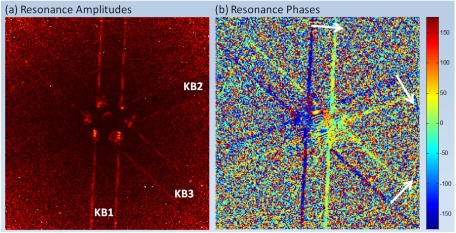
In order to map the directions of atomic motions and their amplitudes, we needed to follow the temporal changes of each pixel in the pattern. However, analyzing all million pixels in the images is nontrivial. We developed a fast Fourier transform approach that allows us to select changes, as a function of time, of both the amplitudes and phases. For each pixel, a peak in the Fourier spectra that corresponds to the resonance frequency of 33 GHz was integrated to determine the amplitude and phase. We then reconstructed the amplitude-phase image for this particular resonance. The results are shown in Fig. 5. From the amplitude distributions in the image (Fig. 5A), one can see that the strongest change is for Kikuchi band KB1, followed by KB2 and KB3, which display somewhat equal amplitudes (KB3 might seem somewhat larger but the difference is within the noise). The strong HOLZ ring is completely absent, demonstrating the robustness of the analysis and consistency with the transverse nature of the motion.

Fig. 5.

Fourier analysis images of phases and amplitudes at the resonance frequency. Shown are (A) resonance amplitude and (B) phase images at 33 GHz, obtained by the Fourier transform of the convergent beam ultrafast electron diffraction frames (Fig. 3). It is clear from image A that the KB1 band oscillates with the highest amplitude, whereas KB2 and KB3 display significantly less amplitude oscillations. The phase image (B) confirms the out-of-phase behavior of the bands’ edges. Moreover, the white arrows indicate the relative movements of the bands, which are readily used to derive the polarization direction of the elastic waves (see text). The scale bar, which is in degrees, is for the phase image.

In Fig. 5B, we display the phases of the Fourier transform for each pixel. The image clearly indicates the out-of-phase behavior of the two sides (band edges) of the three Kikuchi bands. More importantly, they show the relative shift direction of the bands, as indicated by the white arrows in the figure. From this relative motion alone, one can reason that the shear polarization must lie between KB2 and KB3. Such a polarization would produce the strongest oscillation for KB1, explaining both the amplitude and phase images observed. Quantitative treatment was made for the amplitudes, phases, and polarizations (SI Text); giving the polarization vector to be 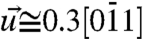, where the amplitude is in milliradian.

Laterally Propagating Elastic Waves

From these observations, it is now possible to elucidate the nature of atomic motions in the nanoslab waveguide. In general, the three different polarizations (and hence, three different velocities) of elastic waves in an anisotropic crystal have to be considered. However, for a shear-horizontally (SH) polarized wave, the waveguide propagation is well defined (Fig. 1), and we have already shown 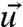to be perpendicular to the sample wedge and parallel to surfaces. Treating this displacement as a part of an SH wave means that 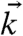must be perpendicular to 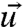, i.e., to 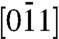. Due to the free-motion boundaries, a standing wave condition defines the magnitude of 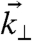, i.e., k_⊥ = (nπ/b), where b is the slab thickness and 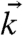is a vector with parallel-to-surface (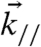) and perpendicular (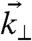) components (Fig. 1). It follows that the acoustic waveguide dispersion relation can be expressed as (21, 22)

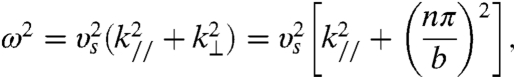[2]

where n = 0,1,2,… and υ_s is the magnitude of the shear-wave phase velocity which can be derived for anisotropic acoustic wave propagation of three polarizations (see SI Text). The oscillation angular frequency is ω.

For our case, b = 130 nm and n = 1, one obtains k_⊥ = 2.4 × 10⁷ m^-1. And by using Eq. 2 with measured ω = 2π33 GHz (from resonance oscillations in Fig. 4) and calculated υ_s of 5.84 km/s, the value of k_// is 2.6 × 10⁷ m^-1. Therefore, the angle of SH waves in the nanoguide is arctan(k_///k_⊥) = 47⁰, which satisfies the total internal reflection condition for the silicon–vacuum boundary (21). The displacement fields of the lowest antisymmetric mode (n = 1) are sketched in Fig. 1, and one can see that the atomic displacements of this mode uniquely predicts the observed temporal behavior of Kikuchi bands. Moreover, the total lateral movement of the top- and bottommost atomic layers can be estimated to be (0.3 mrad) × (130 nm/2) = 0.2 Å. This value is significant when compared to the size of the hydrogen atom, suggesting that such displacement may be exploited to generate atomic movements on the nanoscale. We note that higher-order modes (n > 1) cannot be supported at the observed frequency and slab thickness because Eq. 2 results in a negative propagation wave vector (k_//). Similarly, the first symmetric eigenmode (n = 0), which shifts the atomic columns transversely without tilting, has a higher k_// value corresponding to a wavelength comparable to the probe size (see SI Text).

The time and length scales involved in the motion are reflected in the results of Fig. 4. The transverse wavelength is λ_// = (2π/k_//) and has the value of 240 nm. In order to detect such lateral resonance modulations, one must use a spatial probe whose dimension is smaller than (λ_///2), which is the case in our convergent-beam microscopy experiments; parallel-beam illumination cannot detect such resonances, because it would average the spatiotemporal modulations of the traveling wave. Moreover, the envelope shape of the amplitude of resonance oscillations depicted in Fig. 4 indicates that the waves originated at a distance away from the measurement point (Fig. 1), because t = 0 was established in the same diffraction pattern as mentioned before. The maximum of the flux arrives to the observation point at 130 ps. With the transverse group-wave speed being 4.3 km/s along [001], the arrival time translates to a distance of 560 nm. This spatial propagation reflects the gradient in the temperature which is determined in silicon by carrier excitations and electron-phonon heating of the lattice in a few picoseconds (23–25).

Concluding Remarks

In this contribution, we have introduced the use of Kikuchi ultrafast diffraction to experimentally observe the transverse elastic wave atomic motions with nanoscale spatial resolution. The amplitudes, phases, and polarizations of the coherent waves have been characterized for a silicon waveguide. The wave (group) packet exhibits real-time oscillatory resonance with unique coherent envelope. The electron probe is smaller than the lateral wavelength, making possible the recording of the evolution in space and time. Because of the probe size, which can be focused to the scale of a unit cell in electron microscopy, and time resolution, Kikuchi together with conventional Bragg diffraction enable the mapping of anisotropic structural dynamics in 3D. With the variant techniques (18, 26–29) of convergent-beam electron microscopy, such as with energy filtering, we expect a range of applications in materials science and including studies of structural dynamics in site-selected molecular transformations.

Materials and Methods

The experiments were conducted in our microscope, UEM-2, which, as detailed elsewhere (10), is equipped with laser systems operating in the stroboscopic and single-pulse modes. The time-resolved convergent-beam arrangement is similar to that reported in ref. 16. Here, the electron packets are accelerated to 200 keV corresponding to de Broglie wavelength of 2.5 pm and wave vector of 40 Å^-1. Femtosecond infrared pulses were up-converted to the ultraviolet at 347 nm and sent to the cathode for photoelectron extraction. Synchronously, green pulses of 5 μJ output at 520 nm were directed to the sample after entering the microscope to initiate (or clock) the elementary excitations. The temporal evolution was recorded by varying the path length between these two pulses.

The sample was oriented such that the 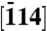crystalline direction was parallel to the incident electron packets; see Fig. 3, Inset for the relevant directions. A low-symmetry zone axis, such as 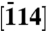, was preferred over a high-symmetry one, such as [011], in order to contain the complete HOLZ ring within the CCD camera range. The beam of electron packets can be focused down onto typically a 10-nm probe (16) and, in this work, the electron packets are focused onto a probe of 100-nm diameter, instead of the micron scale used in conventional parallel-beam probing. The second condenser lens of the microscope was used for such focusing and the shadow image of the sample was invoked to determine the optimum focus in diffraction patterns. The silicon nanoslab specimen with a 4° wedge angle was prepared by mechanical polishing along the (011) planes, followed by ion milling for final smoothing.