Reassessing optimal neural population codes with neurometric functions

Abstract

Cortical circuits perform the computations underlying rapid perceptual decisions within a few dozen milliseconds with each neuron emitting only a few spikes. Under these conditions, the theoretical analysis of neural population codes is challenging, as the most commonly used theoretical tool—Fisher information—can lead to erroneous conclusions about the optimality of different coding schemes. Here we revisit the effect of tuning function width and correlation structure on neural population codes based on ideal observer analysis in both a discrimination and a reconstruction task. We show that the optimal tuning function width and the optimal correlation structure in both paradigms strongly depend on the available decoding time in a very similar way. In contrast, population codes optimized for Fisher information do not depend on decoding time and are severely suboptimal when only few spikes are available. In addition, we use the neurometric functions of the ideal observer in the classification task to investigate the differential coding properties of these Fisher-optimal codes for fine and coarse discrimination. We find that the discrimination error for these codes does not decrease to zero with increasing population size, even in simple coarse discrimination tasks. Our results suggest that quite different population codes may be optimal for rapid decoding in cortical computations than those inferred from the optimization of Fisher information.

Neuronal ensembles transmit information through their joint firing patterns (1). This fact raises challenging theoretical questions on how the encoding accuracy of such population codes is affected by properties of individual neurons and correlations among them. Any answer to these questions necessarily depends on the measure used to compare the performance of different population codes. A principled approach to define such a measure is to use the concept of a Bayesian ideal observer (2, 3). This concept requires choosing a specific task: In a stimulus reconstruction task, we ask how well a Bayes-optimal decoder can estimate the true value of the presented stimulus on the basis of the noisy neural response (Fig. 1A). In a stimulus discrimination task, we ask how well it is able to decide which of two stimuli was presented on the basis of the response pattern (Fig. 1B).

Fig. 1.

(A) The stimulus reconstruction framework. Orientation is represented in the noisy firing rates of a population of neurons. The error of estimating this stimulus orientation optimally from the firing rates serves as a measure of coding accuracy. (B) The stimulus discrimination framework. The error of an optimal classifier deciding whether a noisy rate profile was elicited by stimulus 1 or 2 is taken as a measure of coding accuracy. (C) A neurometric function is a graph of the minimum discrimination error (MDE) as a function of the difference between a fixed reference orientation (upper right) and a second varied stimulus orientation (x axis). (D) The MDE for two Gaussian firing rate distributions with different mean rates corresponds to the gray area. The optimal classifier selects the stimulus more likely to have caused the observed firing rate. (E) The optimal discrimination function in the case of two neurons, whose firing rates are described by a bivariate Gaussian distribution, is a straight line if the stimulus change causes only a change in the mean. (F) If it also changes the covariance matrix, the optimal discrimination function is quadratic.

Most theoretical studies of neural coding (4–12) have chosen the stimulus reconstruction paradigm. For the sake of simplicity and analytical tractability, these studies have evaluated population codes almost exclusively with regard to Fisher information, assuming its inverse approximates the average reconstruction error of an ideal observer, the minimum mean squared error. Others have chosen the stimulus discrimination paradigm, linking Fisher information to the discriminability between two stimuli, given the neural responses (4, 13, 14). In addition to this large body of theoretical work, many experimental studies have used Fisher information to interpret their results (15–17).

The relationship between Fisher information and the error of an ideal observer in a reconstruction task has mostly been justified using the Cramér–Rao bound, which states that the conditional mean squared error of an unbiased estimator 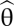of a stimulus θ is bounded from below by the inverse of the Fisher information J_θ:

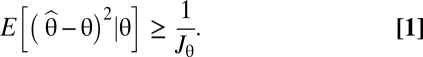More precisely, this argument is based on the fact that under certain assumptions the maximum a posteriori estimator is asymptotically normally distributed around the true stimulus with variance equal to the Cramér–Rao bound (4, 18, 19). Alternatively, using Fisher information to approximate the error of an ideal observer in a stimulus discrimination task has been justified by noting that the just noticeable distance is approximately proportional to the inverse square root of the Fisher information (4). The proof of this relationship similarly relies on a Gaussian approximation of the posterior distribution.

Whereas it is usually taken for granted that Fisher information is an accurate tool for the evaluation and comparison of population codes, the examples studied by Bethge et al. (18) suggest that the assumptions necessary to relate Fisher information to the error in the reconstruction or the discrimination task may be violated in interesting population coding scenarios. This risk is particularly severe when the codes are optimized for Fisher information and the signal-to-noise ratio for individual neurons is low—that is, exactly in the regime in which neural circuits frequently operate. Perceptual decisions are computed in <100 ms (20, 21) and firing rates in cortex are often low (15, 22), such that neural circuits compute with a few spikes at best. In this regime, Fisher information may yield an incorrect assessment of optimal reconstruction and discrimination performance. Although it is known in principle that this failure of Fisher information results from its locality, the precise factors that determine when the validity of Fisher information breaks down are often complex.

To achieve a more precise understanding of this problem we investigate neural population codes by computing the full neurometric function of an ideal observer in the stimulus discrimination paradigm (23). A neurometric function shows how the discrimination error achieved by a population code depends on the difference between the two stimuli. We use it to revisit the question of optimal population coding with two goals: First, we show that optimal discrimination and optimal reconstruction lead to qualitatively similar results regarding the effect of tuning function width and of different noise correlation structures on coding accuracy; in contrast, Fisher information favors coding schemes that are severely suboptimal for both reconstruction and discrimination at low signal-to-noise ratio. Second, we use the diagnostic insights provided by neurometric functions in a discrimination task to obtain an analytical understanding of the poor performance of Fisher-optimal population codes. In particular, we show that the tuning functions and correlation structures favored by Fisher information show strikingly bad performance in simple coarse discrimination tasks.

Results

Studying Neural Population Codes Using Neurometric Functions.

We obtain neurometric functions by fixing one reference stimulus at orientation θ, varying the second stimulus, and then plotting the error of the ideal observer trying to discriminate the two on the basis of their neural representation as a function of the difference Δθ (illustrated in Fig. 1C). This graph contains information about the performance of the population code both in fine and in coarse discrimination tasks.

The ideal observer in such a discrimination task is the Bayes classifier (24)

where r is the population response, s ∈ {θ, θ + Δθ} is the stimulus, and This equation means that the classifier chooses the class that was more likely to have caused the observed response pattern on the basis of the stimulus conditional response distributions. Consider a single neuron with a Gaussian response distribution, for which the mean response increases from stimulus 1 to stimulus 2 (Fig. 1D). The response will be classified as being caused by stimulus 2 whenever the neuron responds with a firing rate larger than a certain threshold (Fig. 1D, dashed line) even if it was caused by stimulus 1. Therefore, the error of the ideal observer, the minimum discrimination error (MDE), corresponds to the gray area under the lower of the two probability densities. In general, the classifier achieving the MDE can have a complex shape, reflecting the equal probability contours of the response distributions. The MDE is given by (24)

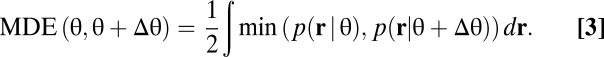For a population with Gaussian response distributions, the optimal classifier is linear if the covariance matrix is the same for both stimuli (Fig. 1E) and quadratic if the covariance matrices are different (Fig. 1F). We evaluate Eq. 3 for populations with several hundred neurons using Monte Carlo techniques (SI Methods 2 and ref. 23). As a measure of the overall performance of a population code we compute the integrated minimum discrimination error (IMDE), the average performance over all possible discrimination angles (Methods, Eq. 8).

In addition to the MDE, we compute the minimum mean squared error (MMSE) and the Fisher information J_θ (Methods, Eqs. 9 and 10). The latter yields the minimum asymptotic error (MASE), the approximation of the MMSE obtained from averaging over the Cramér–Rao bound (18):

In the case of asymptotic normality, the MASE yields a good approximation for the MMSE. For a summary of the acronyms we use to refer to the different measures, see Table 1.

Table 1.

Definition of acronyms

Acronym	Definition
MDE	Minimum discrimination error, Eq. 3; ideal observer error in a discrimination task
IMDE	Integrated minimum discrimination error, Eq. 8; average MDE over all Δθ
MMSE	Minimum mean squared error, Eq. 9; ideal observer error in a reconstruction task
MASE	Mean asymptotic squared error, Eq. 4; approximation to the MMSE obtained by averaging over the inverse of Fisher information

Optimal Tuning Function Width for Individual Neurons.

For all three measures (MASE, MMSE, and IMDE), we investigate how the coding quality of a population with 100 independent neurons with bell-shaped tuning functions depends on the tuning width of individual neurons at different time intervals available for decoding (10, 100, 500, and 1,000 ms). The population activity is assumed to follow a multivariate Gaussian distribution with Poisson-like noise, where variances are identical to mean spike counts (Methods). In this model, the signal-to-noise ratio per neuron increases with the expected spike count, which depends on both the average firing rates as specified by the tuning functions and the observation time. Here, we vary only the observation time, which is linearly related to the single neuron signal-to-noise ratio (SI Methods 1).

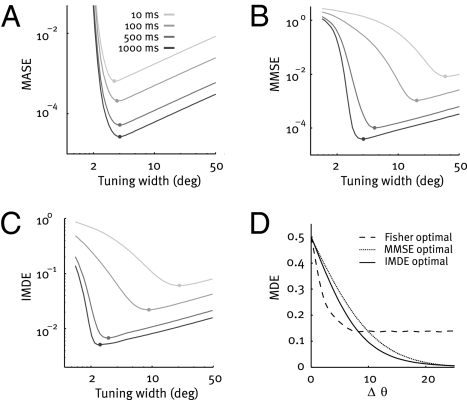
We first study the effect of tuning width on the coding accuracy in the reconstruction task. We compute the MASE on the basis of Fisher information as an approximation to the MMSE. According to this measure, narrow tuning functions are advantageous over broad tuning functions independent of the length of the time interval used for decoding (Fig. 2A and Fig. S1 A and B) as has been reported before (e.g., refs. 9–11). For the reason for the slight time dependence of the Fisher-optimal tuning width, see Fig. S2. In striking contrast, numerical evaluation of the MMSE reveals that the optimal tuning width critically depends on the available decoding time, confirming results of earlier studies (18, 25): For short times, broad tuning functions were advantageous over narrow ones (Fig. 2B and Fig. S1 C and D).

Fig. 2.

Optimal tuning function width. (A) Mean asymptotic error (MASE) of a population of 100 independent neurons as a function of tuning width for four different integration times (T = 10, 100, 500, and 1,000 ms; light gray to black). The MASE is the average inverse Fisher information. Dots mark the optimum. (B) As in A, but MMSE of the same population. For short integration times, broad tuning functions are optimal in terms of MMSE, in striking contrast to the predictions based on Fisher information. (C) As in A, but IMDE of the same population. Results obtained with the IMDE agree well with those based on the MMSE, although the former corresponds to the minimal error in a discrimination task and the latter to that in a reconstruction task. (D) Neurometric function of a population with Fisher-optimal (dashed line), MMSE-optimal (dotted line), and IMDE-optimal tuning width (solid line) for a short time interval (10 ms).

We next evaluate the effect of tuning width in the discrimination paradigm by computing the average error of an ideal observer, the IMDE. We find that the optimal tuning width in terms of IMDE depends on decoding time as well (Fig. 2C): Wide tuning functions are preferable for short integration times, whereas narrow ones for long integration times (Fig. S1 E and F). Despite the fact that the IMDE and the MMSE measure different quantities (discrimination error vs. reconstruction error), their dependence on tuning width is very similar (compare Fig. 2B with 2C). For short integration times, Fisher information thus failed to reflect the effect of tuning width on coding performance both in the reconstruction and in the discrimination task. These results also hold in the case of discrete Poisson noise and for Fano factors different from 1 (Fig. S3).

Neurometric functions allow us to analyze the difference between the results based on Fisher information and the ideal observer analysis (MMSE and IMDE) in more detail. To do so, we compute the neurometric functions for populations with Fisher-, MMSE-, and IMDE-optimal tuning functions when decoding time is short (T = 10 ms; Fig. 2D). We find that Fisher-optimal tuning functions are advantageous in fine discrimination over the tuning functions optimal for the ideal observers. However, the performance of Fisher-optimal codes levels off for larger Δθ at a nonzero error. The neurometric functions computed for populations with MMSE- and IMDE-optimal tuning width do not show this saturation behavior.

To explain this striking discrepancy, we investigate the coding properties of a population with Fisher-optimal tuning functions systematically. We compute the Fisher-optimal tuning width for populations of different size at different integration times and find that the Fisher-optimal tuning width is inversely proportional to the population size (Fig. 3A). Whereas Fisher information suggests that the error achieved by these populations should decay like 1/N as a function of the population size for all time windows considered (Fig. 3B), the ideal observer error (IMDE) for the same populations saturates with increasing population size so that adding more neurons does not improve the quality of the code (Fig. 3C).

Fig. 3.

Performance of Fisher-optimal codes. (A) Optimal tuning width as a function of population size for T = 1,000 ms. (B) MASE of a neural population with independent noise and Fisher-optimal width for 10 different integration times T (values logarithmically spaced between 10 and 1,000; light to dark gray). The width of the tuning functions is optimized for each N separately and chosen such that it minimizes the MASE. (C) IMDE for the same Fisher-optimal populations as in B. (D) Family of neurometric functions for Fisher-optimal population codes at T = 10 ms for n = 10 to n = 190 (right to left). Δθ_S is the point of saturation, and P is the pedestal error, also marked by the gray dashed line. (E) The pedestal error P is independent of the population size N (T = 1,000 ms not shown for clarity). (F) The pedestal error P depends on the integration time (black; independent of N) and analytical approximation for P (gray). (G) For each population size, approximately three neurons are activated by each stimulus (red), independent of the population size. (H) For coarse discrimination (red vs. green), the two stimuli activate disjoint sets of neurons determining the pedestal error (red vs. green; error bars show 2 SD). For fine discrimination, the activated populations overlap, determining the initial region (red vs. blue). (I) Dependence of the point of saturation Δθ_S on the population size N. (J) Two parts of the neurometric function of Fisher-optimal population codes: the pedestal error P (light gray) and the initial region (dark gray). Together they determine the IMDE. The neurometric function is shown in units of difference in preferred orientation; therefore it does not depend on N. The pedestal error is reached at Δθ_S ~ 2Δφ (Fig. S4). As N → ∞, the x axis is rescaled and the area of the initial region A_IR goes to zero (SI Text) and the IMDE converges to πP.

The reason for the observed saturation is that the neurometric functions of populations with different size asymptote at a “pedestal error” P (Fig. 3D). We can provide a lower bound for this pedestal error using the MDE of an auxiliary population of neurons with additive instead of Poisson-like noise. In this way, we show that the pedestal error is nonzero for finite T (see SI Text for formal treatment):

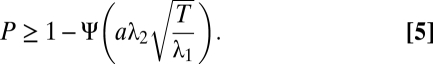Here, λ₁ determines the baseline firing rate, λ₂ sets the gain of the tuning function, and a is a constant independent of N. Ψ is the cumulative normal distribution function. Thus, the pedestal error does not decay with increasing population size but is determined by the available decoding time alone, in agreement with our numerical results (Fig. 3 E and F). Intuitively, this is because in Fisher-optimal codes the tuning width is inversely proportional to N, such that only three cells are active for each stimulus, independent of N (Fig. 3G). For coarse discrimination, the two stimuli activate two disjoint groups of neurons (Fig. 3H, red and green neurons). Thus, the error in discriminating two orientations far away from each other (the pedestal error) is determined solely by the ability to determine which of these two groups of three neurons is active in the presence of background noise. Using this argument we obtain a linear approximation of the pedestal error, which has a similar form to Eq. 5 (Fig. 3F and SI Text, Eq. S2). In contrast, if the two orientations are very close, the sets of activated neurons overlap and classification is more difficult (Fig. 3H, red and blue neurons). As can be seen in Fig. 3H, the point Δθ_s at which the neurometric function reaches its saturation level is approximately twice the difference of the preferred orientation of two adjacent neurons (Δφ), independent of the population size (Fig. S4). As the population size increases, Δφ goes to zero and, consequently, Δθ_s as well (Fig. 3I and SI Text).

Together, these results explain why Fisher-optimal tuning widths lead to saturation of the ideal observer performance in the large N limit. The IMDE is determined by the area of the initial region of the neurometric function A_IR and the pedestal error P (Fig. 3J):

For fixed T, the pedestal error is independent of N. In contrast, A_IR shrinks toward zero with N, because Δθ_S goes to zero. In the large N limit, the IMDE therefore converges to the pedestal error. To complete the picture, we note that for fixed N, the pedestal error converges to zero in the large T limit, such that eventually P ≪ A_IR. Here, Fisher information, which is related to A_IR (23), and the IMDE will lead to similar conclusions.

In summary, the discrepancy at low signal-to-noise ratio between the optimal tuning width predicted by Fisher information and that found by evaluating the performance of ideal observer models can be explained by the fact that Fisher-optimal population codes show poor performance for simple coarse discrimination tasks. In particular, we find that Fisher information yields a valid approximation of the ideal observer performance only when the pedestal error P characteristic for coarse discrimination tasks is small compared with the area of the initial region.

Optimal Noise Correlation Structure.

We next investigate whether the relative advantages of different noise correlation structures are accurately captured by Fisher information. Noise correlations are correlations among the firing rates of pairs of neurons when the stimulus is constant. Many theoretical studies have investigated the effect of these shared trial-to-trial fluctuations on the representational accuracy of a population code using Fisher information (5–8). Although their magnitude in cortex is debated (15, 16, 26), an accurate assessment of the potential impact of different noise correlation structures on population coding is important. In our model, the correlation structure can be one of the following (Fig. 4A and SI Methods 1): All pairs can have the same correlation (“uniform correlations”), correlations can be increasing with firing rates (“stimulus-dependent correlations”), pairs with similar orientation preference can have stronger correlations than pairs with dissimilar preference (“limited-range correlations”), or the latter two can be combined.

Fig. 4.

Effect of noise correlations. (A) Correlation coefficient matrices. Dark values indicate high correlations. Neurons are arranged according to their preferred orientation, so correlations between cells with similar tuning properties are close to the main diagonal. Diagonal entries have been removed for visualization. (B–D) MASE, MMSE, and IMDE for a population of n = 100 neurons for the four different noise correlation structures shown relative to the independent population in logarithmic units. Colors are as shown in A. (E and F) MASE (dashed lines) and IMDE (solid lines) for a population of 100 neurons with stimulus-dependent (red) or uniform correlations (blue) at 500 ms (E) and 10 ms (F) as a function of average correlation strength. Data are shown relative to the independent population in logarithmic units. (G and H) Neurometric functions for the four correlation structures at 500 ms (G) and at 10 ms (H). The square marks Δθ_c; from there on stimulus-dependent correlations perform worse than uniform correlations. In H, the crossing point lies effectively at Δθ = 0. Data are also shown relative to the independent population, smoothed and in logarithmic units on the y axis in the Insets.

We evaluate how the correlation structure affects the performance of the population code in populations of 100 neurons with varying noise correlation structure for a range of time intervals (T = 10–1,000 ms) and intermediate correlation strength (). We compute the MASE (Fig. 4B) as well as the ideal observer errors, MMSE (Fig. 4C) and IMDE (Fig. 4D).

We find that all three measures agree that noise correlations with limited-range structure are harmful compared with uncorrelated noise. Similarly, uniform noise correlations lead to a better code than uncorrelated noise with regard to all three measures (although the advantage with regard to the ideal observer errors is less pronounced). Surprisingly, however, they disagree on the effect of stimulus-dependent correlations: Fisher information suggests that a population with such correlations shows even better coding accuracy than one with uniform noise correlations, in line with previous results (7). In remarkable contrast, MMSE and IMDE suggest that stimulus-dependent correlations are advantageous over uniform correlations only for time intervals >100–200 ms and perform worse at shorter ones (Fig. 4 C and D). For time windows <50–100 ms, they are even harmful compared with uncorrelated noise. In addition, Fisher information falsely indicates an increasingly superior performance of stimulus-dependent correlations over uniform correlations with increasing correlation strength for all time intervals (Fig. 4 E and F). The ideal observer shows this behavior only for long time intervals (Fig. 4E). For short time intervals the dependency is reversed: The higher the average correlation is, the worse stimulus-dependent correlations perform (Fig. 4F). The results for short times obtained here for the Gaussian noise distribution also hold for a discrete binary noise distribution (tested for n ≤ 15), where each neuron emits either one spike or none (23).

Neurometric functions again allow us to gain additional insights into this behavior (Fig. 4 G and H): For sufficiently coarse discrimination uniform correlations always lead to a superior population code over stimulus-dependent correlations. In contrast, stimulus-dependent correlations are always superior for sufficiently fine discrimination. With decreasing decoding time, however, the critical Δθ_c, where the neurometric functions cross, shifts more and more toward zero (Fig. S5). Therefore, uniform correlations lead to superior performance over stimulus-dependent correlations for almost all Δθ when decoding time is short (Fig. 4H). Whereas Fisher information predicts that relative performance of the correlation structures is independent of time, the IMDE reveals that stimulus-dependent correlation may be beneficial for long decoding intervals, but detrimental for short ones.

Discussion

In the present study, we revisited optimal population coding using Bayesian ideal observer analysis in both the reconstruction and the discrimination paradigm. Both lead to very similar conclusions with regard to the optimal tuning width (Fig. 2 B and C) and the optimal noise correlation structure (Fig. 4 C and D). Importantly, the signal-to-noise ratio—which is critically limited by the available decoding time—plays a crucial role for the relative performance of different coding schemes: Population codes well suited for long intervals may be severely suboptimal for short ones. In contrast, Fisher information is largely ignorant of the limitations imposed by the available decoding time—codes that are favorable for long integration intervals seem favorable for short ones as well.

Whereas Fisher information yields an accurate approximation of the ideal observer performance in the limit of long decoding time windows, this is not necessarily true in the limit of large populations. We showed analytically that the ideal observer error for a population with Fisher-optimal tuning functions does not decay to zero in the limit of a large number of neurons but saturates at a value determined solely by the available decoding time (Fig. 3C). In contrast, Fisher information predicts that the error scales like the inverse of the population size, independent of time (Fig. 3B). Thus, the “folk theorem” that Fisher information provides an accurate assessment of coding quality in the limit of large population size is correct only if the width of the tuning functions is not optimized as the population grows.

In the discrimination task, we explained this behavior by showing that the coarse discrimination error is independent of the population size for ensembles with Fisher-optimal tuning curves. In the reconstruction task, large estimation errors play a similar role to the coarse discrimination error. The convergence of the reconstruction error to a normal distribution with variance equal to the inverse Fisher information relies on a linear approximation of the derivative of the log-likelihood (19). If the tuning function width scales with population size—as it does if the tuning functions are optimized for Fisher information—the quality of this linear approximation does not improve with increasing population size because the curvature of the tuning functions is directly coupled to the tuning width. As a consequence, the Cramér–Rao bound from Eq. 1 is not tight even asymptotically leading to the observed discrepancies between Fisher information and the MMSE.

Similarly, Fisher information also fails to evaluate the ideal observer performance for different noise correlation structures correctly when the time available for decoding is short. The reason is that the link between Fisher information and the optimal reconstruction or discrimination error also relies on the central limit theorem (4, 18, 19). Therefore, in the presence of noise correlations, the approximation of the ideal observer error obtained from Fisher information can converge very slowly or not at all to the true error for increasing population size, because the observations gathered from different neurons are no longer independent. In fact, our results show that it is crucial not to rely on the asymptotic approach of Fisher information alone to determine the relative quality of different correlation structures.

In contrast to our study, earlier studies using the discrimination framework mostly measured the minimal linear discrimination error or computed the fine discrimination error only (4, 13, 27–29). Two other studies used upper bounds on the MDE, which are tighter than the minimal linear discrimination error (13, 30), but no study has so far computed the exact MDE for the full range of the neurometric function. For a detailed discussion of these studies see SI Discussion. Information theoretic approaches provide a third framework for evaluating neural population codes in addition to the reconstruction and discrimination framework studied here. For example, stimulus-specific information (SSI) has been used to assess the role of the noise level for population coding in small populations (31) and in the asymptotic regime, SSI and Fisher information seem to yield qualitatively similar results (32). In contrast to neurometric function analysis, information theoretic approaches are not directly linked to a behavioral task.

In conclusion, neurometric function analysis offers a tractable and intuitive framework for the analysis of neural population coding with an exact ideal observer model. It is particularly well suited for a comparison of theoretical assessment of different population codes with results from psychophysical or neurophysiological measurements, as the two-alternative forced choice orientation discrimination task is much studied in many neurophysiological and psychophysical investigations in humans and monkeys (33, 34). In contrast to Fisher information, neurometric functions are informative not only about fine, but also about coarse discrimination performance. For example, two codes with the same Fisher information may even yield different neurometric functions (Fig. S6). Our results suggest that the validity of the conclusions based on Fisher information depends on the coding scenario being investigated: If the parameter of interest induces changes that either impair or improve both fine and coarse discrimination performance (e.g., when studying the effect of population size for fixed, wide tuning functions), Fisher information is a valuable tool for assessing different coding schemes. If, however, fine discrimination performance can be improved at the cost of coarse discrimination performance (as is the case with tuning width), optimization of Fisher information will impair the average performance of the population codes. In this case, quite different population codes are optimal than those inferred from Fisher information.

Methods

Population Model.

We study orientation coding in an idealized, homogenous population of N neurons with bell-shaped tuning functions,

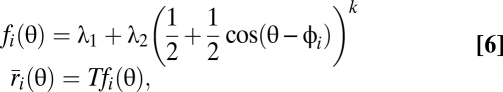where θ is the stimulus orientation, φ_i is the preferred orientation of neuron i, and T is the observation time. The parameter k controls the width of the tuning curves. Large k corresponds to steep tuning curves with small width. The parameters λ₁ and λ₂ set the baseline rate to 5 Hz and the maximal rate to 50 Hz.

The stimulus-conditional response distribution is modeled as a multivariate Gaussian so that

where 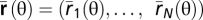is a vector of average spike counts. We use a flexible model for the covariance matrix Σ(θ), allowing for different noise correlation structures (SI Methods 1 and Fig. 4A). Noise is Poisson-like; i.e., the variance is equal to the mean firing rate. In this model, the signal-to-noise ratio per neuron is proportional to the observation time T (SI Methods 1).

Neurometric Function Analysis.

The minimal discrimination error MDE(θ, θ + Δθ) is given by Eq. 3. We compute it numerically using Monte Carlo integration (SI Methods 2). The necessary software is available online at http://www.kyb.tuebingen.mpg.de/bethge/reproducibility/BerensEtAl2011/index.php. MDE_θ (Δθ) = MDE(θ, θ + Δθ) is the neurometric function relative to the reference direction. The IMDE quantifies the average performance of a code independent of Δθ:

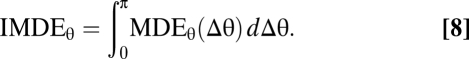It is equal to the area under the neurometric function. A modified version of the IMDE could have variable weights for the error at different Δθ to represent the relative importance of different discriminations; this would not change the conclusions of Fig. 3. We average the neurometric function MDE_θ(Δθ) and the integrated MDE over θ to make them independent of the reference direction.

Minimum Mean Squared Error and Fisher Information.

The MMSE is the error of an ideal observer in the reconstruction task and minimizes

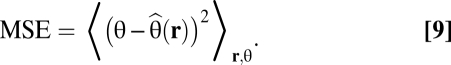We compute it numerically using Monte Carlo integration (SI Methods 3). The necessary software is available online at http://www.kyb.tuebingen.mpg.de/bethge/reproducibility/BerensEtAl2011/index.php. In the Gaussian case, the Fisher information is given by

where the dependence on θ of the right-hand side is omitted for clarity. are the derivatives of 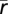and Σ with respect to θ. The inverse of J_θ can be used to bound the conditional error variance of an unbiased estimator according to Eq. 1. By averaging over θ, we obtain a lower bound on the MMSE, the MASE (Eq. 4). For long decoding time windows (T → ∞), the MMSE and the MASE coincide (18, 19). Fisher-optimal codes were computed by numerically minimizing the MASE for the tuning width parameter for each N and T.