Abstract
DNA methylation is a key regulator of gene function in a multitude of both normal and abnormal biological processes, but tools to elucidate its roles on a genome-wide scale are still in their infancy. Methylation sensitive restriction enzymes and microarrays provide a potential high-throughput, low-cost platform to allow methylation profiling. However, accurate absolute methylation estimates have been elusive due to systematic errors and unwanted variability. Previous microarray preprocessing procedures, mostly developed for expression arrays, fail to adequately normalize methylation-related data since they rely on key assumptions that are violated in the case of DNA methylation. We develop a normalization strategy tailored to DNA methylation data and an empirical Bayes percentage methylation estimator that together yield accurate absolute methylation estimates that can be compared across samples. We illustrate the method on data generated to detect methylation differences between tissues and between normal and tumor colon samples.
Keywords: DNA methylation, Epigenetics, Microarray
1. INTRODUCTION
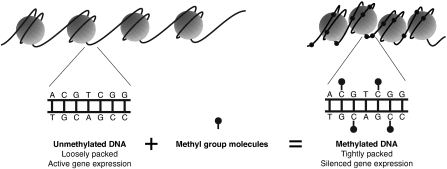
DNA methylation is a chemical modification of DNA that plays a key role in regulation of gene expression (Figure 1). As an “epigenetic” mark, it encodes an additional layer of heritable information on top of DNA without changing the underlying genetic sequence. While all cell types in an organism share nearly the same genome sequence, their DNA methylation patterns can be markedly different (Song and others, 2005; Meissner and others, 2008). DNA methylation marks help encode tissue-specific transcriptional programs in diverse cell types and allow these gene expression patterns to be passed down to daughter cells. Chemically, DNA methylation involves the modification of a cytosine (C) base to form methyl-cytosine. These methylation marks are recognized by specialized proteins that bind the methylated DNA and inhibit the expression of neighboring genes (Bird, 2002). In adult cells of mammals, this modification occurs almost exclusively at cytosines that are immediately followed by a guanine (G) in the 5′ to 3′ direction, denoted “CpG.”
Fig. 1.
DNA (black strand) is wrapped around histone proteins (gray spheres). Unmethylated DNA (left) tends to be loosely packed. Genes in such regions are accessible to the cell's transcriptional machinery and can be expressed. DNA methylation involves the addition of methyl group molecules to cytosine bases. Highly methylated DNA (right) is tightly packed resulting in silenced gene expression.
The health implications of deciphering the DNA methylation code have recently received much attention both in the scientific literature and in the media (Issa, 2007; Cloud, 2010; SchuBeler, 2009). Work in the rapidly evolving field of stem cell biology, for example, has shown that DNA methylation can contribute to the cellular memory mechanism used by the stem cells to retain their pluripotent state during repeated cell divisions (Sen and others, 2010). In cancer biology, it is clear that aberrations in DNA methylation almost universally accompany the initiation and progression of cancers (Feinberg and Tycko, 2004). Much of the excitement surrounding epigenetics relates to the promise of therapies that alter the epigenetic code, activating or silencing disease-related genes. While the majority of such treatments are still hypothetical or experimental, 2 epigenetic drugs that reactivate tumor suppressor genes by removing methylation marks have recently received U.S. Food and Drug Administration approval (Sharma and others, 2010; Kaminskas and others, 2005). These studies and therapies highlight the medical promise of mapping and understanding the role of DNA methylation.
Fully describing the methylation profile of a given cell requires measuring the methylation state of every CpG. However, current practical laboratory protocols do not permit single cell methylation measurements and because studied cell populations are known to be heterogeneous, methylation measurements are expected to be continuous rather than binary. Therefore, for any given cell type, we aim to measure the percentage of methylated cells at each CpG site. These measurements can be made by treating DNA with sodium bisulfite, which selectively converts unmethylated cytosine (C) to uracil (U) while leaving methylated C as is, followed by DNA amplification and sequencing (Clark and others, 2006; Frommer and others, 1992). However, although considered a gold standard, this procedure comes at significant cost when applied genome-wide due to the amount of sequencing coverage required. Therefore, this technology is not yet suitable for affordable genome-wide measurements. The methods presented in this paper are motivated by the demand for high-throughput measurements necessary to construct genome-wide methylation profiles.
Recent advances in microarray technology and laboratory protocols provide an alternative high-throughput platform for assessing DNA methylation. Since methylation of adjacent cytosines in small regions of a few hundred base pairs tends to be highly correlated (Eckhardt and others, 2006), lower resolution strategies based on methylated DNA enrichment provide a cost-effective alternative to bisulfite sequencing. These approaches employ proteins that selectively bind (affinity purification) (Weber and others, 2005) or cut (restriction enzymes) DNA depending on its methylation status. Following a procedure that enriches for either methylated or unmethylated DNA, microarrays are used to detect the DNA fragments. Coupled with suitable analytical tools, these strategies can provide accurate genome-wide methylation profiles. A recent comparison of methods É found that the restriction enzyme McrBC, which selectively cuts methylated DNA (Sutherland and others, 1992; Ordway and others, 2006), has higher sensitivity than the commonly used methylated DNA immunoprecipitation (MeDIP) affinity purification protocol, É in regions of lower CpG density (Irizarry and others, 2008). While analytical methods have been developed for MeDIP (Down and others, 2008; Pelizzola and others, 2008), tools are currently lacking for McrBC DNA methylation data.
The microarray measurements produced by the procedures described above present new statistical challenges. We have developed an empirical Bayes estimation strategy that, when combined with appropriately normalized McrBC-enriched DNA microarray data, produces accurate percentage methylation estimates with a mean error of 10% compared to bisulfite sequencing estimates. As in applications of empirical Bayes methods to other microarray data settings (Efron and others, 2001; Smyth, 2004; Irizarry and others, 2003), we take advantage of the massively parallel structure of the data to borrow information across the ensemble of probes. Since accurate methylation estimates are highly dependent on suitable pre-processing to remove systematic biases, we also present a novel normalization strategy. In so doing, we demonstrate that well-established methods, developed largely in the context of gene expression analysis, are often inappropriate for DNA methylation data. While these methods have been widely and successfully used in a variety of other microarray applications, certain key assumptions underlying the strategies are violated in the DNA methylation setting leading to inaccurate estimates.
This article is organized as follows. We begin with a description of our example data sets in Section 2. Section 3 lays out limitations of existing methods for preprocessing DNA methylation data. In Section 4, we describe our normalization strategy and the empirical Bayesian estimator of percentage methylation. Results demonstrating the utility of our methods are presented in Section 5. We conclude with a discussion in Section 6. Derivations and practical issues including microarray data quality control are included in the supplementary material available at Biostatistics online.
2. DATA DESCRIPTION
2.1. Microarray data
DNA methylation assays typically involve random fragmentation of a DNA sample, followed by an enrichment step that selects for either methylated or unmethylated DNA. Prior to enrichment, the DNA is split into 2 fractions one of which is left untreated. Methylation estimates are based on the relative quantities of DNA in the enriched fraction compared to the untreated (total input) fraction. In this paper, we use 2 data sets generated using the restriction enzyme McrBC (NCBI GEO Accession No. GSE23841). The first is derived from human liver, brain and spleen, with 5 samples from each tissue. The second consists of 5 normal colon and 5 colon cancer samples. The samples are described in Irizarry and others (2009). Each sample was processed and hybridized to microarrays as detailed in Ordway and others (2006) and Irizarry and others (2008). Briefly, the assay involves enrichment of unmethylated DNA using the McrBC enzyme and the Comprehensive high-throughput arrays for relative methylation (CHARM) DNA methylation microarray (Irizarry and others, 2008) available from Nimblegen. The CHARM microarray is a 2.1 million probe 2-color array designed for maximal CpG coverage.
2.2. Bisulfite-sequencing validation data
We generated an independent verification data set using the same samples analyzed on the CHARM microarrays. Ten regions containing an average of 12 CpGs and spanning an average of 220 base pairs were selected for methylation analysis by bisulfite treatment followed by sequencing. A total of 110 sequencing runs were performed with a subset of samples chosen for each region, generating percentage methylation estimates for each CpG.
3. MOTIVATION
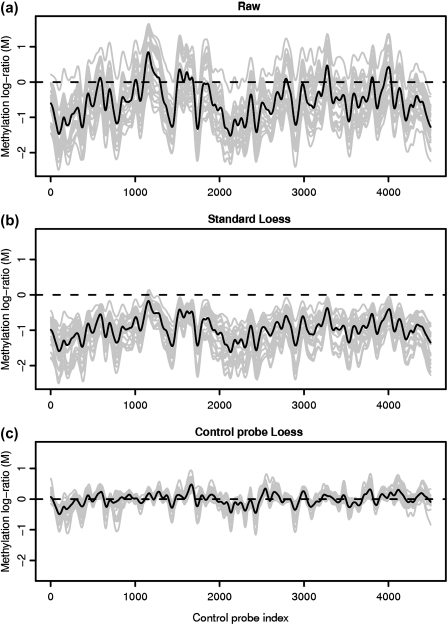
A key prerequisite for estimation of absolute methylation levels from microarray data is preprocessing to accurately establish the baseline signal level associated with unmethylated regions. The basic measurement used to quantify methylation is the log ratio (M) of intensities observed in the treated and control (total input) channels. Within-sample normalization aims to transform the log ratios such that zero represents unmethylated regions and higher M-values represent more methylation. A plot of the microarray methylation log ratio for probes from unmethylated regions reveals several problems with the raw signal (Figure 3(a)). First, the M-values are not centered on zero as is desirable for regions without methylation. Second, there is a strong sequence-dependent bias in the signal manifested as a “wave” in a plot of signal by genomic location. This wave is similar to that observed in array-comparative genomic hybridization data (Marioni and others, 2007), and can lead to both false negatives and false positives, particularly in calls of absolute methylation levels. The effect represents a sequence-specific bias as evidenced by its strong conservation across samples and is partly explained by probe GC content. The ability to minimize between-probe variation in GC content during array design is limited since options for probe placement are constrained by the denseness of tiling. Accurate assessment of absolute methylation levels is therefore highly dependent on an analysis approach that adequately corrects for these biases. The Loess normalization strategy which has been widely and successfully used for other 2-color microarray applications (Yang and others, 2002) fails to adequately normalize the methylation log ratio (Figure 3(b)).
Fig. 3.
Methylation log ratio across 30 unmethylated control regions in a CHARM microarray. The light gray lines show individual sample profiles while the dark lines represent the median signal across samples, clearly showing strong conservation of the “wave” artifact between samples. Neither the raw data (a) nor the standard Loess normalized (b) signals are zero centered as is desirable for unmethylated regions. Control probe Loess normalization (c) achieves both a mean-zero signal for unmethylated regions and an 80% reduction in variation compared to the raw signal.
As with other microarray applications, the strong nonlinear dependence of M on signal intensity is a significant source of bias. This effect is evident in a plot of M versus A, where A is the average of the 2 channels' log signals. The key Loess assumptions are that the majority of probes represent regions without signal (M = 0), and that signal intensity-dependent deviations are an artifact. In applications such as differential gene expression analysis or transcription factor binding profiling, these assumptions typically hold and Loess regression can effectively be used to estimate and remove signal intensity-dependent bias. In methylation experiments, however, both of these assumptions are violated. Since we expect many sites to be methylated, the average probe behavior no longer represents regions without signal. The baseline signal level estimated through Loess represents the mean methylation level rather than no methylation. If Loess normalization were used here, and we define M = 0 as the average value of unmethlyated sites, then one would incorrectly force M = 0 for many of the probes associated with methylation. This effect is clear from Figure 3(b) where virtually all unmethylated probes have M < 0.
The second Loess assumption that the methylation log ratio (M) should be independent of the average individual channel signal intensity (A) is also invalid in the methylation data setting. DNA methylation levels are related to CpG (and hence GC) density; CpG dense regions, referred to as CpG islands tend to be unmethylated, while lone CpGs are usually methylated. Since signal intensity is also known to be influenced by GC content the true M is related to A. Forcing the methylation level to be independent of A through Loess normalization thus actually introduces bias.
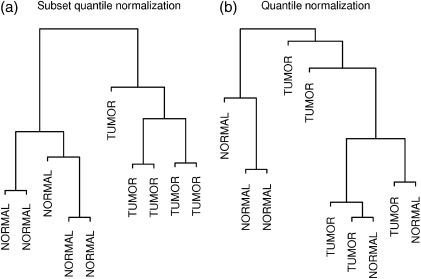
A further problem that remains unresolved after Loess normalization is the considerable variability between biological replicates. While established between-sample microarray normalization techniques such as quantile normalization (Bolstad and others, 2003) are in many cases suitable for addressing this problem in DNA methylation data, we have identified important situations in which alternatives are necessary. Most methods were developed in the context of gene expression data and typically make the assumption that the overall amount of gene expression, and hence signal, should be the same across samples. While not strictly true, this assumption has proved reasonable for most gene expression data. In studies of DNA methylation, similarly, we have found this assumption reasonable for comparisons between normal tissues. In many situations of particular interest, however, such as comparisons between cancer and normal tissues, there may be significant global differences in methylation levels. Total methylation levels are known to vary significantly between, for example, cancer versus normal cells or stem cells versus differentiated cells (Jones and Baylin, 2007; Laurent and others, 2010). As a result, normalizing such samples in a way that equalizes their total signal level may introduce bias. This is illustrated by a hierarchical clustering dendrogram of the colon tissue data set following quantile normalization (Figure 4(b)). One would expect the biological replicates within the cancer and normal tissue groups to cluster together, but the biological differences are obscured by technical artifacts.
Fig. 4.
Hierarchical clustering dendrogram of 5 normal colon and 5 colon tumor samples following (a) subset quantile normalization and (b) quantile normalization. Subset quantile normalization results in perfect group separation. The top 10 000 most variable probes are used in each case.
Developments in laboratory tools have provided researchers with a promising platform for accurately and rapidly assaying DNA methylation. As described above, however, signal biases and limitations in current analytical methods present a barrier to making the most effective use of this promising technology.
4. METHODS
We present a 2-component strategy for estimating absolute methylation levels. We first normalize the methylation log ratios to remove systematic bias (Sections 4.1 and 4.2) and then transform the normalized log ratios into percentage methylation estimates (Section 4.3). All normalization techniques depend on identifying individual features or overall array characteristics that can be assumed to be constant across samples. Normalization transforms the data to equalize these features between samples. With this in mind, we aim to select control probes to serve dual purposes during the normalization process: to set the zero-level for the methylation signal within each sample and to reduce between sample technical variation.
4.1. Within-sample normalization
To address the limitations of Loess normalization, we employ a method that uses knowledge of genome sequence, assay properties, and DNA methylation patterns to select a subset of probes for which its assumptions do hold. By fitting a Loess regression to these control probes, we obtain a valid correction curve that can be applied to the remaining probes. The key step in selecting control probes is to identify unmethylated regions of the genome. Since mammalian DNA is almost exclusively methylated at CpG sites, we can typically achieve this by selecting probes from CpG-free regions, guaranteeing a signal that represents unmethylated DNA. For these probes, we expect both that M equal zero and that M be independent of A. Ideally, such control probes are included on the array by design. The CHARM microarray, for example, contains 4500 probes located in CpG-free regions to be used for this purpose. Alternatively, a suitable subset of probes can be identified for many standard array designs, allowing the use of our method with a broad set of platforms.
In addition to setting the zero level using the control probe Loess procedure, a simple scale normalization with minimal assumptions is useful to establish the signal level associated with fully methylated regions. We typically scale the methylation log ratios such that the 99th percentile has an M-value corresponding to 99% methylation (see Section 4.3). This is roughly equivalent to the assumption that the top 1% of probes represent almost completely methylated regions.
Since methylation estimates are derived from the log ratio of signal intensity in the 2 channels, the presence of background signal biases these estimates toward zero. To address this, we implement background removal prior to the log-ratio calculation using a modified robust multichip average (RMA) convolution model (Irizarry and others, 2003) that takes advantage of background signal probes as detailed in Section 3 of the Supplementary Material available at Biostatistics online.
4.2. Between-sample normalization
In many situations of particular interest in DNA methylation studies, such as comparisons between cancer and normal tissues, samples might be expected to exhibit significant global differences in methylation levels. In these cases, we propose the use of subset quantile normalization (Wu, 2009), a modified version of quantile normalization that avoids assumptions about total signal level. It takes advantage of control probes representing regions known to exhibit the same behavior across samples. While spike-in controls can serve this purpose, it has recently been shown that negative control probes can also be used (Wu, 2009). Since negative controls by design measure nonbiological signals they provide a good basis for assessing technical variation between arrays. We find that probes from non-CpG regions (Section 4.1) serve this purpose well. Such probes measure quantities that are not dependent on the methylation status of individual samples and technical variation due to probe effects can be expected to be constant across samples. Since the control probes will be used as reference points during between-sample normalization, a further consideration is that their sequence characteristics should represent those of the array as a whole, particularly in terms of GC content.
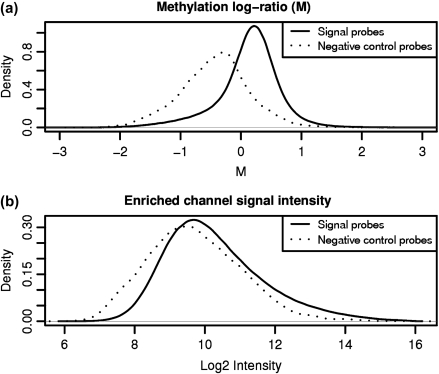
Due to significant probe effects (Wu, 2009), the negative control features from unmethylated regions span almost the entire dynamic range of signal within the enriched channel (Figure 2(b)). This is explained by the observation that differences in individual probe hybridization efficiencies and the effects of varying amounts of cross-hybridization are frequently of similar magnitude as the biological differences of interest (Irizarry and others, 2003; Johnson and others, 2006; Li and Wong, 2001; Wu and others, 2004).
Fig. 2.
While negative control features representing unmethylated regions have lower signals than the signal probes on the M (log ratio) scale (a), they span almost the entire dynamic range of signal in the enriched channel (b) as a result of probe effects.
The use of subset quantile normalization allows us to take advantage of the facts that the individual negative control features should show the same behavior across all samples, and that they also cover the dynamic range of the signal probes. In this approach, the control probes are used as “anchors” when normalizing the data. First, an empirical reference distribution is created by quantile normalizing the control features. A target distribution is created from a weighted average of this empirical distribution and normal mixture distribution to allow extrapolation beyond the range of control probe signals. We then map probes that fall in the qth quantile of control probes on their array to the qth quantile of the target distribution.
We have adapted subset quantile normalization, originally proposed in the context of single-color microarray data, to the 2-color setting. Figure 2 motivates the use of subset quantile normalization on the enriched channel data rather than directly on the methylation log ratios (M). On the M scale, where probe effects have mostly been cancelled out, the control probes span a smaller fraction of the signal probe dynamic range and are therefore less useful as normalization anchors. Prior to normalizing the enriched channel we establish a common baseline by first normalizing the total input channel, leaving M-values unchanged. As the total input channel represents genomic DNA which can be assumed to be essentially identical in all samples, it is reasonable to make an even stronger assumption than that of quantile normalization, and instead set each total input probe to its median value across all samples.
4.3. Percentage methylation estimates
The final preprocessing step involves estimation of percentage methylation from the normalized data. The use of a Bayesian estimator ensures that the values are constrained to the appropriate range. The procedures described in Sections 4.1 and 4.2 serve to remove the major within- and between-sample biases. The observed signal intensities in the total input (T) and enriched (E) channels for probe i can be then be modeled as IiT = φiϵiT and IiE = (1 − pi)φiϵiE respectively. pi represents the proportion of methylated CpGs at a given locus i, φi captures the probe effect, and ϵi are error terms. The log ratio of the observed intensities is given by mi = qi + ei, where qi = − log(1 − pi) and ei = logϵiT − logϵiE. Larger values of qi represent more methylation with zero representing no methylation. Preprocessing ensures that the error term, ei, is centered at 0 and examination of empirical distributions (supplementary Figure 3 available at Biostatistics online) suggests a log-normal model is reasonable. To allow for the nonzero probability of no methylation (qi = 0), we model qi as a mixture of a point mass at 0 and an exponential distribution. Under these conditions, we are able to derive a closed-form estimator of qi. This model is similar to the RMA convolution model with the differences that the normal component, ei, is centered at 0 and not truncated, and that the signal component, qi, is modeled as a mixture rather than an exponential distribution. We calculate the expected value of qi given the observed log ratio, mi, and then solve for pi.
| (4.1) |
where ai = mi − ασ2 and α and σ are hyperparameters corresponding to qi and ei, respectively. Parameter estimation and the derivation of (4.1) are detailed in Section 1 of the Supplementary Material avialable at Biostatistics online.
5. RESULTS
5.1. Within-sample normalization
Figure 3(c) shows the methylation signal in unmethylated regions following our control probe Loess procedure. Data from the 25 individual samples is shown in gray with the median across samples in black. Unlike Loess normalization (Figure 3(b)), our procedure effectively establishes the baseline zero level necessary to make accurate estimates of absolute methylation levels. In addition, we find that over 80% of the variation due to the wave effect in McrBC/CHARM DNA methylation data is explained by a nonlinear function of the individual channel intensities and can therefore be mitigated by our control probe Loess procedure.
5.2. Between-sample normalization
As might be expected, when comparing samples with significantly different overall levels of DNA methylation, we find that quantile normalization introduces biases that can obscure true biological differences. This is evident in a hierarchical clustering dendrogram of the colon tissue data set (Figure 4). Panel (a) shows samples clustered following subset quantile normalization. The biological differences between cancer and normal tissue clearly divides the samples into 2 groups. On the other hand, the sample clustering breaks down following quantile normalization (panel b), suggesting that artifacts have been introduced, obscuring the biological differences.
As a second metric of ability to retain biological variation while suppressing technical variation, we also examined the behavior of the top 10 000 most variable probes by calculating F-statistics for group differences. Probes with low-quality scores were excluded from the analysis (Section 2 of the Supplementary Material available at Biostatistics online. Given that we expect true differences between tumor and nontumor tissue, larger F-statistics are desirable and indicative of better ability to detect between-group differences. The mean F-statistics following quantile and subset quantile normalization are 4.8 and 8.5, respectively, suggesting that subset quantile normalization retains considerably more real biological signal while reducing technical variability. On the other hand, when comparing F-statistics for the normal tissue data set where the samples have similar global methylation levels, full quantile normalization achieves greater between-group separability.
5.3. Validating microarray percentage methylation estimates
We compared array-derived estimates of percentage methylation with an independent bisulfite sequencing data set targeting 10 regions. We summarized the sequencing reactions by the median percentage methylation across the CpGs in the region for a total of 110 methylation estimates across the 25 samples. Corresponding microarray estimates are derived from the median of the 2–8 probes in the region.
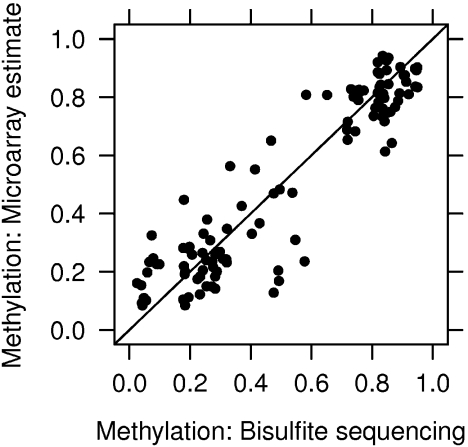
Figure 5 plots array-derived percentage methylation estimates against the bisulfite sequencing data. The correlation between the microarray estimates and bisulfite sequencing data is high at 93% with an average discrepancy of 10%, suggesting that the microarray-derived estimates are a good proxy for bisulfite sequencing data. The most accurate estimates are obtained in regions with high ( > 70%) and low ( < 30%) methylation levels, while the correlation is significantly lower when only regions of intermediate methylation are considered.
Fig. 5.
Percentage methylation estimates. The y-axis shows microarray DNA methylation estimates derived from the median of the probes in each validation region. The x-axis shows methylation from an independent gold-standard validation data set obtained by bisulfite treatment and sequencing. The mean difference between microarray and gold-standard estimates is 10%, with highest accuracy at high ( > 70%) and low ( < 30%) methylation levels.
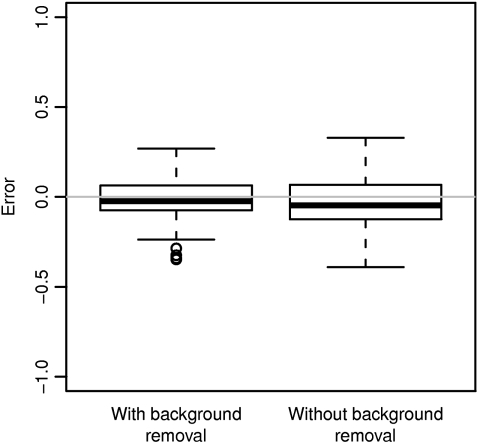
Our results also highlight the importance of background subtraction when estimating methylation levels. Figure 6 shows the error in microarray estimates of percentage methylation made with and without background removal, as compared to the bisulfite sequencing verification data. Only when background removal is used as part of the preprocessing procedure are the microarray-derived estimates centered on the gold-standard methylation values.
Fig. 6.
Error in microarray estimates of percentage methylation with and without background removal. Bisulfite sequencing was used as the gold-standard measurement.
6. DISCUSSION & CONCLUSION
The strategy presented here involves a closed-form Bayesian estimator of percentage methylation coupled with normalization methods tailored to DNA methylation microarray data. We demonstrate that the technique, together with data generated using the McrBC methylation-sensitive restriction enzyme and the CHARM DNA methylation microarray, achieves a high degree of correlation with bisulfite sequencing data with an average discrepancy of 10%.
Both the within-sample (between-channel) and between-sample normalization methods hinge on identifying suitable control probes from unmethylated regions. Since adult mammalian cells are almost exclusively methylated at CpG sites, this can typically be achieved by identifying stretches of CpG-free DNA. Depending on the properties of the methylation assay, it may be possible to relax this CpG-free requirement. Since most methylation-sensitive restriction enzymes only recognize CpGs when flanked by specific bases, other CpGs are essentially invisible to the enzyme and need not be excluded when selecting control regions. Choosing suitable control probes is slightly more difficult in systems where cells may have significant levels of non-CpG methylation, as has been demonstrated in stem cells (Lister and others, 2009; Ramsahoye and others, 2000). One solution is to choose to study only CpG sites through the use of a CpG-specific enrichment strategy. In this case, non-CpG methylation is undetectable and the standard control probe selection procedure can be applied.
Between-sample normalization is complicated by the possibility of significantly different levels of total DNA methylation between samples. Such comparisons, such as between cancer and normal cells, are often of particular interest from a DNA methylation perspective. Our results suggest that in situations where we have strong a priori reason to believe that global methylation differences exist, subset quantile normalization is superior to quantile normalization since it avoids the assumption of equality in global methylation levels. When this assumption is significantly violated, quantile normalization introduces significant bias that may mask the underlying biological signal. In situations where overall methylation levels are not drastically different, on the other hand, the stronger assumptions of quantile normalization are to be preferred. Since subset quantile normalization makes weaker assumptions about the data, it therefore has less ability to correct large between-sample biases. In effect, successful use of subset quantile normalization is dependent on high-quality data to a greater extent than quantile normalization.
While this paper has focused on DNA methylation data from the McrBC/CHARM platform, much of the statistical methodology is applicable more widely. The control probe loess procedure can be applied in the context of other 2-color tiling array DNA methylation protocols, regardless of enrichment strategy since the wave artifact is a general feature of these data. The subset quantile normalization procedure is even more widely applicable as it is not tied to microarray data. It will be useful in any DNA methylation assay where samples exhibit significant global methylation differences. This will remain true as assays increasingly shift away from microarrays to high-throughput sequencing.
As genomics seeks to unravel the diverse methylomes represented across cell types, it will be essential to have accurate and affordable high-throughput methods to query methylation. The analytical methods presented here will help provide a cost-effective means to globally profile DNA methylation by leveraging what we already know about genome structure and methylation patterns.
SUPPLEMENTARY MATERIAL
Supplementary material is available at http://www.biostatistics.oxfordjournals.org.
FUNDING
National Institutes of Health / National Cancer Institute (P50CA58236 and 2P50HG003233-06); Department of Defense Prostate Cancer Research Program (PC073533); the Maryland Stem Cell Research Fund (MSCRFE_0102-00).
Acknowledgments
Conflict of Interest: None declared.
References
- Bird A. DNA methylation patterns and epigenetic memory. Genes and Development. 2002;16:6–21. doi: 10.1101/gad.947102. [DOI] [PubMed] [Google Scholar]
- Bolstad BM, Irizarry RA, Astrand M, Speed TP. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics. 2003;19:185–193. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]
- Clark SJ, Statham A, Stirzaker C, Molloy PL, Frommer M. DNA methylation: bisulphite modification and analysis. Nature Protocols. 2006;1:2353–2364. doi: 10.1038/nprot.2006.324. [DOI] [PubMed] [Google Scholar]
- Cloud J. Why Genes Aren't Destiny. 2010. Time. New York. Volume 175. [PubMed] [Google Scholar]
- Down TA, Rakyan VK, Turner DJ, Flicek P, Li H, Kulesha E, Gräf S, Johnson N, Herrero J, Tomazou EM and others. A Bayesian deconvolution strategy for immunoprecipitation-based DNA methylome analysis. Nature Biotechnology. 2008;26:779–785. doi: 10.1038/nbt1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckhardt F, Lewin J, Cortese R, Rakyan VK, Attwood J, Burger M, Burton J, Cox TV, Davies R, Down TA and others. DNA methylation profiling of human chromosomes 6, 20 and 22. Nature Genetics. 2006;38:1378. doi: 10.1038/ng1909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Tibshirani R, Storey J, Tusher V. Empirical Bayes analysis of a microarray experiment. Journal of the American Statistical Association. 2001;96:1151–1160. [Google Scholar]
- Feinberg AP, Tycko B. The history of cancer epigenetics. Nature Reviews Cancer. 2004;4:143–153. doi: 10.1038/nrc1279. [DOI] [PubMed] [Google Scholar]
- Frommer M, McDonald LE, Millar DS, Collis CM, Watt F, Grigg GW, Molloy PL, Paul CL. A genomic sequencing protocol that yields a positive display of 5-methylcytosine residues in individual DNA strands. Proceedings of the National Academy of Sciences of the United States of America. 1992;89:1827–1831. doi: 10.1073/pnas.89.5.1827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irizarry RA, Hobbs B, Collin F, Beazer-Barclay YD, Antonellis KJ, Scherf U, Speed TP. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics (Oxford, England) 2003;4:249–264. doi: 10.1093/biostatistics/4.2.249. [DOI] [PubMed] [Google Scholar]
- Irizarry RA, Ladd-Acosta C, Carvalho B, Wu H, Brandenburg SA, Jeddeloh JA, Wen B, Feinberg AP. Comprehensive high-throughput arrays for relative methylation (CHARM) Genome Research. 2008;18:780–790. doi: 10.1101/gr.7301508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irizarry RA, Ladd-Acosta C, Wen B, Wu Z, Montano C, Onyango P, Cui H, Gabo K, Rongione M, Webster M and others. The human colon cancer methylome shows similar hypo- and hypermethylation at conserved tissue-specific CpG island shores. Nature Genetics. 2009;41:178–186. doi: 10.1038/ng.298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Issa JP. Ghost in your genes [interview transcript]. PBS NOVA. 2007 http://pbs.org/wgbh/nova/genes/issa.html. [Google Scholar]
- Johnson W, Evan L, Wei M, Clifford A, Gottardo R, Carroll JS, Brown M, Liu XS. Model-based analysis of tiling-arrays for ChiP-chip. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:12457–12462. doi: 10.1073/pnas.0601180103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones PA, Baylin SB. The epigenomics of cancer. Cell. 2007;128:683–692. doi: 10.1016/j.cell.2007.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaminskas E, Farrell A, Abraham S, Baird A, Hsieh L-S, Lee S-L, Leighton JK, Patel H, Rahman A, Sridhara R and others. Approval summary: azacitidine for treatment of myelodysplastic syndrome subtypes. Clinical Cancer Research. 2005;11:3604–3608. doi: 10.1158/1078-0432.CCR-04-2135. [DOI] [PubMed] [Google Scholar]
- Laurent L, Wong E, Li G, Huynh T, Tsirigos A, Ong CT, Low HM, Kin Sung KW, Rigoutsos I, Loring J and others. Dynamic changes in the human methylome during differentiation. Genome Research. 2010;20:320–331. doi: 10.1101/gr.101907.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Wong WH. Model-based analysis of oligonucleotide arrays: expression index computation and outlier detection. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:31–36. doi: 10.1073/pnas.011404098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lister R, Pelizzola M, Dowen RH, Hawkins RD, Hon G, Tonti-Filippini J, Nery JR, Lee L, Ye Z, Ngo QM and others. Human DNA methylomes at base resolution show widespread epigenomic differences. Nature. 2009;462:315–322. doi: 10.1038/nature08514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marioni JC, Thorne NP, Valsesia A, Fitzgerald T, Redon R, Fiegler H, Andrews TD, Stranger BE, Lynch AG, Dermitzakis ET and others. Breaking the waves: improved detection of copy number variation from microarray-based comparative genomic hybridization. Genome Biology. 2007;8:R228. doi: 10.1186/gb-2007-8-10-r228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meissner A, Mikkelsen TS, Gu H, Wernig M, Hanna J, Sivachenko A, Zhang X, Bernstein BE, Nusbaum C, Jaffe DB and others. Genome-scale DNA methylation maps of pluripotent and differentiated cells. Nature. 2008;454:766. doi: 10.1038/nature07107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ordway J, Bedell J, Citek R, Nunberg A, Garrido A, Kendall R, Stevens J, Cao D, Doerge R, Korshunova Y and others. Comprehensive DNA methylation profiling in a human cancer genome identifies novel epigenetic targets. Carcinogenesis. 2006;27:2409. doi: 10.1093/carcin/bgl161. [DOI] [PubMed] [Google Scholar]
- Pelizzola M, Koga Y, Urban AE, Krauthammer M, Weissman S, Halaban R, Molinaro AM. MEDME: an experimental and analytical methodology for the estimation of DNA methylation levels based on microarray derived MeDIP-enrichment. Genome Research. 2008;18:1652–1659. doi: 10.1101/gr.080721.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsahoye BH, Biniszkiewicz D, Lyko F, Clark V, Bird AP, Jaenisch R. Non-CpG methylation is prevalent in embryonic stem cells and may be mediated by DNA methyltransferase 3a. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:5237. doi: 10.1073/pnas.97.10.5237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schübeler D. Epigenomics: methylation matters. Nature. 2009;462:296. doi: 10.1038/462296a. [DOI] [PubMed] [Google Scholar]
- Sen GL, Reuter JA, Webster DE, Zhu L, Khavari PA. DNMT1 maintains progenitor function in self-renewing somatic tissue. Nature. 2010;463:563. doi: 10.1038/nature08683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma S, Kelly T, Jones P. Epigenetics in cancer. Carcinogenesis. 2010;31:27. doi: 10.1093/carcin/bgp220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth GK. Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. 2004 doi: 10.2202/1544-6115.1027. Statistical Applications in Genetics and Molecular Biology 3, Article3. [DOI] [PubMed] [Google Scholar]
- Song F, Smith JF, Kimura MT, Morrow AD, Matsuyama T, Nagase H, Held WA. Association of tissue-specific differentially methylated regions (TDMs) with differential gene expression. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:3336–3341. doi: 10.1073/pnas.0408436102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutherland E, Coe L, Raleigh EA. McrBC: a multisubunit gtp-dependent restriction endonuclease. Journal of Molecular Biology. 1992;225:327–348. doi: 10.1016/0022-2836(92)90925-a. [DOI] [PubMed] [Google Scholar]
- Weber M, Davies JJ, Wittig D, Oakeley EJ, Haase M, Lam WL, Schübeler D. Chromosome-wide and promoter-specific analyses identify sites of differential DNA methylation in normal and transformed human cells. Nature Genetics. 2005;37:853–862. doi: 10.1038/ng1598. [DOI] [PubMed] [Google Scholar]
- Wu Z. Baltimore, MD: Department of Biostatistics Working Papers. Johns Hopkins Univeristy; 2009. Subset quantile normalization using negative control features. Working Paper 191. http://www.bepress.com/jhubiostat/paper191. [Google Scholar]
- Wu Z, Irizarry RA, Gentleman R, Martinez-Murillo F, Spencer F. A model-based background adjustment for oligonucleotide expression arrays. Journal of the American Statistical Association. 2004;99:909–917. [Google Scholar]
- Yang YH, Dudoit S, Luu P, Lin DM, Peng V, Ngai J, Speed TP. Normalization for cDNA microarray data: a robust composite method addressing single and multiple slide systematic variation. Nucleic Acids Research. 2002;30:e15. doi: 10.1093/nar/30.4.e15. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.