Inference of Mutation Parameters and Selective Constraint in Mammalian Coding Sequences by Approximate Bayesian Computation

Abstract

We develop an inference method that uses approximate Bayesian computation (ABC) to simultaneously estimate mutational parameters and selective constraint on the basis of nucleotide divergence for protein-coding genes between pairs of species. Our simulations explicitly model CpG hypermutability and transition vs. transversion mutational biases along with negative and positive selection operating on synonymous and nonsynonymous sites. We evaluate the method by simulations in which true mean parameter values are known and show that it produces reasonably unbiased parameter estimates as long as sequences are not too short and sequence divergence is not too low. We show that the use of quadratic regression within ABC offers an improvement over linear regression, but that weighted regression has little impact on the efficiency of the procedure. We apply the method to estimate mutational and selective constraint parameters in data sets of protein-coding genes extracted from the genome sequences of primates, murids, and carnivores. Estimates of CpG hypermutability are substantially higher in primates than murids and carnivores. Nonsynonymous site selective constraint is substantially higher in murids and carnivores than primates, and autosomal nonsynonymous constraint is higher than X-chromsome constraint in all taxa. We detect significant selective constraint at synonymous sites in primates, carnivores, and murid rodents. Synonymous site selective constraint is weakest in murids, a surprising result, considering that murid effective population sizes are likely to be considerably higher than the other two taxa.

WHAT fraction of new mutations in the genome are influenced by natural selection? One way to address this question is to compare levels of between-species nucleotide divergence at classes of candidate selectively evolving and neutrally evolving sites. For example, under the assumptions that nonsynonymous mutations are either strongly deleterious or neutral and there exists a class of sites that evolves neutrally, the proportion of deleterious amino acid-changing mutations in a protein-coding gene can be estimated from

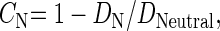(1)

where D_N and D_Neutral are rates of nonsynonymous and neutral substitutions between the species pair, respectively. C_N is referred to as the selective constraint. In the absence of positive selection, C_N is expected to lie in the range [0, 1]. However, C_N < 0 can be taken as evidence of the presence of many adaptive amino acid substitutions (but see Parmley and Hurst 2007).

The neutral substitution rate, D_Neutral, has often been assumed to be equal to D_S, the rate of synonymous substitutions in protein-coding genes. That assumption, however, is not justified in many species (reviewed by Hershberg and Petrov 2008), and even in mammals some form of selection appears to operate on synonymous mutations (Chamary et al. 2006). For example, between-species divergence at fourfold degenerate sites is significantly lower than in ancestral transposable element repeats (ARs) (Eöry et al. 2010), and ARs are among the best candidates for a class of sites that evolves neutrally (Lunter et al. 2006; Meader et al. 2010; Pollard et al. 2010). If we employ ARs as a neutral reference, nonsynonymous and synonymous selective constraint can be estimated as

(2)

and

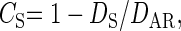(3)

respectively, where D_AR is the substitution rate for intronic ARs. Note that intronic ARs represent a better local neutral reference than intergenic ARs, since mutation rates may differ between transcribed and nontranscribed DNA due to transcription-coupled repair. In a genome-wide analysis employing ARs as a neutral reference, Eöry et al. (2010) estimated mean C_S of 0.24 and 0.11 for hominids and murid rodents, respectively, suggesting that mammalian synonymous sites are subject to net purifying selection, albeit at modest levels. Eöry et al. (2010) noted that the higher C_S estimate in hominids was unexpected, because recent effective population size (N_e) has been estimated to be two orders of magnitude higher in wild mice than hominids (Eyre-Walker et al. 2002; Halligan et al. 2010). This difference in N_e would lead to more effective selection against suboptimal synonymous mutations in murids than hominids, if selection coefficients at these sites are similar in the two taxa. In contrast, higher values of C_N in murids than primates have consistently been observed (Ohta 1993, 1995; Li 1997, Chap. 8; Eöry et al. 2010), suggesting that selection against new amino acid mutations is more effective in murids and that there is a significant fraction of nearly neutral amino acid mutations in hominids (Eyre-Walker et al. 2002). It is unclear, however, whether the synonymous and nonsynonymous selective constraint values inferred by Eöry et al. (2010) are typical of mammals in general.

There are several limitations of previous approaches that compare evolutionary rates between categories of sequence to estimate selective constraint. First, mutational parameters and constraint have been estimated separately, whereas in principle it is desirable to jointly estimate all of the relevant parameters within the same analysis. Second, CpG sites outside of CpG islands in mammals are hypermutable and their frequency differs between coding and noncoding DNA, complicating inference of substitution rates. In several previous analyses (e.g., Meunier and Duret 2004; Keightley et al. 2005; Eöry et al. 2010), the ad hoc procedure of excluding sites preceded by C or followed by G (CpG-prone sites) has been employed, but this excludes selective constraint at CpGs. The procedure of estimating separate evolutionary rates at sites that are C followed by G in either species (CpG sites) and non-CpG sites has also been frequently employed (e.g., Ebersberger et al. 2002; Hardison et al. 2003; Hellmann et al. 2003; Subramanian and Kumar 2003; Chimpanzee Sequencing and Analysis Consortium 2005; Parmley et al. 2006), but this has been shown to be biased, potentially seriously for closely related species (Gaffney and Keightley 2008). Finally, in several analyses, only fourfold degenerate synonymous sites and zerofold degenerate nonsynonymous sites have been considered, whereas selection on twofold sites has been excluded.

Here, we develop a method on the basis of approximate Bayesian computation (ABC) to jointly estimate mutation rates and selective constraint at nonsynonymous and synonymous sites at CpG and non-CpG sites. We attempt to capture several of the complexities of mutation and selection operating simultaneously on coding and noncoding sequences, particularly the context-dependent hypermutability of CpG dinucleotides in mammals. The ABC approach described here has its origins in the rejection sampling method described by Tavaré et al. (1997), with enhancements introduced by Beaumont et al. (2002) (reviewed by Csilléry et al. 2010). In ABC, multiple, independent simulated data sets resembling the real data set are generated according to an appropriate model. The parameters for each simulation are sampled from prior distributions (typically uniform) that have wide limits encompassing the plausible true parameter values for the real data under analysis. From each simulation replicate, a set of easy-to-compute summary statistics, correlated with the hard-to-estimate parameters of interest are computed. The same set of summary statistics is computed for the real data. A posterior distribution of parameters for the real data can be approximated by parameter values of simulations whose summary statistics closely match the real data (Tavaré et al. 1997). In the approach described by Beaumont et al. (2002), parameter estimation is by multiple weighted regression within the set of simulations that best match the real data, where match to the data is measured by Euclidean distance. Here, our starting point is the local linear regression approach of Beaumont et al. (2002). We also investigate whether incorporating quadratic regression and an alternative measure of the distance between the simulated and actual data (the Mahalanobis distance) can improve the accuracy of estimates. We simulate coding and noncoding sequences, incorporating hypermutability at CpG sites, and transition:transversion mutation rate bias, and infer mutation and selective constraint parameters simultaneously within the same model. We use simulations to investigate the performance of the method. We then apply the method to estimate constraint at synonymous and nonsynonymous sites along with mutation rate parameters in the genomes of primates (Homo sapiens vs. Macaca mulatta), murid rodents (Mus domesticus vs. Rattus norvegicus), and carnivores (Felis catus vs. Canis familiaris).

METHODS

General description of the model:

Ancestral protein-coding gene sequences and intronic noncoding sequences closely linked to the coding sequences are assumed to be at or near equilibrium for base composition, then to evolve independently along a pair of lineages. The mutation rates for noncoding and coding sequences of the gene are assumed to be equal. We assume different mutation rates for sites within and outside the CpG dinucleotide context, and different transition and transversion rates at both CpG and non-CpG sites. With the exception of CpG dinucleotides, mutations are assumed to occur independently in each sequence. The mutation rate parameters of the model are listed in Table 1.

TABLE 1.

Mutation and selection parameters fitted in the model and limits for uniform priors

Parameter	Meaning	Limits of uniform prior
knCG	Mutation rate at non-CpG sitesa	0, 0.4
α	CpG:non-CpG mutation rate ratio	2, 20
βnCG	Transition:transversion ratio at non-CpG sites	1, 5
βCG	Transition:transversion ratio at CpG sites	1, 20
CN	Constraint at nonsynonymous sites	−1, 1
CS	Constraint at synonymous sites	−1, 1

^aThe mutation rate refers to the rate down one of the two lineages.

Selective elimination of deleterious mutations and fixation of advantageous mutations are modeled by constraint parameters, C_S and C_N, for synonymous and nonsynonymous sites, respectively (Table 1). In the absence of fixed differences driven by positive selection, C_S and C_N represent the fractions of mutations that are strongly deleterious and eliminated by natural selection. The values of C_S and C_N would then be in the range [0, 1]. However, in our model, we also allow for the possibility of adaptive evolution at synonymous and nonsynonymous sites, and allow C_S and C_N to take negative values.

Evolutionary model:

We simulated sequence evolution using a discrete-time algorithm in which the period since the most recent common ancestor is divided into s steps. Let n_CG and n_nCG be the number of bases within and outside of the CpG context, respectively. Write k_CG and k_nCG for the probabilities of a mutation occurring at each such site during the time since most recent common ancestor, and let α = k_CG/k_nCG be the ratio of mutation rates within vs. outside the CpG context. We determined the number of mutations that occurred in a single time step by sampling from Poisson distributions with parameter n_CG k_CG/(2s) for CpG sites and with parameter n_nCG k_nCG/(2s) for non-CpG sites. CpG and non-CpG mutations were sampled in random order at random CpG and non-CpG contexts, respectively. Mutations at CpG contexts were randomly allocated to the C or G base. A mutation was a transition with probability β_CG/(2 + β_CG) or β_nCG/(2 + β_nCG) for CpG and non-CpG sites, respectively, where β_CG and β_nCG are the respective transition:transversion ratios (Table 1); otherwise, it was a transversion.

For neutral sequences, a mutation led to a substitution with probability 1. For coding sequences, the substitution probability was (1 − C_S) if the mutation caused a synonymous change, and (1 − C_N) if the mutation caused a nonsynonymous change. If the sampled value of C_S or C_N was negative, then all mutations resulted in substitutions. We further generated an additional number of adaptive substitutions by sampling from Poisson distributions with parameters −C_x n_CG k_CG/(2s) for CpG sites and −C_x n_nCG k_nCG/(2s), where C_x = C_S or C_N for synonymous and nonsynonymous sites, respectively.

We began each simulation with a random sequence of nucleotides. We then allowed the ancestral sequence to evolve for s = 50 steps. To accelerate the convergence of the ancestral sequence to an equilibrium base composition, the mutation rate in this initial period was set to k_nCG = 10, a value that assures that almost all sites in the genome will have experienced multiple hits, particularly CpG sites. The speciation event then occurred, and each descendant lineage evolved for an additional s = 50 steps. Increasing the number of steps to 100 had no appreciable effect on the outcome of simulations (supporting information, Figure S1).

Inference by approximate Bayesian computation:

For parameter estimation, our starting point is the ABC method described by Beaumont et al. (2002). Inference is based on a set of summary statistics, calculated from real or simulated data, correlated with the parameters of interest. Multiple simulated data sets are generated under the model using parameter values sampled independently from uniform prior distributions. In analyzing simulated data sets for the purpose of evaluating the inference method, we used priors with the limits shown in Table 1. The true values of simulated parameter values were chosen to fall well within these limits. In analyzing real data, by definition we do not know the true parameter values, so assigning limits for priors can therefore be problematic. We therefore assigned limits for the mutation rate parameter priors that are wide ranges about empirically estimated values for mammals (Siepel and Haussler 2004; Zhang et al. 2007). The prior limits for C_S and C_N include the maximum possible value (1) and a rate of synonymous or nonsynonymous evolution twice the neutral rate (i.e., C_S and C_N = −1). In analyzing the real data, the prior limits were as shown in Table 1, with the exception that the upper limit of the prior for α was raised to 30, because a significant number of estimates exceeded 20, especially in the case of primates. There is a trade-off between accurately estimating parameters, i.e., values within the acceptance range should be within the prior limits for each gene analyzed; however, the computing time increases with the range of the priors. Vectors of summary statistics, s and s′ for the real data and each simulation replicate, respectively, are calculated and then scaled (by the mean and standard deviation across all simulations for each statistic). We considered two measures of the distance between the vectors s and s′, the Euclidean distance and the Mahalanobis distance measure (Morrison 1976). We expected the Mahalanobis distance to be more powerful because it takes into account correlations between the summary statistics. Using the distance measure for each simulation, the proportion P_δ of simulations whose summary statistics are closest to the real data is retained. Finally, multiple regression is used to obtain parameter estimates. Regression is carried out separately for each simulated parameter using the “lm” function in the R statistical computing language (www.r-project.org). We carry out either weighted or unweighted, linear or quadratic multiple regression of the simulated parameter values on the matrix of summary statistics. For weighted regression, we employed the Epanechnikov kernel scheme suggested by Beaumont et al. (2002). Quadratic regression is carried out by including all squared summary statistics in the multiple regression formula. Parameter estimates, obtained by taking fitted values at the observed summary statistics from the fitted model, correspond to the posterior mean (see Beaumont et al. 2002).

A simulated data set consisted of a coding sequence that matches the total lengths of the exons of the gene under consideration, and a concatenated noncoding sequence that matches the length of the concatenated ARs that form the neutral standard for the gene under consideration. The bases preceding and following the AR or exon boundary of the real data and the simulations were used to determine whether the first and last base, respectively, is part of a CpG dinucleotide. We used 12 summary statistics for parameter estimation: the fractions of transition and transversion differences at CpG and non-CpG sites at nonsynonymous, synonymous, and AR sites. These counts are easy to compute by a simple comparison of two sequences and are expected to be correlated to the corresponding rates of substitution that we wish to estimate. However they do not account for multiple hits, and the correlation is expected to decrease with increasing sequence divergence. We investigated the inclusion of additional summary statistics computed from fractions of differences at non-CpG-prone sites, but found that they made little difference to the results.

In analyzing simulated data for the purpose of testing the method, the lengths of the sequences to be analyzed and the simulated sequences used for ABC inference were identical. However, real genes vary in length, so it was not feasible to generate simulated sequences of identical length to each gene in the analysis. We therefore generated approximate summary statistic for each gene as follows. We simulated noncoding and coding sequences of lengths 50,000 and 5000 bases, respectively, and we stored summary statistics for the maximum sequence lengths, and then in steps decreasing by 20% down to a minimum of 100 bases. For each gene analyzed, we used linear interpolation within ordered lists of summary statistics to generate statistics corresponding to the actual noncoding and coding lengths. If the real data sequence length exceeded the maximum simulated sequence length, the sequence was truncated.

Data:

Genomic sequence data were downloaded from the Ensembl MySQL server through the Perl API interface. We obtained BLASTZ alignments for human–chimpanzee and mouse–rat and downloaded the EPO-LOW-COVERAGE alignments for dog–cat and realigned these using MAVID (Bray and Pachter 2004). Gene annotations from Ensembl release 57 were used, and genes that fulfilled the following system of criteria for orthology were analyzed. We assumed any transcript to be orthologous between the reference and target species if both started in a start and ended in a stop codon, did not contain premature stop codons, and were not subject to frameshift mutations. Genes were considered to be valid if they contained at least one valid homologous transcript in the target genome. In cases of genes with multiple transcripts, a single transcript was chosen randomly and used in the analysis. Transposable element (TE) annotations were also downloaded from Ensembl and those TEs with a putatively orthologous sequence in the target genome (ARs) were used as neutral standards. The distribution of insertion–deletion substitution suggest that these are among the best candidates for a category of neutrally evolving sequence in mammals (Lunter et al. 2006). Overlapping dust and low complexity regions, tandem and microsatellite repeats were masked off from the analysis, since sequencing and alignment of these regions may be problematic. Gaps and bases opposite gaps were removed from alignments.

The genome was divided into 1-Mb blocks. The ABC analysis was carried out using summary statistics on a gene-by-gene or block-by-block basis. If the analysis was carried out block by block, the exons of each gene within each block were concatenated up to the limit of 5000 bases that could be used in the ABC analysis (see above). The neutral reference was the concatenated ARs mapped in the introns of that block up to the maximum of 50,000 bases (see above). If the analysis was gene by gene and the amount of noncoding sequence exceeded 50,000 bases, ARs within the focal gene were preferentially used and then random ARs from the block up to the maximum sequence length. To avoid a contribution of excessively noisy parameter estimates from genes having few nucleotide differences, a gene was rejected from the ABC analysis if its number of neutral reference bases was <1000 or its number of coding bases was <400. The numbers of genes and 1-Mb blocks that met these criteria are shown in Table 2. Standard errors of mean parameter estimates were obtained by bootstrapping by block 1000 times.

TABLE 2.

Numbers of loci and 1-Mb blocks analyzed in three species pairs

Species pair	No. loci	No. 1-Mb blocks
Human–macaque	12,992	2145
Mouse–rat	13,215	1893
Cat–dog	816	302

RESULTS

Simulations:

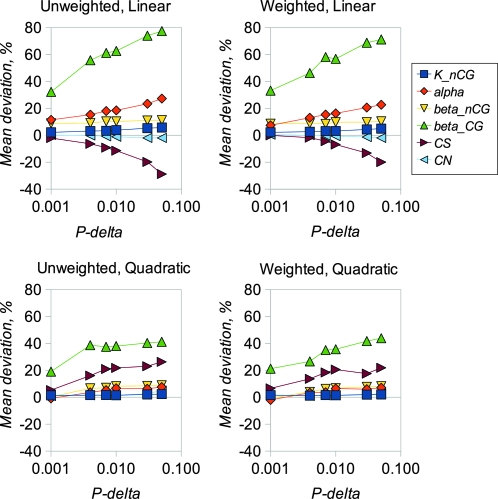
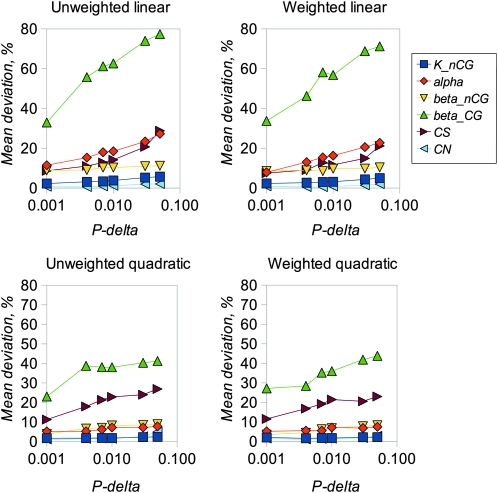
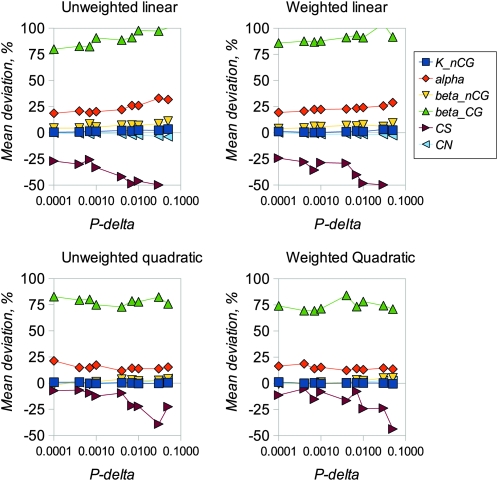
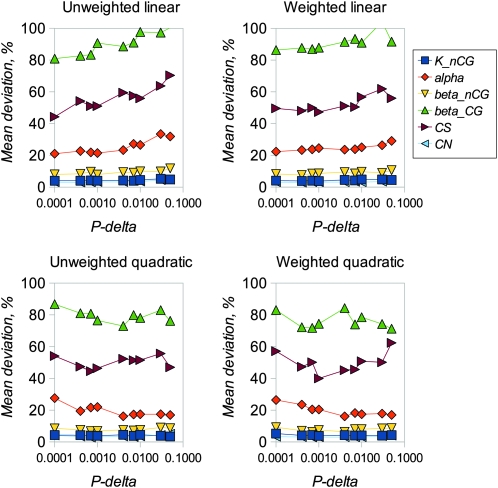
We examined the performance of the ABC inference procedure in simulations using four regression models and a range of values for the proportion of simulations accepted, P_δ. We first compared the results from analyzing long sequences of 100,000 bp of coding and noncoding DNA (Figures 1 and 2) with results for sequences of lengths comparable to mammalian genes (2000 coding and 10,000 noncoding bases, Figures 3 and 4). Figures 1 and 3 show the estimated amounts of bias for each parameter, expressed as mean percentage deviation from the true parameter values, plotted a function of P_δ. Figures 2 and 4 show the error of each parameter estimate, expressed as mean percentage absolute deviation from the true parameter values, also plotted a function of P_δ. As expected, mean bias is smaller for longer sequences (compare Figures 1 and 3), and bias tends to decline as P_δ decreases. Interestingly, in these analyses there is little advantage to using a weighted regression, whereas quadratic regression can offer an appreciable advantage over linear regression.

Figure 1.—

Mean deviation of estimated parameter values from simulated true values. Each point is the mean of 100 replicates. There were 100,000 neutral and 100,000 coding sites analyzed in each replicate. There were 10⁵ independent simulations used for ABC inference. The simulated parameter values were k_nCG = 0.1, α = 10, β_nCG = 2, β_CG = 5, C_S = 0.2, and C_N = 0.8.

Figure 2.—

Mean absolute deviation of estimated parameter values from true values corresponding to results shown in Figure 1.

Figure 3.—

Mean deviation of estimated parameter values from true values. Each point is the mean of 100 replicates. There were 10,000 neutral and 2000 coding sites and 10⁶ simulations used for inference. Simulated parameter values are as in Figure 1.

Figure 4.—

Mean absolute deviation of estimated parameter values from true values for simulations corresponding to Figure 3.

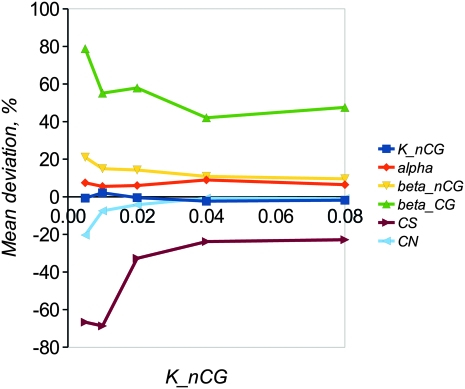
Different parameters are subject to different amounts of bias, presumably as a consequence of varying amounts of information in the data that can be used to estimate them. In particular, it is difficult to get unbiased estimates of the transition:transversion ratio at CpG sites, presumably because there are few informative sites. Estimates of C_N are reasonably unbiased in all scenarios investigated. Estimates of C_S can also be reasonably unbiased, but only with small values of P_δ, quadratic regression, and (particularly) if a large number of simulations is used in the analysis. The amount of variability among estimates for each parameter tends to decline as P_δ decreases (Figures 2 and 4). However, if a very small number of replicates is used in the analysis (i.e., P_δ = 0.0001 with 10⁶ simulations or 100 simulations retained), variability starts to increase if a small amount of sequence data is analyzed. This suggests that, for analysis of real data, at least 10⁶ replicates and P_δ of 0.001 is appropriate. We then investigated the extent to which the divergence between the sequences of the two species affects the amount of bias. The results (Figure 5) suggest that bias increases for most parameters if sequence divergence is low (k_nCG < 0.02). Finally, we compared the results obtained using Euclidean distance vs. Mahalanobis distance (Figure S2). In general the amount of bias does not differ greatly between the two methods, with the exception of C_S, which tends to be overestimated for Euclid and underestimated for Mahalanobis. At P_δ = 0.0001, Mahalanobis distance appears to slightly outperform Euclid.

Figure 5.—

Effect of amount of sequence divergence (k_nCpG) on mean percentage bias of parameter estimates. Each point is the mean of 100 replicates. Other parameters are as in Figure 1.

Parameter inference by ABC analysis of coding sequences in primates, murids, and carnivores:

We used the ABC procedure described in methods to analyze gene sequence data from primates (human vs. macaque), murid rodents (mouse vs. rat), and carnivores (dog vs. cat) using 1.5 × 10⁶ simulation replicates. We used quadratic unweighted regression and Euclidean distance to select P_δ = 0.001 of the simulation replicates for analysis. Mutational and constraint parameter estimates are presented in Table 3. The estimates of the CpG:non-CpG mutation rate ratio (α) suggest that, as expected, the CpG mutation rate is about one order of magnitude higher than the non-CpG mutation rate in all taxa. Notably, the α estimate in primates is nearly twice that of murids and carnivores. Estimates of transition:transversion mutational parameters (β_CG and β_nCG) are fairly similar between the two taxa and broadly agree with previous estimates from a different approach (i.e., β_CG = ∼10 and β_nCG = ∼4, respectively; Zhang et al. 2007).

TABLE 3.

Mean ABC estimates of mutation and selective constraint parameters

	Parameter estimate (SE)
Parameter	Human–macaque	Mouse–rat	Cat–dog
2knCG	0.042 (0.0002)	0.140 (0.0004)	0.178 (0.0019)
α	24.5 (0.12)	15.3 (0.09)	12.7 (0.24)
βnCG	3.43 (0.007)	3.17 (0.008)	2.93 (0.032)
βCG	11.4 (0.06)	12.1 (0.05)	11.0 (0.15)
CN	0.689 (0.003)	0.796 (0.003)	0.824 (0.008)
CS	0.205 (0.004)	0.093 (0.005)	0.112 (0.020)

Estimates of mean selective constraint for nonsynonymous sites also varies between the taxa. Mean nonsynonymous site constraint (C_N) is substantially higher in murids than primates, a result that agrees with Eöry et al. (2010), who obtained, for example, estimates of 0.70 and 0.80 for single transcript genes in hominids and murids, respectively. This is consistent with more effective selection associated with a higher effective population size in murids (Halligan et al. 2010). Surprisingly, however, the highest C_N estimate comes from carnivores, and the estimate is substantially higher than that in murids. The ranking is therefore the opposite of what would be expected on the basis of differences in effectiveness of selection brought about by differences in effective population size, assuming that predators have the smaller N_e. Estimates for synonymous sites are also in general agreement with Eöry et al. (2010). Mean constraint at synonymous sites is substantially higher in primates than murid rodents. We also observe significant selective constraint at synonymous sites in carnivores. To check the sensitivity of the results to the length of sequence analyses, we concatenated genes within 1-Mb blocks and recomputed ABC estimates. Results are similar to the estimates computed locus by locus (Table S1).

We then estimated C_N and C_S separately for autosomal and X-linked loci (Table 4). In all three taxa, autosomal C_N is higher than chromosome X C_N, and the difference is highly significant in primates and murids. This effect has been documented previously in birds and mammals (Mank et al. 2010). The higher constraint at nonsynonymous sites for autosomal loci is consistent with a lower N_e for X-linked loci and with the presence of nearly neutral amino acid mutations. This pattern is also consistent with a higher rate of positively selected substitutions on X-linked than autosomal loci, that can result from several processes (Charlesworth et al. 1987). Surprisingly, C_S is significantly higher for murid X-linked than autosomal loci (Table 4). A possible explanation is the presence of stronger selection on synonymous sites of X-linked genes, as has been suggested to occur in Drosophila species (Vicoso et al. 2008).

TABLE 4.

Mean ABC estimates of CN and CS for autosomal and X-linked loci

	CN (SE)			CS (SE)
	Human–macaque	Mouse–rat	Cat–dog	Human–macaque	Mouse–rat	Cat–dog
Autosomes	0.693 (0.003)	0.801 (0.003)	0.827 (0.007)	0.206 (0.004)	0.089 (0.005)	0.114 (0.021)
Chr X	0.618 (0.017)	0.706 (0.023)	0.765 (0.041)	0.192 (0.022)	0.150 (0.022)	0.062 (0.080)
P	<0.002	<0.002	0.10	0.43	0.002	0.53

The P-values are the probability of observing at least as large a difference between autosomal and chromosome (Chr) X mean constraint under the null hypothesis that there is no difference, calculated from bootstrap estimates, assuming a two-tailed test.

DISCUSSION

In this article, we have explored the utility of ABC in the context of estimating mutational and selection parameters from whole-genome sequence data from a pair of species. Our principal conclusions from these analyses are that CpG hypermutability varies between mammalian taxa, and that there is variation in the strength of selection on both nonsynonymous and synonymous mutations between taxa and between the X chromosome and autosomes.

Our model has several simplifying assumptions made necessary by the limited number of parameters that can be estimated simultaneously by ABC. By restricting the analysis to pairs of species, we have needed to make the assumption of equilibrium nucleotide frequencies. However, G/C content is believed not to be at equilibrium in mammalian taxa (Duret and Arndt 2008), and it has been suggested that G/C rich isochores are gradually vanishing from mammalian genomes (Duret et al. 2002). To account for the nonequilibrium G/C content it would, for example, be necessary to extend the approach to three species and to incorporate additional summary statistics and parameters. Within our model, we found it necessary to generate a minimum of 10⁶ simulation replicates, only 0.1% of which were retained for the regression analysis on the basis of similarity to the data. Unfortunately, as the number of parameters increases, the number of replicates needed increases nonlinearly. We found that the weighted regression scheme suggested by Beaumont et al. (2002) provided little advantage over unweighted regression. On the other hand, a quadratic regression led to less biased estimates than linear regression, a result consistent with observations of Blum and François (2010). We also see potential improvement from using the Mahalanobis rather than Euclidean distance, although only if a small proportion of simulations are accepted in the analysis. Further improvements could potentially be made by combining ABC with Markov chain Monte Carlo (MCMC) to focus on proposals that generate summary statistics close to the data (Wegmann et al. 2009). However, this approach did not fit easily within our implementation, since we generated simulations that are used to analyze multiple genes of variable length by storing summary statistics for a range of gene lengths and use linear interpolation to generate approximate summary statistic values.

As expected, estimates of mutation parameters reveal CpG hypermutability and higher transition than transversion mutation rates (Table 3). In agreement with previous work (Siepel and Haussler 2004; Zhang et al. 2007), the transition:transversion mutation rate ratio is substantially higher at CpG than non-CpG sites. The transition:transversion ratio parameters are fairly consistent across the three taxa, but this contrasts with the substantial differences among taxa in the CpG:non-CpG mutation rate (α), most notably in primates. We obtained a similar estimate of α to the human–macaque data set reported here in an analysis of a genome-wide data set of human–chimpanzee genes (results not shown). There are also substantial differences in selective constraint at nonsynonymous sites. In agreement with several previous analyses (Ohta 1993, 1995; Li 1997, Chap. 8; Eöry et al. 2010), mean C_N (primates) < C_N (murids). Since the effective population size in wild house mouse populations in the ancestral range approaches two orders of magnitude higher than recent hominid N_e (Halligan et al. 2010) this can be taken as evidence for a reduction in the effectiveness of selection in the primate lineage at amino acid sites. More surprising is our observation of mean C_N (carnivores) > C_N (murids). Since population sizes of murids are likely to be higher than carnivores (Piganeau and Eyre-Walker 2009), this result runs contrary to the idea that effective population size differences explain differences in selective constraint (see also Eöry et al. 2010). A possible contributing factor is that slightly deleterious nonsynonymous polymorphism increases apparent nonsynonymous divergence disproportionately for closely related species (Wolf et al. 2009). Alternatively, it is also possible that the rather limited set of carnivore genes that we analyzed is biased toward highly conserved genes, since carnivore genes are frequently annotated on the basis of human annotations. Distinguishing between theses alternatives could be helped by an analysis restricted to orthologs present in all six species.

Eöry et al. (2010) also reported mean C_S (primates) > C_S (murids), and our results also show this pattern (Table 3). Furthermore, we observe significant selective constraint at synonymous sites of carnivores. Further evidence from additional species pairs may help to clarify whether murids are exceptional among mammals in showing low selective constraint at synonymous sites. This observation is another piece of evidence suggesting that differences in N_e may not be the sole cause of differences in selective constraint between taxa and that more detailed information about the nature of selection on synonymous sites in mammals may be necessary to fully understand the observed patterns.