Abstract
Robustness seems to be the opposite of evolvability. If phenotypes are robust against mutation, we might expect that a population will have difficulty adapting to an environmental change, as several studies have suggested1–4. However, other studies contend that robust organisms are more adaptable5–8. A quantitative understanding of the relationship between robustness and evolvability will help resolve these conflicting reports and will clarify outstanding problems in molecular and experimental evolution, evo-devo, and protein engineering. Using a general population-genetic model, we demonstrate here that mutational robustness can either impede or facilitate adaptation, depending on the population size, the mutation rate, and the structure of the fitness landscape. In particular, neutral diversity in a robust population can accelerate adaptation provided the number of phenotypes accessible to an individual by mutation is smaller than the total number of phenotypes in the fitness landscape. These results provide a quantitative resolution to a significant ambiguity in evolutionary theory.
The relationship between robustness and evolvability is complex because robust populations harbor a large diversity of neutral genotypes that may play an important role in adaptation9–11. Although neutral mutations do not change an organism’s phenotype, they may nevertheless have epistatic consequences for the phenotypic effects of subsequent mutations12–18. In particular, a neutral mutation can alter an individual’s “phenotypic neighborhood” – the set of distinct phenotypes that the individual can access through a further mutation. Pioneering studies based on RNA folding and network dynamics suggest that genotypes expressing a particular phenotype are often linked by neutral mutations into a large neutral network, and that members of a neutral network differ widely in their phenotypic neighborhoods1,19–21. Numerous studies have documented the importance of neutral variation in allowing a population to access adaptive phenotypes5,17,18,22–24, and neutral networks have consequently been hypothesized to facilitate adaptation9–11.
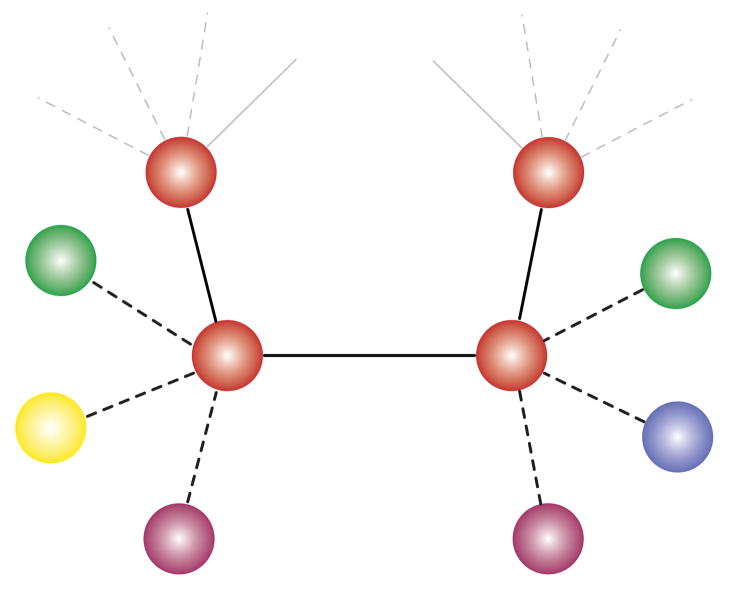
Here we analyze the relationship between robustness and evolvability using a population-genetic model that specifies statistical properties of the fitness landscape. Our approach bypasses the tremendous complexity of explicit neutral networks1,11,17,19,21,22 to focus instead on the essential evolutionary consequences of epistatic mutations. We consider a population of N individuals reproducing according to the discrete-time, infinite-sites Moran model. In each time step, a randomly chosen individual produces one offspring. Upon replication, a mutation occurs with probability μ, producing a novel genotype. With probability q, the mutation is neutral. The parameter q therefore quantifies robustness, which is assumed to be the same for all genotypes on a network. With probability 1 − q the mutation is non-neutral and it changes the offspring’s phenotype to one of K phenotypes accessible from a given genotype. Each genotype has a specific set of K accessible phenotypes that constitute its phenotypic neighborhood; these K phenotypes are drawn uniformly from P possible alternatives. Phenotypic neighborhoods are assumed independent, such that the K accessible phenotypes are redrawn whenever a mutation occurs (we relax this and other assumptions below). When the number of phenotypes accessible to an individual, K, is significantly smaller the total number of alternative phenotypes in the landscape, P, neutral mutations can profoundly alter an individual’s phenotypic neighborhood. This genotype-phenotype map is illustrated in Figure 1.
FIG. 1. Illustration of Genotype-Phenotype Model.
A schematic representation of the genotype-phenotype map used in our analysis. Each circle corresponds to a genotype; colors denote phenotypes. The model parameter q quantifies robustness: a proportion q of mutations are neutral (solid lines), and the remaining mutations are non-neutral (dotted lines). A non-neutral mutation changes an individual’s phenotype to one of the K accessible alternatives that form the individual’s phenotypic neighborhood. When K is smaller than the total number of alternative phenotypes in the landscape, P, then individuals may have different phenotypic neighborhoods. The central pair of adjacent genotypes shown here express the same phenotype, but they have different phenotypic neighborhoods.
Our model implicitly represents a space of adjacent neutral networks. Neutral mutations produce other genotypes on the focal network, while non-neutral mutations produce genotypes on adjacent networks, each expressing one of P alternative phenotypes. To study evolution on the focal network, we assume that initially all of the P alternative phenotypes are lethal (our results hold more generally, see SI section 5). We analyze the relationship between robustness, q, and the time required to adapt to a novel environment; this analysis is outlined in Box 1 and detailed in SI section 1.
Box 1. Analysis of Adaptation Time.
Following an environmental change, we study the time required until the newly beneficial phenotype arises in a population with robustness q. A genotype is called “adaptable” if its phenotypic neighborhood contains the beneficial phenotype; our analysis links the stochastic evolution of these adaptable types to the adaptation time. Let p(t, y)dy denote the probability that there are y adaptable individuals at time t, scaling space and time by the factor . p (t, y)is well-approximated by the solution to
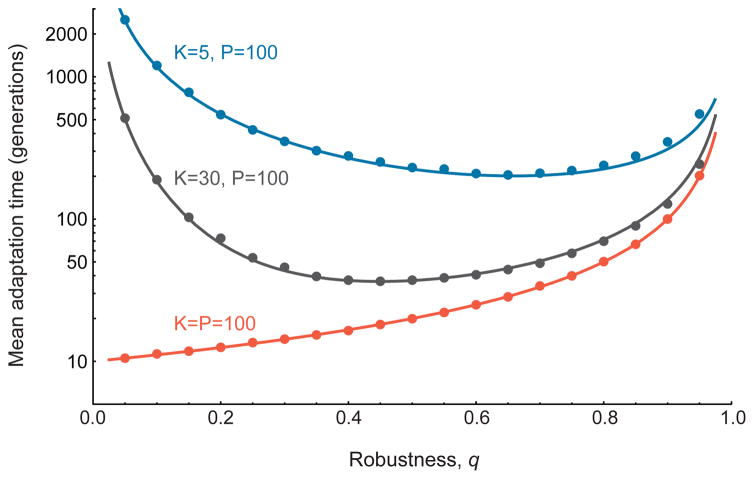
where β = Nμ. The first term in this expression quantifies genetic drift, the second term quantifies the increase in adaptable individuals through mutation, and the third term describes the rate of mutations that produce the beneficial phenotype. The conflicting effects of robustness on adaptation are evident in this expression: an increase in robustness (q) increases the supply of adaptable individuals, but it also reduces the rate at which beneficial mutations arise in such individuals. Solving a boundary value problem related to this equation produces an analytic expression for the expected arrival time of the beneficial phenotype (see SI sec. 1), a graph of which is shown in Figure 2.
We find that a robust population may adapt either more slowly or more quickly than one that is less robust (Figure 2). Starting from a steady-state population with robustness q, we considered an environmental shift that assigns one of the P alternative phenotypes the highest fitness. We derived an analytic expression for the mean waiting time before this fittest phenotype subsequently arises in the population (see SI sec. 1.4). When all phenotypes are accessible from any genotype (K = P), neutral mutations have no epistatic consequences and we observe the naive expectation: more robust populations always adapt more slowly (Figure 2). However, when the phenotypic neighborhood size, K, is smaller than the total number of phenotypes, P, we find a surprising pattern: the relationship between robustness and evolvability is non-monotonic. In particular, populations with an intermediate amount of robustness adapt more quickly than populations with little or no robustness (Figure 2).
FIG. 2. Robustness and Adaptation Time.
The relationship between robustness, q, and the average waiting time before the arrival of a specific beneficial mutation, for three fitness landscapes. Points show the means of 10,000 replicate Monte Carlo simulations, and lines show our analytic predictions (see Box 1 and SI sec. 1). When all possible phenotypes in the landscape are directly accessible by a mutation from any genotype (i.e. when K = P), robustness always inhibits adaptation (red curve). However, when phenotypic neighborhoods are small (i.e. when K<P), neutral mutations have epistatic consequences and the resulting relationship between robustness and adaptation time is non-monotonic: adaptation is most rapid at intermediate levels of robustness. N = 10,000, μ =0.001, P = 100.
There is a simple explanation for this counter-intuitive result. In a population with little robustness (q small), most mutations are lethal and little genetic variation accumulates. As a result, the population may not contain any “adaptable” individuals – i.e. those that are a single mutation away from the beneficial phenotype. Thus, when q is small the population may need to wait a long time before an adaptable individual arises, and then wait further for the adaptive phenotype itself to arise. However, slightly more robust populations contain a greater diversity of neutral genotypes, each of which has an independent chance (probability K/P) of being adaptable; thus, more robust populations may adapt more quickly.
Adaptation is most rapid when a population assumes an intermediate level of robustness. Moreover, this optimal level of robustness increases as the ratio K/P decreases (Figure 2). This trend confirms the primary intuition behind our result: when phenotypic neighborhoods are small, less robust populations contain few individuals who are “prepared to adapt”. In this range, increasing robustness results in a larger repertoire of phenotypes accessible to the population, thereby accelerating adaptive evolution.
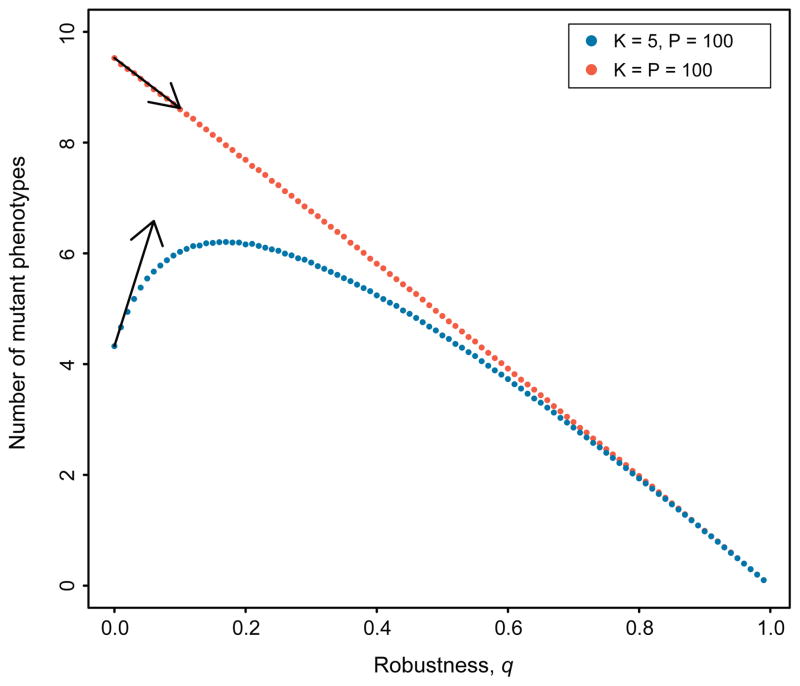
In addition to adaptation time, we also studied another measure of evolvability: the diversity of phenotypes produced by mutations in a population at steady state. Again, the naive expectation is that as robustness increases, fewer non-neutral mutants are produced each generation, and so the diversity of mutant phenotypes should decrease. However, increasing robustness also increases the neutral genetic diversity within a population, and, when K is less than P, each additional neutral type may increase the number of phenotypes accessible to the population through mutation. Thus, as with adaptation time, a surprising non-monotonic relationship is apparent when K < P : more robust populations can produce greater phenotypic diversity than their less-robust equivalents (Figure 3). We have derived an analytic expression to quantify the range of parameters for which this relationship is non-monotonic (see SI sec. 2). Our analysis shows that when K is smaller than a threshold determined by P, N and μ, the diversity of mutant phenotypes is maximized at an intermediate level of robustness.
FIG. 3. Robustness and Diversity.
The relationship between robustness, q, and the diversity of phenotypes produced by mutation in each generation, for two fitness landscapes. Points show the means of 100,000 replicate simulations; arrows depict slopes calculated analytically (see SI sec. 2). As these results demonstrate, an increase in robustness can increase phenotypic diversity, but only when the level of robustness, q, is small, and the number of phenotypes accessible from a single genotype, K, is less than the total number of phenotypes in the landscape, P. Parameters values: N = 10,000, μ =0.001.
There is an interesting difference between adaptation times and phenotypic diversity: increasing the population size or mutation rate moves the relationship between robustness and adaptation time closer to the naive monotonic prediction, whereas it moves phenotypic diversity further away from monotonicity (see SI sec. 4). While these influences of population size and mutation rate have some intuitive basis, they demonstrate that even qualitative predictions about the robustness-adaptability relationship require an explicit population-genetic model.
Our analysis has relied on several strong assumptions: 1) a neutral mutation completely changes the phenotypic neighborhood; 2) the number of phenotypes, K, in a genotype’s neighborhood is independent of its robustness q; 3) the values of K and q do not vary across the neutral network; and 4) alternative phenotypes are generally lethal. Relaxing each of these assumptions does not change our qualitative results (see SI sec. 5). Briefly, we relax the first assumption by introducing a parameter, f, the fraction of K neighbors that are redrawn following a neutral mutation. Allowing correlations between the phenotypic neighborhoods of neutral neighbors (i.e. allowing f < 1) still preserves the non-monotonic relationship between robustness and evolvability. Furthermore, a strong linear correlation between K and q, or variation in either quantity across the network, does not change our results. When q varies across the network, the population evolves towards elevated robustness as predicted by previous studies25,26. Nonetheless, the time required to acquire a new adaptive phenotype is still accurately described by our analytic formula, replacing the fixed value q by the average q in the population. The same relationship between robustness and adaptation also holds when alternative phenotypes are moderately deleterious, as opposed to lethal. Therefore, our conclusions are not sensitive to any of the strong assumptions used to derive our analytical results.
Our results above reveal a complex relationship between robustness and evolvability. In some situations, increasing robustness will decrease evolvability, whereas in other situations it will accelerate adaptation. The latter phenomenon can occur only when the number of phenotypes accessible to an individual, K, is smaller than the total number of alternative phenotypes in the landscape, P. To assess the plausibility of this condition, and to test the assumptions and predictions of our abstract model using an empirical, mechanistic genotype-phenotype map, we examined the folding and evolution of simulated RNA molecules. We used the Vienna folding software to estimate reasonable values of K, P, and f for RNA. Since these parameters vary among genotypes in an RNA neutral network, we determined appropriate averages of K, P, and f (see SI). For sequences of length 40 nucleotides, we estimated that K ≈ 19 and P is greater than 60,000, confirming that K<P for RNA. Furthermore, we found that f ≈ 0.3, indicating that neutral mutations substantially alter phenotypic neighborhoods. Finally, we evolved RNA populations in silico with varying levels of robustness, and we observed a non-monotonic relation between evolvability and robustness, which was predicted accurately by our abstract model (see SI sec. 6).
Recent studies have used theoretical27,28 or biological5,8 examples to argue that robustness increases evolvability. Another study has argued that robustness can either increase or decrease evolvability, depending upon the level at which robustness is described11. Although that study provided important intuition, it did not analyze the effect of robustness on adaptation time in an evolving population. By contrast, our analysis describes the population genetics connecting these important properties. This perspective allows a quantitative resolution to opposing informal arguments, and it highlights the complex interplay of influences shaping mutational robustness29,30.
Our analysis also reveals general patterns than may guide future experimental studies. First, the relationship between robustness and evolvability can be non-monotonic. In light of this complexity, empirical studies must go beyond pairwise comparisons of high-and low-robustness strains8 to measure evolvability over a broad range of robustness. Second, the population size and mutation rate in part determine whether robustness increases or decreases adaptation time. This insight was not apparent from informal arguments linking robustness and evolvability9–11, and it has not yet been considered in any empirical work. Finally, the parameters K, f, and P provide a new way to quantify epistasis beyond the conventional paradigm of synergistic and antagonistic interactions among selected sites.
Even though most standing genetic variation is neutral, the epistatic consequences of neutral mutations have received little experimental study. Our results demonstrate that conditionally neutral mutations strongly influence a population’s capacity to adapt, and so this form of “neutral epistasis” deserves direct experimental interrogation.
Supplementary Material
Acknowledgments
The authors thank Paul Turner and members of the Plotkin lab for advice and feedback. JBP acknowledges funding from the Burroughs Wellcome Fund, the David and Lucile Packard Foundation, the James S. McDonnell Foundation, the Alfred P. Sloan Foundation, the Defense Advanced Research Projects Agency (HR0011-05-1-0057), and the National Institute of Allergy and Infectious Diseases (U54AI057168). GPW acknowledges funding from the John Templeton Foundation and the Perinatology Research Branch of the NIH.
Footnotes
Competing Interests: The authors declare that they have no competing interests.
Author contributions: JAD, JBP, and GPW designed the project. JAD and JBP wrote the paper; GPW and TLP edited the paper. JAD performed the simulations. TLP performed most of the analysis, with contributions from JBP and JAD. JAD, TLP, and JBP wrote the SI.
References
- 1.Ancel LW, Fontana W. Plasticity, evolvability, and modularity in RNA. J Exp Zool. 2000;288:242–283. doi: 10.1002/1097-010x(20001015)288:3<242::aid-jez5>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 2.Carter AJR, Hermisson J, Hansen TF. The role of epistatic gene interactions in the response to selection and the evolution of evolvability. Theor Popul Biol. 2005;68:179–196. doi: 10.1016/j.tpb.2005.05.002. [DOI] [PubMed] [Google Scholar]
- 3.Cowperthwaite MC, Economo EP, Harcombe WR, Miller EL, Meyers LA. The ascent of the abundant: How mutational networks constrain evolution. PloS Computational Biology. 2008;4(7) doi: 10.1371/journal.pcbi.1000110. doi:10.1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Parter M, Kashtan N, Alon U. Facilitated variation: how evolution learns from past environments to generalize to new environments. PLoS Comput Biol. 2008;4(11) doi: 10.1371/journal.pcbi.1000206. doi:10.1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bloom JD, Labthavikul ST, Otey CR, Arnold FH. Protein stability promotes evolvability. Proc Natl Acad Sci USA. 2006;103:5869–5874. doi: 10.1073/pnas.0510098103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Aldana M, Balleza E, Kauffman S, Resendiz O. Robustness and evolvability in genetic regulatory networks. J Theor Biol. 2007;245:433–448. doi: 10.1016/j.jtbi.2006.10.027. [DOI] [PubMed] [Google Scholar]
- 7.Elena SF, Sanjuan R. The effect of genetic robustness on evolvability in digital organisms. BMC Evol Biol. 2008;8:284. doi: 10.1186/1471-2148-8-284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.McBride RC, Ogbunugafor CB, Turner PE. Robustness promotes evolvability of thermotolerance in an RNA virus. BMC Evol Biol. 2008;8:231. doi: 10.1186/1471-2148-8-231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.de Visser JAGM, et al. Perspective: Evolution and detection of genetic robustness. Evolution. 2003;57:1959–1972. doi: 10.1111/j.0014-3820.2003.tb00377.x. [DOI] [PubMed] [Google Scholar]
- 10.Lenski RE, Barrick JE, Ofria C. Balancing robustness and evolvability. PLoS Biol. 2006;4(12) doi: 10.1371/journal.pbio.0040428. doi:10.1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wagner A. Robustness and evolvability: a paradox resolved. Proc Biol Sci. 2008;275:91–100. doi: 10.1098/rspb.2007.1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rutherford S, Lindquist S. Hsp90 as a capacitor for morphological evolution. Nature. 1998;396:336–342. doi: 10.1038/24550. [DOI] [PubMed] [Google Scholar]
- 13.Bergman A, Siegal M. Evolutionary capacitance as a general feature of complex gene networks. Nature. 2003;424:549–552. doi: 10.1038/nature01765. [DOI] [PubMed] [Google Scholar]
- 14.Kirschner M, Gerhart J. The plausibility of life: resolving Darwin’s dilemma. Yale University Press; New Haven: 2005. [Google Scholar]
- 15.Wagner A. Robustness and evolvability in living systems. Princeton University Press; Princeton, N.J: 2005. [Google Scholar]
- 16.Meyers L, Ancel F, Lachmann M. Evolution of genetic potential. PloS Comp Bio. 2005;1(3) doi: 10.1371/journal.pcbi.0010032. doi:10.1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.van Nimwegen E. Influenza escapes immunity along neutral networks. Science. 2006;314:1884–1886. doi: 10.1126/science.1137300. [DOI] [PubMed] [Google Scholar]
- 18.Blount ZD, Borland CZ, Lenski RE. Historical contingency and the evolution of a key innovation in an experimental population of Escherichia coli. Proc Natl Acad Sci USA. 2008;105:7899–7906. doi: 10.1073/pnas.0803151105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fontana W, Schuster P. Continuity in evolution: on the nature of transitions. Science. 1998;280:1451–1455. doi: 10.1126/science.280.5368.1451. [DOI] [PubMed] [Google Scholar]
- 20.Ciliberti S, Martin OC, Wagner A. Innovation and robustness in complex regulatory gene networks. Proc Natl Acad Sci USA. 2007;104:13591–13596. doi: 10.1073/pnas.0705396104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sumedha, Martin OC, Wagner A. New structural variation in evolutionary searches of RNA neutral networks. Biosystems. 2007;90:475–485. doi: 10.1016/j.biosystems.2006.11.007. [DOI] [PubMed] [Google Scholar]
- 22.Koelle K, Cobey S, Grenfell B, Pascual M. Epochal evolution shapes the phylodynamics of interpandemic influenza a (H3N2) in humans. Science. 2006;314:1898–1903. doi: 10.1126/science.1132745. [DOI] [PubMed] [Google Scholar]
- 23.Cambray G, Mazel D. Synonymous genes explore different evolutionary landscapes. PloS Genetics. 2008;4(11) doi: 10.1371/journal.pgen.1000256. doi:10.1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Isalan M, et al. Evolvability and hierarchy in rewired bacterial gene networks. Nature. 2008;452:840–845. doi: 10.1038/nature06847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.van Nimwegen E, Crutchfield J, Huynen M. Neutral evolution of mutational robustness. Proc Natl Acad Sci USA. 1999;96:9716–9720. doi: 10.1073/pnas.96.17.9716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Forster R, Adami C, Wilke CO. Selection for mutational robustness in finite populations. Journal of Theoretical Biology. 2006;243:181–190. doi: 10.1016/j.jtbi.2006.06.020. [DOI] [PubMed] [Google Scholar]
- 27.Daniels BC, Chen YJ, Sethna JP, Gutenkunst RN, Myers CR. Sloppiness, robustness, and evolvability in systems biology. Curr Opin Biotechnol. 2008;19:389–395. doi: 10.1016/j.copbio.2008.06.008. [DOI] [PubMed] [Google Scholar]
- 28.Wilds R, Kauffman SA, Glass L. Evolution of complex dynamics. Chaos. 2008;18:033109. doi: 10.1063/1.2962223. [DOI] [PubMed] [Google Scholar]
- 29.Wilke C, Wang J, Ofria C, Lenski R, Adami C. Evolution of digital organisms at high mutation rates leads to survival of the flattest. Nature. 2001;412:331–333. doi: 10.1038/35085569. [DOI] [PubMed] [Google Scholar]
- 30.Krakauer D, Plotkin J. Redundancy, antiredundancy, and the robustness of genomes. Proc Natl Acad Sci USA. 2002;99:1405–1409. doi: 10.1073/pnas.032668599. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.