Fluorescence fluctuation spectroscopy: ushering in a new age of enlightenment for cellular dynamics

Abstract

Originally developed for applications in physics and physical chemistry, fluorescence fluctuation spectroscopy is becoming widely used in cell biology. This review traces the development of the method and describes some of the more important applications. Specifically, the methods discussed include fluorescence correlation spectroscopy (FCS), scanning FCS, dual color cross-correlation FCS, the photon counting histogram and fluorescence intensity distribution analysis approaches, the raster scanning image correlation spectroscopy method, and the Number and Brightness technique. The physical principles underlying these approaches will be delineated, and each of the methods will be illustrated using examples from the literature.

Introduction

In fields as diverse as data transmission, stock market analysis and rock music, the saying “One man’s noise is another man’s signal” often comes to mind. This saying is particularly appropriate for the technique of fluorescence fluctuation spectroscopy (FFS). Serious interest in fluctuations dates to 1827 with the observations by Robert Brown (Brown 1828) that pollen grains from the American plant Clarkia pulchella, when suspended in water, demonstrated a continuous jittery movement. In his own words “While examining the form of these particles immersed in water, I observed many of them very evidently in motion; their motion consisting not only of a change of place in the fluid, manifested by alterations in their relative positions, but also not unfrequently of a change of form in the particle itself.” And then: “These motions were such as to satisfy me, after frequently repeated observations, that they arose neither from currents in the fluid, nor from its gradual evaporation, but belonged to the particle itself.” Jan Ingenhousz, famous for his discovery of photosynthesis, had made similar observations on coal dust on the surface of alcohol in 1785. Ingenhousz’s work, however, did not appear to attract the same attention as did Brown’s, which in fact created a lively debate about the cause and even the existence of such fluctuations. The phenomenon actively attracted the attention of physicists after the publications of Albert Einstein (Einstein 1905) and Marian Ritter von Smolan Smoluchowski (Smoluchowski 1906), respectively, which developed the theory underlying such fluctuations. In 1911, in an effort to verify the theory, Theodor H.E. Svedberg observed the fluctuations in the number of colloidal gold particles in a small volume observed under a microscope (Svedberg and Inouye 1911). These works, and a series of elegant studies by Jean Baptiste Perrin, eventually firmly established the existence of atoms and molecules. Interestingly, in his classic book, Les Atomes (Perrin 1913), Perrin stated: “I had hoped to perceive these fluctuations in dilute solutions of fluorescent substances. I have found, however, that such bodies are destroyed by the light which makes them fluoresce.” Thus Perrin almost anticipated fluorescence fluctuation studies.

As pointed out by Elliott Elson, in a marvelous overview of the historical development of FCS (Elson 2004), the theory and experimental realization of both relaxation kinetics and dynamic light scattering (DLS) attracted significant attention in the 1950s and 1960s. These relaxation methods typically used small perturbations of temperature or pressure to displace the system from its equilibrium position, and then the kinetics of the return to equilibrium was monitored. Dynamic light scattering, which had been used in the 1960s to study the diffusion rates of biological macromolecules, was also applied to studies of chemical kinetics in the hopes of observing systems in the absence of external perturbations, but technical difficulties hampered these efforts. Fluorescence offered solutions to these difficulties, and in the early 1970s Magde, Elson, and Webb published seminal papers on the theory and application of fluorescence fluctuation analysis, specifically fluorescence correlation spectroscopy (FCS) (Elson and Magde 1974; Magde et al. 1972, 1974). This technique, originally developed to study the kinetics of chemical reactions in the absence of external perturbations, and specifically to study the binding of ethidium bromide to DNA, eventually engendered a revolution in quantitative fluorescence microscopy which now provides unparalleled insights into the dynamics of cellular interiors. Wide-spread applications of FCS had to wait though until the 1990s when the advent of confocal and two-photon microscopy greatly reduced the observation volume and thus significantly improved the sensitivity of the method, even extending it to single-molecule levels (Denk et al. 1990; Eigen and Rigler 1994; Maiti et al. 1997; Qian and Elson 1991; Webb 2001). A number of commercial instruments are now available which can carry out different types of FFS measurements; these include instruments from ISS (www.ISS.com), Zeiss (www.zeiss.com/micro), Olympus (www.olympusamerica.com), Leica (www.leica-microsystems.com), and Sensor Technologies LLC (Lake Hiawatha, NJ). Once the province solely of physicists and physical chemists, the availability of commercial FFS instruments, coupled with the explosion in the use of recombinant fluorescent proteins, is bringing FFS into the mainstream of cell biology.

In this brief overview we shall define and describe some of the more popular FFS methods presently being applied to problems of cellular dynamics. The particular methods we shall focus on include (1) fluorescence correlation spectroscopy (FCS), (2) scanning FCS (sFCS), (3) fluorescence cross-correlation spectroscopy (FCCS), (4) photon counting histogram (PCH) and fluorescence intensity distribution analysis (FIDA), (5) raster scanning image correlation spectroscopy (RICS), and (6) Number and Brightness (N&B) analysis.

Before beginning this discussion, however, we should mention the various ways in which fluorescent molecules are introduced into living cells. In rare cases one may be interested in the natural autofluorescence of the cell, but since our understanding of the origins of autofluorescence—besides the more obvious sources, such as the pyridinic and flavin coenzymes, lipofuscin, porphyrins, elastin, and collagen—are incomplete, FFS studies on autofluorescence are rare (see, however, Brock et al. 1998). Perhaps the most popular method, and the method most researchers would first consider, is the attachment of a naturally fluorescent protein to the target protein via genetic techniques. As most readers will appreciate, the number of fluorescent proteins now available is large and ever increasing (see, for example, Nienhaus and Wiedenmann 2009). Another genetic method finding application is the use of the so-called FlAsH or ReAsH tags, wherein a tetracysteine motif (such as CCPGCC) is attached to the protein of interest using standard genetic techniques, and then a profluorescent compound is microinjected into the cell that attaches preferentially to the genetically introduced motif, becoming fluorescent upon the attachment (Gaietta et al. 2002; Griffin et al. 1998). More recently, the method of bimolecular fluorescence complementation was introduced in which the DNA coding for a fluorescent protein (such as YFP or CFP) is split into two parts after which one part is attached to the one target protein and the complementary part is attached to another target protein (Kerppola 2008). If the two target proteins form a complex in the cell, one may find that the fully fluorescent protein can develop and provide the signal. Alternatively, one may simply label the purified target protein in vitro and then microinject some into the cell (Paradise et al. 2007).

Fluorescence correlation spectroscopy (FCS)

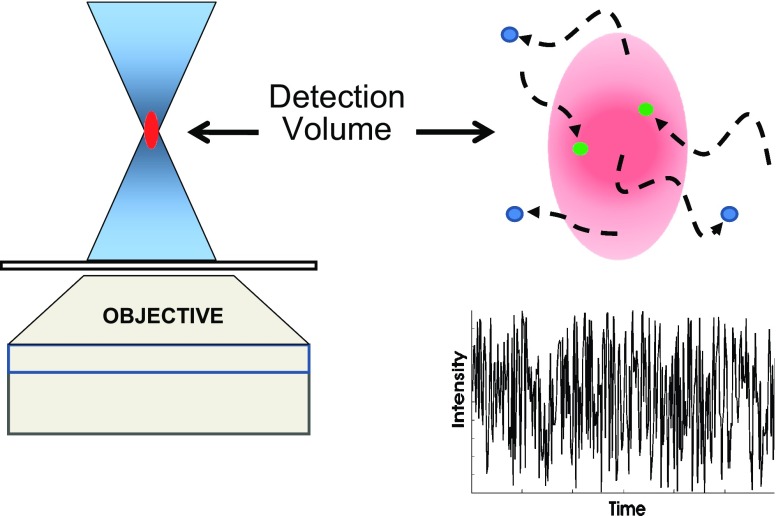
In an FCS measurement, the sample—whether in vitro or a living cell—is illuminated by a light source focused to a very small volume, typically on the order of 1 femtoliter or less. The fluorescence originating from particles diffusing in and out of the detection volume, which usually does not correspond to the entire illumination volume, is recorded. This concept is illustrated in Fig. 1. While in the illumination volume, the fluorescent particles may be excited more than once and may also undergo chemical or photophysical processes which alter their fluorescence properties. Examples of such processes are the “blinking” demonstrated by green fluorescent protein (GFP; Dickson et al. 1997; Nirmal et al. 1995) and by quantum dots (Yao et al. 2005) and alterations in fluorophore quantum yields upon binding to macromolecules (e.g., ethidium bromide binding to DNA). All of these considerations lead to fluctuations in the detected fluorescence signal. The data stream thus corresponds to the time course of the fluctuating fluorescence signal as depicted in Fig. 1.

Fig. 1.

A sketch illustrating excitation of a small sample volume and detection of emission from that volume. Also illustrated is the fluctuation in the fluorescence intensity to be expected as fluorophores diffuse into and out of the illumination/detection volume

Nowadays, FCS experiments are almost always conducted using a microscope. As in traditional confocal microscopy, the basic requirements for FCS microscopy are: a stable monochromatic excitation source, a high numerical aperture (NA) objective, dichroic and/or emission filters, and efficient photon detection [using either photomultiplier tubes (PMT) or avalanche photodiodes (APD)], combined with some additional electronics, such as autocorrelators, to process the data stream and appropriate software for data analysis. A stable excitation source is crucial because FCS experiments measure the time dependence of the signal fluctuation, and if there is a time-dependence inherent in the excitation intensity, that fluctuation will also be present in the recorded data. Technical aspects of the instrumentation, commercial and homebuilt, used to acquire FCS data have been reviewed many times and shall not be repeated here. Readers interested in such technical information are referred to more specialized discussions (such as those given in Berland et al. 1995; Borejdo 1979; Bulseco and Wolf 2007; Dertinger et al. 2008; Hess and Webb 2002; Lieto et al. 2003; Schwille et al. 1997a). For discussions of FCS applied to total internal reflection fluorescence (TIRF), the reader should see Lieto et al. (2003) and Ries et al. (2008). We should note that in order to extract diffusion rates from the FCS data, the precise shape of the detection volume, termed the point spread function (PSF), must be known (for an excellent discussion of point spread functions, the reader should view the lecture by Unruh and Colyer given at the 2006 Advanced Fluorescence Workshop and available on the website of the Laboratory for Fluorescence Dynamics at http://www.lfd.uci.edu/workshop/2006). Typically, FCS practitioners do not determine the PSF directly but, rather, a standard of known diffusional rate, such as fluorescein or rhodamine, is used to calibrate the system. In the literature one often sees a “standard” diffusion rate of 300 µm² s⁻¹ assigned to these fluorophores—yet this value appears to be anecdotal. Recent careful determinations of diffusional rates of various xanthene-based dyes (fluorescein, rhodamine, Alexa) suggests that a value near 430 µm² s⁻¹ would be more accurate (Müller et al. 2008; Petrasek and Schwille 2008).

One technical aspect that warrants consideration from the beginning is the use of either one- or two-photon excitation. In principle, FCS and the other fluorescence fluctuation techniques can be conducted using either excitation mode, but some practical considerations influence the use of one over the other. With one-photon excitation and confocal optics, all fluorophores exposed to the illumination beam are excited, but only the emission from those at the focal spot is detected. Out-of-focus fluorescence is eliminated by spatial filtering through a pinhole at a position which is confocal to the focal spot within the sample. In two-photon excitation, a very high local photon density [usually at near infra-red (IR) wavelengths] is achieved at the focal spot of the objective, and fluorophores can experience two-photon absorption, essentially the simultaneous absorption of two photons resulting in excitation of the fluorophore to the first excited singlet state, normally achieved via a one-photon process (for discussions of multiphoton methods and of two-photon cross-sections of various fluorophores, see Bestvater et al. 2002; Kim and Cho 2009; Pawlicki et al. 2009). As such, there is no need for a pinhole since fluorophores outside of the focal spot are not excited. Two-photon excitation is increasingly popular in FFS work on cells due to (1) its inherent optical sectioning, i.e., confocal aspect, (2) the fact that photo-toxicity of the out-of-focus near-IR illumination is generally much lower than that of one-photon excitation, and (3) the ability to eliminate Rayleigh or Raman scatter from the observed emission. Also, the illumination volume generated by two-photon excitation can be facilely placed almost anywhere within the cell. A typical PSF for two-photon excitation resembles an ellipsoid, being around 0.3 µm in the XY directions and 1.5 µm in the Z direction. Of course, there is one great advantage of one-photon excitation sources (such as laser diodes or small gas lasers) versus two-photon sources, namely cost. Two-photon sources have become smaller physically over the years, but they still remain very expensive.

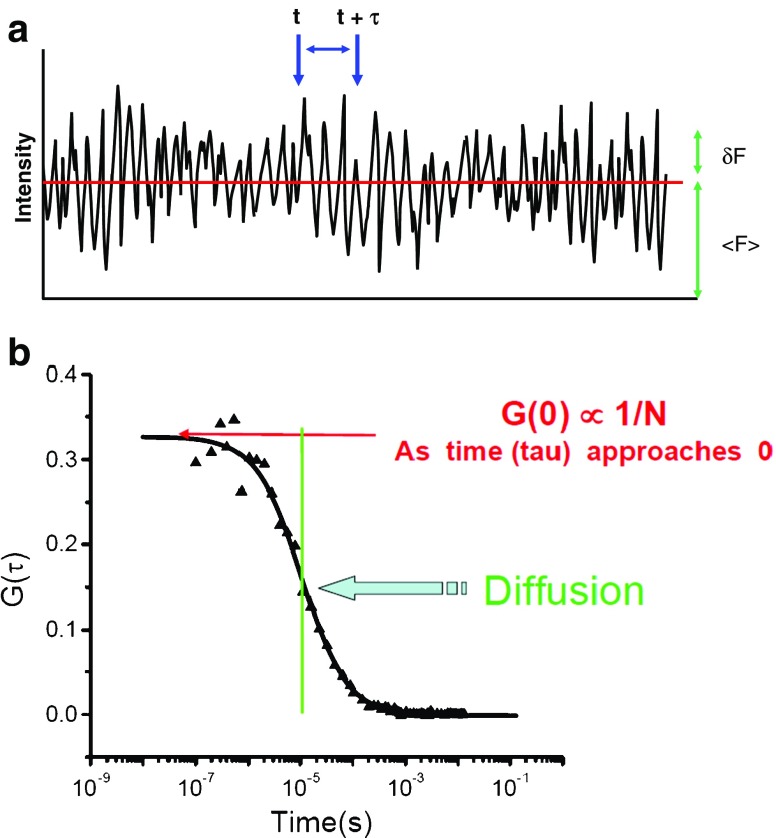
An FCS data stream can be treated in different ways—but in this section we shall only consider the autocorrelation function, G(τ). The autocorrelation function is essentially the time-dependent decay of the fluorescence intensity fluctuations. Consider the data stream depicted in Fig. 2. The average fluorescence intensity in the data stream is termed <F(t)>, while the variation of any point from the average is termed δF(t). To calculate the autocorrelation function, G(τ), one multiplies the intensity at some time, t, with the intensity at a later time, t + τ, as illustrated in Fig. 2. The average of the product of these two intensities is then divided by the square of the average fluorescence intensity for each value of τ.

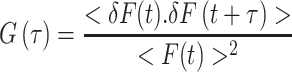1

Fig. 2.

a Fluorescence correlation spectroscopy (FCS) data intensity stream indicating the average intensity, <F(t)>, the deviation in intensity from the average at a particular time point, δF(t), and a time interval, t to t + τ. b Autocorrelation curve indicating the characteristic diffusion time of the curve and the value of the autocorrelation function extrapolated to τ = 0, i.e. G(0), which is proportional to the reciprocal of the number of particles, N. (The authors acknowledge Enrico Gratton for sketch B, which is from his lecture in the 2007 Advanced Fluorescence Workshop presented by the Laboratory for Fluorescence Dynamics)

As this calculation is made over many τ values, one eventually builds up an entire autocorrelation curve, as shown in Fig. 3. It is easy to understand why an autocorrelation curve has this general shape. Namely, when the signals at times close to one another are multiplied, they are likely to have nearly the same absolute magnitude, since it is likely that the fluorescent particle has not diffused far between the two moments in time. Hence, the shorter the time intervals in which the signals are compared, i.e., t to t + τ, the more likely they are to be correlated. However, as the interval between these two points increases, it is less likely that the signals will correlate, which will result in a decrease in the autocorrelation function.

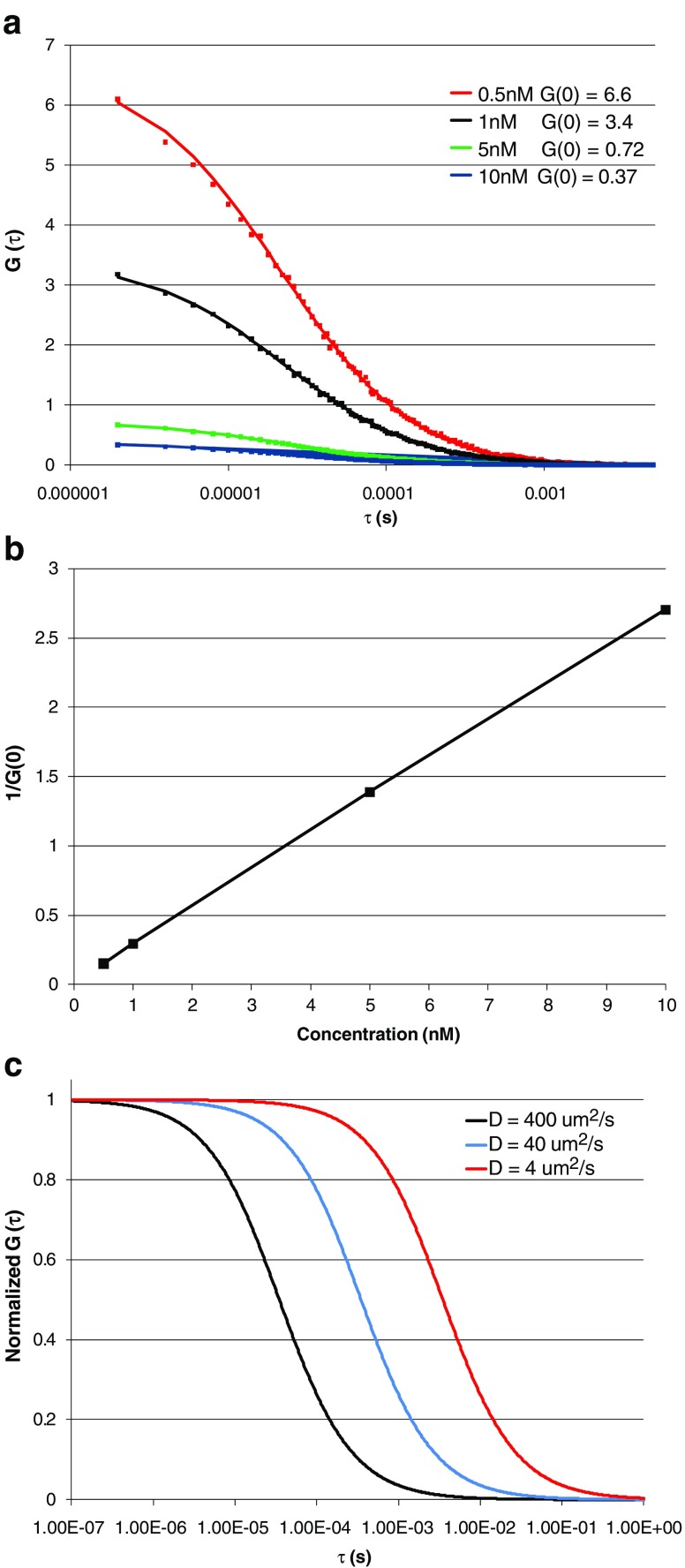
Fig. 3.

a Autocorrelation curves obtained for aqueous solutions of rhodamine 110 (Rh 100) at 22°C. The concentrations used are indicated on the figure. Squares indicate experimental data while solid lines represent the fit of the data to a Gaussian–Lorentzian point spread function (PSF) with the diffusion constant of 430 µm² s⁻¹. Data were acquired on an ISS Alba FCS spectrometer (www.ISS.com) using 800 nm excitation from a Chameleon Ti:Sapphire laser (Coherent, Santa Clara, CA). b Plot of the reciprocal of G(0) (which is proportional to <N>) as a function of Rh 110 concentration. Note that the calculated 1/G(0) values vary in proportion to the fluorophore concentration, as expected. c Simulation of the autocorrelation function of molecules with different diffusion coefficients with the G(0) normalized to 1

Alternatively, the autocorrelation function may be calculated using Fourier transforms. This approach has the advantage that it is much less computationally intensive, particularly for large data sets.

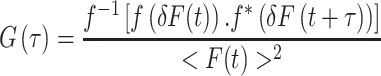2

where f is the Fourier transform, f ⁻¹ is the inverse transform, and f* is the complex conjugate. If the excitation volume and shape are known, one can relate G(τ) to the translational diffusion of the target molecule. For the case of a three-dimensional (3D) Gaussian excitation volume:

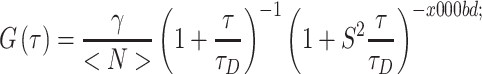3

where γ is a geometric scaling factor [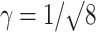 for one-photon 3D Gaussian or 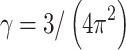for two-photon Gaussian–Lorentzian], <N> is the average particle number, τ_D is the characteristic diffusion time of the particle, also termed the residence time, and S = ω/z is the ratio of the axial/radial dimensions of the observation volume. Since the characteristic diffusion time, τ_D, is related to the diffusion coefficient, D, by 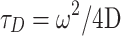, the autocorrelation function thus leads directly to the diffusion rate of the target molecule, which in turn provides information on the size of the molecule via the Stokes–Einstein–Sutherland equation:

4

where k is Boltzmann’s constant, T is the absolute temperature, η is the viscosity of the solvent, and r is the Stokes radius of the particle.

We should note another very important feature of FCS data, namely that the method permits determination of the absolute concentration of the target fluorophore in the illumination/detection volume. Although this parameter may be obvious when dealing with homogeneous solutions of known concentration, it is extremely difficult to obtain when working with living cells and may be an important parameter in such studies.

For many years, diffusion rates were the main point of the experiment. Diffusion rates, for example, provided information on the interaction of the fluorophore with other molecules, as in the case of the original use of the method, ethidium bromide binding to DNA. As the method matured and as instrumentation became commercially available, an increasing number of in vitro studies appeared. Since this review is primarily concerned with applications of FFS to cells, we shall not give detailed descriptions of such in vitro applications. However, since many in vitro FCS studies illustrate the type of problems which can be studied with the method and may hold interest to some readers, we provide a brief, though obviously incomplete, list of such studies.

1. The association and dissociation kinetics of the interaction of α-bungarotoxin with detergent solubilized nicotinic acetylcholine receptors (AChR) of Torpedo californica was studied by Rauer et al. (Rauer et al. 1996).

2. The aggregation of α-synuclein, which plays a key role in Parkinson’s disease, was studied by Gerard et al. (Gerard et al. 2006; Humpolickova et al. 2006) and the binding of α-synuclein to lipid vesicles was quantified by Rhoades et al. (Rhoades et al. 2006).

3. Prion aggregation has been investigated by Riesner (2001) (Elson Rigler book).

4. Aggregation of β-amyloid-peptide using FCS has been reported by several groups, including Tjernberg et al. (Tjernberg et al. 1999) and Garai et al. (Garai et al. 2007).

5. Hazlett et al. (Hazlett et al. 2005) reviewed the use of FCS to quantify antigen–antibody interactions.

6. Sanchez et al. (Sanchez et al. 2001) described the use of two-photon FCS to follow the interaction of a phospholipase with single-lipid and mixed-lipid giant unilamellar vesicles.

7. The activation of fibrinogen by thrombin and the early stages of the aggregation of fibrin monomers into fibrin polymers was followed by Bark et al. (Bark et al. 1999).

8. Orden and Jung (Orden and Jung 2008) reviewed the application of FFS methods to study nucleic acid hairpin conformations in aqueous solutions.

9. Anomalous diffusion in highly concentrated random-coiled polymer and globular protein solutions, imitating the crowded cellular environment, was studied by Banks and Fradin (Banks and Fradin 2005).

10. Sengupta et al. (Sengupta et al. 2003) carried out theoretical and experimental studies on errors in FCS measurements and, in particular, demonstrated a method for extracting information on distributions of diffusion rates for highly heterogeneous systems.

11. Sanchez et al. (Sanchez et al. 2004) used FCS and brightness analysis (vide infra) to study the dimer–monomer dissociation of αβ tubulin induced by guanidinium hydrochloride.

12. Sanchez and Gratton wrote an excellent review (Sanchez and Gratton 2005) of the application of two-photon FCS to study lipid–protein interactions in giant unilamellar vesicles.

13. FCS methodologies are also now being implemented in high throughput screening—see, for example, Komura et al. (2005) and Sugiki et al. (2009)

14. We also note a series of theoretical studies by Földes-Papp (Földes-Papp 2006, 2007a, b), which present thought-provoking discussions of “true” single molecule FCS approaches.

The use of the autocorrelation function for studies in living cells, however, is more limited. The technique is certainly useful for certain applications, such as the binding of ligands to receptors on the cell surface. An excellent review of this area has been written by Briddon and Hill (Briddon and Hill 2007) who describe many such studies, including binding to GABA(A) receptors on hippocampal neurons (Meissner and Haberlein 2003), binding of proinsulin C-peptide to intact and detergent solubilized human skin fibroblasts (Henriksson et al. 2001), and transferrin binding to human transferrin receptor (Schuler et al. 1999), to mention but a few. As more FCS studies on living cells began to appear, however, it became clear that the diffusional rates of many proteins in cellular interiors were much slower than expected. Studies in the 1980s and 1990s on the cellular interiors, using a variety of techniques, had suggested that the translational diffusion of proteins in the crowded milieu of the cytoplasmic environment was about threefold slower than that expected in water. As more sophisticated cell imaging methods became available, however, the existence of networks of diffusional barriers became more evident (reviewed by Luby-Phelps 1994). It now appears that—with few exceptions—the translational diffusions of proteins in the cell interior are significantly slower than one expects from a simple consideration of the molecular mass. An examination of thousands of proteins in yeast cells has shown that the translational diffusion rates, measured by FCS, are much slower than the theoretical values, both in the cytoplasm and in the nucleus (the recording of a lecture on Proteosome-Wide Fluctuation Analysis on Saccharomyces cerevisiae by Winfried Wiegraebe, presented at the 2008 Weber Symposium, can be viewed at http://www.lfd.uci.edu/weber/symposium/2008/). A recent study from the Berland lab (Wu et al. 2009b) bears on these issues. Namely, these researchers studied the intracellular dynamics of nuclear import receptors (karyopherins), both wildtype and mutants [expressed as enhanced (E)GFP constructs], in human embryonic kidney cells, using both classic autocorrelation functions and brightness analysis (described below). They observed that karyopherins had two- to fivefold lower diffusion coefficients in cells than calculated based on their molecular weights and on the diffusion coefficient of EGFP in cells. This reduction in the diffusional rates indicated that the karyopherins are associated with huge (mega-Dalton) complexes, and not just with their cargo. Brightness analysis showed that the karyopherins were monomeric at all observed concentrations—from 100 to 1000 nM—and thus the slow diffusion was not due to receptor aggregation. Using FCS, Paradise et al. (2007) also noted the reduced mobility of nuclear transport proteins, both in the cytoplasm and in the nucleus, and also used photobleaching methods to ascertain the contribution from an immobile fraction. Dross et al. (2009) studied the diffusion of EGFP in cell interiors and also present a useful discussion of the FCS-specific artifacts typically encountered in live cell studies as well as strategies for minimizing them.

Scanning FCS

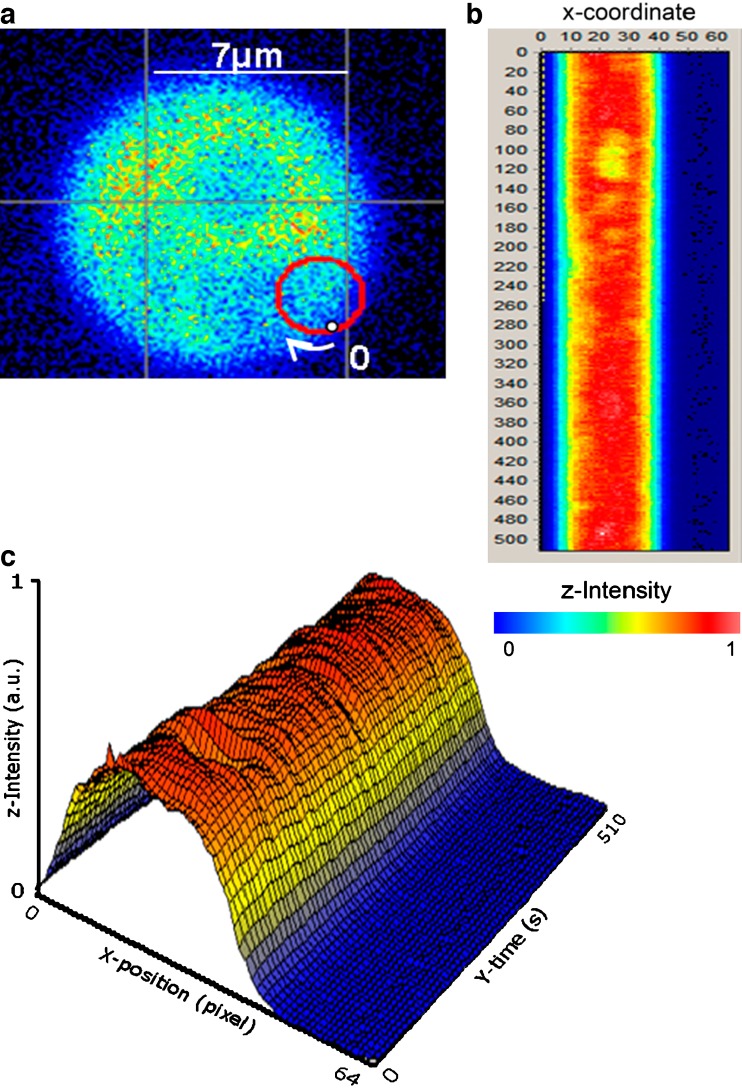
A particular variant of FCS that deserves mention is scanning FCS (sFCS). By sFCS, we do not mean simple raster-type scanning of a laser to accumulate an image. Rather, we refer to the method of scanning the excitation in a particular pattern—usually circular, but sometimes a simple line scan—while obtaining FCS data at each point along the scan. Although the earliest implementations of the scanning approach to FFS utilized fixed illumination and a translating sample stage (Petersen et al. 1986; Weissman et al. 1976), present-day scanning is almost always accomplished by keeping the sample stationary while scanning the laser (see, for example, Berland et al. 1996; Ruan et al. 2004; Skinner et al. 2005). The sFCS method is particularly useful in cases wherein it is difficult to localize the excitation beam precisely in a target area—for example, a membrane. By scanning across the membrane, one is sure to have the beam traverse the target area, and if a circular scan is utilized, the beam will cross the membrane twice during each scan. The data stream can then be presented as a “carpet” that renders evident which data are associated with particular regions. An example of a circular scan and the associated carpet is shown in Fig. 4 (obtained from Garcia-Marcos et al. 2008). In this case, different ribosomal stalk proteins were linked with EGFP, and the image of the resulting yeast cell is shown in Fig. 4a along with a red circle depicting the scan. The “carpet” corresponding to the scan is shown in Fig. 4b with the X-coordinate displaying the number of the scan and the Y-coordinate displaying the time along a particular scan. For each line in the “carpet”, PCH analysis (discussed below) was carried out to determine how many EGFP-labeled proteins were in each ribosome, which addressed the question of the distribution of different stalk proteins among the ribosome population in the living yeast cell. One should note that the diffusional rate of the target fluorophore should be slower than the orbital scanning rate to avoid biasing the recovered diffusion coefficient. Recently, Ries et al. (2009) used line-scan FCS (the data are collected along a single scan line) to obtain the diffusion coefficients and absolute concentrations of probes associated with biological membranes, while Petrasek et al. (2008) utilized scanning FCS to study the dynamics of the PAR-2 protein in the cytoplasm and on the cortex of Caenorhabditis elegans eggs before asymmetric cell division.

Fig. 4.

a Intensity image of a yeast cell expressing enhanced green fluorescent protein (EGFP)-labeled ribosomal stalk proteins. The scanning orbit is depicted by the red circle (radius 1.52 µm). The point labeled 0 corresponds to the beginning of the scan (point 0 in the X-position column in the ‘‘carpet’’) and the end of the scan (point 63 in the X-position column in the ‘‘carpet’’). b XY transformation of the raw scanning FCS. The X-position columns represent points along one circular scan, and the Y-position rows represent successive scans, with each scan taking 1 ms. The color scale indicates the relative intensities of the sections, with orange being the most intense and blue corresponding to intensities outside of the cell. Data were acquired at 64 kHz. c The time–intensity–position data of the ‘‘carpet’’ shown in b are replotted as a surface. The intensity–color scale is the same. (From Garcia-Marcos et al. 2008)

We note that an excellent source of information on RICS and other advanced FCS approaches, such as scanning FCS and N&B analysis (discussed below), can be found on the website for the Laboratory for Fluorescence Dynamics, and in particular on the sites presenting the lectures from the annual advanced workshops: http://www.lfd.uci.edu/workshop/.

Fluorescence cross-correlation spectroscopy

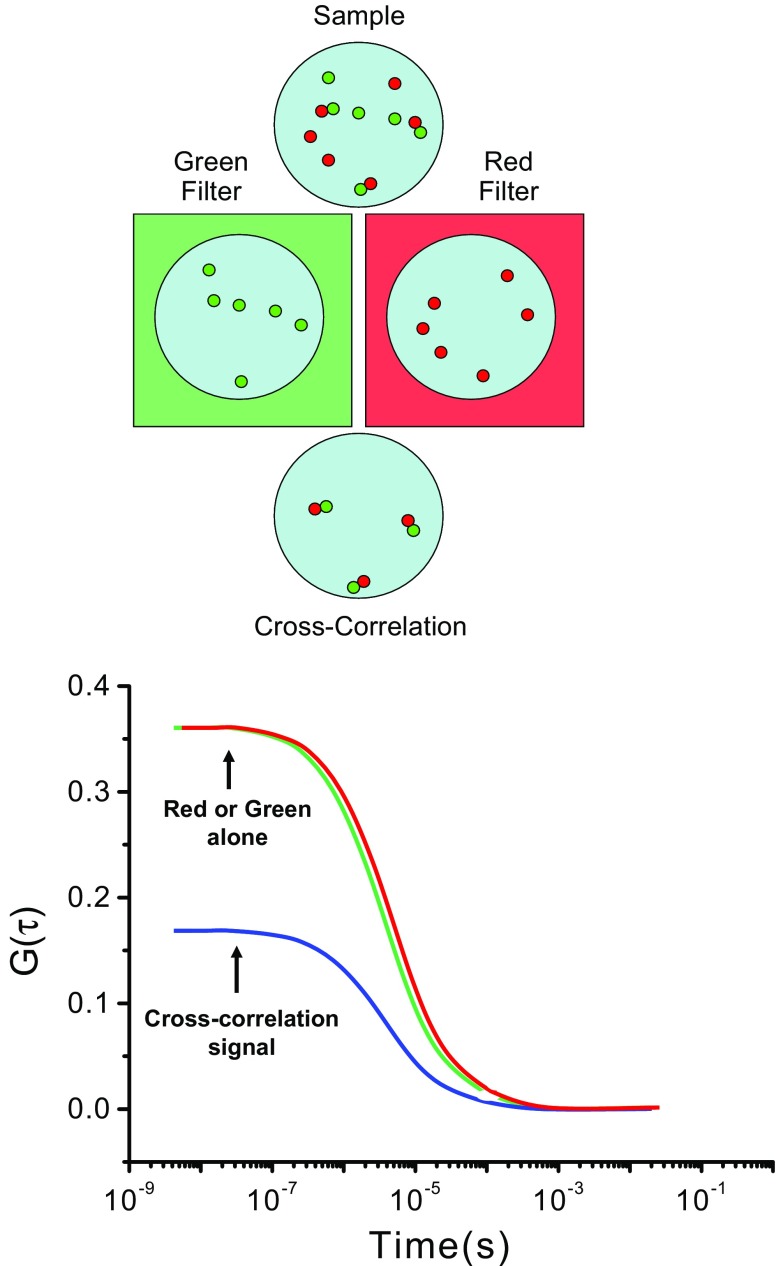
The suggestion that the signals from two different fluorophores, associated in some manner, could be followed by cross-correlation was first made by Rigler and Eigen (Eigen and Rigler 1994), and the first experimental realization of this approach was made by Schwille et al. (1997b). In the original manifestation of this method, two different laser beams, of two different wavelengths, were used in a one-photon mode to excite two different fluorophores. The development and wide-spread utilization of two-photon lasers has greatly simplified the FCCS approach since typical fluorophores have sufficiently broad two-photon absorption cross sections, such that one excitation wavelength can effectively excite two different fluorophores. An example of this approach is given in Fig. 5. As indicated, the sample has two different fluorophores, indicated as red and green, whose emission can be separated by appropriate filters. The most common applications in cells utilize different fluorescent proteins, such as EGFP and mCherry. Each fluorophore will give rise to its own distinct autocorrelation curve, but it is also possible to cross-correlate the signals. In other words, the signal at one particular time for fluorophore 1 can be correlated with the signal at a different time for fluorophore 2. If the two fluorophores are in some way linked, then the resulting cross-correlated signal will show correlation, as indicated in Fig. 5. (For examples and reviews of this approach, see Berland 2004; Bacia et al. 2002 , 2006; Bacia and Schwille 2003; Hwang and Wohland 2007; Rarbach et al. 2001; Ruan and Tetin 2008; Weidtkamp-Peters et al. 2009.) The great advantage of this approach over fluorescence resonance energy transfer (FRET) methods commonly used to determine the proximity of fluorophores is that there is no requirement regarding the orientation or distance between the fluorophores. All that is required is that the movements of the two fluorophores are associated.

Fig. 5.

Illustration depicting a dual color cross-correlation scenario. A sample containing both “green” and “red” proteins can be viewed through green or red filters that pass only one color. In this case, since the number of proteins and their diffusion rate are shown to be the same, the autocorrelation curves for data acquired through either green or red filters should look similar. When the green and red signals are cross-correlated, however, only the dimers containing both green and red proteins will contribute to the cross-correlated signal

Photon counting histogram/fluorescence-intensity distribution analysis

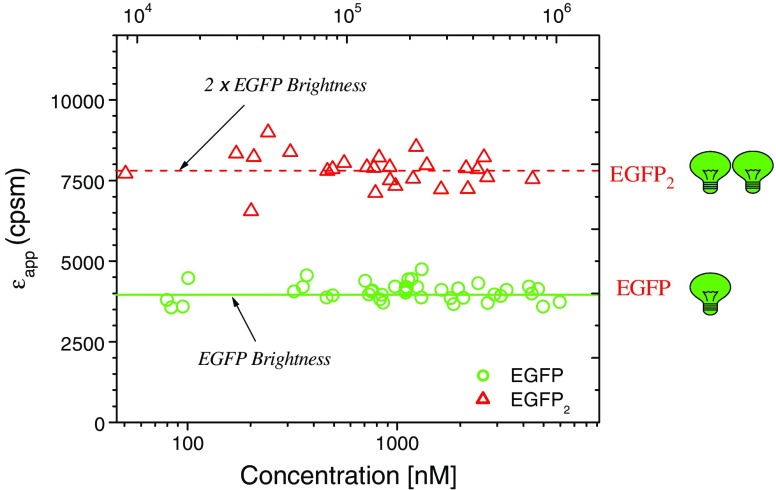
Although the kinetics or temporal behavior of fluorescence fluctuations is best described by the autocorrelation function, the intensity of these fluctuations may also be analyzed in terms of a distribution. Initial approaches to this problem were presented by Palmer and Thompson (1987, 1989). Qian and Elson (1990a, b) then developed a technique based on the analysis of first and second moments of the photon counts. In 1999, two groups, from the USA and Germany independently extended this approach (Chen et al. 1999; Kask et al. 1999). The two groups named their methods photon counting histogram (PCH) (Chen et al.) and fluorescence-intensity distribution analyisis (FIDA) (Kask et al.). In 2004, Müller developed the related fluorescence cumulant analysis (FCA) approach (Müller 2004). All of these methods rely on the determination of the inherent “brightness” of a fluorophore, i.e., the actual counts per second per molecule (CPSM), which depends, of course, on the specific illumination and detection conditions of the particular experiment. The utility of the brightness approach to study protein complexes in living cells has been demonstrated by several groups (Chen et al. 2003; Chen and Müller 2007; Garcia-Marcos et al. 2008; Wu et al. 2009a, b). An illustration of the brightness principle is shown in Fig. 6 (taken from J. Müller; redrawn from Chen et al. 2003). In a recent tour de force of the application of brightness analysis, Chen et al. (2009) used the method to determine the stoichiometry of HIV-1 Gag proteins in viral-like particles (VLP) in COS-1 cells—finding values ranging from 750–2500, while the size of the VLPs remained relatively constant, as measured by the diffusion coefficients, which fit to a hydrodynamic diameter of 130 nm.

Fig. 6.

Molecular brightness of EGFP and EGFP₂ as a function of average photon count rate and protein concentration. Note that the brightness levels are independent of concentration. Each data point represents the brightness measured in different cells expressing either EGFP or EGFP₂. (Adapted from Chen et al. 2003)

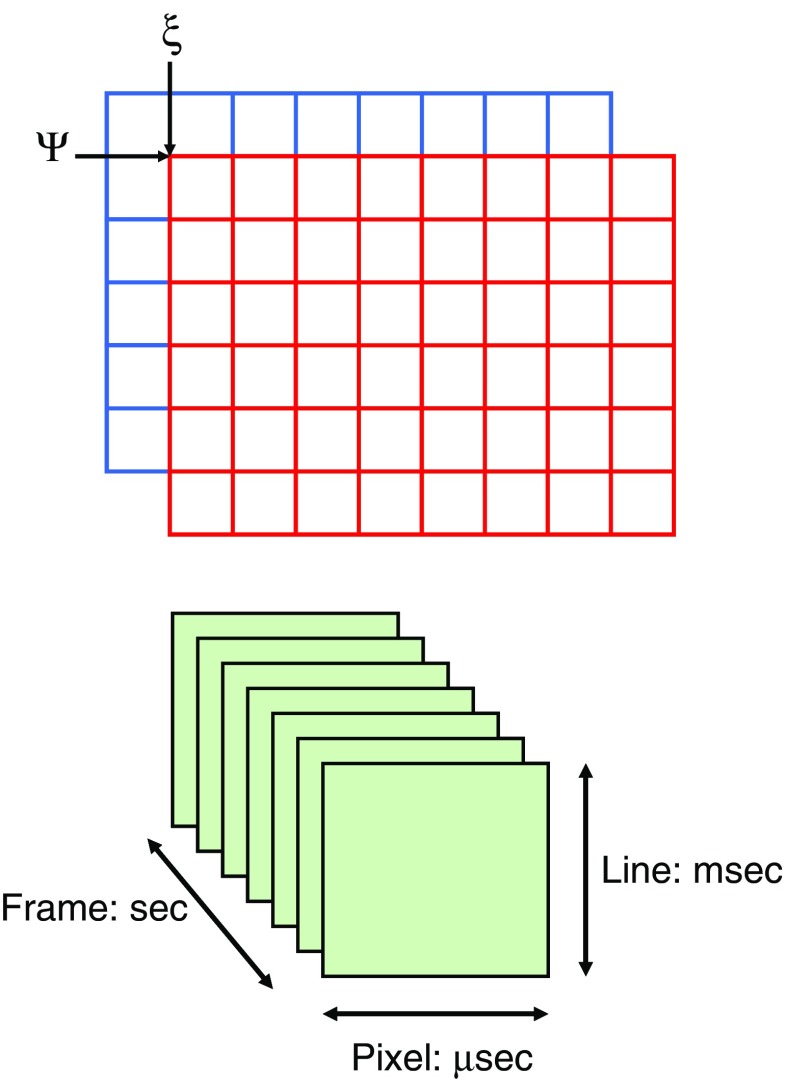
Raster scanning image correlation spectroscopy

Raster scanning image correlation spectroscopy (RICS) is one form of image correlation spectroscopy (ICS). The latter was originally developed by Nils Petersen (Petersen 1986; Petersen et al. 1986) as an image analog of traditional FCS. In ICS, spatial autocorrelations are calculated from stacks of images obtained in a time-series. This method was extended in Enrico Gratton’s lab (Digman et al. 2005a, b; Digman and Gratton 2009) to use a laser-scanning microscope to probe the time structure in images to spatially correlate pixels separated by microseconds (adjacent pixels in a line), milliseconds (pixels in successive lines), and seconds (pixels in different frames). Many other variants of the ICS method have appeared including TICS, ICCS, STICS, kICS, and PICS, and the bewildered reader should consult the excellent review by Kolen and Wiseman (Kolin and Wiseman 2007), which will guide him/her through this acronym jungle. The diffusion of a particle in a uniform medium can be described by the relation:

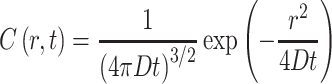5

where C(r, t) represents the concentration of the particle at position r and time t, and D is the diffusion coefficient. In a RICS experiment, we are concerned with the spatial aspect. In this method, the spatial autocorrelation is similar to the time-dependent autocorrelation function carried out in traditional FCS except that the correlation is carried out on different spatial points in the image, as illustrated in Fig. 7. In this case, the autocorrelation is defined as:

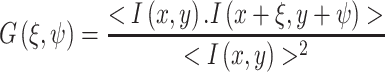6

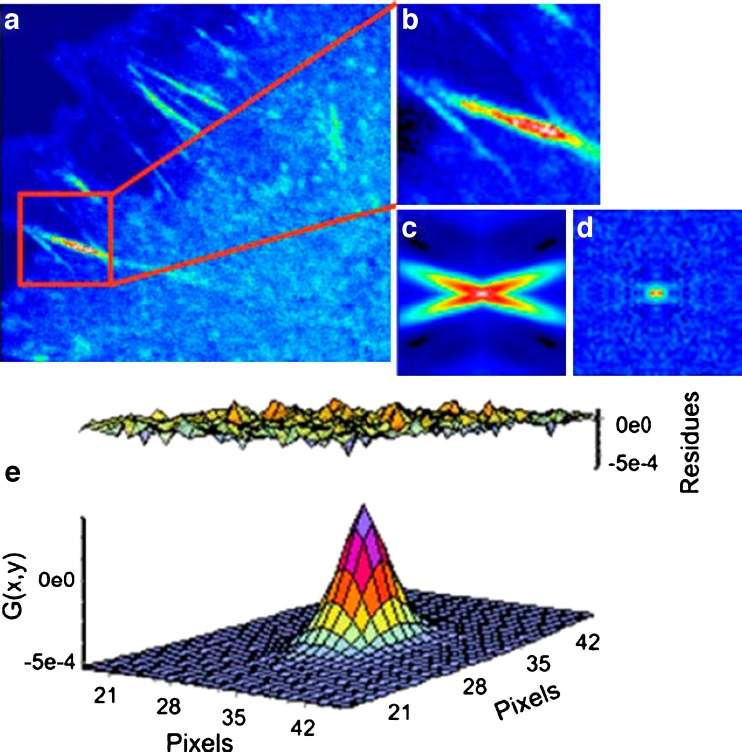
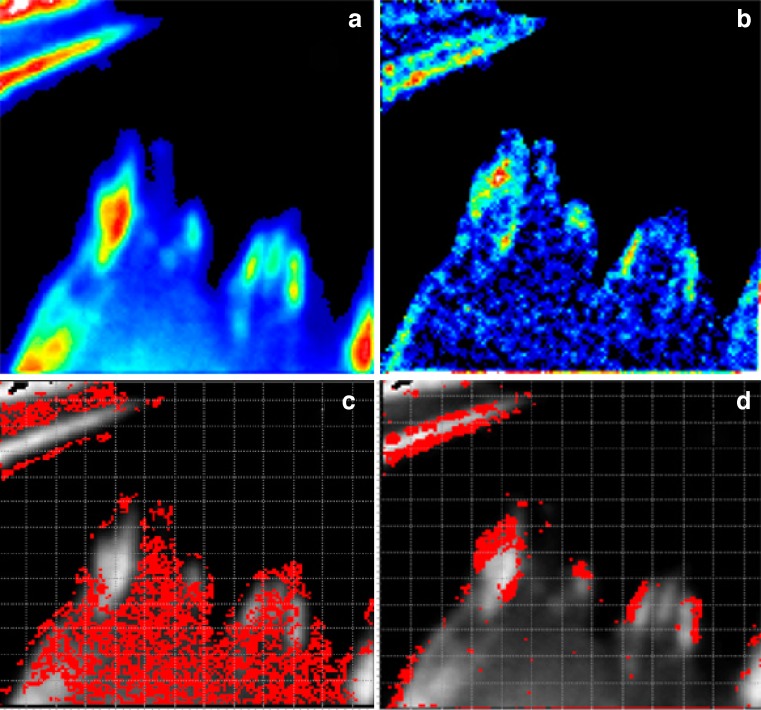
where ξ and ψ represent the spatial increments in the x and y directions, respectively, which are correlated. Spatial correlation functions are illustrated in Fig. 8b–e. One must bear in mind that in a RICS experiment the scan rate must be compatible with the diffusion being examined, or for that matter with any process which affects this diffusion. Details on this consideration can be found in the initial publications by Digman et al. ( 2005a, b). An example of a RICS analysis is shown in Fig. 8 from Digman et al. (2008a). As shown, an important aspect of the RICS method is that it permits the subtraction of immobile components and hence allows one to better quantify dynamic aspects of the system. In the paxillin study, the authors were able to study the assembly and disassembly of paxillin aggregates at focal adhesions in various loci in the cell. A recent study by Gielen et al. (Gielen et al. 2009) used the RICS approach to measure the diffusion of lipid-like probes in artificial and natural membranes.

Fig. 7.

Sketch illustrating the multiple-shifting operation carried out to calculate a spatial correlation function. The time scale associated with each aspect of an image is also shown. Typically, 50 to 100 frames are required for a raster scanning image correlation spectroscopy (RICS) analysis

Fig. 8.

a Image of a CHO-K1 cell expressing paxillin–EGFP. b 64 × 64 subframe in the cytosolic part of a focal adhesion structure. c, d Spatial autocorrelation before (c) and after (d) the subtraction of immobile structures. e Fit of the spatial correlation function in d. The diffusion coefficient in this cell region is 0.49 µm² s⁻¹. (From Digman et al. 2005a)

Number and brightness

The number and brightness (N&B) approach to image analysis was recently introduced by Enrico Gratton’s laboratory (Digman et al. 2008b, 2009). This technique can be applied to images acquired using confocal microscopy or TIRF (Unruh and Gratton 2008) as long as the pixel dwell time is less than the characteristic diffusion time of the particle. The N&B approach can be considered the imaging equivalent of the PCH method; however, N&B does not require a non-linear fit of the data, and the average particle number <N> and particle brightness B are extracted directly from the image intensity data.

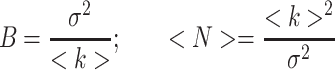7

where <k> = Σk_i-/M is the average number of counts, k is the number of counts for each image i, M is the total number of images, 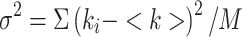is the variance of the number of counts. This analysis is carried out for each pixel. However there is also a contribution to the variance of the signal due to the shot noise of the detector; thus, the true number of molecules, n, and brightness, ε, are given by:

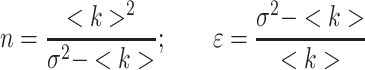8

It should be noted that the PCH method requires acquisition of a large number of photons at each point for reasonable precision of the oligomeric state of the target molecule and as such does not readily lend itself to image analysis. The N&B approach, although not as precise at each pixel in the image as the PCH method, nonetheless allows for a rapid estimation of aggregate size. The general concept is illustrated in Fig. 9 (modified from Digman et al. 2008a). The N&B approach has thus far only been applied to relatively few biological systems. One of the more recent applications was by Sanabria et al. (2008) who used N&B and RICS to investigate the effect of calcium on eGFP–calmodulin and its interaction with other cellular proteins.

Fig. 9.

An example of number and brightness (N&B) analysis from Digman et al. (2008b). Paxillin–EGFP was expressed in CHO-K1 cells. a Image intensity map showing paxillin accumulating at focal adhesions (image size 31 × 31 μm). b Brightness image showing that larger B values are at the borders of some adhesions. c All pixels having brightness values of 1150 counts/s/molecule (corresponding to EGFP monomers) are selected. Note that these points accumulate in the cytosol. d All pixels of 11,500 counts/s/molecule are selected. Note that these pixels are at the borders of the adhesions

Closing remarks

The preceding discussion has briefly covered several of the FFS methods currently being applied to cell biology. These techniques are becoming ever more accessible to biologists as commercial instrumentation becomes less expensive and as specialized workshops and courses teaching the latest methodologies reach increasing numbers of students. Given these considerations, coupled with the continual appearance of new and exciting genetic and molecular biological manipulations, one can expect ever increasing applications of FFS in the life sciences. We hope this review will motivate some readers to learn more about this exciting area and to consider using FFS to shed light on their favorite biological mystery.