Multiply robust inference for statistical interactions

Abstract

A primary focus of an increasing number of scientific studies is to determine whether two exposures interact in the effect that they produce on an outcome of interest. Interaction is commonly assessed by fitting regression models in which the linear predictor includes the product between those exposures. When the main interest lies in the interaction, this approach is not entirely satisfactory because it is prone to (possibly severe) bias when the main exposure effects or the association between outcome and extraneous factors are misspecified. In this article, we therefore consider conditional mean models with identity or log link which postulate the statistical interaction in terms of a finite-dimensional parameter, but which are otherwise unspecified. We show that estimation of the interaction parameter is often not feasible in this model because it would require nonparametric estimation of auxiliary conditional expectations given high-dimensional variables. We thus consider ‘multiply robust estimation’ under a union model that assumes at least one of several working submodels holds. Our approach is novel in that it makes use of information on the joint distribution of the exposures conditional on the extraneous factors in making inferences about the interaction parameter of interest. In the special case of a randomized trial or a family-based genetic study in which the joint exposure distribution is known by design or by Mendelian inheritance, the resulting multiply robust procedure leads to asymptotically distribution-free tests of the null hypothesis of no interaction on an additive scale. We illustrate the methods via simulation and the analysis of a randomized follow-up study.

1 Introduction

A primary focus of an increasing number of scientific studies is to determine whether two given exposures interact to produce their effect, i.e. to determine whether the effect of one exposure is modified by the second. For instance, in many longitudinal studies, the question of whether the time evolution of the response differs for subjects with different baseline characteristics/interventions is of primary interest. In genetic association studies of complex disorders, the discovery of gene-enviroment and gene-gene interactions is of great interest, because most complex disorders are thought to be caused by numerous genes and environmental factors, a subset of which may act synergistically. The development of robust and powerful tests of gene-gene interaction is of special interest to geneticists, since, when the effect of one locus is modified by alleles at another locus, the power to detect a phenotypic association with the first locus can be greatly reduced unless the interaction is explicitly modelled (Cordell, 2002).

When the outcome is continuous or positive-constrained and uncensored, the presence of effect modification between exposures A₁ and A₂ is commonly assessed by fitting a linear or loglinear conditional mean model for the outcome Y, in which the linear predictor includes the product between these exposures. To be specific, let X be a vector of measured pre-exposure variables such that conditioning on X suffices to control for confounding when estimating the effects of A₁ and A₂ on outcome Y. Then the term β* in the conditional mean model

$$E(Y\mid \mathbf{A},\mathbf{X})=g({\gamma }_0^{\ast }+{\gamma }_1^{\ast }{A}_1+{\gamma }_2^{\ast }{A}_2+{\gamma }_3^{{\ast }^{\prime }}\mathbf{X}+{\beta }^{\ast }{A}_1{A}_2)$$ (1)

with A = (A₁, A₂)’ and g (x) = x or g (x) = e^x known, encodes the degree to which exposure A₂ modifies the effect of A₁ on outcome (on the scale g), and vice versa. Specifically, the choice β* = 0 expresses that the effect of exposure A₁ on outcome is the same (on the scale g), regardless of the other exposure A₂. It thus encodes the absence of effect modification (on scale g). More generally, one may fit a conditional mean model of the form

$$E(Y\mid \mathbf{A},\mathbf{X})=g\left\{m(\mathbf{A},\mathbf{X};{\beta }^{\ast },{\gamma }^{\ast })\right\}$$ (2)

where

$$m(\mathbf{A},\mathbf{X};\beta ,\gamma )=q_3(\mathbf{A},\mathbf{X};\beta )+q_2(\mathbf{X},A_2;{\gamma }_2)+q_1(\mathbf{X},A_1;{\gamma }_1)+h(\mathbf{X};{\gamma }_0)$$

with g defined as before, with q₃ (A, X; β) a known function smooth in β and satisfying q₃ (A, X; β) = 0 when A₁A₂ = 0, with q₂ (X, A₂; γ₂), q₁ (X, A₁; γ₁) and h (X; γ₀) known functions smooth in $\gamma ={({\gamma }_0^{\prime },{\gamma }_1^{\prime },{\gamma }_2^{\prime })}^{\prime }$ (and γ₀, γ₁ and γ₂ variation independent parameters), satisfying q₁ (X, 0; γ₁) = q₂ (X, 0; γ₂) = 0, with β* ∈ R^p and γ* ∈ R^q unknown parameters and with the joint law of (A, X) unrestricted. In this model, the term q₃ (A, X; β) encodes the statistical interaction between exposures A₁ and A₂ (possibly as a function of X). Without loss of generality, we can require q₃ (A, X; β) to satisfy q₃ (A, X; 0) = 0 so that β* = 0 continues to encode the absence of statistical interaction. The functions q₂ (X, A₂; γ₂) and q₁ (X, A₁; γ₁) encode the main effects (possibly as functions of X) of the exposures A₂ and A₁, respectively. Finally, h (X; γ₀) encodes the main effect of the extraneous factors X. For instance, model (1) is the special case in which q₃ (A, X; β) = βA₁A₂, q₂ (X, A₂; γ₂) = γ₂A₂, q₁ (X, A₁; γ₁) = γ₁A₁ and h(X; γ₀) = γ₀ + γ’₃X.

In observational studies, X will typically be high-dimensional with a number of continuous components. For instance, in genetic association studies, X might include a high-dimensional collection of substructure-informative loci (Epstein, Allen and Satten, 2007). This makes models for the main exposure effects q₂ (X, A₂; γ₂), q₁ (X, A₁; γ₁) and for the association h(X; γ₀) of extraneous factors X with outcome prone to misspecification. These models are not in themselves of scientific interest when the primary goal is to test for statistical interaction between the exposures A₁ and A₂. As such, standard tests of β* = 0 and inference for statistical interaction under the above model is less than satisfactory. This is so because standard tests for statistical interaction tend to be heavily sensitive to misspecification of the models for the main exposure effects (Greenland, 1993). In particular, they may fail to attain the nominal significance level when these nuisance models are misspecified. Similarly as demonstrated in the simulation study of Section 5, estimates of statistical interaction may be severely biased under misspecification of these nuisance models. As a consequence, in longitudinal studies, standard tests to determine whether the change in outcome mean over time depends on a particular baseline exposure may be compromised when the time evolution or main exposure effect is misspecified, or when important interactions with extraneous variables X have been neglected or mismodelled. In genetic association studies, tests for gene-gene or gene-environment interaction may be biased when the main effect of the gene/environment is incorrectly modelled (e.g. when a dominant genetic model was assumed but not appropriate) or interactions with extraneous confounders have been inadvertently omitted.

Our concern about the consequence of misspecifying the main exposure effects or the association between outcome and extraneous factors in statistical interaction tests is additionally motivated by a problem arising in the Sufficient-component cause framework (Rothman, 1976). It is well known that whether two variables statistically interact may depend on the particular model being used (e.g. on the chosen scale g in model (1)) (Mantel et al., 1977, Greenland, 1993). Specifically, two variables that have an interaction under one statistical model, may not have an interaction under a different model (e.g. with a different link function). When the outcome and exposures are dichotomous, it has been argued (Rothman, 1976; Koopman, 1981) that there is a natural, scale-independent way in which to assess the presence of interactions between two exposures, based on the Sufficient-component cause framework. This framework makes reference to the actual causal mechanisms involved in bringing about the outcome: when two or more binary causes participate in the same causal mechanism, it becomes proper to speak of Sufficient cause interactions. In recent work, VanderWeele and Robins (2007, 2008) derived various conditions which necessarily entail the presence of Sufficient cause interactions. When the exposure effects are assumed to be monotone (Greenland, 1993; VanderWeele and Robins, 2007), these conditions involve testing for effect modification on the risk difference scale. This scale suggests a Bernoulli regression model with linear link as the natural choice to test for sufficient cause interactions. Our interest in semiparametric tests now stems from the fact that such models are likely misspecified because for dichotomous outcomes they may not yield expected outcomes between 0 and 1. See the supplemental material (Vansteelandt et al., 2008) for further discussion of the relation between the estimators we derive below and interactions in the Sufficient cause framework (see also VanderWeele (2008)).

A number of approaches have been developed which avoid modelling the effects of extraneous factors and/or main exposure effects. Robins, Mark and Newey (1992) propose G-estimation which avoids modelling the effects of extraneous factors when a model is specified for the conditional mean exposure given these extraneous factors. Correlated data methods, such as conditional likelihood estimation (Verbeke, Spiessens and Lesaffre, 2001), regression of changes (Louis, 1988) and regression on within- and between-cluster effects (Neuhaus and Kalbfleisch, 1998) can be viewed as variants of this approach in the case of the linear link (Goetgeluk and Vansteelandt, 2007). However, all these approaches require a correct model for the main exposure effects.

In the context of longitudinal studies, Zeger and Diggle (1994) avoid modelling a main exposure effect (i.e. the time effect) via a backfitting algorithm which iterates between kernel estimation of the main time effect and generalized least squares estimation of the remaining parameters. When measurements are collected at discrete time points, Lin and Ying (2001) avoid nonparametric smoothing via a weighted least squares approach that is equivalent to G-estimation. Fan and Li (2004) relax these authors’ restriction of measurements being taken at discrete time points via an approximate regression of changes and profile least squares estimation. These approaches were specifically designed for longitudinal data and, with exception of the approximate regression of changes (Fan and Li, 2004), they require modelling the effects of extraneous factors X. Multivariate adaptive regression splines (MARS) (Friedman, 1991) and interaction spline models (Chen, 1994) avoid parametric modelling assumptions on all exposures and extraneous factors. Although well suited for high-dimensional problems, they still suffer from the curse of dimensionality when the predictor space is large.

In this article, we develop a novel semiparametric approach that can perform well in moderate sized samples even when X is high dimensional. In contrast to previous approaches, the performance guarantees offered by our new approach depend on the extent of prior knowledge concerning the joint exposure distribution f (A₁, A₂|X) conditional on the covariates. Previous approaches do not make use of information concerning this law; as described below, by incorporating such information our estimators have certain multiple robustness properties described in detail in the next section. By incorporating information on the joint conditional exposure distribution f(A₁, A₂|X), the class of estimators derived below also essentially encompasses a ‘propensity score’ approach to the estimation of interaction parameters.

Specifically suppose first that the joint law of A₁ and A₂ is known, as could be the case in either a clinical trial with A₁ and A₂ both randomly assigned or in a family-based gene-gene interaction study where the law of the genetic markers A₁ and A₂ is determined by Mendelian inheritance. In this setting, when g is the identity link, our approach delivers consistent and asymptotically normal (CAN) estimators of the interaction β* and an asymptotically distribution free (ADF) test of the hypothesis β* = 0 of no interaction, even when the models q₂ (X, A₂; γ₂), q₁ (X, A₁; γ₁), h(X; γ₀) are all misspecified. In contrast, we prove that, even with f (A₁, A₂|X) known, if the vector X has a continuously distributed component and none of the models q₂ (X, A₂; γ₂), q₁ (X, A₁; γ₁), h(X; γ₀) is guaranteed to be correct, it is impossible to obtain either a CAN estimator of β* or an ADF test of no interaction when g is the exponential function.

Suppose next A₁ and A₂ are correctly assumed to be conditionally independent given X so f (A₁, A₂|X)=f (A₁|X) f (A₂|X), but neither the models q₂ (X, A₂; γ₂), q₁ (X, A₁; γ₁), h(X; γ₀) nor models f (A₁|X; α₁) and f (A₂|X; α₂) (with α₁ and α₂ variation independent parameters) for f (A₁|X) and f (A₂|X) are guaranteed correct. This would often be the case in population-based gene-environment interaction studies of a genetic marker score A₁ and an environmental exposure A₂ or in a population-based gene-gene interaction study where the two genetic markers A₁ and A₂ are unlinked, provided Sufficient information on ethnicity and geographic origin, or on parental genetic markers are recorded in X to remove the effects of population stratification. In this setting, with g the identity link, we construct a CAN estimator of β* under a union model that assumes at least one of the following four statements is true: (i) the models f (A₁|X; α₁) and f (A₂|X; α₂) are both correct, (ii) the models q₂ (X, A₂; γ₂), q₁ (X, A₁; γ₁), h(X; γ₀) are all correct, (iii) the models f (A₁|X; α₁) and q₁ (X, A₁; γ₁) are both correct, or (iv) the models f (A₂|X; α₂) and q₂ (X, A₂; γ₂) are both correct. We refer to our estimation approach as quadruply robust as only one of (i)−(iv) need to hold to obtain a CAN estimator of β*. For g the exponential link, it is only triply robust, delivering CAN estimators of β* if at least one of (ii), (iii), or (iv) holds.

Finally suppose A₁ and A₂ are not known to be conditionally independent, given X, and we therefore specify a model f (A₁, A₂|X; α) = f (A₁|A₂, X; α₁) × f (A₂| X; α₂) that allows for conditional dependence. None of the models q₂ (X, A₂; γ₂), q₁ (X, A₁; γ₁), h(X; γ₀), f (A₁|A₂, X; α₁), f (A₂| X; α₂) is guaranteed correct. Then we shall see that, even for the identity link, quadruply robust estimators are not possible, because there do not exist compatible models f (A₁|A₂, X; α₁) and f (A₂|A₁, X; α₂) with variation independent parameters. Specifically in this setting, with g the identity link, we construct a CAN estimator of β* which we refer to as triply robust because it is CAN under a union model that assumes at least one of the following three statements is true: (i) the models f (A₁|A₂, X; α₁) and f (A₂|X; α₂) are both correct, (ii) the models q₂ (X, A₂; γ₂), q₁ (X, A₁; γ₁), h(X; γ₀) are all correct, (iii) the models f (A₁|A₂, X; α₁) and q₁ (X, A₁; γ₁) are both correct. For g the exponential link, our approach is also triply robust when (i) just above is replaced by the more restrictive condition that the models f (A₁|A₂, X; α₁), f (A₂|X; α₂) and q₂ (X, A₁; γ₂) are all correct.

In summary, because of the multiple robustness property enjoyed by our approach, we would recommend that, when X is high dimensional, it be used quite generally because an inference concerning an interaction e ect under our approach, unlike under previous approaches, has multiple chances, rather than only one chance, to be correct or nearly correct.

The paper is organized as follows. In Section 2 we introduce semiparametric statistical interaction models. These parameterize the statistical interaction between exposures A₁ and A₂ (on the chosen scale g) as a function of exposures and extraneous variables X in terms of a finite number of parameters, but leave the observed data law otherwise unrestricted. In particular, the proposed models leave the main effects of both exposures on the outcome unspecified, along with their interactions with extraneous variables. We examine properties of these models. We show that, due to the curse of dimensionality, no general ADF test for statistical interaction exists that is guaranteed to perform well in realisitic-sized samples because estimation of the interaction parameters requires the auxiliary estimation of conditional expectations given high-dimensional variables. We therefore introduce parametric models that we characterize as ‘working’ models because they are not guaranteed to be correct. In Sections 3 and 4, we show how to construct the multiply robust estimators described above. In Section 3, we do so under the assumption that A₁ and A₂ are conditionally independent given X. In Section 4 we allow for conditional dependence. We illustrate the performance of our methods via simulation studies in Section 5 and the analysis of a randomized follow-up study in Section 6.

2 Model and inference

Consider a study whose design calls for measurements on a vector of variables (Y_i, A_i, X_i) to be recorded for each of i = 1, …, n independent subjects. Here, Y_i is the outcome of interest, A_i = (A_i1, A_i2)’ is a vector of exposure variables A_i1 and A_i2, and X_i is a vector of extraneous variables, such as confounders for the association between exposure A_i and outcome Y_i. The goal of the study is to assess whether the association between the exposure A₁ and the outcome Y is modified by A₂ on either an additive or multiplicative scale.

To investigate whether there exist ADF tests of the null hypothesis that the interaction parameter β* = 0, we consider the semiparametric interaction model $\mathcal{A}$ which relaxes some of the parametric restrictions of model (2). Specifically, model $\mathcal{A}$ is defined by the conditional mean model

$$E(Y\mid \mathbf{A},\mathbf{X})=g\left\{m(\mathbf{A},\mathbf{X};{\beta }^{\ast })\right\}$$ (3)

where

$$m(\mathbf{A},\mathbf{X};\beta )=q_3(\mathbf{A},\mathbf{X};\beta )+q_2(\mathbf{X},A_2)+q_1(\mathbf{X},A_1)+h\left(\mathbf{X}\right)$$

with q₃ (A, X; β) defined as before, q₂ (X, A₂), q₁ (X, A₁) and h(X) being unknown functions satisfying q₁ (X, 0) = q₂ (X, 0) = 0, with the joint law of (A, X) unrestricted, with g(.) known and either the identity or exponential function, and with β* ∈ R^p an unknown parameter vector. For instance, we may postulate that

$$E(Y\mid \mathbf{A},\mathbf{X})=g\{{\beta }^{\ast }{A}_1{A}_2+q_2(\mathbf{X},A_2)+q_1(\mathbf{X},A_1)+h(\mathbf{X}\left)\right\}$$ (4)

for unknown functions q₂ (X, A₂), q₁ (X, A₁) and h(X).

Theorem 1 gives the influence functions of regular asymptotically linear (RAL) estimators of β* in model $\mathcal{A}$ and will form the basis of our argument as to why estimation of β* in model $\mathcal{A}$ is infeasible when X is high dimensional. The proof of this and other results are given in the supplemental material (Vansteelandt et al., 2008).

Theorem 1. If $\widehat{\beta }$ is a regular asymptotically linear (RAL) estimator of β* in model $\mathcal{A}$, then there exists a p × 1 function d(A, X) in the set D of all p × 1 functions of (A, X) satisfying

$$E\{\mathbf{d}(\mathbf{A},\mathbf{X})\mid A_1,\mathbf{X}\}=E\{\mathbf{d}(\mathbf{A},\mathbf{X})\mid A_2,\mathbf{X}\}=0,$$ (5)

such that $\widehat{\beta }$ has influence function d(A,X)∊(β), where ∊(β) = Y − m(A,X; β) when g (x) = x and ∊(β) = Y exp {−m(A,X; β)} − 1 when g (x) = e^x. That is, $n^{1∕2}\left(\widehat{\beta }-{\beta }^{\ast }\right)=n^{-1∕2}{\sum }_{i=1}^n\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i){∊}_i\left(\beta \right)+o_p\left(1\right)$.

By standard results from semiparametric theory in Bickel et al. (1993), Theorem 1 implies that all regular and asymptotically linear (RAL) estimators of β* in model $\mathcal{A}$ can be obtained (up to asymptotic equivalence) as the solution $\tilde{\beta }\left(\mathbf{d}\right)$ to the equation

$$\sum _{i=1}^n\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i){∊}_i\left(\beta \right)=0,$$ (6)

for some d ∈ D. The solution $\tilde{\beta }\left(\mathbf{d}\right)$ to this equation is an infeasible estimator as the set of functions D satisfying (5) depends on the unknown conditional law f(A_i|X_i) of exposure A_i, given X_i, and ∊_i(β) depends on the unknown functions q₂ (X_i, A_i2), q₁ (X_i, A_i1) and h(X_i). A feasible RAL estimator is not possible unless some of the unknowns q₂ (X_i, A_i2), q₁ (X_i, A_i1), h(X_i), and f(A_i|X_i) can be consistently estimated. While smoothing methods could in principle be used, with the sample sizes found in practice, the data available to estimate the density f(A_i|X_i) and the main effects q₂ (X_i, A_i2), q₁ (X_i, A_i1) and h(X_i) will be sparse when X_i is a vector with at least several continuous components. As a consequence any feasible estimator of β* under model $\mathcal{A}$ will exhibit poor finite sample performance when the predictor space is large. It follows that in general inference about β* in model $\mathcal{A}$ is infeasible due to the curse of dimensionality and that dimension-reducing (e.g. parametric) working models must be used to estimate the unknowns q₂ (X_i, A_i2), q₁ (X_i, A_i1), h(X_i) and f(A_i|X_i). In the following 2 sections, we demonstrate that multiply robust estimators of β* are obtained when the parameters of these models are estimated in an appropriate fashion. In Section 3, we assume that A₁ and A₂ are conditionally independent given X. This assumption is dropped in Section 4.

3 Conditionally independent exposures

As discussed in the introduction, there are important settings in which A₁ and A₂ are known to be conditionally independent given X. Therefore define ${\mathcal{A}}_{\text{cip}}$ like model $\mathcal{A}$, but with the additional assumption that A₁ ∐ A₂|X. Under this model, the set of estimating equations (6) with d ∈ D can equivalently be rewritten as

$$\begin{array}{cc}\hfill 0=& \sum _{i=1}^n[\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)-E\{\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i1},{\mathbf{X}}_i\}-E\{\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i2},{\mathbf{X}}_i\}\hfill \\ \hfill & +E\{\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid {\mathbf{X}}_i\}\left]{∊}_i\right(\beta )\hfill \end{array}$$ (7)

where d = d(A_i, X_i) is a member of the set of p × 1 functions of (A_i, X_i). The solution $\tilde{\beta }\left(\mathbf{d}\right)$ to this equation is still an infeasible estimator for the reasons discussed previously.

We consider 4 possible dimension-reducing strategies based on working models. The first strategy is to postulate the parametric model (2), i.e., to postulate a parametric model ${\mathcal{M}}_y$ for $q_2(\mathbf{X},A_2)=q_2(\mathbf{X},A_2;{\gamma }_2^{\ast })$, $q_1(\mathbf{X},A_1)=q_1(\mathbf{X},A_1;{\gamma }_1^{\ast })$ and $h\left(\mathbf{X}\right)=h(\mathbf{X};{\gamma }_0^{\ast })$ with ${\gamma }^{\ast }\equiv {({\gamma }_0^{\ast \prime },{\gamma }_1^{\ast \prime },{\gamma }_2^{\ast \prime })}^{\prime }$ unknown finite dimensional parameters, and with γ₀, γ₁ and γ₂ variation independent. The second strategy is to postulate a parametric model ${\mathcal{M}}_a$ for the conditional densities of A_j, given X for j = 1, 2, i.e.

$$f(A_j\mid \mathbf{X})=f(A_j\mid \mathbf{X};{\alpha }_j^{\ast }),$$

where f(A₁|X; α₁) and f(A₂|X; α₂) are known densities smooth in variation independent parameters α₁ and α₂, ${\alpha }_1^{\ast }$, ${\alpha }_2^{\ast }$ are unknown finite-dimensional parameters and ${\alpha }^{\ast }\equiv {({\alpha }_1^{{\ast }^{\prime }},{\alpha }_2^{{\ast }^{\prime }})}^{\prime }$. The third (fourth) strategy is to postulate the model ${\mathcal{M}}_{yaj}$, j = 1 (j = 2) that assumes $q_j(\mathbf{X},A_j)=q_j(\mathbf{X},A_j;{\gamma }_j^{\ast })$ and $f(A_j\mid \mathbf{X})=f(A_j\mid \mathbf{X};{\alpha }_j^{\ast })$.

Since we cannot be certain that any of these 4 models are correct, we aim to find an estimator $\widehat{\beta }$ of β* that is guaranteed to be CAN when any one of them (but not necessarily more than 1 of them) is correct. That is, we wish to find estimators $\widehat{\beta }$ that are CAN in the union submodel ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}\equiv {\mathcal{A}}_{\text{cip}}({\mathcal{M}}_y\cup {\mathcal{M}}_a\cup {\mathcal{M}}_{ya1}\cup {\mathcal{M}}_{ya2})$ of model ${\mathcal{A}}_{\text{cip}}$ that assumes that at least one of ${\mathcal{M}}_y$, ${\mathcal{M}}_a$, ${\mathcal{M}}_{ya1}$ and ${\mathcal{M}}_{ya2}$ is true. In line with Robins, Rotnitzky and van der Laan (2000), Robins and Rotnitzky (2001) and van der Laan and Robins (2003), we will refer to such estimators as quadruply robust and, more generally, as multiply robust estimators (Vansteelandt, Rotnitzky and Robins, 2007). Part (i) of Theorem 2 below shows that, under mild regularity conditions, when g(.) is the identity link, the estimators ${\widehat{\beta }}_{\text{cip}}\equiv {\widehat{\beta }}_{\text{cip}}\left(\mathbf{d}\right)$ are multiply robust (in the sense of being CAN for β* under model ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}$) for ${\widehat{\beta }}_{\text{cip}}\left(\mathbf{d}\right)$ the solution to

$$\begin{array}{cc}\hfill 0=& \sum _{i=1}^n[\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)-E\{\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i1},{\mathbf{X}}_i;{\widehat{\alpha }}_2\}\hfill \\ \hfill & -E\{\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i2},{\mathbf{X}}_i;{\widehat{\alpha }}_1\}+E\{\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid {\mathbf{X}}_i;\widehat{\alpha }\}]{∊}_i(\beta ,\widehat{\gamma }(\beta \left)\right)\hfill \end{array}$$ (8)

with ∊_i(β, γ) = Y_i − m(A_i, X_i; β, γ), d(A_i, X_i) an arbitrary p × 1 function of (A_i, X_i), $\widehat{\alpha }={({\widehat{\alpha }}_1^{\prime },{\widehat{\alpha }}_2^{\prime })}^{\prime }$, with ${\widehat{\alpha }}_j$ satisfying

$$0=\sum _{i=1}^n{\mathbf{H}}_{ij}\left({\widehat{\alpha }}_j\right)\equiv \sum _{i=1}^n\frac{\partial }{\partial {\alpha }_j}\ln f{(A_{ij}\mid {\mathbf{X}}_i;{\alpha }_j)}_{\mid {\alpha }_j={\widehat{\alpha }}_j}$$

for j = 1, 2, and $\widehat{\gamma }\left(\beta \right)$ solving the system of equations

$$0=\sum _{i=1}^n{\mathbf{G}}_{i0}(\beta ,\gamma )\equiv \sum _{i=1}^n{\mathbf{c}}_0({\mathbf{A}}_i,{\mathbf{X}}_i){∊}_i(\beta ,\gamma )$$ (9)

$$0=\sum _{i=1}^n{\mathbf{G}}_{i1}(\beta ,\gamma ,{\widehat{\alpha }}_1)\equiv \sum _{i=1}^n[{\mathbf{c}}_1({\mathbf{A}}_i,{\mathbf{X}}_i)-E\{{\mathbf{c}}_1({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i2},{\mathbf{X}}_i;{\widehat{\alpha }}_1\}]{∊}_i(\beta ,\gamma )$$ (10)

$$0=\sum _{i=1}^n{\mathbf{G}}_{i2}(\beta ,\gamma ,{\widehat{\alpha }}_2)\equiv \sum _{i=1}^n[{\mathbf{c}}_2({\mathbf{A}}_i,{\mathbf{X}}_i)-E\{{\mathbf{c}}_2({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i1},{\mathbf{X}}_i;{\widehat{\alpha }}_2\}]{∊}_i(\beta ,\gamma )$$ (11)

for arbitrary vector functions c₀(A_i, X_i), c₁(A_i, X_i) and c₂(A_i, X_i) of bthe dimension of γ₀, γ₁ and γ₂, respectively. The arguments of Robins and Rotnitzky (2001) imply that a necessary condition for the existence of such quadruply robust estimator of β* in model $A_{\text{cip}}\cap ({\mathcal{M}}_y\cup {\mathcal{M}}_a\cup {\mathcal{M}}_{ya1}\cup {\mathcal{M}}_{ya2})$ is that there exists an unbiased estimating equation for β* (with non-trivial power against local alternatives) were any of the following four statements to hold: (1) q₂ (X, A₂), q₁ (X, A₁) and h (X) are all known, (1) f(A₂|X) and f(A₁|X) are both known, (3) q₁ (X, A₁) and f(A₁|X) are both known, (4) q₂ (X, A₂) and f(A₂|X) are both known. The main step in the proof of Theorem 2 is showing that, for j = 1, 2, 3, 4, (8) is an unbiased estimating equation for β* when statement j holds and the known values of the functions specified in statement j are substituted for their estimated values in (8). The proof is then completed by showing that all of the following are true: $f(A_{ij}\mid {\mathbf{X}}_i;{\widehat{\alpha }}_j)$ is a CAN estimator of f(A_ij|X_i) in models ${\mathcal{M}}_a$ and ${\mathcal{M}}_{yaj}$, j = 1, 2, $q_j(\mathbf{X},A_j;{\widehat{\gamma }}_j({\beta }^{\ast }\left)\right)$ is a CAN estimator of q_j (X, A_j) in models ${\mathcal{M}}_y$ and ${\mathcal{M}}_{yaj}$, j = 1, 2, and $h(\mathbf{X};{\widehat{\gamma }}_0({\beta }^{\ast }\left)\right)$ is a CAN estimator of h (X) in model ${\mathcal{M}}_y$.

Part (i) of Theorem 2 further shows that when g(.) is the exponential link, all estimators ${\widehat{\beta }}_{\text{cip}}\equiv {\widehat{\beta }}_{\text{cip}}\left(\mathbf{d}\right)$ obtained by solving (8) with ∈_i(β, γ) = Y_i exp {—m(A_i, X_i; β, γ)} — 1 are multiply robust in the sense of being CAN in the union model ${\mathcal{B}}_{\text{cip}}^{\exp }=A_{\text{cip}}\cap ({\mathcal{M}}_y\cup {\mathcal{M}}_{ya1}\cup {\mathcal{M}}_{ya2})$ when the above conditions hold. As discussed in the introduction, unlike under the identity link, the estimators ${\widehat{\beta }}_{\text{cip}}\left(\mathbf{d}\right)$ are not CAN in model ${\mathcal{A}}_{\text{cip}}\cap {\mathcal{M}}_a$. In fact, as mentioned above, a necessary condition for any estimator to be CAN in model ${\mathcal{A}}_{\text{cip}}\cap {\mathcal{M}}_a$, and thus in model $A_{\text{cip}}\cap ({\mathcal{M}}_y\cup {\mathcal{M}}_a\cup {\mathcal{M}}_{ya1}\cup {\mathcal{M}}_{ya2})$, is that an unbiased estimating equation for β* (with non-trivial power against local alternatives) exists when f(A₂|X) and f(A₁|X) are known. But in Lemmas 1-3 of the supplemental materials (Vansteelandt et al., 2008) we show that no such unbiased estimating equation need exist when g is the exponential function and X has continuous components. The lack of an unbiased estimating equation in this setting is connected with the following non-collapsibility property of multiplicative interactions.

Remark

Non-Collapsibility of Multiplicative Interactions: Consider again model (4) and suppose A and X are independent. The model $E(Y\mid \mathbf{A})=g({\kappa }^{\ast }{A}_1{A}_2+{\eta }_1^{\ast }{A}_1+n_2^{\ast }{A}_2+{\eta }_0^{\ast })$ is derived from model (4) by collapsing over X. Note that this model is saturated when A₁ and A₂ are dichotomous. If g(x) = x, then β* = κ*, so additive interactions are collapsible over X. However, a trivial calculation shows that if g(x) = exp(x), even β* = 0 fails to imply κ* = 0.

Theorem 2

Suppose that the regularity conditions stated in the supplemental materials (Vansteelandt et al., 2008) hold and that β, γ₁, γ₂, α₁ and α₂ are variation independent.

(i) Then, when g(x) = x (g(x) = exp(x)), $\sqrt{n}({\widehat{\beta }}_{\text{cip}}-{\beta }^{\ast })$ is RAL under model ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}\left({\mathcal{B}}_{\text{cip}}^{\exp }\right)$ with influence function

$$E^{-1}\left\{\frac{\partial }{\partial \beta }{\mathbf{U}}_i^{\ast }{(\beta ,\tilde{\gamma }({\beta }^{\ast }),\tilde{\alpha })}_{\mid \beta ={\beta }^{\ast }}\right\}{\mathbf{U}}_i^{\ast }({\beta }^{\ast },\tilde{\gamma }({\beta }^{\ast }),\tilde{\alpha })$$

and thus converges in distribution to a N (0,_γ), where

$$\gamma =E\left({\left[E^{-1}\left\{\frac{\partial }{\partial \beta }{\mathbf{U}}_i^{\ast }{(\beta ,\tilde{\gamma }({\beta }^{\ast }),\tilde{\alpha })}_{\mid \beta ={\beta }^{\ast }}\right\}{\mathbf{U}}_i^{\ast }({\beta }^{\ast },\tilde{\gamma }({\beta }^{\ast }),\tilde{\alpha })\right]}^{\otimes 2}\right)$$

with $\tilde{\gamma }\left(\beta \right)$ and $\tilde{\alpha }$ denoting the probability limits of the estimators $\widehat{\gamma }\left(\beta \right)$ and $\widehat{\alpha }$ respectively, and

$$\begin{array}{cc}\hfill {\mathbf{U}}_i^{\ast }(\beta ,\gamma ,\alpha )& ={\mathbf{U}}_i(\beta ,\gamma ,\alpha )-E\left\{\frac{\partial }{\partial \gamma }{\mathbf{U}}_i(\beta ,\gamma ,\alpha )\right\}{E}^{-1}\left\{\frac{\partial }{\partial \gamma }{\mathbf{G}}_i(\beta ,\gamma ,\alpha )\right\}{\mathbf{G}}_i(\beta ,\gamma ,\alpha )\hfill \\ \hfill -& [E\left\{\frac{\partial }{\partial \alpha }{\mathbf{U}}_i(\beta ,\gamma ,\alpha )\right\}-E\left\{\frac{\partial }{\partial \gamma }{\mathbf{U}}_i(\beta ,\gamma ,\alpha )\right\}{E}^{-1}\left\{\frac{\partial }{\partial \gamma }{\mathbf{G}}_i(\beta ,\gamma ,\alpha )\right\}\phantom{]}\hfill \\ \hfill \times E& \phantom{[}\left\{\frac{\partial }{\partial \alpha }{\mathbf{G}}_i(\beta ,\gamma ,\alpha )\right\}]E^{-1}\left\{\frac{\partial }{\partial \alpha }{\mathbf{H}}_i\left(\alpha \right)\right\}{\mathbf{H}}_i\left(\alpha \right)\hfill \end{array}$$ (12)

with ${\mathbf{H}}_i\left(\alpha \right)\equiv {\left({\mathbf{H}}_{i1}^{\prime }\right(\alpha ),{\mathbf{H}}_{i2}^{\prime })}^{\prime }$ and ${\mathbf{G}}_i(\beta ,\gamma ,\alpha )\equiv {({\mathbf{G}}_{i0}^{\prime }(\beta ,\gamma ),{\mathbf{G}}_{i1}^{\prime }(\beta ,\gamma ,{\alpha }_1),{\mathbf{G}}_{i2}^{\prime }(\beta ,\gamma ,{\alpha }_2))}^{\prime }$.

(ii) Furthermore, let $\widehat{\beta }(\mathbf{d},{\mathbf{G}}_{\left(1\right)},{\mathbf{H}}_{\left(1\right)})$ and $\widehat{\beta }(\mathbf{d},{\mathbf{G}}_{\left(2\right)},{\mathbf{H}}_{\left(2\right)})$ be 2 estimators of β* under model ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}\left({\mathcal{B}}_{\text{cip}}^{\exp }\right)$ corresponding to the same index functions d, but different unbiased estimating functions G₍₁₎ and G₍₂₎ for γ under model ${\mathcal{M}}_y$ and H₍₁₎ and H₍₂₎ for α* under model ${\mathcal{M}}_a$. Then, $\sqrt{n}\left\{\widehat{\beta }\left({\mathbf{G}}_{\left(1\right)}\right),{\mathbf{H}}_{\left(1\right)}-\widehat{\beta }({\mathbf{G}}_{\left(2\right)},{\mathbf{H}}_{\left(2\right)})\right\}=o_p\left(1\right)$ at the intersection submodel ${\mathcal{A}}_{\text{cip}}\cap {\mathcal{M}}_y\cap {\mathcal{M}}_a$.

Part (i) of Theorem 2 suggests that multiply robust estimators of β* in model ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}\left({\mathcal{B}}_{\text{cip}}^{\exp }\right)$ can be obtained by solving an equation of the form (8). General results on doubly robust estimation in Robins and Rotnitzky (2001) further imply that any regular CAN estimator of β* in model ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}\left({\mathcal{B}}_{\text{cip}}^{\exp }\right)$ has the same asymptotic distribution as ${\widehat{\beta }}_{\text{cip}}\left(\mathbf{d}\right)$ can be obtained in this way. Part (ii) of Theorem 2 suggests that the choice of estimators for α* and γ* has no impact on the efficiency of ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}\left({\mathcal{B}}_{\text{cip}}^{\exp }\right)$ when the models ${\mathcal{M}}_y$ and ${\mathcal{M}}_a$ are correctly specified. Thus the fact that ${\gamma }_1^{\ast }$ and ${\gamma }_2^{\ast }$ are estimated by G-estimators solving (10) and (11), respectively, rather than by their more effcient maximum likelihood estimators under model ${\mathcal{A}}_{\text{cip}}\cap {\mathcal{M}}_y$ has no effect on the asymptotic variance of ${\widehat{\beta }}_{\text{cip}}$ when the law of the data lies in ${\mathcal{A}}_{\text{cip}}\cap {\mathcal{M}}_y\cap {\mathcal{M}}_a$. Nonetheless, the use of such G-estimators is critical to control bias. Indeed, while the solution to (8) is a CAN estimator under model ${\mathcal{A}}_{\text{cip}}\cap ({\mathcal{M}}_y\cap {\mathcal{M}}_a)$ with γ* is replaced by an arbitrary CAN estimator under model ${\mathcal{A}}_{\text{cip}}\cap {\mathcal{M}}_y$, it is not CAN under the less restrictive model ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}$ (or ${\mathcal{B}}_{\text{cip}}^{\exp }$).

It follows as a corollary of Theorem 4 in Section 4 that, when the residual outcome variance is constant in A, i.e. $\mathrm{Var}\left\{∊\right({\beta }^{\ast }\mid \mathbf{A},\mathbf{X}\left)\right\}={\sigma }^2\left(\mathbf{X}\right)$ for some function σ²(X), the efficient estimating equation at β in model ${\mathcal{A}}_{\text{cip}}$ is obtained by replacing d (A_i, X_i) in equation (8) with

$${\sigma }^{-2}\left({\mathbf{X}}_i\right)\frac{\partial }{\partial \beta }{q}_3({\mathbf{A}}_i,{\mathbf{X}}_i;\beta )$$

For example, when q₃(A_i, X_i;β) = q₃(X_i;β)A_i1A_i2, we obtain

$$0=\sum _{i=1}^n\frac{\partial q_3({\mathbf{X}}_i;\beta )}{\partial \beta }\{A_{i1}-E(A_{i1}\mid {\mathbf{X}}_i;{\widehat{\alpha }}_1)\}\{A_{i2}-E(A_{i2}\mid {\mathbf{X}}_i;{\widehat{\alpha }}_2)\}\frac{{∊}_i(\beta ,\widehat{\gamma }(\beta \left)\right)}{{\sigma }^2\left({\mathbf{X}}_i\right)}$$ (13)

It can be deduced from Robins and Rotnitzky (2001) that the semiparametric variance bound in models ${\mathcal{A}}_{\text{cip}}$ and ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}\left({\mathcal{B}}_{\text{cip}}^{\exp }\right)$ are identical whenever the model ${\mathcal{M}}_y\cap {\mathcal{M}}_a$ is true, and thus that solving (13) then yields a semiparametric efficient estimator under model ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}\left({\mathcal{B}}_{\text{cip}}^{\exp }\right)$ at the intersection model ${\mathcal{M}}_y\cap {\mathcal{M}}_a$. Note that (13) merely requires specifying the conditional means of A₁ and A₂, given X, and not the entire conditional distribution. In practice, unless the variance function σ²(X) is further assumed not to depend on X, the unknown function σ²(X) in (13) must be replaced by an estimator.

The homoscedasticity assumption that ${\mathcal{M}}_y\cap {\mathcal{M}}_a$ does not depend on A, may often be implausible and is logically impossible for count data with g(x) = exp(x). When this assumption fails, the efficient estimating equation at β* in model ${\mathcal{A}}_{\text{cip}}$ can be obtained following the methods developed in the next section.

4 Conditionally dependent exposures

In this section, we relax the previous assumptions by allowing for the exposures A₁ and A₂ to be conditionally dependent given X.

4.1 Estimation

We first consider the special case of binary exposures. When A₁ and A₂ are dichotomous, as when testing for gene-gene interaction between 2 possibly linked bi-allelic markers each with dominant or recessive mode of inheritance, then an arbitrary function d(A_i, X_i) can be written as A_i2A_i1d₁₁ (X_i) + A_i2(1 − A_i1)d₀₁ (X_i) + (1 − A_i2)A_i1d₁₀ (X_i) + (1 − A_i2)(1 − A_i1)d₀₀ (X_i) for given functions d_kl(X_i), k, l = 0, 1. It follows that the set D of functions (A, X) satisfying (5) is the set D = {d^‡(X)Δ(A, X);d^†(X) ∈ R^p} where

$$\begin{array}{cc}\hfill \Delta (\mathbf{A},\mathbf{X})\equiv & \frac{A_1{A}_2}{E\{A_1{A}_2\mid \mathbf{X}\}}+\frac{(1-A_1)(1-A_2)}{E\{(1-A_1)(1-A_2)\mid \mathbf{X}\}}\hfill \\ \hfill & -\frac{A_1(1-A_2)}{E\{A_1(1-A_2)\mid \mathbf{X}\}}-\frac{(1-A_1)A_2}{E\{(1-A_1)A_2\mid \mathbf{X}\}}\hfill \end{array}$$ (14)

$$={\left\{f\right(A\mid X\left)\right\}}^{-1}[I\{A_1=A_2\}-I\{A_1\ne A_2\}]$$ (15)

Hence the estimating equations (6) with d ∈ D can equivalently be written as

$$0=\sum _{i=1}^n{\mathbf{d}}^{†}\left({\mathbf{X}}_i\right)\Delta ({\mathbf{A}}_i,{\mathbf{X}}_i){∊}_i\left(\beta \right)$$ (16)

where d^† is a member of the set of all p × 1 functions of X.

When the exposures A_i1 and A_i2 are not both dichotomous and dependent conditional on X_i, we can use the following characterization of the set D of functions (A, X) satisfying (5).

Lemma (Tchetgen and Robins, 2008)

Let f* (A|X) = f* (A₁|X) f* (A₂|X) be any fixed density for A|X with A₁ and A₂ conditionally independent given X that is absolutely continuous with respect to the true density f (A|X). Then the set of functions D satisfying (5) is the set {d^‡(A, X, r); r = r(A,X) ∈ R^p} where

$$\begin{array}{cc}\hfill {\mathbf{d}}^{‡}(\mathbf{A},\mathbf{X},\mathbf{r})=& \frac{f^{\ast }(\mathbf{A}\mid \mathbf{X})}{f(\mathbf{A}\mid \mathbf{X})}[\mathbf{r}(\mathbf{A},\mathbf{X})-E^{\ast }\{\mathbf{r}(\mathbf{A},\mathbf{X})\mid A_1,\mathbf{X}\}\hfill \\ \hfill & -E^{\ast }\{\mathbf{r}(\mathbf{A},\mathbf{X})\mid A_2,\mathbf{X}\}+E^{\ast }\{\mathbf{r}(\mathbf{A},\mathbf{X})\mid \mathbf{X}\}]\hfill \end{array}$$ (17)

and where the expectations E*(.) are taken w.r.t. f* (A|X).

When A₁ and A₂ are dichotomous and we choose f* (A|X) ≡ 1/4 w.p.1 and r (A, X) = 4d^†(X_i) [I {A₁ = A₂} - I {A₁ ≠ A₂}], we obtain d^‡(A, X, r) = d^†(X_i)Δ(A_i, X_i), thus establishing equation (16) as a special case of equation (17). For non-dichotomous A₁ and A₂, given any (user-supplied) density f* (A|X) = f* (A₁|X) f* (A₂|X) satisfying the conditions of the lemma, we can apply equation (17) to an arbitrary (user-supplied) function, say d⁽¹⁾(A, X), to obtain a function d^‡(A_i, X_i, d⁽¹⁾) that satisfies equation (5).

An alternative way to map an arbitrary function d⁽¹⁾(A, X) to an element of D is to apply the alternating conditional expectations (ACE) algorithm (Breiman and Friedman, 1985; Bickel et al., 1993). This is an iterative algorithm which, starting from d⁽¹⁾(A_i, X_i), computes the repeating conditional expectations

$${\mathbf{d}}^{\left(2m\right)}({\mathbf{A}}_i,{\mathbf{X}}_i)={\mathbf{d}}^{(2m-1)}({\mathbf{A}}_i,{\mathbf{X}}_i)-E\{{\mathbf{d}}^{(2m-1)}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i1},{\mathbf{X}}_i\}$$ (18)

$${\mathbf{d}}^{(2m+1)}({\mathbf{A}}_i,{\mathbf{X}}_i)={\mathbf{d}}^{\left(2m\right)}({\mathbf{A}}_i,{\mathbf{X}}_i)-E\{{\mathbf{d}}^{\left(2m\right)}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i2},{\mathbf{X}}_i\}$$ (19)

for m = 1, 2, … until convergence at d(A_i, X_i, d⁽¹⁾) = lim_m→∞ d^(2m+1) (A_i, X_i). The function d(A_i, X_i, d⁽¹⁾) then satisfies equation (5). Although both in D, d(A_i, X_i, d⁽¹⁾) and d^‡(A_i, X_i, d⁽¹⁾) will generally differ. The function d^‡(A_i, X_i, d⁽¹⁾) exists in closed form and is easy to compute. In contrast, the function d(A_i, X_i, d⁽¹⁾) cannot be expressed in closed form when A₁ and A₂ are both continuous, unlike when A₁ and/or A₂ is discrete (Bickel et al., 1993); even so, in general, d(A_i, X_i, d⁽¹⁾) remains more difficult to compute than d^‡(A_i, X_i, d⁽¹⁾). Furthermore, we shall see below that (a weighted version) of d(A_i, X_i, d⁽¹⁾) is needed to obtain a locally semiparametric efficient estimator.

Unlike in the previous section, there do not exist compatible models f (A₁|A₂, X; α₁) and f (A₂|A₁, X; α₂) with variation independent parameters when conditional dependence between both exposures is allowed for. Inference for β* therefore cannot be made robust to misspecification of either one of these conditional densities, and thus no consistent estimators can be obtained under model $\mathcal{A}\cap ({\mathcal{M}}_{ya1}\cup {\mathcal{M}}_{ya2}\cup {\mathcal{M}}_{ya1})$.

Remark

More precisely, it can be shown that we could construct compatible models for f (A₁|A₂, X) and f (A₂|A₁, X) with variation independent parameters α₁ and α₂ if we assume that, for chosen values a₁₀, a₂₀, the generalized odds ratio function ρ (A₁, A₂, X) = f(A₁|A₂, X)f(A₁ = α₁₀|A₂ = α₂₀, X)/{f(A₁ = α₁₀|A₂, X)f(A₁|A₂ = α₂₀, X)} is a known function, simply by specifying models f(A₁|A₂ = α₂₀, X; α₁) and f (A₂|A₁ = α₁₀, X; β₂) for f (A₁|A₂ = α₂₀, X) and f (A₂|A₁ = α₁₀, X). However, in practice, the assumption that ρ (A₁, A₂, X) is known would never be reasonable, except in the special case that the generalized odds ratio function is the constant function 1, which is equivalent to again assuming A₁ and A₂ are conditionally independent given X. However, if we did not restrict attention to variation independent models, it is possible to drop the assumption that ρ (A₁, A₂, X) is known and specify a model ρ (A₁, A₂, X; ς) for ρ (A₁, A₂, X) depending on a parameter vector ς. Then the model ρ (A₁, A₂, X; ς) together with the aforementioned models f (A₁|A₂ = α₂₀, X; α₁) and f (A₂|A₁ = α₁₀, X; α₂) induce compatible models for f (A₁|A₂, X) and f (A₂|A₁, X) with the parameter ς occurring in both. We could then construct consistent estimators of β* when either the model for f (_A1|A₂, X) or the model for f (A₂|A₁, X) is correct, because, using methods described in Chen (2007) and Tchetgen and Robins (2008), the common parameter ς can be consistently estimated if either the model f (A₁|A₂ = α₂₀, X; α₁) or the model f (A₂|A₁ = α₁₀, X; α₂) is correct.

We will therefore conduct inference for β* under model ${\mathcal{B}}^{\mathrm{id}}\equiv \mathcal{A}({\mathcal{M}}_y\cup {\mathcal{M}}_a\cup {\mathcal{M}}_{ya1})$, where we redefine ${\mathcal{M}}_a$ to be a parametric model for the conditional density of A, given X, of the form

$$f(\mathbf{A}\mid \mathbf{X})=f(\mathbf{A}\mid \mathbf{X};{\alpha }^{\ast })=f(A_1\mid \mathbf{X},A_2;{\alpha }_1^{\ast })f(A_2\mid \mathbf{X};{\alpha }_2^{\ast }).$$

Here, f(A₁|X, A₂; α₁) and f(A₂|X; α₂) are known densities smooth in α₁ and α₂, and ${\alpha }^{\ast }={({\alpha }_1^{{\ast }^{\prime }},{\alpha }_2^{{\ast }^{\prime }})}^{\prime }$ is an unknown finite-dimensional parameter. Further, we define ${\mathcal{M}}_{ya2}^{\ast }\equiv {\mathcal{M}}_{ya2}\cap {\mathcal{M}}_a$. Let $\widehat{\alpha }={\left({\widehat{\alpha }}_1^{\prime },{\widehat{\alpha }}_2^{\prime }\right)}^{\prime }$ satisfy

$$0=\sum _{i=1}^n{\mathbf{H}}_{i1}\left({\widehat{\alpha }}_1\right)\equiv \sum _{i=1}^n\frac{\partial }{\partial {\alpha }_1}\ln f{(A_{i1}\mid A_{i2},{\mathbf{X}}_i;{\alpha }_1)}_{\mid {\alpha }_1={\widehat{\alpha }}_1}$$ (20)

$$0=\sum _{i=1}^n{\mathbf{H}}_{i2}\left({\widehat{\alpha }}_2\right)\equiv \sum _{i=1}^n\frac{\partial }{\partial {\alpha }_2}\ln f{(A_{i2}\mid {\mathbf{X}}_i;{\alpha }_2)}_{\mid {\alpha }_2={\widehat{\alpha }}_2}$$ (21)

Hence ${\widehat{\alpha }}_2$ is the MLE of ${\alpha }_2^{\ast }$ under model ${\mathcal{M}}_a$, while ${\widehat{\alpha }}_1$ is the MLE of ${\alpha }_1^{\ast }$ under both models ${\mathcal{M}}_a$ and ${\mathcal{M}}_{ya1}$.

Let $\Delta ({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })$, ${\mathbf{d}}^{‡}({\mathbf{A}}_i,{\mathbf{X}}_i,{\mathbf{d}}^{\left(1\right)};\widehat{\alpha })$ and $\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i,{\mathbf{d}}^{\left(1\right)};\widehat{\alpha })$ be Δ(A_i, X_i), d^‡(A_i, X_i, d⁽¹⁾), and d(A_i,X_i, d⁽¹⁾), except with the expectations now evaluated under $f(\mathbf{A},\mathbf{X};\widehat{\alpha })$. Given d^†(X_i) and d⁽¹⁾(A_i, X_i), let $\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })$ be ${\mathbf{d}}^{†}\left({\mathbf{X}}_i\right)\Delta ({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })$ when A_i1 and A_i2 are binary and let $\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })$ be either $\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i,{\mathbf{d}}^{\left(1\right)};\widehat{\alpha })$ or ${\mathbf{d}}^{‡}({\mathbf{A}}_i,{\mathbf{X}}_i,{\mathbf{d}}^{\left(1\right)};\widehat{\alpha })$ otherwise, where the dependence of $\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })$ on d^† or d⁽¹⁾ is suppressed. In all cases, the function $\mathbf{d}\left(\widehat{\alpha }\right)=\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })$ is an element of $\mathbf{D}\left(\widehat{\alpha }\right)$, where the set $\mathbf{D}\left(\widehat{\alpha }\right)$ is defined like the set D but with $f({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })$ replacing f (A_i|X_i) in equation (5).

Theorem 3 below shows that when g(.) is the identity link, the estimators $\widehat{\beta }\equiv \widehat{\beta }\left(\mathbf{d}\right(\widehat{\alpha }\left)\right)$ for a given $\mathbf{d}\left(\widehat{\alpha }\right)=\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })$ are multiply robust (in the sense of being CAN for β* under model ${\mathcal{B}}^{\mathrm{id}}$), where $\widehat{\beta }\left(\mathbf{d}\right(\widehat{\alpha }\left)\right)$ solves

$$0=\sum _{i=1}^n{\mathbf{U}}_i(\beta ,\widehat{\gamma }(\beta ),\widehat{\alpha })=\sum _{i=1}^n\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha }){∊}_i(\beta ,\widehat{\gamma }(\beta \left)\right)$$ (22)

with $\widehat{\beta }\equiv \widehat{\beta }\left(\mathbf{d}\right(\widehat{\alpha }\left)\right)$ still defined as in Section 3. Theorem 3 further shows that when g(.) is the exponential link, the estimators $\widehat{\beta }\equiv \widehat{\beta }\left(\mathbf{d}\right(\widehat{\alpha }\left)\right)$ obtained by solving (22) with ∊_i(β, γ) = Y_i exp {−m(A_i, X_i,; β, γ)} − 1 are multiply robust in the sense of being CAN in the union model ${\mathcal{B}}^{\exp }$.

Theorem 3

Suppose that the regularity conditions stated in the supplemental materials (Vansteelandt et al., 2008) hold and that, β₁, γ₂, γ₁ and α₂ are variation independent. Suppose $\mathbf{d}\left(\widehat{\alpha }\right)\in \mathbf{D}\left(\widehat{\alpha }\right)$. Then Parts 1 and 2 of Theorem 2 continue to hold with $\widehat{\beta }\equiv \widehat{\beta }\left(\mathbf{d}\right(\widehat{\alpha }\left)\right)$ replacing ${\widehat{\beta }}_{\text{cip}}$ and model ${\mathcal{B}}^{\mathrm{id}}\left({\mathcal{B}}^{\exp }\right)$ replacing ${\mathcal{B}}_{\text{cip}}^{\mathrm{id}}\left({\mathcal{B}}_{\text{cip}}^{\exp }\right)$, with $A_{i1}\left({\widehat{\alpha }}_1\right)$ and $A_{i2}\left({\widehat{\alpha }}_2\right)$ now defined as in (20) and (21).

We propose two practical strategies for implementing the ACE algorithm when when A₁ and A₂ are both continuous. The first strategy is a numerical integration approach whereby the integrals

$$E\{\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\alpha )\mid A_{ij},{\mathbf{X}}_i;\alpha \}=\int \mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\alpha )f(A_{i{j}^{\prime }}\mid A_{ij},{\mathbf{X}}_i;\alpha )d{A}_{i{j}^{\prime }}$$

for j, j’ = 1, 2, j ≠ j’ in the ACE algorithm are approximated via numerical integration methods, such as the composite Simpson’s rule (with α replaced by $\tilde{\alpha }$). This requires that we can evaluate the function d^(2m)(A_i, X_i; α) (and thus that we run the ACE algorithm) at a Sufficient number M of points (a_i11, a_i21), …, (a_i1M, a_i2M ), spread across the support of (A₁, A₂). These may be chosen for each given X_i separately by drawing a random sample from the joint distribution of (A_i1, A_i2), given X_i, and should additionally include the observed data points at the given X_i. Note that we opt for the composite Simpson’s rule because this merely requires knowing the function values of d^(2m)(A_i, X_i; α) at the selected M points.

The second strategy is an ad-hoc approach which involves postulating separate high-dimensional models for the conditional expectations in (18) and (19) and fitting these each time using standard regression techniques (thus without postulating a model for f(A|X)), as in Breiman and Friedman (1985). A drawback of this approach is that it does not guarantee congenial models for the conditional expectations in (18) and (19) (i.e. there may be no joint law f(A|X) for which the postulated conditional expectations (18) and (19) hold for m = 1, 2, …). Nevertheless, we recommend this approach for data analysis because the numerical integration approach is computer intensive, generally does not lead to improved results in simulation studies (see Section 5) and, to the best of our knowledge, its convergence properties have not been studied, unlike those of the ad-hoc approach (Breiman and Friedman, 1985). Furthermore, while there may be concerns over using automatic model fitting for the conditional expectations in (18) and (19) in the sense that these may be more likely misspecified, these concerns are mitigated to some extent by the robustness property of our estimators.

Remark

Using (12) to estimate the asymptotic variance of $\tilde{\beta }$ requires knowing the derivative E{∂U_i(β, γ, α)/∂α}. This is difficult when d(A_i, X_i; α) is obtained via the ACE algorithm because it then has no closed-form expression. However, a variance estimate can still be obtained by noting that, as shown in the supplemental materials (Vansteelandt et al., 2008), under models B_id (B_exp),

$$E{\left\{\frac{\partial }{\partial \alpha }{\mathbf{U}}_i^{\ast }({\beta }^{\ast },\tilde{\gamma }({\beta }^{\ast }),\alpha )\right\}}_{\mid \alpha =\tilde{\alpha }}=-E\left\{\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\tilde{\alpha }){\mathbf{S}}_i\right(\tilde{\alpha }\left){∊}_i({\beta }^{\ast },\tilde{\gamma }({\beta }^{\ast }\left)\right)\right\}$$ (23)

where ${\mathbf{S}}_i\left(\tilde{\alpha }\right)$ is the score for under model ${\mathcal{M}}_a$, evaluated at $\tilde{\alpha }$.

Expression (23) is not useful under the ad-hoc implementation of the ACE algorithm because the score S_i(α) is then unknown. In that case, one might for simplicity choose to ignore estimation of α* when calculating the standard error of $\widehat{\beta }$. Indeed, Theorem 2.3 in van der Laan and Robins (2003) assures that, if model ${\mathcal{M}}_a$ holds, ignoring efficient estimation of α* leads to conservative inferences for β* under model B_id (B_exp). Furthermore, because $E{\{\partial {\mathbf{U}}_i({\beta }^{\ast },\tilde{\gamma },\alpha )∕\partial \alpha \}}_{\mid \alpha =\tilde{\alpha }}=0$ and $E{\{\partial {\mathbf{G}}_i({\beta }^{\ast },\tilde{\gamma },\alpha )∕\partial \alpha \}}_{\mid \alpha =\tilde{\alpha }}=0$ when model ${\mathcal{M}}_y$ is correctly specified, estimation of α* does not affect the distribution of our estimator for β* at model ${\mathcal{M}}_y$ (see expression (12)). This approach is not attractive, however, because simulation studies in Section 5 show that ignoring estimation of α* in constructing our variance estimator may imply a serious loss of power when model ${\mathcal{M}}_y$ is misspecified. We therefore recommend the nonparametric bootstrap for inference under ad-hoc implementations of the ACE algorithm, as the bootstrap always provides a consistent estimator of the asymptotic variance under our assumptions.

4.2 Local semiparametric efficiency

We now consider how to obtain locally semiparametric efficient estimators. The key to doing so is the following characterization of the efficient score in model A. Let σ²(A, X) ≡ Var {∊(β*)|A, X}. In Theorem 4, we show that when A_i1 and A_i2 are binary, the efficient score for β* is S_eff = d_opt(A_i, X_i)∊_i(β*) in model A with ${\mathbf{d}}_{\mathit{opt}}({\mathbf{A}}_i,{\mathbf{X}}_i)={\mathbf{d}}_{\mathit{opt}}^{†}\left({\mathbf{X}}_i\right)\Delta ({\mathbf{A}}_i,{\mathbf{X}}_i)$ and

$${\mathbf{d}}_{\mathit{opt}}^{†}\left({\mathbf{X}}_i\right)=\mathrm{E}{\left\{{\Delta }^2({\mathbf{A}}_i,{\mathbf{X}}_i){\sigma }^2({\mathbf{A}}_i,{\mathbf{X}}_i\mid {\mathbf{X}}_i)\right\}}^{-1}\mathrm{E}\left\{\Delta ({\mathbf{A}}_i,{\mathbf{X}}_i)\frac{\partial }{\partial \beta }{q}_3{({\mathbf{A}}_i,{\mathbf{X}}_i;\beta )}_{\mid \beta ={\beta }^{\ast }}\mid {\mathbf{X}}_i\right\}.$$

When A_1i and A_2i are both continuous, the efficient score S_eff = d_opt(A_i,X_i)∊_i(β*) does not exist in closed form. However, regardless of the sample spaces of A₁ and A₂, we show in Theorem 4 that d_opt(A_i,X_i) = lim_m→∞ d^(2m+1)(A_i,X_i) is always the function to which the ν—weighted ACE algorithm defined by

$${\mathbf{d}}^{\left(2m\right)}({\mathbf{A}}_i,{\mathbf{X}}_i)={\mathbf{d}}^{(2m-1)}({\mathbf{A}}_i,{\mathbf{X}}_i)-\upsilon ({\mathbf{A}}_i,{\mathbf{X}}_i)\frac{E\{{\mathbf{d}}^{(2m-1)}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i1},{\mathbf{X}}_i\}}{E\{\upsilon ({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i1},{\mathbf{X}}_i\}}$$ (24)

$${\mathbf{d}}^{(2m+1)}({\mathbf{A}}_i,{\mathbf{X}}_i)={\mathbf{d}}^{\left(2m\right)}({\mathbf{A}}_i,{\mathbf{X}}_i)-\upsilon ({\mathbf{A}}_i,{\mathbf{X}}_i)\frac{E\{{\mathbf{d}}^{\left(2m\right)}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i2},{\mathbf{X}}_i\}}{E\{\upsilon ({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{i2},{\mathbf{X}}_i\}}$$ (25)

for m = 1, 2, …, converges for the choices ν (A_i,X_i) = σ⁻²(A_i,X_i) and d⁽¹⁾(A_i,X_i) = σ⁻²(A_i,X_i)∂q₃(A_i,X_i; β)_β=β*/∂β. The unweighted ACE algorithm defined by equations (18) and (19) is the special case of the ν—weighted ACE algorithm with ν (A_i,X_i) = ν* (X_i) only a function of X_i. For any d⁽¹⁾(A_i,X_i) ∊ R^p and any always-positive function ν (A_i,X_i), the ν—weighted algorithm, like the unweighted algorithm converges to a function d_ν(A_i,X_i; d⁽¹⁾), that satisfies equation (5). This last statement follows from the following arguments. First, $\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)-\upsilon ({\mathbf{A}}_i,{\mathbf{X}}_i)\frac{E\{\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{ij},{\mathbf{X}}_i\}}{E\{\upsilon ({\mathbf{A}}_i,{\mathbf{X}}_i)\mid A_{ij},{\mathbf{X}}_i\}}$ for j ∊ {1, 2}, is the orthogonal projection of the univariate function d(A_i, X_i) on the closed linear subspace Λ_j = {d(A_i, X_i); E {d(A_i, X_i)|A_ij, X_i} = 0} in the Hilbert space of functions of (A_i, X_i) with inner product ⟨d₁, d₂⟩ ≡ E [{ν (A_i, X_i)}⁻¹ d₁(A_i, X_i)d₂(A_i, X_i)]. It then follows from a theorem of Von Neumann (Bickel et al., 1993, p.436) that d_ν(A_i, X_i; d⁽¹⁾) is the projection of d⁽¹⁾(A_i, X_i) on the linear space Λ = Λ₁ ⋂ Λ₂, which is precisely the subspace satisfying equation (5).

We now explain how to obtain a locally efficient estimator of β*. Consider the model

$$\mathrm{Var}\left(∊\right({\beta }^{\ast })\mid \mathbf{A},\mathbf{X})={\sigma }^2(\mathbf{A},\mathbf{X};{\eta }^{\ast })$$ (26)

where σ²(A, X; η) is a known function, smooth in η, and η* is an unknown parameter vector. Let $\widehat{\eta }$ satisfy

$$0=\sum _{i=1}^n{\mathbf{H}}_{i3}\left(\widehat{\eta }\right)=\sum _{i=1}^n\mathbf{s}({\mathbf{A}}_i,{\mathbf{X}}_i)\left\{{∊}_i^2(\widehat{\beta },\widehat{\gamma }(\widehat{\beta }\left)\right)-{\sigma }^2({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\eta })\right\}$$

where s(A_i, X_i) is a vector of user-supplied functions of the dimension of η, and $\widehat{\beta }=\widehat{\beta }\left(\mathbf{d}\right(\widehat{\alpha }\left)\right)$ for a given $d\left(\widehat{\alpha }\right)=\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })\in \mathbf{D}\left(\widehat{\alpha }\right)$. Note that, with any positive ν (A_i, X_i) and any d⁽¹⁾(A_i, X_i) as input, the ν—weighted ACE algorithm, based on $f({\mathbf{A}}_i\mid {\mathbf{X}}_i;\widehat{\alpha })$ rather than on f (A_i|X_i), outputs a function $\mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })\in \mathbf{D}\left(\widehat{\alpha }\right)$.

Theorem 4

(i)The efficient score for β* in model $\mathcal{A}$ is d_opt(A_i,X_i)∊_i(β*)

1. with ${\mathbf{d}}_{\mathit{opt}}({\mathbf{A}}_i,{\mathbf{X}}_i)={\mathbf{d}}_{\mathit{opt}}^{†}\left({\mathbf{X}}_i\right)\Delta ({\mathbf{A}}_i,{\mathbf{X}}_i)$ for binary A_i1 and A_i2;

2. with d_opt(A_i,X_i) = lim_m→∞ d^(2m+1)(A_i,X_i) in the ν—weighted ACE algorithm with ν (A_i, X_i) = σ⁻²(A_i, X_i) and d⁽¹⁾ (A_i, X_i) = σ⁻²(A_i, X_i) ×∂q₃(A_i, X_i; β)_|β=β*|/∂β in general.

(ii) Let $\widehat{\beta }\left(\mathbf{d}\right(\widehat{\alpha }\left)\right)$ and $\widehat{\beta }\left({\mathbf{d}}_{\mathrm{opt}}(\widehat{\alpha },\widehat{\eta })\right)$ solve (22) where $\mathbf{d}\left(\widehat{\alpha }\right)\equiv \mathbf{d}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha })\in \mathbf{D}\left(\widehat{\alpha }\right)$ and ${\mathbf{d}}_{\mathrm{opt}}(\widehat{\alpha },\widehat{\eta })={\mathbf{d}}_{\mathrm{opt}}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\alpha },\widehat{\eta })\in \mathbf{D}\left(\widehat{\alpha }\right)$ is the function to which the ν—weighted ACE algorithm based on $f({\mathbf{A}}_i\mid {\mathbf{X}}_i;\widehat{\alpha })$ converges for $\upsilon ({\mathbf{A}}_i,{\mathbf{X}}_i)={\sigma }^{-2}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\eta })$ and ${\mathbf{d}}^{\left(1\right)}({\mathbf{A}}_i,{\mathbf{X}}_i)={\sigma }^{-2}({\mathbf{A}}_i,{\mathbf{X}}_i;\widehat{\eta })\partial q_3{({\mathbf{A}}_i,{\mathbf{X}}_i;\beta )}_{\beta ={\beta }^{\ast }}∕\partial \beta$. Then, $\widehat{\beta }\left(\mathbf{d}\right(\widehat{\alpha }\left)\right)$ and $\widehat{\beta }\left(d_{\mathrm{opt}}\right(\widehat{\alpha },\widehat{\eta }\left)\right)$ are RAL estimators in models ${\mathcal{B}}^{\mathrm{id}}$ or ${\mathcal{B}}^{\exp }$. If, in addition, the true distribution of the data lies in the intersection submodel $\mathcal{A}\cap {\mathcal{M}}_y\cap {\mathcal{M}}_a$ and model (26) holds, then the difference between the asymptotic variance matrices of $\widehat{\beta }\left(\mathbf{d}\right(\widehat{\alpha }\left)\right)$ and $\widehat{\beta }\left(d_{\mathrm{opt}}\right(\widehat{\alpha },\widehat{\eta }\left)\right)$ is non-negative definite, with the asymptotic variance of $\widehat{\beta }\left(d_{\mathrm{opt}}\right(\widehat{\alpha },\widehat{\eta }\left)\right)$ equalling {Var (S_eff)}⁻¹ = [Var {d_opt(A_i,X_i)∊_i(β*)}]⁻¹.

It follows from Part (ii) of Theorem 4 that $\widehat{\beta }\left(d_{\mathrm{opt}}\right(\widehat{\alpha },\widehat{\eta }\left)\right)$ is a locally semiparametric efficient of β* in model A (and following the general results in Robins and Rotnitzky (2001) then also in models B^id or B^exp) at the intersection submodel in which model (26) and models ${\mathcal{M}}_y$ and ${\mathcal{M}}_a$ all hold.

5 Simulation study

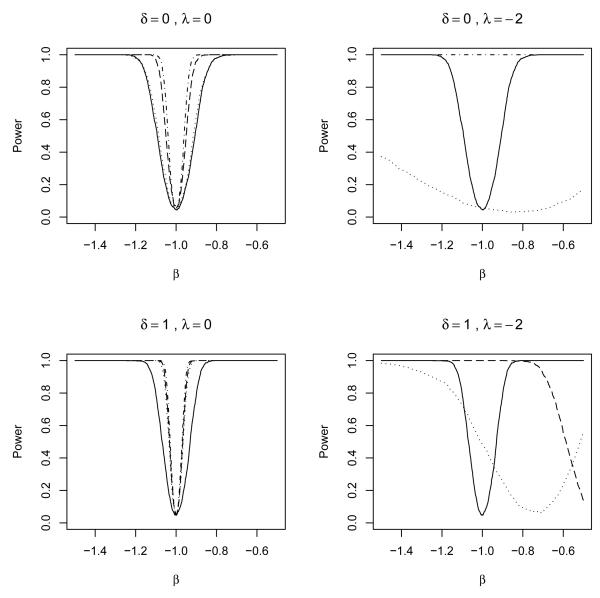
We conducted a simulation experiment to evaluate the behaviour in finite samples of the multiply robust estimators for statistical interaction parameters. Each experiment was based on 1000 replications of random samples of size 500 generated as follows. Exposures were generated as A₁ = 1 + X + δU + ∊₁ and A₂ = 1 — X + δU + ∊₂, where X, U, ∊₁ and ∊₂ are four independent standard normal variates and where δ was set to 0 or 1 to represent settings without and with conditionally independent exposures, given X, respectively. The outcome was generated as Y = −1 + A₁ + A₂ — A₁A₂ + X + λ(A₁ — A₂)X + ∊, where ∊ is a standard normal variate and λ was set to 0 and −2.

In each simulation experiment, 4 estimators were calculated under model A with q₃(A, X; β) = βA₁A₂. The first is an ordinary least squares (OLS) estimate under working model ${\mathcal{M}}_y$, which is defined by $q_2(A_2,X;{\gamma }_2^{\ast })={\gamma }_2^{\ast }{A}_2$, $q_1(A_1,X;{\gamma }_1^{\ast })={\gamma }_1^{\ast }{A}_1$ and $h(X;{\gamma }_0^{\ast })={\gamma }_{0,0}^{\ast }+{\gamma }_{0,1}^{\ast }X$. The second is an efficient G-estimate (G) (Robins, Mark and Newey, 1992), assuming that $q_2(A_2,X;{\gamma }_2^{\ast })={\gamma }_2^{\ast }{A}_2$ and $q_1(A_1,X;{\gamma }_1^{\ast })={\gamma }_1^{\ast }{A}_1$ and that, in addition, model ${\mathcal{M}}_y$ holds or model M_2G holds, which is defined by (correctly specified) second-order linear regression models for E(A_j|X), j = 1, 2 and a (correctly specified) third-order linear regression model for E(A₁A₂|X). The third (CI) is obtained by solving (7) assuming that either model ${\mathcal{M}}_y$ holds, or model M_2CI holds, which is defined by second-order linear regression models for E(A_j|X), j = 1, 2 and the assumption that A₁ ∐ A₂|X. The fourth (ACE) is obtained by solving (22) under working model ${\mathcal{M}}_y$, having first applied the ACE algorithm under the ad-hoc strategy of Section 4, using linear regression models for the conditional expectations in (18) and (19) which involve third-order poly-nomials in A_j (j = 1 and 2, respectively) along with interactions with X, and third-order polynomials in X, and assuming a constant residual variance.

The results of the simulation study are summarized in Table 1 and Figure 1. Variance estimates were obtained via the ordinary nonparametric bootstrap based on 500 resamples for the ACE- and CI-estimate, using sandwich estimators for the G-estimator and using the Fisher information matrix for the OLS estimator. Reported coverage for the ACE and CI-estimates is based on 95% basic bootstrap intervals.

Table 1.

Bias, variance, empirical variance and Type I error rate (α) of tests performed at the 5% signi cance level.

(δ, λ)	Estimator	Bias	Variance	Empirical Var	α
(0,0)	ACE	9 10-5	0.0023	0.0023	0.045
	CI	6 10-4	0.0025	0.0024	0.037
	G	8 10-4	0.00067	0.00072	0.066
	OLS	4 10-4	0.00041	0.00042	0.058
	NI	6 10-4	-	0.0010	-
(0,-2)	ACE	9 10-5	0.0023	0.0023	0.045
	CI	-0.024	0.14	0.11	0.066
	G	1.32	0.0056	0.0058	1.00
	OLS	2.40	0.0050	0.019	1.00
	NI	0.063	-	0.028	-
(1,0)	ACE	3 10-4	0.0013	0.0013	0.050
	CI	3 10-3	0.00059	0.00052	0.053
	G	1 10-4	0.00028	0.00029	0.054
	OLS	5 10-5	0.00023	0.00023	0.050
	NI	5 10-4	-	0.0011	-
(1,-2)	ACE	0.00029	0.0013	0.0013	0.050
	CI	0.12	0.016	0.016	0.24
	G	0.57	0.0062	0.0063	1.00
	OLS	1.33	0.0056	0.029	1.00
	NI	-0.30	-	0.035	-

Figure 1.

Power of 4 statistical interaction tests of the null hypothesis that β* = −1: OLS (long-short dashed), G (long dashed), CI (dotted), ACE (solid).

The results indicate that the ad-hoc implementation of the ACE algorithm yields unbiased estimators for the statistical interaction parameter under each of the four data-generating models. This is because the chosen conditional mean models for (18) and (19) in the ACE algorithm were Sufficiently flexible to yield approximately correctly specified models. None of the other estimators shares this property: the OLS and G-estimates are biased whenever the main effects of A₁ and A₂ are misspecified (i.e. λ ≠ 0), although the OLS estimates are more severely biased. Estimate CI is biased when, in addition, A₁ and A₂ are conditionally dependent, given X (i.e. λ ≠ 0 and δ ≠ 0). The price to pay for the increased robustness of our estimators is a loss of efficiency. This loss can be important when the conditional mean model for the outcome is correctly specified, but overall, reasonable efficiency was obtained with the semiparametric approach. Estimates obtained via the ACE algorithm were substantially more precise than those obtained under the conditional independence assumption (CI) when the conditional mean model ${\mathcal{M}}_y$ was incorrectly specified, even when the exposures were conditionally independent given X. This is in conformity with the fact that, whenever model ${\mathcal{M}}_y$ is incorrectly specified, one may gain efficiency by estimating the exposure distribution under a model that fails to impose a priori known restrictions such as the conditional independence of the exposures (van der Laan and Robins, 2003). Curiously, the CI estimate is much more precise than the estimate obtained using the ACE algorithm when the conditional independence assumption fails and the conditional mean model ${\mathcal{M}}_y$ is correctly specified. This is because the index function d(A_i, X_i) of the CI estimate is much more variable than the corresponding function obtained via the ACE algorithm when the exposures are conditionally dependent, given X. For example, in the extreme case that A₁ = A₂ w.p.1, d(A_i, X_i) = 0 is the only solution to (5) and hence no multiply robust root-n estimators for β* exist under laws at which A₁ = A₂ w.p.1, whilst the estimating functions in (7) yield root-n estimators of β* under such laws (however, only when the conditional mean model ${\mathcal{M}}_y$ is correctly specified). We also evaluated doubly robust estimators obtained by replacing γ* by an ordinary least squares estimate (instead of a G-estimate). This had no impact on the bias and variance of the doubly robust estimators obtained by the ACE algorithm because these are based on correctly specified models for the exposure distribution f(A|X). However, it did impact the bias and variance of the CI estimators under the simulation experiments with conditional dependence: (δ, λ) = (1, 0) (bias −3 10⁻⁴, bootstrap variance 0.00034, empirical variance 0.00035, Type I error rate 0.063) and (δ, λ) = (1, −2) (bias 0.23, bootstrap variance 0.017, empirical variance 0.019, Type I error rate 0.48).

Table 1 further shows results for the numerical integration approach of Section 4 with m = 100 and using (correctly specified) third-order linear regression models with constant variance and normal errors for the conditional distributions of A₁, given (A₂, X), and of A₂, given (A₁, X). The complexity of these models warrants use of the bootstrap for inference. However, no bootstrap-based variance estimates are reported because the numerical integration approach was extremely time-consuming. Table 1 shows that the obtained estimates (NI) are more efficient than those obtained under the ad-hoc strategy when the conditional mean model for the outcome is correctly specified, but they are biased and have greater imprecision otherwise. This is due to numerical approximation error and the fact that, when the conditional mean model for the outcome is incorrectly specified, the estimation procedure relies more heavily on restriction (5), and thus on the numerical integration. Indeed, the bias of the estimates diminished noticeably upon repeating the numerical integration approach for m = 200, at the expense of a serious increase in computation time.

6 Data analysis

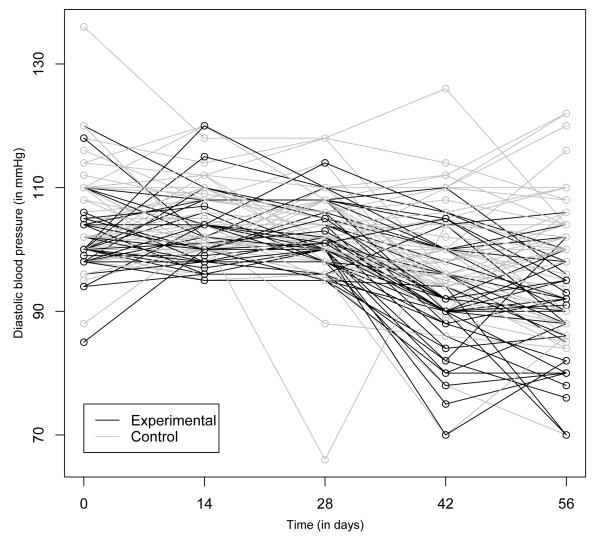
To illustrate the methods, we re-analyze data from a placebo-controlled randomized trial conducted in 1989-1990 in the UK to study blood pressure reduction, as described in Goetghebeur and Lapp (1997). The trial started with a run-in period of 4 weeks whereby all patients received placebo tablets and after which they were randomized to 4 weeks of one of two active treatments (A or B) or placebo. Diastolic blood pressure measurements were taken every 2 weeks. For illustration, we analyze the subset of 105 patients randomized to treatment A or placebo, ignoring 2 patients with missing outcome data. Figure 2 shows a profile plot of the data.

Figure 2.

Profile plot of diastolic blood pressure in 2 treatment arms.

Let Y denote diastolic blood pressure, A₁ be a binary variable taking the value 1 for patients randomized to the experimental treatment A during the active study period and 0 otherwise, A₂ denote time in days since enrollment into the study and X measure centered body weight (in kg). Fitting the following model

$$E(Y\mid A_1,A_2,X)={\gamma }_0+{\gamma }_{1}X+{\gamma }_2{A}_2+{\beta }_1{A}_1{A}_2+{\beta }_2{A}_1{A}_{2}X$$

using generalized estimating equations with exchangeable working correlation, yields ${\widehat{\beta }}_1=-0.12$ (SE 0.029) and ${\widehat{\beta }}_2=0.0089$ (SE 0.0044). This suggests that the average change in diastolic blood pressure per day is 0.12 (95% CI 0.067 - 0.18) higher in the experimental treatment arm than in the placebo arm among patients of average body weight. This difference reduces with 0.0089 (95% CI 0.00027 - 0.017) per kg increase in body weight.

To examine whether these results continue to hold, even under possible misspecification of the time evolution and possible interactions of time with body weight, we use the methods developed in this article. These methods, including the efficient score expressions, continue to hold for correlated data provided that scalar outcomes Y_i are replaced by vectors that contain all outcome measurements for the ith cluster, and likewise for the remaining data A_i, X_i, etc. In the analyses below, we let σ²(X_i; β, γ) in (26) be the working covariance matrix obtained via generalized estimating equations and use the bootstrap for inference. Under the valid assumption that the observation times are independent of assigned treatment, given body weight, we now estimate that the average change in diastolic blood pressure per day is 0.14 (95% CI 0.075 - 0.18) higher in the experimental treatment arm than in the placebo arm among patients with average body weight. This difference reduces with 0.014 (95% CI −0.0044 - 0.023) per kg increase in body weight. These estimates are distribution-free because E(A₁|X) = E(A₁) by the fact that randomization happened independently of body weight, and likewise, because E(A₂|X) = E(A₂) by the fact that the study design was completely balanced in time. In particular, the obtained estimates will be valid, even if the main effects of time and body weight (and possible interactions between both) have been incorrectly specified. Using the ACE algorithm we obtain similar, but slightly less efficient estimates of 0.13 (95% CI 0.075 - 0.18) for the main effect and 0.017 (95% CI −0.0078 - 0.028) for the interaction. All results confirm that the reduction in blood pressure over time is significantly different in both treatment arms. Given that standard estimates for statistical interactions can be very sensitive to the model for the main effects, these new results are more trustworthy, at the expense of a relatively limited degree of precision loss.

Alternatively we could have used randomization inference (Rosenbaum, 2002) for estimating the 2 considered interactions. This would also yield distribution-free inference by the fact that the ‘main’ effect of A₁ can be assumed to be zero and thus its misspecification is not at issue. Even so, the proposed multiply robust estimators enjoy a greater attraction than estimators obtained from a computationally more involved randomization inference, because they are available in closed-form. Furthermore, it is unclear how randomization inference could protect against misspecification of both main exposure effects. For further discussions on randomization inference versus semiparametric inference, see Robins (2002).

7 Conclusion

In this article, we have developed multiply robust estimators for statistical interaction parameters indexing additive or multiplicative conditional mean models. The estimators in the additive model are especially attractive in settings where the distribution of exposure given the extraneous covariates X is known, as is generally the case in randomized follow-up studies and family-based genetic association studies, because they can be used to construct asymptotically distribution-free tests of the no-interaction hypothesis, even when the vector X is high dimensional with continuous components. This makes our approach distinct from existing approaches, which ignore prior information on the exposure distribution. Our proposed approach can be used quite generally, even when, as in most observational studies, no such prior information is available, because an inference concerning an interaction effect under our approach has multiple chances, rather than only one chance, to be correct or nearly correct. In future work, we will apply the proposed estimators to develop scale-invariant interaction tests based on the Sufficient-component cause framework. In addition, we will extend the proposed methods to allow for ascertainment conditions, such as frequently encountered in genetic association studies, whereby data are sampled conditional on the outcome.