Abstract
Gene duplication is an important mechanistic antecedent to the evolution of new genes and novel biochemical functions. In an attempt to assess the contribution of gene duplication to genome evolution in archaea and bacteria, clusters of related genes that appear to have expanded subsequent to the diversification of the major prokaryotic lineages (lineage-specific expansions) were analyzed. Analysis of 21 completely sequenced prokaryotic genomes shows that lineage-specific expansions comprise a substantial fraction (∼5%–33%) of their coding capacities. A positive correlation exists between the fraction of the genes taken up by lineage-specific expansions and the total number of genes in a genome. Consistent with the notion that lineage-specific expansions are made up of relatively recently duplicated genes, >90% of the detected clusters consists of only two to four genes. The more common smaller clusters tend to include genes with higher pairwise similarity (as reflected by average score density) than larger clusters. Regardless of size, cluster members tend to be located more closely on bacterial chromosomes than expected by chance, which could reflect a history of tandem gene duplication. In addition to the small clusters, almost all genomes also contain rare large clusters of size ≥20. Several examples of the potential adaptive significance of these large clusters are explored. The presence or absence of clusters and their related genes was used as the basis for the construction of a similarity graph for completely sequenced prokaryotic genomes. The topology of the resulting graph seems to reflect a combined effect of common ancestry, horizontal transfer, and lineage-specific gene loss.
“Natural selection merely modified while redundancy created.” (Susumu Ohno 1970)
This millenial year marks the thirtieth anniversary of the publication of Evolution by Gene Duplication, Ohno's treatise on the primacy of gene duplication as an evolutionary force (Ohno 1970). This seminal work is characterized by a relentless emphasis on the importance of gene duplication in creating new genes and novel functions. Ohno's model of evolution by gene duplication rests on the assertion that duplication creates the redundancy necessary to free one copy of a gene from the constraints of purifying selection. Once thus liberated, the redundant gene is free to accumulate once-forbidden mutations and evolve a new function. Ohno's particular model of evolution by gene duplication and, specifically, the role of natural selection in the process, has been contended on several fronts (Hughes and Hughes 1993; Zhang et al. 1998; Hughes 1999; Stoltzfus 1999); however, the importance of gene duplication in genome evolution remains unquestioned.
The availability of numerous complete genome sequences, primarily those of prokaryotes (archaea and bacteria), provides a wealth of data that can be examined to assess various aspects of the role of gene duplication in genome evolution. Families of paralogs (related genes within the same genome) comprise a significant proportion of prokaryotic gene sets (Brenner et al. 1995; Koonin et al. 1995; Labedan and Riley 1995; Huynen and van Nimwegen 1998). This work is specifically concerned with the contribution of gene duplication to the genomic differences between lineages of prokaryotes. A lineage as defined here corresponds to a completely sequenced representative of a single archaeal or bacterial genus. At the time that this work was commenced, there existed 24 completely sequenced bacterial genomes representing 21 lineages. The evolutionary depth of different lineages defined in this fashion may vary depending on the number of completely sequenced genomes for a given phylogenetic group. For example, because there are a number of complete Proteobacteria genomes, Proteobacterial lineages are shallower than the Deinococcus lineage, where the entire phylogenetic group is represented by a single complete genome sequence. Comparative genomic sequence analyses were employed to delineate and examine what will hereafter be referred to as lineage-specific expansions. Lineage-specific expansions are groups of paralogous genes (duplicated copies from the same genome) generated subsequent to the divergence of the prokaryotic lineages analyzed.
Quantitative analyses of lineage-specific expansions were employed to address several specific questions: First, what fraction of each prokaryotic genome is comprised of genes that have duplicated subsequent to the divergence of individual lineages? Second, how does the extent of lineage-specific expansion depend on the genome size? Third, what is the frequency distribution and level of sequence conservation for clusters of lineage-specific expansions of different sizes (different numbers of genes)? Fourth, how are members of lineage-specific expansions distributed along bacterial chromosomes? It was also hoped that examination of the patterns of gene duplication in individual bacterial lineages would yield some clues as to the genomic determinants of phenotypic evolution and adaptation of microbes to their specific lifestyles. Finally, the phyletic distribution of genes related to those involved in lineage-specific expansions was analyzed to produce a graph of genome similarity for completely sequenced bacterial genomes.
RESULTS AND DISCUSSION
Contribution of Lineage-Specific Expansions to Bacterial Genomes
A set of 21 completely sequenced archaeal and bacterial genomes, each representing a unique lineage (genus), was assayed for the presence of lineage-specific expansions. Lineage-specific expansions are defined here as expansions of paralogous groups of genes that could be inferred to have occurred subsequent to the divergence of the prokaryotic lineages. Candidate lineage-specific expansions were delineated using both the BLAST (Altschul et al. 1997) program to perform amino acid sequence similarity searches and the SEALS program suite (Walker and Koonin 1997) to organize and postprocess the data, as described in the Methods section. This initial fully automated procedure included the use of a single-linkage algorithm as the final step in cluster construction. Clusters generated by such a method may contain nonhomologous protein pairs bridged via multidomain proteins (Watanabe and Otsuka 1995; Koonin et al. 1996). To correct for this artifact, all clusters of size ≥3 proteins were manually inspected to ensure that they contain only homologous proteins. A total of 812 such clusters were analyzed, and 120 (∼15%) required revision, resulting in a total of 856 verified clusters (size ≥3 proteins). Altogether, a total of 2730 clusters among the 21 genomes was detected, each encoded by paralogous genes that probably evolved via lineage-specific duplications.
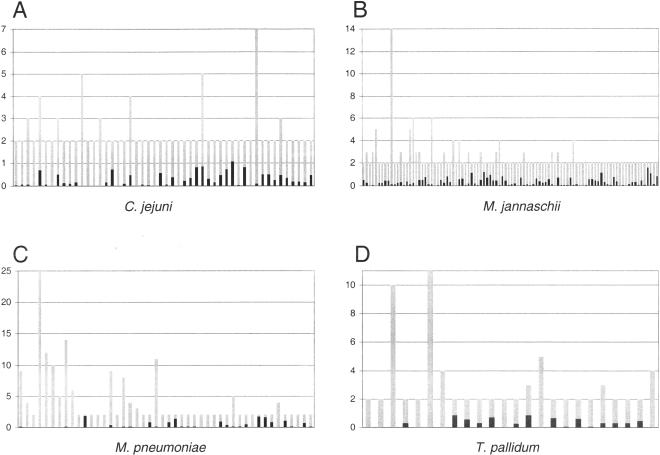
To further assess the robustness of these potential lineage-specific expansions, all clusters were reanalyzed using the best hits (BeTs) approach that underlies the construction of clusters of orthologous groups of proteins (COGs; Tatusov et al. 1997, 2000). A BeT is the best BLAST hit (highest score or lowest e value) retrieved from a single genome for any given query sequence. If a cluster represents a unique terminal expansion of genes, then all cluster members should converge on one BeT (or no BeTs at all if there is no significant hit) when queried against any other genome. Each cluster from a given genome was queried against all other complete genomes, and the number of BeTs for each cluster was recorded. The vast majority (∼94%) of clusters had either 0 or 1 BeTs in any other genome. For example, a comparison between the cluster sizes for four representative genomes and the average number of BeTs per cluster in all other genomes shows that virtually all clusters average <1 BeT per genome (Fig. 1). Approximately 22% of clusters do not have any significant hits in any other genome (Table 1). These unique clusters represent lineage-specific expansions in the strictest sense. The narrow phyletic distribution of these clusters suggests that they were either derived de novo in their current lineage or that they have diverged to such an extent that significant sequence similarity to homologs in other lineages is no longer readily apparent. Thus, such clusters seem to be particularly likely to possess some adaptive significance for the lineage of organisms in which they are found.
Figure 1.
Cluster sizes in number of genes (Y-axis, gray bars) for four representative species, (A) Campylobacter jejuni, (B) Methanococcus janaschii, (C) Mycoplasma pneumoniae, and (D) Treponema pallidum, compared to the average number of best hits (BeTs) for each cluster (Y-axis, black bars) in all other completely sequenced bacterial genomes.
Table 1.
Lineage-Specific Gene Family Expansions Detected by Analysis of Completely Sequenced Genomes
| Domain | Division | Species | Genes | Lineage-specific clusters | Genes in lineage-specific clusters | Percent genome in lineage-specific clusters | Average score density | No. of clusters with no significant BeTs in other genomes | Percent of clusters with no significant BeTs in other genomes |
|---|---|---|---|---|---|---|---|---|---|
| Archaea | Euryarchaeota | A. fulgidus | 2407 | 197 | 553 | 23.0 | 0.75 | 35 | 17.8 |
| M. thermoautotrophicum | 1869 | 97 | 265 | 14.2 | 0.76 | 19 | 19.6 | ||
| M. jannaschii | 1715 | 96 | 238 | 13.9 | 0.71 | 12 | 12.5 | ||
| P. horikoshii | 2064 | 129 | 310 | 15.0 | 0.60 | 8 | 6.2 | ||
| Crenarchaeota | A. pernix | 2694 | 64 | 138 | 5.1 | 0.64 | 14 | 21.9 | |
| Bacteria | Aquificales | A. aeolicus | 1522 | 80 | 184 | 12.1 | 0.71 | 9 | 11.3 |
| Thermotogales | T. maritima | 1846 | 93 | 261 | 14.1 | 0.72 | 12 | 12.9 | |
| Deinococcus group | D. radiodurans | 3103 | 201 | 525 | 16.9 | 0.66 | 38 | 18.9 | |
| Spirochaetales | B. burgdorferi | 1255 | 61 | 220 | 17.5 | 0.86 | 39 | 63.9 | |
| T. pallidum | 1031 | 24 | 74 | 7.2 | 0.52 | 9 | 37.5 | ||
| Chlamydia group | C. pneumoniae | 1052 | 35 | 129 | 12.3 | 0.63 | 14 | 40.0 | |
| Cyanobacteria | Synechocystis sp. | 3169 | 238 | 785 | 24.8 | 0.72 | 59 | 24.8 | |
| Firmicutes | B. subtilis | 4100 | 437 | 1202 | 29.3 | 0.76 | 83 | 19.0 | |
| M. pneumoniae | 677 | 46 | 191 | 28.2 | 0.69 | 7 | 15.2 | ||
| U. urealyticum | 611 | 25 | 83 | 13.6 | 0.70 | 9 | 36.0 | ||
| M. tuberculosis | 3918 | 350 | 1309 | 33.4 | 0.70 | 128 | 36.6 | ||
| Proteobacteria | E. coli | 4289 | 383 | 1031 | 24.0 | 0.81 | 59 | 15.4 | |
| H. influenzae | 1709 | 44 | 96 | 5.6 | 1.12 | 2 | 4.6 | ||
| C. jejuni | 1634 | 50 | 119 | 7.3 | 0.68 | 11 | 22.0 | ||
| H. pylori | 1553 | 65 | 203 | 13.1 | 0.85 | 22 | 33.9 | ||
| R. prowazekii | 834 | 15 | 40 | 4.8 | 0.65 | 3 | 20.0 |
Despite the fact that, by definition, the duplications that generated lineage-specific expansions have occurred relatively recently over evolutionary time, these events contribute substantially to coding capacity of bacterial genomes (Table 1). Among the 21 complete genomes analyzed here, recently expanded clusters of genes encode from ∼5% to >33% of an individual genome's predicted proteins. These results underscore the potential adaptive significance of lineage-specific expansions. Similar sequence similarity–based approaches have been employed in individual genome studies (e.g., White et al. 1999; Heidelberg et al. 2000; Read et al. 2000; Tettelin et al. 2000) to determine the extent of recent gene duplications. These individual studies also reveal substantial numbers of recent lineage-specific duplications. However, to our knowledge, this study is the first systematic comparative analysis of this kind.
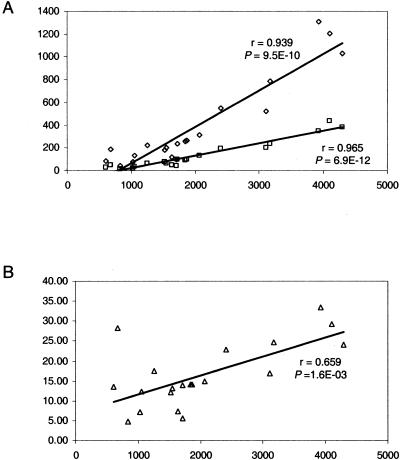
Not surprisingly, there is a strong positive correlation between genome size (represented as the number of predicted protein encoding genes) and the number of recently duplicated genes (Fig. 2A). Larger genomes will tend to have higher numbers of recently duplicated genes simply because of the fact that they possess more genes overall. Less expected is the positive correlation found between genome size and the proportion of the genome made up of recently duplicated genes (Fig. 2B); an exception to this general trend is Mycoplasma pneumoniae, a small genome with a high level of lineage-specific gene family expansion (Table 1; Fig. 2B). This correlation may reflect the fact that genomes consist of a subset from a finite pool of gene families (Chothia 1992; Zhang and DeLisi 1998; Wolf et al. 2000). As genome size increases and the number of families represented in the given genome approaches the total number of gene families, the likelihood of adding a new family falls and the proportion of the genome made up by paralogous genes, including recently duplicated ones, is expected to increase. A complementary explanation would posit that lineage-specific duplications possess significant adaptive value (see also below) and, thereby, are favored in certain lineages, resulting in the overall increase in the genome size.
Figure 2.
Linear correlation between genome size (in number of genes) and the parameters of lineage-specific expansions. Correlation coefficients (r) and significance levels (P) were determined using ordinary least squares linear regression. (A) For completely sequenced prokaryotic genomes, genome size (X-axis) is plotted against the number of genes in lineage-specific clusters (diamonds) and the number of such clusters (squares). (B) Genome size (X-axis) is plotted against the percentage of the genome made up of lineage-specific clusters (triangles).
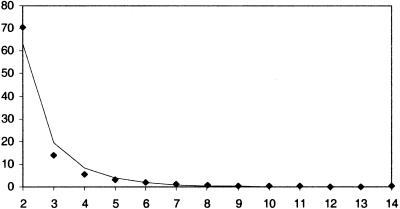
Consistent with the notion that these analyses reveal recently duplicated genes, the majority of lineage-specific clusters consist of very few genes. While cluster size ranges from two to 90 genes, >70% of the clusters are of size 2, and clusters of sizes 2–4 genes account for >90% of all clusters (Fig. 3). Large clusters are much more rare; for instance, there are only 13 clusters of size ≥20. The frequency distribution (99% quantile) of cluster sizes was fit with the logarithmic approximation (Fig. 3). Previously, frequency distributions for gene families for a number of different genomes were found to be compatible with power law distributions (Huynen and van Nimwegen 1998). Because the lineage-specific expansions analyzed here represent more recent duplications, the cluster sizes are smaller and the distribution has a less substantial tail than those seen for more ancient gene families (Huynen and van Nimwegen 1998). The logarithmic approximation fits the distribution seen here slightly better than the power law approximation, although the difference between the two fits is not significant. However, neither theoretical distribution has a significant fit to the data, and so it is difficult to reach any meaningful biological conclusion concerning the shape of the cluster size frequency distribution.
Figure 3.
Frequency distribution (99% quantile) of lineage-specific expansion cluster sizes (X-axis in numbers of genes). Observed data are shown with diamonds. These data were fit using the logarithmic approximation (line).
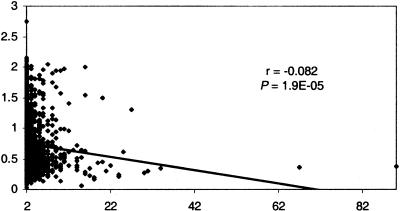
Levels of sequence similarity among the encoded products of the clusters detected here were assessed using score density in the protein sequence alignment as the criterion (see Methods). The average cluster score densities per genome also provide some indication that the clusters are comprised of relatively recently duplicated genes. Most of these average values are in the narrow range between 0.6 and 0.9 (Table 1), with an average over all genomes of ∼0.73, which corresponds to an average of ∼40% pairwise sequence identity. For comparison, the median of the distribution of the identity level between orthologs in pairs of genomes from different bacterial lineages typically lies at ∼30% (Grishin et al. 2000). In addition, a slight but statistically significant negative correlation between cluster size and score density (Fig. 4) indicates that smaller and presumably more recently duplicated clusters tend to have higher score densities. However, cluster size only explains a small fraction of the variability in score density.
Figure 4.
Linear correlation between cluster size in number of genes (X-axis) and average score density per cluster (Y-axis). Correlation coefficients (r) and significance levels (P) were determined using ordinary least squares linear regression. Removal of the two largest clusters (size 67 and 90) results in a greater magnitude of r and a lower P value (i.e., a stronger negative correlation).
Chromosomal Distribution of Cluster Members
The process of gene duplication often results in the presence of tandem or closely linked paralogous genes (Li 1997). Subsequent genome rearrangements may then dissolve these physical associations. Genome rearrangement seems to be a particularly potent force in bacterial genome evolution, as there is relatively little conservation of gene order, at least on a greater than operon scale, between even closely related species (Koonin and Galperin 1997; Watanabe et al. 1997). Because lineage-specific expansions consist of relatively recently duplicated genes, it could be expected that the history of tandem gene duplication would still be reflected in the chromosomal distribution of cluster members. However, initial examination of the chromosomal distribution of the genes that belong to lineage-specific paralogous families failed to immediately reveal systematic clustering. Therefore, to address this issue, a statistical method was developed that tests the null hypothesis that cluster members are distributed uniformly on the chromosome. This method tests each cluster independently, assessing the probability of the observed minimum length between adjacent genes, and pools the data for all clusters in a genome (see Methods). For almost every genome, the null hypothesis of random distribution could be rejected with high statistical significance (Table 2). Thus, cluster members tend to be closer together on the chromosome than expected by chance. An exception to this pattern is seen only for the crenarchaeon Aeropyrum pernix. Analysis of A. pernix clusters results in only a marginally significant rejection of the null hypothesis. This is probably because of the fact that the A. pernix proteome is vastly overpredicted and likely consists of far fewer genes than reported (Natale et al. 2000).
Table 2.
Test For Non-Random Chromosomal Distribution of Cluster Members Based on Analysis of All Clusters in a Genome
| Domain | Division | Species | χ2a | dfb | Pc |
|---|---|---|---|---|---|
| Archaea | Euryarchaeota | A. fulgidus | 754.13 | 394 | 6.77E-25 |
| M. thermoautotrophicum | 443.55 | 194 | 1.38E-21 | ||
| M. jannaschii | 332.79 | 192 | 1.23E-09 | ||
| P. horikoshii | 533.90 | 258 | 2.2E-21 | ||
| Crenarchaeota | A. pernix | 157.41 | 128 | 4.0E-02 | |
| Bacteria | Aquificales | A. aeolicus | 307.94 | 160 | 1.97E-11 |
| Thermotogales | T. maritima | 354.70 | 186 | 1.23E-12 | |
| Spirochaetales | T. pallidum | 145.31 | 48 | 1.01E-11 | |
| Chlamydia group | C. pneumoniae | 270.18 | 70 | 2.67E-25 | |
| Cyanobacteria | Synechocystis sp. | 800.46 | 476 | 6.94E-19 | |
| Firmicutes | B. subtilis | 1623.13 | 874 | 1.44E-47 | |
| M. pneumoniae | 227.86 | 92 | 1.61E-13 | ||
| U. urealyticum | 136.53 | 50 | 5.82E-10 | ||
| M. tuberculosis | 1323.16 | 700 | 6.90E-41 | ||
| Proteobacteria | E. coli | 1227.99 | 766 | 5.08E-24 | |
| H. influenzae | 173.99 | 88 | 1.33E-07 | ||
| C. jejuni | 276.12 | 100 | 2.04E-18 | ||
| H. pylori | 278.28 | 130 | 8.17E-13 | ||
| R. prowazekii | 68.24 | 30 | 8.33E-05 |
Value obtained by combining all p-values for individual clusters in a genome (see Methods).
Degrees of freedom = 2 *number of clusters in a genome.
Probability associated with the χ2 value and the degrees of freedom.
Because of the fact that the vast majority of clusters are small in size, as well as the conservative nature of the statistical test described above, the statistical signal in the whole genome test is derived almost entirely from these small clusters. Thus, in addition to the whole genome tests, the large clusters (size ≥20) were analyzed individually to test for random chromosomal distribution. The test employed for the large clusters was based on a comparison between the observed distribution of relative distances between adjacent genes of a single cluster and the expected distribution of distances estimated using the exponential approximation (Wolf et al. 2000). The results of this test reveal that the large clusters are also nonrandomly distributed along the chromosome (Table 3).
Table 3.
Test For Non-Random Chromosomal Distribution of Cluster (Size ≥20) Members Using Exponential Distribution
| Species | Cluster size | dmaxa | Pb |
|---|---|---|---|
| A. fulgidus | 24 | −0.1176 | 2.43 E-07 |
| E. coli | 31 | 0.1107 | 1.19 E-10 |
| H. pylori | 34 | 0.0931 | 3.92 E-09 |
| M. pneumoniae | 25 | 0.2119 | 8.34 E-25 |
| M. tuberculosis | 20 | 0.5198 | 2.61 E-94 |
| M. tuberculosis | 21 | 0.0836 | 0.0042 |
| M. tuberculosis | 24 | 0.8272 | 0 |
| M. tuberculosis | 67 | 0.2634 | 5.73 E-271 |
| M. tuberculosis | 90 | 0.1854 | 9.94 E-248 |
| Synechocystis sp. | 20 | 0.1917 | 3.42 E-13 |
| Synechocystis sp. | 22 | 0.2016 | 1.66 E-17 |
| Synechocystis sp. | 27 | 0.1346 | 6.82 E-12 |
| Synechocystis sp. | 30 | 0.1011 | 2.05 E-08 |
The maximum deviation (dmax) between the expected values based on the exponential distribution and observed values based on the relative distances between adjacent cluster members.
The probability associated with dmax.
Potential Adaptive Significance of Large Lineage-Specific Clusters
Among the recently duplicated genes analyzed here, small clusters predominate. There are only 13 large clusters of size ≥20 (Table 4). The presence of rare large clusters of recently duplicated genes is particularly likely to reflect selective pressure for their increased or varied coding capacity. Of interest is the obvious excess of large lineage-specific clusters in Actinomycetes (Mycobacterium tuberculosis; Table 4), although we presently cannot link this observation to this organism's lifestyle in specific terms. Presented here are several cases where the potential adaptive significance of these rare large clusters is explored.
Table 4.
Domain Composition and Functions of Lineage-Specific Clusters of Size ≥ 20a
| Species | Cluster size | Average score density | Domain organizationb | Function |
|---|---|---|---|---|
| M. tuberculosis | 90 | 0.38 | Multitransmembrane proteins; PPE family | Predicted surface protein, interaction with host cells |
| M. tuberculosis | 67 | 0.37 | Signal-peptide-containing, non-globular proteins, consist mostly of glycine-rich repeats; PE family | Predicted surface protein, interaction with host cells |
| H. pylori | 34 | 0.34 | Outer membrane protein | Predicted surface protein, interaction with host cells |
| E. coli | 31 | 0.30 | Helix-turn-helix DNA-binding domain (LysR family), solute-binding domain | Transcription regulation of various metabolic operons |
| Synechocystis sp. | 30 | 0.26 | Histidine kinase | Signal transduction, sensing of environmental stimuli |
| M. pneumoniae | 25 | 0.62 | Predicted non-globular domain | Unknown |
| M. tuberculosis | 24 | 0.21 | Signal-peptide-containing protein | Predicted surface protein (mce1), interaction with host cells |
| A. fulgidus | 24 | 0.23 | Histidine kinase | Signal transduction, sensing of environmental stimuli |
| Synechocystis sp. | 22 | 0.39 | Diguanylate cyclase/phosphodiesterase (GGDEF and EAL domains) | Signal transduction, sensing of environmental stimuli |
| M. tuberculosis | 21 | 0.29 | Short chain dehydrogenase | Dehydrogenases with different specificities (related to short-chain alcohol dehydrogenases) |
| M. tuberculosis | 20 | 0.45 | Beta-ketoacyl synthase, acyl transferase, thioesterase | Polyketide synthase |
Two more clusters of size ≥20a included transposases and were omitted.
Analyzed using the SMART, PSI-BLAST and SEG programs.
The nonrandom distribution of cluster members may be caused by the recent history of tandem duplication, as suggested above. However, in cases of close proximity of cluster members, such gene arrangement may also be maintained in evolution because of coregulation of recently duplicated genes. A cluster of size 24 in M. tuberculosis exemplifies this possibility. This cluster consists of four groups of six contiguous genes. These genes are located within four duplicated operons with identical organization. The operons are not well characterized, but each encodes one copy of the mammalian cell entry protein (mce1-4), one copy of a membrane lipoprotein (lprK-N), and several other predicted membrane proteins (Cole et al. 1998; Tekaia et al. 1999a; Wiker et al. 1999). The mce1 protein has been shown to be involved in entry and survival inside macrophages, which is critical to the organism's ability to escape host defenses (Arruda et al. 1993). M. tuberculosis has also been shown to invade epithelial cell lines (Arruda et al. 1993; Bermudez et al. 1995). The presence of four operons, each with identical organization but diverged coding sequences, seems to provide for a substantially variable cell invasion repertoire. It is even possible that the different operons mediate entry into different cell types. Thus, duplication of the mce operons could represent an adaptation that aids long-term survival of the bacterium in an infected host.
Several of the large clusters consist of outer membrane proteins of pathogenic bacteria presumed to be involved in interaction with target cells of their host organism (Table 4). These include the Helicobacter pylori outer membrane protein (Hop) family (Tomb et al. 1997; Alm et al. 2000) as well as the PE and PPE families of M. tuberculosis (Cole et al. 1998; Tekaia et al. 1999a). The surface variability conferred by the mulitple coding capacities of these families is also likely to play a role in the avoidance and escape from host immune surveillance. The PE and PPE families may, in fact, represent the main source of anitgenic variation in M. tuberculosis (Cole et al. 1998). Genes belonging to these recently expanded families of outer membrane proteins demonstrate a number of different mechanisms that generate surface variability. These include changes in gene expression mediated by slipped-strand mispairing at mono- and dinucleotide repeats (Tomb et al. 1997) and conversion between paralogous genes within a genome (Jordan et al. 2001).
One of the large clusters detected in M. tuberculosis (size 21) is unique in that it consists of genes that encode metabolic enzymes (Table 4). Most of the members of this cluster are uncharacterized homologs of short-chain alcohol dehydrogenases. The cluster also contains several characterized members, including the dehydrogenases fabG2, fabG3, and acrA1, which are involved in fatty acid biosynthesis. AcrA1 is involved in the biosynthesis of mycolic acids (Yuan et al. 1995), a major component of mycobacterial cell walls. This expansion may also reflect adaptive evolution of the bacterial cell surface. However, in this case, variability in surface components appears to be achieved through modification of enzymes that synthesize the surface structures (lipids) as opposed to the previous examples, where the surface structures (proteins) themselves were modified.
Two large clusters that expanded in diverse lineages, namely the archaeon Archaeoglobus fulgidus (Klenk et al. 1997) and the cyanobacterium Synechocystis sp. (Kaneko et al. 1996), consist of signal-transduction histidine kinases (Table 4). Smaller expansions of histidine kinases are also seen in many other lineages. The presence of multiple lineage-specific signal-transduction histidine kinases probably allows microbes to process environmental cues in a highly specific manner. Interestingly, A. fulgidus encodes far fewer response regulators than signal-transduction histidine kinases (Klenk et al. 1997). Seemingly, each response regulator must be capable of receiving multiple inputs from different signal-transduction histidine kinases. Such interactions mediated by multiple unique signal-tansduction histidine kinases could result in combinatoric levels of complexity and facile adaptive responses to challenges posed by differing environments.
Yet another type of adaptation is probably represented by the major expansion of LysR-family transcriptional regulators in Escherichia coli (Table 4) that provide for the versatility of metabolic regulation critical for this bacterium's lifestyle.
In addition to true functional diversification, it is conceivable that the adaptive value of some of the lineage-specific gene family expansions could lie in the potential for dosage regulation of the respective gene proteins and/or differential regulation of gene expression in response to environmental stimuli.
Genome Clustering Based on the Distribution of Lineage-Specific Expansions
The procedure employed to assess the robustness of the clusters encompassing lineage-specific expansions relied on a COG-like approach where, for each organism analyzed, the number of BeTs corresponding to each cluster was recorded. This analysis resulted in a wealth of data with potential relevance to the relationships between bacterial genomes. Specifically, the presence or absence of counterparts (typically, in the form of single genes; see above) to the lineage-specific clusters present in the given genome in another genome can be taken as a measure of similarity between the two genomes. Similar approaches have been employed using the presence or absence of all proteins encoded by a set of complete genomes (Fitz-Gibbon and House 1999; Snel et al. 1999; Tekaia et al. 1999b). The narrow phyletic distribution of genes homologous to any given cluster may have some added utility for this type of approach because clusters and their counterparts represent a data set enriched for shared derived character states (synapomorphies) that can unite related genomes via a parsimony graph.
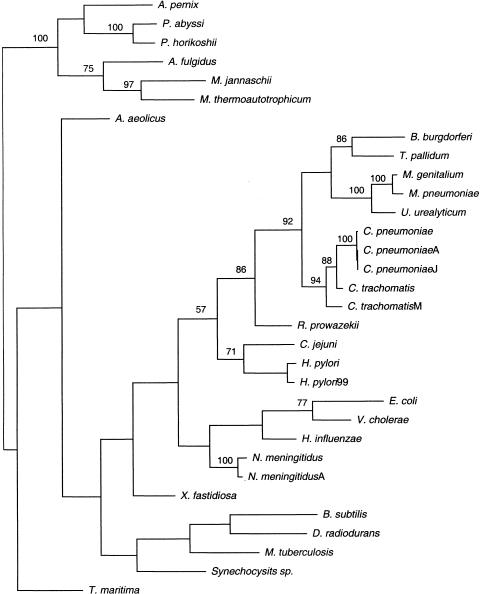
For each of the 32 complete archaeal and bacterial genomes, each of the 2730 clusters was scored with 0 if there were no homologs to cluster members or with 1 if there was at least one homolog. This resulted in a binary matrix with 2730 character states for each genome. This matrix was used in parsimony graph reconstruction of the 32 complete archaeal and bacterial genomes (Fig. 5). The resulting graph does not represent a phylogeny in sensu strictu, as the signal in the data may be derived from horizontal transfer and gene loss in addition to the pattern of speciation. The branching pattern is therefore considered to represent a graph of genome similarity.
Figure 5.
Maximum parsimony graph for completely sequenced archaeal and bacterial genomes. The root was provisionally placed between archaea and bacteria.
This genome similarity graph shows some interesting patterns (Fig. 5). The archaea and bacteria form two separate well-supported groups, as expected. Within the archaea, the grouping of two methanogens, M. jannaschii and M. thermoautotrophicum, is confidently retained, probably reflecting common ancestry as well as, possibly, horizontal gene exchange. More unexpected is the grouping of the crenarcheon A. pernix with the two species of Pyrococci (although this node is not strongly statistically supported). Similar clustering has been observed in the analysis of cooccurrence of genomes in the COGs and may reflect a similar pattern of gene loss (Natale et al. 2000). The two hyperthermophilic bacteria, Aquifex aeolicus and Thermotoga maritima, come as the most basal branches of the bacterial group. While this is consistent with phylogenetic reconstructions based on rRNA sequences (Pace 1997), it is also likely to reflect the contribution of horizontal transfer between organisms in similar extreme environments, particularly exchange of genes between archaea and bacteria (Aravind et al. 1998; Nelson et al. 1999). The largest and most strongly supported assemblage within the bacterial part of the graph consists of the small pathogenic bacteria. This grouping appears to reflect similarity caused by substantial gene loss rather than the pattern of speciation. This is illustrated by the clustering of the Mycoplasma and Ureaplasma genomes whose phylogenetic affinity clearly lies with the Gram-positive bacteria (represented by Bacillus subtilis in the analyzed set of genomes) with the Spirochetes and Chlamydia. There is a group (albeit poorly supported) of large bacterial genomes that consists of B. subtilis, M. tuberculosis, Deinococcus radiodurans, and the cyanobacterium Synechocystis sp. This grouping may reflect retention of genes that have been lost in other lineages in addition to the pattern of speciation. In contrast, the β-γ-proteobacterial group (E. coli, Vibrio cholerae, Haemophilus influenzae, and Neisseria meningitidis) clearly reflects a phylogenetic relationship that overshadows the effect of lineage-specific gene loss. Thus, the graph topology recovered from the data on lineage-specific gene expansions reflects a combined effect of phylogenetic relationships, common patterns of gene loss, and horizontal transfer.
Conclusions
Paralogous gene families that have expanded subsequent to the divergence of archaeal and bacterial lineages comprise a significant fraction of the genome coding capacity. As such, these families seem likely to contribute substantially to the genomic determinants of phenotypic differences between bacterial lineages. Examination of rare large clusters of recently duplicated genes gives some clue as to the potential adaptive significance of lineage-specific expansions. A systematic experimental study of these differentially expanded families could advance our understanding of the diverse routes of adaptation in prokaryotes.
METHODS
Genome Sequence Data
Completely sequenced archaeal and bacterial genomes available on the NCBI ftp server (ftp://ncbi.nlm.nih.gov/genbank/genomes/bacteria) as of March 1, 2000, were analyzed to uncover lineage-specific expansions of gene families. Lineage-specific expansions are considered here to result from gene duplications that occur subsequent to the divergence of prokaryotic genera. To conform to this criterion, congeneric pairs of genomes were not considered together in the analysis. For the four congeneric pairs available at that time, the larger of the two genomes (in numbers of predicted proteins) was chosen for analysis. This resulted in a final set of 21 complete genomes: Aeropyrum pernix K1, Archaeoglobus fulgidus, Aquifex aeolicus VF5, Borrelia burgdorferi, Bacillus subtilis, Campylobacter jejuni, Chlamydia pneumoniae CWL029, Deinococcus radiodurans R1, Escherichia coli K-12 (MG1655), Haemophilus influenzae Rd, Helicobacter pylori 26695, Methanococcus jannaschii, Mycoplasma pneumoniae M129, Methanobacterium thermoautotrophicum delta H, Mycobacterium tuberculosis H37Rv, Pyrococcus horikoshii OT3, Rickettsia prowazekii Madrid E, Synechocystis sp. PCC6803, Thermotoga maritima, Treponema pallidum, and Ureaplasma urealyticum.
Identification and Characterization of Lineage-Specific Expansions
A database was constructed with all of the predicted protein sequences encoded in the selected 21 complete genomes. In a fully automated procedure, the SEALS program (Walker and Koonin 1997) was used to implement a series of 43,052 BLAST (Altschul et al. 1997) searches (e value cut-off 10−7) against this database, using all predicted protein sequences as queries.
BLAST results from each genome were parsed separately to isolate protein sequences that showed more similarity to protein sequences encoded by that same genome than to protein sequences encoded by any of the other genomes. Such sets of protein sequences and their corresponding genes represent candidate lineage-specific expansions. A single-linkage clustering algorithm was then used to group together related sets of proteins encoded by genes involved in lineage-specific expansions. Under the single-linkage clustering method, multidomain protein(s) may occasionally bridge together two or more unrelated protein families (Watanabe and Otsuka 1995; Koonin et al. 1996). To eliminate this effect, the automatically produced clusters were further refined to ensure that each cluster consisted entirely of proteins with homologous domains. The process of cluster refinement involved the use of several programs for identification of protein domains and multiple alignment analysis including SMART (Schultz et al. 2000), SEG (Wootton and Federhen 1996), COGnitor (Tatusov et al. 2000), and CLUSTALX (Thompson et al. 1997). Concomitantly, the results produced with these programs and the results of additional, iterative database searches with the PSI-BLAST program BLAST (Altschul et al. 1997) were used to predict the functions of uncharacterized clusters.
All clusters were further analyzed by searching cluster members against a database created from the predicted proteins encoded by all 32 of the complete genomes available on the NCBI ftp server as of August 1, 2000. Using BLAST implemented in SEALS (e value cut-off 10−4), each member of a cluster was queried against genome-specific predicted protein sequence databases and the best hit (BeT) to each database was retrieved. The number of BeTs from each cluster to each genome-specific database was recorded.
Pairwise sequence similarity among the encoded products of cluster members was measured in terms of score density. For all pairwise amino acid sequence comparisons, the score density was calculated as the BLAST score divided by the length of subject sequence included in the high-scoring segment pair. Average score densities were calculated for each cluster, and cluster score densities were averaged for each genome.
Statistical Analysis
Two methods were used to evaluate the chromosomal distribution of cluster members. Both methods are based on the relative positions of cluster members expressed in terms of the chromosomal order of genes. The first method evaluates each cluster in the genome based on the minimum relative distance M between any consecutive pair of genes in the cluster. The null hypothesis assumes that the g genes in a cluster are distributed uniformly around a circular genome of length L. The probability that M ≤ m is
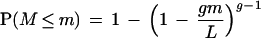 |
1 |
The p values for all clusters in a genome are combined using the Fisher Omnibus test (Bailey and Gribskov 1998). If there are N clusters with p values pI(I = 1,2, …, N), then
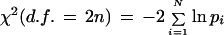 |
2 |
has a χ2 distribution with 2n degrees of freedom.
To evaluate the chromosomal distribution of individual clusters of size ≥20, the exponential probability
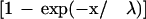 |
3 |
was used to approximate a random cumulative distribution of relative distances between adjacent genes in the cluster (Makarova et al. 1999). The value of λ was numerically approximated using the average distance between adjacent genes in the cluster. The maximum deviation (dmax) between the expected values based on the exponential distribution and observed values based on the relative distances between adjacent cluster members was evaluated using the Kolmogov-Smirnov test (Zar 1999), where
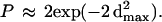 |
4 |
The frequency distribution of cluster sizes was fit with a logarithmic distribution where
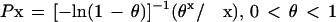 |
5 |
The value of θ was numerically approximated using maximum likelihood.
Parsimony Analysis
The results of the BeTs analysis of the clusters were modified to construct a character matrix for parsimony analysis of the total set of complete bacterial genomes available on the NCBI ftp server as of August 1, 2000. For each cluster in a given genome, every other genome was scored 0 if it had no significant BLAST hits to that cluster or 1 if it had any significant BLAST hits to the cluster. This resulted in a binary matrix of 2730 characters by 32 genomes. This matrix was analyzed using the maximum parsimony method implemented in the PAUP* v4.0 (Swofford 1998) program. The full heuristic search option was used with tree-bisection-reconnection branch swapping and random stepwise addition (10 replicates) of sequences. A single most parsimonious graph requiring 8431 steps was obtained. One hundred bootstrap replicates were performed using the same search options as above. The root was assumed to lie between archaea and bacteria.
Availability of the Complete Results
A complete list of gi numbers (NCBI genInfo identifiers) corresponding to lineage-specific gene family expansions in prokaryotes is available at ftp://ncbi.nlm.nih.gov/pub/koonin/expansions.
Acknowledgments
K.S.M. was supported by grants DE-FG02–98ER62583, DE-FG02–97ER62492, and DE-FG07–97ER20293 from the U.S. Department of Energy and grant 5R01-GM39933–09 from the National Institutes of Health.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL koonin@ncbi.nlm.nih.gov; FAX (301) 480-9241.
Article published on-line before print: Genome Res., 10.1101/gr.166001.
Article and publication are at www.genome.org/cgi/doi/10.1101/gr.166001.
REFERENCES
- Alm RA, Bina J, Andrews BM, Doig P, Hancock RE, Trust TJ. Comparative genomics of helicobacter pylori: Analysis of the outer membrane protein families. Infect Immun. 2000;68:4155–4168. doi: 10.1128/iai.68.7.4155-4168.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–33402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aravind L, Tatusov RL, Wolf YI, Walker DR, Koonin EV. Evidence for massive gene exchange between archaeal and bacterial hyperthermophiles. Trends Genet. 1998;14:442–444. doi: 10.1016/s0168-9525(98)01553-4. [DOI] [PubMed] [Google Scholar]
- Arruda S, Bomfim G, Knights R, Huima-Byron T, Riley LW. Cloning of an M. tuberculosis DNA fragment associated with entry and survival inside cells. Science. 1993;261:1454–1457. doi: 10.1126/science.8367727. [DOI] [PubMed] [Google Scholar]
- Bailey TL, Gribskov M. Combining evidence using p-values: Application to sequence homology searches. Bioinformatics. 1998;14:48–54. doi: 10.1093/bioinformatics/14.1.48. [DOI] [PubMed] [Google Scholar]
- Bermudez LE, Shelton K, Young LS. Comparison of the ability of Mycobacterium avium, M. smegmatis and M. tuberculosis to invade and replicate within HEp-2 epithelial cells. Tuber Lung Dis. 1995;76:240–247. doi: 10.1016/s0962-8479(05)80012-7. [DOI] [PubMed] [Google Scholar]
- Brenner SE, Hubbard T, Murzin A, Chothia C. Gene duplications in H. influenzae. Nature. 1995;378:140. doi: 10.1038/378140a0. [DOI] [PubMed] [Google Scholar]
- Chothia C. Proteins: One thousand families for the molecular biologist. Nature. 1992;357:543–544. doi: 10.1038/357543a0. [DOI] [PubMed] [Google Scholar]
- Cole ST, Brosch R, Parkhill J, Garnier T, Churcher C, Harris D, Gordon SV, Eiglmeier K, Gas S, Barry CE, III, et al. Deciphering the biology of Mycobacterium tuberculosis from the complete genome sequence. Nature. 1998;393:537–544. doi: 10.1038/31159. [DOI] [PubMed] [Google Scholar]
- Fitz-Gibbon ST, House CH. Whole genome-based phylogenetic analysis of free-living microorganisms. Nucleic Acids Res. 1999;27:4218–4222. doi: 10.1093/nar/27.21.4218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grishin NV, Wolf YI, Koonin EV. From complete genomes to measures of substitution rate variability within and between proteins. Genome Res. 2000;10:991–1000. doi: 10.1101/gr.10.7.991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heidelberg JF, Eisen JA, Nelson WC, Clayton RA, Gwinn ML, Dodson RJ, Haft DH, Hickey EK, Peterson JD, Umayam L, et al. DNA sequence of both chromosomes of the cholera pathogen Vibrio cholerae. Nature. 2000;406:477–483. doi: 10.1038/35020000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes AL. Adaptive evolution of genes and genomes. New York: Oxford University Press; 1999. [Google Scholar]
- Hughes MK, Hughes AL. Evolution of duplicate genes in a tetraploid animal, Xenopus laevis. Mol Biol Evol. 1993;10:1360–1369. doi: 10.1093/oxfordjournals.molbev.a040080. [DOI] [PubMed] [Google Scholar]
- Huynen MA, van Nimwegen E. The frequency distribution of gene family sizes in complete genomes. Mol Biol Evol. 1998;15:583–589. doi: 10.1093/oxfordjournals.molbev.a025959. [DOI] [PubMed] [Google Scholar]
- Jordan IK, Makarova KS, Wolf YI, Koonin EV. Gene conversions in genes encoding outer-membrane proteins in H. pylori and C. pneumoniae. Trends Genet. 2001;17:7–10. doi: 10.1016/s0168-9525(00)02151-x. [DOI] [PubMed] [Google Scholar]
- Kaneko T, Sato S, Kotani H, Tanaka A, Asamizu E, Nakamura Y, Miyajima N, Hirosawa M, Sugiura M, Sasamoto S, et al. Sequence analysis of the genome of the unicellular cyanobacterium Synechocystis sp. strain PCC6803. II. Sequence determination of the entire genome and assignment of potential protein-coding regions. DNA Res. 1996;3:109–136. doi: 10.1093/dnares/3.3.109. [DOI] [PubMed] [Google Scholar]
- Klenk HP, Clayton RA, Tomb JF, White O, Nelson KE, Ketchum KA, Dodson RJ, Gwinn M, Hickey EK, Peterson JD, et al. The complete genome sequence of the hyperthermophilic, sulphate-reducing archaeon Archaeoglobus fulgidus. Nature. 1997;390:364–370. doi: 10.1038/37052. [DOI] [PubMed] [Google Scholar]
- Koonin EV, Galperin MY. Prokaryotic genomes: The emerging paradigm of genome-based microbiology. Curr Opin Genet Dev. 1997;7:757–763. doi: 10.1016/s0959-437x(97)80037-8. [DOI] [PubMed] [Google Scholar]
- Koonin EV, Tatusov RL, Rudd KE. Sequence similarity analysis of Escherichia coli proteins: Functional and evolutionary implications. Proc Natl Acad Sci. 1995;92:11921–11925. doi: 10.1073/pnas.92.25.11921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ————— Protein sequence comparison at genome scale. Methods Enzymol. 1996;266:295–322. doi: 10.1016/s0076-6879(96)66020-0. [DOI] [PubMed] [Google Scholar]
- Labedan B, Riley M. Widespread protein sequence similarities: Origins of Escherichia coli genes. J Bacteriol. 1995;177:1585–1588. doi: 10.1128/jb.177.6.1585-1588.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li WH. Molecular evolution. Sunderland, MA: Sinauer Associates; 1997. [Google Scholar]
- Makarova KS, Wolf YI, White O, Minton K, Daly MJ. Short repeats and IS elements in the extremely radiation-resistant bacterium Deinococcus radiodurans and comparison to other bacterial species. Res Microbiol. 1999;150:711–724. doi: 10.1016/s0923-2508(99)00121-7. [DOI] [PubMed] [Google Scholar]
- Natale DA, Shankavaram UT, Galperin MY, Wolf YI, Aravind L, Koonin EV. Genome annotation using clusters of orthologous groups of proteins (COGs) towards understanding the first genome of a Crenarchaeon. Genome Biol. 2000;1:9.1–9.19. doi: 10.1186/gb-2000-1-5-research0009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson KE, Clayton RA, Gill SR, Gwinn ML, Dodson RJ, Haft DH, Hickey EK, Peterson JD, Nelson WC, Ketchum KA, et al. Evidence for lateral gene transfer between Archaea and bacteria from genome sequence of Thermotoga maritima. Nature. 1999;399:323–329. doi: 10.1038/20601. [DOI] [PubMed] [Google Scholar]
- Ohno S. Evolution by gene duplication. New York: Springer; 1970. [Google Scholar]
- Pace NR. A molecular view of microbial diversity and the biosphere. Science. 1997;276:734–740. doi: 10.1126/science.276.5313.734. [DOI] [PubMed] [Google Scholar]
- Read TD, Brunham RC, Shen C, Gill SR, Heidelberg JF, White O, Hickey EK, Peterson J, Utterback T, Berry K, et al. Genome sequences of Chlamydia trachomatis MoPn and Chlamydia pneumoniae AR39. Nucleic Acids Res. 2000;28:1397–1406. doi: 10.1093/nar/28.6.1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz J, Copley RR, Doerks T, Ponting CP, Bork P. SMART: A web-based tool for the study of genetically mobile domains. Nucleic Acids Res. 2000;28:231–234. doi: 10.1093/nar/28.1.231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snel B, Bork P, Huynen MA. Genome phylogeny based on gene content. Nat Genet. 1999;21:108–110. doi: 10.1038/5052. [DOI] [PubMed] [Google Scholar]
- Stoltzfus A. On the possibility of constructive neutral evolution. J Mol Evol. 1999;49:169–181. doi: 10.1007/pl00006540. [DOI] [PubMed] [Google Scholar]
- Swofford DL. PAUP*: Phylogenetic analysis using parsimony (* and other methods). Sunderland, MA: Sinauer; 1998. [Google Scholar]
- Tatusov RL, Koonin EV, Lipman DJ. A genomic perspective on protein families. Science. 1997;278:631–637. doi: 10.1126/science.278.5338.631. [DOI] [PubMed] [Google Scholar]
- Tatusov RL, Galperin MY, Natale DA, Koonin EV. The COG database: A tool for genome-scale analysis of protein functions and evolution. Nucleic Acids Res. 2000;28:33–36. doi: 10.1093/nar/28.1.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tekaia F, Gordon SV, Garnier T, Brosch R, Barrell BG, Cole ST. Analysis of the proteome of Mycobacterium tuberculosis in silico. Tuber Lung Dis. 1999a;79:329–342. doi: 10.1054/tuld.1999.0220. [DOI] [PubMed] [Google Scholar]
- Tekaia F, Lazcano A, Dujon B. The genomic tree as revealed from whole proteome comparisons. Genome Res. 1999b;9:550–557. [PMC free article] [PubMed] [Google Scholar]
- Tettelin H, Saunders NJ, Heidelberg J, Jeffries AC, Nelson KE, Eisen JA, Ketchum KA, Hood DW, Peden JF, Dodson RJ, et al. Complete genome sequence of Neisseria meningitidis serogroup B strain MC58. Science. 2000;287:1809–1815. doi: 10.1126/science.287.5459.1809. [DOI] [PubMed] [Google Scholar]
- Thompson JD, Gibson TJ, Plewniak F, Jeanmougin F, Higgins DG. The CLUSTAL_X windows interface: Flexible strategies for multiple sequence alignment aided by quality analysis tools. Nucleic Acids Res. 1997;25:4876–4882. doi: 10.1093/nar/25.24.4876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomb JF, White O, Kerlavage AR, Clayton RA, Sutton GG, Fleischmann RD, Ketchum KA, Klenk HP, Gill S, Dougherty BA, et al. The complete genome sequence of the gastric pathogen Helicobacter pylori. Nature. 1997;388:539–547. doi: 10.1038/41483. [DOI] [PubMed] [Google Scholar]
- Walker DR, Koonin EV. SEALS: A system for easy analysis of lots of sequences. Ismb. 1997;5:333–339. [PubMed] [Google Scholar]
- Watanabe H, Otsuka J. A comprehensive representation of extensive similarity linkage between large numbers of proteins. Comput Appl Biosci. 1995;11:159–166. doi: 10.1093/bioinformatics/11.2.159. [DOI] [PubMed] [Google Scholar]
- Watanabe H, Mori H, Itoh T, Gojobori T. Genome plasticity as a paradigm of eubacteria evolution. J Mol Evol. 1997;44:S57–S64. doi: 10.1007/pl00000052. [DOI] [PubMed] [Google Scholar]
- White O, Eisen JA, Heidelberg JF, Hickey EK, Peterson JD, Dodson RJ, Haft DH, Gwinn ML, Nelson WC, Richardson DL, et al. Genome sequence of the radioresistant bacterium Deinococcus radiodurans R1. Science. 1999;286:1571–1577. doi: 10.1126/science.286.5444.1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiker HG, Spierings E, Kolkman MA, Ottenhoff TH, Harboe M. The mammalian cell entry operon 1 (mce1) of mycobacterium leprae and mycobacterium tuberculosis. Microb Pathog. 1999;27:173–177. doi: 10.1006/mpat.1999.0298. [DOI] [PubMed] [Google Scholar]
- Wolf YI, Grishin NV, Koonin EV. Estimating the number of protein folds and families from complete genome data. J Mol Biol. 2000;299:897–905. doi: 10.1006/jmbi.2000.3786. [DOI] [PubMed] [Google Scholar]
- Wootton JC, Federhen S. Analysis of compositionally biased regions in sequence databases. Methods Enzymol. 1996;266:554–571. doi: 10.1016/s0076-6879(96)66035-2. [DOI] [PubMed] [Google Scholar]
- Yuan Y, Lee RE, Besra GS, Belisle JT, Barry CE., III Identification of a gene involved in the biosynthesis of cyclopropanated mycolic acids in Mycobacterium tuberculosis. Proc Natl Acad Sci. 1995;92:6630–6634. doi: 10.1073/pnas.92.14.6630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zar JH. Biostatistical analysis. Upper Saddle River, NJ: Prentice-Hall; 1999. [Google Scholar]
- Zhang C, DeLisi C. Estimating the number of protein folds. J Mol Biol. 1998;284:1301–1305. doi: 10.1006/jmbi.1998.2282. [DOI] [PubMed] [Google Scholar]
- Zhang J, Rosenberg HF, Nei M. Positive Darwinian selection after gene duplication in primate ribonuclease genes. Proc Natl Acad Sci. 1998;95:3708–3713. doi: 10.1073/pnas.95.7.3708. [DOI] [PMC free article] [PubMed] [Google Scholar]