Abstract
Time series associated with single-molecule experiments and/or simulations contain a wealth of multiscale information about complex biomolecular systems. We demonstrate how a collection of Penalized-splines (P-splines) can be useful in quantitatively summarizing such data. In this work, functions estimated using P-splines are associated with stochastic differential equations (SDEs). It is shown how quantities estimated in a single SDE summarize fast-scale phenomena, whereas variation between curves associated with different SDEs partially reflects noise induced by motion evolving on a slower time scale. P-splines assist in “semiparametrically” estimating nonlinear SDEs in situations where a time-dependent external force is applied to a single-molecule system. The P-splines introduced simultaneously use function and derivative scatterplot information to refine curve estimates. We refer to the approach as the PuDI (P-splines using Derivative Information) method. It is shown how generalized least squares ideas fit seamlessly into the PuDI method. Applications demonstrating how utilizing uncertainty information/approximations along with generalized least squares techniques improve PuDI fits are presented. Although the primary application here is in estimating nonlinear SDEs, the PuDI method is applicable to situations where both unbiased function and derivative estimates are available.
Keywords: . Penalized-splines, semiparametric regression, time-inhomogeneous stochastic differential equation modeling
1. Introduction
Our primary interest is modeling time series associated with single-molecule simulations/experiments [1, 2, 3, 4, 5, 6, 7, 8, 9]. We demonstrate how information in such time series can be summarized into scatterplot data [8, 10] and how a new method introduced here, the P-splines using Derivative Information (PuDI) method, can be used to gain better quantitative understanding of these time series containing information about multiple time scales in situations where the dynamics are homogeneous or an external force causes the stochastic evolution rules to be time inhomogeneous. The latter case is demonstrated in this article.
However, the PuDI method is a general “semiparametric” method that utilizes regression splines referred to as Penalized-splines (P-splines) [11, 12]. We use a simple design matrix that simultaneously uses noisy function and derivative scatterplot information to approximate nonlinear curves. The use of both the function and its derivative as “response” data in a P-spline is a unique part of our approach. The method is applicable to situations where noisy function and derivative estimates are available at design points. If uncertainty information about the (possibly correlated) estimates is available, the PuDI method can readily handle this situation. Applications where such data are available include economics [13], geosciences [14], and single-molecule dynamics [1, 2, 3, 4, 6, 7, 8, 9].
We focus on showing how the PuDI method can be used to better understand noisy time series coming from single-molecule applications. One utility of the approach is that the contributions from the local drift and diffusion can be more accurately estimated from noisy position versus time data. The function and derivative information mentioned in the previous paragraph are inferred from observed time series data in the single-molecule applications studied. The approach reported can also be modified to explicitly estimate/model “measurement noise” in cases where this noise can be modeled as a Gaussian. How to separate “thermal noise” from measurement noise in experimental single-molecule time series data is shown elsewhere [6, 8, 15]. In this article, the focus is on a benchmark all-atom molecular dynamics simulation of the gramicidin A ion channel [7].
The local parametric models used have a loose physical interpretation in terms of local effective force and friction. This feature allows one a better physical understanding of the effective evolution rules in single-molecule and atomistic modeling applications. The PuDI method provides one a means to patch together local parametric models to form global nonlinear models in cases where a global parametric nonlinear model is unknown. For example in “simple” proteins studied at fine scales, it is known that classic nonlinear polymer physics models, such as the worm-like chain [16], can provide only rough approximations of the dynamics. At smaller length and time scales, these polymer models become more inaccurate, and in more complex biomolecules the dynamics are poorly quantitatively understood from a priori considerations. A semiparametric approach where the estimated local parameters have a physical interpretation shows promise in learning from time ordered single-molecule data in such situations [6, 7, 8, 10, 15]. It should be noted that purely nonparametric models [17, 18] can be difficult to reliably estimate (and check the statistical validity of) when a time-inhomogeneous driving term is present, as in the cases we report.
The following notation will be used: xi denotes a design point, f (xi) represents the function of interest evaluated at xi, ∂ f (xi) represents the corresponding derivative (df(x)/dx|x=xi), and ε1, ε2 represent mean zero noise processes, discussed in more detail later, associated with the noisy estimates of f(xi), ∂ f (xi), respectively. The design matrix constructed for the PuDI method exploits some of the advantageous properties associated with the truncated power function (TPF) basis set [12, 19] and overcomes the well-known ill-conditioning issue associated with this basis by using a recently developed stable and efficient algorithm for computing the penalized least squares solutions associated with the P-spline problem [20]. However, other spline bases can be entertained, such as the B-spline basis as advocated when P-splines were introduced [11]. Smoothing splines can also be considered [21], but the ability of P-splines to parsimoniously represent complex nonlinear functions has appeal in longitudinal data [12] and functional data analysis [22] applications; these techniques show promise in providing a better quantitative understanding of batches of complex single-molecule time series [6, 15, 23]. We demonstrate how information about the (possibly correlated) noise processes can be utilized to improve function estimates using established generalized least squares (GLS) techniques [24] to modify the PuDI design matrix. Illustrative examples demonstrating how undesirable results can be obtained when differences in the noise processes (ε1, ε2) are ignored are presented.
This article is organized as follows. Section 2 quickly reviews established P-spline results [12]. Section 3 presents the basic ideas behind the PuDI method. The background and challenges associated with modeling single-molecule dynamics are presented in section 4, although we remind the reader that the PuDI method is motivated by single-molecule data sets, and it is applicable to other scatterplot situations where derivative information is available (see, e.g., [13, 14]). Section 5 presents results from both controlled and single-molecule data situations. Section 6 presents the conclusions and outlook. MATLAB scripts for fitting general P-splines with our method are provided in the Supporting Material which is available online from http://www.caam.rice.edu/tech_reports/2009/PuDI_demo_mfiles.zip.
2. Review of P-spline notation
The basic regression problem considered here is to approximate a continuous nonlinear function, f(·), evaluated at fixed points, xi, using discrete noisy measurements, yi, where i = 1, …, m and m represents the number of individual samples collected. The model is written as
| (2.1) |
where it is assumed that the error vector, ε = (ε1, …, εm), has a mean zero distribution with general, square, covariance matrix R of dimensions m × m. For practical reasons, we assume that the vector of residuals ε possesses a multivariate normal distribution. We allow for the possibility of nonzero covariance between arbitrary εl and εq, where l ≠ q, i.e., Rlq = cov(εl, εq) ≠ 0. Most P-spline approximations take the form
| (2.2) |
where the Bj(·) represent the selected spline basis used. We introduce the following notation: Bj ≡ [Bj(x1), …, Bj(xm)]⊤, Z ≡ [B1, …, BK], u ≡ [ζ1, …, ζK]⊤, β ≡ [η0, η1, …, ηp]⊤, , and y ≡ [y1, …, ym]⊤. With this notation we can write the model specified by (2.1) and (2.2) as
| (2.3) |
P-splines offer the flexibility of different types of penalties, but we will focus on penalized least squares problems that minimize , where C = (X, Z) is the design matrix of size m × {(p + 1) + K} and β′ = (β⊤, u⊤)⊤ is the matrix of coefficients of size {(p + 1) + K} × 1. To fit this model we can pick a relatively large number of knots, K, and let the penalized minimization select which knots are most relevant [12]. In this article we use generalized cross validation (GCV) to pick the “optimal” smoothing parameter α̂ ≡ argminα GCV(y, α;; C).
3. The PuDI method
The PuDI method assumes a noisy unbiased sample of the underlying function, and the corresponding derivatives are available. In this situation we write the observed data as
| (3.1) |
where is assumed normally distributed with mean zero and covariance matrix R = W W⊤, where W denotes the Cholesky factor of the symmetric matrix R. Throughout we assume that R is invertible and not poorly conditioned.
The design matrix we propose makes use of the TPF basis; e.g., in (2.2) one sets , where (·)+ is a function that takes real arguments and is the identity for arguments ≥ zero and is zero otherwise. We construct the various design matrices using minor transformation of
| (3.2) |
In terms of the model presented in (2.3), the first p + 1 columns correspond to X, and the last K columns correspond to Z. With the TPF basis, including derivative information in the P-spline is straightforward.
We do not claim that the TPF basis is optimal in any sense. However, it can readily handle derivative information estimation in situations where the knot spacing is not uniform, a feature not shared by other popular spline bases, such as B-splines [11, 19].
3.1. The importance of weighting derivatives
We next provide a simple illustration demonstrating the importance of weighting measurements of different qualities. After we apply simple GLS techniques to CPuDI defined in (3.2), the resulting structure is similar to a system of uncorrelated linear regression equations. Because the penalized regression spline problem requires the estimation of a regularization smoothing parameter, α, and the selection of the number of splines used, K, it is more involved than standard multivariate regression. However, it is established that by selecting K to be large enough and letting the smoothing parameter emphasize the importance of certain splines, the problem is simplified greatly [12].
At each design point xi with i = 1, …, m, we observe a nearly unbiased estimate z = {y(f) (xi), y(∂f) (xi)}, where y(f)(xi) is an estimate of the function and y(∂f) (xi) is an estimate of the derivative. The PuDI method can be viewed as using two different design matrices to estimate one regression coefficient β′. These design matrices are associated with different conditional expectations, i.e.,  {y(f)(x)} = C(f)(x)β′ and
{y(f)(x)} = C(f)(x)β′ and  {y(∂f)(x)} = C(∂f)(x)β′, where C(f)(x) and C(∂f) (x) represent the two distinct design matrices depending on the vector of design points x. Note that the design matrix shown in (3.2) consists of two matrix blocks; i.e., the block C(f)(x) is stacked on top of C(∂f)(x). The importance of using GLS can be readily seen with the following simplified multivariate example.
{y(∂f)(x)} = C(∂f)(x)β′, where C(f)(x) and C(∂f) (x) represent the two distinct design matrices depending on the vector of design points x. Note that the design matrix shown in (3.2) consists of two matrix blocks; i.e., the block C(f)(x) is stacked on top of C(∂f)(x). The importance of using GLS can be readily seen with the following simplified multivariate example.
Suppose we are given two sets of independent observations: ( ) possessing mean μ and variance σ2 for all xi and ( ) having mean μ and variance cσ2 for all xi, where c > 1 (c serves as an amplification factor and a common population mean μ is used to simplify the exposition). A possible naive estimate would use only the y(f) data: . If the unequal variances are ignored, one might take . The weighted GLS estimate would read . All three estimates have mean μ, and the variances in this example are easy to compute explicitly:
The variance of the GLS estimate is less than that of the other two for all c considered (i.e., c > 1). If c > 3, the unweighted estimate has larger variance than the naive estimator.
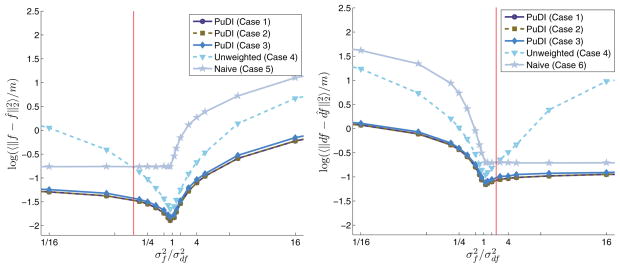
For cases where GLS is applied, the results associated with Figure 5.1 provide a demonstration of the improvement obtainable for different c values in a PuDI application; these results show that the simple example above carries through to a more involved penalized regression spline setting. The main point of this example was to demonstrate how using an unweighted estimate can do worse than the naive approach. Note also that as c → ∞ the GLS case tends to the naive case, so if one estimator is very noisy relative to the other, then the improvement gained by simultaneously using the function and derivative estimations in the P-spline fit diminishes. However, we show that even for fairly disparate noise magnitudes a substantial gain can be achieved in various situations.
Fig. 5.1.
AMSE of f(x) (left panel) and ∂f(x) (right panel) using various semiparametric estimators. The x-axis plots the ratio of the variance of the f noise to that of the ∂f noise, and the y-axis contains the AMSE measured over 1 × 104 Monte Carlo simulations. In each case the weighted PuDI methods (Cases 1–3) outperform the other estimators. These plots also demonstrate how findings from simple multivariate arguments carry through to these nonlinear semiparametric regression spline fits. The vertical (red) lines indicate the point at which the naive estimator (using only f or ∂f information) outperforms the PuDI estimator using f and ∂f but weights all the observations equally (i.e., Case 4). See the text for additional details.
4. Single-molecule dynamics
The purpose of this section is to briefly describe single-molecule dynamic experiments/simulations and the data that often arise from them. Recent technological advances in single-molecule physics have made it possible to manipulate individual macromolecules and measure various kinetic and thermodynamic properties associated with complex molecules, such as proteins and nucleic acids, at nanoscale resolution without artifacts associated with bulk measurements obscuring results. For example, a high resolution atomic force microscope (AFM) was recently used to measure the force time series associated with repeatedly unfolding and refolding a single protein. The study demonstrated that modifying the chemical environment via ligand concentration alters the protein folding kinetics [9]. Information of this sort can provide researchers with a new level of fundamental understanding and can also be exploited in novel nanotechnology/molecular medicine applications. However, the complexity of the underlying system and the stochastic dynamics inherent at small scales rarely permit a single simple parametric model to accurately approximate the global stochastic dynamics. Another complication stems from the fact that the external forces introduced into the system typically result in nonstationary time series. Furthermore, there are often unresolved degrees of freedom making important contributions to the dynamics. We demonstrate how the PuDI method can help in addressing some of these complications.
Our approach uses a time series, , as input and then applies local maximum likelihood methods (in state space) to transform the time sequence into a scatterplot sequence of the form , where m is substantially less than the number of temporal observations N. The “ψj” can be thought of as local average x value, explained further below. We then apply the PuDI method to this sequence. We demonstrate that incorporating the derivative information substantially improves the model calibrated from observed time series. We stress that this procedure is repeated for different time series realizations, and substantial variation can be measured between the curves estimated by P-splines. This variation is due both to the standard uncertainty associated with a finite number of scatterplot observations and to a latent process, unique to each time series realization, modulating the dynamical response. The variability observed in the curves estimated from different time series is of physical interest and suggests more sophisticated statistical analysis as future work, e.g., functional data analysis, which considers functions as the individual observations, and/or a longitudinal analysis, which involves the study of measurements made on the same individuals over time. This type of “functional” variability has proved to be important to thermodynamic and kinetic computations associated with some single-molecule systems [6, 7, 23].
4.1. Modeling single-molecule dynamics
At time scales currently accessible to many single-molecule experiments, classical statistical mechanics is often assumed to be a highly accurate model of the system dynamics. These models often involve many degrees of freedom because each atom possesses a position and momentum vector. Let NDOF denote the number of degrees of freedom. Fairly sophisticated computer simulation algorithms have been developed to include this high level of detail [25]. Let the vector Γ, the “phase space vector,” represent all the degrees of freedom of the system. There is interest in determining simplified dynamical summaries, e.g., in using x ∈ ℝr to construct a reduced order model of Γ ∈ ℝNDOF with r ≪ NDOF. Various motivations exist for appealing to model reduction. The high dimensionality of Γ complicates computer simulations due to the small time step sizes that must be used to ensure numerical stability in numerical integration; a reduced order model can often be simulated for longer length and time scales [26]. In experiments, one can usually dynamically track only a small number of degrees of freedom accurately but can explore longer length and time scales where various events of scientific interest typically occur [8]. Constructing accurate reduced stochastic dynamical models from time series coming either from single-molecule experiments or computer simulations is one way of comparing these two information sources [8]. Rapid technological advances are closing the time scale gaps in data that can be obtained from experiments and simulations. The smaller time scale gap will facilitate the comparison of models calibrated from experimental and simulation data [25], so new tools quantitatively comparing output from these two information sources are desirable.
Denote the degrees of freedom directly observable, or measured from the simulation, by the vector x. The term “reaction coordinate” is sometimes applied to x-type variables. Some researchers in chemical physics believe that an ideal, or “good,” reaction coordinate should be associated with the slowest relevant mode(s) of molecular motion. When this is the case, there is hope for using an effective potential, or potential of mean force denoted here by  (x), to approximate the dynamics of the high-dimensional system at longer time scales [27]. The approximate force acting on this coordinate is obtained by taking the gradient, ∇
(x), to approximate the dynamics of the high-dimensional system at longer time scales [27]. The approximate force acting on this coordinate is obtained by taking the gradient, ∇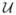 (x). In practice, it is rarely true that an ideal reaction coordinate is known or measurable from experiments; in these situations, one should think of the potential as
(x). In practice, it is rarely true that an ideal reaction coordinate is known or measurable from experiments; in these situations, one should think of the potential as 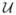 (x; Γ) [8]. The unobserved degrees of freedom serve as a latent process and modulate the dynamical response. For simplicity assume the variable χ is a scalar variable that evolves on a time scale much longer than that associated with x and that this variable (along with x) adequately summarizes the effective dynamical information contained in Γ. In this situation, one should really think of the effective forces as being governed by ∇
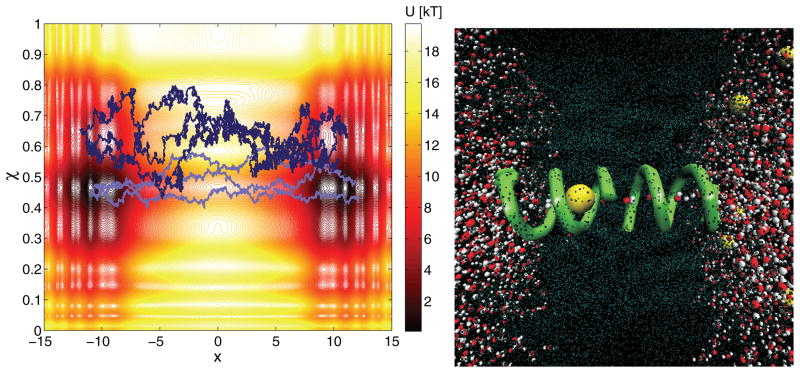
(x; Γ) [8]. The unobserved degrees of freedom serve as a latent process and modulate the dynamical response. For simplicity assume the variable χ is a scalar variable that evolves on a time scale much longer than that associated with x and that this variable (along with x) adequately summarizes the effective dynamical information contained in Γ. In this situation, one should really think of the effective forces as being governed by ∇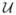 (x; χ), and this type of situation is illustrated in Figure 4.1. In molecular modeling, a -type variable can be one characterizing large-scale conformational fluctuations [26]; in a protein, this might be a certain dihedral angle. The presence of the slowly evolving latent χ causes physically relevant variability in the P-spline curves we estimate from time series data. The next section outlines more specifically how we transform time series coming from single-molecule experiments or simulations into scatterplot data.
(x; χ), and this type of situation is illustrated in Figure 4.1. In molecular modeling, a -type variable can be one characterizing large-scale conformational fluctuations [26]; in a protein, this might be a certain dihedral angle. The presence of the slowly evolving latent χ causes physically relevant variability in the P-spline curves we estimate from time series data. The next section outlines more specifically how we transform time series coming from single-molecule experiments or simulations into scatterplot data.
Fig. 4.1.
Contour plot of a fictitious free energy landscape and some sample trajectories (left panel). x represents the observable process, and the variable χ characterizes the latent process. Three sample trajectories are depicted using two distinct initial values. Two distinct initial conditions are used to stress that randomness is inherent to the reduced dynamics, and the initial condition modulates the dynamics (even if the same x value is present at time zero). Since we assume ignorance of the underlying value of χ, we would estimate slightly different effective forces (and local diffusion coefficients). Snapshot of the gramicidin A channel (right panel). The helical structure represents a protein complex consisting of two gramicidin A monomers. The large spheres denote potassium ions; the multiple colored spheres denote water molecules, and the lightly colored portion represents the lipid bilayer molecules. x corresponds to the ion’s distance from the channels’ plane of symmetry, and χ corresponds to a dihedral angle characterizing the complex. Each atom was modeled explicitly (plot generated using the VMD program [28]).
4.2. Modeling observable quantities
Assume batches of time series are collected from the system, where the superscript is used to index the trajectory number and the subscript to index a time ordering of a scalar observable. In the molecular dynamics community, time series are often referred to as “trajectories.” For a given trajectory we attempt to fit a stochastic differential equation (SDE) having the form
| (4.1) |
where Γ represents the degrees of freedom introduced in the previous section, μ(·, ·) and σ2(·) are the nonlinear deterministic drift and diffusion functions (respectively), and Bt represents the standard Brownian motion [17]. We introduce the terminology “local diffusion coefficient” ≡ D̃ (x; Γ):= σ2 (x; Γ) in order to distinguish the coefficient in the SDE above from the diffusion coefficient usually implied in the physical sciences: we estimate the former using P-splines. The term “diffusion coefficient” used in statistical physics [29] is not necessarily the same as D̃ (x; Γ). If unresolved coordinates in Γ do not substantially modulate the dynamics, the two definitions are effectively identical.
Diffusion models of the reaction coordinates can be used to approximate a wide range of molecular dynamics simulations [7, 23, 26]. Unfortunately a parametric model is usually not known a priori for the drift and diffusion functions. Other SDE estimation approaches can be entertained [17, 18], but, for reasons described more fully in the next section and elsewhere [6, 8, 10, 23], we appeal to local maximum likelihood estimation (MLE) methods. Briefly, the nonstationary nature of the single-molecule data considered here complicates one’s ability to use purely nonparametric methods. The full degrees of freedom vector, Γ, is retained in the drift and diffusion functions to remind us that a latent process is modulating the dynamics. We stress that, for each observed time series, we estimate a new SDE model.
4.3. From local MLEs to global SDEs via P-splines
The so-called over-damped Langevin equation is a useful approximation in statistical physics [27]. In externally driven systems, the approximation assumes μ (x, t):= (kBT)−1D̃ (x; Γ){F (x; Γ) + FExt(x, t)}, where kBT represents the product of Boltzmann’s constant and the system temperature, FExt (x, t) denotes the time-dependent force added to the system, and F (x; Γ) denotes the effective internal force due to intermolecular interactions. One appeal of overdamped Langevin approximations is that drift and diffusion functions can be physically interpreted, although other SDEs can be entertained. The use of this structure is not necessary, but it does illustrate how our approach is not a traditional nonparametric approach (i.e., it is locally parametric). The goodness-of-fit of the models calibrated from nonstationary data can be checked using the omnibus tests of Hong and Li [30]. These tests have been shown to have adequate power for identifying some interesting physical features in molecular dynamics time series [8, 26, 31].
In single-molecule experiments/simulations, we often have detailed knowledge of the time-dependent external force added. The use of a local parametric model facilitates incorporating the known time-dependent force added to the single-molecule system in the SDE model. However, we do not know the global functional form of the local force F (x; Γ) or local diffusion coefficient D̃ (x; Γ). We use polynomials to model these quantities locally, namely in each neighborhood centered around . The constant denotes a specified point where we wish to evaluate the Taylor-type expansion of the expression in (4.2). In this article, it corresponds to the temporal average of window ℓ1 The following local approximation is used:
| (4.2) |
where the local parameter vector, , is estimated using . The subscript ℓ is an index of a partition, 1:= T0 < · · ·<Tℓ · · · < Tm:= N, used to divide the total time series into m disjoint local windows. The results reported were constructed to have ≈ 250 observations2 fall within a given local window, but “optimal” bandwidth rules in this type of application would be of interest. Note that suitably normalized MLEs of parametric models are asymptotically mean zero normal random vectors when the assumed parametric model generates the data and mild technical assumptions are satisfied [17]. Said differently (for a correctly specified model), MLE often provides asymptotically unbiased point estimates of functions and derivatives. Recall that goodness-of-fit tests [30] are used to test the statistical validity of our local parameter estimates.
The global nonlinear force is constructed by applying the PuDI method to the points . The σ (x; Γ) function is obtained in a similar fashion. The scatterplot data is obtained by finding the maximizing a likelihood approximation [32] of a local parametric SDE possessing the drift and diffusion given by (4.2) and the external force we add to the system. This is done for m windows. The two functions of interest, F (·; Γ) and σ(x; Γ), have different degrees of smoothness and were estimated independently of one another. We have changed from the generic notation of used in the introduction to emphasize that the scatterplot information is not directly measured. We have suppressed the superscript indexing the time series number, (j), because each estimated P-spline function constructed in this article uses information from only one time series. The vector is modelled as a normally distributed noise with mean zero and a covariance matrix R. This covariance is meant to reflect parameter uncertainty due to finite length of the discrete time series and can be estimated using Monte Carlo simulation of a genuine SDE. More specifically, the P-spline curves, i.e., the drift and diffusion functions, estimated from trajectory j scatterplot data, were used to construct a nonlinear SDE. This SDE was used to simulate multiple new sample paths (here we used 1,000), corresponding to trajectory j. We then obtained m sets of local MLE parameters on each simulated path and used this information to approximate the uncertainty in the ’s; the empirical covariance between the m vectors was then computed to approximate the parameter uncertainty. This procedure was repeated for each trajectory.
5. Applications
Three sets of applications are studied. The first set of results present Monte Carlo simulation data obtained using discrete samples of known highly oscillatory nonlinear functions contaminated with a noise of known distribution. A relatively small number of scatterplot samples are used to estimate each curve. The intention is to quantitatively study how using derivative information, along with uncertainty estimates, influences the P-spline estimates in a situation where the parameter distribution is known precisely. The function constructed was meant to mimic the function measured in the ion-channel system of interest, which is what we turn to after results on the first controlled example are discussed. We then discuss some basic features of the molecular dynamics simulation and present results and discussion associated with this second application. Finally we present a situation where the SDEs generating the data are known precisely but the finite parameter distribution is unknown (and is not necessarily Gaussian). The intent is to illustrate some points introduced in the ion-channel example and to show how the PuDI method can help in estimating a nonlinear drift (containing a time-inhomogeneous term) in situations where the scatterplot data are estimated from a finite set of data.
The discussion that follows is relevant to all three applications. If the original problem is to find the least squares solution to Cβ′ = y, then, for a given weight matrix 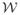 , the GLS analogue of this problem would be to find the solution to
, the GLS analogue of this problem would be to find the solution to 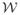 Cβ′ =
Cβ′ = 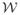 y. Under the assumption that
y. Under the assumption that 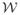 is invertible and not ill-conditioned, which is the situation in the cases studied here, the GLS problem can then be viewed as an ordinary least squares problem in a new coordinate system;3 i.e., find the least squares solution to C̃β′ = ỹ. The penalized least squares problem associated with the P-spline problem requires finding the β′ = (β⊤, u⊤) ⊤ vector that minimizes
We use several different weight matrices to construct standard least squares problems, and these matrices require us to define some parameters: nMC is a parameter determining the number of vectors drawn from a mean zero normal distribution possessing the covariance R. These vectors are used to form a simple empirical estimate of R. Note that in the first application the R associated with the scatterplot data is known and used to generate the Monte Carlo samples; in the second application we assume that the parameter distribution of the local MLE procedure can be adequately approximated by a normal distribution, although the associated covariance is not known to us in closed form; the procedure we use in this application was described earlier. The various weight and design matrices considered are listed below.
is invertible and not ill-conditioned, which is the situation in the cases studied here, the GLS problem can then be viewed as an ordinary least squares problem in a new coordinate system;3 i.e., find the least squares solution to C̃β′ = ỹ. The penalized least squares problem associated with the P-spline problem requires finding the β′ = (β⊤, u⊤) ⊤ vector that minimizes
We use several different weight matrices to construct standard least squares problems, and these matrices require us to define some parameters: nMC is a parameter determining the number of vectors drawn from a mean zero normal distribution possessing the covariance R. These vectors are used to form a simple empirical estimate of R. Note that in the first application the R associated with the scatterplot data is known and used to generate the Monte Carlo samples; in the second application we assume that the parameter distribution of the local MLE procedure can be adequately approximated by a normal distribution, although the associated covariance is not known to us in closed form; the procedure we use in this application was described earlier. The various weight and design matrices considered are listed below.
Case 1. , and W1 is the Cholesky factor of the measurement noise covariance: recall that this is known exactly in the first benchmark application.
Case 2. , and W2 is the Cholesky factor of the estimated measurement noise covariance using nMC = 5 × 104.
Case 3. , and W3 is the Cholesky factor of the estimated measurement noise covariance using nMC = 1 × 103
Case 4. C4 = CPuDI.
Case 5. C5 = P1CPuDI, where P1 = (Im×m, 0 m×m); i.e., use only function information.
Case 6. C6 = P2CPuDI, where P2 = (0m×m, Im×m); i.e., use only derivative information.
The CPuDI design matrix was formed using the TPF basis parameters K = 20 and p = 2. The quantiles were used to select the knot locations [33, 34]. The regularization/smoothing parameter was selected using GCV in all cases. The results did not change appreciably if we used other criteria, e.g., AIC, if we used p = 3, or if we increased K [12].
5.1. Benchmarking PuDI on a smooth nonlinear function
Here we quantitatively study how a PuDI-type design matrix can assist in the estimation of a known function:
| (5.1) |
Samples contaminated with noise (of known noise distributions) are taken from this function. For each known noise distribution studied we generate scatterplot data and fit P-splines using the design matrices presented in the previous section. Recall that this function was constructed to mimic the salient features of curves coming from single-molecule data studied later.
5.1.1. Data generation
Each grid point xi was associated with the noisy measurements and . Throughout we set the number of scatterplot points m to take a value m = 40. An independent and identically distributed (i.i.d.) two-dimensional Gaussian noise with mean zero and covariance matrix
was used to generate the noise for each grid point xi. The diagonal of this 2 × 2 matrix was varied, one diagonal component was always set to be unity, and the correlation coefficient, ρ, between each and was set to zero in the plot shown in this subsection. The net covariance matrix, R, associated with the P-spline scatterplot data was sparse due to the i.i.d. noise structure used. In the ρ = 0 case, R is a diagonal matrix defined by the vector . The ρ > 0 case covariance had the same structure plus two off-diagonal bands, each consisting of m repeated entries of the product ρσf σ∂f. Tables reporting results with ρ = 0.5 and ρ = 0 can be found in the Supplementary Material which is available online from http://www.caam.rice.edu/tech_reports/2009/PuDI_demo_mfiles.zip; the same qualitative trends are observed in each case.
5.1.2. Results and discussion
Figure 5.1 plots the logarithm of the average mean square error (AMSE) associated with predicted f and ∂f for various R’s. The PuDI estimates using the weights, design matrices C1– C3, outperform all other methods. In both f and ∂f, as the ratio of the diagonal terms of R tends to 0 or ∞, the PuDI estimate approaches that of the “naive estimator.” The naive estimator uses design matrix C5 or C6, with the selection depending on σf/σ∂f, as shown in Figure 5.1. The limits of 0 or ∞ mentioned above indicate that the extra information provided by using both f and ∂f is negligible in relation to the information accessible to the naive estimator. However, there is significant gain for a large range of σf/σ∂f values. Also note that using an empirical covariance approximation was nearly identical to the case where the exact covariance R was used. Note also that the estimate of the Cholesky factor, obtained using nMC sample vectors of the R matrix, was dense, whereas the known underlying Cholesky factor, W, was highly sparse. The sampling noise caused the estimated Cholesky factor to appear dense, but this artifact did not hurt the PuDI estimate utilizing W2 or W3.
The vertical lines denote the point where the average AMSE estimator using both f and ∂f but ignoring the different noise variances, i.e., using design matrix C4, is greater than that of applying the naive estimator to the less noisy random vector. The intuition gained from the two-dimensional normal variable result dictates that this crossover should occur when the noisier estimate is a factor of three greater than the other estimate. Recall that our situation is more involved due to the smoothing parameter selection and other tunable parameters, but nonetheless the crossover occurs close to three. The exact crossover point depended on whether f was noisier than ∂f or vice versa. Note that, in the PuDI design matrix cases, we utilized estimates of f(xi) and ∂f (xi) and selected α̂, which minimized the GCV consistent with both measurements. Since the smoothness is different in each function, the resulting α̂ represents a type of weighted average between the α̂ that would have been selected had only f(xi) or ∂f (xi) been used individually.
5.2. Applying PuDI to estimate SDEs characterizing ion-channel dynamics
For those not interested in the fine details, one can think of this application as a type of study in longitudinal data analysis [12]. There are several subject specific responses, and the deviations from the mean population function provide useful information about the individual curves, which here correspond to unobserved, but physically important, phase space variables. The interest is in the different types of effective forces experienced by a potassium ion as it travels across a pore formed by a single protein lodged in a lipid bilayer. This lipid bilayer serves as a boundary between the interior and exterior of a cell and does not permit water or ions to easily pass in the absence of an open ion channel. A schematic of the gramicidin A ion channel studied is provided in Figure 4.1. This particular system was selected because it has been extensively studied both experimentally and theoretically. This ion channel is commonly used as a benchmark in molecular dynamics simulations [35]. The results we study introduce an external force into the system to “steer” an ion across the channel in a prescribed time. Measurements from these simulations can be used to back out a potential of mean force and diffusion coefficient using recently developed nonequilibrium statistical mechanics methods. These quantities are often of interest in a variety of single-molecule simulations. We demonstrate how capturing the variation induced by χ-type variables is important for making predictions. The physical relevance of this type of variability is described in detail elsewhere [7].
5.2.1. Data generation
The NAMD program [36] was used to generate steered molecular dynamics simulations [27] consisting of 36,727 atoms. Constant particle number, pressure, and temperature (NpT) simulations were used. The x coordinate corresponds to the distance between the center of mass of the channel and the ion’s axial location within the channel; this position was recorded every 0.1 ps for 1 ns. The resulting time series were then divided into m = 40 disjoint windows, and the P-spline data was obtained from the sequence of local MLEs taken along this partition. In all cases, the estimated local MLE parameters along with the in sample time series passed goodness-of-fit tests appropriate for the nonstationary data [30]. A more detailed account of the simulation methodology is reported in [7].
5.2.2. Results and discussion
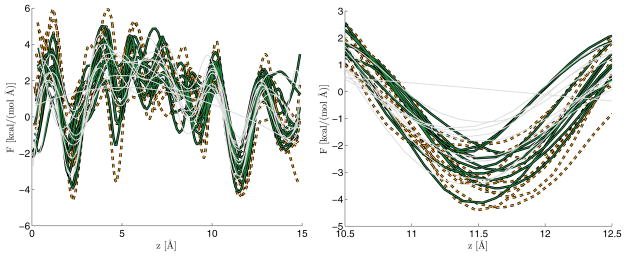
Figure 5.2 displays the global nonlinear effective force obtained using 10 separate steered molecular dynamics realizations. Only results obtained using design matrices C2, C4, and C5 were considered because the true R is unknown and the interest is in the function itself (not the derivative). We observe that results obtained using C2, C4 appear roughly similar, but C5 appears to be oversmoothing due to the lack of derivative information. The rightmost panel focuses on a major binding pocket of the channel, between 10.5 to 12.5Å. This binding pocket is a local minimum on the free energy landscape; here we see that the differences between the C2 and C4 curves are more pronounced.
Fig. 5.2.
The different curves correspond to the effective force estimated from 10 realizations of time series data. After processing these time series, we obtained sets of 10 scatterplot data. These data sets were then processed with design matrices C2 (dark solid), C4 (dashed), and C5 (light grey). The underlying scatterplot data is the same regardless of the design matrix used; differences in curves are due only to the P-spline design matrix. The left panel shows the entire realizations, while the right panel zooms into a major binding pocket of the channel. Note that in this plot the variable z corresponds to the state of the resolved coordinate denoted by x in the text. z is often used to denote axial position in this system; in this figure, z does not have the meaning used in section 3.
Once the P-spline is estimated, we can construct a global nonlinear SDE (see section 4.3) and then simulate multiple realizations of the process using a large number of Brownian paths. The multiple Brownian paths are supposed to quantify the inherent variability caused by neglecting unresolved fast-scale motion in the detailed dynamics. This type of variability, associated with one steered molecular dynamics path, can be important in several contexts [8, 10]. In our final controlled multiscale example, we elaborate on this point.
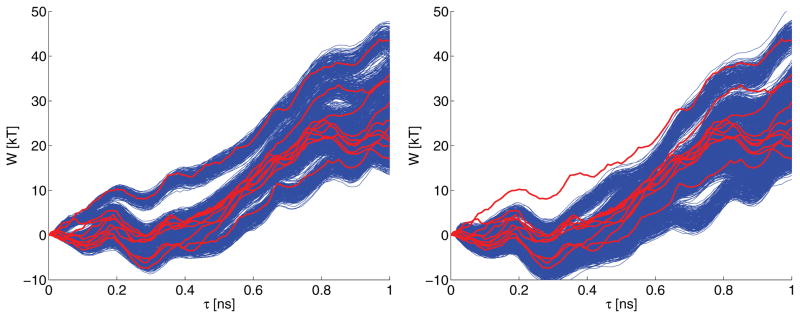
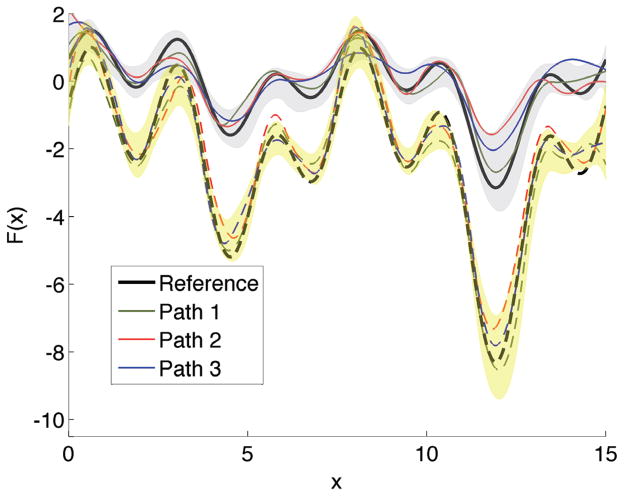
The nonequilibrium work associated with steered molecular dynamics simulations is one example illustrating the item above. The work tubes associated with a single steered molecular dynamics realization can be computed using the estimated SDEs. We can use the SDEs to simulate the nonequilibrium work and compare the variability between these work tubes. Each tube is computed from information contained in one SDE corresponding to one molecular dynamics trajectory. The variability between tubes provides information about the fluctuations induced by a latent χ-type process, whereas the width of each single tube can be attributed to fast-scale noise experienced by the steered molecular dynamics path. Figure 5.3 demonstrates that the different level of smoothing associated with C2 and C4 substantially affects the predictive ability of the corresponding global SDE model. Note that the underlying scatterplot points are the same in all cases; only the P-spline design matrix changes. The different predictions have consequences in physical quantities computed from these simulated work paths. For example, using C2 gives improved potential of mean force and diffusion coefficient estimates compared to other methods [7]. Note also that the work was not used as a fitting criterion, and this demonstrates that the estimated nonlinear models have predictive power.
Fig. 5.3.
The work tubes simulated using the 10 SDEs constructed from stitching together local SDE models by P-spline design matrices C2 (left panel) and C4 (right panel). Each work tube is made of 1,000 work trajectory simulations using the 10 global SDEs previously mentioned. The thick lighter color curves correspond to the work trajectories measured directly from the 10 steered molecular dynamics simulation (one work trajectory per steered molecular dynamics trajectory). The P-splines used the same scatterplot data in the left and right panels; only the design matrix changes, and this alone explains the difference in the estimated curves.
5.3. PuDI applied to a controlled multiscale example
In order to illustrate some of the aforementioned points on a toy model, take the following example:
| (5.2) |
| (5.3) |
| (5.4) |
| (5.5) |
where x represents the coordinate we can measure or resolve and τ ≡ ετk; ετ is set to a value of 1×10−3 to make the “unresolved” variables χ and 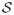 slow relative to x, and k represents a harmonic spring constant whose value is set to 20. The variables χ and S represent dynamically evolving “location” and “scale” parameters, respectively, which are assumed to influence the dynamics but whose value as a function of time is assumed unavailable to the researcher; the constants χo and
slow relative to x, and k represents a harmonic spring constant whose value is set to 20. The variables χ and S represent dynamically evolving “location” and “scale” parameters, respectively, which are assumed to influence the dynamics but whose value as a function of time is assumed unavailable to the researcher; the constants χo and 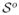 represent the mean of these variables (values reported later). We set kB T = 0.6 in reduced units (corresponding to T = 300K) and specify
.
represent the mean of these variables (values reported later). We set kB T = 0.6 in reduced units (corresponding to T = 300K) and specify
.
A random number generator can be used to generate a batch of Brownian paths to simulate the SDE system above. For a fixed set of evolution rules, the variation induced by different W1 path draws is supposed to mimic unresolved fast-scale motion. If the evolution rules are describing atomistic motion, such fast-scale motion could correspond to dynamical contributions coming from bond vibration and/or solvent bombardment. This type of motion is assumed to occur on time scales that cannot be accurately resolved at the temporal frequency at which measurements are made over. The inability to resolve all degrees of freedom motivates the use of inherently stochastic evolution rules. Note that “unresolved” ≠ “uninteresting”; the magnitude of the effective noise coefficients needs to be estimated and can relate to important molecular level events and can also change as a function of the resolved coordinate x [6, 8, 15, 23, 37]. However, the focus of this example is on the effective force (the local diffusion functions are constants whose value is fixed to the value of for all components throughout).
The coordinates χ and S are constructed to evolve stochastically but exhibit small fluctuations centered around the constants χo and 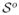 over the time scale observations are made over. The values χo and
over the time scale observations are made over. The values χo and 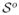 take should be thought of as random variables which arise from a discrete or continuous distribution (the latter is relevant to situations where a portion of phase space does not have a well-defined “state” [31]). Each time series is associated with a different set of (χo,
take should be thought of as random variables which arise from a discrete or continuous distribution (the latter is relevant to situations where a portion of phase space does not have a well-defined “state” [31]). Each time series is associated with a different set of (χo, 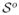 ), and in this controlled example the different (χo,
), and in this controlled example the different (χo, 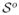 ) values result in a different effective force for each observed time series. The values of (χo,
) values result in a different effective force for each observed time series. The values of (χo, 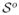 ) are assumed unobserved. The variability between the “subject specific curves” indexed by different latent (χo,
) are assumed unobserved. The variability between the “subject specific curves” indexed by different latent (χo, 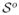 ) values is another source of variability important to both equilibrium [26] and nonequilibrium [7, 10, 23, 31] settings. Here these variables are supposed to represent physically important, but experimentally unresolved, degrees of freedom. In the ion channel, they could correspond to coordinates needed to describe the orientation of the channel in the lipid bilayer [7].
) values is another source of variability important to both equilibrium [26] and nonequilibrium [7, 10, 23, 31] settings. Here these variables are supposed to represent physically important, but experimentally unresolved, degrees of freedom. In the ion channel, they could correspond to coordinates needed to describe the orientation of the channel in the lipid bilayer [7].
5.3.1. Data generation
To make the above discussion more transparent, we will consider only two cases, (χo, 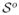 ) = (0, 1) and (χo,
) = (0, 1) and (χo, 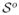 ) = (2, 2). For each of these two cases, 100 Brownian paths
will be simulated and used to approximate sample paths associated with (5.5) for a given fixed (χo,
) = (2, 2). For each of these two cases, 100 Brownian paths
will be simulated and used to approximate sample paths associated with (5.5) for a given fixed (χo, 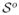 ). The initial condition used was (15, χo,
). The initial condition used was (15, χo, 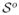 ) for all simulations. 10,000 uniformly spaced discrete observations were recorded for each path simulation (the simulation step size was 0.01, but observations were recorded every 0.1 time units), and each time series was divided into m = 40 local windows. Parameter estimates in the local windows are obtained from these local windows, and the covariance is estimated by the Monte Carlo procedure discussed previously.4 In this example, it should be noted that the parameter distribution covariance is unknown in closed form (in contrast to the first control case studied) due to the fact that the parameters are estimated from a finite set of discrete observations.
) for all simulations. 10,000 uniformly spaced discrete observations were recorded for each path simulation (the simulation step size was 0.01, but observations were recorded every 0.1 time units), and each time series was divided into m = 40 local windows. Parameter estimates in the local windows are obtained from these local windows, and the covariance is estimated by the Monte Carlo procedure discussed previously.4 In this example, it should be noted that the parameter distribution covariance is unknown in closed form (in contrast to the first control case studied) due to the fact that the parameters are estimated from a finite set of discrete observations.
5.3.2. Results and discussion
The results are reported in Figure 5.4. The thin lines denote the PuDI spline estimate calibrated using design matrix C3. The thick lines denote the reference function of interest evaluated at (χo, 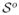 ). The shaded region denotes the rough 95% pointwise confidence band obtained from evaluating the spline over a fine uniform grid for each of the estimated spline coefficients and then computing the average and standard deviation at this point. The fact that the function of interest falls within these simple confidence bands demonstrates that the basic features of a nonlinear function can be estimated using scatterplot data inferred from observed (noisy) position versus time data, even when slow latent processes are modulating the dynamics (see the discussion in the next paragraph). Other methods can be used to construct confidence bands [12], and such methods can be helpful in better understanding complex multiscale signals. Furthermore, we would like to note that our formulation of the P-spline problem (namely the structure given in (2.3)) allows one to plug into the machinery of mixed models [12]. Mixed models and functional data analysis [22] show great promise as tools for attempting to quantify the variability induced by slow latent (χo,
). The shaded region denotes the rough 95% pointwise confidence band obtained from evaluating the spline over a fine uniform grid for each of the estimated spline coefficients and then computing the average and standard deviation at this point. The fact that the function of interest falls within these simple confidence bands demonstrates that the basic features of a nonlinear function can be estimated using scatterplot data inferred from observed (noisy) position versus time data, even when slow latent processes are modulating the dynamics (see the discussion in the next paragraph). Other methods can be used to construct confidence bands [12], and such methods can be helpful in better understanding complex multiscale signals. Furthermore, we would like to note that our formulation of the P-spline problem (namely the structure given in (2.3)) allows one to plug into the machinery of mixed models [12]. Mixed models and functional data analysis [22] show great promise as tools for attempting to quantify the variability induced by slow latent (χo, 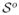 )-type coordinates in single-molecule modeling applications [6, 7, 23]. This is especially important when ergodic sampling does not occur in a single time series [26] and the system exhibits substantial hysteresis [6]. The PuDI method demonstrated here can help in providing a more accurate estimate of smooth curves calibrated from noisy observations in such situations, but methods exploring more systematic techniques for understanding variability induced by latent processes is left to future work.
)-type coordinates in single-molecule modeling applications [6, 7, 23]. This is especially important when ergodic sampling does not occur in a single time series [26] and the system exhibits substantial hysteresis [6]. The PuDI method demonstrated here can help in providing a more accurate estimate of smooth curves calibrated from noisy observations in such situations, but methods exploring more systematic techniques for understanding variability induced by latent processes is left to future work.
Fig. 5.4.
Simulation results from the three-dimensional multiscale example. The thick lines denote the reference function of interest evaluated at (χo, 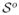 o), and the thin lines represent PuDI estimates coming from a single sample path calibrated using the symbols as input (as well as the corresponding derivative estimate at this point). The shaded regions denote the pointwise 95% confidence bands estimated from 100 SDE realizations. The same Brownian paths were used for two different values of (χo,
o), and the thin lines represent PuDI estimates coming from a single sample path calibrated using the symbols as input (as well as the corresponding derivative estimate at this point). The shaded regions denote the pointwise 95% confidence bands estimated from 100 SDE realizations. The same Brownian paths were used for two different values of (χo, 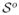 o), where the solid lines represent (χo,
o), where the solid lines represent (χo, 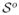 o) = (0, 1) results and the dashed lines represent (χo,
o) = (0, 1) results and the dashed lines represent (χo, 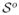 o) = (2, 2) results.
o) = (2, 2) results.
The stochastic dynamics of the unresolved coordinates coupled to x in this example introduce a (slow) non-Markovian noise source. This noise source increased the width of the approximate 95% pointwise confidence band. Goodness-of-fit tests can be used to statistically assess if unresolved noise sources are “fast” enough or “slow” enough to justify the use of low-dimensional diffusive SDEs to approximate the dynamics of data generated from a more complex system. This is discussed extensively in [26, 31]; we just note that all of the data presented here passed the goodness-of-fit test (appropriate for nonstationary signals) proposed by Hong and Li [30], which means that, for the amount of data we have, deviations from an effective diffusive (Markovian) SDE cannot be detected in the data. Knowledge of having “statistically acceptable” scatterplot points inferred from observed position versus time data is important if one wants to use the PuDI method to construct models used for predictive purposes [7, 26, 31].
6. Conclusions and outlook
We demonstrated how a single-molecule time series can be transformed, via local maximum likelihood-type methods, into scatterplot data approximating pointwise function and derivative information associated with an SDE. The functions needed by an SDE approximating the global dynamics of the time series were obtained using P-spline techniques. The PuDI design matrix was shown to be useful in this context. The PuDI design matrix exploited some of the advantageous properties of the TPF basis; numerical difficulties were overcome with a recent algorithm [20]. The use of GLS along with P-splines was shown to influence the estimated curves, and the difference was shown to be relevant in regards to predicting/simulating physical quantities of interest. For example, the work computation associated with the ion-channel system studied benefited substantially from the GLS implementation. When this procedure was repeated for different time series, it was shown that the global SDE functions estimated from different time series exhibited variation in part due to a latent process; i.e., our data consisted of “subject specific curves.” We briefly discussed why this is relevant information to modern biophysics applications [4, 26].
Although we focused on simulation data, the methodology is also applicable to experimental data [6, 8, 15]. Applications making fuller use of pointwise function estimates and derivative proxies calibrated from time series, as the PuDI method was demonstrated to do, show promise as tools that can be used for understanding the rich amount of information contained in recent single-molecule experiments and computer simulations. Other areas where function and derivative scatterplot information is available and a PuDI might be helpful include geosciences [14] and finance [13]. MATLAB scripts illustrating the PuDI method can be found in the Supporting Material which is available online from http://www.caam.rice.edu/tech_reports/2009/PuDI_demo_mfiles.zip.
Supplementary Material
Acknowledgments
This author’s work was funded by NIH grant T90 DK070121-04.
This author’s work was supported by a postdoctoral training grant from the National Cancer Institute (CA90301).
This author’s work was partially supported by AFOSR grant FA9550-09-1-0225 and by NSF grant CCF-0634902.
CPC would like to thank Lorant Janosi and Ioan Kosztin for sharing the gramicidin simulation data.
Carroll’s research was supported by a grant from the National Cancer Institute (R37-CA057030).
Footnotes
This work was performed by an employee of the U.S. Government or under U.S. Government contract. The U.S. Government retains a nonexclusive, royalty-free license to publish or reproduce the published form of this contribution, or allow others to do so, for U.S. Government purposes. Copyright is owned by SIAM to the extent not limited by these rights.
In the “constant velocity” molecular dynamics experiments studied, the nature of the external forcing makes using the average in the local window a natural candidate because the data is centered roughly around this point. However, other selection criteria, such as quantiles or user selected points, can be used to specify .
Cases using m = 25 corresponding to ≈ 400 observations were studied (not reported) and demonstrated features similar to the ones reported here.
If R happens to be ill-conditioned, numerical methods exist for treating this situation [24].
A more “optimal” approach to estimating this covariance would be interesting future work.
Contributor Information
RAYMOND J. CARROLL, Email: carroll@stat.tamu.edu.
DANNY C. SORENSEN, Email: sorensen@rice.edu.
References
- 1.Smith SB, Cui Y, Bustamante C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- 2.Clausen-Schaumann H, Rief M, Gaub HE. Sequence-dependent mechanics of single DNA molecules. Nat Struct Biol. 1999;6:346–349. doi: 10.1038/7582. [DOI] [PubMed] [Google Scholar]
- 3.Lu H, Isralewitz B, Krammer A, Vogel V, Schulten K. Unfolding of titin immunoglobulin domains by steered molecular dynamic simulations. Biophys J. 1998;75:662–671. doi: 10.1016/S0006-3495(98)77556-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fuller DN, Raymer DM, Kottadiel VI, Rao VB, Smith DE. Single phage T 4 DNA packaging motors exhibit large force generation, high velocity, and dynamic variability. Proc Natl Acad Sci USA. 2007;104:16868–16873. doi: 10.1073/pnas.0704008104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kou S. Stochastic modeling in nanoscale biophysics: Subdiffusion within proteins. Ann Appl Stat. 2008;2:501–535. [Google Scholar]
- 6.Calderon CP, Chen WH, Harris N, Lin KJ, Kiang CH. Quantifying DNA melting transitions using single-molecule force spectroscopy. J Phys Condens Matter. 2009;21:034114. doi: 10.1088/0953-8984/21/3/034114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Calderon CP, Janosi L, Kosztin I. Using stochastic models calibrated from nanosecond nonequilibrium simulations to approximate mesoscale information. J Chem Phys. 2009;130:144908. doi: 10.1063/1.3106225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Calderon CP, Harris N, Kiang CH, Cox DD. Quantifying multiscale noise sources in single-molecule time series. J Phys Chem B. 2009;113:138–148. doi: 10.1021/jp807908c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Junker JP, Ziegler F, Rief M. Ligand-dependent equilibrium fluctuations of single calmodulin molecules. Science. 2009;323:633–637. doi: 10.1126/science.1166191. [DOI] [PubMed] [Google Scholar]
- 10.Calderon CP. On the use of local diffusion for path ensemble averaging in potential of mean force computations. J Chem Phys. 2007;126:084106. doi: 10.1063/1.2567098. [DOI] [PubMed] [Google Scholar]
- 11.Eilers PHC, Marx BD. Flexible smoothing with B-splines and penalties (with discussion) Statist Sci. 1996;11:89–121. [Google Scholar]
- 12.Ruppert D, Wand MP, Carroll RJ. Semiparametric Regression. Cambridge University Press; New York: 2003. [Google Scholar]
- 13.Hall P, Yatchew A. Nonparametric estimation when data on derivatives are available. Ann Statist. 2007;35:300–323. [Google Scholar]
- 14.Cox DD. Approximation of method of regularization estimators. Ann Statist. 1990;16:694–712. [Google Scholar]
- 15.Calderon CP, Harris N, Kiang CH, Cox DD. Analyzing single-molecule manipulation experiments. J Mol Recognit. 2009;22:356–362. doi: 10.1002/jmr.959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fernandez VI, Kosuri P, Parot V, Fernandez JM. Extended Kalman filter estimates the contour length of a protein in single molecule atomic force microscopy experiments. Rev Sci Instrum. 2009;80:113104. doi: 10.1063/1.3252982. [DOI] [PubMed] [Google Scholar]
- 17.Prakasa Rao BLS. Statistical Inference for Diffusion Type Processes. Hodder Arnold; London: 1999. [Google Scholar]
- 18.Pokern Y, Stuart AM, Vanden-Eijnden E. Remarks on drift estimation for diffusion processes. Multiscale Model Simul. 2009;8:69–95. [Google Scholar]
- 19.de Boor C. A Practical Guide to Splines. Springer-Verlag; New York: 2001. [Google Scholar]
- 20.Calderon CP, Martinez JG, Carroll RJ, Sorensen DC. Technical report. Rice University; Houston, TX: 2009. A Stable and Efficient Penalized Spline Algorithm Avoiding Unnecessary Numerical Approximations. available online from http://www.caam.rice.edu/tech_reports/2009/TR09-15.pdf. [Google Scholar]
- 21.Mardia KV, Kent JT, Goodall CR, Little JA. Kriging and splines with derivative information. Biometrika. 1996;83:207–221. [Google Scholar]
- 22.Ramsay J, Silverman BW. Functional Data Analysis. Springer-Verlag; New York: 2005. [Google Scholar]
- 23.Calderon CP, Chelli R. Approximating nonequilibrium processes using a collection of surrogate diffusion models. J Chem Phys. 2008;128:145103. doi: 10.1063/1.2903439. [DOI] [PubMed] [Google Scholar]
- 24.Golub GH, van Loan CF. Matrix Computations. The Johns Hopkins University Press; Baltimore, MD: 1996. [Google Scholar]
- 25.Sotomayor M, Schulten K. Single-molecule experiments in vitro and in silico. Science. 2007;316:1144–1148. doi: 10.1126/science.1137591. [DOI] [PubMed] [Google Scholar]
- 26.Calderon CP, Arora K. Extracting kinetic and stationary distribution information from short MD trajectories via a collection of surrogate diffusion models. J Chem Theory Comput. 2009;5:47–58. doi: 10.1021/ct800282a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Park S, Schulten K. Calculating potentials of mean force from steered molecular dynamics simulations. J Chem Phys. 2004;120:5946–5961. doi: 10.1063/1.1651473. [DOI] [PubMed] [Google Scholar]
- 28.Humphrey W, Dalke A, Schulten K. VMD—Visual Molecular Dynamics. J Mol Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 29.Zwanzig R. Nonequilibrium Statistical Mechanics. Oxford University Press; New York: 2001. [Google Scholar]
- 30.Hong Y, Li H. Nonparametric specification testing for continuous-time models with applications to term structure of interest rates. Rev Financ Stud. 2005;18:37–84. [Google Scholar]
- 31.Calderon CP. Detection of subtle dynamical changes induced by unresolved conformational coordinates in single-molecule trajectories via goodness-of-fit tests. J Phys Chem B. 2010;114:3242–3253. doi: 10.1021/jp911124z. [DOI] [PubMed] [Google Scholar]
- 32.Jimenez JC, Ozaki T. An approximate innovation method for the estimation of diffusion processes from discrete data. J Time Ser Anal. 2006;27:77–97. [Google Scholar]
- 33.Ruppert D. Selecting the number of knots for penalized splines. J Comput Graph Statist. 2002;11:735–757. [Google Scholar]
- 34.Baladandayuthapani V, Mallick BK, Carroll RJ. Spatially adaptive Bayesian penalized regression splines (P-splines) J Comput Graph Statist. 2005;14:378– 394. [Google Scholar]
- 35.Allen TW, Bastug T, Kuyucak S, Chung SH. Gramicidin A channel as a test ground for molecular dynamics force fields. Biophys J. 2003;84:2159–2168. doi: 10.1016/S0006-3495(03)75022-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Phillips J, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Calderon CP. A data-driven approach to decomposing complex enzyme kinetics. Phys Rev E (3) 2009;80:061118. doi: 10.1103/PhysRevE.80.061118. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.