The application of naive Bayes model averaging to predict Alzheimer's disease from genome-wide data

Abstract

Objective

Predicting patient outcomes from genome-wide measurements holds significant promise for improving clinical care. The large number of measurements (eg, single nucleotide polymorphisms (SNPs)), however, makes this task computationally challenging. This paper evaluates the performance of an algorithm that predicts patient outcomes from genome-wide data by efficiently model averaging over an exponential number of naive Bayes (NB) models.

Design

This model-averaged naive Bayes (MANB) method was applied to predict late onset Alzheimer's disease in 1411 individuals who each had 312 318 SNP measurements available as genome-wide predictive features. Its performance was compared to that of a naive Bayes algorithm without feature selection (NB) and with feature selection (FSNB).

Measurement

Performance of each algorithm was measured in terms of area under the ROC curve (AUC), calibration, and run time.

Results

The training time of MANB (16.1 s) was fast like NB (15.6 s), while FSNB (1684.2 s) was considerably slower. Each of the three algorithms required less than 0.1 s to predict the outcome of a test case. MANB had an AUC of 0.72, which is significantly better than the AUC of 0.59 by NB (p<0.00001), but not significantly different from the AUC of 0.71 by FSNB. MANB was better calibrated than NB, and FSNB was even better in calibration. A limitation was that only one dataset and two comparison algorithms were included in this study.

Conclusion

MANB performed comparatively well in predicting a clinical outcome from a high-dimensional genome-wide dataset. These results provide support for including MANB in the methods used to predict outcomes from large, genome-wide datasets.

Introduction

Predicting clinical and biological outcomes from available evidence is an important task. Clinical examples include prognosis, diagnosis, and prediction of response to therapy. Biological applications include many areas of molecular biology where we wish to understand the influence of one set of biological variables on another set, such as genetics on gene expression.

Increasingly, data are becoming available in the form of high-throughput, molecular biological measurements. Examples include microarray expression data, proteomic data, and genome-wide single nucleotide polymorphism (SNP) data. These data may contain measurements on hundreds of thousands or even millions of features, such as SNP measurements. It is computationally challenging to develop machine-learning methods for predicting outcomes well, using such large sets of features.

Naives Bayes (NB) is a machine-learning method that has been used for over 50 years in biomedical informatics.¹ It is very efficient computationally and has often been shown to perform classification surprisingly well, even when compared to much more complex methods.^{2 3} However, NB is known to be miscalibrated and this problem is generally accentuated when there are large numbers of features; it tends to make predictions with posterior probabilities that are too close to 0 and 1.^{4 5}

One way to cope with a large number of features is to perform feature selection, which remains an open and important area of research.^{6 7} If a subset of features is strongly predictive of the target outcome and it can be located, then selecting those features may result in excellent classification. When there are no strongly predictive features, however, combining the effects of moderately predictive features may perform classification best. The approach described in this paper can adapt to both of these scenarios, as well as other scenarios, such as when some predictors are strong and others are moderate or even weak. In particular, the approach averages over the predictions of models that contain different sets of features, weighted by the posterior probability of each model. When there are only a few strong predictors, model averaging is similar to feature selection; in other less extreme scenarios, model averaging will average over the predictive effects of many features. Model averaging has a sound theoretical basis, and moreover, it has been shown to work well in practice.⁸ However, in general it is computationally expensive.

This paper describes a model-averaged naive Bayes (MANB) method that was previously developed, is highly efficient, and has been shown to work well empirically.^{9 10} However, to our knowledge the method has not been applied to datasets with a very large number of features (eg, >100 000 features). MANB is suitable not only for predicting outcomes, but also for ranking features, although the main focus of this paper is the former. We apply the MANB method to a genome-wide dataset with a large number of features to predict a clinical outcome. We conjectured that it would be efficient and perform well. A positive result would support using the method in analyzing other genome-wide datasets, including next-generation genome-wide datasets that contain a very large number of features.

Background

This section provides background information about genome-wide association studies, NB models, Bayesian model averaging (BMA), and Alzheimer's disease, because we apply an NB model averaging algorithm to predict Alzheimer's disease using genome-wide data.

Genome-wide association studies

Genome-wide association studies (GWASs) use high-throughput genotyping technologies to assay hundreds of thousands or even millions of SNPs, with the goal typically being to identify SNPs that are predictive of a disease or a trait. The degree to which GWASs are expected to be successful in identifying genes associated with a disease is based in large part on the common disease–common variant hypothesis. This hypothesis posits that (a) common diseases are due to relatively common genetic variants that occur in individuals who manifest the disease,¹¹ and (b) individually many of these variants have low penetrance and hence have small to moderate influence in causing the disease.¹¹ A competing hypothesis is the common disease–rare variant hypothesis, which posits that many rare variants underlie common diseases and each variant causes disease in relatively few individuals with high penetrance.¹¹ However, it is likely that common disease–common variant and common disease–rare variant hypotheses both play a role in common diseases in which underlying genetic variants may range from rare to the common SNPs.¹² Though GWASs were originally developed to detect common variants, larger sample sizes and new analytical methods will likely make them useful for detecting rare variants as well.¹³

GWASs have been widely utilized for identifying the genetic variations underlying common diseases such as Alzheimer's disease, type 2 diabetes, and coronary artery disease. Since the first GWAS was published 5 years ago, more than 450 GWASs and the associations of more than 2000 SNPs have been reported.¹⁴

The naive Bayes model

The NB model assumes that predictive features X₁, X₂, …, X_n are independent of each other conditioned on the state of a target (class) variable T. That is, for all values of X₁, X₂, …, X_n, and T we assume that:

$$P(X_1,X_2,\mathrm{\dots },X_n|T)=\prod _{i=1}^{n}P\left(X_i\right|T)$$

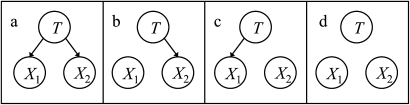
We then assess the prior probability distribution P(T) and apply Bayes' theorem to derive P(T | X₁, X₂, …, X_n). Figure 1A shows an example of a small NB model with two features. In this paper, we will assume the features and target are discrete variables.

Figure 1.

Four naive Bayes models. T is the target node, and X₁ and X₂ are feature nodes.

NB models have been used widely for classification and prediction in many domains, including bioinformatics, because they (1) can be constructed quickly and easily from data, (2) are compact in terms of space complexity, (3) allow rapid inference, and (4) often perform well in practice, even when compared with more complex learning algorithms.^{2 3}

A feature-selection naive Bayes algorithm

In the experiments reported below, we also applied a version of NB that selects the features to include in the model (FSNB). In particular, we started with the model with no features. We then used a forward stepping greedy search that added the feature to the current model that most increased the score. If no additional feature increased the score, the search stopped. We scored models using the conditional marginal likelihood method described in Kontkanen et al,¹⁵ combined with a binomial structure prior, which is described below. This method tries to locate the smallest set of features that predict the target variable well.

Bayesian model averaging

Often in statistical modeling and in machine-learning a single model is learned from data and then applied to make a prediction. Such an approach is called model selection. Often search is performed using training data D to select a good model M (according to some score) to use in predicting a targeted outcome T of interest based on patient features X, namely, P(T | X, M). In doing so, an assumption is being made that model M is correct, that is, P(M | D)=1. However, we usually do not have such total confidence in the correctness of any given model. BMA is based on the notion of averaging over a set of possible models and weighting the prediction of each model according to its probability given training data D,¹⁶ as shown in equation 1.

$$P\left(T\right|\text{X})=\sum _{M}P\left(T\right|\text{X},M\left)P\right(M\left|D\right)$$ (1)

As an example, consider the four NB models on two features X₁ and X₂ in figure 1 and suppose that given D the models a, b, c, and d are assigned probabilities of 0.5, 0.1, 0.3, and 0.1, respectively. Suppose further that for the current case in which X₁=true and X₂=false, the models a, b, c, and d predict T=true as 0.9, 0.5, 0.8, and 0.7, respectively. Then, according to equation 1, the model averaged estimate of P(T=true | X₁=true, X₂=false) is 0.5×0.9+0.1×0.5+0.3×0.8+0.1×0.7=0.81.

Madigan and Raftery show that BMA is expected to give better predictive performance on a test case than any single model.¹⁷ This theoretical result is supported by a wide variety of case studies in practice.¹⁸ Yeung et al applied BMA to predict breast cancer from DNA microarray data and showed that the method performed comparably to other methods in the literature, but required many fewer gene expression levels to do so.¹⁹ They obtained similar results in predicting leukemia. However, for computational reasons, their method is limited to considering the interactions among only 30 genes at a time. Hoeting et al provide a good overview of BMA, including its desirable theoretical properties, as well as several clinical case studies in which BMA performed better than various types of model selection.⁸ They highlight that ‘the development of more efficient computational approaches’ is an important problem needing further research. Koller and Friedman provide a good introduction to BMA in the context of Bayesian network models.¹⁶

Model-averaged naive Bayes algorithm

We have applied BMA to the NB model. In particular, the model-averaged naive Bayes (MANB) algorithm derives P(T | X) by model averaging over all 2ⁿ NB models, where n is the total number of features in the dataset. In the example in figure 1, n is 2 and there are 2²=4 NB models over which we average. As n increases, the number of NB models soon becomes enormous. For n=100, 2¹⁰⁰≥10³⁰, which is far too many models to average over in an exhaustive way. For current genome-wide datasets, n is now often 500 000 or more features that represent, for example, SNP measurements.

As it turns out, the independence relationships inherent in NB models enable dramatically more efficient model averaging. For Bayesian networks, Buntine describes how to use a single conditional probability distribution to compactly represent the model-averaged relationship between a child node and a set of its parents.²⁰ Dash and Cooper investigate how such a compact representation can be used to efficiently perform model averaging over all NB models on a set of features.^{9 10} Remarkably, by using this method, MANB inference becomes linear in the number of features, and it is almost as efficient as NB inference. Thus, rather than requiring O(2ⁿ) time to perform inference using model averaging, it only requires O(n) time. Details about how to implement the MANB algorithm are given in the online appendix and in Dash and Cooper.⁹

Key assumptions needed to obtain such efficiency are global parameter independence and parameter modularity.²¹ The first assumption holds that belief about the conditional probability of a feature given its parents is independent of belief about any other feature given its parents. The second assumption holds that belief about the conditional probability of a feature given its parents is independent of the structure of network that involves other features. It is also assumed that the prior probability of an arc from target T to a feature X_i is independent of the presence or absence of other arcs in the network model.

Dash and Cooper present the results of experiments with simulated and real datasets which support that MANB often has classification performance that is as good as or better than that of NB in terms of the area under the receiver operating characteristic (ROC) curve (AUC).^{9 10} Those positive results and the efficiency of training a MANB model led us to apply the MANB algorithm to predict a clinical outcome, namely Alzheimer's disease, from genome-wide data.

Alzheimer's disease

Alzheimer's disease (AD) is a neurodegenerative disease and is the most common cause of dementia associated with aging.²² It is characterized by slowly progressing memory failure, language disturbance, and poor judgment.²³ Genetically, AD is divided into two forms.²⁴ The early-onset familial AD typically begins before 65 years of age. This form of AD is rare and exhibits an autosomal dominant mode of inheritance. The genetic basis of early-onset AD is well established, and mutations in one of three genes (amyloid precursor protein gene, presenelin 1, or presenelin 2) account for most cases of familial AD.

The more common form of AD, accounting for approximately 95% of all AD, is called late-onset AD (LOAD) since the age of onset of symptoms is typically after 65 years. LOAD is heritable but has a more genetically complex mechanism compared to familial AD. One genetic risk factor for LOAD that has been consistently replicated is the apolipoprotein E (APOE) locus. The APOE gene has three common alleles, ε2, ε3, and ε4, determined by the combined genotypes at the loci rs429358 and rs7412. The ε4 APOE allele increases the risk of development of LOAD, while the ε2 allele may have a protective effect.²⁵

In the past few years, GWASs have identified several additional genetic loci associated with LOAD. The AlzGene database lists over 40 candidate LOAD risk modifiers obtained from systematic meta-analyses of 15 AD GWASs.²⁶

Methods

Dataset

The LOAD GWAS data we used were collected and analyzed originally by Reiman et al.²⁷ The genotype data were collected on 1411 individuals, of which 861 had LOAD and 550 did not; 644 were APOE ε4 carriers (one or more copies of the ε4 allele) and 767 were non-carriers. Of the 1411 individuals, 1047 are brain donors in whom the status of LOAD or control was neuropathologically determined, and 364 are living individuals in whom the status was clinically determined. The average age of the brain donors at death was 73.5 years for LOAD and 75.8 years for controls. The average age of the living individuals is 78.9 years for LOAD and 81.7 years for controls. The target outcome we predicted is the binary LOAD variable. In this dataset, 61% (861 of 1411) had LOAD. For each individual, the genotype data consists of 502 627 SNPs that were measured on an Affymetrix chip; the original investigators analyzed 312 316 SNPs after applying quality controls. We used those 312 316 SNPs, plus two additional APOE SNPs from the same study namely, rs429358 and rs7412.

Experimental methods

We applied the NB, FSNB, and MANB algorithms to predict LOAD from the genome-wide SNP data. In all three algorithms, we used Laplace parameter priors, which assume that for P(X_i | T) every distribution is equally likely a priori. For FSNB and MANB, we used binomial structure priors, which assume that the probability of a given model structure (in terms of the arcs present) is p^m (1–p)^n−m, where n is the total number of features in the dataset, m is the number of features with arcs from T, and p is the probability of an arc from T being present. For the LOAD dataset, we have n=312 318. We assumed p=20/312 318, which implies an expectation of 20 SNPs that are predictive of LOAD. The value 20 was set subjectively, informed by the number and strength of the SNP predictors of LOAD that have been reported in the literature.

We evaluated the algorithms using fivefold cross-validation. The dataset was randomly partitioned into five approximately equal sets such that each set had a similar proportion of individuals who developed LOAD. For each algorithm, we trained a model on four sets and evaluated it on the remaining test set, and we repeated this process once for each possible test set. We thus obtained a LOAD prediction for each of the 1411 cases in the data. The AUC and calibration results reported below are based on these 1411 predictions. This fivefold cross-validation process generated five models for each of the algorithms. For a given algorithm, the training time results reported below are the average training times over the five models learned by the algorithm.

We ran all three algorithms on a PC with a 2.33 GHz Intel processor and 2 GB of RAM.

We used two performance measures: one measures discrimination and the other measures calibration. For discrimination we used the AUC. For calibration we used calibration plots and the Hosmer–Lemeshow goodness-of-fit statistic, for which small p-values support that the calibration curve is not along the 45° line as desired (shown as a dotted line in the results section). For each machine-learning method, we also recorded the time required for model construction on the training cases and for model inference on the test cases.

Results

Table 1 shows that NB and MANB required only about 16 s to train a model (not including about 27 s to load the data into the main memory), while FSNB required about 1684 s. For all three algorithms, the time required to predict each test case was less than 0.1 s.

Table 1.

Mean model training time in seconds

NB	FSNB	MANB
15.6 s	1684.2 s	16.1 s

FSNB, naive Bayes algorithm with feature selection; MANB, model-averaged naive Bayes; NB, naive Bayes.

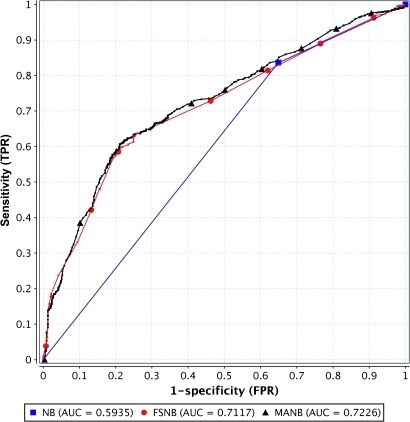
FSNB and MANB had AUCs of about 0.71 and 0.72, respectively, and they are statistically close in performance (the 95% CI of their AUC difference is −0.008 to 0.029). Figure 2 shows that NB has an AUC of about 0.59, which is statistically significantly different than the AUC of MANB (p<0.00001).

Figure 2.

ROC curves and areas. FSNB (naive Bayes algorithm with feature selection) and MANB (model-averaged naive Bayes) are at the top and overlap. Naive Bayes (NB) is the solid line below.

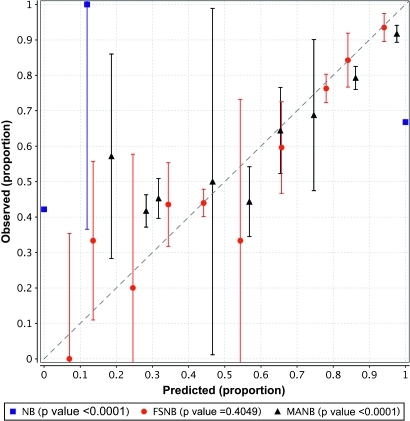
NB predicted almost all the test cases as having a posterior probability for LOAD of ∼0 or ∼1; such extreme predictions tend to occur with NB when there are a large number of features in the model. Figure 3 shows that NB (the squares) is very poorly calibrated. MANB is better calibrated (triangles) than NB. The only decile bin in which both NB and MANB predicted more than one case is the bin representing predictions of 0.9 or greater. In that bin, we removed cases that were predicted by both MANB and NB and on the remaining cases we compared the proportion of LOAD cases that were predicted only by MANB to the proportion of LOAD cases that were predicted only by NB. The proportion for MANB was 0.85, which is statistically significantly different than the proportion for NB which was 0.63 (p=0.0401), indicating that MANB is significantly better calibrated than NB in this bin. FSNB is even better calibrated. FSNB constructed models with no more than 4 features (mean 2.4).

Figure 3.

Calibration curves with 95% CIs around the mean calibration. The p-values are for the Hosmer–Lemeshow goodness-of-fit statistic; a higher value indicates better calibration.

A side-effect of applying the MANB algorithm is the generation of a rank order of all 312 318 SNPs according to their posterior probability of having an association with LOAD. We applied MANB to all the 1411 cases, following the same procedure that was used in training the MANB model, as described above. We tallied the posterior probability of there being an arc (association) from LOAD to every SNP. Table 2 shows the 10 SNPs that had the highest posterior probabilities. The first three SNPs (rs429358, rs4420638, and rs7412) have been identified previously in the literature as strongly associated with LOAD.²⁸ SNPs rs429358 and rs7412 are located in the APOE gene and their combined genotypes determine the APOE allelic status. In this study, we assessed SNPs rs429358 and rs7412 independently and not jointly; hence we did not directly assess the association of the APOE genotype to LOAD. A recent study estimated the OR to be 4.4 for individuals who have the rs429358(T) allele for developing LOAD.³⁰ SNP rs4420638 is located on the APOC1 gene which is close to the APOE gene on chromosome 19. This SNP is in linkage disequilibrium (LD) with the APOE gene and is known to be associated with increased risk for LOAD.²⁶ Using the D' measure of LD, we obtained an LD value between rs429358 and rs4420638 of 0.843 for the dataset we analyzed in this paper, which is close to the value of 0.86 reported in Coon et al.³¹

Table 2.

The 10 single nucleotide polymorphisms (SNPs) that were found to have the highest posterior probability of an association with late-onset Alzheimer's disease

Rank	SNP rs identifier	Probability of association	Physical location of the SNP	Related gene
1	rs429358	1	Chr 19 Pos: 45411941	APOE28
2	rs4420638	1	Chr 19 Pos: 42227269	APOC128
3	rs7412	0.88734	Chr 19 Pos: 45412079	APOE28
4	rs3732443	0.16331	Chr 3 Pos: 72950735	Unknown
5	rs16974268	0.08957	Chr 15 Pos: 69070827	Unknown
6	rs13414200	0.07169	Chr 2 Pos: 13431146	Unknown
7	rs3905173	0.0682	Chr 1 Pos: 33223772	Unknown
8	rs16939136	0.06635	Chr 8 Pos: 72612135	Unknown
9	rs9453276	0.04112	Chr 6 Pos: 64239921	Unknown
10	rs10824310	0.03579	Chr 10 Pos: 47291511	PRKG129

The SNPs ranked 4 through 9 in table 2 are not on chromosome 19 and to our knowledge have not been associated with known genes. However, the 10th SNP rs10824310, which is on chromosome 10, was reported to have a strong association with LOAD in one study,²⁹ but not in another study.³²

Discussion

The results show that MANB performed significantly better than NB, in terms of both AUC and calibration. MANB and FSNB had similar AUCs, but MANB performed model training more than 100 times faster than FSNB. The predictive performance of all the models was strongly influenced by a single APOE SNP (rs429358) that is highly predictive of LOAD.

FSNB was better calibrated than MANB, which is likely due to FSNB including a small number of features in its models. Calibration analysis is best applicable to data obtained from cross-sectional or prospective cohort studies in which prevalence can be estimated reliably. The dataset that we used is obtained from a convenience sample of brain donors and living individuals. However, the prevalence of 61% LOAD in this dataset is not far from what may be expected for individuals whose mean ages range from early 70s to early 80s. AD afflicts about 10% of persons over 65 years of age and almost 50% of those over 85 years of age.²⁷ Thus, the analysis of calibration is a reasonable thing to do for this dataset, even though it is a convenience sample.

In an earlier paper, we and our colleagues applied logistic regression, support vector machines, and a Bayesian network method to these same LOAD training and test datasets.³³ The training time for logistic regression and support vector machines, for example, was about 4400 s, almost all of which was devoted to feature selection by the ReliefF algorithm. No method had an AUC greater than 0.73, even when we performed a sensitivity analysis over the number of features to include in training. For example, logistic regression had an AUC that varied between 0.613 (when using the top 500 features, according to ReliefF) and 0.732 (when using the top 10 features).

Limitations

A main limitation of the current paper is the use of only one genome-wide dataset, although it is an interesting dataset on an important disease. In future research, we plan to investigate the performance of MANB on additional genome-wide datasets to predict both clinical and biological outcomes. Based on the results obtained in the current paper, we estimate that given a genome-wide training dataset consisting of 10 million predictors and 1000 cases, MANB could construct a model in less than 8 min on a standard desktop PC. Another limitation is that we did not use informative prior probabilities for encoding prior knowledge/belief from the literature about the associations between LOAD and individual SNPs; the MANB algorithm allows informative priors and including them in the analysis is an interesting area for study. In future research, we also plan to include additional prediction algorithms with which to compare MANB.

Future considerations

Other future research includes investigating the use of informative structure priors that are based on the literature. We also plan to explore the use of algorithms that perform efficient model averaging on Bayesian network models that are more general than NB models, as described in Dash and Cooper.¹⁰

Conclusion

MANB had excellent comparative performance among the three algorithms we applied in this paper, based on the results of AUC, calibration, and training time. Using only about 16 s of training time on a dataset consisting of hundreds of thousands SNP measurements, MANB was able to predict LOAD patients with an AUC of 0.72. At the same time, it identified SNPs that were the most predictive of LOAD, according to its measure of association. These results provide support for including MANB in the methods used to predict clinical outcomes from high-dimensional genome-wide datasets.