Fluorescence Correlation Spectroscopy Simulations of Photophysical Phenomena and Molecular Interactions: A Molecular Dynamics/Monte Carlo Approach

Abstract

Fluorescence correlation spectroscopy (FCS) is being applied increasingly to study diffusion and interactions of fluorescently labeled macromolecules in complex biological systems. Fluctuations in detected fluorescence, δF(t), are expressed as time-correlation functions, G(τ), and photon-count histograms, P(k;ΔT). Here, we developed a generalized simulation approach to compute G(τ) and P(k;ΔT) for complex systems with arbitrary geometry, photophysics, diffusion, and macromolecular interactions. G(τ) and P(k;ΔT) were computed from δF(t) generated by a Brownian dynamics simulation of single-molecule trajectories followed by a Monte Carlo simulation of fluorophore excitation and detection statistics. Simulations were validated by comparing analytical and simulated G(τ) and P(k;ΔT) for diffusion of noninteracting fluorophores in a three-dimensional Gaussian excitation and detection volume. Inclusion of photobleaching and triplet-state relaxation produced significant changes in G(τ) and P(k;ΔT). Simulations of macromolecular interactions and complex diffusion were done, including transient fluorophore binding to an immobile matrix, cross-correlation analysis of interacting fluorophores, and anomalous sub- and superdiffusion. The computational method developed here is generally applicable for simulating FCS measurements on systems complicated by fluorophore interactions or molecular crowding, and experimental protocols for which G(τ) and P(k;ΔT) cannot be computed analytically.

Introduction

Fluorescence correlation spectroscopy (FCS) is being applied increasingly to study diffusive phenomena and macromolecular interactions in complex systems, including aqueous and membranous compartments in living cells.^1–3 Typically, fluorescence intensity in a detection volume, F(t), is monitored over time. Fluctuations in F(t) are produced by kinetic processes that alter the number and/or intrinsic fluorescence of molecules in the detection volume. The fluorescence time course thus contains information about molecular diffusion and/or photophysical and chemical dynamics. The FCS approach has been used most widely to measure fluorophore diffusion coefficients and concentrations,^4,5 though many other biologically relevant phenomena are in principle measurable, including fluorophore rotation,^6,7 surface adsorption dynamics,⁸ and fluorophore binding interactions.^9,10

Although all information in an FCS measurement is contained in F(t), derived functions are computed to extract useful information from F(t). The commonly used derived functions are the time-correlation function G(τ)^5,11 and the photon-count histogram, P(k;ΔT),^12,13 where k represents the number of photons in a time interval ΔT. G(τ) characterizes the temporal memory of the fluorescence signal, while P(k;ΔT) characterizes the static distribution of fluorescence intensities over a specified time interval. Analytical expressions for G(τ) have been obtained for a few simple situations involving simple Brownian diffusion of fluorophores with a Gaussian detection volume with and without triplet-state photophysics¹⁴ and fluorophore binding to a relatively immobile substrate.¹⁵ Deviations from these analytical G(τ) cases have been noted or are anticipated for anomalous diffusion,^16,17 confined diffusion,¹⁸ non-Gaussian detection volumes,^19,20 large diffusing particles compared to detection volume,²¹ photobleaching,^22-24 and Förster resonance energy transfer.^10,25 Expressions for P(k;ΔT) have been obtained for Brownian fluorophore diffusion.^12,26 The influence of triplet-state photophysics and other nonideal conditions mentioned above on P(k;ΔT) has not been investigated.

Measurements in cellular systems are complicated by geometric and phase heterogeneities that produce confined diffusion within organelles and/or macromolecular crowding. Molecular crowding by fixed and mobile obstacles can dramatically alter particle diffusion and interactions through excluded volume effects and spatial organization.^27,28 We have used photobleaching methods extensively to characterize the diffusion of macromolecules in cellular compartments²⁹ and have developed analytical and computational methods to deal with complex diffusive behavior³⁰ and organelle geometry.^31,32 In principle, FCS measurements can contain greater information content about diffusive and reaction dynamics than fluorescence recovery after photobleaching, in part because single-molecule events are recorded over many orders of magnitude of time.

In this study we establish a general approach to simulate FCS data for complex systems. The motivation for this work was the need to extract quantitative information on diffusion and binding from FCS measurements in complex systems. The computational method involves a Brownian dynamics simulation of particle trajectories followed by a Monte Carlo simulation of fluorescence statistics. The G(τ) and P(k;ΔT) derived functions are computed from the simulated F(t). The simulation approach was validated and applied to examine the effects of photophysical phenomena and intermolecular interactions on G(τ) and P(k;ΔT).

Experimental Section

Overview

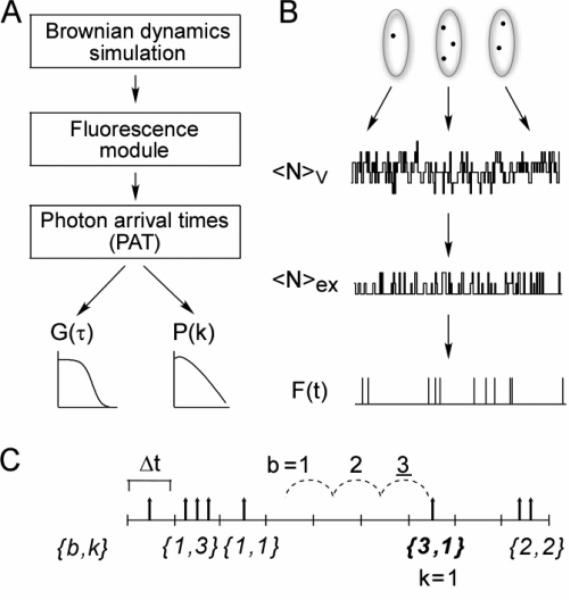
The simulation of an FCS measurement was conducted in three stages: (a) generation of molecular trajectories, (b) generation of detected fluorescence time course, F(t), on the basis of the molecular trajectories, and (c) computation of G(τ) and P(k;ΔT) from F(t) (Figures 1A and 1B). Computations for each stage were handled independently of the other stages. Molecular trajectories were generated by Brownian dynamics simulations using the GROMACS molecular dynamics package.³³ The trajectories were filtered through a fluorescence statistics module to generate F(t), which was stored efficiently as a list of photon arrival times. F(t) was processed to generate G(τ) and P(k;ΔT) using an algorithm based on the photon arrival times. As discussed below, the simulations utilized different time scale intervals: dt, for the Brownian dynamics time step; δt, for the time interval over which fluorescence is calculated from the molecular trajectories to generate F(t); and Δt, for the minimum bin time used for the generation of G(τ). In general, dt ≤ δt ≤ Δt, where δt and Δt are integer multiples of dt.

Figure 1.

Simulation method. (A) Simulations were done in three steps: computation of Brownian dynamics trajectories using GROMACS software; computation of fluorescence time courses using custom software; and computation of correlation functions and photon-count histograms from photon arrival times. (B) Brownian dynamics trajectories were generated to give coordinates of a collection of molecules in a periodic box. The number of molecules within a subvolume of the box at each time, N_V, was computed. A fraction of these molecules, N_ex, were excited, and a fraction of the excited molecules emitted photons, generating a fluorescence time course, F(t). (C) Photon arrival time format. Given a user-defined time bin, Δt, fluorescence photon counts are stored as a data pair: the first element is the number of empty bins, b, separating bins containing photons, and the second element is the number of photons, k, within the latter bin. Shown in the figure is the entry 3,1. The dashed lines demonstrate that b = 3, and the single photon at the end of the dashed lines indicates k = 1, forming the entry 3,1.

Brownian Dynamics Simulations

A system of molecules evolving by Brownian dynamics in an isotropic highly damping hydrodynamic fluid is described by the modified Langevin equation: dr_i/dt = F_i/γ_i + δ_i, where r_i is the position of molecule i, F_i is the force acting on the molecule, γ_i is the friction coefficient of the molecule in the hydrodynamic fluid, and δ_i is a randomly varying force.³⁴ This equation was integrated using the GROMACS package, version 3.1.2,³³ to obtain $\mathrm{d}{\mathbf{r}}_i=({\mathbf{F}}_i∕{\gamma }_i)\mathrm{d}t+\sqrt{2k_{\mathrm{B}}T\left(\mathrm{d}t\right)∕{\gamma }_i}{\delta }_0$, where k_B is Boltzmann's constant, T is absolute temperature, dt is the simulation time step, and δ₀ is a Gaussian-distributed random number with average zero and standard deviation 1. The uniform random number generator in GROMACS, version 3.1.2, was replaced by the program ran2 of Press et al.³⁵ (with a random number generation period of ~10¹⁸), and the Gaussian transformation was replaced by the program gasdev of Press et al.³⁶ The GROMACS-parametrized friction coefficient, γ, was calibrated by simulating a system of identical spherical particles of known mass and radius a and comparing the diffusion coefficient from the simulation, $D_{\mathrm{sim}}=\langle r^2\rangle ∕6t$, with the diffusion coefficient calculated from the Stokes–Einstein equation, D_SE = k_BT/6πηa. The friction coefficient varied with the mass of the particle.

Intermolecular forces between the atoms i and j, F_ij, were estimated by Lennard-Jones potentials, F_ij(r_ij) = A_ij/r_ij¹² – C_ij/r_ij⁶, where r_ij is the distance between atoms i and j and A_ij and C_ij are particle-specific coefficients governing the strength of the interaction. Electrostatic interactions were ignored. For most simulations reported here, C_ij = 0, yielding a collection of Lennard-Jones repulsive spheres. For crowding simulations, the short-range repulsion was made softer by adding terms with C_ij < 0. For specified A_ii and C_ii, the effective length of the potential (and thus the effective radius of the particle) was operationally defined as the distance at which the potential reached kT. To simulate binding of a fluorophore to a large immobile object, the spatial coordinates of the fluorophore were frozen for a specified length of time. Whether binding occurs and the length of time remaining bound were specified in a Monte Carlo fashion with constant probability characterized by two time constants, τ_on and τ_off. These time constants correspond to the reciprocal pseudo-first-order forward and reverse rate constants for binding, respectively.

In a typical simulation, the trajectory of 1000 molecules, whose initial positions were chosen at random, was computed in a 10 × 10 × 10 μm³ box with periodic boundary conditions and no pressure coupling (equivalent concentration 1.7 nM). We found that trajectories run for times greater than 200 times the characteristic diffusion time gave results independent of run time. All simulations were run at 300 °K. The system was typically equilibrated by a run of 3 s, followed by a production run of 1 s. The time step dt was set to 1–200 ns. The time step was chosen to give a potential energy that did not vary abruptly upon close intermolecular approach. The GROMACS software was compiled and run on a Pentium 4 computer running Linux emulation software on Windows XP. Dynamics for low particle concentrations were generated at a rate of ~2 × 10⁶ steps/h for a 2.8 MHz Pentium 4. Simulations at high particle concentrations were run on the Xeon cluster at the National Center for Supercomputer Applications at the University of Illinois, Urbana-Champaign.

Fluorescence Statistics

F(t) was calculated from the Brownian dynamics trajectories according to

$$F\left(t\right)=\sum _{i=1}^N\left[{\int }_{t^{\prime }}^t{p}_{\mathrm{ex}}({\mathbf{r}}_i^{\prime },{\omega }_i^{\prime };t^{\prime })p_{\mathrm{ph}}({\mathbf{r}}_i,{\omega }_i;t\mid {\mathbf{r}}_i^{\prime },{\omega }_i^{\prime };t^{\prime })p_{\mathrm{em}}({\mathbf{r}}_i,{\omega }_i;t)Q_{\det }\left({\omega }_i\right)\delta t^{\prime }\right]$$ (1)

where N is the number of molecules, $p_{\mathrm{ex}}({\mathbf{r}}_i^{\prime },{\omega }_i^{\prime };t^{\prime })$ is the probability that molecule i at position ${\mathbf{r}}_i^{\prime }$ with orientation ${\omega }_i^{\prime }$ is excited at time t′, $p_{\mathrm{ph}}({\mathbf{r}}_i,{\omega }_i;t\mid {\mathbf{r}}_i^{\prime },{\omega }_i^{\prime };t^{\prime })$ is the conditional probability that a molecule excited at time t′ undergoes a photo-physical conversion by a later time t, p_em(r_i,ω_i;t) is the probability that a molecule subsequently emits a photon, and Q_det(ω_i) is the quantum yield of detecting emitted photons from a molecule in orientation ω_i (assuming negligible time to detection). The quantum yield of photon detection was assumed to be independent of the polarization of emitted photons and thus molecular orientation: Q_det(ω_i) ≈ Q_det. The bracketed integral in eq 1 is computed in units of δt, the fundamental fluorescence query interval. Each of the conditional probability terms as used in the simulations is defined explicitly below. Generation of the fluorescence trace, F(t), and calculations of G(τ) and P(k;ΔT) were implemented in Compaq Visual FORTRAN 90 (source code and computational details available upon request).

Molecular Excitation

The probability molecule i is excited at a time t′ can be expressed as

$$p_{\mathrm{ex}}({\mathbf{r}}_i^{\prime },{\omega }_i^{\prime };t^{\prime })=p_{{\mathrm{S}}_0}\left(i\right)∊\left({\omega }_i^{\prime }\right)I_{\mathrm{app}}\left({\mathbf{r}}_i^{\prime }\right)$$ (2)

where p_S0(i) is the probability (0 or 1) that molecule i is in the ground state (S₀) (available for excitation), ε(ω) is the orientation-dependent absorption probability per unit time, and I_app(r) is the normalized apparent excitation profile. Here, we follow the convention of Rigler et al.³⁷ in using I_app(r) for the convolution of the excitation intensity profile and the detection efficiency profile.^38,39 For the simulations presented here, rotational correlation times were assumed to be much faster than the Brownian dynamics time step, permitting replacement of ε(ω) by an orientationally averaged $\stackrel{‒}{∊}$. For a three-dimensional Gaussian, I_app(r), the excitation probability of molecule i at position r_i = (x_i,y_i,z_i) is then

$$p_{\mathrm{ex}}({\mathbf{r}}_i^{\prime },{\omega }_i^{\prime };t{,}^{\prime })=p_{{\mathrm{S}}_0}\left(i\right)•\stackrel{‒}{∊}\exp \left[-\left(\frac{{(x_i-x_0)}^2+{(y_i-y_0)}^2+{((z_i-z_0)∕\kappa )}^2}{2{w_{xy}}^2}\right)\right]$$ (3)

where w_xy is the standard deviation of the Gaussian profile in the radial direction centered at (x₀,y₀,z₀) and κ = w_z/w_xy, where w_z is the standard deviation of the Gaussian profile in the axial direction. For each fluorescence query interval, δt, eq 3 was evaluated for each molecule and compared to a uniformly distributed random number between 0 and 1 to determine whether excitation occurred (see below for long-lived photo-dynamics). Typically, $\stackrel{‒}{∊}$ was adjusted to yield 10⁴–10⁵ detection events per second. For some computations, the functional form of I_app(r) was adjusted to accommodate other excitation profiles.

Photophysical Conversions

Molecules in the excited state were allowed to relax via fluorescence, intersystem crossing, or photobleaching mechanisms as described below.

Fluorescence

The fluorescence lifetime of the excited state, τ_F, was assumed to be much faster than the time step of the Brownian dynamics simulation so that excitation and de-excitation occurred during the same time step $({\tau }_{\mathrm{F}}\ll \delta t)$. Fluorescence photons were emitted with a constant quantum yield, Q_F, simulated by comparing a specified Q_F with a uniformly distributed random number in the range 0–1

$$\begin{array}{c}\hfill p_{\mathrm{ph}}({\mathbf{r}}_i,{\omega }_i;t\mid {\mathbf{r}}_i^{\prime },{\omega }_i^{\prime };t^{\prime })=\delta (t-t^{\prime })\hfill \\ \hfill p_{\mathrm{em}}({\mathbf{r}}_i,{\omega }_i;t)=Q_{\mathrm{F}}\hfill \end{array}$$ (4)

Since molecules are regenerated immediately after excitation–emission, p_S0(i) = 1 for all i in eq 2.

Intersystem Crossing

Excited molecules were allowed to cross over into a triplet state with a constant probability, Q_T. Once in the triplet state, they were allowed to decay nonradiatively to the ground state with a constant probability defined by a characteristic exponential time constant, τ_t > δt

$$\begin{array}{c}\hfill p_{\mathrm{ph}}({\mathbf{r}}_i,{\omega }_i;t\mid {\mathbf{r}}_i^{\prime },{\omega }_i^{\prime };t^{\prime })=Q_{\mathrm{T}}∕{\tau }_{\mathrm{T}}\hfill \\ \hfill p_{\mathrm{em}}({\mathbf{r}}_i,{\omega }_i;t)=0\hfill \end{array}$$ (5)

Molecules in the triplet state were excitable again only after relaxing to the ground state, while in the triplet state p_S0(i) was set to 0 in eq 2. Molecules in the triplet state that crossed a periodic boundary of the simulation box were assumed to have “escaped” and so were returned to the ground state.

Photobleaching

Excited molecules were forced to become unexcitable permanently with constant probability Q_B

$$\begin{array}{c}\hfill p_{\mathrm{ph}}({\mathbf{r}}_i,{\omega }_i;t\mid {\mathbf{r}}_i^{\prime },{\omega }_i^{\prime };t^{\prime })=Q_{\mathrm{B}}∕{\tau }_{\mathrm{B}}\hfill \\ \hfill p_{\mathrm{em}}({\mathbf{r}}_i,{\omega }_i;t)=0\hfill \end{array}$$ (6)

with p_S0(i) = 0. Photobleached molecules were regenerated (p_S0(i) set to 1) once they crossed the periodic boundary of the simulation box to prevent continuous depletion and non-steady-state effects.

Correlation Function and Histogram Computations

F(t), calculated from eq 1, was stored as a paired list of times between the consecutive photons and the number of photons (photon arrival times (PATs)) (Figure 1C). To maximize computational efficiency where the simulation time step was much smaller than the characteristic time of photon arrival, a binned PAT format was used in which the number of bins, b, between consecutive bins with photons (bins i and i + b) was recorded along with the number of photons counts, k, registered in bin (i + b). For a list of PAT pairs, the time autocorrelation function of fluorescence fluctuations was computed as

$$G(\tau =b\left(j\right)\Delta \tau )=[\left({(B-b\left(j\right))}^{-1}\sum _{i=1}^{M-1}\sum _{j=i+1}^{M}k\left(i\right)k(j-1)\right)∕{(K∕B)}^2]-1$$ (7)

where M is the length of the PAT list, K is the total number of photons counted $\left({\sum }_{j=1}^{M}k\left(j\right)\right)$, and B is the total number of bins between the first and the last detected photons $\left({\sum }_{j=2}^{M}b\left(j\right)\right)$.

For calculation of cross-correlation functions using paired F_x(t) and F_y(t), an absolute PAT format (absPAT) was used instead, in which b(j) entries are replaced by the absolute time in which photons arrive (in units of Δt): p^abs(j) = {b^abs(j),k(j)}. For two absPAT records, $p_x^{\mathrm{abs}}\left(j\right)=\{b_x^{\mathrm{abs}}\left(j\right),k_x\left(j\right)\}$ and $p_y^{\mathrm{abs}}\left(j\right)=\{b_y^{\mathrm{abs}}\left(j\right),k_y\left(j\right)\}$, the cross-correlation function was computed as

$$G_{\mathrm{cross}}(\tau =[b_x\left(i\right)-b_y\left(j\right)]\Delta \tau )=\frac{{(B_{\min }-[b_x\left(i\right)-b_y\left(j\right)])}^{-1}\sum _{i=1}^{M_x}\sum _{j=1}^{M_y}{k}_x\left(i\right)k_y\left(j\right)}{(K_x∕B_x)(K_y∕B_y)}-1$$ (8)

where B_min = Min[B_x,B_y]. Equation 8 can be used to compute simultaneously the forward (τ > 0) and reverse (τ < 0) cross-correlation functions, G_xy(τ) and G_yx(τ), respectively.

Computation of the correlation function using photon arrival times as described above is more efficient than the conventional direct approach using the fluorescence trace, scaling approximately as M² (M is the number of PAT pairs) instead of as B² (B is the total number of simulation time bins). For a 2 s simulation with a 200 ns time step, a photon-count rate of 100 kHz/molecule and an average of 1 molecule in the observation volume, M ≤ 2 × 10⁵, whereas B = 10⁷. In this case, computing the correlation function using the direct approach took 7 h on a 2.8 MHz Pentium 4, whereas the PAT method took 30 min.

The calculation of G(τ) as described by eqs 7 and 8 is similar to that of Davis et al.⁴⁰ that mimics the computation in hardware correlator cards. In our method, G(τ) is computed at each τ by multiplication of PAT counts corresponding to that photon arrival time, whereas G(τ) is computed by Davis et al. by addition. In principle, the computation of G(τ) by multiplication becomes efficient for large photon-count rates where the number of bins containing more than one count is significant; multiple additions would then be necessary as opposed to a single multiplication. In practice, we found a <1 s difference in computation time between the two methods for a 1 s simulation with a 50–100 kHz count rate.

To mimic the temporal resolution and time-binning structure of hardware correlators used in FCS experiments, G(τ) values were averaged in a quasi-logarithmic manner.^41,42 Briefly, G(τ) values within each of the first eight successive time blocks Δτ were averaged for a total of eight initial averaged values of G(τ); here, Δτ = 32 or 200 ns, corresponding to the resolution of commercially available hardware cards. Each subsequent group of eight G(τ) values was averaged using a width that was twice that of the preceding group. For example, averaged G(τ) values 9–16 were obtained with width 2Δτ, G(τ) values 17–24 had width 4Δτ, and so on. The averaging procedure was continued until all simulated G(τ) values were averaged.

Functions were fit to averaged and binned G(τ) by nonlinear least-squares regression. The fits were weighted by the standard deviation of G(τ), determined from multiple simulations done with the same set of parameters but with different starting configurations and random number seeds.^43,44 Nonlinear least-squares regression was conducted in Microsoft Excel⁴⁵ or Igor Pro 4 (WaveMetrics, Inc., Lake Oswego, OR). Identical values of fitted parameters were obtained using Mathematica 4.0 (Wolfram Research, Champaign, IL).

The photon-count histogram (PCH), P(k;ΔT), was computed by rebinning the PAT using a specified time bin, ΔT, followed by tabulating the number of counts, k, in the rebinned PAT list. PCH data were fitted by numerical integration of the equations of Chen et al.¹² using a Levenberg–Marquardt algorithm implemented in Mathematica 4.0 (Wolfram Research, Inc., Champaign, IL). The two fitting parameters were N̄, the average number of molecules in the excitation volume, and $\stackrel{‒}{∊}$, the average specific brightness, in counts (time bin)⁻¹ molecule⁻¹.

FCS Measurements

FCS measurements on 1–5 nM aqueous solutions of calcein (Molecular Probes, Inc., Eugene, OR) were done on a home-built instrument⁴⁶ in which the 488 nm beam from a diode laser (Coherent, Inc., Santa Clara, CA) was directed through a 100× oil objective lens using a Nikon TE-300 inverted epifluorescence microscope. The excitation light was focused on thin fluid layers sandwiched between cover glasses. Emitted fluorescence passed through a 510 nm dichroic mirror and a 525 ± 25 nm band-pass filter (Chroma Technologies, Corp., Rockingham, VT) and was focused onto a 100 μm diameter fiberoptic cable (Fico, Inc., Tyngsboro, MA). Photon counts were detected using an avalanche photodiode (Perkin-Elmer Optoelectronics, Ltd.) and correlated with an ALV-5000 correlator card (ALV–Laser Vertriebsgesellschaft mbH, Langen, Germany).

Results

Validation: Brownian Diffusion

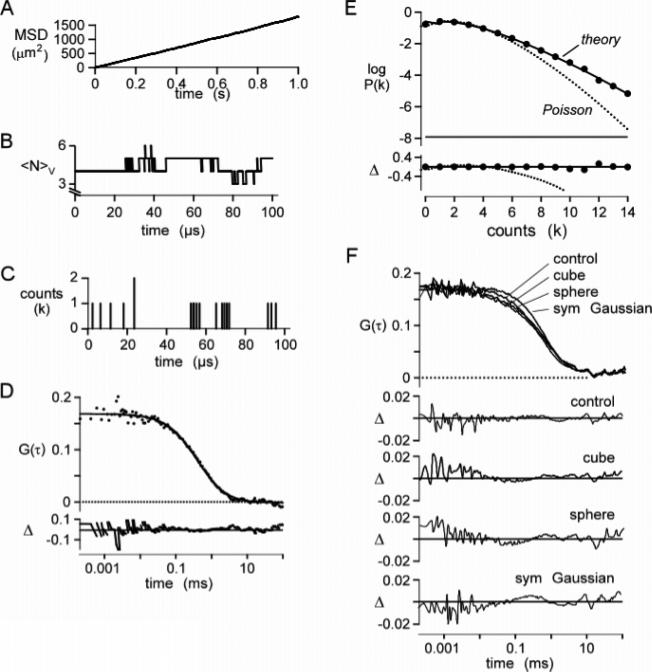
To validate our computational approach, FCS simulations of Brownian diffusion in a Gaussian excitation volume were carried out where analytical expressions exist for G(τ) and P(k;ΔT). Figure 2A shows a linear plot of mean-square displacement (MSD) versus time (r > 0.99), confirming a lack of correlation in the 10¹⁰ random numbers generated for the Brownian dynamics simulation. The diffusion coefficient computed from the slope was 298 μm²/s, in agreement with 300 μm²/s used in the simulation.

Figure 2.

Validation of simulation method. The Brownian dynamics simulation of particle diffusion was run for 1 s using a 200 ns time step for 1000 molecules with a diffusion coefficient of 300 μm²/s in a 10 × 10 × 10 μm³ box (average concentration 1 particle/μm³; 1.7 nM). (A) Mean-square displacement plot of particle positions. The fitted slope gives a diffusion coefficient of 298 μm²/s. (B) Representative plot of the number of particles, N_V, in a 1 × 1 × 3 μm³ cubic observation volume. (C) Corresponding plot for detected photons. Molecules were excited with a Gaussian excitation profile of w_xy = 0.354 μm, w_z = 1.061 μm (κ = 3), and specific brightness 17 kHz/molecule. (D) Autocorrelation function, G(τ), computed from F(t) from four separate simulations. The solid line is fitted G(τ) for a simple diffusion (eq 9) (see text for fitted parameters), with fractional deviation (Δ) shown in the lower panel. (E) Photon-count histogram, P(k;ΔT), generated from the fluorescence trace with ΔT = 20 μs. Data were fitted with the P(k;ΔT) for the Poisson distribution (dotted curve) and the super-Poissonian model (theory; solid curve) (Chen et al.¹²). (F) Effect of the excitation profile on G(τ). Trajectories were generated as above. The fluorescence module was modified to produce cubic, spherical, and symmetric Gaussian (ω_x = ω_y = ω_z) excitation profiles. Simulated data were fitted with eq 9, and the fractional deviation between fit and simulation (Δ) was plotted.

A 1 × 1 × 3 μm³ observation box was set up at the center of the 10 × 10 × 10 μm³ simulation box, and the number of particles within the observation volume tracked throughout a 1 s simulation time. The average number of particles in the observation volume was 3.02, as expected from the observation volume of 3 μm³ and the specified concentration of 1 particle/μm³. The number of particles in the observation volume varied from 0 to 13 during the simulation. Figure 2B shows representative fluctuations in the number of particles in the observation volume over a representative 100 μs time interval. Figure 2C shows the number of fluorescence detection events (binned in 200 ns time intervals) during the same time after processing through the fluorescence filtering module.

Figure 2D shows G(τ) computed from F(t), together with a fit of the analytical equation for Stokes–Einstein diffusion in a volume defined by a Gaussian excitation beam profile³⁷

$$G\left(\tau \right)=G\left(0\right){(1+\tau ∕{\tau }_{\mathrm{D}})}^{-1}{(1+\tau ∕{\kappa }^2{\tau }_{\mathrm{D}})}^{-1∕2}$$ (9)

where τ_D is the characteristic diffusion time through the excitation volume and κ is the ratio w_xy/w_z. The simulated data were fitted well, with a τ_D value of 405 ± 15 μs (standard deviation) from an average of four separate 1 s simulations, in agreement with 419 μs calculated using the diffusion coefficient derived from Figure 2A and the specified Gaussian illumination width in the xy-plane (ω_xy): τ_D = (2w_xy)²/4D. The fitted G(0) was 0.169 ± 0.003, in agreement with 0.169 calculated from the particle concentration, C_N, and the specified Gaussian illumination volume: G(0) = (8π^3/2C_Nκw_xy³)⁻¹. Figure 2E shows P(k;ΔT) computed from F(t), together with a fit to the theory given by Chen et al.¹² The simulated P(k;ΔT) was in excellent agreement with the theory predicting a “super-Poissonian” function but quite different from a single Poisson distribution shown for comparison.

Additional computations were done to validate the model, including demonstrating predicted effects on τ_D and G(0) of changing particle concentrations and diffusion coefficients: τ_D was not affected by concentration and was inversely proportional to the friction coefficient, while G(0) was not affected by the friction coefficient and was inversely proportional to concentration (not shown). Simulations done with non-Gaussian excitation and emission profiles (spherical, cubic, and symmetric Gaussian) at constant volume revealed small though significant changes in the G(τ) curve shape (Figure 2F) that could be misinterpreted as anomalous or other types of complex diffusion.

Effect of Intersystem Crossing on G(τ) and P(k;Δt)

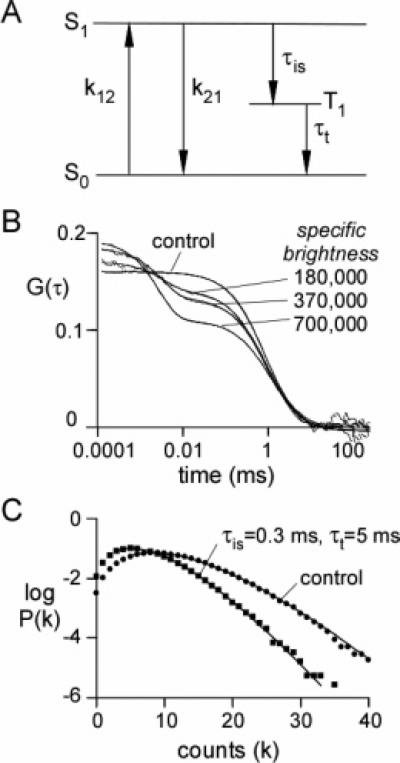
The effect of triplet-state intersystem crossing on G(τ) was simulated by allowing an excited molecule in state S₁ to enter the triplet state (T₁) as a first-order kinetic process characterized by time constant τ_is (Figure 3A). Decay from the triplet state to the ground state was also simulated as a first-order kinetic process characterized by triplet lifetime τ_t. Molecules in the triplet state were not subject to excitation, and decay from the triplet state occurs without detectable photon emission.

Figure 3.

Simulations of intersystem crossing. (A) Kinetic scheme for intersystem crossing. (B) Simulated G(τ). Brownian dynamics trajectories (1 s) generated for 192 spherical molecules with a diffusion coefficient of 107 μm²/s in a 4 × 4 × 12 μm³ box (1 molecule/μm³; 1.7 nM) with a step time of 50 ns×(total of 10⁷ steps), with k₁₂ = k₂₁ = 2.0 × 10⁷ s⁻¹, τ_is = 0.3 μs⁻¹, and ${\stackrel{‒}{\tau }}_{\mathrm{t}}=5\mu \mathrm{s}$. F(t) was generated using a Gaussian excitation beam (w_xy = 0.354 μm and w_z = 1.061 μm) with the indicated specific brightness (in kHz/molecule). The smooth curves (which follow the simulated data very closely) are fits of eq 10 (see text for fitted parameters). (C) Effects of intersystem crossing on P(k;ΔT) with ΔT = 20 μs. Data were simulated as in part B with a specific brightness of 370 kHz/molecule (in the absence of intersystem crossing). Solid lines are fits of the super-Poissonian model with the parameters: control (observed simulation values in parentheses), N̄ = 2.06 (2.16), $\stackrel{‒}{∊}=5.07\left(4.86\right)$; triplet state, N̄ = 2.01 (2.62), $\stackrel{‒}{∊}=3.41\left(2.62\right)$.

Figure 3B shows G(τ) for simulations with intersystem crossing as a function of excitation intensity at constant τ_is = 0.3 μs and τ_t = 5 μs. Excitation intensities in Figure 3B are expressed in terms of the specific brightness (detector counts per molecule per second) obtained from simulations done in the absence of triplet-state population. For this combination of τ_is and τ_t, which are typical of values obtained experimentally,¹⁴ high specific brightness is required to appreciably populate the triplet state.

For the case of isotropic diffusion in a hydrodynamic medium in which the time scale of triplet-state kinetics is much faster than that of diffusion kinetics (the conditions under which Figure 3B was simulated), G(τ) is given as¹⁴

$$G\left(\tau \right)=G\left(0\right){(1+\tau ∕{\tau }_{\mathrm{D}})}^{-1}{(1+\tau ∕{\kappa }^2{\tau }_{\mathrm{D}})}^{-1∕2}\left(\frac{1+\stackrel{‒}{T}({\mathrm{e}}^{-\tau ∕{\stackrel{‒}{\tau }}_{\mathrm{T}}}-1}{1-\stackrel{‒}{T}}\right)$$ (10)

where T̄ is the steady-state fraction of molecules in the triplet state and ${\stackrel{‒}{\tau }}_t$ is the characteristic time for triplet-state decay. T̄ and ${\stackrel{‒}{\tau }}_{\mathrm{T}}$ are spatial averages weighted by the square of the fluorescence intensity across the excitation profile.¹⁴T̄ was calculated numerically by dividing the simulation cell into subcells of 0.1 μm³, tabulating the square of the fluorescence intensity (i²) and the fraction of molecules in the triplet state (T) for each subcell, and then summing the product over the simulation box and over all time steps: T̄ = ∑i²F/∑F, where F = T/(1 – T). τj_T was calculated for each subcell by determining the triplet-state lifetime (τ_t) of molecules entering the triplet state in that subcell, then summing the product: T̄ = (∑τ_Ti²F/c)/(∑i²F/c), where c is the concentration of molecules in the subcell. The time constant τ_t is related to the triplet lifetime, τ_t, by 1/τ_t = 1/τ_T – k₁₂/τ_is(k₁₂ + k₂₁).

The smooth curves in Figure 3B (which track the simulations very closely) are fits of eq 10 to simulated G(τ). The triplet-state state parameters obtained from the fit (T̄ = 0.17, 0.28, and 0.43 and ${\stackrel{‒}{\tau }}_{\mathrm{t}}=3.6$, 3.3, and 2.8 μs, for specific brightnesses 1.8 × 10⁵, 3.7 × 10⁵, and 7.0 × 10⁵, respectively) were in good agreement with those calculated from the parameters used to generate the simulation (T̄ = 0.16, 0.27, and 0.40 and ${\stackrel{‒}{\tau }}_{\mathrm{t}}=3.5$, 3.4, and 2.9 μs, respectively).

Figure 3C shows the effect of triplet-state kinetics on the PCH. As expected, triplet-state kinetics lowered the most probable count rate. Interestingly, P(k;ΔT) for triplet-state kinetics were fitted well by the “super-Poissonian” theory applicable in the absence of triplet-state kinetics, albeit with altered specific brightness and concentration, indicating the inability to detect triplet-state phenomena by PCH analysis alone.

Effects of Photobleaching on G(τ) and P(k;ΔT

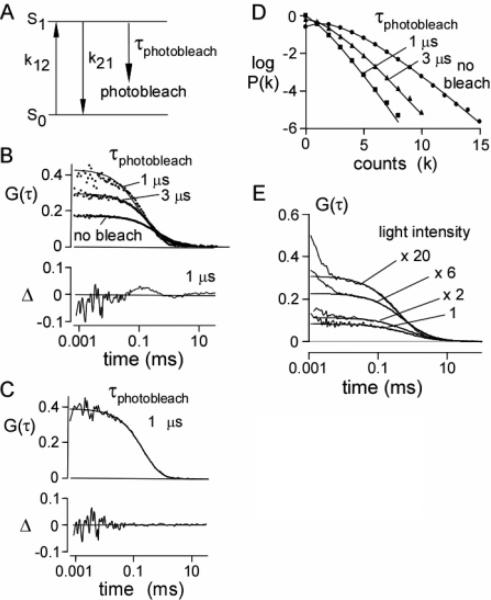
Photo-bleaching was simulated by including a first-order kinetic process that converts an excited molecule into a permanently dark state (Figure 4A). G(τ) and P(k;ΔT) were compared in the absence of photobleaching and for different photobleaching rates as given in Figures 4B and 4C. In the absence of photobleaching, G(τ) was described by eq 9 with fitted G(0) and τ_D (0.168 and 0.422 ms) in agreement with parameters used in the simulation (0.169 and 0.419 ms). As the photobleaching rate increased, simulated G(τ) values were still described reasonably well by eq 9, with deviations apparent at the highest photobleaching rate (1 μs). Photobleaching produced an increase in apparent G(0) (0.296 and 0.428 for τ_bl = 3 and 1 μs, respectively) and decrease in τ_D (0.244 and 0.130 μs). Qualitatively, the increase in G(0) with photobleaching arises from the reduced steady-state fluorophore concentration in the illuminated volume, and the decrease in τ_D arises from enhanced apparent mobility as bleached fluorescent molecules disappear from the excitation volume. Photobleaching can be taken into account approximately by the inclusion of an additional exponential term in the correlation function^23,47

$$G\left(\tau \right)=G_{\mathrm{D}}\left(\tau \right)(1+B({\mathrm{e}}^{-\tau ∕{\tau }_{\mathrm{b}1}}-1))$$ (11)

where G_D(τ) is the autocorrelation function with no photo-bleaching (eq 9), B is the average fraction of excited molecules that photobleach, and τ_bl is the average photobleach time constant. Figure 4C shows that this modified correlation function describes G(τ) well for τ_bl = 1 μs. Figure 4D shows the effect of photobleaching on P(k;ΔT). As expected, the count rate decreased with photobleaching, from 104 kHz (no photobleach) to 51.2 kHz (τ_bl = 3 μs) to 25.4 kHz (τ_bl = 1 μs). As was the case for triplet-state kinetics (Figure 3C), the P(k;ΔT) values for photobleaching were fit well by the super-Poissonian theory applicable in the absence of photobleaching, indicating the inability to identify photobleaching by PCH analysis alone.

Figure 4.

Simulations of photobleaching. (A) Kinetic scheme for photobleaching. (B) Effect of photobleaching on G(τ). Brownian dynamics trajectories generated as in Figure 2. F(t) was generated using a Gaussian excitation beam (w_xy = 0.354 μm, w_z = 1.061 μm) with indicated photobleaching time constants. The specific brightness was 17 kHz/molecule (in the absence of photobleaching). Data were simulated at a constant excitation light intensity. The solid lines are fits of eq 9 (see text for values of fitted parameters) with fractional deviation (Δ) at τ_bl = 1 μs shown in the lower panel. (C) Fit of eq 11 with parameters: G(0) = 0.40, τ_D = 0.34 ms, B = 0.86, and τ_bl = 0.53 ms with fractional deviation (Δ). (D) Effect of photobleaching on P(k;ΔT). Data were binned with ΔT = 20 μs. The solid lines are fits to the super-Poissonian model (with observed simulation values in parentheses): control, N̄ = 2.16 (2.0862), $\stackrel{‒}{∊}=0.9463\left(0.98\right)$; 3 μs bleach, N̄ = 1.30 (1.19), $\stackrel{‒}{∊}=0.70\left(0.76\right)$; 1 μs bleach, N̄ = 0.99 (0.88), $\stackrel{‒}{∊}=0.45\left(0.51\right)$. (E) Effect of excitation light intensity on G(τ) for calcein. The solid lines are fits of eq 9 to the data (starting at 10 μs). Fitted parameters: G(0) = 0.082, 0.11, 0.23, 0.31 and τ_D = 0.60, 0.63, 0.43, 0.22 ms for relative light intensities of 1, 2×, 6×, and 20×, respectively.

The predictions from the simulations of the effects of photo-bleaching were tested experimentally by FCS measurements on aqueous calcein solutions. Representative G(τ) values shown in Figure 4E indicate an increase in G(0) and reduction in τ_D with increased excitation light intensity. The experimental data are in qualitative agreement with the predictions of Figure 4B, though the experimental data also show evidence for increased triplet-state population with increased excitation intensity.

Two-Color Cross-Correlation Validation and Effects of Beam Misalignment

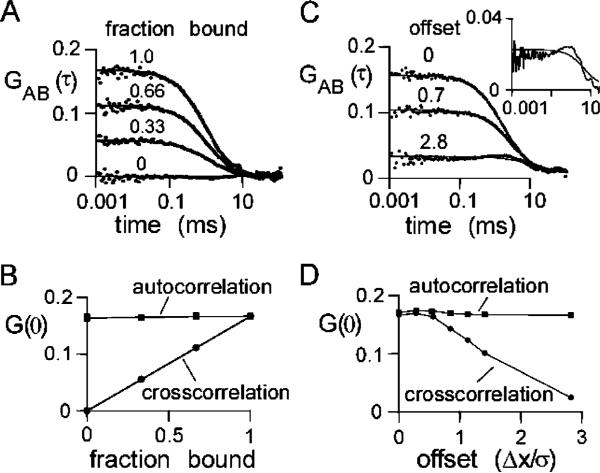
The effects of dimer formation on auto- and cross-correlation G(τ) in two-color FCS were simulated by configuring a system consisting of equal numbers of two kinds of particles, A and B, each separately excited and detected. A specified fraction of A and B were bound permanently as A–B rigid-rod dimers with a 50 nm bond length. Figure 5A shows the cross-correlation function, G_AB(τ), of A and B as a function of the fraction held bound. As expected, G_AB(0) increased with fraction bound. Figure 5B shows that G_AB(0) increased linearly with fraction bound, while the autocorrelation functions, G_AA(0) and G_BB(0), are not sensitive to binding, as expected.

Figure 5.

Simulations of TCFCS. Brownian dynamics trajectories (1 s) generated for 192 spherical particles of type A and 192 spherical particles of type B (each with a diffusion coefficient of 273 μm²/s) in a 4 × 4 × 12 μm³ box using a step time of 100 ns for 10⁷ steps. F(t) generated using a Gaussian excitation beam (w_xy = 0.354 μm and w_z = 1.061 μm) and a specific brightness of 17 kHz/molecule. (A) Effect of dimer formation on the cross-correlation function. Indicated fractions of A and B were constrained as 50 nm rigid-rod A–B dimers. Solid lines are a fit of eq 9. Fitted parameters: G(0) = 0.055, 0.112, and 0.165 and τ_D = 0.97, 0.97, and 0.83 ms for bound fractions 0.33, 0.66, and 1.00, respectively. For unbound A and B, G(0) = 0.163 and τ_D = 0.42 ms (data not shown). (B) Dependence of G(0) on fraction bound. The autocorrelation of the A molecules, G_AA(0), is shown. G_BB(0) (not shown) was identical to G_AA(0). (C) Effect of beam misalignment on cross-correlation function. A and B were constrained as 50 nm rigid-rod A–B dimers. Illumination and detection profiles for A and B were displaced in the x-direction by indicated distances. The solid lines represent a fit of eq 9 to the data. Fitted parameters: G(0) = 0.158, 0.102, and 0.026 and τ_D = 1.63, 1.38, and 5.96 μs for offset Δx/σ = 0.0, 0.7, and 2.8, respectively. Δx is the offset of the centers of the Gaussian excitation profiles, and σ is the standard deviation in the x-direction. The inset shows the lower curve on an expanded y-scale. (D) Effect of misalignment of the beams on auto- and cross-correlation G(0).

The simulated effect of beam misalignment on FCS measurements on a collection of rigid A–B dimers is shown in Figure 5C. For these simulations, identical Gaussian excitation/detection profiles were used, and the centers of the two profiles were offset. The offset in the x-direction was expressed as a fraction of the standard deviation of the Gaussian profile. As expected, G_AB(0) decreased with greater offset. The inset to Figure 4C shows an expansion of the lower curve, revealing a peak in cross-correlation at 1 μs when the beams are separated by 2.8 times the standard deviation. This peak in cross-correlation occurs near the characteristic diffusion time of 1.6 μs and corresponds to the cross-correlation arising from diffusion of the A–B dimer from one detection volume to the other. Figure 5D shows that G_AB(0) is relatively unaffected until the centers of the excitation profiles are separated by more than 0.2 times the standard deviation of the Gaussian excitation profile.

Effects of Binding on G(τ)

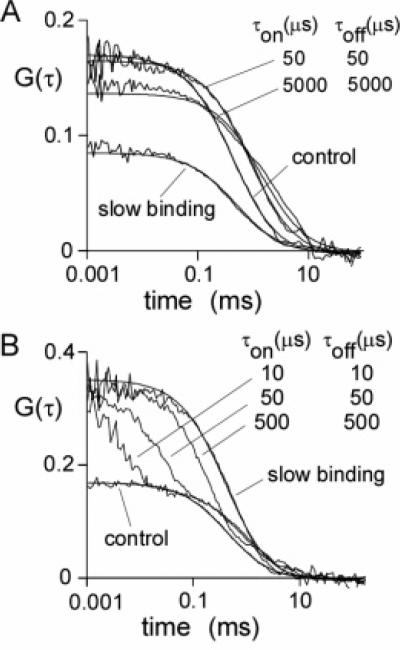
Simulations of binding were done for an ensemble of molecules in which there was a constant probability that a molecule would stop in its trajectory (characterized by time constant τ_on), and once stopped, a constant probability to resume its trajectory (characterized by time constant τ_off). This system corresponds to binding of a fluorophore to an immobile object with on and off rate constants 1/τ_on and 1/τ_off, respectively. Simulations for τ_on/τ_off = 1 are shown in Figure 6A. For τ_on = τ_off = 50 μs, G(0) is only mildly affected, but apparent τ_D increases. Similar data were obtained for τ_on = τ_off = 500 μs (not shown). As the on–off times increase to 5000 μs, G(0) decreases and τ_D increases. The increase in apparent τ_D is related to slowed fluorophore diffusion in the excitation volume because of binding; the reduced G(0) with slow on—off rates arises from fluorophores that do not escape the excitation beam over the course of the simulation, acting as background fluorescence. In the limit of very slow binding, bound fluorophores do not move whereas the free fluorophores diffuse without binding. Since τ_on/τ_off = 1 and half of the fluorophores are bound for the simulations in Figure 6A, G(0) is reduced to half of its original value with no change in τ_D.

Figure 6.

Simulations of binding effects on FCS. Brownian dynamics trajectories (1 s) generated for 192 spherical particles in a 4 × 4 × 12 μm³ box using a time step of 100 ns for 10⁷ steps. F(t) values were generated using a Gaussian excitation beam (w_xy = 0.354 μm and w_z = 1.061 μm) and a specific brightness of 17 kHz/molecule. Trajectories were modified by fixing the positions of particles for a given time, as described in the text, characterized by association time, τ_on, and dissociation time, τ_off. To simulate slow binding, particles selected at random were held fixed throughout the course of the simulation, and no additional particles were allowed to bind. The fraction of particles was held fixed at τ_off/(τ_on + τ_off) = 0.5. (A) Effect of binding on G(τ) with equally fluorescent bound and free particles. Solid lines are a fit of eq 5, with fitted parameters: G(0) = 0.170, 0.166, 0.136, and 0.085 and τ_D = 0.45, 0.93, 1.52, and 0.52 ms for control, τ_on = 50 μs, τ_on = 5000 μs, and slow binding, respectively. (B) Same as in part A, except that bound particles were nonfluorescent. The solid curves are a fit of eq 9 with: G(0) = 0.170 and 0.356 and τ_D = 0.45 and 0.41 ms for control and slow binding, respectively.

Simulations were also done for the case where the bound complex is nonfluorescent (Figure 6B). A second component is seen in autocorrelation functions, corresponding to a flickering of the fluorescence signal produced by binding–unbinding. As the binding rate slows, the second component becomes more prominent until, in the limit of infinitely slow binding–unbinding, the system behaves as a collection of fluorophores at half of the concentration of the control. The fitted G(0) (0.170 and 0.357) and τ_D (0.45 and 0.41 ms) for control and slow binding support this interpretation. For the slow binding data in Figure 6B, 50% of fluorophores are dark at any one time, producing a 2-fold increase in G(0) but no change in τ_D.

Effects of Anomalous Diffusion and Crowding on G(τ)

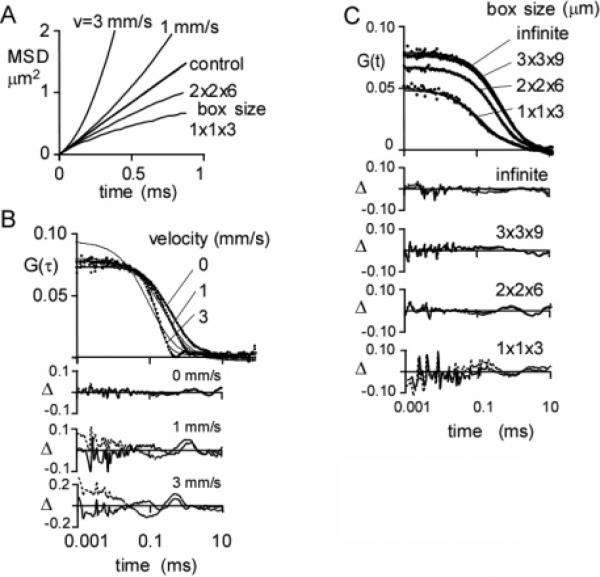
Anomalous superdiffusion was modeled by inclusion of drift in the Brownian dynamics simulation. Increasing drift (velocity from 0 to 3 mm/s) produced greater upward curvature in the MSD plot (Figure 7A), signifying superdiffusion. The corresponding G(τ) curve shape differed significantly from that for simple diffusion (Figure 7B) but fit reasonably well to the semiempirical equation often used for FCS measurements of anomalous diffusion⁵⁰

$$G\left(\tau \right)=G\left(0\right){(1+{(\tau ∕{\tau }_{\mathrm{D}})}^{\alpha })}^{-1}{(1+{(\tau ∕{\kappa }^2{\tau }_{\mathrm{D}})}^{\alpha })}^{-1∕2}$$ (12)

Fitted α values were 1.5 and 2.5 for drifts of 1 and 3 mm/s, respectively.

Figure 7.

Simulations of anomalous diffusion. (A) MSD plots for simulated super- and subdiffusion. Brownian dynamics trajectories were generated for 0.73 μm particles at a concentration of 2 particles/μm³ for 100 ms using a 200 ns time step (average of 50 trajectories). Superdiffusion was simulated by a constant velocity (v) in the x-direction. Subdiffusion was simulated by confining the particle to a rectangular box of indicated dimensions. (B) Superdiffusion. F(t) values were generated with a Gaussian excitation profile of w_xy = 0.354 μm, w_z = 1.061 μm (κ = 3), and a specific brightness of 17 kHz/molecule. G(τ) as a function of velocity is shown along with deviations (Δ) between the fit of eq 9 (dashed line) or 11 (solid line) and the simulation. Fitted parameters are given in Table 1. (C) Subdiffusion. F(t) and fits were generated as in part B. Infinite box size refers to a 3 × 3 × 9 μm³ box with periodic boundary conditions.

Anomalous subdiffusion was modeled by confining diffusion to a box with reflecting boundaries. At box sizes comparable to the size of the Gaussian excitation beam (width 0.7 × 0.7 × 2.1 μm³), MSD plots were downward-curved (Figure 7A), signifying subdiffusion. MSD plots leveled out at long times (data not shown). Corresponding G(τ) values (Figure 7C) were fitted using eq 12 with α values of 1.0 and 0.9 for box sizes of 2 × 2 × 6 and 1 × 1 × 3 μm³, respectively.

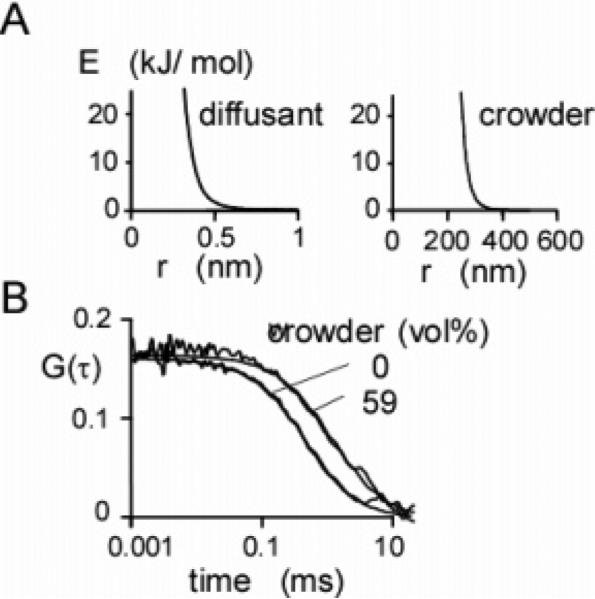
As another possible cause of anomalous subdiffusion, molecular crowding, was modeled by simulating the diffusion of small fluorophores (radius 0.73 nm) in a crowded environment containing large nonfluorescent mobile spheres (radii of 150 nm). Intermolecular interactions were specified by the nonbonding potentials shown in Figure 8A. At a crowder volume fraction of 59%, there was an increase in apparent τ_D by 2.5-fold without a change in G(0) (Figure 8B). The crowder volume fraction was calculated by taking the effective crowder radius as the distance at which the intermolecular potential increased to kT. Others have used energies up to 2kT.⁵¹ With the larger energy, the crowder radius decreases to 143 nm, and the volume fraction decreases to 0.50.

Figure 8.

Simulations of crowding. (A) Nonbonding potentials used in crowding simulations. The radius of the particles was defined operationally as the distance from the center of the particle at which the potential dropped to kT. (B) Effect of crowding on G(τ). Brownian dynamics trajectories (100 ms) were generated for 81 spherical diffusing particles (diffusion coefficient 95 μm²/s, effective radius 0.45 nm) and 420 large crowding particles (diffusion coefficient 0.67 μm²/s, effective radius 300 nm) in a 3 × 3 × 9 μm³ box for a volume exclusion of 59%. The solid lines represent a fit of eq 9 to the data. Fitted parameters: G(0) = 0.161 and 0.164 and τ_D = 0.80 and 2.01 ms for volume fractions 0% and 59%, respectively.

The MSD plots were linear with a 2.5-fold decrease in slope at 59% crowder volume fraction (data not shown). MSD plots of the large crowder particles were also linear over the simulation time course. The G(τ) shape was described adequately by a model without anomalous diffusion (eq 9) as predicted from the linear MSD plot. Because of computation time constraints, it was not practical to carry out crowding simulations at more highly crowded volume fractions or using smaller crowder sphere diameters where greater slowing of diffusion is predicted.

Discussion

The purpose of this study was to develop a generalized computational approach for simulation of correlation functions and intensity histograms to investigate phenomena that are expected to complicate the interpretation of FCS measurements on biological systems. Such simulations enable analysis of systems for which analytical expressions for G(τ) or P(k;ΔT) do not exist, such as non-Gaussian detection volumes, complex photophysical phenomena, diffusion through complex, inhomogeneous, or anisotropic media, or nonequilibrium effects. The simulations described here were applied to analyze the impact on FCS of photobleaching, intersystem crossing, misaligned focal volume elements in two-color FCS (TCFCS) experiments, transient fluorophore binding to an immobile substrate, and anomalous diffusion.

Simulation Method

Our simulation approach used three distinct modules for computation of particle trajectories, simulation of photon statistics to generate F(t), and computation of correlation functions and histograms from F(t). Trajectories were computed as Brownian molecular dynamics trajectories to enable the time and spatial resolution needed to simulate rapid photophysical effects and interparticle interactions. In contrast, in most FCS simulation methods^40,48 trajectories are generated by random jumps between lattice points on a grid. While lattice methods are computationally efficient, intra- and intermolecular interactions are difficult to simulate. Here, we generated trajectories using the Langevin equation appropriate for a highly damped system of independent particles. This approximation is valid for low concentrations of small particles over time scales much greater than the characteristic relaxation time for particle motion.³⁴ The relaxation time is given by the ratio of particle mass to the solvent friction coefficient. For small molecules in aqueous solutions the relaxation time is on the order of femtoseconds and thus much smaller than the simulated millisecond diffusion times. The close agreement between the simulated data and that predicted theoretically (Figure 2) supports the approach used here to compute trajectories for FCS simulation.

Decoupling the trajectory module from the fluorescence module allows efficient simulation of various complex phenomena such as the effects of conformation and mobility of polymers on FCS experiments. Photophysical phenomena and different illumination profiles are easily simulated without recomputing trajectories. Such effects are not easily computed using simulation approaches in which dynamics and fluorescence generation are directly coupled.^42,49

Diffusion through structures having complex geometries, such as cellular organelles, can produce significant deviations from G(τ) compared to isotropic diffusion (eq 9). For example, significant deviations from eq 9 are found for diffusion of small molecules through dendritic tubules with diameters much smaller than the focal volume,¹⁸ anomalous subdiffusion through cell cytoplasm,⁵⁰ and non-Gaussian excitation profiles.²⁰ The simulation approach described here is readily adapted to include these phenomena. Restricted diffusion is simulated by computing appropriate Brownian molecular dynamics trajectories and non-Gaussian excitation profiles by modifying the fluorescence statistics module.

The raw fluorescence trace data were stored in a PAT format. As discussed by Eid et al.⁵² and Laurence et al.,⁵³ the PAT is the most efficient way to encode photon-count data when the number of photon counts is much smaller than the number of available time bins in the data acquisition hardware. We developed an efficient approach to compute intensity auto- and cross-correlation functions and photon-count histograms using PAT information directly. Storing F(t) and calculating G(τ) and P(k;ΔT) using the PAT format obviates the need to store and carry out computations of time bins that have zero counts.

Effects of Photophysics on G(τ) and P(k;ΔT

FCS experiments at high excitation light intensities with photolabile fluorophores can be complicated by triplet-state kinetics as well as by photobleaching (Figures 3 and 4). These two phenomena are often found concurrently: Excitation to higher energy levels increases the probability of both intersystem crossing and photobleaching. The effects can be simulated independently in our method.

Analytical forms for G(τ)¹⁴ and P(k;ΔT)⁴⁸ have been developed for molecules that undergo intersystem crossing into the triplet state. Simulations with triplet-state photophysics (Figure 3B) showed excellent agreement with G(τ) predicted from theory. The histogram analysis in Figure 3C showed that P(k;ΔT) computed with triplet-state kinetics can be fit well by the super-Poissonian theory neglecting photophysical effects. Palo et al.⁴⁸ propose that the effects of triplet-state trapping on P(k;ΔT) may be accounted for by using apparent specific brightness and concentration values according to

$$\begin{array}{c}\hfill {\stackrel{‒}{N}}_{\mathrm{app}}\propto c_{\mathrm{app}}\left(\Delta T\right)=\frac{c}{{\Gamma }_{\mathrm{trip}}\left(\Delta T\right){\Gamma }_{\mathrm{diff}}\left(\Delta T\right)(1+\kappa \tau )}\hfill \\ \hfill {\stackrel{‒}{∊}}_{\mathrm{app}}=q_{\mathrm{app}}\left(\Delta T\right)=q{\Gamma }_{\mathrm{trip}}\left(\Delta T\right){\Gamma }_{\mathrm{diff}}\left(\Delta T\right)\hfill \end{array}$$ (13)

where ΔT is the histogram bin time, κ is the singlet–triplet transition rate, τ is the triplet lifetime, and Γ_trip(ΔT) and Γ_diff(ΔT) are correction factors for triplet events and diffusive mixing, respectively, occurring within the time ΔT. For triplet-state dynamics

$${\Gamma }_{\mathrm{trip}}\left(\Delta T\right)=\left\{2\lambda f(1+f-\lambda (1-\exp [-(1+f)∕\lambda ]))\right\}∕{(1+f)}^3$$ (14)

where λ = τ/ΔT and f = κτ. Using eq 14, however, leads to a significant underestimation of the specific brightness and particle concentration compared to the values from the simulation and those obtained fitting P(k;ΔT) to the histogram data (Figure 3C). Significantly, this implies that the current theory described by Palo et al.⁴⁸ is insufficient for determining triplet-state parameters from P(k;ΔT).

Photobleaching effects become apparent on G(0) and τ_D (with little change in the shape of G(τ)) when the characteristic time constant for photobleaching is as low as 1% of the diffusion time (Figure 4B). The simulations of photobleaching (Figure 4) are qualitatively consistent with what is expected from removal of fluorophores from the excitation volume. Ignoring the effects of photobleaching on G(τ) can produce significant underestimation of particle concentration and overestimation of particle mobility. An important finding from our simulations is that the P(k;ΔT) profile shape is quite insensitive to photo-bleaching dynamics, as was also found for triplet-state dynamics. The main determinants of P(k;ΔT) are the steady-state fluorescence properties of the molecules, even if the time scales for P(k;ΔT) binning are comparable to the time scale of the kinetics.

There is no analytical expression for the fluorescence auto-correlation as a function of photobleach time because the probability of photobleaching depends in an unknown way on the nonuniform excitation across the excitation volume. Eggeling et al.²³ and Dittrich and Schwille⁴⁷ have developed an approximate expression for G(τ) (eq 11) assuming the excitation probability is uniform across the excitation volume. Equation 11 describes the data well (Figure 4C), indicating that photo-bleaching in FCS experiments can be thought of as a unimolecular kinetic process independent of the diffusional motion of the fluorophore through the excitation beam. According to this view, effects of photobleaching on FCS experiments become apparent when the effective photobleaching time (τ_bl of eq 11) becomes comparable to the characteristic time for diffusion through the excitation beam (e.g., τ_bl = 0.53 ms and τ_D = 0.34 ms for the conditions in Figure 4C).

Molecular Interactions

Two-color FCS has been used to measure the concentration of bound fluorophores,⁵⁴ which relies on the fact that G(0) and τ_D of the cross-correlation function contain information only about bound fluorophores. As predicted, our simulations showed that at constant fluorophore concentration G(0) parallels the fraction of bound fluorophores (Figures 5A and 5B). The fitted diffusion time for the cross-correlation function (0.83–0.97 ms) was greater than that of the monomer (0.42 ms), as expected for slower dimer diffusion. G(0) for the cross-correlation function at 100% bound (0.165) was similar to that for the autocorrelation function (0.163), indicating that all fluorophores are detected. These simulations validate the use of cross-correlation methods to measure concentrations of bound fluorophores.

In a commonly used implementation of TCFCS, two laser beams are used, with each laser beam exciting a single class of fluorophores. It is generally advised that the two laser beams be of equal intensity and superimposed if G(τ) is to be analyzed by simple diffusional models.⁵⁵ Imperfect beam alignment was modeled as an application of the TCFCS simulation. Our results (Figure 4D) indicate that the beams may be displaced as much as 20% of the width of the excitation beam without significant effects on G(τ). However, an offset of several times the width can lead to a peak in the cross-correlation (Figure 4C). Such a peak in G_AB(τ) is also seen for transient association of A and B¹⁰ so that misregistration of the two excitation beams in TCFCS could be wrongly interpreted as bimolecular kinetic phenomena.

Fluorophore binding can also change G(τ) curve shape.⁵⁶ Dynamic effects were simulated by stopping a fluorophore in its trajectory for a randomly chosen time so as to produce first-order kinetics. When binding occurs without a change in quantum yield and on the time scale of diffusion through the illumination volume (Figure 6A), significant effects on G(0) and τ_D were found even though the G(τ) curve shape was well described by simple diffusion (eq 9). The G(τ) curve shape differed from that predicted by simple diffusion when the diffusion time was increased by 10-fold. When binding occurs with a change in quantum yield (Figure 6B), there were significant changes in G(τ) curve shape for all binding rates. Thus, fluorophore binding to a slowly diffusing or immobile object on a time scale of the diffusion time or faster may not be detected from a curve-shape analysis of G(τ) unless there is a change in fluorescence quantum yield upon binding.¹⁰ Furthermore, immobile fluorophores are not detected, producing an overestimate (Figure 6A) or underestimate (Figure 6B) in fluorophore concentration.

Anomalous Diffusion and Molecular Crowding

In general terms, anomalous diffusion can be defined as diffusion in which the MSD of a particle is not linear with time. Another commonly used definition of anomalous diffusion is that the MSD is proportional to t^α, where α is not equal to 1. In the analysis of FCS data, the parameter α has been determined by fitting eq 12 to the data. The parameter α is often used as a semiempirical measure of anomalous diffusion.⁵⁰ The approach used here was to investigate the effect of three “nonnormal” diffusive models (normal diffusion plus drift, reflecting boundary conditions, and crowding) on FCS data. The effects were investigated by fitting eq 12 to the simulated data.

Anomalous diffusion has been reported for molecular diffusion in crowded biological environments such as membranes and cytoplasm.^50,57 Anomalous superdiffusion, characterized by upward-curved MSD plots, can be produced by directed movement by convective or motor-driven processes. Anomalous subdiffusion, seen as downward-curved MSD plots, can be produced by confined or restricted diffusion. Anomalous diffusion in FCS analysis has been analyzed semiempirically using eq 12, in which a parameter α is included. The parameter α describes the power-law behavior of the MSD plot: r² ≈ t^α. An α of unity signifies simple diffusion, with α < 1 indicating subdiffusion and α > 1 superdiffusion.

Simulations of superdiffusion and subdiffusion in Figure 7 produced nonlinear MSD plots and altered G(τ) curve shape. Superdiffusion, modeled by convection, produced an upwardly curved MSD plot (Figure 7A) as expected. Significant deviations in G(τ) from simple diffusion were found (Figure 7B). G(0) was unaffected by drift velocity, indicating the average number of particles in the excitation beam was unaffected by drift velocity. However, the apparent diffusion time τ_D increased with drift velocity as a consequence of the reduced time a particle remains in the excitation volume. Notably, G(τ) values were fitted reasonably well with eq 12 with α > 1, providing the first direct validation for the use of eq 12 in FCS analysis of anomalous diffusion.

Subdiffusion, modeled by confining particles to a rectangular box with reflecting boundary conditions, produced downward-curved MSD plots (Figure 7A). When the dimensions of the box became comparable to those of the excitation volume, both G(0) and τ_D decreased, with a small change in α. G(0) decreases because of the apparent increase in particle concentration as particles are unable to diffuse out of the beam. τ_D decreases because collisions with the box walls keep the particles within the excitation volume, leading to an apparent decrease in transit time across the excitation volume. An important implication of these simulations is that FCS analysis of solute diffusion in a small confined compartments (such as an intracellular organelle) could produce overestimations of solute diffusion and concentration without significant change in G(τ) shape.

Molecular crowding, defined as the volume exclusion of solvent by a crowder, can strongly slow solute diffusion and potentially produce anomalous subdiffusion.^27,46,58 Calculation of solute diffusion in crowded solutions using statistical mechanical theories and comparison with experimental data suggest that the solute and crowder can be modeled effectively as hard spheres with the solvent modeled as a continuum. Extensions to this model include attractive potentials⁵⁸ and Lennard-Jones and Coulomb interactions.⁵⁹ Here, crowding was simulated using Brownian dynamics with repulsive interactions between crowder and solute (Figure 8). With large spheres at 59 vol % as the crowder, solute diffusion was slowed 2.5-fold with G(τ) fitting well to a simple diffusion model (α = 1). These results are in agreement with experimental data showing nonanomalous diffusion of the small solute Rhodamine G with Ficoll-70 crowder concentrations of up to 60 wt %, producing a 140-fold slowing of diffusion.⁴⁶

Measurement of the diffusion of larger solutes with Ficoll-70 as a crowding agent also shows nonanomalous diffusion.^46,60 However, Weiss et al.⁵⁰ found anomalous diffusion of large dextrans (10–2000 kDa) and IgG when cell cytoplasm was used as a crowding agent. This apparent discrepancy has not been resolved. Because of computational time constraints, it was not possible here to carry out the computationally intensive simulations of crowding by large numbers of diffusing particles.

In conclusion, we have reported a general method for simulation of FCS data. The method was used to investigate effects of beam geometry, photophysical processes, binding, anomalous diffusion, and crowding. Our approach should prove useful in the design and analysis of FCS studies on systems with complex diffusive phenomena.

TABLE 1.

Fitted Parameters for Simulations of Anomalous Diffusion in Figure 7

	simple diffusion		anomalous diffusion
simulation	G(0)	τD (ms)	G(0)	τD (ms)	α
superdiffusion, control	0.081	0.41	0.079	0.409	1.07
superdiffusion, v = 1 mm/s	0.085	0.28	0.074	0.31	1.50
superdiffusion, v = 3 mm/s	0.098	0.11	0.074	0.17	2.50
subdiffusion, control	0.080	0.39	0.077	0.39	1.08
subdiffusion, 3 × 3 × 9 μm3	0.086	0.47	0.085	0.48	1.03
subdiffusion, 2 × 2 × 6 μm3	0.070	0.30	0.068	0.30	1.07
subdiffusion, 1 × 1 × 3 μm3	0.049	0.13	0.051	0.12	0.89