Abstract
Proteins with multiple binding sites play important roles in cell signaling systems by nucleating protein complexes in which, for example, enzymes and substrates are co-localized. Proteins that specialize in this function are called by a variety names, including adapter, linker and scaffold. Scaffold-mediated nucleation of protein complexes can be either constitutive or induced. Induced nucleation is commonly mediated by a docking site on a scaffold that is activated by phosphorylation. Here, by considering minimalist mathematical models, which recapitulate scaffold effects seen in more mechanistically detailed models, we obtain analytical and numerical results that provide insights into scaffold function. These results elucidate how recruitment of a pair of ligands to a scaffold depends on the concentrations of the ligands, on the binding constants for ligand-scaffold interactions, on binding cooperativity, and on the milieu of the scaffold, as ligand recruitment is affected by competitive ligands and decoy receptors. For the case of a bivalent scaffold, we obtain an expression for the unique scaffold concentration that maximally recruits a pair of monovalent ligands. Through simulations, we demonstrate that a bivalent scaffold can nucleate distinct sets of ligands to equivalent extents when the scaffold is present at different concentrations. Thus, the function of a scaffold can potentially change qualitatively with a change in copy number. We also demonstrate how a scaffold can change the catalytic efficiency of an enzyme and the sensitivity of the rate of reaction to substrate concentration. The results presented here should be useful for understanding scaffold function and for engineering scaffolds to have desired properties.
Keywords: Multivalent binding, synthetic biology, biological design principles, ternary complex, prozone effect, combinatorial inhibition, adaptor
1. Introduction
Proteins involved in cell signaling typically possess multiple binding sites, and as a result, a common feature of these proteins is their ability to interact with several binding partners to form heterogeneous protein complexes [1]. Some proteins specialize in the nucleation of protein complexes [2]. For example, Ste5 is a well-studied scaffold protein that acts in a yeast MAP kinase cascade; it binds all three kinases of the cascade, Ste11, Ste7, and Fus3 [3]. The interaction of Fus3 with Ste5 is modulated by multisite phosphorylation of Ste5 [4]. One function of Ste5 is to co-localize enzyme-substrate pairs (e.g., Ste11 and Ste7) in the cascade [5], which contributes to switch-like cellular responses to signals [4]. Two well-known examples of scaffold-like proteins that nucleate protein complexes in mammalian signaling systems are the Grb2 adapter protein in the epidermal growth factor receptor (EGFR) pathway [6] and the LAT linker protein in the T cell receptor (TCR) pathway [7, 8, 9]. The binding sites in LAT are activated by tyrosine phosphorylation, and as a result, the valence of LAT and the abundance of functional LAT binding sites can be quickly changed by changes in kinase and phosphatase activities, with these changes serving to modulate the effect of LAT on signaling [10]. In addition to proteins with dedicated scaffold functions, proteins that have catalytic activities and protein complexes, such as ligand-induced receptor dimers, can also function as scaffolds, i.e., take on the function of facilitating the formation of multicomponent complexes through multivalent binding.
Many functions have been ascribed to scaffold proteins [2, 9, 11, 12, 13, 14]. For example, scaffolds have been suggested to control the specificities of enzymes, coordinate spatiotemporal aspects of signaling, and amplify or attenuate signals. To better understand the mechanisms by which scaffolds influence cell signaling, researchers have formulated mathematical models to study the effects of scaffolds on specific signaling systems and to study the generic properties of scaffolds [15, 16, 17, 18, 19, 20, 21, 4, 22]. The ability of a scaffold to either amplify or attenuate signaling was demonstrated by Levchenko et al. [16] using a mathematical model for a MAP kinase cascade. In this model, scaffold enhancement of signaling results from scaffold-mediated nucleation of an enzyme with its substrate, whereas scaffold inhibition of signaling results from excess scaffold, which separates enzyme and substrate into distinct enzyme-scaffold and substrate-scaffold complexes. This effect is equivalent to the well-known prozone effect in antibody-antigen reactions [15]. Heinrich et al. [17] further studied these effects of scaffolds on protein kinase cascades. More recently, Locasale et al. [20] studied how scaffolds affect competition between phosphatases and kinases, finding that scaffolds can have positive and negative effects on signaling for reasons related to the kinetics of signaling events.
Modeling has improved our understanding of scaffold function, but many of the reported modeling studies of scaffold function have been based solely on simulations, which makes the results dependent on the parameter values considered in simulations. In addition, many of the models used to study scaffolds incorporate mechanistic details that are likely to be extraneous for understanding scaffold function broadly. Greater theoretical understanding of the design principles of scaffolds could perhaps be obtained by focusing on minimalist models that are relatively easy to analyze. With a better understanding of scaffold design principles, we can hope to manipulate scaffold function through precise tuning of scaffold and system properties. Manipulating the properties of a scaffold or its milieu to alter the behavior of a cell signaling system is known to be feasible [5, 23, 24]. For example, Lim and co-workers have demonstrated that the response of a cell to a signal can be changed qualitatively by altering the binding specificities of a scaffold [5].
Here, by considering minimalist models for multivalent scaffold-ligand interaction, we investigate the recruitment of ligands to a scaffold and the effects of a scaffold on an enzymatic reaction. We obtain a number of analytical and numerical results, mostly for a model that characterizes the equilibrium formation of a ternary complex composed of a scaffold and two binding partners. In this ternary-complex model, the scaffold is bivalent and and its monovalent binding partners are taken to be an enzyme-substrate pair. Each binding partner, or ligand, interacts with one of the two binding sites of the scaffold. We evaluate the relevance of the ternary-complex model through comparisons with more mechanistically detailed models for cell signaling systems that involve scaffolds. The ternary-complex model is similar in mathematical form to a variety of models that have been used to study receptor signaling [25, 26] and multivalent ligand-receptor binding [27, 28, 29].
The remainder of this report is organized as follows. In Section 2, we introduce models and present analytical results relevant for understanding the effects of scaffold valence, negative and positive cooperativity in binding of multiple ligands to a scaffold, competitive inhibitors of ligand-scaffold interactions, and decoy receptors. We also develop an approximate rate law for scaffold-mediated enzyme kinetics. Our most significant analytical result is a design equation that characterizes how the scaffold concentration that maximally nucleates a ternary complex depends on equilibrium binding constants and ligand concentrations. Interestingly, this scaffold concentration is independent of cooperativity in ligand binding. In Section 3, we present numerical results that complement the analytical results. The numerical results include a demonstration that our simple ternary-complex model recapitulates scaffold effects seen in more mechanistically detailed models and a demonstration that a single scaffold can nucleate distinct signaling complexes at different scaffold concentrations. We conclude with a brief discussion (Section 4).
2. Models and Analytical Results
The models that we will consider are illustrated in Fig. 1 and described below, along with various analytical results relevant for understanding scaffold function.
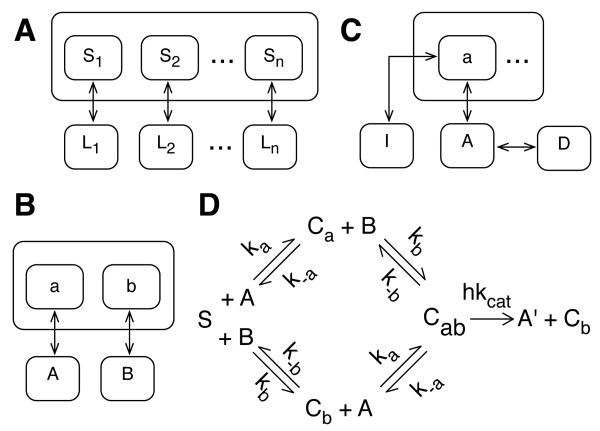
Figure 1.
Minimalist models for ligand-scaffold interactions. (A) A scaffold with n sites (S1,…, Sn). Each site Si interacts with a distinct ligand Li. (B) Ternary-complex model. A bivalent scaffold with sites a and b interacts with monovalent ligands A and B, respectively. (C) A scaffold site a interacts with a ligand A and a competitive inhibitor I. The ligand A interacts with a decoy receptor D. (D) A reaction scheme for a scaffold-mediated enzymatic reaction that produces a product A′. The substrate is scaffold ligand A and the enzyme is scaffold ligand B. See text for discussion.
2.1. Multivalent scaffold with independent binding sites
We consider a scaffold protein with n ≥ 2 binding sites. Each scaffold binding site i interacts independently with a distinct monovalent ligand i, as illustrated in Fig. 1(A). Thus, we consider the following reactions:
| (1) |
where Si represents free site i, Li represents free ligand i, and Bi represents bound site i (or equivalently, bound ligand i). Using the same symbols for chemical species in Eq. (1) for the corresponding concentrations, we can write the following equilibrium relations, which are derived from the law of mass action:
| (2) |
where Ki is an equilibrium dissociation constant. Assuming conservation of mass, such that S0 = Si + Bi and Li0 = Li + Bi, where S0 is the total concentration of scaffold protein and Li0 is the total concentration of ligand i, we find from Eq. (2) that
| (3) |
From the quadratic formula and the physical constraint that Bi < min(Li0, S0), it further follows that
| (4) |
This equation and the mass conservation relations given above can be used to completely determine the equilibrium state of the system described in Fig. 1(A).
We will now show that there is a unique scaffold concentration that maximizes Cn, the equilibrium concentration of scaffold protein with all n sites occupied. The analytical results that follow complement numerical results obtained in earlier modeling studies of scaffold function [11, 15, 16, 17].
We note that the equilibrium quantity Bi/S0 can be interpreted as the probability that scaffold binding site i is occupied at equilibrium. Likewise, Cn/S0 can be interpreted as the joint probability that all n scaffold binding sites are occupied. Thus, because each scaffold binding site is assumed to interact with its cognate ligand independently, we can write
| (5) |
Trivially, for the case S0 = 0, Cn = 0. In other words, there is no complex in the absence of scaffold. Also, from Eq. (5), we can see that limS0→∞Cn = 0, because each Bi is finite. In fact Bi can be no greater than Li0. From inspection of Eqs. (4) and (5), one can see that Cn is a continuous and differential function of S0. Thus, from the mean value theorem, the derivative of Cn with respect to S0 must vanish at some finite value of S0, which we will denote as . In other words,
| (6) |
Because is unique, as we will show below, and Cn is positive for all finite S0 (on physical grounds), Cn is maximum at .
To see that is unique, consider the following expression, which is derived from Eq. (5) by differentiating Cn with respect to S0:
| (7) |
where
| (8) |
Note that gn is the slope of the plot of log Cn vs. log S0. The expression for bi was obtained by differentiating each term in Eq. (3) with respect to S0 and then solving for dBi/dS0. From inspection of Eq. (8), one can see that 0 < bi < 1 for finite S0. In fact, it can be shown that limS0→0 bi = 1 and limS0→∞ bi =0. From these considerations and inspection of Eq. (7), one can see that is unique if bi decreases monotonically as S0 increases for all i. Differentiating the expression for bi given in Eq. (8) with respect to S0, we find
| (9) |
Note that the terms Bi – Li0, Bi – S0, and are all negative. Thus, each bi is a monotonically decreasing function, as is gn by extension, and as a result, is unique.
The results presented above provide insight into the shape of the log-log scaffold dose-response curve, meaning the plot of log Cn vs. log S0. Recall that the slope of this curve, which is concave, is given by Eq. (7). As can be seen from Eq. (7), for , whereas for . For n = 2, |g2| approaches 1 as S0 approaches either 0 or ∞. However, for n ≥ 3, the two asymptotic limits of |gn| are different, with the curve becoming steeper at some point in the excess scaffold regime than at any point in the regime where . Thus, the log-log scaffold dose-response curve is asymmetric.
To gain insight into the effect of scaffold valence on scaffold function, measured by nucleation of a complex in which all scaffold binding sites are occupied, let us consider two scaffolds in the same milieu with the same properties except that one scaffold has an extra binding site n and cognate binding partner Ln. We impose this equivalence constraint to ensure a fair comparison [30, 31]. We will denote the valences of the two scaffolds as m ≥ 2 and n = m + 1. From Eq. (5) and our equivalence constraint, it follows that Cn = CmBn/S0 and further that Cn < Cm for any given scaffold concentration. Thus, with all factors being as equal as possible, scaffold-mediated nucleation of Cn is less efficient than nucleation of Cm. Another inherent effect of valence on scaffold function is greater sensitivity of Cn to changes in scaffold concentration in the excess scaffold regime. From Eq. (7), for S0 sufficiently large such that gm < 0 and gn < 0, it can be seen that gn is larger in magnitude than gm. This result is consistent with our earlier discussion of asymmetry in the log-log scaffold dose-response curve.
2.2. Bivalent scaffold with cooperative ligand binding
We will now consider a bivalent scaffold that interacts with a pair of monovalent ligands A and B (Fig. 1(B)). Ligand A interacts with a scaffold binding site a, and ligand B interacts with a scaffold binding site b. Equation (1) with n = 2 applies, but we will not use the nomenclature of Eq. (1) in our treatment of this special case, which because of its simplicity will allow us to obtain an analytical expression for the scaffold concentration that maximizes formation of the ternary complex composed of A, B and the scaffold. Nucleation of this complex can be taken as a measure of the functional activity of the scaffold if A and B constitute an enzyme and substrate or if instead the two ligands constitute functionally related enzymes recruited to the scaffold to act in concert, as in substrate channeling [32]. We will relax the assumption that ligands interact with the scaffold independently and allow for cooperative binding. Thus, using the law of mass action, we write the following equilibrium relations:
| (10) |
| (11) |
| (12) |
where Sf is the concentration of free scaffold, Af and Bf are the concentrations of free ligands A and B, Ka is an equilibrium dissociation constant that characterizes a-A interaction, Ca is the concentration of the binary complex composed of A and the scaffold, Kb is an equilibrium dissociation constant that characterizes b-B interaction, Cb is the concentration of the binary complex composed of B and the scaffold, and Cab is the concentration of the ternary complex composed of A, B, and the scaffold. The factor ϕ, which is positive and dimensionless, is introduced to characterize cooperativity in binding of A and B to the scaffold: ϕ < 1 indicates negative cooperativity, ϕ > 1 indicates positive cooperativity, and ϕ = 1 indicates that the ligands bind the scaffold independently. We will assume conservation of mass, such that the following relations hold:
| (13) |
| (14) |
| (15) |
where S0 is the total scaffold concentration, A0 is the total concentration of ligand A, and B0 is the total concentration of ligand B.
We will now derive an expression for , the total scaffold concentration that maximizes Cab, or equivalently, the total scaffold concentration for which dCab/dS0 = 0. From Eqs. (10) and (12), we find
| (16) |
We note that, for ϕ=1, Cab = CaCb/Sf = (Ca + Cab)(Cb + Cab)/S0, which is equivalent to Eq. (5) with n = 2. From Eqs. (10) and (14), we find
| (17) |
Similarly, from Eqs. (11) and (15), we find
| (18) |
| (19) |
where
| (20) |
Differentiating each term in Eq. (19) with respect to S0, we find
| (21) |
From this equation, one can see that the derivative dCab/dS0 uniquely vanishes at . Thus, is the value of S0 at which . Using Eqs. (17) and (18), we can rewrite Eq. (13) as follows:
| (22) |
Substituting for Sf in Eq. (22), we find
| (23) |
Notably, is independent of the cooperativity factor ϕ. For the special case . For the special case .
It is straightforward to find an expression for the maximum concentration of scaffold-nucleated ternary complex, which we will denote as . We simply use the quadratic formula to solve Eq. (19) for the case where . This expression for R is obtained by substituting for Sf in Eq. (20). Unlike , depends on ϕ (because R depends on ϕ). For the special case where ϕ = 1, Ka = Kb = KD and A0 = B0 = L0, we find .
2.3. Effect of a competitor or decoy receptor
The in vivo milieu of a scaffold is complex. A given binding site on the scaffold may interact with a specific ligand as well as a number of competitors. Likewise, the ligand may interact a number of binding partners besides the scaffold. To study the effects of the milieu on the function of a scaffold, we consider the simple scenario illustrated in Fig. 1(C). A ligand A interacts with a scaffold binding site a in competition with an inhibitor I. The ligand also interacts with a decoy receptor D. Thus, we consider the following equilibrium relations:
| (24) |
| (25) |
| (26) |
where Sa is the concentration of free scaffold binding site a, Af is the concentration of free ligand A, Ba is the concentration of scaffold bound to ligand A, If is the concentration of free inhibitor I, Bc is the concentration of scaffold bound to competitive inhibitor I, Df is the concentration of free decoy receptor D, and Bd is the concentration of ligand A bound to decoy receptor D. The equilibrium dissociation constants Ka, Kc and Kd characterize a-A interaction, a-I interaction and A-D interaction, respectively. We will assume that the following mass conservation relations hold: S0 = Sa + Ba + Bc, where S0 is the total scaffold concentration, and A0 = Af + Ba + Bd, where A0 is the total ligand concentration.
To quantify the effect of a competitive inhibitor or decoy receptor on interaction between a scaffold binding site and a ligand, we can find the apparent equilibrium dissociation constant satisfying the relation (cf. Eq. (24)), where is the apparent concentration of free scaffold binding site a and is the apparent concentration of free ligand A. From these considerations and Eqs. (24)–(26), we find
| (27) |
Thus, a competitive inhibitor or decoy receptor simply has the effect of reducing the apparent affinity of a ligand for its scaffold binding site.
In the previous section, we provided equations that elucidate how and depend on binding constants. Given Eq. (27), we can now interpret these equations as also defining how competitive inhibitors and decoy receptors in the milieu of a scaffold affect and . A competitive inhibitor or decoy receptor can shift the total scaffold concentration that maximally nucleates a signaling complex. For example, under certain conditions, a competitive inhibitor can promote scaffold-mediated nucleation of a signaling complex by reversing the effect of excess scaffold (i.e., the effect of ). Thus, the function of a scaffold might be controlled by regulating the expression levels of competitive inhibitors and decoy receptors. It should also be noted that competitive inhibitors and decoy receptors can obscure the relationship between in vivo and binding parameters determined in vitro.
2.4. Effect of a scaffold on the rate of an enzyme-catalyzed reaction
To study the effect of a scaffold on the rate of an enzyme-catalyzed reaction, we consider the scheme presented in Fig. 1(D). This scheme represents a simple extension of the classical Michaelis-Menten reaction scheme:
| (28) |
where A is a substrate, B is an enzyme, (AB) is an enzyme-substrate complex, A′ is a product, and k1, k−1 and kcat are rate constants. As is well known, a pseudo steady-state assumption leads to the following approximate expression for the rate of product formation V ≡ kcat(AB):
| (29) |
where Af is the concentration of free substrate, B0 is the total concentration of enzyme, and Km = (k−1 + kcat)/k1. For simplicity, we will assume that kcat ≪ k−1 such that Km ≈ k−1/k1. When Km is set equal to k−1/k1, it can be said that Eq. (29) depends on a rapid equilibrium assumption.
To obtain an expression analogous to that of Eq. (29) for the reaction scheme of Fig. 1(D), we will assume that V′, the rate of product formation when an enzyme and substrate are co-localized on a scaffold, is proportional the concentration of the ternary complex of the scaffold, enzyme and substrate, which we will denote as Cab. In other words, we will assume that V′ ≡ hkcatCab = hkcat(B0 − Bf − Cb), where h ≥ 0 is a constant introduced to characterize the effect on reactivity of scaffold-controlled positioning of the enzyme and substrate. Positioning/orientation of an enzyme-substrate pair is a known function of some scaffolds [14]. Note that we have assumed conservation of enzyme, such that B0 = Bf + Cb + Cab, where B0 is the total concentration of enzyme, Bf is the concentration of free enzyme, and Cb is the concentration of the binary complex of enzyme and scaffold (Fig. 1(D)). Under a rapid equilibrium assumption, we take the following relations to hold: KbCb = SfBf and KaCab = AfCb, where Sf is the concentration of free scaffold and Ka and Kb are equilibrium dissociation constants. Note that Ka = k−a/ka and Kb = k−b/kb, where ka, k−a, kb and k−b are rate constants in the reaction scheme of Fig. 1(D). Thus,
| (30) |
where . If h in Eq. (30) is approximately 1 (i.e., scaffold effects on the reactivity of scaffold-tethered enzyme and substrate are inconsequential, which can be the case [5]), then the effect of a scaffold on the rate of an enzyme-catalyzed reaction lies in the difference between Km and the apparent Micheaelis-Menten constant for the scaffold-mediated reaction. Note that is unrelated to Km and is determined by the affinities of the enzyme and substrate for binding sites on the scaffold and by the concentration of free scaffold. Thus, a scaffold can profoundly affect the catalytic efficiency of an enzyme even if the stereochemical effects of the scaffold on reactivity (captured in h) are inconsequential.
3. Numerical Results
3.1. Relevance of simple ternary-complex model
To investigate scaffold-mediated nucleation of signaling complexes, we will focus, except as noted, on a bivalent scaffold that recruits a pair of monovalent ligands, i.e., on our ternary-complex model given by Eqs. 10–15 and illustrated in Fig. 1(B). To demonstrate the relevance of this minimalist model, we will consider two more mechanistically detailed models for cell signaling systems reported in the literature. The first of these models characterizes the effect of a scaffold on a MAP kinase cascade [16]. The second model characterizes early events of immunoreceptor signaling, in which a ligand-induced receptor dimer nucleates a signaling complex [33, 34].
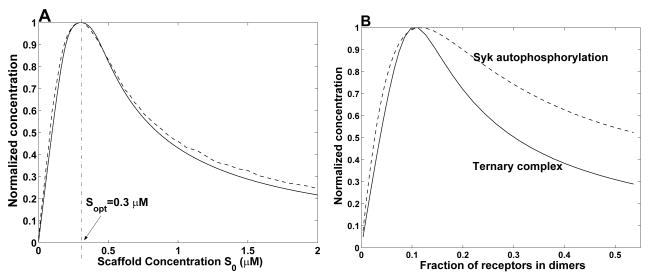
In the model of Levchenko et al. [16], MAPK is phosphorylated as a result of a cascade of binding and phosphorylation reactions in which a scaffold co-localizes MAPK with its kinase, MAPKK. In Fig. 2A, we plot the steady-state level of phosphorylation of MAPK predicted by the model of Levchenko et al. [16] as a function of scaffold concentration. In addition, we plot the dependence of scaffold-nucleated ternary complex concentration (Cab) on scaffold concentration using the parameters that characterize the binding reactions of MAPK, MAPKK and scaffold in the original model. As can be seen, if we assume that MAPK phosphorylation is related to the amount of MAPK and MAPKK co-localized by scaffold, then our simple model closely predicts the steady-state level of MAPK phosphorylation predicted by the model of Levchenko et al. [16] even though the simple model omits many of the reactions included in the more mechanistically detailed model. This result suggests that the steady-state output of the MAP kinase cascade is dominated by co-localization of MAPK and MAPKK by the scaffold. We note that the MAPK-scaffold and MAPKK-scaffold equilibrium dissociation constants in the model of [16] are each 5 nM. As a result, is largely determined by the concentrations of MAPK (0.4 μM) and MAPKK (0.2 μM), as can be seen from Eq. (23).
Figure 2.
Comparison of predictions of the ternary-complex model and more mechanistically detailed models capturing the effects of scaffolds. (A) Comparison between the results of the ternary-complex model (solid line) and a model for a MAP kinase cascade incorporating a scaffold [16]. The broken line corresponds to the concentration of phosphorylated MAPK in Ref. [16]. Parameter values correspond to those used in Ref. [16]: A0 = 0.2 μM, B0 = 0.4 μM and Ka = Kb = 5 nM. (B) Comparison between the results of the ternary-complex model (solid line) and a model for early events in IgE receptor signaling [33, 34]. The broken line corresponds to the amount of Syk autophosphorylation predicted by the model of Ref. [34] for the case of 4 × 104 Syk molecules per cell, as in Fig. 3 of Ref. [1]. Other parameter values are as in Ref. [34]. Note that the KD for Syk binding to phosphorylated receptor is 2167 molecules per cell.
In the mechanistic model for early events in IgE receptor (FcεRI) signaling developed by Goldstein et al. [33] and Faeder et al. [34], a bivalent ligand induces receptor dimerization; receptor phosphorylation; recruitment of Syk, a cytosolic protein tyrosine kinase, to phosphorylated receptors; and autophosphorylation of receptor-associated Syk. In this model, a phosphorylated receptor dimer acts as a scaffold that co-localizes two copies of Syk, enabling one copy of Syk to phosphorylate its neighboring copy of Syk. In Fig. 2B, we plot the steady-state level of Syk autophosphorylation predicted by the detailed model with the parameters of Ref. [34] as a function of receptor dimer concentration. We also plot the dependence of Cab on phosphorylated receptor dimer (the effective scaffold) concentration using the parameters of Ref. [34] that characterize the binding reactions of phosphorylated receptor and Syk. As can be seen, if we assume that Syk autophosphorylation is related to the number of receptor dimers associated with two copies of Syk, then the ternary-complex model accurately predicts the amount of ligand-induced receptor dimers that yields maximum Syk autophosphorylation. This result further demonstrates that the minimalist ternary-complex model can provide insights into the effects of a scaffold on cell signaling.
We caution that the ternary-complex model is not guaranteed to recapitulate the system properties of more sophisticated, more mechanistic models. Our point is only that the model, despite its simplicity, can be useful for gaining insights into signaling events in which scaffold-mediated nucleation plays a role, as illustrated by the qualitative similarities of the two sets of curves in Fig. 2. The ternary-complex model can fail to capture the effects of a scaffold in the context of a specific cell signaling system for myriad reasons. For example, an important caveat of the model is that it is an equilibrium model. Thus, if interactions of binding partners with a scaffold are slow relative to the time scale of processes affected by scaffold-mediated nucleation, then the ternary-complex model will fail to capture the true effects of the scaffold, which will be dominated by the kinetics of ligand-scaffold interactions. Also, the scope of the ternary-complex model is rather circumspect. For example, it does not account for the process of Syk dephosphorylation in the model of Refs. [33, 34], or more generally, downstream influences on events triggered by scaffold-mediated nucleation. This feature of the ternary-complex model (e.g., omission of processes affecting Syk phosphorylation status, including dephosphorylation mediated by phosphatases) explains the quantitative discrepancy between the two curves of Fig. 2(B).
3.2. Concentration-dependent scaffold functionality
A bivalent scaffold, depending on its concentration, can recruit different pairs of ligands. In Fig. 3A, we show that two ligand pairs can be recruited to the same scaffold and to the same maximal extent at different scaffold concentrations. Co-localization of the first ligand pair is maximum at a scaffold concentration of 0.055 μM, whereas co-localization of the second ligand pair is maximum at 9.8 μM. In general, such a scenario requires that the ligand pairs have different total concentrations and/or scaffold affinities (Fig. 3B). The contour plot of Fig. 3B shows how , the concentration of ternary complex at , depends on ligand concentration and affinity for the special case where A0 = B0 = L0 and Ka = Kb = KD. Thus, at different concentrations, a scaffold can produce quantitatively identical outputs, as measured by co-localization of its binding partners, but qualitatively distinct outputs, because the binding partners differ. Any scaffold is potentially multifunctional, as the concentration of a scaffold can be adjusted through regulation of gene expression. In addition, the effective concentration of a scaffold can be adjusted without changes in gene expression through post-translational modifications, e.g., phosphorylation-dependent binding sites on a scaffold can be turned on and off by kinases and phosphatases, effectively changing the amount of scaffold available for interaction with ligands.
Figure 3.
A scaffold is potentially multifunctional. (A) According to the ternary-complex model, a scaffold can recruit different ligand pairs at different scaffold concentrations. Parameters used in calculations are as follows: A0 = B0 = 0.05 μM and Ka = Kb = 5 nM (solid line); A0 = B0 = 1.0 μM and Ka = Kb = 8.8 μM (broken line). Competition of ligand pairs was not considered explicitly in our calculations because competition is insignificant for this particular example. (B) A contour plot showing log10 ( /1 μM) as a function of ligand concentration L0 (μM) and equilibrium dissociation constant KD (μM). We assume that Ka = Kb = KD and A0 = B0 = L0. Along any contour line, is constant while varies in accordance with Eq. (23).
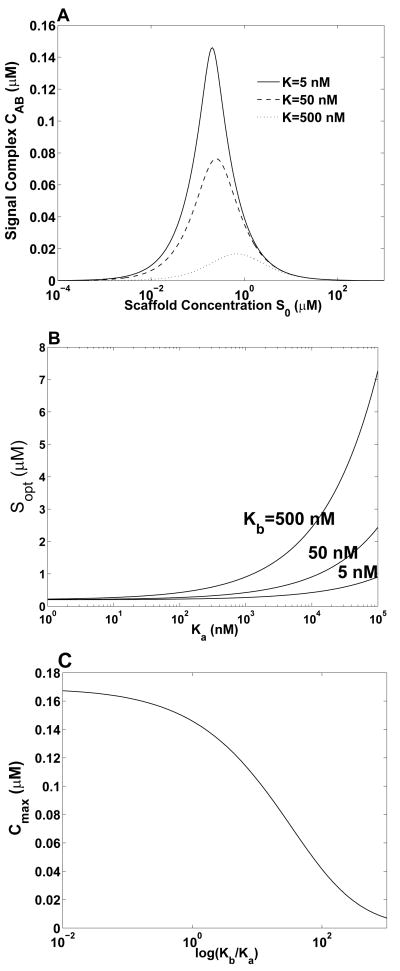
3.3. Dependence of complex formation on binding constants
Figure 4 illustrates how the maximum concentration of ternary complex, , and the scaffold concentration at which depend on the binding constants that characterize ligand-scaffold interactions. In Fig. 4A, we can see that increases as the equilibrium dissociation constant KD (Ka = Kb = KD for the results shown in this panel) increases, or equivalently, as affinity decreases. In Fig. 4B, we can see how changes as the equilibrium dissociation constant for scaffold interaction with ligand A (Ka) is varied while Kb is held constant at 5, 50, and 500 nM. The value of is least sensitive to changes in Ka and Kb for small values of Ka and Kb (i.e., for high ligand-scaffold affinities). Figure 4C shows how depends on Ka and Kb. In this example, is affected by changes of Ka and Kb, but large changes of Ka or Kb result in only modest changes of Cmax. For example, a 100-fold increase in Kb from 5 nM (Kb/Ka = 1) to 0.5 μM (Kb/Ka = 100) results in a only an approximate four-fold decrease of from 0.15 μM to 0.04 μM. As indicated by Eq. (27), the sensitivities of and to an increase in a binding constant is analogous to the sensitivities of these quantities to an increase in the concentration of a competitive inhibitor or decoy receptor.
Figure 4.
Effects of binding constants on optimal scaffold concentration and maximum concentration of ternary complex . (A) The value of Cab is plotted as the function of S0 for three different values of KD. In these calculations, Ka and Kb are each set equal to KD and A0 = B0 = 0.2 μM. (B) The value of is shown as a function of Ka for three different values of Kb. Ligand concentrations are the same as for panel (A). (C) The value of is plotted as a function of the ratio of the equilibrium dissociation constants (Kb/Ka). In this panel, Ka is held fixed at 5 nM and ligand concentrations are the same as for panel (A).
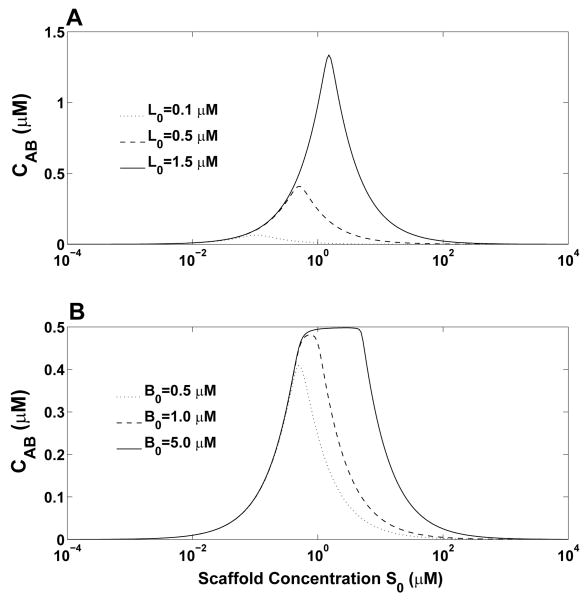
3.4. Dependence of complex formation on ligand concentrations
Figure 5 illustrates how the maximum concentration of ternary complex, , and the scaffold concentration at which depend on ligand concentrations. The results shown in Fig. 5 complement those of Eq. (23) and Fig. 3. In Fig. 5A, we can see that increases as both ligand concentrations (A0 = B0 = L0) increase simultaneously. Increasing ligand concentrations also increases . Thus, inhibition of ternary complex formation by excess scaffold can be reversed by increasing ligand concentrations. For example, 10 μM scaffold inhibits formation of the ternary complex at L0 = 0.5 μM. In contrast, when L0 = 1.5 μM, is increased by nearly three fold and there is a significant amount of ternary complex at a 10 μM concentration of scaffold (Fig. 5A). In Fig. 5B, we show how Cab depends on the total scaffold concentration S0 for three different values of B0 (0.5, 1 and 5 μM). For all three curves, the value of A0 is the same (0.5 μM). As can be seen, when the two ligand concentrations are different, the value of Cab can be nearly maximal over a broad range of scaffold concentrations. For example, at B0 = 5.0 μM and A0 = 0.5 μM, Cab is nearly maximal for scaffold concentrations between 1 and 5 μM. Over this range, ligand B is in excess and ligand A is limiting (i.e, nearly all A is bound to scaffold and the amount of ternary complex is approximately equal to the concentration of ligand A). At higher scaffold concentrations, free B is consumed and Cab becomes less than maximal because of the excess scaffold effect [15, 16].
Figure 5.
Dependence of scaffold-nucleated complex formation on ligand concentrations according to the ternary-complex model. (A) The amount of ternary complex Cab is plotted as a function of total scaffold concentration S0 for three different values of L0. In these calculations, A0 and B0 are each set equal to L0 and Ka = Kb = 5 nM. (B) Cab vs. S0 for three different total concentrations of ligand B (B0) with A0 held fixed at 0.5 μM. The equilibrium dissociation constants are the same as for panel (A).
3.5. Cooperative binding
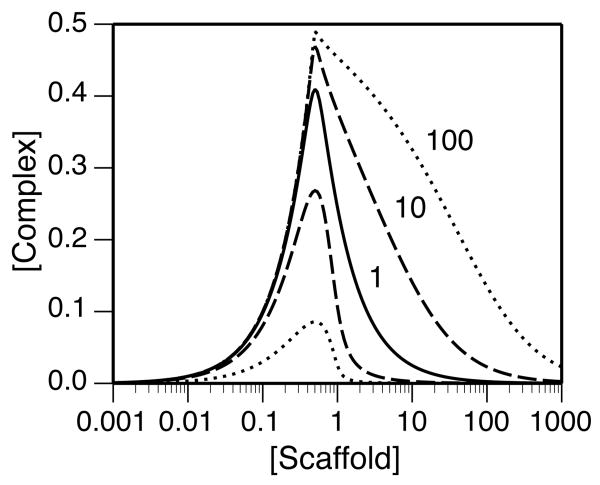
Cooperative binding of ligands A and B to a scaffold is illustrated in Fig. 6. In accordance with Eq. (23), Sopt is independent of the value of ϕ. However, for ϕ > 1, Cab takes on a nearly maximal value over a broader range of scaffold concentrations. For ϕ < 1, the maximal value of Cab is attenuated.
Figure 6.
The effect of cooperativity on scaffold-mediated nucleation of ternary complex: Cab (μM) is plotted as a function of S0 (μM) for five different values of the cooperativity factor ϕ. The solid line corresponds to independent binding of ligands A and B to the scaffold (ϕ = 1). The broken line and dotted line below the solid line correspond to negativity cooperativity: ϕ = 0.1 and ϕ = 0.01, respectively. Similarly, the broken line and dotted line above the solid line correspond to positive cooperativity: ϕ = 10 and ϕ = 100, respectively. Calculations are based on the following ligand concentrations and binding constants: A0 = B0 = L0 = 0.5 μM and Ka = Kb = KD = 5 nM. In accordance with Eq. (23), μM for all curves.
3.6. Higher-order complexes
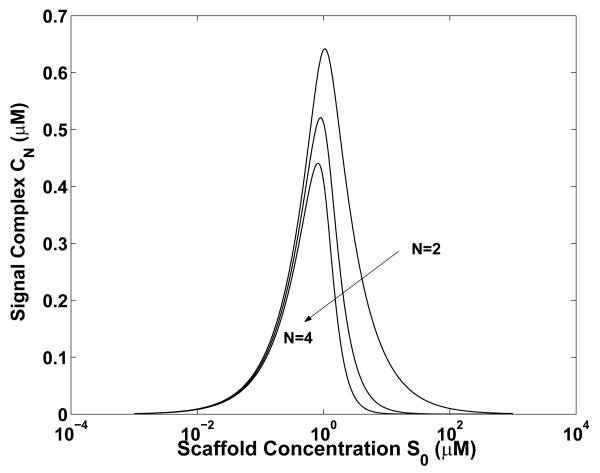
So far, we have considered ternary complexes nucleated by a bivalent scaffold. Here, we consider scaffold-nucleated complexes containing two or more ligands per scaffold. In other words, we consider the reaction scheme of Eq. 1, which is illustrated in Fig. 1A. In Fig. 7, we show how C2, C3 and C4 depend on the total scaffold concentration S0, where Cn is the concentration of scaffold bound to n ligands. As can be seen, for a larger value of n, the maximum value of Cn is reduced (in a controlled comparison). In addition, the scaffold concentration at which Cn is maximum is reduced. These results are consistent with the intuition that it is more difficult to form a scaffold-nucleated complex that contains more ligands. The results of Fig. 7 are essentially the same as those obtained by Heinrich et al. [17] through the analysis of a more mechanistically detailed model, which provides further support for the relevance of the minimalist models considered in this study. The asymmetry seen in the curves of Fig. 7 is explained by the asymptotic limits of |gn|, which is given by Eq. (7), as S0 approaches 0 and ∞.
Figure 7.
The effects of scaffold valence n on nucleation of a complex containing n ligands (L1,…, Ln). The concentration of complex containing all n ligands, Cn, is plotted as a function of the total scaffold concentration, S0, for three different valences: n = 2, 3 and 4. Calculations are based on Eqs. (4) and (5) and the following parameter values: Li0 = 1 μM and Ki = 0.05 μM for all i.
3.7. Effects of a scaffold on an enzymatic reaction
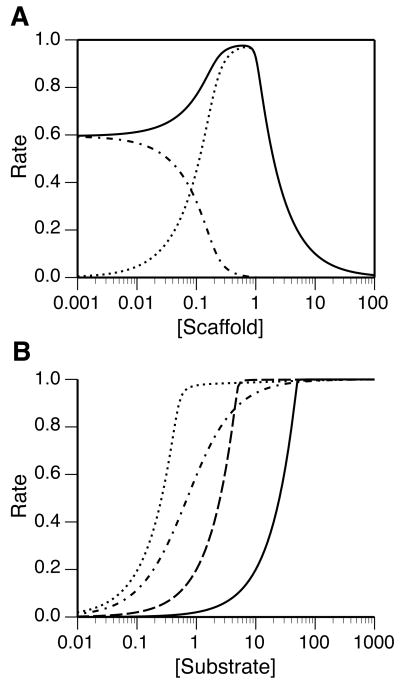
In accordance with Eq. (30), an enzyme-scaffold complex can be regarded as an effective enzyme, one that has a different maximal rate of reaction and one that achieves the half maximal rate at a different substrate concentration, which can be lower or higher than the corresponding concentration in the absence of scaffold. Figure 8 complements these insights, showing how a scaffold that co-localizes a substrate and enzyme can affect the initial rate of enzyme-catalyzed conversion of the substrate to product. As can be seen in Fig. 8A, a scaffold can significantly accelerate the rate of reaction relative to the situation where the reaction proceeds in the absence of the scaffold. However, scaffold-mediated acceleration occurs only within a certain range of scaffold concentrations. A scaffold concentration outside this range, in the excess scaffold regime, can have the effect of inhibiting the enzyme-catalyzed reaction. In Fig. 8B, the rate of reaction is shown as a function of substrate concentration for different concentrations of scaffold and for the case of no scaffold. As can be seen, the dose-response curve can be shifted by the involvement of a scaffold, and in addition, the slope of the curve can be altered, i.e., the sensitivity of reaction rate to a change in substrate concentration can be altered. For the case of Fig. 8B, the effect of the scaffold is to increase the sensitivity of the initial reaction rate to a change in substrate concentration.
Figure 8.
The effect of a scaffold on an enzymatic reaction under the assumption of rapid equilibrium. The initial normalized rate of reaction is plotted as a function of (A) total scaffold concentration S0 (μM) and (B) total substrate concentration A0 (μM). In panel (A), A0 = 1 μM. The dash-dot curve corresponds to V/(kcatB0) (Eq. (29)), the dotted curve corresponds to V′/(hkcatB0) (Eq. (30)), and the solid curve corresponds to V/(kcatB0)+V′/(hkcatB0). In panel (B), the dash-dot curve corresponds to the case of a classical Michaelis-Menten reaction (no scaffold). The other curves correspond to different scaffold concentrations: 0.5 μM (dotted line), 5 μM (broken line) and 50 μM (solid line). Calculations are based on Eqs. (10)–(15) with ϕ = 1 and with Eqs. (14) and (15) each modified to include a term for the concentration of (AB), which is taken to be Af Bf/Km. The following parameter values were used in all calculations: Ka = Kb = 0.005 μM, Km = 0.6 μM, and B0 = 0.2 μM.
4. Discussion
Elucidating the design principles of cellular regulatory systems is recognized as an important goal of systems biology [35, 36, 37], which is facilitated by the tools of synthetic biology [38, 39]. Understanding the design principles of scaffold-mediated nucleation of a multicomponent complex, a motif in cell signaling [14], is important for a number of reasons, including understanding how scaffold function is conserved across species, interpreting the functional consequences of protein copy number variation in diseases, and engineering scaffolds to have desired properties [40].
Here, we have used minimalist models for which analytical results can be obtained to reveal principles that govern the recruitment of ligands to a scaffold. We have shown that the simplest model considered here, the ternary-complex model, captures essential features predicted by more sophisticated and mechanistically detailed models, which can only be analyzed via simulation (Fig. 2). For the the ternary-complex model, we derived a number of analytical expressions, which can serve as basic design equations, in that these equations can potentially be used to guide the manipulation of intrinsic scaffold properties or scaffold milieu to achieve desired effects on the system-level properties of scaffold-dependent processes. Perhaps the most significant analytical result is Eq. (23). Special cases of this equation have been reported in studies of multivalent ligand-receptor binding. For example, Mack et al. [29] obtained a similar equation in a study of bivalent ligand-receptor binding (cf. Eq. (16) in Ref. [29] and Eq. (23) here in this report). In studies specifically focused on scaffolds, earlier work has largely relied on simulation. The parameter-dependent nature of simulation results can lead to incomplete understanding. For example, on the basis of simulation results, Levchenko et al. [16, 41] reported that scaffold function is insensitive to binding constants, which is definitely the case in certain parameter regimes. However, as can be seen from Eq. (23) and as illustrated in Figs. 3 and 4, binding constants can have a significant impact on scaffold function.
For the ternary-complex model, in our presentation of Eqs. (10)–(23), we have shown that the maximum concentration of the ternary complex, , and the scaffold concentration that yields this maximum concentration, , depend on ligand-scaffold binding constants and ligand concentrations (Eq. (23)). In addtion, , but not , depends on the cooperativity of ligand A and ligand B binding to the scaffold. Levchenko et al. [16] reported that cooperativity shifts the optimal scaffold concentration (see Fig. 4B in Ref. [16]). This finding is inconsistent with the equilibrium binding properties of a scaffold (Eq. 23). The shift of dose-response curves seen in the study of Levchenko et al. [16] is perhaps attributable to kinetic binding properties of a scaffold in the specific context of a MAP kinase cascade. The above mentioned analytical results are complemented by the simulation results of Figs. 3–6. In our presentation of Eqs. (1)–(9), we have shown that scaffold-mediated nucleation depends asymmetrically on total scaffold concentration, which is illustrated in Fig. 7. This finding is consistent with the simulation results of Heinrich et al. [17] (see Fig. 8 in Ref. [17]). We also considered competitive ligands and decoy receptors, the presence of which can be mimicked by an increase in the equilibrium binding constants for ligand-scaffold interactions (Eq. (27)). Finally, we found that a scaffold can reprogram the catalytic efficiency of an enzyme (Eq. (30) and Fig. 8).
The results of Fig. 3A suggest that scaffolds could have multiple context-dependent functions. A scaffold, depending on its concentration, can nucleate distinct sets of ligands. Thus, in a given cellular context, only a subset of a scaffold's known binding partners may be physiologically relevant. In addition, in cases where the (effective) scaffold concentration depends on the strength of a signal, a scaffold may enable a cell to respond differentially to signal strength. An example where effective scaffold concentration depends on signal strength via post-translational modifications and other fast events (and not gene expression) is provided by the model of Goldstein et al. [33] and Faeder et al. [34] for signaling by the high-affinity receptor for IgE antibody (FcεRI). In this model, phosphorylated receptors in ligand-induced receptor dimers serve to co-localize two copies of the protein tyrosine kinase Syk, which is necessary for Syk autophosphorylation and downstream Syk-dependent signaling events. Furthermore, the number of receptor dimers depends on the concentration of (multivalent) ligand that induces receptor aggregation. Thus, given the results of Fig. 3A, receptor dimers in this system, which have a scaffold-like function, could nucleate different signaling complexes at different ligand doses [1, 42], with these complexes potentially eliciting different cellular responses. We are not aware of a signaling system where scaffold concentration controls the formation of complexes that lead to distinct cellular responses, but given the number of binding partners of a typical signaling protein, we expect that scaffold multifunctionality, such as that illustrated in Fig. 3A, could be found.
Results such as those shown in Fig. 4C can be used to engineer a scaffold with non-native ligand-scaffold interactions to obtain a desired scaffold-dependent cellular response to a signal, assuming ternary complex formation correlates with the cellular response of interest. Park et al. [5] engineered the yeast scaffold protein Ste5 to interact with one of its binding partners, Ste7 or Ste11, via a non-native protein-protein interaction. In these experiments, the Ste7 or Ste11 binding site on Ste5 was disrupted by a mutation of Ste5 (V763A/S861P or I504T) and Ste5 was fused to the PDZ domain of syntrophin. In addition, Ste7 or Ste11 was fused to the PDZ domain of neuronal nitric oxide synthase (nNOS). The nNOS and syntrophin PDZ domains heterodimerize with a KD of 0.6 μM [43]. In contrast, the native interaction between Ste5 and Ste7 or Ste11 is characterized by a KD of about 0.1 μM [44, 45]. Using measured concentrations of Ste5 (35 nM), Ste11 (39 nM) and Ste7 (68 nM) reported by Maeder et al. [44], we can calculate the effect of increasing KD from 0.1 to 0.6 μM. We find that this change is expected to cause a 15-fold decrease in the amount of the ternary complex composed of Ste5, Ste7 and Ste11. This prediction is consistent with the decrease in phosphorylation of Fus3 observed by Park et al. [5] for the engineered Ste5-Ste7 or Ste5-Ste11 interaction.
We have focused on equilibrium properties of scaffolds that nucleate ternary and higher-order protein complexes. We also considered the effect of a scaffold on the rate of an enzyme-catalyzed reaction under a rapid equilibrium assumption. The results that we have found should be useful for understanding cellular responses that depend on the concentration and composition of a scaffold-nucleated complex, assuming that these responses are insensitive to the kinetics of complex formation. As Locasale et al. [20, 21] and Thalhauser and Komarova [22] have shown, the kinetics of scaffold-mediated complex formation can have physiological relevance. Thus, an important caveat of the results presented here is the assumption of equilibrium or pseudo equilibrium. Another caveat is the assumption of monovalent ligands. If the ligands that interact with a multivalent scaffold are themselves multivalent, then complex dose-response behavior can arise, such that complex formation is maximal at multiple scaffold concentrations [1, 42].
An interesting future application of the results presented here might be interpretation of comparative proteomics data. It has been observed that protein copy number tends to be conserved across species [46, 47, 48]. Because the function of a scaffold is affected by the relative abundances of the scaffold and its ligands, conservation of relative abundances of the proteins in a “scaffold motif” would suggest conservation of function of the motif, whereas the opposite would suggest the acquisition of a new function or compensatory modifications of scaffold properties and/or milieu, which could perhaps be more easily understood or predicted in light of this report.
Highlights.
> In this study, we consider minimalist models for scaffold interaction with ligands.
> We obtain analytical expressions that indicate how scaffold-mediated nucleation depends on ligand concentrations, binding constants, cooperativity, and scaffold valence. > We also study the effect of a scaffold on an enzymatic reaction. > A scaffold can reprogram the catalytic efficiency of an enzyme and change sensitivity of the rate of reaction to substrate concentration.
Acknowledgments
This work was supported by NIH grants GM076570 and RR18754, Department of Energy contract DE-AC52-06NA25396, and NSFC grant 30870477. J.Y. thanks Dr. Zhen Wang for helpful discussions and the Center for Nonlinear Studies for support that made travel to Los Alamos possible.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Jin Yang, Email: jinyang2004@gmail.com.
William S. Hlavacek, Email: wish@lanl.gov.
References
- 1.Hlavacek WS, Faeder JR, Blinov ML, Perelson AS, Goldstein B. The complexity of complexes in signal transduction. Biotechnol Bioeng. 2003;84:783–794. doi: 10.1002/bit.10842. [DOI] [PubMed] [Google Scholar]
- 2.Pawson T, Scott JD. Signaling through scaffold, anchoring, and adaptor proteins. Science. 1997;278:2075–2080. doi: 10.1126/science.278.5346.2075. [DOI] [PubMed] [Google Scholar]
- 3.Elion EA. The Ste5p scaffold. J Cell Sci. 2001;114:3967–3978. doi: 10.1242/jcs.114.22.3967. [DOI] [PubMed] [Google Scholar]
- 4.Malleshaiah MK, Shahrezaei V, Swain PS, Michnick SW. The scaffold protein Ste5 directly controls a switch-like mating decision in yeast. Nature. 2010:101–105. doi: 10.1038/nature08946. [DOI] [PubMed] [Google Scholar]
- 5.Park SH, Zarrinpar A, Lim WA. Rewiring MAP kinase pathways using alternative scaffold assembly mechanisms. Science. 2003;299:1061–1064. doi: 10.1126/science.1076979. [DOI] [PubMed] [Google Scholar]
- 6.Rozakis-Adcock M, Fernley R, Wade J, Pawson T, Bowtell D. The SH2 and SH3 domains of mammalian Grb2 couple the EGF receptor to the Ras activator mSos1. Nature. 1993;363:83–85. doi: 10.1038/363083a0. [DOI] [PubMed] [Google Scholar]
- 7.Zhang W, Sloan-Lancaster J, Kitchen J, Trible RP, Samelson LE. LAT: the ZAP-70 tyrosine kinase substrate that links T cell receptor to cellular activation. Cell. 1998;92:83–92. doi: 10.1016/s0092-8674(00)80901-0. [DOI] [PubMed] [Google Scholar]
- 8.Samelson LE. Signal transduction mediated by the T cell antigen receptor: the role of adapter proteins. Annu Rev Immunol. 2002;20:371–94. doi: 10.1146/annurev.immunol.20.092601.111357. [DOI] [PubMed] [Google Scholar]
- 9.Burack WR, Cheng AM, Shaw AS. Scaffolds, adaptors and linkers of TCR signaling: theory and practice. Curr Opin Immunol. 2002;14:312–316. doi: 10.1016/s0952-7915(02)00347-3. [DOI] [PubMed] [Google Scholar]
- 10.Nag A, Monine MI, Faeder JR, Goldstein B. Aggregation of membrane proteins by cytosolic cross-linkers: theory and simulation of the LAT-Grb2-SOS1 system. Biophys J. 2009;96:2604–2623. doi: 10.1016/j.bpj.2009.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Burack WR, Shaw AS. Signal transduction: hanging on a scaffold. Curr Opin Cell Biol. 2000;12:211–216. doi: 10.1016/s0955-0674(99)00078-2. [DOI] [PubMed] [Google Scholar]
- 12.Pawson T. Dynamic control of signaling by modular adaptor proteins. Curr Opin Cell Biol. 2007;19:112–116. doi: 10.1016/j.ceb.2007.02.013. [DOI] [PubMed] [Google Scholar]
- 13.Zeke A, Lukács M, Lim WA, Reményi A. Scaffolds: interaction platforms for cellular signalling circuits. Trends Cell Biol. 2009;19:364–374. doi: 10.1016/j.tcb.2009.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Good MC, Zalatan JG, Lim WA. Scaffold proteins: hubs for controlling the flow of cellular information. Science. 2011;332:680–686. doi: 10.1126/science.1198701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bray D, Lay S. Computer-based analysis of the binding steps in protein complex formation. Proc Natl Acad Sci USA. 1997;94:13493–13498. doi: 10.1073/pnas.94.25.13493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Levchenko A, Bruck J, Sternberg PW. Scaffold proteins may biphasically affect the levels of mitogen-activated protein kinase signaling and reduce its threshold properties. Proc Natl Acad Sci USA. 2000;97:5818–5823. doi: 10.1073/pnas.97.11.5818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Heinrich R, Neel BG, Rapoport TA. Mathematical models of protein kinase signal transduction. Mol Cell. 2002;9:957–970. doi: 10.1016/s1097-2765(02)00528-2. [DOI] [PubMed] [Google Scholar]
- 18.Swain PS, Siggia ED. The role of proofreading in signal transduction specificity. Biophys J. 2002;82:2928–2933. doi: 10.1016/S0006-3495(02)75633-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Prehoda KE, Lim WA. How signaling proteins integrate multiple inputs: a comparison of N-WASP and Cdk2. Curr Opin Cell Biol. 2002;14:149–154. doi: 10.1016/s0955-0674(02)00307-1. [DOI] [PubMed] [Google Scholar]
- 20.Locasale JW, Shaw AS, Chakraborty AK. Scaffold proteins confer diverse regulatory properties to protein kinase cascades. Proc Natl Acad Sci USA. 2007;104:13307–13312. doi: 10.1073/pnas.0706311104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Locasale JW, Chakraborty AK. Regulation of signal duration and the statistical dynamics of kinase activation by scaffold proteins. PLoS Comput Biol. 2008;4:e1000099. doi: 10.1371/journal.pcbi.1000099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thalhauser CJ, Komarova NL. Signal response sensitivity in the yeast mitogen-activated protein kinase cascade. PLoS One. 2010;5:e11568. doi: 10.1371/journal.pone.0011568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bashor CJ, Helman NC, Yan S, Lim WA. Using engineered scaffold interactions to reshape MAP kinase pathway signaling dynamics. Science. 2008;319:1539–1543. doi: 10.1126/science.1151153. [DOI] [PubMed] [Google Scholar]
- 24.Chapman SA, Asthagiri AR. Quantitative effect of scaffold abundance on signal propagation. Mol Syst Biol. 2009;5:313. doi: 10.1038/msb.2009.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jacobs S, Cuatrecasas P. The mobile receptor hypothesis and ‘cooperativity’ of hormone binding. Application to insulin. Biochim Biophys Acta. 1976;433:482–495. doi: 10.1016/0005-2736(76)90275-3. [DOI] [PubMed] [Google Scholar]
- 26.De Lean A, Stadel JM, Lefkowitz RJ. A ternary complex model explains the agonist-specific binding properties of the adenylate cyclase-coupled β-adrenergic receptor. J Biol Chem. 1980;255:7108–7117. [PubMed] [Google Scholar]
- 27.Perelson AS, DeLisi C. Receptor clustering on a cell surface. I. Theory of receptor cross-linking by ligands bearing two chemically identical functional groups. Math Biosci. 1980;48:71–110. [Google Scholar]
- 28.Sulzer B, Perelson AS. Equilibrium binding of multvalent ligands to cells: effects of cell and receptor density. Math Biosci. 1996;135:147–185. doi: 10.1016/0025-5564(96)00022-3. [DOI] [PubMed] [Google Scholar]
- 29.Mack E, Perez-Castillejos R, Suo Z, Whitesides G. Exact analysis of ligand-induced dimerization of monomeric receptors. Anal Chem. 2008;80:5550–5555. doi: 10.1021/ac800578w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Savageau MA. The behavior of intact biochemical control systems. Curr Top Cell Reg. 1972;6:63–130. [Google Scholar]
- 31.Savageau MA. Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology. Addison-Wesley; Reading, MA: 1976. [Google Scholar]
- 32.Dueber JE, Wu GC, Malmirchegini GR, Moon TS, Petzold CJ, Ullal AV, Prather KLJ, Keasling JD. Synthetic protein scaffolds provide modular control over metabolic flux. Nat Biotechnol. 2009;27:753–759. doi: 10.1038/nbt.1557. [DOI] [PubMed] [Google Scholar]
- 33.Goldstein B, Faeder JR, Hlavacek WS, Blinov ML, Redondo A, Wofsy C. Modeling the early signaling events mediated by FcεRI. Mol Immunol. 2002:1213–1219. doi: 10.1016/s0161-5890(02)00066-4. [DOI] [PubMed] [Google Scholar]
- 34.Faeder JR, Hlavacek WS, Reischl I, Blinov ML, Metzger H, Redondo A, Wofsy C, Goldstein B. Investigation of early events in FcεRI-mediated signaling using a detailed mathematical model. J Immunol. 2003;170:3769–3781. doi: 10.4049/jimmunol.170.7.3769. [DOI] [PubMed] [Google Scholar]
- 35.Savageau MA. Design principles for elementary gene circuits: elements, methods, and examples. Chaos. 2001;11:142–159. doi: 10.1063/1.1349892. [DOI] [PubMed] [Google Scholar]
- 36.Wall ME, Hlavacek WS, Savageau MA. Design of gene circuits: lessons from bacteria. Nat Rev Genet. 2004;5:34–42. doi: 10.1038/nrg1244. [DOI] [PubMed] [Google Scholar]
- 37.Alon U. An Introduction to Systems Biology: Design Principles of Biological Circuits. Chapman and Hall/CRC; Boca Raton, FL: 2006. [Google Scholar]
- 38.Mukherji S, van Oudenaarden A. Synthetic biology: understanding biological design from synthetic circuits. Nat Rev Genet. 2009;10:859–871. doi: 10.1038/nrg2697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bashor CJ, Horwitz AA, Peisajovich SG, Lim WA. Rewiring cells: synthetic biology as a tool to interrogate the organizational principles of living systems. Annu Rev Biophys. 2010;39:515–537. doi: 10.1146/annurev.biophys.050708.133652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lim WA. Designing customized cell signalling circuits. Nat Rev Mol Cell Biol. 2010;11:393–403. doi: 10.1038/nrm2904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Levchenko A, Bruck J, Sternberg PW. Regulatory modules that generate biphasic signal response in biological systems. Syst Biol. 2004;1:139–148. doi: 10.1049/sb:20045014. [DOI] [PubMed] [Google Scholar]
- 42.Nag A, Faeder JR, Goldstein B. Shaping the response: the role of FcεRI and Syk expression levels in mast cell signalling. IET Syst Biol. 2010;4:334–347. doi: 10.1049/iet-syb.2010.0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Harris K, Lamson RE, Nelson B, Hughes TR, Marton MJ, Roberts CJ, Boone C, Pryciak PM. Role of scaffolds in MAP kinase pathway specificity revealed by custom design of pathway-dedicated signaling proteins. Curr Biol. 2001;11:1815–1824. [PubMed] [Google Scholar]
- 44.Maeder CI, Hink MA, Kinkhabwala A, Mayr R, Bastiaens PIH, Knop M. Spatial regulation of Fus3 MAP kinase activity through a reaction-diffusion mechanism in yeast pheromone signalling. Nat Cell Biol. 2007:1319–1326. doi: 10.1038/ncb1652. [DOI] [PubMed] [Google Scholar]
- 45.Slaughter BD, Schwartz JW, Li R. Mapping dynamic protein interactions in MAP kinase signaling using live-cell fluorescence fluctuation spectroscopy and imaging. Proc Natl Acad Sci USA. 2007;104:20320–20325. doi: 10.1073/pnas.0710336105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Schrimpf SP, Weiss M, Reiter L, Ahrens CH, Jovanovic M, Malmström J, Brunner E, Mohanty S, Lercher MJ, Hunziker PE, Aebersold R, von Mering C, Hengartner MO. Comparative functional analysis of the Caenorhabditis elegans and Drosophila melanogaster proteomes. PLoS Biol. 2009;7:e1000048. doi: 10.1371/journal.pbio.1000048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Weiss M, Schrimpf S, Hengartner MO, Lercher MJ, von Mering C. Shotgun proteomics data from multiple organisms reveals remarkable quantitative conservation of the eukaryotic core proteome. Proteomics. 2010;10:1297–1306. doi: 10.1002/pmic.200900414. [DOI] [PubMed] [Google Scholar]
- 48.Laurent JM, Vogel C, Kwon T, Craig SA, Boutz DR, Huse HK, Nozue K, Walia H, Whiteley M, Ronald PC, Marcotte EM. Protein abundances are more conserved than mRNA abundances across diverse taxa. Proteomics. 2010;10:4209–4212. doi: 10.1002/pmic.201000327. [DOI] [PMC free article] [PubMed] [Google Scholar]