Separating intrinsic from extrinsic fluctuations in dynamic biological systems

Abstract

From molecules in cells to organisms in ecosystems, biological populations fluctuate due to the intrinsic randomness of individual events and the extrinsic influence of changing environments. The combined effect is often too complex for effective analysis, and many studies therefore make simplifying assumptions, for example ignoring either intrinsic or extrinsic effects to reduce the number of model assumptions. Here we mathematically demonstrate how two identical and independent reporters embedded in a shared fluctuating environment can be used to identify intrinsic and extrinsic noise terms, but also how these contributions are qualitatively and quantitatively different from what has been previously reported. Furthermore, we show for which classes of biological systems the noise contributions identified by dual-reporter methods correspond to the noise contributions predicted by correct stochastic models of either intrinsic or extrinsic mechanisms. We find that for broad classes of systems, the extrinsic noise from the dual-reporter method can be rigorously analyzed using models that ignore intrinsic stochasticity. In contrast, the intrinsic noise can be rigorously analyzed using models that ignore extrinsic stochasticity only under very special conditions that rarely hold in biology. Testing whether the conditions are met is rarely possible and the dual-reporter method may thus produce flawed conclusions about the properties of the system, particularly about the intrinsic noise. Our results contribute toward establishing a rigorous framework to analyze dynamically fluctuating biological systems.

All biological systems are networks of individual agents that interact probabilistically in changing environments. Fluctuations in population sizes—whether of chemical species in cells (1) or of organismic species in ecosystems (2)—thus arise both from probabilistic births and deaths at low numbers (“intrinsic noise”) and the randomizing effects of the physical and biological environment (“extrinsic noise”). The stochastic dynamics of any given species therefore reflects all directly and indirectly connected processes, many of which are poorly characterized. This explains why fluctuations are so prevalent in biology, but also why they can be overwhelmingly difficult to analyze. For example, even an accurate microscopic model of gene expression could not predict fluctuations in protein levels without accounting for variations in, e.g., RNA polymerases and ribosomes, which in turn depend on yet other components.

An ingeniously simple approach to this seemingly intractable problem is to embed a second independent system in the same environment and observe the two copies simultaneously. Correlations between the systems then reflect the influence of the common environment, whereas differences between them reflect the spontaneous noise created within each system (Fig. 1). Such approaches promise to distinguish the intrinsic or extrinsic origin of fluctuations in one fell swoop without knowledge of the microscopic details of either the system or its environment. For example, in microrheology two-particle methods have been used to disentangle material inhomogeneities from diffusion effects (3), whereas twin studies attempt to separate genetic from environmental influences during human development (4).

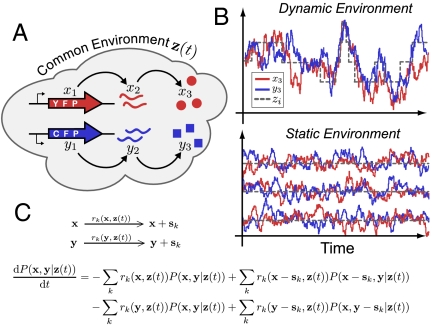
Fig. 1.

The dual-reporter setup. (A) Cartoon illustrating an example dual-reporter setup in which a common cellular environment affects the rates of gene activation, transcription, and translation of two different fluorescent proteins. (B) Signal of two reporters (red and blue lines) subject to a common environment (dashed gray line) reflecting two sources of variability: stochastic events within a system leading to uncorrelated fluctuations; changes in the common environment leading to correlated fluctuations. In contrast to a dynamic environment, a static heterogenous environment takes different but constant values. (C) Jump processes for two copies of identical and independent stochastic systems with intrinsic variables x = x₁,x₂,x₃,…x_n and y = y₁,y₂,y₃,…y_n undergoing reactions with step size s_k and rates r_k that depend on a common time-dependent set of environmental variables z(t). General master equation for the time evolution of the joint conditional probability distribution P(x,y|z(t)) of the two reporters given a realization of the stochastic environment Z = z(t).

Here we derive generally applicable methods but focus on dual-reporter applications in molecular biology that are used to identify the cellular sources of fluctuations in protein numbers. The normalized covariance between two reporter proteins within a gene regulatory network has been used as a measure of extrinsic noise defining the remaining noise as intrinsic (5–8), allowing each category to be modeled and evaluated separate from the other. To ensure that this is a mechanistically sound interpretation rather than an arbitrary definition, early theoretical analyses reported that the total noise indeed can be decomposed into intrinsic and extrinsic parts by conditioning on the state of the shared environment (9) and that the dual-reporter method can identify those two parts. However, the authors later emphasized relations that contradict key steps of the original proof (10). This implies that the originally reported decomposition allows only for static environmental heterogeneity (Fig. 1B). This may be approximately true in special systems, but in many biological networks the environment and the system are expected to change on similar time scales because they are governed by similar types of processes. For example, in the first experimental analysis (5) based on this approach, the extrinsic noise was traced back to the influence of a repressor that is expected to change at least as quickly as the fluorescent proteins measured.

The main practical reason for decomposing noise into separate terms is to more effectively evaluate models without having to specify both the intrinsic and extrinsic mechanisms simultaneously—simplifying analyses greatly by reducing the number of ad hoc assumptions and free parameters. However, for that approach to work, the top-down statistical decomposition that is inherent to the dual-reporter method must capture the same noise terms as correct bottom-up mechanistic mathematical models. This is often taken for granted (6–8) but is in fact nontrivial.

Here we address these key questions of fluctuations in biology: How can intrinsic and extrinsic types of noise be separated in complex systems? What do the two categories mean biologically? How should measurements be compared to mechanistic models?

Decomposing Noise with the Dual-Reporter Method

Noise arising from the inherently probabilistic reactions within a system is typically called intrinsic or internal, whereas the effect of environmental fluctuations on a system is called extrinsic or external (11). The distinction thus depends on what is defined as system and environment in any particular experiment. The two contributions have been suggested to add up to the total variance with the extrinsic noise identified by the covariance between independent and identical reporters. For example, with x and y denoting the levels of the dual-reporter proteins (Fig. 1) observed in single cells we would have

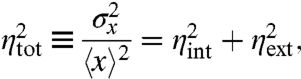[1]

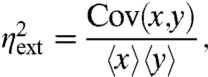[2]

where averages correspond to an ensemble snapshot over a population of cells (5). Here we discuss the idealized scenario of dual reporters that are strictly identical and independent. This assumption is fundamental to the approach and always needs to be established experimentally as in the original dual-reporter study (5) in which the marginal distributions of the two reporters were almost indistinguishable and the addition of a second reporter did not significantly affect the distribution of the first. In addition to the natural heterogeneity, experimental errors can contribute to the observed intrinsic and extrinsic variability. For example, the fluorescence from reporter proteins may imperfectly reflect the actual protein copy numbers due to slow fluorophore maturation. Here we consider only the dynamics of the proteins themselves rather than any technical issues associated with specific experimental methods to infer protein copy numbers.

Because intrinsic and extrinsic noise have physical meanings that reflect the origin of fluctuations, the above equations are not definitions but interpretable claims. To prove that the dual-reporter covariance can identify the origin of fluctuations we must thus show that the total noise can be meaningfully decomposed according to Eq. 1 and that the extrinsic noise is given by Eq. 2.

In the limit where all noise is either intrinsic or extrinsic, this is trivially true: Statistically independent variables by definition do not covary, whereas identical deterministic systems subject to the same inputs by definition take the same values, so that the covariance equals the variance. However, the fact that a decomposition “works” in the limit where there is nothing to decompose in no way suggests that it is suitable to separate the two noise contributions. There are in fact infinitely many pairwise statistical measures that converge to zero in the limit of deterministic extrinsic dynamics and to the covariance in the limit of deterministic intrinsic dynamics, but produce different values for intermediate scenarios. Because the whole purpose of the approach is to separate between the noise sources, it is thus essential to find a decomposition that provably performs this separation. That was indeed the great appeal of the original motivation (5, 9), though later results (10) imply that it unfortunately applies only to static environments. Furthermore, for any decomposition to be of practical value beyond a phenotypic classification, the noise terms obtained should also be relatable to mathematical models that account for one type of noise without the other. We will thus establish if the intrinsic part of the total noise corresponds to the fluctuations exhibited by the system in the absence of environmental variability and if the extrinsic part of the total noise corresponds to the fluctuations the system would exhibit in the absence of intrinsic variability.

Decomposing Noise by the State of the Environment.

The effect of specific variables could in principle be accounted for by conditioning experimental data on the state of those variables, for example, by gating data based on morphology. To summarize this effect in a single number for the whole dataset, the conditional variance so obtained can be averaged over the full process. This is formalized by the law of total variance that splits up the variance of any variable into the expectation of a conditional variance and the variance of a conditional expectation. For example, looking at gene expression with X denoting the number of molecules (of a protein in interest) in a given cell, we can always rewrite the observed cell-to-cell variability 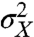by conditioning the data on the state Z of environmental variables such as the number of polymerases, ribosomes, etc.

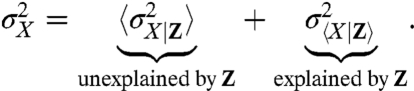[3]

Here 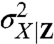is the variance of X in the subpopulation of cells with some given value of Z, and the angular brackets denote averages over all such subpopulations, whereas 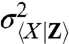is the variance of the conditional average of X given Z (Appendix). Though formulated differently, this is mathematically equivalent to the noise decomposition used previously in the motivation for dual-reporter methods (9) and is also the most common approach to account for the influence of observable variables.

To illustrate the biological implications of the above decomposition, consider a toy system in which a fluctuating extrinsic variable z affects the birth rate of the intrinsic variable x:

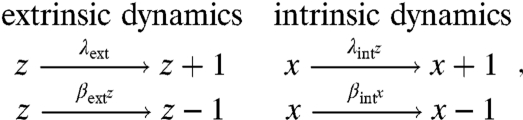[4]

where the reaction rates are transition probabilities per unit time. At stationarity, the total variance of x is then

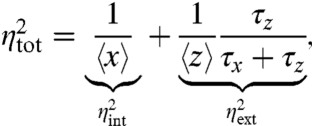[5]

where τ_z = 1/β_ext and τ_x = 1/β_int are the respective average lifetimes of the environmental and intrinsic components (12). Eq. 5 is an exact result for the variance of the above system and highlights two distinct terms: the first term comes from the intrinsic stochastic reactions in X and the second term comes from extrinsic fluctuations in Z levels that are inherited by X in a time-averaged way because as Z changes, X levels adjust only partially before the value of Z changes again. In this example the total noise is thus indeed the sum of a purely intrinsic noise 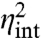that is unaffected by environmental fluctuations and a purely extrinsic noise that is unaffected by the intrinsic stochasticity. The corresponding decomposition using (Eq. 3) is less straightforward to derive because conditional master equations are harder to formulate or solve, which perhaps explains why decompositions are rarely illustrated explicitly in specific examples. Here we derive an exact analytical recurrence relation for the conditional average 〈x|z〉 of the system defined in reaction scheme 4 (SI Appendix), leading to the following unexplained and explained parts of the normalized stationary state variance:

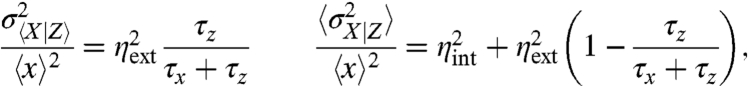[6]

with 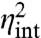and 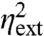as given in Eq. 5. The above noise decomposition based on the state of the environment thus exaggerates the intrinsic noise and underestimates the extrinsic noise (Fig. 2). Even in the limit in which the average 〈x〉 is so large that intrinsic fluctuations 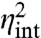are negligible, and X levels respond deterministically to a fluctuating environment, the decomposition of Eq. 3 reports substantial intrinsic noise (Fig. 2A). Hence, even if we could experimentally measure the current state of all environmental variables, we thus still cannot infer the variability that is due to those variables, simply because the whole history matters. Conditioning on the state of the environment captures the correct contributions only in the limit of infinitely slow environmental fluctuations (τ_z≫τ_x). But few if any cellular components are slow compared to the stable fluorescent proteins studied, let alone static. Conditioning on the state of an environmental variable thus does not identify how much it contributes to the overall variance if the environment is dynamic. This problem applies to the motivation of the dual-reporter method and to the many studies that first gate data based on morphology or other observable features. Cell size and age are to some extent excepted from this problem, because the current state is a good predictor of the recent history (unless growth rates fluctuate rapidly) but another type of decomposition is still needed.

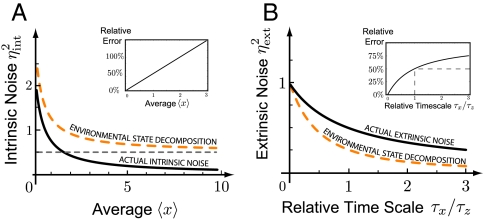
Fig. 2.

Decompositions based on the current state of the environment do not separate between intrinsic and extrinsic origins of fluctuations in dynamical systems. (A) Comparing the true intrinsic noise (black line) of the system defined in reaction scheme 4 with the decomposition that conditions on the current state of the environment (dashed orange line) given in Eq. 6 for different values of the intrinsic reporter average 〈x〉. The decomposition reports substantial intrinsic noise (dashed gray line) even in the deterministic limit 〈x〉 → ∞. Only in the absence of extrinsic noise, or for infinitely slow environmental fluctuations (τ_x ≪ τ_z), do the two measures agree. (B) Comparing the true extrinsic noise (black line) with the decomposition of Eq. 6 (dashed orange line) for different values of the relative time scale of fluctuations τ_x/τ_z. Only in the limit of very slow environmental fluctuations does the extrinsic noise estimate based on an environmental value decomposition converge to the true value. (Insets) Respective relative errors 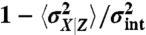and 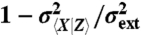. The curves represent families of systems (cf. Eq. 6), with example rate parameters corresponding to (A) λ_ext = 2 and β_ext, β_int = 1 while varying λ_int and (B) λ_ext, λ_int, β_ext = 1 while varying β_int.

Decomposing Noise by the History of the Environment.

To identify the noise contributions in dynamical systems, we instead condition on the full histories of the extrinsic variables (13) and then average the instantaneous conditional averages over all possible histories. The law of total variance then gives

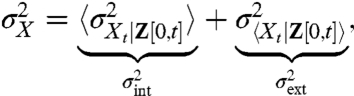[7]

where the intrinsic term is the variance of X_t in a group of cells sharing an environmental history Z[0,t] averaged over all possible histories, and the extrinsic term is the variance of the average X_t over different sample paths of the history Z[0,t], where time t = 0 corresponds to the infinite past. To stress the time dependence of the conditional averages we have introduced the subscript t for the random variable in the above equation and will use this notation for the remainder of the article. For ergodic systems, averaging over all possible histories is equivalent to averaging a single trace over time (Appendix). The so-defined extrinsic noise can then be interpreted as the variation of the average over time, whereas the intrinsic noise 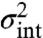corresponds to the variation around that average (Fig. 3). Applying those definitions to the example system of reaction scheme 4 leads to the correct intrinsic and extrinsic noise contributions as given in Eq. 5.

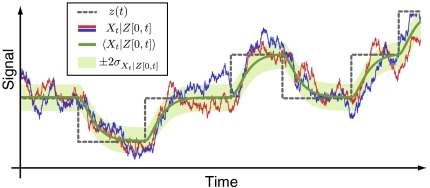
Fig. 3.

Physical definition of intrinsic and extrinsic noise for dynamical systems. Illustrated are two stochastic realizations (red and blue lines) of the intrinsic system subject to a given environmental time trace z(t) (dashed gray line). The extrinsic noise corresponds to the variability of the conditional intrinsic average trace (solid green line), whereas the intrinsic noise is determined by the average variability of the conditioned intrinsic system (indicated by light green corridor).

In principle, the generalized decomposition Eq. 7 could be experimentally obtained by simultaneously observing a large number of identical reporters in the same cell. However, the two noise contributions can also be obtained using just two reporters. If systems X and Y are identical and independent reporters embedded in the same environment—requiring that the two reporters cannot affect environmental variables, affect each other’s reaction rates, or be stoichiometrically coupled in any chemical reaction (14)—the time evolution of the conditional averages satisfy 〈X_tY_t|Z[0,t]〉 = 〈X_t|Z[0,t]〉〈Y_t|Z[0,t]〉 and 〈X_t|Z[0,t]〉 = 〈Y_t|Z[0,t]〉 (Appendix). The covariance between two independent and identical reporters thus corresponds to the extrinsic noise as defined in Eq. 7, for any nonlinear or multivariate process:

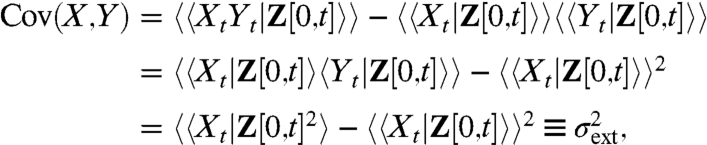[8]

where the outer brackets denote time averages. Hence measuring the covariance between two reporters can replace an infinite number of reporters to decompose the total noise.

Periodic Versus Stochastic Environmental Influences.

In some cases the unknown environmental influence z(t) may have a more or less deterministic component that varies periodically over time. For example, many cellular processes are coupled to the cell cycle, and in population biology much of the overall variation is explained by the seasons. Previously such a periodic signal has been treated as just one example of a varying extrinsic variable (9). However, periodically changing environments are different from truly stochastic environments, not only because the variability has little to do with noise, but also because the current value of the environment explains much of the variability in the recent history. Asynchronous cell populations then exhibit a nonrandom source of heterogeneity simply because cells at different stages of the cell cycle are different on average. Levels of independent reporters will thus correlate creating an extrinsic “noise” that may completely overshadow truly stochastic sources of extrinsic noise (15). The question is thus if we can separate such nonrandom variability due to a periodic but deterministic extrinsic signal from stochastic sources of extrinsic noise.

The heterogeneity due to unsynchronized observations can be identified by conditioning on the phase t^∗, with 0 < t^∗ < T where T is the period of the environmental signal. The total observed variability for asynchronous cells is then given by (outer brackets denote averages over the cell-cycle phase) 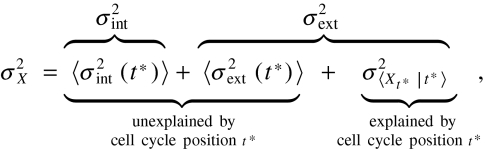9 where the intrinsic and extrinsic contributions for synchronized cells are given by (SI Appendix)

with outer brackets denoting averages over all histories Z[0,t^∗] that end at the specific phase t^∗ within the periodic cell cycle. The three contributions in Eq. 9 can be inferred from the dual-reporter covariance of asynchronous populations by additionally measuring bulk averages of synchronized populations, making the intrinsic and extrinsic noise contributions experimentally accessible without having to follow a synchronized population at the level of single cells. Observing dual reporters in synchronized cells in turn allows for direct control experiments because the extrinsic noise term is related to the phase dependent dual-reporter covariance in synchronized cells (SI Appendix): .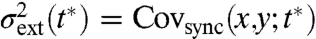

Another important experimental consideration is that growing populations of cells generally exhibit an age structure, with more newborn cells than dividing cells. Bulk observations of asynchronous cells will thus correspond to averages over a nonuniform distribution of cell-cycle positions. Eq. 9 can be applied to averages over any distribution of cell-cycle times, but must be used consistently for all measurements. In the following we use it exclusively to analyze decompositions that correspond to cell-cycle averages obtained by picking cells at random times during the cell cycle with uniform probability.

Analyzing Intrinsic Versus Extrinsic Sources of Noise

The above results show that a noise decomposition based on environmental history can separate intrinsic and extrinsic noise contributions regardless of microscopic details and that the contributions can be experimentally identified using just two independent reporters. This provides independent interpretations of the intrinsic and extrinsic categories and ensures that the approach is self-consistent without resorting to circularity. However, this level of description is entirely phenotypic and not connected to mechanistic representations of the underlying system. There is in fact no guarantee that the intrinsic and extrinsic contributions correspond to what is typically thought of as intrinsic and extrinsic processes, except in the trivial and nonuseful limit that there is only one type of noise.

Specifically, we ask: Can each noise term be compared to models that account only for either intrinsic or extrinsic mechanisms rather than the whole complex system that is subject to both types of noise? That is arguably the main purpose of the whole approach and has been taken for granted in practical applications of the dual-reporter method (6–8).

To address this issue we differentiate between different classes of systems. We call the system linear in intrinsic variables if all reaction rates r_k are linear functions of x—still allowing nonlinear effects with respect to the environmental variables—so that the total fluxes follow R(x,z) = a(z) + J(z)x, for some vector a and Jacobian matrix J. Borrowing terminology from stochastic differential equations we then call the environment additive when the matrix J is independent of z, and multiplicative otherwise. Multiplicative noise is the rule rather than exception in biology: The rate of encounters between predators and prey depends on the product of population sizes, just as the rates of degradation, transcription, and translation depend on the products of substrate and enzyme levels.

Modeling Extrinsic Noise.

The response of a deterministic system to extrinsic variables is described by a conventional deterministic equation with rates r_k where the continuous variables 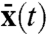respond to changes in the environment, according to

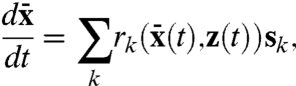[10]

for a given environmental sample path z(t). If such a model could be rigorously compared to the extrinsic noise in Eq. 7, we could analyze the nature of extrinsic variability without having to specify details of the intrinsic stochastic reactions, such as burst sizes. Starting from the conditional master equation and without specifying the unknown environmental influences we can prove that for systems linear in intrinsic variables, the conditional average 〈X_t|Z[0,t]〉 follows the above time evolution equation for the deterministic system 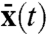(Appendix). The extrinsic noise of the full system thus indeed equals the noise of the intrinsically deterministic system (Eq. 10) subjected to the fluctuating environment: 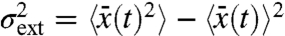, where brackets denote time averages. As long as the system is linear in intrinsic variables the extrinsic noise obtained from the covariance between dual reporters can thus be rigorously analyzed by a simple deterministic model where the rate “constants” vary in time. This is true regardless of the details of the system and allows for arbitrary, nonlinear environmental influences of both stochastic or periodically changing nature. The condition of intrinsic linearity is less restricting than it may seem because many reporter systems have been constructed to be linear in this sense (5, 6). The dual-reporter method is thus broadly applicable to analyze extrinsic fluctuations in complex networks and effectively reduces the number of unknown parameters that would otherwise be necessary to specify the system’s intrinsic stochasticity on top of the environmental dynamics. If the rates r_k instead are nonlinear functions of the intrinsic variables, the system generally does not satisfy 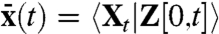with 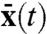following Eq. 10. The extrinsic noise, according to the top-down definition of Eq. 7, can then still be extracted using the dual-reporter method, but it cannot be rigorously analyzed using mathematical models that ignore the intrinsic stochasticity.

Modeling Intrinsic Noise.

Many studies instead focus on intrinsic noise and use dual reporters to eliminate the need to account for unknown or complex environmental influences. The remaining intrinsic fluctuations in gene expression are often thought of as the variability within a population of cells “identical not just genetically but also in the concentrations and states of their cellular components” (5).

This can be modeled in several ways. For example, if molecules of species X are degraded with a variable degradation rate β(z)x, a constant environment could be created by replacing β(z) by its average. But such approaches, which have been modeled using Langevin approximations (10), do not capture the correct average abundances and therefore will not capture the correct intrinsic noise that is greatly affected by abundances. We follow an alternative approach by replacing the fluctuating rate “constants” by true constants that ensure that the average abundance and lifetime of X are preserved.

For systems that are linear in intrinsic variables and subject to additive environmental influences, the noise decomposition based on the environmental history can be obtained analytically. The master equation (Fig. 1C) determines the time evolution of the ensemble variance for a given environmental time trace, and by time averaging the conditional ensemble variance 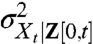we can calculate the intrinsic noise 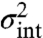for arbitrary additive environmental fluctuations. This shows (SI Appendix) that the intrinsic noise is captured by models that replace the fluctuating rates by their averages, which for such systems is equivalent to using rate constants that preserve the average abundances. The intrinsic noise can then be modeled and interpreted separately from extrinsic noise.

For multiplicative environments we first consider the simplest example where X molecules are produced with rate λ(z) and degraded with rate β(z) per molecule:

[11]

where both β and λ depend in some unspecified way on the fluctuating environment. Replacing the fluctuating rates with constants that ensure correct average abundances and average lifetimes of X leads to a model that correctly captures the intrinsic noise (SI Appendix)—even though noise terms generally are not superimposable in systems with multiplicative noise (10, 14, 16). Unfortunately this is a special case, and the same strategy fails already if we simply allow for molecules to be produced in bursts instead of one by one, i.e., 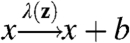. The approach then misleadingly produces the expected scaling with 〈x〉 but with an incorrect burst size (Fig. 4A).

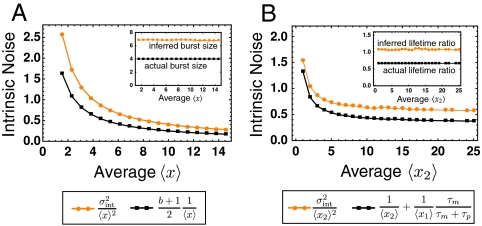
Fig. 4.

Intrinsic noise cannot be modeled independently of extrinsic fluctuations. (A) Numerical results for the normalized intrinsic noise of the the simple birth and death process (reaction scheme 11) with bursts of synthesis. The top-down intrinsic noise as measured by the dual-reporter method (orange dots) differs from the fluctuations exhibited by the system in the absence of environmental fluctuations (black squares; see formula in legend). (Inset) Inferred versus the actual value of the burst size. (B) Analyzing the mRNA-protein model (reaction scheme 12). The dual-reporter intrinsic noise measure (orange dots) differs from the normalized fluctuations exhibited by the system in the absence of environmental fluctuations (black squares; see formula in legend). (Inset) Inferred time-averaging factor τ_m/(τ_p + τ_m) when incorrectly interpreting the intrinsic noise as the fluctuations exhibited by the system in the absence of environmental fluctuations versus its actual value determined by the respective average mRNA and protein lifetimes τ_m and τ_p. Note the inferred nonsensical value of a time-averaging factor larger than one. Parameters used: λ(z) = α, β(z) = 10z, b = 4 and λ₁ = 1, β₁ = 0.5, λ₂(z) = αz, β₂ = 1, where α was varied to generate systems of different averages. The extrinsic variable z followed simple Poissonian dynamics (cf. reaction scheme 11) with τ_z = 10 and τ_z = 1/3, respectively.

Such discrepancies are the rule rather than the exception. Consider for example the commonly used toy model for gene expression (cf. Fig. 1A) where mRNAs x₁ and proteins x₂ follow:

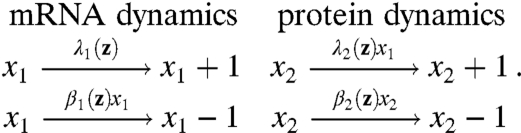[12]

Replacing the fluctuating rates with a constant environment such that average abundances and lifetimes are preserved will not reproduce the intrinsic noise. This inevitably leads to incorrect inferences of key features, such as how much noise in protein levels is inherited from mRNA fluctuations (Fig. 4B). Because multiplicative noise is the expectation in virtually all systems, due to bimolecular interactions, this is a severe limitation: Interpreting the intrinsic noise 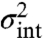from dual-reporter experiments in terms of models that ignore the environmental influences does not work even for systems that are linear in all intrinsic variables. The approach also fails for systems with additive environmental influences but nonlinear intrinsic mechanisms, because the average behavior is directly affected by the fluctuations around the average.

Discussion

From biochemistry to embryonic development, population dynamics and social interactions, many processes are both inherently stochastic as well as affected by a wide range of fluctuating inputs (1, 2, 17–23). Experimental observations must then be compared to models that account for both the system of interest as well as its environment, often introducing so many variables that mathematical analysis can degrade from hypothesis testing to mere curve fitting. The effect of “uninteresting” variables can to some extent be accounted for by physically or statistically holding them constant, but not all relevant variables are experimentally accessible or even known. Alternatively one could use identical pairs of reporters to infer the influence of a shared environment. For example, genetically identical twins can be used to determine what fraction of the phenotypic variance across a population is explained by the shared genes.

Here we extend this approach to dynamically changing environments and prove how, e.g., two protein reporters can be used to determine how much protein noise is explained by variations in the intracellular environment. We show that the extrinsic noise can often be analyzed by models that ignore intrinsic fluctuations, whereas the same approach applied to intrinsic noise will lead to misinterpretations of data. The reason is that, by construction, the law of total variance separates an explained contribution from an unexplained rest—it does not identify multiple explained contributions. Even if a random variable is only a function of two statistically independent other random variables, the contributions explained by each of those do not sum up to the total—if 40% of the total variability is explained by extrinsic fluctuations in gene expression, the remaining 60% is not explained by intrinsic fluctuations, except in very special cases. Unfortunately it is not possible to reverse the roles of intrinsic and extrinsic: Two proteins cannot share the same physical copies of genes and mRNAs and at the same time be in different cells.

Despite these limitations, dual-reporter methods are still preferable to using a single reporter, where interpretations always rely on detailed assumptions about both the intrinsic and extrinsic mechanisms. In addition to identifying extrinsic contributions, dual reporters can estimate intrinsic contributions in any situation where these completely dominate. Also, comparing distributions across a population of dual-reporter cells to the distribution across single-reporter cells can reveal feedback or competition effects. Even in cases when dual-reporter data cannot be interpreted without explicit model assumptions about both system and environment, measuring a second reporter allows for more rigorous model testing by providing access to different types of measurable outputs without introducing new parameters.

We have shown that dual-reporter methods facilitate quantitative analysis in many ways, without relying on detailed assumptions about every aspect of the system. However, because many biological processes are nonstationary, have nonlinear rate functions, and are subject to multiplicative environmental influences, complementary mathematical approaches are also required. Accounting for fluctuations in single cells may facilitate rather than complicate such analyses, for example, by providing conditional independences (24, 25) where the unknown mechanisms are accounted for via the fluctuations they create. Such methods will be key for quantitative biology, both because they account for the stochastic mechanisms and because they rigorously deal with complex and poorly characterized networks.

Appendix

In this appendix we clarify the mathematical definitions and perspectives introduced in the main text. The proofs of our technical results (the example environmental state decomposition, the noise decomposition in periodically changing environments, and intrinsic noise models in additive or multiplicative environments) are detailed in SI Appendix.

Law of Total Variance.

By introducing conditional averages the total variance 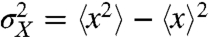can be written as

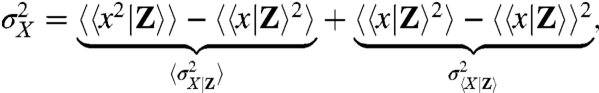where the outer brackets indicate averages over all states of Z.

Averaging Over All Possible Histories.

For ergodic systems the average over all histories can be written as a time average of the time-dependent ensemble average:

where x^j(t) for j = 1,2,3,… are different realizations of the reporter signal subjected to the same given sample path of the environmental time trace Z = z(t).

Conditional Independence of Dual Reporters.

Overall X, Y are not statistically independent, or there would be no covariance to discuss. However, assuming that the dual reporters are independent in a mechanistic sense, i.e., they do not influence each other in any way (directly or indirectly through feedbacks to the environment), implies that the dual reporters are statistically independent for a given sample path of the environment. That means for a fixed environmental history Z[0,t] = z(t) we require that the marginal distribution of X_t at time t given an environmental history is not affected by knowing the value of Y_t implying that 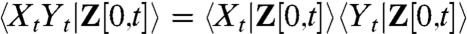. This condition of causal independence is not the same as assuming that 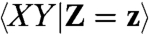is equal to 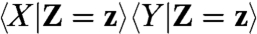, which only holds for static environmental variability but not for dynamically changing environments.

Modeling Extrinsic Noise.

For systems with fluxes that are linear functions of the intrinsic variables the conditional average given a sample path of the environmental time trace Z[0,t] = z(t) follows:

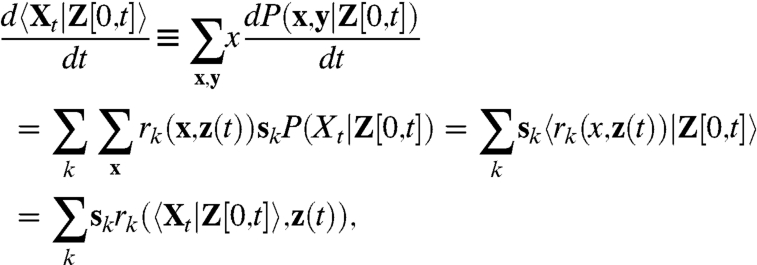because by assumption the rates r_k(x,z(t)) are linear functions of the intrinsic variable x. That means that the extrinsic noise 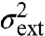as given by Eq. 7 corresponds to the variability exhibited by the above deterministic system (cf. Eq. 10) responding to a variable environmental input z(t).