Direct and indirect effects of biological factors on extinction risk in fossil bivalves

Abstract

Biological factors, such as abundance and body size, may contribute directly to extinction risk and indirectly through their influence on other biological characteristics, such as geographic range size. Paleontological data can be used to explicitly test many of these hypothesized relationships, and general patterns revealed through analysis of the fossil record can help refine predictive models of extinction risk developed for extant species. Here, I use structural equation modeling to tease apart the contributions of three canonical predictors of extinction—abundance, body size, and geographic range size—to the duration of bivalve species in the early Cenozoic marine fossil record of the eastern United States. I find that geographic range size has a strong direct effect on extinction risk and that an apparent direct effect of abundance can be explained entirely by its covariation with geographic range. The influence of geographic range on extinction risk is manifest across three ecologically disparate bivalve clades. Body size also has strong direct effects on extinction risk but operates in opposing directions in different clades, and thus, it seems to be decoupled from extinction risk in bivalves as a whole. Although abundance does not directly predict extinction risk, I reveal weak indirect effects of both abundance and body size through their positive influence on geographic range size. Multivariate models that account for the pervasive covariation between biological factors and extinction are necessary for assessing causality in evolutionary processes and making informed predictions in applied conservation efforts.

All species eventually go extinct, and biological correlates of extinction risk have been the focus of many studies of extant and extinct taxa (1–4). Most studies have analyzed biological factors separately, tacitly assuming independence among them. However, few biological characteristics are independent, and unaccounted for covariation confounds causal interpretation, weakens the power of predictive models, and inhibits successful synthesis. In addition, most studies have considered only the direct effects of biological factors on extinction. However, factors can contribute both directly and indirectly through their influence on other more proximal biological characteristics, and thus, accounting for indirect effects can be important when assessing the relative influence of multiple factors (5–7).

Here, I investigate the direct and indirect effects of multiple biological factors on extinction risk using the early Cenozoic marine fossil record of the eastern United States. I focus on the contributions of abundance, body size, and geographic range size to the observed stratigraphic range (termed duration hereafter) of species. Measures of geographic range and abundance are commonly used to set conservation priorities (8), and empirical support exists for the influence of both on extinction risk over geologic time scales (9–14). Body size is also widely believed to influence extinction risk, although support is equivocal (15–19). These three factors often covary, although most of our understanding of these relationships is restricted to extant birds and mammals (20, 21), and little is known about their variation over evolutionary time. Abundance, body size, and geographic range are dynamic attributes, and for this study, I use maximum abundance, maximum body size, and cumulative geographic range size.

Marine bivalves are well-suited for testing models relating biological factors to extinction risk over a range of spatial and temporal scales. The bivalve fossil record is relatively complete (22) and preserves ecological data such as relative abundance with considerable fidelity (23–25). Extensive research on the Paleogene (65.5–28.4 mya) sedimentary deposits of the US Gulf and Atlantic Coastal Plains has generated a well-resolved taxonomic (26, 27) and stratigraphic framework (28, 29) in which to conduct these analyses.

Using species in three ecologically disparate superfamilies of marine bivalves (the shallow infaunal Carditoidea, epifaunal Pectinoidea, and shallow to deep infaunal Veneroidea), I ask three questions. (i) What are the direct effects of abundance, body size, and geographic range size on the duration of species, and do estimates of these effects change when covariation between factors is taken into account? (ii) Do abundance and body size contribute indirectly to species duration through their influence on geographic range size? (iii) Do biological correlates of duration vary markedly among clades?

Results

Linear regression models were used to assess the direct effects of biological factors on extinction risk. When each factor is considered separately (Fig. 1A and Table 1), geographic range size exerts the strongest direct effect on the duration of bivalve species. Species with larger geographic ranges persisted over longer intervals of time than those species with smaller geographic ranges. Abundance also positively affects species duration, although its influence is weaker. In contrast, body size has no measurable direct effect on duration. These results are robust to distributional assumptions, remaining when nonparametric rank order correlation is used to assess the association between biological factors and duration (Table S1).

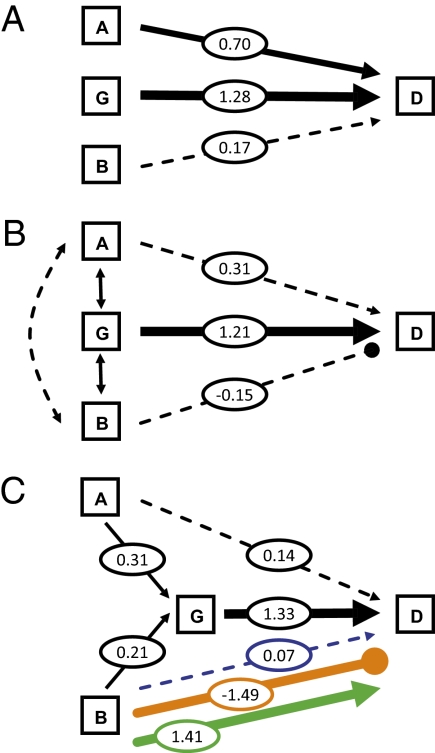
Fig. 1.

Models of the direct and indirect effects of biological factors on extinction risk in Cenozoic bivalves depending on whether covariation between factors is accounted. A, abundance; B, body size; G, geographic range size; D, species duration. Values are model coefficients. Solid lines denote significant effects at α = 0.05. Dashed lines are hypothesized but nonsignificant effects. Positive and negative effects are indicated by arrows and filled circles, respectively. Clade-independent coefficient estimates are black, and clade-specific coefficient estimates are colored blue (Carditoidea), orange (Pectinoidea), and green (Veneroidea). (A) When biological factors are assumed to be independent in their effects on extinction risk, geographic range is the strongest predictor, with abundance also contributing. (B) When covariation is taken into account, geographic range seems to be the only factor that contributes directly to extinction risk. (C) A multigroup model that includes both direct and indirect effects has the greatest support and identifies weak indirect effects of abundance and body size on extinction risk through the influence on geographic range size and opposing direct effects of body size on extinction risk among clades.

Table 1.

Direct effects of biological factors on extinction risk when factors are assessed using separate regression models or a single multiple regression model

	Coefficient	R2	AIC	AW
Abundance	0.70 ± 0.33	0.04	576.53	<<0.01
Body size	0.17 ± 0.34	<0.01	580.67	<<0.01
Geographic range	1.28 ± 0.31	0.13	565.33	0.82
A + B + G	A, 0.31 ± 0.34; B, −0.15 ± 0.33; G, 1.21 ± 0.34	0.14	568.34	0.18

Coefficients are presented as ±1 SE. Significance at α < 0.05 is indicated by bold type. R² measures model fit. Akaike’s information criterion (AIC) is used for model selection. The relative support for each model is summarized by the Akaike weights (AW). Geographic range size exerts the primary direct effect on extinction risk, and an apparent direct effect of abundance is explained entirely by its covariation with geographic range.

The relative strengths of these direct effects are confounded by the lack of independence between factors. Abundance is positively correlated with geographic range size (Spearman ρ = 0.36, P < 0.05) as are body size and geographic range (Spearman ρ = 0.19, P = 0.05). Abundance negatively covaries with body size in some marine and terrestrial systems (30, 31), but this relationship depends on the spatial and phylogenetic scale of analysis (32, 33). Across species in the three superfamilies analyzed here, abundance and body size are only weakly coupled (Spearman ρ = 0.17, P = 0.07).

To measure the unique direct effect of each biological factor on species duration, I used multiple linear regression. Abundance no longer has a direct effect when its covariation with geographic range size is taken into account (Fig. 1B and Table 1), but geographic range remains a strong predictor of extinction risk. The simpler model in which geographic range size directly affects duration is moderately better supported [Akaike’s information criterion (AIC) = 565.33, Akaike weight (AW) = 0.82] than the multiple regression model in which abundance and body size also directly contribute (AIC = 568.34, AW = 0.18).

Structural equation modeling was used to evaluate the impact that indirect effects have on predictions of extinction risk (7). In the indirect effects model, abundance and body size contribute directly to species duration and indirectly through their influence on geographic range size. Among marine invertebrates, body size and fecundity may positively covary (34), and increased fecundity could result in broader geographic distributions through propagule pressure (14, 35, 36). Abundance may also contribute positively to variation in geographic range size over the history of a species, with species with larger local populations having greater opportunity to disperse and establish new populations on the landscape (37, 38).

The indirect effects model is much better supported than a model consisting only of direct effects (AIC_indirect = 21.47, AW_indirect > 0.99, AIC_direct = 34.635, AW_direct < 0.01), and the covariance structure implied by the indirect effects model does not deviate significantly from the observed data [χ² = 3.47, degrees of freedom (df) = 1, P = 0.06]. The indirect effects model provides additional support for a strong direct effect of geographic range on species duration (Table 2, clade-independent model and Fig. S1) and reveals weak indirect effects of abundance and body size on duration through their positive contributions to geographic range size. The indirect effects of abundance and body size are of comparable magnitude and are measured as the product of the coefficients linking each factor to duration (Table 2).

Table 2.

Direct and indirect effects of biological factors on extinction risk depending on whether structural equation models are fit to the data for all species (clade-independent) or fit simultaneously to data for each of the three superfamilies (clade-dependent)

	Direct effects			Indirect effects
Model	Abundance	Body size	Geographic range	Abundance	Body size
Clade-independent	0.31 ± 0.33	−0.15 ± 0.32	1.21 ± 0.34	0.32 ± 0.09	0.17 ± 0.09
Clade-dependent	0.14 ± 0.31	C, 0.07 ± 0.43; P, −1.49 ± 0.70; V, 1.41 ± 0.66	1.33 ± 0.34	0.31 ± 0.09	0.21 ± 0.09

Paths linked directly to duration are direct effects. Paths linked to duration through geographic range are indirect effects. Coefficients are presented as ±1 SE. Significance at α < 0.05 is indicated by bold type. A clade-independent model of direct and indirect effects is better supported than a clade-independent model of only direct effects. However, a clade-dependent multigroup model of direct and indirect effects, in which the direct effects of body size on duration vary among superfamilies, has the greatest support.

To assess whether the direct and indirect effects of biological factors on extinction risk observed across this broad taxonomic sampling of bivalves are widely applicable, I compared structural equation models for the three bivalve superfamilies using multigroup analysis (7, 39). Multigroup analysis involves specifying a candidate set of models in which coefficients are either constrained to be equal across groups or allowed to vary. Multigroup models, in which some of the associations between biological factors and extinction risk differ among superfamilies, have the greatest support (Fig. 1C and Table S2). Models in which all effects are assumed to be equal across groups (AW = 0.04, χ² = 23.36, df = 13, P < 0.05) or in which all effects freely vary (AW < 0.01, χ² = 8.787, df = 3, P < 0.05) are not supported (Table S2).

The multigroup models with the greatest support (Table S2, models 1 and 2) are those models in which the direct effects of body size on extinction risk differ among clades (Table 2). Larger size is associated with greater extinction risk in pectinoid species, whereas the opposite is true among veneroid species (Fig. 1C and Table 2). All of the remaining paths linking biological factors directly or indirectly to extinction risk are clade-independent. There is no support for variation among clades in the direct effects of geographic range or the direct and indirect effects of abundance (Table S2). There is equivocal support for variation in the indirect effects of body size (Table S2), but this more complex model does not provide a significantly better fit to the data than the model presented in Fig. 1C (P = 0.13 for a single df χ² test). Multigroup analysis corroborates the general structure of direct and indirect effects linking biological factors and extinction risk in fossil bivalves, and it reveals additional factors that contribute to extinction dynamics at finer phylogenetic and ecological scales.

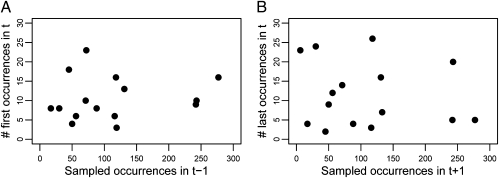
These results indicate that geographic range size is a general predictor of the observed durations of bivalve species in the early Cenozoic fossil record. However, sampling and incomplete preservation can affect estimates of the temporal and spatial distributions of fossil taxa. Incomplete sampling can truncate the observed durations of fossil species (40), although stratigraphic range extension can also occur when preservation is poor (2, 25, 41). If the quality of sampling strongly affects the observed durations of species, then the frequency of species’ first and last occurrences in a given time interval should correlate with the quality of sampling in the preceding and subsequent intervals, respectively (42). Poor sampling should result in an observed increase in the number of last occurrences in the preceding time interval and an increase in the number of first occurrences in the subsequent interval. I use the number of occurrences in a time interval—defined here as the unique occurrence of a species at a locality—as a measure of sampling quality and find no correlation between sampling in an interval and the frequency of first (Spearman ρ = −0.03, P = 0.9) and last occurrences (Spearman ρ = −0.03, P = 0.9) in the preceding and subsequent intervals (Fig. 2). Temporal variation in sampling intensity did not contribute greatly to the durations of fossil species analyzed here.

Fig. 2.

Relationship between sampling quality and the observed distribution of species’ first (A) and last (B) stratigraphic occurrences. If variation in sampling strongly affects the observed durations of species, a negative correlation is expected between the frequency of first occurrences in time bin t and the number of sampled occurrences in the preceding bin (t − 1). Conversely, poor sampling in interval t + 1 is expected to generate an excess of last occurrences in time bin t. No correlation exists between quality of sampling and the temporal distribution of observed stratigraphic range endpoints.

Measures of geographic range for fossil taxa are also sensitive to variation in the spatial extent of preserved and sampled sedimentary rocks. To account for this variation, geographic range size in the analyses presented above was estimated as the observed extent of a species scaled to the maximum extent possible (i.e., the maximum distance between fossil occurrences in the study area) over its observed duration. Uncorrected measures of geographic extent show a stronger association with species duration because of the pooling of species from intervals characterized by different degrees of sampling (Table S3). Because measures of extent may be sensitive to geographic outliers (43, 44), I also estimated the occupancy of each species. Occupancy is strongly correlated with extent (Spearman ρ = 0.76, P < 0.05) and is also associated with species duration (Table S4).

Most species are rare in that they have narrow geographic ranges and low local abundances, and the results of this study indicate that narrow geographic ranges are associated with elevated extinction risk. However, rare species are also less likely to be sampled, which can artificially elevate apparent rates of extinction. The analyses presented above include species known from only a single county as well as species present only in museum collections and/or published faunal lists. Abundance for these museum-only species was estimated using ref. 45. If the most narrowly distributed species are excluded, geographic range still has a strong direct effect on species duration (Table S5). If hyperrare museum-only species are excluded from the analysis, the apparent direct effect of abundance on duration weakens, whereas geographic range remains a strong predictor of extinction risk (Table S5).

For the 28% of species with observed durations greater than two time intervals, mean sampling probability can be estimated, and its correlation with each biological factor can be directly assessed. Sampling probability was calculated as (H − 2)/(R − 2), where H is the number of intervals in which a species is observed and R is its observed stratigraphic range (46). Both terms are conditioned on the species having a first and last occurrence in the database. Sampling probability is generally high (mean = 0.84) and not correlated with abundance (Spearman ρ = 0.14, P > 0.05), body size (Spearman ρ = 0.17, P > 0.05), or geographic range (Spearman ρ = −0.18, P > 0.05), providing another indication that the results presented here are robust to sampling artifacts.

Discussion

Although many studies have attempted to pinpoint biological factors that influence the extinction of species, the interrelationships among these factors are rarely evaluated. Charles Darwin observed over 150 years ago that broadly distributed species also tend to be locally abundant, and both geographic range size and abundance are widely used today to assess extinction risk (3, 47). However, studies that have attempted to untangle their unique contributions are rare. The analyses presented here show the impact that accounting for such covariation can have on models of extinction risk. When analyzed separately, both abundance and geographic range seem to directly influence the duration of fossil bivalve species. When the covariation between abundance and geographic range is taken into account, geographic range size is the only factor among those factors examined here that has a consistent direct effect on species duration in each clade.

Whereas abundance does not directly contribute to extinction risk, there are reasons to expect abundance and body size to contribute indirectly through their contributions to variation in geographic range size. Larger-bodied individuals and larger local population sizes are both hypothesized to contribute positively to geographic range size among marine invertebrates through propagule pressure and by acting as source populations, respectively (14, 34–38). This prediction was borne out in these analyses, because structural equation models that incorporated both direct and indirect effects had the greatest support.

Geographic range is increasingly recognized as a primary determinant of extinction risk (10, 11, 14, 48–51). In most studies, however, correlates of extinction risk are assessed by pooling taxa from different clades with markedly different evolutionary histories and biological characteristics. Variation among clades in their biology and patterns of survivorship may generate patterns of association between biological factors and extinction risk that are not applicable at finer ecological or phylogenetic scales. By comparing the covariation between biological factors and species duration across several ecologically disparate bivalve superfamilies using multigroup structural equation modeling, I showed marked clade dependence in some of these relationships. This result is in accord with other recent analyses of extant and extinct taxa (3, 47, 52), and it highlights the importance of accounting for clade effects in predictive models of extinction risk. Despite clade-level differences, however, the strong direct effect of geographic range was ubiquitous, and most direct and indirect effects were general characteristics of marine bivalves. It is encouraging that multigroup analysis corroborates the important biological differences between clades but still reveals correlates of extinction risk that transcend the idiosyncratic natural histories of individual clades.

Body size is an important factor in extinction risk in two of three superfamilies analyzed here. However, body size operated in opposing directions such that larger-bodied veneroid species were relatively buffered from extinction, whereas larger-bodied pectinoid species were at greater risk. These opposing directions of selection explain the apparent lack of a relationship between body size and extinction risk across bivalves as a whole, a result in accord with many other paleontological studies (16, 17). Body size covaries with many biological characteristics (53), and its effect on extinction risk likely reflects the contributions of other covariates such as metabolic rate or fecundity. Among burrowing bivalves, body size also covaries with infaunal depth, which has been hypothesized to buffer species from environmental stress and reduce predation pressure (13, 54–57). The differences in the effect of body size on duration in the Pectinoidea and Veneroidea may reflect variations in life history traits between epifaunal and infaunal species or a common response to environmental stress diminishing in intensity with increasing infaunal depth. Because body size in species with indeterminate growth reflects such diverse factors as growth rate, ambient temperature, and age, additional work is needed to tease apart the relationships between shell size and life history traits.

The analyses presented here support a role for biological factors, particularly geographic range, in determining extinction risk over geologic time. However, multiple processes may underlie the strong positive relationship between geographic range and duration. Broad range size may buffer lineages from extinction, but older lineages also have more time to spread geographically; thus, the relationship between geographic range and duration may be reciprocal rather than unidirectional, which is often assumed. Furthermore, a positive relationship between range and duration could reflect chance survivorship or substantially different ways in which broad vs. narrowly distributed species establish and maintain their ranges. Some paleobiological studies have begun to address these questions (10, 12, 14, 48, 58), but additional work is necessary before analyses of the fossil record can be used fully to inform predictive models of extinction risk developed for extant species.

Last, it is perhaps surprising that abundance had no direct effect on the duration of fossil bivalve species given its importance in the management of endangered species today. Abundance is an important factor in some multivariate analyses of extinction risk in extant species (3, 50, 51), although it generally contributes less than geographic range. This mismatch between contemporary conservation practice and empirical data on the role of abundance in extinction risk in the fossil record is likely an issue of scale. Demographic stochasticity becomes important at very low population sizes (59), but such rare species may be less likely to be preserved and/or sampled in the fossil record (60, 61). Although geographic range size is the most general biological determinant of species susceptibility to extinction, conservation efforts still need to account for and counteract low abundance after species are at elevated risk.

Conclusions

Biological factors, such as abundance, may contribute directly to extinction risk and indirectly through their influence on other biological characteristics. When examined individually, both geographic range and abundance have an apparent direct effect on extinction risk. However, abundance, body size, and geographic range size are not independent, which confounds causal interpretation of these relationships. When covariation between factors is accounted, geographic range emerges as the only consistent predictor of extinction risk among the factors considered here. This result is widely applicable across three diverse clades that differ in many other biological characteristics, and it provides support for the important role of geographic range in diversity dynamics over the history of life. Clade-level effects can be equally strong however, and multigroup modeling provides a useful analytical framework for assessing general vs. specific determinants of extinction risk among extant and extinct species.

Materials and Methods

Database Compilation.

A database containing the occurrence, size, and abundance of fossil marine bivalve species in three superfamilies (Carditoidea, Pectinoidea, and Veneroidea) was assembled for the Paleogene of the Gulf and Atlantic Coastal Plains of the eastern United States. Occurrence and abundance data were collected through fieldwork by the author and supplemented by the use of collections at the Paleontological Research Institution, National Museum of Natural History, Florida Museum of Natural History, and Academy of Natural Sciences Philadelphia, records in the Paleobiology Database (http://paleodb.org), and the published literature. The database consists of ∼3,600 occurrences of species over the Paleogene (65–28.4 mya) distributed over 14 states and 153 counties in the eastern United States (Fig. S2). Analyses were restricted to 108 species for which abundance, body size, geographic range, and duration could be measured or estimated (Dataset S1). These 108 species include 39 species in the Carditoidea, 28 species in the Pectinoidea, and 41 species in the Veneroidea.

Geographic Range.

The cumulative geographic range of each species was measured as the maximum great circle distance between the centroids of counties in which the species occurred. As has been observed by others (14), cumulative geographic range size strongly correlates with the maximum geographic range size that a species attains in a given interval within its duration (partial correlation with duration held fixed for species that span two or more intervals; Spearman ρ = 0.69, P < 0.05). Cumulative range is used here, because it allows all occurrences to be used in measuring range size, including those occurrences that are temporally not as well-constrained. Counties were used as species occurrences in museum collections and the literature cannot be resolved consistently to finer spatial scales. Most counties in the Coastal Plain are of similar size (mean length = 39 ± 13 km); thus, this measure is analogous to using equal area cells. Owing to variation in the preserved and sampled sedimentary record over the Paleogene, the extent of each species was scaled relative to the maximum distance between counties in the study area containing fossiliferous sedimentary rocks over its duration. The extent of species restricted to a single county was estimated as the mean length of a county in Coastal Plain states containing fossils (39 km). Variation in sampling extent over time can, however, generate markedly different measures of proportional extent for these single county taxa (58). To account for these variations, the minimum geographic extent was subtracted from the observed extent of all species, thus setting the extent of single county species equal to zero. The results presented here do not depend on the value of geographic extent assigned to species restricted to a single county.

Occupancy is an alternative measure of the geographic distribution of species (43, 44). Occupancy was calculated as the number of counties in which a species occurred over its observed duration relative to the total number of counties containing fossils during that same interval of time. A value of one was subtracted from the numerator to standardize the occupancy of all single county species as described above. Species occupancy is strongly correlated with extent, and model results are qualitatively similar, regardless of which geographic range metric is used.

Body Size.

The body size of each species was calculated as the geometric mean of shell length and width (13, 16) using specimens in museum collections and plates in taxonomic monographs. The median number of measurements for each species was 12 specimens. Because these species show indeterminate growth, the maximum size of species was analyzed in all models (16).

Abundance.

The relative abundance of species was estimated using counts of specimens recovered in bulk samples of fossiliferous sediment collected by the author for this study as well as published data compiled in the Paleobiology Database and other literature reports. The relative abundance of each species at a locality was calculated as the number of specimens of that species relative to the total number of bivalve specimens in a sample. Where possible, data from replicate bulk samples were pooled to provide an estimate of the abundance of species in that environment at the locality scale. The abundance of species at a locality known from museum collections but absent from the current sample of specimens (N) was assumed to be 1/N (45). The dataset contains counts of 84,870 specimens from 71 localities spanning the Paleogene. The median sample size for each locality was 502 specimens, and the mean was 1,195. Samples containing exclusively calcitic bivalves were excluded from the abundance estimates to minimize the effects of taphonomic biases such as dissolution.

Because most species are rare in most localities and only some are common somewhere within their geographic range, the maximum abundance for each species was analyzed in all extinction models. Using maximum abundance may approximate the peak abundance of species in their favored habitats and should minimize the effects of temporal variation in the environmental breadth of sampling. Abundance estimates for each species were derived from 1 to 17 samples, with a median of 2 and a mean of 3.5.

Duration.

The duration of each species was measured from the midpoint of the stratigraphic unit in which it first occurred to the midpoint of the stratigraphic unit in which it last occurred. This value was then rounded to the nearest 1 million year. All species restricted to a single stratigraphic unit were assigned a duration of zero, because there are insufficient data to determine their durations within the unit in which they occur. Alternative methods of calculating durations (e.g., assuming species, including those species restricted to a single interval, ranged from the base of the unit of first occurrence to the top of the unit of last occurrence) generate equivalent results.

Modeling Extinction Risk.

Two methods were used to assess the relative contribution of biological factors to species duration: (i) linear regression and (ii) structural equation modeling (7). Both methods model linear relationships between factors. In structural equation modeling, however, multiple response variables can be considered (direct and indirect effects), and models can be fit simultaneously to data for multiple groups (multigroup analysis). Before analysis, each covariate (geographic range, abundance, and body size) was normalized and scaled to zero mean and unit variance to satisfy assumptions of normality and allow relative effects to be assessed on a comparable scale. An arcsine square root transformation commonly applied to proportional data was used to normalize abundance and extent followed by logarithmic transformation of abundance and body size values; extent could not be logarithmically transformed, because these data include values of zero. Structural equation models were fit to the observed data using AMOS (62), and all other analyses were conducted using R (63). AIC was used for model selection, with AW used to summarize the relative support for each model in the set. To assess the support for structural equation models in which biological factors contribute both directly and indirectly to extinction risk, the observed and expected covariance matrices were also compared; P > 0.05 associated with the model χ² (i.e., a lack of significant difference) indicates an acceptable fit of a structural equation model to the observed data.