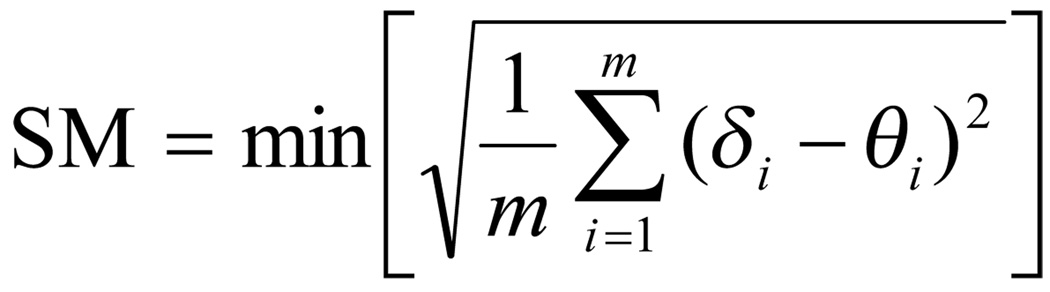Abstract
A complete, isostructural series of complexes with La-Lu (except Pm) with the ligand TREN-1,2-HOIQO has been synthesized and structurally characterized by means of single-crystal X-ray analysis. All complexes are 1D-polymeric species in the solid state, with the lanthanide being in an eight-coordinate, distorted trigonal-dodecahedral environment with a donor set of eight unique oxygen atoms. This series constitutes the first complete set of isostructural complexes from La-Lu (without Pm) with a ligand of denticity greater than two. The geometric arrangement of the chelating moieties slightly deviates across the lanthanide series, as analyzed by a shape parameter metric based on the comparison of the dihedral angles along all edges of the coordination polyhedron. The apparent lanthanide contraction in the individual Ln-O bond lengths deviates considerably from the expected quadratic decrease that was found previously in a number of complexes with ligands of low denticity. The sum of all bond lengths around the trivalent metal cation, however, is more regular, showing an almost ideal quadratic behavior across the entire series. The quadratic nature of the lanthanide contraction is derived theoretically from Slater’s model for the calculation of ionic radii. In addition, the sum of all distances along the edges of the coordination polyhedron show exactly the same quadratic dependence as the Ln-X bond lengths. The universal validity of this coordination sphere contraction, concomitant with the quadratic decrease in Ln-X bond lengths, was confirmed by reexamination of four other, previously published series of lanthanide complexes. Due to the importance of multidentate ligands for the chelation of rare-earth metals, this result provides a significant advance for the prediction and rationalization of the geometric features of the corresponding lanthanide complexes, with great potential impact for all aspects of lanthanide coordination.
1 Introduction
The coordination chemistry of the lanthanides shows much structural diversity. However, there is often only a limited degree of predictability due to the absence of strong ligand field effects, resulting in small energetic differences between different geometric arrangements and/or coordination numbers. One of the few reliable cornerstones for the rationalization of geometric features around lanthanide cations is the well-known phenomenon of the lanthanide contraction.1,2 Recently, it has been shown that in this context the monotonic decrease of certain parameters, such as Ln-X (X = Lewis-basic donor), can be best described by a second-order polynomial. This dependence was established by the examination of isostructural series of lanthanide complexes published in the literature.3 Subsequently, this dependence has also been observed for a few other examples of incomplete series including solid state materials,4 as well as coordination compounds.5 Due to the rarity of isostructural series over the whole range from La to Lu (excluding Pm), only limited structural information is available for the further analysis of the lanthanide contraction and geometrical ramifications thereof. Specifically, for complexes with ligands of higher denticity, which are often most relevant for the application of lanthanides (e.g. luminescence,6 MRI,7 radioisotope labeling,8 etc.), no example of a complete isostructural series with La-Lu (without Pm) has been presented.9 We report here the first case of such a series of complexes with a multidentate ligand and a detailed analysis of the structural changes corresponding to the lanthanide contraction as seen here and in previous systems.
2 Results and Discussion
2.1 Complex Syntheses
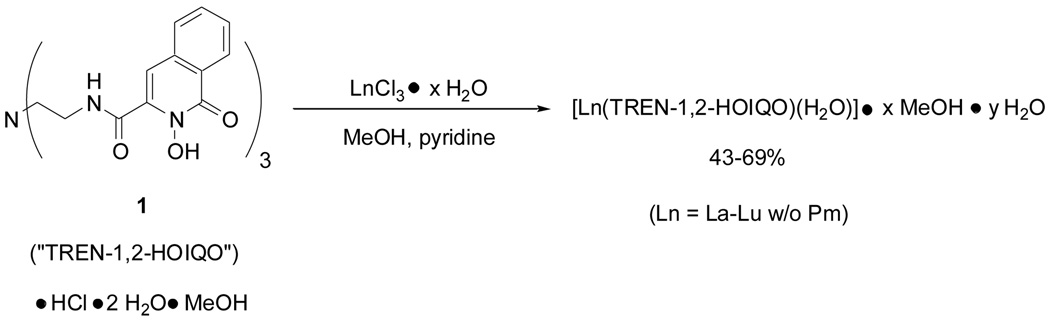
We recently introduced the tripodal ligand TREN-1,2-HOIQO (1, Scheme 1) as a new ligand for iron(III) and lanthanide(III) cations (Ce, Eu, Gd, Lu).9 The lanthanide complexes were prepared as previously described by refluxing equimolar amounts of the ligand TREN-1,2-HOIQO and the corresponding lanthanide chloride (hydrated or anhydrous) in methanol with pyridine as the base (Scheme 1).
Scheme 1.
Synthesis of lanthanide complexes with TREN-1,2-HOIQO.
2.2 Crystal Structures
Single crystals of the resultant lanthanide complexes were grown by diffusion of water into solutions of the complexes in DMF. Unit cell determinations and further analyses revealed that all structures crystallized in the monoclinic system P21/c with very similar lattice parameters (Tables 1 and 2).
Table 1.
Crystal data for lanthanide complexes (La-Gd) with TREN-1,2-HOIQO (1).
| [La(1)(H2O)] • H2O | [Pr(1)(H2O)] • H2O | [Nd(1)(H2O)] • H2O | [Sm(1)(H2O)] • H2O | [Eu(1)(H2O)] • H2O | [Gd(1)(H2O)] • H2O | |
|---|---|---|---|---|---|---|
| formula | C36H34LaN7O11 | C36H34N7O11Pr | C36H34N7NdO11 | C36H34N7O11Sm | C36H34EuN7O11 | C36H34GdN7O11 |
| mol. weight | 879.61 | 881.61 | 884.94 | 891.05 | 892.66 | 897.95 |
| crystal app. | colorless plate | red plate | red plate | red plate | colorless plate | colorless plate |
| crystal system | monoclinic | monoclinic | monoclinic | monoclinic | monoclinic | monoclinic |
| space group | P21/c | P21/c | P21/c | P21/c | P21/c | P21/c |
| a [Å] | 12.3545(11) | 12.3482(14) | 12.355(5) | 12.3528(13) | 12.380(3) | 12.3590(18) |
| b [Å] | 26.745(2) | 26.594(3) | 26.521(5) | 26.371(3) | 26.314(5) | 26.307(4) |
| c [Å] | 10.6674(9) | 10.6089(12) | 10.605(5) | 10.6066(11) | 10.612(2) | 10.5933(15) |
| α [°] | 90 | 90 | 90 | 90 | 90 | 90 |
| β [°] | 97.018(2) | 96.581(2) | 96.512(5) | 96.441(2) | 96.470(4) | 96.343(3) |
| γ [°] | 90 | 90 | 90 | 90 | 90 | 90 |
| volume [Å3] | 3498.3 (5) | 3460.9(7) | 3452(2) | 3433.3(6) | 3435.0(12) | 3423.1(9) |
| Z | 4 | 4 | 4 | 4 | 4 | 4 |
| ρ [g cm−1] | 1.67 | 1.69 | 1.70 | 1.72 | 1.73 | 1.74 |
| μ [mm−1] | 1.30 | 1.48 | 1.58 | 1.79 | 1.90 | 2.01 |
| crystal size [mm3] | 0.24×0.22×0.09 | 0.27×0.13×0.09 | 0.30×0.15×0.08 | 0.28×0.13×0.06 | 0.15×0.07×0.04 | 0.19×0.13×0.06 |
| temperature [K] | 160(2) | 157(2) | 156(2) | 159(2) | 158(2) | 164(2) |
| radiation [Å] | MoKα (λ=0.71073) | MoKα (λ=0.71073) | MoKα (λ=0.71073) | MoKα (λ=0.71073) | MoKα (λ=0.71073) | MoKα (λ=0.71073) |
| θ max [°] | 26.40 | 26.37 | 26.39 | 26.40 | 26.37 | 26.42 |
| meas. refls. | 19871 | 19631 | 19552 | 19446 | 19433 | 19276 |
| indep. refls. | 7071 | 7016 | 6951 | 6953 | 6936 | 6861 |
| refls. in ref. | 5080 (I ≥ 2σ(I)) | 4840 (I ≥ 2σ(I)) | 4620 (I ≥ 2σ(I)) | 4741 (I ≥ 2σ(I)) | 4280 (I ≥ 2σ(I)) | 4343 (I ≥ 2σ(I)) |
| parameters | 496 | 496 | 496 | 496 | 496 | 496 |
| R[a] | 0.0610 | 0.0507 | 0.0530 | 0.0483 | 0.0584 | 0.0564 |
| wR[b] | 0.1474 | 0.1086 | 0.1130 | 0.1042 | 0.1183 | 0.1138 |
| R[a] (all data) | 0.0897 | 0.0860 | 0.0951 | 0.0849 | 0.1120 | 0.1054 |
| wR (all data) | 0.1598 | 0.1194 | 0.1264 | 0.1148 | 0.1345 | 0.1285 |
| GoF | 1.050 | 1.035 | 1.030 | 1.026 | 1.008 | 1.003 |
| Δρmax [e/Å3] | 4.39 (near La) | 1.01 | 1.48 | 1.39 | 1.36 | 1.85 |
| Δρmin [e/Å3] | −0.14 | −0.64 | −0.86 | −0.87 | −0.75 | −0.73 |
R factor definition: R = Σ (‖F0| – |Fc‖) / Σ |F0|.
SHELX-97 wR factor definition: wR = [Σ w(F02 – Fc2)2 / Σ w(F02)]1/2. Weighting scheme: w = 1 / [σ2(F0)2 + (np)2], p = [F02 + 2 Fc2] / 3.
Table 2.
Crystal data for lanthanide complexes (Tb-Lu) with TREN-1,2-HOIQO (1).
| [Tb(1)(H2O)] • H2O | [Dy(1)(H2O)] • H2O | [Ho(1)(H2O)] • H2O | [Er(1)(H2O)] • H2O | [Tm(1)(H2O)] • H2O | [Yb(1)(H2O)] • H2O | [Lu(1)(H2O)] • H2O | |
|---|---|---|---|---|---|---|---|
| formula | C36H34N7O11Tb | C36H34DyN7O11 | C36H34HoN7O11 | C36H34ErN7O11 | C36H34N7O11Tm | C36H34N7O11Yb | C36H34LuN7O11 |
| mol. weight | 899.62 | 903.20 | 905.63 | 907.96 | 909.63 | 913.74 | 915.67 |
| crystal app. | yellow plate | colorless plate | colorless plate | colorless plate | colorless needle | red plate | colorless plate |
| crystal system | monoclinic | monoclinic | monoclinic | monoclinic | monoclinic | monoclinic | monoclinic |
| space group | P21/c | P21/c | P21/c | P21/c | P21/c | P21/c | P21/c |
| a [Å] | 12.3216(14) | 12.3472(15) | 12.345(2) | 12.3589(18) | 12.3920(13) | 12.336(5) | 12.417(2) |
| b [Å] | 26.295(3) | 26.188(3) | 26.153(4) | 26.132(4) | 26.162(3) | 26.006(10) | 26.193(4) |
| c [Å] | 10.5618(12) | 10.5624(12) | 10.5557(17) | 10.5565(15) | 10.5522(12) | 10.546(4) | 10.5619(17) |
| α [°] | 90 | 90 | 90 | 90 | 90 | 90 | 90 |
| β [°] | 96.335(2) | 96.220(2) | 96.306(3) | 96.277(2) | 96.357(3) | 96.443(5) | 96.436(4) |
| γ [°] | 90 | 90 | 90 | 90 | 90 | 90 | 90 |
| volume [Å3] | 3401.0(7) | 3395.2(7) | 3387.3(10) | 3388.9(8) | 3400.0(6) | 3362(2) | 3413.4(10) |
| Z | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| ρ [g cm−1] | 1.76 | 1.77 | 1.78 | 1.78 | 1.78 | 1.81 | 1.78 |
| μ [mm−1] | 2.16 | 2.23 | 2.41 | 2.55 | 3.21 | 2.86 | 3.56 |
| crystal size [mm3] | 0.24×0.22×0.09 | 0.18×0.16×0.06 | 0.18×0.09×0.06 | 0.22×0.08×0.06 | 0.09×0.01×0.01 | 0.15×0.07×0.04 | 0.10×0.04×0.02 |
| temperature [K] | 159(2) | 162(2) | 161(2) | 165(2) | 173(2) | 158(2) | 173(2) |
| radiation [Å] | MoKα (λ=0.71073) | MoKα (λ=0.71073) | MoKα (λ=0.71073) | MoKα (λ=0.71073) | synchro. (λ=0.7749) | MoKα (λ=0.71073) | synchro. (λ=0.7749) |
| θ max [°] | 26.40 | 26.45 | 26.39 | 26.39 | 29.19 | 26.44 | 25.62 |
| meas. refls. | 19325 | 19202 | 19179 | 19114 | 35089 | 16284 | 20804 |
| indep. refls. | 6901 | 6888 | 6833 | 6866 | 7007 | 6475 | 4946 |
| refls. in ref. | 4833 (I ≥ 2σ(I)) | 5033 (I ≥ 2σ(I)) | 4390 (I ≥ 2σ(I)) | 4446 (I ≥ 2σ(I)) | 5731 (I ≥ 2σ(I)) | 3542 (I ≥ 2σ(I)) | 4578 (I ≥ 2σ(I)) |
| parameters | 496 | 496 | 496 | 496 | 496 | 496 | 496 |
| R[a] | 0.0517 | 0.0456 | 0.0551 | 0.0489 | 0.0474 | 0.0594 | 0.0313 |
| wR[b] | 0.1189 | 0.1027 | 0.1079 | 0.0986 | 0.1107 | 0.1059 | 0.0804 |
| R[a] (all data) | 0.0849 | 0.0725 | 0.1045 | 0.0976 | 0.0597 | 0.1432 | 0.0340 |
| wR (all data) | 0.1299 | 0.1121 | 0.1219 | 0.1118 | 0.1149 | 0.1312 | 0.0820 |
| GoF | 1.024 | 1.037 | 1.013 | 0.993 | 1.096 | 0.964 | 1.097 |
| Δρmax [e/Å3] | 2.54 | 1.35 | 1.10 | 1.15 | 1.63 | 2.61 | 1.66 |
| Δρmin [e/Å3] | −0.84 | −0.88 | −0.93 | −1.04 | −1.97 | −0.84 | −0.73 |
R factor definition: R = Σ (‖F0| – |Fc‖) / Σ |F0|.
SHELX-97 wR factor definition: wR = [Σ w(F02 – Fc2)2 / Σ w(F02)]1/2. Weighting scheme: w = 1 / [σ2(F0)2 + (np)2], p = [F02 + 2 Fc2] / 3.
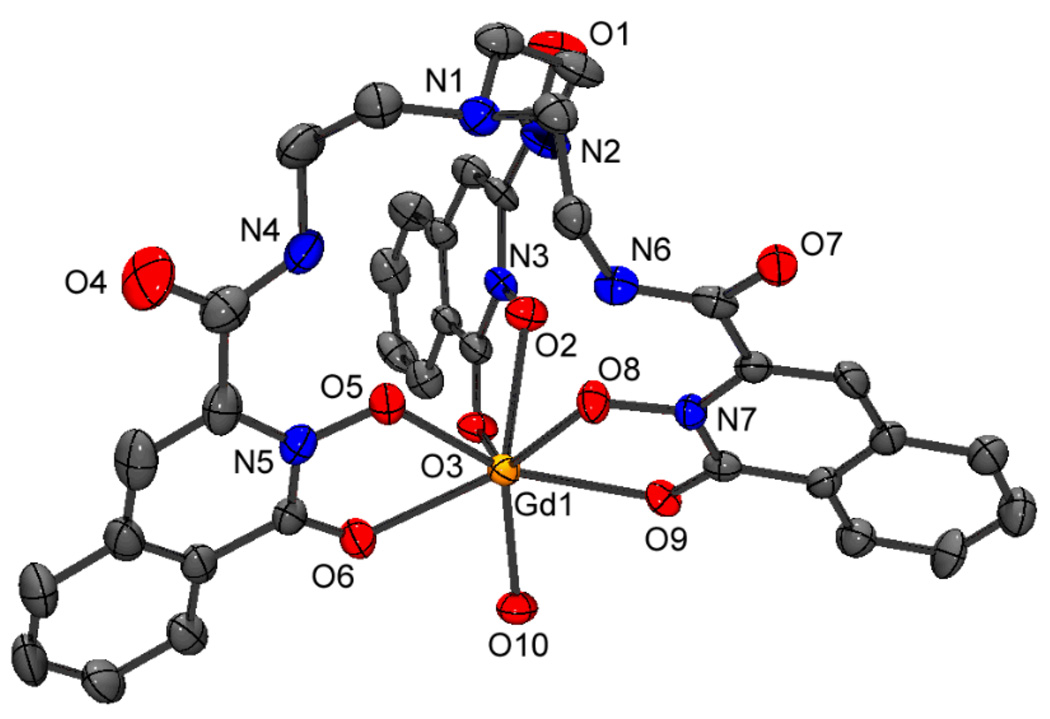
The structures were readily solved by direct methods. All the complexes are isostructural, with the same polymeric nature that was previously reported for the cerium complex of 1.9 The ligand chelates the lanthanide in a heptadentate fashion through three pairs of oxygen donors from the cyclic hydroxamic acid derivative 1,2-HOIQO and one bridging amide oxygen of a neighboring complex (Figure 1). The coordination sphere is completed by a water molecule to give an eight-coordinate lanthanide center with an approximately trigonal-faced dodecahedral geometry (vide infra).
Figure 1.
Asymmetric unit of [Gd(1)(H2O)] • H2O. Thermal ellipsoid plot (ORTEP-3 for Windows,10 50% probability level) with atom numbering scheme. Hydrogens and the isolated water molecule are omitted for clarity. O7 is coordinated to a neighboring complex.
2.3 Structural Analysis
2.3.1 Isostructural Behavior
For the analysis of the lanthanide contraction and its ramifications, it is essential that the subjects of the study have the same or very similar structure to ensure that the nature of the lanthanide is the only changing parameter. In the literature on the lanthanide contraction to date, however, terms like “isostructural” and ‘isotypical” have been used in a rather qualitative fashion, although there have been some efforts to develop a more quantitative measure for the similarity of coordination compounds.11 For the investigation of the present series of lanthanide complexes, a shape measure approach was utilized based on the dihedral angles along the edges of the coordination polyhedron.12
As the reference polyhedron the gadolinium complex was chosen due to the central position within the lanthanide series. Table 3 shows the dihedral angles of all complexes as well as the shape measure deviation SMGd relative to this standard.
Table 3.
Dihedral angles along the edges of the coordination polyhedra [°] of the lanthanide complexes with TREN-1,2-HOIQO (1). Shape measure SMGd (deviation relative to the gadolinium complex).
| Edge | La | Ce[a] | Pr | Nd | Sm | Eu | Gd | Tb | Dy | Ho | Er | Tm | Yb | Lu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O7-O8 | 55.07 | 55.68 | 56.25 | 56.68 | 57.31 | 57.75 | 57.94 | 58.37 | 58.77 | 58.70 | 58.85 | 59.35 | 59.72 | 60.10 |
| O7-O5 | 41.41 | 41.56 | 41.77 | 42.10 | 42.00 | 42.24 | 42.42 | 42.09 | 42.36 | 42.54 | 42.75 | 42.31 | 43.00 | 41.60 |
| O7-O6 | 49.04 | 48.85 | 49.16 | 49.02 | 49.25 | 49.54 | 49.40 | 49.45 | 49.51 | 49.18 | 49.02 | 49.47 | 48.91 | 50.19 |
| O7-O10 | 56.74 | 57.09 | 57.40 | 57.55 | 57.88 | 57.89 | 57.86 | 57.90 | 58.21 | 58.17 | 58.30 | 58.38 | 59.55 | 57.81 |
| O7-O9 | 47.45 | 46.36 | 45.77 | 45.51 | 44.62 | 43.87 | 43.60 | 43.44 | 42.49 | 42.23 | 42.41 | 42.03 | 40.98 | 41.47 |
| O6-O10 | 61.63 | 61.31 | 61.04 | 60.82 | 60.79 | 60.78 | 61.22 | 60.70 | 60.74 | 60.98 | 60.80 | 60.54 | 60.87 | 61.31 |
| O9-O10 | 68.17 | 69.12 | 68.39 | 68.26 | 68.38 | 68.31 | 68.07 | 67.95 | 68.35 | 68.79 | 68.42 | 68.37 | 69.03 | 68.33 |
| O3-O9 | 30.36 | 29.78 | 30.81 | 31.32 | 31.28 | 31.93 | 32.46 | 32.32 | 32.54 | 32.67 | 33.06 | 33.07 | 31.99 | 33.02 |
| O2-O9 | 40.79 | 41.52 | 40.91 | 41.39 | 41.47 | 40.91 | 41.13 | 42.01 | 42.00 | 42.25 | 42.33 | 42.69 | 43.26 | 43.33 |
| O2-O8 | 63.81 | 63.67 | 63.64 | 63.10 | 63.33 | 63.25 | 63.29 | 62.81 | 62.97 | 62.61 | 62.80 | 62.40 | 62.70 | 62.62 |
| O2-O5 | 62.25 | 62.23 | 62.55 | 62.98 | 63.87 | 64.15 | 64.18 | 63.98 | 64.33 | 64.58 | 64.75 | 64.47 | 65.26 | 64.65 |
| O3-O5 | 13.68 | 13.98 | 13.05 | 13.10 | 12.47 | 12.02 | 11.46 | 11.93 | 11.56 | 11.64 | 11.57 | 12.06 | 11.18 | 11.71 |
| O2-O3 | 86.69 | 87.41 | 87.47 | 87.83 | 88.45 | 88.63 | 88.64 | 89.19 | 89.63 | 89.89 | 89.75 | 89.33 | 89.71 | 89.14 |
| O5-O6 | 80.45 | 80.35 | 80.54 | 80.37 | 80.85 | 81.14 | 81.17 | 81.17 | 81.44 | 81.28 | 81.53 | 81.25 | 81.25 | 81.69 |
| O3 -O6 | 57.05 | 57.54 | 57.88 | 57.78 | 58.11 | 58.46 | 58.73 | 59.02 | 59.53 | 59.43 | 59.37 | 59.66 | 59.67 | 59.85 |
| O10-O3 | 72.70 | 72.39 | 72.08 | 71.85 | 71.41 | 71.10 | 70.54 | 70.02 | 69.50 | 69.50 | 69.21 | 68.65 | 68.80 | 67.86 |
| O9-O8 | 68.95 | 68.61 | 68.48 | 67.87 | 67.32 | 67.16 | 67.06 | 66.82 | 66.48 | 66.52 | 66.14 | 66.11 | 65.35 | 65.52 |
| O8-O5 | 57.52 | 57.45 | 57.87 | 57.78 | 57.83 | 57.87 | 57.83 | 58.56 | 58.19 | 58.03 | 57.95 | 58.62 | 57.91 | 58.68 |
| SMGd | 2.01 | 1.78 | 1.44 | 1.24 | 0.89 | 0.70 | 0 | 0.65 | 0.69 | 0.72 | 0.74 | 0.94 | 1.27 | 1.26 |
Ref. 9.
As can be seen in Table 3, the structures vary subtly with the dihedral angles varying by as much as ca. 5° (e.g. along edge O7–O8). On average, the differences are small as expressed by SMGd, which only shows a maximum variation of 1–2° for all complexes relative to the gadolinium species. The reasons for these deviations are not obvious but could be related to small ligand field effects or geometrical constraints imposed by the multidentate ligand (vide infra).
2.3.2 Ln-O Bond Lengths
As the next step, the decrease in Ln-O bond lengths was analyzed as evidence for the lanthanide contraction. In the complexes with TREN-1,2-HOIQO, all eight Ln-O bonds are different from each other, providing a rich source of structural data. Each bond length decreases by approximately 7–8% going from La to Lu in accordance with typical values for the lanthanide contraction (Table 4).
Table 4.
Bond lengths Ln-O in lanthanide complexes with TREN-1,2-HOIQO (1).
| f electrons (Ln3+) | dLn-O3 (σ) [Å] | dLn-O6 (σ) [Å] | dLn-O9 (σ) [Å] | dLn-O2 (σ) [Å] | dLn-O5 (σ) [Å] | dLn-O8 (σ) [Å] | dLn-O10 (σ) [Å] | dLn-O7 (σ) [Å] | ΣdLn-O (σ) [Å] |
|---|---|---|---|---|---|---|---|---|---|
| 0 (La) | 2.482(4) | 2.463(4) | 2.479(4) | 2.447(4) | 2.443(5) | 2.473(4) | 2.581(4) | 2.516(4) | 19.884(34) |
| 1 (Ce)[a] | 2.469(4) | 2.445(4) | 2.450(4) | 2.432(4) | 2.426(4) | 2.445(4) | 2.573(4) | 2.478(4) | 19.718(32) |
| 2 (Pr) | 2.452(4) | 2.427(4) | 2.428(4) | 2.407(4) | 2.405(4) | 2.437(3) | 2.556(4) | 2.473(4) | 19.585(31) |
| 3 (Nd) | 2.434(4) | 2.397(4) | 2.415(4) | 2.395(4) | 2.394(4) | 2.418(4) | 2.536(4) | 2.461(4) | 19.450(32) |
| 4 (Pm) | - | - | - | - | - | - | - | - | - |
| 5 (Sm) | 2.396(4) | 2.381(4) | 2.374(4) | 2.377(4) | 2.377(4) | 2.396(4) | 2.518(4) | 2.434(4) | 19.253(32) |
| 6 (Eu) | 2.384(5) | 2.368(5) | 2.356(5) | 2.361(5) | 2.367(5) | 2.386(5) | 2.501(5) | 2.420(5) | 19.143(40) |
| 7 (Gd) | 2.373(5) | 2.357(5) | 2.349(5) | 2.352(4) | 2.343(5) | 2.376(4) | 2.491(5) | 2.403(5) | 19.044(38) |
| 8 (Tb) | 2.356(4) | 2.338(4) | 2.333(4) | 2.336(4) | 2.332(4) | 2.361(4) | 2.462(4) | 2.381(4) | 18.899(32) |
| 9 (Dy) | 2.340(4) | 2.335(4) | 2.322(4) | 2.329(4) | 2.327(4) | 2.355(4) | 2.460(4) | 2.375(4) | 18.843(32) |
| 10 (Ho) | 2.327(5) | 2.318(5) | 2.313(5) | 2.312(5) | 2.311(5) | 2.333(5) | 2.456(5) | 2.353(5) | 18.723(40) |
| 11 (Er) | 2.314(4) | 2.309(5) | 2.307(4) | 2.307(4) | 2.313(4) | 2.330(4) | 2.442(5) | 2.353(4) | 18.675(34) |
| 12 (Tm) | 2.308(4) | 2.300(4) | 2.294(4) | 2.297(4) | 2.304(4) | 2.324(4) | 2.424(4) | 2.338(4) | 18.589(32) |
| 13 (Yb) | 2.277(6) | 2.282(6) | 2.265(6) | 2.300(6) | 2.286(6) | 2.301(6) | 2.437(6) | 2.333(6) | 18.481(48) |
| 14 (Lu) | 2.288(3) | 2.292(3) | 2.282(3) | 2.294(3) | 2.287(3) | 2.320(3) | 2.418(3) | 2.329(3) | 18.510(24) |
| dLa / dLu | 1.085 | 1.075 | 1.086 | 1.067 | 1.068 | 1.066 | 1.067 | 1.080 | 1.074 |
Ref. 9.
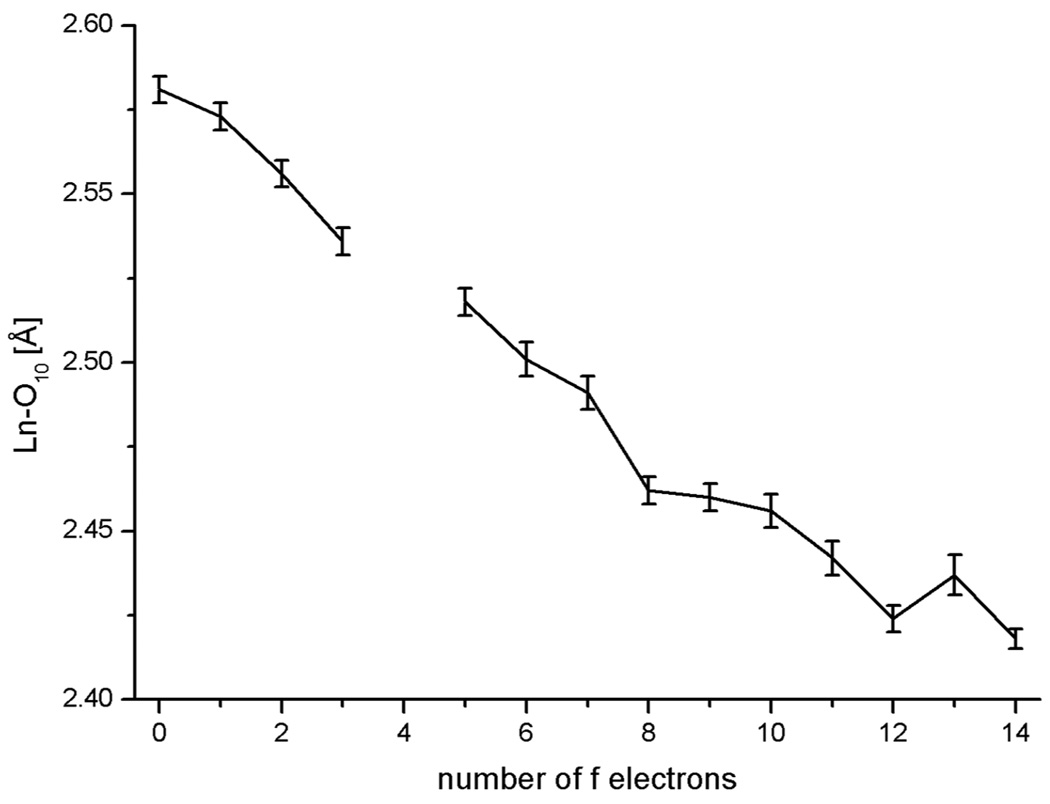
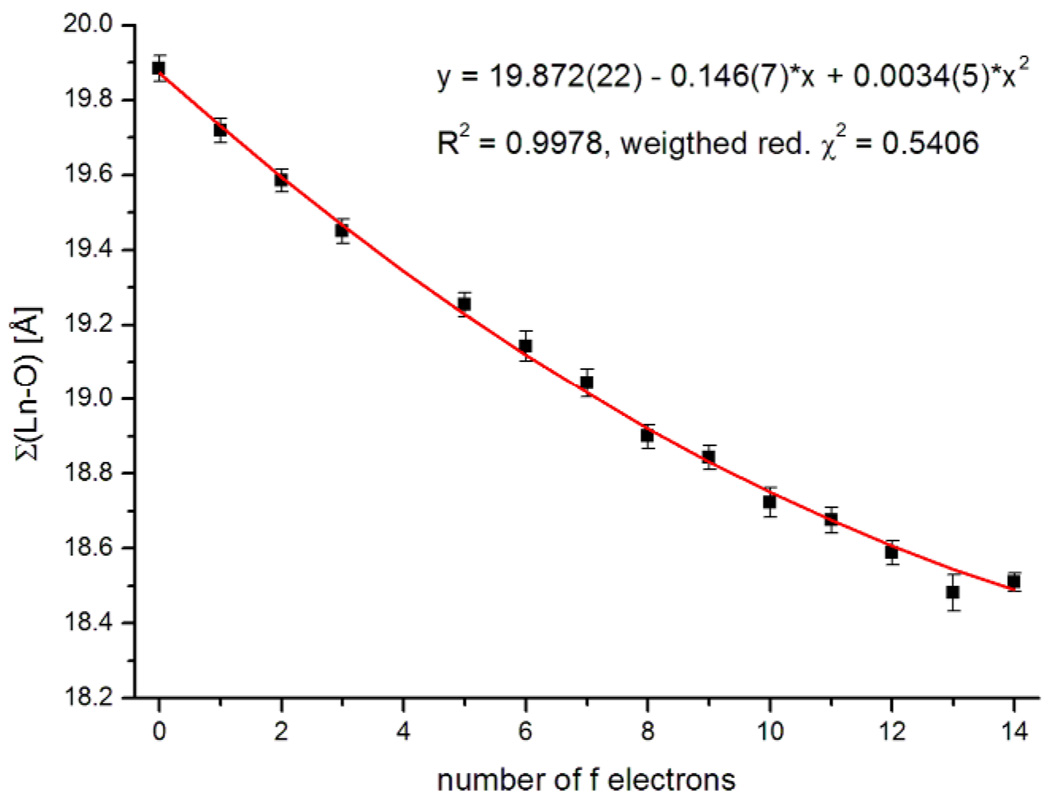
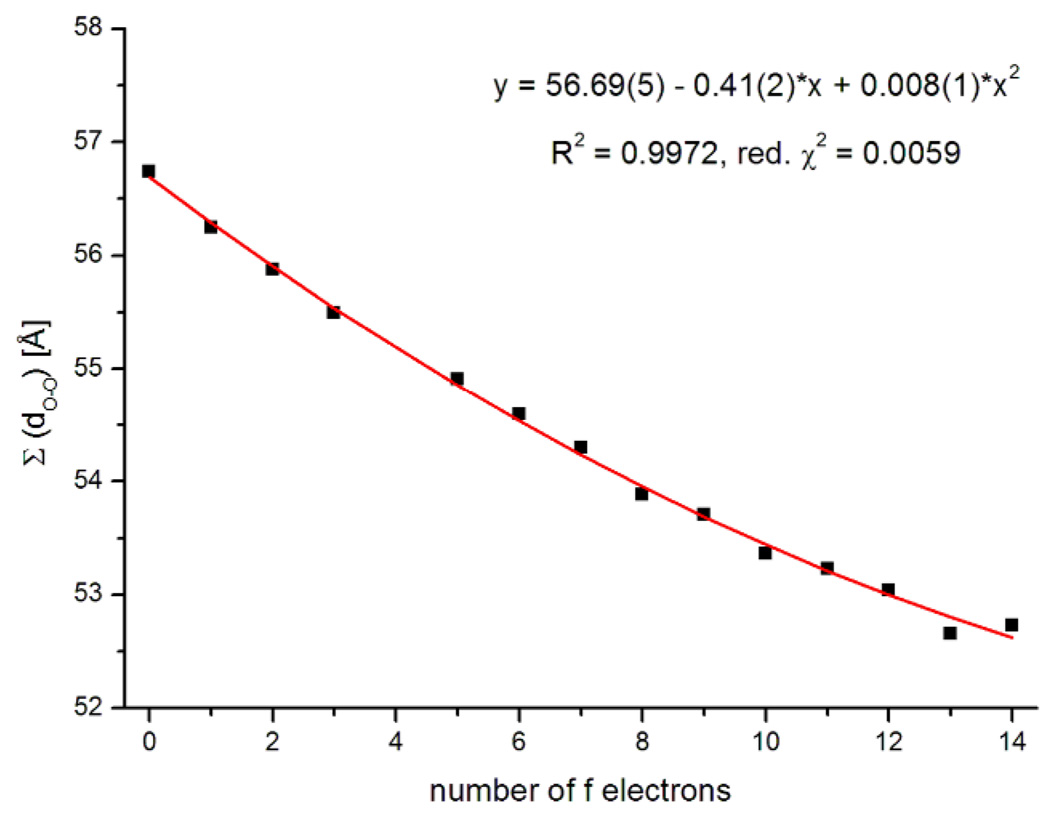
While the general trend of decreasing distances with heavier lanthanide is seen in every case, the individual classes of bond lengths cannot be fit by a second-order polynomial as was proposed.3 Figure 3 shows as an example the dependence of the bond length Ln-O10.13 In effect, the force field of the ligand responds to the change in the average metal ion size to distribute the metal-ligand bond length changes, more in some and less in others. However the sum of all bond lengths Ln-O averages these deviations out and hence shows the expected even contraction.14 The data shown in Figure 4, were well fit by a weighted polynomial regression (with a weighting factor of σ−2, R2 = 0.9978).15
Figure 3.
Decrease in Ln-O10 bond length in [Ln(1)(H2O)] against the number of f electrons of the trivalent lanthanide cation.
Figure 4.
The sum of the Ln-O bond lengths against the number of f electrons. Quadratic fit in red (χ2- weighting factor: σ−2).
That the lanthanide contraction follows a quadratic decay has been experimentally established by others,3 but this dependence has not been derived from a theoretical model. The general reason for the decrease in ionic radii with higher atomic number is well known to be the increase in effective nuclear charge due to incomplete shielding of the (5s, 5p) electrons from the increased nuclear charge by the 4f electrons. This phenomenon can be treated with the theoretical model that was introduced by Slater16 and later modified by others.17 That model utilizes a set of empirical rules for the shielding of the nuclear charge Z from electrons in a particular orbital by inner electron shells, expressed by a screening constant s. The atomic or ionic radius in the Slater model is at the maximum of the radial part of the outermost orbital which has the analytical form:
| (1) |
(with and n: principal quantum number; s: screening constant; n* : effective quantum number.) The maximum of this function is at
| (2) |
In order to get the dependence of the ionic radius rmax with the number of 4f electrons, the expressions s = s0 + kx and Z = Z0 + x (with s0 : screening constant for La3+; k: screening constant for one 4f electron; x: number of 4f electrons; Z0 = 57 : nuclear charge of La) are substituted in (2).
| (3) |
In addition, the value for the ionic radius of La3+ (x = 0) is:
| (4) |
From equations (3) and (4) follows:
| (5) |
Development of the corresponding Taylor series and termination after the third term gives an approximation for r(x):
| (6) |
The sum S(x) over all m Ln-X bond lengths can be written as the sum of all lanthanide ionic radii r(x) and all radii rL(x) of the ligating atoms:
| (7) |
With the assumption that ., the sum in (7) can be rewritten as:
| (8) |
| (9) |
From the equations (9), the screening constant can be determined by the following relationship:
| (10) |
| (11) |
Calculating k with the measured parameters c and b (Figure 4) of the present lanthanide series and a value for (5p electrons17) yields:
| (12) |
The good agreement with the commonly accepted value for the screening constant of k = 0.69 for f electrons shows the validity of the presented model.
2.3.3 O-O Bond Lengths
Most of the investigations reported so far in the literature are limited to the analysis of the Ln-X bond lengths. However, for multidentate ligands there is a considerable constraint on the coordination geometry that must be addressed. In order to assess the behavior of the ligand in this respect, the change in the distances between the eight coordinating donor atoms was investigated (Table 5).
Table 5.
Distances O-O between coordinating O donors in lanthanide complexes with TREN-1,2-HOIQO (1).
| f electrons (Ln3+) |
dO7-O9 [Å] |
dO3-O5 [Å] |
dO7-O5 [Å] |
dO3-O9 [Å] |
dO5-O6 [Å] |
dO9-O10 [Å] |
dO2-O3 [Å] |
dO7-O8 [Å] |
dO7-O10 [Å] |
dO3-O6 [Å] |
dO7-O6 [Å] |
dO10-O3 [Å] |
dO2-O5 [Å] |
dO2-O9 [Å] |
dO9-O8 [Å] |
dO8-O5 [Å] |
dO6-O10 [Å] |
dO2-O8 [Å] |
ΣdO-O [Å] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 (La) | 3.120 | 3.942 | 3.408 | 3.960 | 2.568 | 3.213 | 2.557 | 3.078 | 3.124 | 3.284 | 3.143 | 3.092 | 3.158 | 3.602 | 2.576 | 3.090 | 2.905 | 2.915 | 56.735 |
| 1 (Ce)[a] | 3.109 | 3.902 | 3.379 | 3.912 | 2.555 | 3.159 | 2.562 | 3.043 | 3.104 | 3.224 | 3.122 | 3.064 | 3.128 | 3.555 | 2.574 | 3.065 | 2.907 | 2.881 | 56.245 |
| 2 (Pr) | 3.112 | 3.908 | 3.353 | 3.840 | 2.557 | 3.119 | 2.551 | 3.039 | 3.086 | 3.217 | 3.100 | 3.023 | 3.106 | 3.509 | 2.576 | 3.031 | 2.884 | 2.862 | 55.873 |
| 3 (Nd) | 3.112 | 3.897 | 3.335 | 3.793 | 2.551 | 3.086 | 2.549 | 3.006 | 3.072 | 3.190 | 3.077 | 2.992 | 3.086 | 3.477 | 2.576 | 2.997 | 2.856 | 2.843 | 55.495 |
| 4 (Pm) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 5 (Sm) | 3.085 | 3.865 | 3.319 | 3.703 | 2.562 | 3.023 | 2.567 | 2.986 | 3.040 | 3.135 | 3.054 | 2.931 | 3.040 | 3.428 | 2.573 | 2.959 | 2.839 | 2.795 | 54.904 |
| 6 (Eu) | 3.083 | 3.866 | 3.294 | 3.646 | 2.560 | 2.976 | 2.551 | 2.967 | 3.031 | 3.137 | 3.038 | 2.910 | 3.023 | 3.392 | 2.570 | 2.940 | 2.838 | 2.775 | 54.597 |
| 7 (Gd) | 3.085 | 3.852 | 3.258 | 3.610 | 2.562 | 2.973 | 2.546 | 2.953 | 3.015 | 3.120 | 3.023 | 2.888 | 3.012 | 3.363 | 2.565 | 2.914 | 2.804 | 2.758 | 54.301 |
| 8 (Tb) | 3.067 | 3.823 | 3.253 | 3.578 | 2.556 | 2.936 | 2.534 | 2.928 | 2.976 | 3.074 | 3.004 | 2.850 | 2.995 | 3.326 | 2.567 | 2.890 | 2.774 | 2.749 | 53.880 |
| 9 (Dy) | 3.074 | 3.817 | 3.237 | 3.535 | 2.558 | 2.901 | 2.544 | 2.918 | 2.969 | 3.063 | 3.001 | 2.842 | 2.984 | 3.302 | 2.570 | 2.881 | 2.788 | 2.724 | 53.708 |
| 10 (Ho) | 3.061 | 3.795 | 3.208 | 3.515 | 2.552 | 2.891 | 2.539 | 2.884 | 2.959 | 3.033 | 2.977 | 2.826 | 2.955 | 3.284 | 2.558 | 2.855 | 2.767 | 2.702 | 53.361 |
| 11 (Er) | 3.060 | 3.792 | 3.211 | 3.489 | 2.544 | 2.876 | 2.549 | 2.884 | 2.948 | 3.018 | 2.976 | 2.802 | 2.953 | 3.272 | 2.564 | 2.853 | 2.753 | 2.684 | 53.228 |
| 12 (Tm) | 3.059 | 3.775 | 3.217 | 3.470 | 2.562 | 2.854 | 2.538 | 2.881 | 2.924 | 2.998 | 2.966 | 2.792 | 2.933 | 3.248 | 2.572 | 2.835 | 2.736 | 2.682 | 53.042 |
| 13 (Yb) | 3.042 | 3.738 | 3.188 | 3.412 | 2.542 | 2.824 | 2.521 | 2.856 | 2.920 | 2.958 | 2.954 | 2.788 | 2.927 | 3.221 | 2.544 | 2.809 | 2.741 | 2.669 | 52.654 |
| 14 (Lu) | 3.054 | 3.752 | 3.194 | 3.417 | 2.552 | 2.831 | 2.535 | 2.860 | 2.913 | 2.974 | 2.956 | 2.761 | 2.928 | 3.216 | 2.579 | 2.812 | 2.722 | 2.674 | 52.730 |
| dLa / dLu | 1.022 | 1.051 | 1.067 | 1.159 | 1.006 | 1.135 | 1.009 | 1.076 | 1.072 | 1.104 | 1.063 | 1.120 | 1.079 | 1.120 | 0.999 | 1.090 | 1.067 | 1.090 | 1.076 |
Ref. 9.
Some features seen in the data: 1) Unlike the Ln-O bond lengths, the decrease in O-O distances is not uniformly distributed. While the three rigid hydroxamate moieties (O2–O3, O5–O6, and O8–O9) remain nearly unchanged, the rest of the distances vary greatly (between 1–16%). The average, however, as seen in the sum of all O-O distances, decreases by 7.6%, and agrees well with the values of 7–8% for the shortening of the unconstrained Ln-O bond lengths in [Ln(1)(H2O)] (see 2.3.2). 2) Similar to the trends seen in Ln-O and, presumably for the same reason, the decrease cannot be fit uniformly in other classes of O-O distances.13 Again however, the quadratic nature of the lanthanide contraction can be seen in the averaged O-O distances (Figure 5).
Figure 5.
The sum of the O-O distances against the number of f electrons. Quadratic fit in red.
2.3.4 Generality
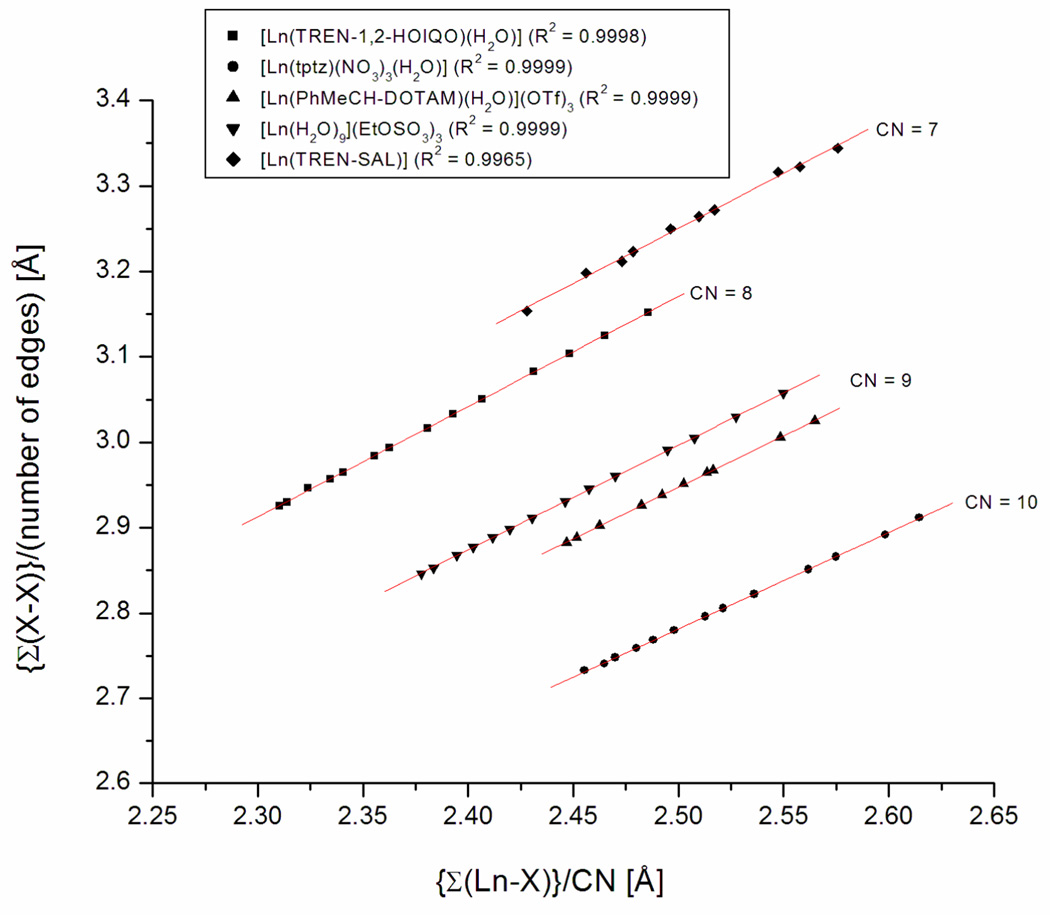
The observation that the sum of either the Ln-O bond lengths or the O-O distances shows an almost perfect quadratic decrease in complexes with a multidentate ligand like TREN-1,2-HOIQO prompted us to compare these results with previously published sets of lanthanide complexes to see whether this phenomenon has general applicability. The following published series of lanthanide complexes were analyzed: (1) [Ln(H2O)9](EtOSO3)3 (highest denticity (HD) = 1, coordination number (CN) = 9);2e (2) [Ln(TREN-SAL)] (HD = 7, CN = 7);18 (3) the present complexes [Ln(TREN-1,2-HOIQO)(H2O)] (HD = 7, CN = 8); (4) [Ln(PhMeCH-DOTAM)(H2O)](OTf)3 (HD = 8, CN = 9);19 (5) [Ln(tptz)(NO3)2(H2O)] (HD = 3, CN = 10).20 These were chosen for several reasons. First, each series has at least ten members of structurally characterized members. Second, series no. 2–5 feature multidentate ligands with medium to high denticities (HD = {3,7,7,8}), different coordination numbers (CN = {7,8,9,10}), and include the most important coordinating atoms for lanthanide coordination (a variety of N and O donors, neutral and anionic). Third, series no. 1 (with only monodentate aqua ligands) functions as a prototype for an unconstrained coordination environment. In addition, it represents the only other complete series of structurally characterized lanthanide complexes.
These literature examples were subjected to the same analysis as just described. The findings are essentially the same as described in these sections, with small additional features: (1) The series [Ln(H2O)9](EtOSO3)3 was used previously to establish the quadratic decrease in Ln-X (X = O).3 In contrast, the complexes with multidentate ligands do not display this dependence in different classes of bond lengths Ln-X (X = N, O) or non-bonded distances X-X (X = N, O). (2) However the average Ln-X (X = N, O) and X-X (X = N, O) shows the expected quadratic behavior in all cases (Table 6).13
Table 6.
Absolute and normalized parameters of the quadratic fits (y = a + bx +cx2) for the lanthanide (Ln-X) and the coordination sphere (X-X) contraction of the series of lanthanide complexes (X = N, O).
| Entry | Series | a (σ) | b (σ) | c (σ) | R2 | norm. a* (a* = a / a) |
norm. b* (b* = b / a) |
norm. c* (c* = c / a) |
|---|---|---|---|---|---|---|---|---|
| 1a | [Ln(H2O)9](EtOSO3)3 (Ln-O) | 22.912(11) | −0.1562(38) | 0.00347(28) | 0.9979 | 1 | −0.0068 | 0.00015 |
| 1b | [Ln(H2O)9](EtOSO3)3 (O-O) | 64.082(49) | −0.434(16) | 0.0091(11) | 0.9978 | 1 | −0.0068 | 0.00014 |
| 2a | [Ln(TREN-SAL)] (Ln-X) | 17.620(24) | −0.107(8) | 0.00165(56) | 0.9955 | 1 | −0.0061 | 0.00009 |
| 2b | [Ln(TREN-SAL)] (X-X) | 50.416(70) | −0.261(23) | 0.0016(17) | 0.9953 | 1 | −0.0052 | 0.00003 |
| 3a | [Ln(TREN-1,2-HOIQO)(H2O)] (Ln-O) | 19.872(22) | −0.146(7) | 0.0034(5) | 0.9978 | 1 | −0.0073 | 0.00017 |
| 3b | [Ln(TREN-1,2-HOIQO)(H2O)] (O-O) | 56.69(5) | −0.411(17) | 0.0086(12) | 0.9972 | 1 | −0.0072 | 0.00015 |
| 4a | [Ln(PhMeCH-DOTAM)(H2O)](OTf)3 (Ln-X) | 23.349(26) | −0.144(7) | 0.00347(44) | 0.9978 | 1 | −0.0062 | 0.00015 |
| 4b | [Ln(PhMeCH-DOTAM)(H2O)](OTf)3 (X-X) | 61.17(10) | −0.376(29) | 0.0088(17) | 0.9951 | 1 | −0.0061 | 0.00015 |
| 5a | [Ln(tptz)(NO3)3(H2O)] (Ln-X) | 26.140(11) | −0.1801(43) | 0.00452(35) | 0.9993 | 1 | −0.0069 | 0.00017 |
| 5b | [Ln(tptz)(NO3)3(H2O)] (X-X) | 61.106(34) | −0.428(12) | 0.00109(9) | 0.9988 | 1 | −0.007 | 0.00018 |
To be able to compare the different series with each other, the fit functions (y = a + bx + cx2) were normalized by scaling the parameters by 1/a (Table 6, three columns on right). The normalized fits show common behavior: In four cases (entries 1, 3–5), the two normalized fits for Σ(Ln-X) (entries a) and the corresponding Σ(X-X) (entries b) are identical within error. Furthermore, the values for a, b, and c are very similar, but show some specificity for a particular ligand. Only for the complexes [Ln(TREN-SAL)] (entries 2a and b), do the values differ more, but are still nearly within error limits.
In addition, the relationship between average bond length ({Σ(Ln-X)}/CN) and average distance X-X ({Σ(X-X)}/number of edges of the coordination polyhedron) was analyzed as a different representation of the phenomenon summarized in Table 6 (Figure 6).13
Figure 6.
The average distance X-X (X = N,O; bound to Ln) against the average Ln-X (X = N,O) bond length for five series of isostructural lanthanide complexes. Linear fits in red.
Figure 6 clearly shows the almost perfect linearity in every case, grouped according to their coordination number. Taken together, these results show that the shortening in Ln-X bond lengths is accompanied by a shrinking of the coordination sphere around the lanthanide that follows the same normalized quadratic decrease. However, this does not describe fully the situation for multidentate ligands because of the constraints in intraligand distances and angles of such ligands. Some donor-donor distances are constrained (e.g. the three bidentate hydroxamate moieties in TREN-1,2-HOIQO) and do not change at all or only very slightly with decreasing Ln-X bond length. This results in greater changes for softer ligand deformations. The wide variation of the extent to which, for example, the individual O-O distances in [Ln(TREN-1,2-HOIQO)(H2O)] (Table 5, last row) decrease over the lanthanide series (1–16%) illustrates this phenomenon.
3 Conclusion
In the course of this investigation we have shown: (1) [Ln(TREN-1,2-HOIQO)(H2O)] represents the first complete set of isostructural complexes from La-Lu (without Pm) with a multidentate ligand. (2) A quadratic decrease is seen in the sum of all distances Ln-X (X = N, O), even in complexes with multidentate ligands. This decrease is modeled successfully by Slater’s model for calculating ionic radii. This result provides a rational analysis and prediction of the geometric features of multidentate ligands for the chelation of rare-earth metals.
4 Experimental Section
4.1 General
The lanthanide chlorides were purchased from commercial suppliers and used as received. The methanol used for the preparation of the metal complexes was HPLC-grade. Pyridine was distilled before use. DMF for the crystallizations was spectrophotometric grade. The elemental analyses were performed in duplicates by the microanalytical facility of the University of California, Berkeley. The syntheses and the analytical data for the ligand TREN-1,2-HOIQO, as well as for the cerium, europium, gadolinium, and lutetium complexes were reported previously.9
4.2 Synthesis of the Lanthanide Complexes
General procedure for complex formation: Under argon, a solution of TREN-1,2-HOIQO (1.0 equiv.) in MeOH was treated with solid LnCl3 • 6 H2O (1.0 equiv.) or LnCl3 (anhydr.) (1.0 equiv.), followed by pyridine and heated to reflux overnight. The resulting fine suspension was cooled to ambient temperature, the precipitate collected on a filter, and washed with MeOH. After drying in vacuo at 50 °C (bath temp.) for 6 h, the lanthanide complexes [Ln(TREN-1,2-HOIQO)(H2O)] • x MeOH • y H2O were obtained in analytically pure form as powders that were soluble in DMF, DMSO, and, only sparingly, in MeOH.
La: Starting with LaCl3 • 6 H2O (9.1 mg, 37 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (30 mg, 37 µmol, 1.0 equiv.), pyridine (62 mg) in 6 mL MeOH gave 19 mg (55%) complex. M.p. >300 °C. Anal. Calcd. for C36H32LaN7O10 • MeOH • 2 H2O (Mr = 929.66): C, 47.80; H, 4.34; N, 10.55. Found: C, 47.62; H, 3.92; N, 10.49.
Pr: Starting with PrCl3 • 6 H2O (14 mg, 40 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (33 mg, 40 µmol, 1.0 equiv.), pyridine (62 mg) in 6 mL MeOH gave 20 mg (55%) complex. M.p. >300 °C. Anal. Calcd. for C36H32N7O10Pr • MeOH (Mr = 895.64): C, 49.62; H, 4.05; N, 10.95. Found: C, 49.29; H, 3.78; N, 10.80.
Nd: Starting with NdCl3 • 6 H2O (13.7 mg, 38.2 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (31.0 mg, 38.2 µmol, 1.0 equiv.), pyridine (62 mg) in 6 mL MeOH gave 15 mg (43%) complex. M.p. >300 °C. Anal. Calcd. for C36H32N7NdO10 • MeOH • H2O (Mr = 916.98): C, 48.46; H, 4.18; N, 10.69. Found: C, 48.51; H, 4.03; N, 10.63.
Sm: Starting with SmCl3 • 6 H2O (41 mg, 113 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (92 mg, 113 µmol, 1.0 equiv.), pyridine (78 mg) in 20 mL MeOH gave 61 mg (60%) complex. M.p. >300 °C. Anal. Calcd. for C36H32N7O10Sm • MeOH (Mr = 905.08): C, 49.10; H, 4.01; N, 10.83. Found: C, 49.29; H, 3.99; N, 10.63.
Tb: Starting with TbCl3 • 6 H2O (14.7 mg, 39.4 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (32.0 mg, 39.4 µmol, 1.0 equiv.), pyridine (62 mg) in 6 mL MeOH gave 16 mg (44%) complex. M.p. >300 °C. Anal. Calcd. for C36H32N7O10Tb • MeOH (Mr = 913.65): C, 48.64; H, 3.97; N, 10.73. Found: C, 48.39; H, 4.06; N, 10.48.
Dy: Starting with DyCl3 • 6 H2O (16.7 mg, 44.3 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (36.0 mg, 44.3 µmol, 1.0 equiv.), pyridine (62 mg) in 6 mL MeOH gave 23 mg (56%) complex. M.p. >300 °C. Anal. Calcd. for C36H32DyN7O10 • 2 H2O (Mr =921.21): C, 46.94; H,3.94; N, 10.64. Found: C, 46.74; H, 3.75; N, 10.45.
Ho: Starting with HoCl3 • 6 H2O (14 mg, 38 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (31 mg, 38 µmol, 1.0 equiv.), pyridine (62 mg) in 6 mL MeOH gave 24 mg (69%) complex. M.p. >300 °C. Anal. Calcd. for C36H32HoN7O10 • MeOH (Mr =919.65): C, 48.32; H, 3.95; N, 10.66. Found: C, 47.98; H, 3.99; N, 10.38.
Er: Starting with ErCl3 • 6 H2O (10.4 mg, 38.2 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (31.0 mg, 38.2 µmol, 1.0 equiv.), pyridine (62 mg) in 6 mL MeOH gave 22 mg (62%) complex. M.p. >300 °C. Anal. Calcd. for C36H32ErN7O10 • MeOH (Mr =921.98): C, 48.20; H, 3.94; N, 10.63. Found: C, 47.81; H, 4.06; N, 10.46.
Tm: Starting with anhydr. TmCl3 (10.5 mg, 38.2 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (31.0 mg, 38.2 µmol, 1.0 equiv.), pyridine (62 mg) in 6 mL MeOH gave 20 mg (57%) complex. M.p. >300 °C. Anal. Calcd. for C36H32N7O10Tm • MeOH (Mr = 923.66): C, 48.11; H, 3.93; N, 10.62. Found: C, 47.82; H, 4.02; N, 10.41.
Yb: Starting with YbCl3 • 6 H2O (9.5 mg, 25 µmol, 1.0 equiv.), TREN-1,2-HOIQO • HCl • 2 H2O • MeOH (20.0 mg, 25 µmol, 1.0 equiv.), pyridine (31 mg) in 5 mL MeOH gave 13 mg (54%) complex. M.p. >300 °C. Anal. Calcd. for C36H32N7O10Yb • 2 MeOH • H2O (Mr = 977.82): C, 46.68; H, 4.33; N, 10.03. Found: C, 46.65; H, 3.89; N, 9.99.
4.3 Single-Crystal X-Ray Analysis
Crystals were grown at room temperature by vapor diffusion of water into DMF solutions of the lanthanide complexes. Measurements for La-Yb (except Tm) were made on a Siemens SMART CCD21 area detector with graphite monochromated Mo-Kα radiation. The data for the structures of the Tm and Lu complexes were collected at the Advanced Light Source (Lawrence Berkeley National Laboratory, Berkeley, USA) using monochromated synchrotron radiation (λ = 0.7749 Å). Data were integrated by the program SAINT22 and corrected for Lorentz and polarization effects. Data were analyzed for agreement and possible absorption using XPREP.23 An empirical absorption correction based on the comparison of redundant and equivalent reflections was applied using SADABS.24 Equivalent reflections were merged. No decay correction was applied. The structure was solved within the WinGX25 package by direct methods (SIR9226) and expanded using Fourier techniques (SHELXL-9727). Hydrogen atoms (except for the two water molecules) were included but not refined. The hydrogen atoms of the water molecules could not unambiguously be assigned. Hydrogen atoms were positioned geometrically, with C–H = 0.93 Å for Carom-H groups, C–H = 0.97 Å for CH2 groups, and N–H = 0.89 Å and constrained to ride on their parent atoms. Uiso(H) values were set at 1.2 times Ueq(C) for all H atoms.
Supplementary Material
Figure 2.
Shape measure SM with δi = observed dihedral angle along the m edges of a coordination polyhedron (angle between normals of adjacent faces) and θi = corresponding dihedral angle for a reference polyhedron.
Acknowledgment
M.S. thanks the German Research Foundation (DFG) for a research fellowship. This work was supported in part by NIH grant R01-HL69832 and by the Director, Office of Science, Office of Advanced Scientific Computing Research, Office of Basic Energy Sciences (U.S. Department of Energy) under contract DE-AC02-05CH11231. Data for the crystal structures of the Tm and Lu complexes were collected at Beamline 11.3.1 of the Advanced Light Source at Lawrence Berkeley National Laboratory operated under DOE contract DE-AC03-76SF00098.
Footnotes
Supporting Information Available. CIF files for the crystal structures of all lanthanide complexes (except for Ce). Additional tables and diagrams for bond lengths and distances for the series [Ln(TREN-1,2-HOIQO)(H2O)], [Ln(TREN-SAL)], [Ln(tptz)(NO3)3(H2O)], [Ln(PhMeCH-DOTAM)(H2O)](OTf)3, and [Ln(H2O)9](EtOSO3)3. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Goldschmidt VM, Barth T, Lunde G. Skrifter Norske Videnskaps-Akademi i Oslo, I. Mat.-Naturv. Klasse. 1925;7:59. [Google Scholar]
- 2.(a) Shannon RD. Acta Crystallogr. A. 1976;32:751. [Google Scholar]; (b) Shannon RD, Prewitt CT. Acta Crystallogr. B. 1969;25:925. [Google Scholar]; (c) Siekierski S. Pol. J. Chem. 1992;66:215. [Google Scholar]; (d) Siekierski S. Inorg. Chim. Acta. 1985;109:199. [Google Scholar]; (e) Gerkin RE, Reppart WJ. Acta Crystallogr. C. 1984;40:781–786. [Google Scholar]; (f) Chatterjee A, Maslen EN, Watson KJ. Acta Crystallogr. B. 1988;44:381–386. [Google Scholar]
- 3.Quadrelli EA. Inorg. Chem. 2002;41:167–169. doi: 10.1021/ic015580v. [DOI] [PubMed] [Google Scholar]
- 4.(a) Deng B, Ellis DE, Ibers JA. Inorg. Chem. 2002;41:5716–5720. doi: 10.1021/ic020324j. [DOI] [PubMed] [Google Scholar]; (b) Yao J, Deng B, Sherry LJ, McFarland AD, Ellis DE, Van Duyne RP, Ibers JA. Inorg. Chem. 2004;43:7735–7740. doi: 10.1021/ic040071p. [DOI] [PubMed] [Google Scholar]
- 5.(a) Baisch U, Belli Dell’Amico D, Calderazzo F, Conti R, Labella L, Marchetti F, Quadrelli EA. Inorg. Chim. Acta. 2004;357:1538–1548. [Google Scholar]; (b) Baisch U, Belli Dell’Amico D, Calderazzo F, Labella L, Marchetti F, Merigo A. Eur. J. Inorg. Chem. 2004:1219–1224. doi: 10.1021/ic049595f. [DOI] [PubMed] [Google Scholar]
- 6.(a) Bünzli J-CG. Acc. Chem. Res. 2006;39:53–61. doi: 10.1021/ar0400894. [DOI] [PubMed] [Google Scholar]; (b) Bünzli J-CG, Piguet C. Chem. Soc. Rev. 2005;34:1048–1077. doi: 10.1039/b406082m. [DOI] [PubMed] [Google Scholar]; (c) Parker D. Chem. Soc. Rev. 2004;33:156–165. doi: 10.1039/b311001j. [DOI] [PubMed] [Google Scholar]
- 7.(a) Caravan P, Ellison JJ, McMurry TJ, Lauffer RB. Chem. Rev. 1999;99:2293–2352. doi: 10.1021/cr980440x. [DOI] [PubMed] [Google Scholar]; (b) Aime S, Botta M, Fasano M, Geninatti Crich S, Terreno E. Coord. Chem. Rev. 1999;185–186:321–333. [Google Scholar]; (c) Tóth E, Helm L, Merbach AE, editors. The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging. Chichester: Wiley; 2001. [Google Scholar]; (d) Raymond KN, Pierre VC. Bioconjugate Chem. 2005;16:3–8. doi: 10.1021/bc049817y. [DOI] [PubMed] [Google Scholar]
- 8.Welch MJ, Redvanly CS, editors. Handbook of Radiopharmaceuticals. Radiochemistry and Applications. Chichester: Wiley; 2003. [Google Scholar]
- 9.Seitz M, Pluth MD, Raymond KN. Inorg. Chem. 2007;46:351–353. doi: 10.1021/ic0614869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Farrugia LJ ORTEP-3 for Windows. J. Appl. Crystallogr. 1997;30:565. [Google Scholar]
- 11.Alvarez S, Alemany P, Casanova D, Cirera J, Llunell M, Avnir D. Coord. Chem. Rev. 2005;249:1693–1708. and refs. cited therein. [Google Scholar]
- 12.(a) Xu J, Radkov E, Ziegler M, Raymond KN. Inorg. Chem. 2000;39:4156–4164. doi: 10.1021/ic000063i. [DOI] [PubMed] [Google Scholar]; (b) Muetterties EL, Guggenberger LJ. J. Am. Chem. Soc. 1974;96:1748–1756. [Google Scholar]; c) Porai-Koshits MA, Aslanov LA. Zh. Strukt. Khim. 1972;13:266. [Google Scholar]
- 13.For more details see the Supporting Information.
- 14.An equivalent alternative description would be the average bond length.
- 15.σ = standard deviation.
- 16.Slater JC. Phys. Rev. 1930;36:57–64. [Google Scholar]
- 17.(a) Clementi E, Raimondi DL. J. Chem. Phys. 1963;38:2686–2689. [Google Scholar]; (b) Clementi E, Raimondi DL, Reinhardt WP. J. Chem. Phys. 1967;47:1300–1307. [Google Scholar]
- 18.(a) Kanesato M, Yokoyama Y. Chem. Lett. 1999:137–138. [Google Scholar]; (b) Kanesato M, Yokoyama Y. Anal. Sci. 2000;16:335–336. [Google Scholar]; (c) Bernhardt PV, Flanagan BM, Riley MJ. Aust. J. Chem. 2000;53:229–231. [Google Scholar]; (d) Bernhardt PV, Flanagan BM, Riley MJ. Aust. J. Chem. 2001;54:229–232. [Google Scholar]
- 19.(a) Batsanov AS, Beeby A, Bruce JI, Howard JAK, Kenwright AM, Parker D. Chem. Commun. 1999:1011–1012. [Google Scholar]; (b) Aime S, Barge A, Batsanov AS, Botta M, Delli Castelli D, Fedeli F, Mortillaro A, Parker D, Puschmann H. Chem. Commun. 2002:1120–1121. doi: 10.1039/b202862j. [DOI] [PubMed] [Google Scholar]; (c) Parker D, Puschmann H, Batsanov AS, Senanayake K. Inorg. Chem. 2003;42:8646–8651. doi: 10.1021/ic030203z. [DOI] [PubMed] [Google Scholar]
- 20.Cotton SA, Franckevicius V, Mahon MF, Ooi LL, Raithby PR, Teat SJ. Polyhedron. 2006;25:1057–1068. [Google Scholar]
- 21.SMART (V5.059) Area-Detector Software Package. Madison, WI: Bruker Analytical X-ray Systems, Inc.; 1995–99. [Google Scholar]
- 22.SAINT (V7.07B) SAX Area-Detector Integration Program. Madison, WI: Siemens Industrial Automation, Inc.; 2005. [Google Scholar]
- 23.XPREP (V6.12) Part of the SHELXTL Crystal Structure Determination Package. Madison, WI: Bruker AXS Inc.; 1995. [Google Scholar]
- 24.SADABS (V2.10) Siemens Area Detector Absorption Correction Program. George Sheldrick; 2005. [Google Scholar]
- 25.Farrugia LJ WinGX 1.70.01. J. Appl. Crystallogr. 1999;32:837–838. [Google Scholar]
- 26.Altomare A, Cascarano G, Giacovazzo C, Guagliardi A SIR92. J. Appl. Crystallogr. 1993;26:343–350. [Google Scholar]
- 27.Sheldrick GM. SHELX97 - Programs for Crystal Structure Analysis (Release 97-2) Germany: Institut für Anorganische Chemie der Universität, Tammanstrasse 4, D-3400 Göttingen; 1998. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.