An intuitive graphical visualization technique for the interrogation of transcriptome data

Abstract

The complexity of gene expression data generated from microarrays and high-throughput sequencing make their analysis challenging. One goal of these analyses is to define sets of co-regulated genes and identify patterns of gene expression. To date, however, there is a lack of easily implemented methods that allow an investigator to visualize and interact with the data in an intuitive and flexible manner. Here, we show that combining a nonlinear dimensionality reduction method, t-statistic Stochastic Neighbor Embedding (t-SNE), with a novel visualization technique provides a graphical mapping that allows the intuitive investigation of transcriptome data. This approach performs better than commonly used methods, offering insight into underlying patterns of gene expression at both global and local scales and identifying clusters of similarly expressed genes. A freely available MATLAB-implemented graphical user interface to perform t-SNE and nearest neighbour plots on genomic data sets is available at www.nimr.mrc.ac.uk/research/james-briscoe/visgenex.

INTRODUCTION

The visualization and analysis of gene expression data plays a central role in biological knowledge discovery (1). A variety of data driven methods are used to identify and classify patterns of gene expression behaviour in transcriptome data. Among the most popular are unsupervised clustering algorithms, including hierarchical clustering (2), k-means clustering (3) and self-organizing maps (SOMs) (sums) (4). Conventionally displayed as red–green plots, these methods give a 1D re-ordering of the genes, in which clusters of co-expressed genes can be seen and used to infer gene function. But these 1D arrangements can be limiting and these techniques suffer from two disadvantages. First, they produce sharp delineations between clusters of co-expressed genes. The validity and the biological logic of the partitioning are not always obvious and it is usually difficult to explore and refine the clustering process. Second, these techniques do not necessarily reveal underlying global patterns in the data, or relationships between the clusters found.

To complement clustering, dimension reduction techniques can be used. In these approaches, the expression data is treated as a collection of data points in high-dimensional space, such that the location of each gene (data point) is defined by its expression level in each of the conditions assayed in the experiment: we will refer to this space as ‘H-space’, for high-dimensional data space and points in it as ‘H-points'. Dimensionality reduction techniques map the H-points onto points in a two or 3D visualization space (V-points in V-space) that, displayed graphically as a scatter plot, provides a humanly interpretable visualization of the data set. A commonly used method for this purpose is principal component analysis (PCA) (5). PCA is a linear projection of the data onto axes oriented so that the greatest variation in the distribution of the H-points is preserved in the V-points. The projection of the first and the second principal components of the data gives a scatter plot that is ‘optimal’ in the sense that the sum of squared distances from the H-points to the V-points is minimized (5). For data sets that are intrinsically 2D, PCA gives a true picture of the data that cannot be improved. But for more complex data sets, such as most gene expression data, PCA typically gives a poor visualization (6).

First, although PCA minimizes global reconstruction error, it may not preserve local proximities of points. In visualizing gene expression data, we are typically more interested in resolving nearby clusters than in preserving the correct distance relationships between genes with very different patterns of expression. But the optimization criterion of PCA results in the opposite priority: the relationship of distant points is depicted as accurately as possible, while small inter-point distances can be distorted. Second, there may be no single linear projection that gives a good view of the data: in such a case, all linear projection methods will fail. PCA provides projections onto planes defined by pairs of principal component vectors: but there are many possible planes onto which to project, and the planes defined by pairs of principal component vectors may not give the best views. Sanguinetti (6) describes an ingenious method for choosing a linear projection that optimally separates clusters. Although this technique works for some types of clustered data, it requires the assumption that the data is arranged in clusters and that the number of clusters is known. This is typically not the case for transcriptome data.

Because of these limitations, nonlinear dimensionality reduction methods have been developed that attempt to preserve local structure in the data (7). Surprisingly, however, their application to biological data has received limited attention. Nonlinear mappings attempt to position data points in V-space in such a way that near-neighbours in H-space are also near-neighbours in V-space. In other words, data points that are close together in H-space are also close, as much as is possible, in the scatter plot, whereas data points that are far apart in H-space may have their relative distances distorted in V-space. We term such visualizations ‘locally valid’. The drawback with these techniques, however, is that the distortions introduced to the projection by nonlinear dimension reductions may not be straightforward to interpret visually: the neighbour relationships in H-space are not necessarily representative of those in V-space. Moreover, unlike PCA, these nonlinear projections do not produce components that are definable in terms of the contributing genes from the data set. It is perhaps because of these difficulties that nonlinear visualization methods have not been widely used for transcriptome data, despite their potential power.

Here, we test the recently developed nonlinear dimensionality reduction algorithm, t-statistic Stochastic Neighbor Embedding (t-SNE) (8), on a variety of real-world transcriptome data sets. The t-SNE algorithm, a variation of Stochastic Neighbor Embedding (9), has been shown to produce visualizations that reveal both local and long-range relationships within a data set in a single mapping. An intuitive description of the t-SNE algorithm and a demonstration of its robustness to noise are given in the Supplementary Data, and a formal description of the algorithm may be found in (7).

We demonstrate that t-SNE is able to efficiently and elegantly map typical, complex gene expression data sets onto a plane in a way that makes the relationships between genes easy to visualize and understand. We develop a visualization technique, which we call ‘nearest neighbour plots' that helps reveal both local and global relationships in the data and significantly enhances the effectiveness of nonlinear dimensionality reduction for gene expression data. Together these methods make the identification of co-expressed genes easy and intuitive. Comparison with conventional clustering techniques demonstrates that t-SNE functions as well or better than the current methods. We show how t-SNE can be used in conjunction with established methods to understand the logic of cluster partitions and to identify co-regulated genes. We have developed a freely available MATLAB-implemented graphical user interface to perform t-SNE and nearest neighbour plots on genomic data sets.

MATERIALS AND METHODS

Transcriptome data sets

The following data sets from published studies were used to investigate and illustrate the performance of t-SNE mappings (for simplicity, the terms probe set and gene are used interchangeably to refer to the set of probes that represent each transcript on an Affymetrix array).

Data set 1: Human embryo

NCBI GEO accession number GSE18887

This study contains transcriptome data from six consecutive stages of human embryonic development covering organogenesis (10) (Carnegie stages 9–14, S9–S14). Embryonic stages S10–S13 were sampled in triplicate, resulting in 12 independent transcription profiles. Stages S9 and S14 were pooled and from this three technical replicates obtained, resulting in an additional six transcription profiles. In total, 18 profiles were analysed using Affymetrix HG-U133A Genechip microarrays (Affymetrix, Santa Clara, CA, USA). The raw expression data were normalized using Robust Multi-array Averaging (RMA) with quantile normalization.

A total of 5441 probe sets were identified as differentially expressed using Extraction of Differential Gene Expression (EDGE)-based methodology (11). This set of data was further analysed using SOM combined with singular value decomposition (SOM-SVD) and SOM-based two-phase gene clustering (10). From this analysis, the authors extracted 2148 differentially expressed probe sets subdivided into 6 clusters. We used this set of 2148 probe sets for our analyses.

Data set 2: Yeast metabolic cycle

NCBI GEO accession number GSE3431

This data set describes the transcriptional changes in the metabolic cycle of budding yeast Saccharomyces cerevisiae (12). In this experiment, gene expression behaved in a periodic manner, comprising a non-respiratory phase followed by a respiratory phase. The transcriptome was assayed every 25 min over three consecutive cycles, resulting in 36 samples (T1–T36). These were profiled using Affymetrix YG_S98 oligonucleotide arrays. Probes that had at least three ‘present’ calls as generated by Affymetrix Gene Chip software were classified as expressed and the data normalized using GeneSpring v7 per-chip normalization. Using a periodicity algorithm described in the original paper, the authors classified 3552 genes as periodic, corresponding to 3656 probe sets. We used this set of 3656 for our analyses.

We furthermore defined differentially expressed probe sets from the original, normalized microarray data by considering corresponding equivalent time points from consecutive cycles as biological replicates, resulting in 12 conditions sampled in triplicate (12D). These were filtered using F-score cut-offs of 0.75 and 0.6, resulting in 2705 and 6218 probe sets, respectively. We used these sets for the analyses in Figure 2d.

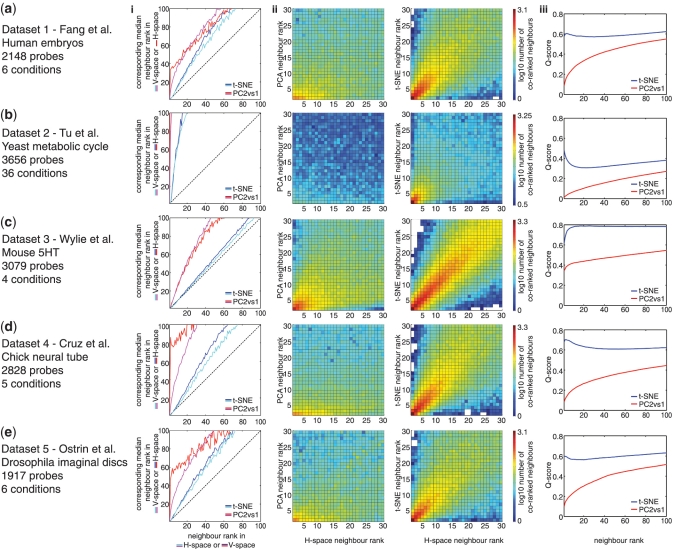
Figure 2.

t-SNE mappings have a high degree of local validity. We compared the quality of t-SNE mappings and projections of the first two PCs for each of the five data sets (a–e). In each case three measures of quality were used: (i) The distance between each data point and all other data points was determined and a rank ordering of neighbours of each data point constructed. The median rank ordering of the neighbours in V-space was compared to the rank orderings in original H-space (Red, PC projection; Blue, t-SNE mapping). Conversely the median rank of the neighbours of data points in H-space was compared to the rank of neighbours in V-space (Magenta, PC projection; Cyan, t-SNE mapping). The closest 100 neighbours are shown in the figure. An optimal method would produce a median rank of neighbours equal to the original rank—this is indicated by the dashed black lines along the main diagonal of the graphs. For each data set, the t-SNE mappings performed better than PCA. (ii) Histogram of co-ranking matrices comparing the rank of neighbours in PC1-PC2 projections (left) or t-SNE maps (right) with the rank of neighbours in H-space (24). The neighbours of every H-point, ranked according to Euclidian distance in H-space, were compared to the distance-ranked neighbours of the corresponding V-point. The joint histogram of these co-ranking matrices was plotted to display the number of neighbours of specific ranks in V-space as a function of the original H-space neighbour ranks. The standard ‘jet’ colour map (MATLAB) was used to indicate the log base 10 of the number of co-ranked neighbours: red indicates high numbers, blue low numbers and the first 30 ranks are displayed. Optimal performance would produce neighbours in the same rank ordering in H-space and V-space. The increased numbers of co-ranked neighbours along the main diagonal shows the increased number of equally ranked neighbours produced by t-SNE compared to PCA. (iii) Plots of the q-score, as defined by Lee and Verleysen (24), for PCA (red) and t-SNE (blue) mappings of each data set. The co-ranking matrix (see above) was used to calculate the error in neighbour ranking in V-space compared to H-space and transformed into a measure of quality of the projections. This measure was plotted as a cumulative score for neighbour ranks. In this plot, higher values of Q for low ranked neighbours (points close together in H-space) indicate better quality local validity in V-space. For each data set, t-SNE outperformed PCA.

In the original study, k-means clustering with Euclidean distance of the entire microarray data was applied to the same 12D data set, resulting in three ‘superclusters': Oxidative, reductive/building and reductive/charging. We used these clusters in Figure 3c and d.

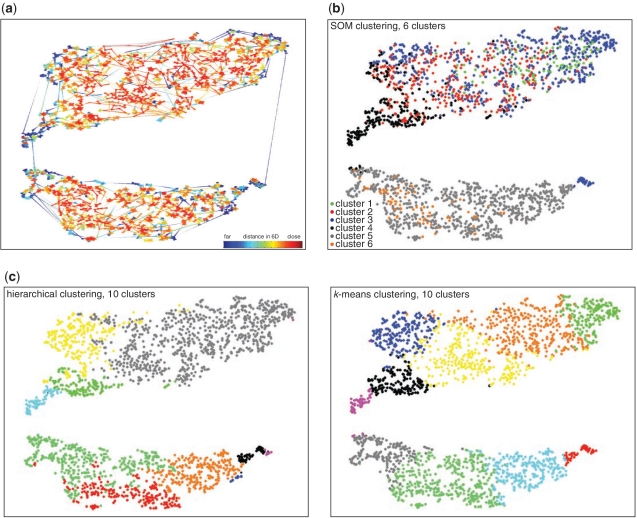
Figure 3.

Data set 1: t-SNE mappings and nearest neighbour plots provide a means to evaluate and refine clustering of co-expressed genes. (a) Nearest neighbour plot of the t-SNE mappings in Figure 1b. Each data point in the t-SNE map was connected to its two nearest neighbours in high-dimensional (6D) space and the connectors coloured according to the distance between these data points in high-dimensional space. Red indicates short, and blue long distances in the higher dimensional space. Thus short red lines indicate faithful projection of distances. (b and c) Overlay of clusters of putatively co-regulated genes on to the t-SNE map obtained from the human embryogenesis data set. Data points are coloured according to cluster membership. (b) Overlay of clusters 1–6 produced using SOMs from the original study (10). (c) Overlay of 10 clusters produced by re-analysis of the original data using hierarchical clustering (left panel) or k-means clustering (right panel), respectively.

Data set 3: Mouse serotonergic neurons

NCBI GEO accession number GSE19474

Data set 3 contains four conditions corresponding to different cell populations in the mouse E12.5 hindbrain (13). Control and 5HT neurons were isolated from rostral and caudal hindbrain, respectively (see original paper for detailed experimental methods). Samples were taken as biological triplicates, resulting in 12 Affymetrix Mouse Genome 430.2 microarray profiles. The raw data were normalized using the Robust MultiChip Averaging (RMA) algorithm as implemented in Bioconductor (14). We defined 3079 differentially expressed probe sets by applying a simple F-score cut-off of 0.85 and used this set for our analyses. In the original study, unsupervised hierarchical clustering was performed on a set of probes selected to be differentially expressed by using the ANOVA test in the Limma Package (15) with an adjusted P-value cut-off of 0.001 and by applying an additional cut-off requiring at least 2-fold change between the groups with highest and lowest average expression value for a probe set. This resulted in eight clusters of which only clusters 1–5 were made available in the publication (13). We used these clusters in Supplementary Figure S3D.

Data set 4: Chick neural tube cells—Sonic Hedgehog signalling

ArrayExpress accession number E-MEXP-2212

In this experiment, the effect of inhibiting or inducing Sonic Hedgehog (Shh) signalling in embryonic chick spinal cord progenitors was analysed (16). The transcriptome was assayed using the Affymetrix Chicken Genome Array at two time points—14 h and 36 h after the perturbation of Shh signalling (see original paper for detailed Experimental methods). Each condition was sampled in triplicate, resulting in 15 independent transcription profiles. The raw data were normalized using Microarray Suite 5.0 (17) (MAS5) and differentially regulated genes identified using multi-class Significance Analysis of Microarrays (18) (SAM) implemented in MeV v4.4 (19,20) with a Q-value cut-off of 5.35%. We used the resulting set of 2828 probe sets for our analyses.

Data set 5: Drosophila imaginal discs—eyeless and atonal targets

NCBI GEO accession number GSE 4008

From this data set (21) of embryonic Drosophila tissue, we analysed five conditions, four of which were assayed as biological triplicates and one condition (wild-type eye discs) assayed as four biological replicates. This resulted in 19 independent transcription profiles obtained using the Affymetrix Drosophila Genome Array 2. Normalization of the raw data was performed with PerfectMatch (22). To filter for differentially expressed genes, we performed one-way ANOVA based on F-scores implemented in MeV v4.4 (19,20), with an adjusted Bonferroni P-value cut-off of 0.05. This resulted in 1917 probe sets that we used for our subsequent analyses with t-SNE.

Hierarchical and k-means clustering

Unsupervised hierarchical and k-means clustering were performed using z-scores of the expression values from the relevant data sets, implemented in MeV v4.4 (19,20). For hierarchical clustering, we used average linking with Euclidean distances. Likewise, Euclidean distances were used for k-means clustering and the number of clusters was set to 10.

Principal component analysis

Principal component analyses of the z-scores of each data set were performed in MATLAB, and the projections of the z-scores of each data point on the first two principal components were plotted.

Data preparation

To prepare the data for t-SNE mapping, the expression values summarized from the arrays were log2 transformed. The values were then normalized so that the mean expression for each gene across the data set was zero, and the rms expression for each gene was one. These z-scores were used for the t-SNE mapping. This normalization procedure was chosen so that distances between genes in H-space would depend upon the pattern of expression across the data set and not on the absolute magnitude of the differences in expression between conditions. The Euclidean distance between these normalized points is also termed the ‘square root Pearson metric’. In addition to facilitating the comparison of gene expression patterns, this normalization procedure has the advantage that a small number of genes with large variations do not unduly influence the PCA.

t-SNE algorithm implementation

The t-SNE algorithm defines a nonlinear mapping of high-dimensional data, the full details of which are given in (8,9,23). For the mappings described here, we used the algorithm to produce 2D projections of the data using Euclidean measures for the distance between data points in the expression space and a perplexity value of 30. A MATLAB implemented GUI that allows data preparation, analysis and exploration of transcriptome data with t-SNE is available at www.nimr.mrc.ac.uk/research/james-briscoe/visgenex.

Nearest neighbour plots

For each point x in the high-dimensional H-space, its K nearest neighbours x₍₁₎, … , x_(K) were determined: in the plots shown, we used K = 2. Edges were then drawn from the visualization point v (x) to the points v (x₍₁₎), … , v(x_(K)).

Edge shape

The edges were drawn as semi-transparent (α = 0.5) wedges, so that edge-overlaps could be seen. Since ‘nearest neighbour’ is an asymmetric relation, in order to indicate the direction of the relation each such edge had greatest width at v (x) and tapered towards its destination point v (x_(i)). Shorter edges were drawn wider, so that the visual impact of short edges would be close but not equal to that of long edges: widths were scaled so that the total area of an edge scaled with the square root of its length in the visualization, plus a small constant. If edge-areas were not scaled in this way, the plots tended to be visually dominated by a small number of longer edges, whereas tight clusters of points in the visualization, many of which were also nearest neighbours in H-space, were inconspicuous.

Colour

Edge colour was used to encode the distances ||x − x_(i)|| in H-space. In the figures, red indicates points that are close in H-space and blue indicates larger distances. The scaling of colours with respect to distances was determined automatically from the histogram of the squared distances of all edges drawn; it is more satisfactory to scale colour differences with squared distance, as this gives a greater spread of colours for the more significant larger neighbour distances. In the figures shown, the standard ‘jet’ colour map of MATLAB was used, as this clearly distinguishes the hues of large from small distances.

RESULTS

t-SNE maps produce realistic visualizations of transcriptome data

In order to demonstrate and evaluate t-SNE and nearest neighbour plots, we used several published, real-world transcriptome data sets (Table 1 and ‘Materials and Methods' section). For illustrative purposes, we focus our attention on Data sets 1 and 2 in the ‘Results' section and we include the analysis of the additional three data sets in Supplementary Data. Data set 1 contains transcriptome data from six consecutive stages of human embryonic development covering organogenesis (10) and Data set 2 describes the transcriptional changes in the metabolic cycle of budding yeast S. cerevisiae (12).

Table 1.

Data sets used in this study

Data set	Accession number	Species	Number of samples	Number of conditions	Number of differentially expressed genes
1	GSE18887	Human	18	6	2148
2	GSE3431	Yeast	36	12*	*F > 0.75: 2705,
				12**	**F > 0.6: 6218;
				36***	***Periodic: 3656
3	GSE19474	Mouse	12	4	3079
4	E-MEXP-2212	Chick	15	5	2828
5	GSE 4008	Fly	19	6	1917

Applying 2D t-SNE mapping to Data sets 1 and 2 produced scatter plots in which each individual gene or probeset in the original data was represented by a data point (Figure 1a and b). Since t-SNE does not define a unique mapping of the data, we ran the algorithm multiple times for each data set and in all cases obtained similar outputs, albeit with different orientations and/or topological transformations of the maps (Supplementary Figure S2). The t-SNE algorithm uses a probabilistic approach to convert the distance between two points in H-space into a conditional probability. The aim is to locate V-points in a way that preserves the computed probabilities and this is achieved using a cost function that finds an arrangement that best preserves neighbour identities. Therefore, the global structure of V-space generated by t-SNE is a consequence of the algorithm maintaining as many close neighbourly relationships from H-space as possible. Genes with similar behaviours—coordinately up- and down-regulated in the same samples—should be positioned close together in the map, reflecting their proximity in the higher dimensional space. Conversely, probes with uncorrelated expression profiles will be distant in higher dimensional space and should be far apart in the t-SNE map. To test whether the mapping had achieved this, we selected small groups of neighbouring points and plotted their expression behaviour across all of the conditions in the data sets (Figure 1a and b). This indicated that the algorithm had effectively grouped together genes with similar behaviours and kept genes with unrelated expression profiles apart.

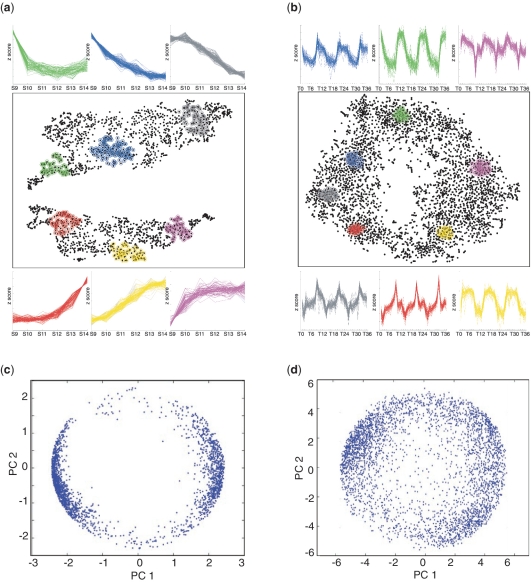
Figure 1.

t-SNE mappings and PCA of two high-dimensional gene expression data sets. (a and b) t-SNE maps of 2148 probe sets identified as differentially expressed between six stages of human embryogenesis (10) (a); and of 3656 probe sets with periodic behaviour over 36 cycles in the yeast metabolic cycle described by Tu et al. (12) (b). Selected groups of neighbouring data points are highlighted and the expression behaviour (plotted as z-scores) of the selected genes over all conditions shown in the corresponding colours. S9–S14: carnegie stages 9–14; T0–T36: time points 0–36. (c and d) Plots of the values of the first and second principal components of the same probe sets used to produce the t-SNE maps in (a and b).

The t-SNE maps offered insight into both local and global gene expression relationships in the data sets. In the case of Data set 1 (Figure 1a), the mapping split the data into two distinct groups. Inspection of the behaviour of the genes in each group revealed that one group contained genes that were highly expressed in the youngest embryos (S9) and then down-regulated in older embryos (S10–S14). Genes in the other group had the opposite behaviour: up-regulated after stage S9. Moreover, the position of individual genes within each of the two groupings revealed a logical organization, with the position of a gene representing the time of transition in its expression. For example, in the case of the genes that were up-regulated during development, genes induced at early stages were positioned at one end of the grouping and genes induced at later developmental times were located progressively further away from this end.

A logical structure was also apparent in the mapping of Data set 2 (Figure 1b). In this case, the data contained genes with a cyclic behaviour and the t-SNE mapping produced a plot with a ring-like shape. Inspection of the behaviour of small groups of genes in the map highlighted the periodicity of the transcriptome and confirmed the presence of the three main periodic behaviours identified in the original study (12) (Figure 1b). In addition, the unbroken circular configuration of the map emphasized the continuous nature of gene expression behaviours. Thus examining the behaviour of genes positioned at regular intervals around the map showed the gradual transformation between the periodicities. Strikingly, we obtained a similar, ring-shaped t-SNE mapping after re-analysing the entire transcriptome reported by Tu et al. (12) using a simple F-score cut-off to select cyclically varying genes instead of the sophisticated periodicity algorithm used in the original study (12) (Figure 4c). This re-analysis highlighted additional cyclic genes, not recognized in the initial study (black data points in Figure 4c). Together, these analyses indicated that t-SNE maps provide an effective visualization of gene expression data and allow the identification of groups of genes with correlated expression profiles.

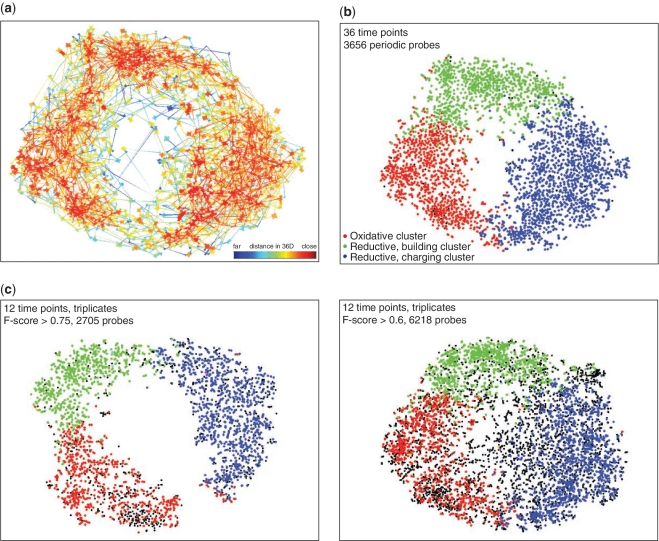
Figure 4.

Data set 2: t-SNE mappings and nearest neighbour plots provide a means to evaluate and refine clustering of co-expressed genes. (a) Nearest neighbour plot of the t-SNE mappings in Figure 1a. Each data point in the t-SNE map was connected to its two nearest neighbours in high-dimensional (36D) space and the connectors coloured according to the distance between these data points in high-dimensional space. Red indicates short, and blue long distances in the higher dimensional space. Thus short red lines indicate faithful projection of distances. (b and c) t-SNE map overlays of three clusters representing the main periodic behaviours in the yeast metabolic cycle as described in Tu et al. (12). Data points are coloured according to cluster membership. (b) Overlay onto the t-SNE map produced from the probe set identified as periodic in the original study. (c) Overlay onto t-SNE maps from the original data set filtered using F-score cut-offs. F-scores were calculated by considering corresponding time points from consecutive cycles as biological replicates.

Comparison of PCA projections and t-SNE maps

We compared t-SNE mappings to PCA (Figure 1c and d). Inspection of a plot of the first two principal components (PCs) of Data set 1 revealed an overall similarity with the t-SNE map (Figure 1c). The first PC separated genes that were expressed at the earliest time points and then down-regulated from genes that were initially low and then up-regulated during the developmental time course, whereas the second PC appeared to reflect the time at which each gene underwent its expression transition. Despite this overall similarity, however, PCA provided less resolution than t-SNE and failed to produce the clear visualization of expression behaviour that the t-SNE mappings offered. In the case of Data set 2, the first two PCs produced a ring-like structure similar to the one in our t-SNE mapping (Figure 1d). As for the t-SNE plot, the three main periodic behaviours were apparent. However, it proved difficult to extract information about the deeper substructure of the data suggesting that t-SNE mappings perform better than PCA.

We systematically evaluated the quality of projections produced by t-SNE and PCA, for each data set, using three objective measures of ‘local validity’ (7,24) (Figure 2a–f). If a visualization has perfect local validity, then, for each gene, its nearest neighbouring gene in H-space would also be its nearest neighbour in V-space, its second-closest neighbour should be its second-closest neighbour in V-space, and so on up to a certain limit of local validity. Using this logic, we determined a straightforward measure of local validity by plotting the median distance rank of the neighbours of all data points in V-space to the distance rank of these neighbours in H-space [panels (i) in Figure 2a–f]. In these ‘neighbour rank’ graphs, a perfect projection would result in the median rank of neighbours in H-space and V-space being equal, producing a line along main diagonal. Similarly, co-ranking matrices [panels (ii) in Figure 2a–f], comparing the ranks of every gene's neighbours in V-space with the ranks of these neighbours in H-space reveal the amount of local validity. In these histograms, as for the neighbour rank graphs, the greater the number of genes that fall along the main diagonal, the greater the local validity (7,24) (Figure 2a–f). Finally, Lee and Verleysen (24) defined a Q-score in which the error in neighbour ranking for each rank between V- and H-space is determined from the co-ranking matrix and plotted as a cumulative function [panels (iii) in Figure 2a–f]: higher values of the Q-score indicate greater overall local validity.

For each measure and for each data set, t-SNE mappings performed significantly better than the corresponding PCA projections (Figure 2). This was particularly noticeable, for example, in the case of Data set 3 where the median ranks of the H-point neighbours of V-points generated by t-SNE were close to optimal [panel (i) in Figure 2c]. In contrast, the projections of the first two PCs of the same data did not preserve close neighbour relationships to the same extent. Moreover, the quality of the output of the t-SNE algorithm appeared relatively robust to changes in the adjustable parameters, including perplexity (a measure of the effective number of neighbours used to embed each data point) and to the distance measure used to determine the conditional probabilities of points in H-space (data not shown). Together, the data indicate that t-SNE produces dimension-reduced mappings of transcriptome data with very good local validity, consistent with our empirical investigation (Figure 1).

Nearest neighbour plots permit ‘visual clustering’ of transcriptome data

Statistics for assessing the overall local validity of a projection allow the general quality of a projection to be determined, but do not help an investigator in the interpretation of any particular region of the visualization. All dimension reduction procedures introduce some distortions in the relationships between data points. It would therefore be helpful to readily see which nearby V-points are truly similar, and which apparent similarities are the results of distortions introduced by the nonlinear mapping. To accomplish this and in order to visualize the underlying relationships between the data points in t-SNE maps, we introduced a technique we term ‘nearest neighbour plots'. This connects pairs of V-points, which are nearest neighbours in H-space and colour-codes them according to the distance between the corresponding data points in H-space. This reveals the pairs of V-points that are truly close, and which pairs are in fact distant in H-space.

We used nearest neighbour plots to visualize the two nearest H-point neighbours of each V-point in Data sets 1 and 2 (Figures 3a and 4a) and Data sets 3–5 (Supplementary Figures S3B, S4B and S5B). This confirmed the validity of the t-SNE mappings: the majority of high dimension nearest neighbours were located close to one another in the t-SNE maps (Figures 3a and 4a, Supplementary Figures S3B, S4B and S5B). In addition, these nearest neighbour plots identified groupings of abundantly inter-connected points indicative of the presence of clusters of co-expressed genes. Consistent with this, inspection of the behaviour of genes comprising interconnected groups indicated that they contained closely co-regulated genes. This suggested the possibility of using t-SNE maps in combination with nearest neighbour plots to visually and interactively partition data sets into clusters of co-expressed genes.

We assessed how this approach to clustering compared to conventional clustering methods used to group co-expressed genes. In the original analysis of Data set 1, a SOM-SVD was used to identify co-expressed genes (10). This method identified six clusters. We overlaid these clusters onto the t-SNE mapping by colouring the data points according to their cluster membership (Figure 3b). Although SOM-SVD clearly segregated genes between the two large groupings present in the t-SNE map, there was significant intermixing of the clusters within each of the large groupings mapped by t-SNE. Closer inspection of the profiles of gene expression in each of the SOM-SVD clusters suggested that this might be expected, because several different clusters appeared to contain genes with similar expression profiles (10). This suggested that SOM-SVD was not providing an optimal classification of the genes within this data set. We therefore asked whether other clustering methods might provide better classifications of the gene expression profiles. To this end, we performed hierarchical and k-means clustering to subdivide the data into 10 clusters (Figure 3c) and overlaid these on the t-SNE map. Using these techniques, clusters were distributed with more spatial integrity on the t-SNE map. Inspection of the average behaviours of the genes in each cluster confirmed that they represented groups of genes with largely distinct expression behaviours.

In some regions of the t-SNE map, the two clustering methods generated clearly distinct divisions of the data. In other areas, the partitions were similar and appeared to correspond to groupings implied by nearest neighbour plots. Subtle differences in the positioning of cluster boundaries were apparent and it was noticeable that differences were often located close to the cluster boundaries in regions where the nearest neighbour plots indicated less tight grouping of the data points in the original higher dimensional space (Figure 3a). This confirmed that in near equivalent clusters, the differences in classification produced by the two methods correspond to the expression behaviours of the genes that differ the most.

This conclusion was supported by the analysis of Data set 2. Tu et al. (12) used k-means clustering of their periodically expressed genes to identify three ‘superclusters' corresponding to the main periodic behaviours. Overlaying these clusters on the t-SNE mapping confirmed that the t-SNE mapping provides a 2D representation of the clustering: genes affiliated with different clusters were spatially grouped in the t-SNE map (Figure 4b). As above, the borders between the clusters appeared fuzzy and ambiguous. Inspection of the expression profiles of genes within these regions indicated that they frequently had periodicities that were somewhere between those associated with the ‘core’ of the superclusters.

Together, therefore, the t-SNE maps combined with nearest neighbour plots provide an intuitive and practical means to understand the relationship between clusters and the affiliation of genes with specific clusters. Employing this approach on the three additional data sets confirmed the utility of the technique (Supplementary Data and Figures).

DISCUSSION

The evaluation of t-SNE and nearest neighbour plots as methods to visualize, explore and cluster gene expression data demonstrates that they represent a novel and powerful approach. Using several diverse gene expression data sets from real-world, published experiments, we show that t-SNE efficiently projects complex gene expression data sets into a 2D mapping in a way that makes the relationships between gene expression behaviours easy to visualize and understand. We provide evidence that the mappings produced by t-SNE have greater local validity than equivalent projections generated by PCA and the t-SNE maps are more appropriate than PCA for this visualization task. The mappings generated by t-SNE provide a global view of gene expression behaviours that offers a coherent understanding of a data set. At the same time, the visualization has sufficient resolution to investigate the relationship between small groups of genes. Obtaining this dual view of a data set is difficult or impossible with other methods. The method can, therefore, be used in conjunction with conventional clustering methods to provide a means to visualize clusters in the context of the entire data set. This opens the ‘black box’ of clustering algorithms and offers a way to investigate and refine cluster boundaries, in order to generate the most appropriate classifications of gene expression behaviour, and to understand the relationships between clusters.

In combination with nearest neighbour plots, t-SNE maps also provide an alternative to currently available clustering methods. Guided by the mappings, clusters can be set in an entirely flexible and intuitive manner. Comparison with conventional clustering techniques demonstrates that t-SNE functions as well or better than the current methods. Moreover, using t-SNE the partitions and composition of clusters can be investigated and altered interactively to produce the most appropriate division of the data. Thus the approach we introduce here opens up new opportunities for exploring and understanding large transcriptome data sets.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

EMBO long-term fellowship (to N.B.); Medical Research Council (U117560541) (to J.B.). Funding for open access charge: MRC (UK).

Conflict of interest statement. None declared.