Physical Limits on Cooperative Protein-DNA Binding and the Kinetics of Combinatorial Transcription Regulation

Abstract

Much of the complexity observed in gene regulation originates from cooperative protein-DNA binding. Although studies of the target search of proteins for their specific binding sites on the DNA have revealed design principles for the quantitative characteristics of protein-DNA interactions, no such principles are known for the cooperative interactions between DNA-binding proteins. We consider a simple theoretical model for two interacting transcription factor (TF) species, searching for and binding to two adjacent target sites hidden in the genomic background. We study the kinetic competition of a dimer search pathway and a monomer search pathway, as well as the steady-state regulation function mediated by the two TFs over a broad range of TF-TF interaction strengths. Using a transcriptional AND-logic as exemplary functional context, we identify the functionally desirable regime for the interaction. We find that both weak and very strong TF-TF interactions are favorable, albeit with different characteristics. However, there is also an unfavorable regime of intermediate interactions where the genetic response is prohibitively slow.

Introduction

Cells respond to many biochemical signals by adjusting their gene expression levels, often in a combinatorial way where the transcription rate of a given gene is a nonlinear function of several inputs. The entire signal transduction cascade, beginning with the detection of the biochemical signals and culminating in a changed intracellular protein concentration, is generally believed to be under strong selective pressure for rapid and well-adjusted responses in competitive environments. An important step in this cascade involves proteins belonging to the large class of transcription factors (TFs) that convey the external signal and trigger the appropriate genetic response by binding to specific binding sites on the genomic DNA. The search process of individual TFs for their functional target sites hidden within millions of nonfunctional sites on the DNA is well characterized (see, e.g., (1–7)). This has led to an understanding of the tradeoffs inherent in the choice of TF-DNA interaction parameters, when both a rapid search as well as sufficient equilibrium discrimination for the functional sites is required (8–10).

However, the experimental timescale for the search process, as inferred, e.g., from single-molecule measurements in vivo (11), is surprisingly short compared to the timescale for significant change in gene expression levels: Whereas a TF target site is occupied within a minute even at low TF concentrations, the concentration of the protein expressed from the target gene typically changes significantly only over a timescale of several minutes, due to the slow kinetics of protein synthesis and degradation. Hence, the search time is only a fraction of the total response time, and it is unclear whether fine-tuning of TF-DNA interaction parameters is needed for kinetic reasons. On the other hand, even in bacteria many genes are coregulated by a combination of different TFs (12–20), whereas the search process studied so far is that of a single TF species, i.e., multiple TF molecules of the same type. A salient question is whether the timescale of transcription control increases with the complexity of the implemented regulatory function.

To explore this question, we consider a simple theoretical model for the kinetics of combinatorial transcription regulation. We focus on the example of an AND-like cis-regulatory function implemented by two TFs, referred to as A and B, which bind cooperatively to two adjacent target sites to activate a gene. This scenario is exemplified by the melAB promoter of Escherichia coli, where CRP and MelR bind cooperatively to activate transcription (19). Our model is sufficiently generic that it can be applied to a variety of cooperative protein-DNA binding situations. However, the example of the AND-gate is particularly well suited to illustrate the basic effects and functional tradeoffs that become apparent when the interaction parameters are varied. Compared to the well-studied case of a single TF-species, the apparent new aspect here is the mutual interaction between the TFs (compare to Fig. 1), that is quantified by the dimensionless cooperativity $\omega =e^{-E_{\mathrm{int}}/k_{\text{B}}T}$.

Figure 1.

Three schematic examples for cooperative protein-DNA binding in gene regulation. In panel A, RNAp is recruited by an activating TF, whereby the signal conveyed by the TF is transferred to the transcription level. In panel B, an activator is assisted by a helper protein which does not contact RNAp itself. In panel C, two different TFs bind cooperatively and contact RNAp. These and other motifs are used by cells to implement regulatory functions (30,41), although the actual arrangement of TF binding sites in bacterial genomes is often more complicated, involving a larger number of sites (42).

This quantity is only a measure of the interaction strength between TFs, with E_int the effective free energy of the interaction and k_BT the energy scale of thermal fluctuations. It is not related to the Hill coefficient, which depends on the number of components involved in a cooperative complex. The strengths of direct protein-protein interactions vary over a broad range with dissociation constants between the femto- and the centimolar regime (21). Biochemically feasible ω-values can therefore span many orders of magnitude, from weak transient interaction with 1 < ω < 1000 to strong dimerization with ω ∼ 10⁷ or larger. Depending on this value, the kinetics of cooperative protein-DNA binding will either be dominated by a monomer pathway or a dimer pathway (22,23).

How do the response time and the steady-state levels of a regulatory module depend on the cooperativity? And which regime of ω-values could be favorable in which functional context?

Our model, illustrated in Fig. 2, generalizes the classic facilitated diffusion model (1) to two interacting protein species. It incorporates the basic kinetic moves, i.e., binding to a DNA site, sliding along the DNA, and unbinding from the DNA, for monomers as well as for dimers. In addition, dimers can form or break up either in solution or while bound to the DNA. We characterize the behavior of our model using a variety of analytical and numerical approaches to calculate equilibrium and kinetic observables over a parameter range chosen to permit the exploration of functional tradeoffs in a bacterial system such as E. coli. For instance, in bacterial transcription regulation, a faster response is generally expected to be advantageous, whereas the steady-state transcription levels of a cis-regulatory function must be adjusted to yield the optimal protein concentrations for the biological conditions represented by the input signals (24–26). Therefore, when considering different choices of ω, we compare regulatory systems that lead to the same steady-state levels. The exploration of our model leads us to two favorable regimes of ω, corresponding to weak (and often promiscuous) interactions and very strong heterodimerization, respectively. On the other hand, our model predicts that the search kinetics will be prohibitively slow at intermediate ω-values, at least when the protein copy number is small as is usually the case for bacterial transcription factors. In the Discussion, we consider biological implications of these theoretical findings and discuss possible experiments to characterize the cooperative search problem and the kinetics of combinatorial transcription regulation.

Figure 2.

Illustration of the energy levels and the kinetic model for the two TF species system with a nonspecific genomic background. (A) Binding of TFs to the DNA reduces the energy by E_ns < 0 compared to the unbound reference state with energy E_free = 0. Additional energy can be gained through sequence-specific contacts (not shown). Upon dimerization of TFs in solution or on the DNA, the energy is further reduced by the interaction energy E_int ≤ 0. The TFs bind to their target site with a specific binding energy E_T. At small dimerization energies E_int, full promoter activation will be reached via the monomer pathway, where TFs arrive at their target independently and consecutively. At large E_int, on the other hand, TFs will predimerize in the DNA-background or in solution and arrive to the targets simultaneously through the dimer pathway. (B) Transcription factors dimerize in solution and bind to the DNA in diffusion-limited binding reactions with a rate constant k_a. The dissociation rate of a free dimer k_d and the dissociation rate k_off of a TF from a DNA site depend on the corresponding energies and follow from detailed balance as explained in the main text. Dimers and monomers can randomly diffuse along the DNA with a rate k_sl, which becomes site-dependent when the binding energy is sequence-specific. When the dissociation of a monomer requires the simultaneous dissociation from a cooperatively bound partner, its off-rate k_off decreases by a factor 1/ω.

Results

Cooperativity and regulatory function

Cooperative protein-DNA binding is employed in diverse functional contexts. For some functions, many molecules of the same protein polymerize along DNA, e.g., RecA for homologous recombination (27) or single-strand-binding-protein during DNA replication (28). In these cases, the role of the protein-protein interaction is to enhance the probability of obtaining continuous DNA coverage rather than a patchwork of randomly positioned molecules. Here we focus on the functional context of transcription regulation where cooperative protein-DNA binding is involved in the processing of input signals. These signals are integrated and transformed into a single output, the transcription rate of a gene (29).

The cooperative binding of a transcription factor (TF) with RNA polymerase (RNAp) transfers a signal, by regulating the effective binding threshold for RNAp via the concentration of active TF (regulated recruitment (29), see Fig. 1 A). When two different TFs bind cooperatively and each makes contact with RNAp to activate transcription, see Fig. 1 C, two signals are effectively integrated into a single output. A similar case is depicted in Fig. 1 B, where TF binding is assisted by a helper protein that does not make contact with RNAp itself. This motif resembles, for instance, the regulation of the melAB promoter, which is codependent on the transcription factors CRP and MelR (19). The helper can also be another molecule of the same TF, making the response to its signal more switchlike (increased effective Hill coefficient).

The molecular function in the signal transfer scenario of Fig. 1 B is quantitatively described by the probability p_b to find a protein B bound as a function of the concentration of a protein A that binds adjacently. In contrast, for the signal integration scenario, the functional activity is captured by the probability p_ab that two DNA sites a and b are both occupied by the matching TF proteins. In the following, we will refer to both quantities, p_b and p_ab, simply as the average activity for the respective scenario. We envisage that selection acts on these average activities as well as on a characteristic timescale, the response time τ, associated with the kinetics of each mechanism. Here, τ corresponds to the typical delay for adjusting the activity to a new average level after a change in the input signal. In a steady state, τ is also a characteristic timescale of spontaneous fluctuations in the activity (noise). Importantly, both the average activity as well as the response time depend on the binding cooperativity ω.

Average activity

Before we introduce our full model, it is instructive to consider the average activity within the simple approximation where we focus only on two binding sites a and b and ignore binding of the TFs to the rest of the DNA. This consideration will be useful in particular as a guide for our detailed study of possible tradeoffs in the choice of ω within the full model.

We first consider the signal transfer scenario as shown in Fig. 1 B. In equilibrium, the probability p_b that site b is occupied by one of N_B available molecules of type B is the normalized sum of the statistical weights for all states where b is occupied (30). In the absence of A, i.e., for N_A = 0, this is just p_b = q_b/(1 + q_b), with the statistical weight for an unoccupied site set to 1 and q_b = N_B/n_b denoting the relative weight for b to be occupied. Here, the binding threshold n_b, which corresponds to the number of B molecules needed to obtain a 50% average occupancy of b in the absence of A, is directly connected to the effective equilibrium binding constant of B to b and the cell volume via n_b = K_dV_cell. In the presence of A, the occupancy of b increases to

$$\begin{array}{l}{p}_b^{\prime }=\frac{q_b^{\prime }}{1+q_b^{\prime }}\mathrm{with}\hfill \\ q_b^{\prime }=q_b\cdot \left[1+\left(\omega -1\right)p_a\right],\hfill \end{array}$$ (1)

where p_a = q_a/(1 + q_a) is the average occupancy of a in the absence of B. Thus, the presence of A boosts the statistical weight for B binding by the regulation factor (30), i.e., the factor in square brackets in Eq. 1. Intuitively, this factor may be thought of either as a boost in the local effective concentration of B (29), or as a decrease in the effective binding threshold n_b (the latter interpretation is closer to the underlying physics).

Importantly, the regulation factor cannot exceed the cooperativity value ω, and it reaches ω only if p_a takes on its maximal value of 1. As a consequence, the cooperativity ω is also an upper bound on the fold-change ϕ in b-occupancy induced by a change in A concentration, because p′_b/p_b ≤ q′_b/q_b. This constitutes a physical constraint on ω that arises from the equilibrium statistics of cooperative protein-DNA binding,

$$\omega >\varphi \left[equilibriumconstraint\right],$$ (2)

i.e., the cooperativity must be larger than the required fold-change ϕ in the output signal (ϕ = p′_b/p_b for the signal transfer scenario). On the molecular level, this constraint can be implemented by a sufficiently strong direct protein-protein interaction or by indirect mechanisms of cooperativity, e.g., via collaborative competition (31) or DNA bending (32).

For the signal integration scenario in Fig. 1 C, the definition of the fold-change ϕ is different, but the constraint in Eq. 2 holds as well. Here, the relevant fold-change is the average activity in the presence of both inputs relative to the average activity with only a single input, ϕ = p_ab/p_a or ϕ = p_ab/p_b, where

$$p_{ab}=\omega q_a{q}_b/\left(1+q_a+q_b+\omega q_a{q}_b\right).$$ (3)

This fold-change is then transferred to the promoter activity in the example considered in Fig. 1 C. Taken together, when considering steady-state activities, both the signal transfer and the signal integration function benefit from larger cooperativities, because large ω-values allow for tight regulation. However, because large binding energies often lead to slow kinetics, we will explore whether a tradeoff exists between the fold-change in average activity and the response time.

Full model

We now introduce a full kinetic model for the cooperative target search that is based on the energies of TF binding states and the transition rates between these states, as illustrated in Fig. 2. We consider a single circular genome of length L_G (in units of basepairs) inside a cell of volume V_cell with a single pair of adjacent target sites for A and B. The unbound state of free TFs in solution is our reference state, with its energy set to E_free = 0. If A and B dimerize in solution, the interaction energy E_int < 0 is gained, while entropy is lost, because the number of possible states is reduced by a factor that we write as V_TF/V_cell, with a microscopic volume V_TF on the order of the size of a TF. Each TF molecule has L_G possible binding sites on the DNA (indexed by i with 0 ≤ i < L_G) with the respective bound-state energies E_i^A and E_i^B. These bound-state energies are either equal to E_ns < E_free, if the protein-DNA interaction is nonspecific, or they take on a lower value if the binding sequence favors specific protein-DNA contacts, E_i^A, E_i^B ≤ E_ns. We denote by L the number of basepairs on the DNA that are occupied by a bound monomer (occupied DNA is inaccessible to other TF molecules), and we posit that A and B can form a DNA-bound dimer only when B binds directly upstream of A.

For the kinetic rates, we assume that all binding reactions are diffusion-limited. For simplicity, we take the same rate constant k_a for the binding of two protein molecules in solution and for the association of a TF molecule with a specified DNA site (thus, the total rate of TF binding anywhere on the DNA is L_Gk_a, if no DNA site is occupied already). The random diffusion of TFs along the DNA contour occurs with the basal sliding rate k_sl. When neighboring sites have different energies, the sliding rate is the basal rate k_sl from the higher to the lower energy state whereas the reverse process occurs at the reduced rate k_sl exp(−ΔE/k_BT), with ΔE > 0 the energy difference, such that detailed balance is respected (in the following we assume all energies to be in units of k_BT, which amounts to setting k_BT = 1). The rates for all other possible reactions are similarly obtained from detailed balance. For instance, the unbinding rate k_off of a monomer from a nonspecific DNA site is determined by k_off/k_a = (V_cell/V_TF)$e^{\left(-E_{\mathrm{free}}+E_{\mathrm{ns}}\right)}$, and the dissociation rate k_d of a free dimer k_d/k_a = (V_cell/V_TF)$e^{E_{\mathrm{int}}}$. Note that monomers can also unbind or slide away from a DNA site while simultaneously dissociating from a cooperatively bound partner (thus disrupting the DNA-bound dimer, see Fig. 2 b, top right). In that case, detailed balance dictates that monomer sliding and dissociation rates decrease by a factor 1/ω due to the loss of the dimerization energy E_int.

Within the framework of this full model, we calculate the steady-state activities as described in Section S1 in the Supporting Material (this exact calculation includes the effect of the genomic background and mutual exclusion of overlapping binding sites, both neglected in the simple discussion above). We determine average search times numerically, using kinetic Monte Carlo simulations as described in Section S2 in the Supporting Material, and we also develop analytical approximations further below and in Section S3 in the Supporting Material.

We choose the parameters of our full model to roughly reflect the situation in a bacterium such as E. coli. We set the genome length to L_G = 5 ⋅ 10⁶ bp, choose a cell volume of V_cell = 5 μm³, and consider DNA binding sites of length L = 15 bp. The sliding rate k_sl can be determined from recent measurements of the one-dimensional diffusion constant for TF sliding on nonspecific DNA (11,33), which obtained values close to 0.05 μm²/s, corresponding to a sliding rate of ∼k_sl = 10⁵/s. The same experiments also determined a residence time of 0.3–5 ms for TF molecules on nonspecific DNA before dissociation. At the given genome length, this fixes our rate constant k_a to be in the range 0.4–6 ⋅ 10⁻³/s, and we set k_a = 10⁻³/s in the following.

Unless otherwise stated, we will assume, for simplicity, that the target sites a, b are the only specific binding sequences in the genome, both with energy E_T. We set the strength of the nonspecific protein-DNA interaction by requiring that a single TF spends, on average, equal time unbound in solution as bound somewhere on the DNA. This parameter choice corresponds to the well-characterized optimum for the search process of a single TF species (4,34); see also the discussion of this point further below. Within our energy model, this corresponds to a nonspecific binding energy E_ns = log(L_G ⋅ V_TF/V_cell) = −5.3, assuming a reaction volume V_TF = 1 nm³. In our model, the effective dimerization rate is increased by the presence of the DNA (which acts as a scaffold for the interaction). A similar increase was observed experimentally in a study of the Jun⋅Fos⋅DNA complex (23).

Quantitative analysis

We now analyze how the quantitative characteristics of the two-protein-species system depend on the cooperativity ω. The cooperative target state where both target sites are occupied can be reached via two distinct kinetic pathways: In the monomer pathway, A and B separately search for their specific target sites in multiple rounds, alternating between one-dimensional diffusion along the DNA and three-dimensional diffusion in the cytoplasm to a new position on the DNA. In this pathway, A and B arrive independently, i.e., one after the other, at their specific target sites. By contrast, in the dimer pathway, the dimer forms beforehand, either in solution or in the DNA background, such that A and B reach their target sites simultaneously (compare to Fig. 2 A).

Clearly, we expect the monomer pathway to dominate for weak TF-TF interactions (small ω), whereas the dimer pathway should dominate for large ω. But what is the behavior of the overall search time τ that results from the kinetic competition between the two pathways?

Before performing the kinetic analysis, we first characterize the steady-state characteristics of our full model. We will focus on the signal integration scenario in the remainder of this study; the behavior in the signal transfer scenario is qualitatively similar. As discussed above, the most relevant steady-state characteristic in the functional context of gene regulation is the attainable fold-change of the average activity, which determines how tightly a gene can be regulated. We assume that the expression level of the regulated gene in the high-activity state, when both TF species can bind the promoter (the ON-state), is constrained to its optimal level by evolutionary selection, e.g., the optimal level of a metabolic enzyme in the presence of its substrate (24,25). The fold-change between the ON-state and the OFF-state (in which only one of the TFs can bind) then determines how tightly the production of the protein can be suppressed under conditions when it would be useless or even detrimental.

Hence, when we consider the system at different cooperativity values ω, we take for granted that another system parameter is adjusted to keep the ON-state level constant. Specifically, we will assume that this compensation occurs via the target binding threshold, which is programmable via the DNA sequence of the target site (10). In other words, we compensate a weaker protein-protein interaction with a stronger protein-target interaction such that the ON-state level p_ab remains constant. In E. coli and yeast, binding sites indeed tend to deviate from the consensus motif when multiple TFs bind next to each other in the cis-regulatory region (15,18,35). For simplicity, we consider a symmetric pair of TFs, which have different binding sequences, but the same energetics, such that q_a = q_b.

Fig. 3 B shows the resulting fold-change ϕ = p_ab/p_a for the full model as a function of the cooperativity (on a double-logarithmic scale), with the three curves corresponding to different ON-state levels p_ab. The fold-change increases monotonously with the cooperativity, roughly as $\varphi \sim \sqrt{\omega }$, before it saturates at a maximal level that depends slightly on the ON-state level. For ω >> 1, the dependence on the ON-state level p_ab is nonmonotonous, with a larger ϕ for p_ab = 0.5 than for both p_ab = 0.1 and p_ab = 0.9. Much of this behavior can be understood already within the simple approximation of Eqs. 1 and 3 as follows: For large ω, cooperative binding to the targets becomes dominant in the ON-state, such that the noncooperative contribution q_a + q_b in the denominator of Eq. 3 can be neglected.

Figure 3.

Characterization of the cooperative search process and steady-state levels as a function of the cooperativity ω and for different on-state levels p_ab, given N = 1 molecule of each TF species. (A) Dimerization probability P_dimer at equilibrium. The dimerization threshold is given by the entropic cost of dimerization and corresponds approximately to the length of the genome L_G. (B) The fold-change ϕ increases with the cooperativity as $\sqrt{\omega }$ below the dimerization threshold and then approaches a maximal value. (C) The cooperative search time τ displays a maximum at an intermediate cooperativity. For large ω, the search time decreases again and settles at an on-state independent value, corresponding to the dimer search time; compare to Fig. 4. (D) The probability W_D that the cooperative target state is reached via the dimer pathway is distinct from P_dimer in panel A, because independent monomeric search and dimeric search have different timescales. Note that the transition from the monomer to the dimer pathway marks the position of the maximal search time.

One then finds that $\varphi \approx \sqrt{\omega }\sqrt{p_{ab}\left(1-p_{ab}\right)}$, explaining the behavior in the intermediate ω-range of Fig. 3 B, i.e., the $\sqrt{\omega }$-dependence and the nonmonotonous dependence on the ON-state level p_ab. However, the saturation of the fold-change at very large ω is beyond this simple approximation, which neglects the background DNA and assumes that the TFs heterodimerize only on the target. This assumption breaks down in the strongly-interacting regime, as shown in Fig. 3 A, which plots the equilibrium probability to find the TFs as a heterodimer. Dimers become prevalent in the background when the cooperativity outweighs the entropic cost of dimerization. If the nonspecific DNA interaction of monomers is optimized for independent search (see below), the dimerization probability is simply P_dimer(ω) = ω/(ω + 2L_G) (see Section S1 in the Supporting Material). Further increase of ω has no significant effect on the fold-change. Hence, the full model confirms our previous conclusion that a large cooperativity is generally beneficial for the steady-state response, but only up to a value of ω ∼ L_G.

Next, we turn to the cooperative search process. We first consider the situation with only one molecule of each type (N_A = N_B = 1). Initially, both monomers are unbound. The cooperative search time τ corresponds to the first point in time when a and b are both occupied. Fig. 3 C shows its mean, 〈τ〉, as a function of ω, for three different ON-state levels p_ab. Here, the symbols represent simulation results, where the average is taken over a large number of simulation runs (see Section S2 in the Supporting Material for details), whereas the solid lines represent an analytical approximation discussed below and in Section S3 in the Supporting Material. Note that 〈τ〉 is plotted in units of the monomer search time 〈τ_M〉, which is defined as the average time needed by a monomer, e.g., of type A, to find its target a in the absence of B.

This kinetic ratio, 〈τ〉/〈τ_M〉, is a direct measure of the slowdown of cooperative regulation relative to the timescale for independent regulation. When the cooperativity is negligible (ω ≈ 1), Fig. 3 C shows that the kinetic ratio is only slightly larger than 1. In this regime, the second protein arrives independently and on the same timescale as the first, while each protein is stably bound by itself, such that the first protein typically does not unbind from its target before the second protein arrives. Indeed, the probability of such a missed encounter depends on the ON-state level p_ab and is simply $1-\sqrt{p_{ab}}$ when ω = 1, which consistently explains the p_ab-dependence (at fixed ω = 1) in Fig. 3 C.

With increasing cooperativity ω, the cooperative search time also becomes longer. Note that our reference timescale, the monomer search time 〈τ_M〉, is independent of ω, such that the ratio plotted in Fig. 3 C shows indeed the ω-dependence of the absolute timescale for cooperative search. The slowdown scales with the square-root of the cooperativity, $\langle \tau \rangle \sim \sqrt{\omega }$. This scaling reflects the mechanism underlying the slowdown, which is produced by an increasing probability of missed encounters: As the cooperativity is increased, our constraint of a constant p_ab implies that a monomer bound to its target becomes less stable and detaches more often before its partner arrives. The cooperative search time is then determined by the number of times a TF must return to its target before finding the other target occupied, which is roughly 1/p_a, the inverse of the probability that a single target is occupied. At intermediate ω, this probability scales as p_a ∼ ω^−1/2, leading to the observed scaling.

The increase of the search time 〈τ〉 with ω is not indefinite, however, because the relative importance of the dimer pathway increases with ω. The contribution of the dimer pathway is shown in Fig. 3 D. It displays a sigmoidal form, with a narrow transition region where the cooperative search switches from the monomer mode to the dimer mode. This transition is accompanied by a peak in the cooperative search time in Fig. 3 C. Note that this transition occurs at significantly smaller ω-values than the transition in the equilibrium probability for heterodimerization shown in Fig. 3 A.

To understand the nonmonotonous behavior of the cooperative search time in Fig. 3 C, it is instructive to consider the extreme case of a purely dimeric search. Fig. 4 shows the purely dimeric search time (dashed line and circles) as a function of the dimer binding ratio, i.e., the relative probability P_d/P_c to find a dimer on the DNA versus in the cytoplasm (top x axis). Here, the binding ratio is varied by changing the nonspecific binding strength E_ns. For comparison, the gray line and squares show the corresponding curve for a monomer (search time for a single target; monomer binding ratio on the bottom x axis). Both curves display the same qualitative behavior, with the well-known optimum (4,34) where the respective binding ratio equals 1 (i.e., the average time spent on the DNA matches the time spent in the cytoplasm).

Figure 4.

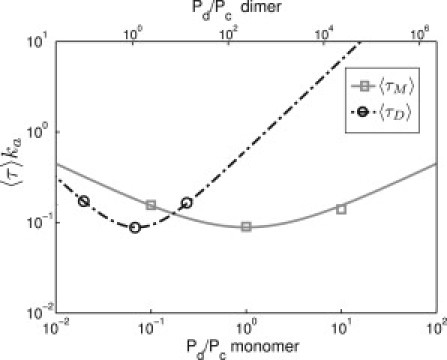
Average search times 〈τ〉 of a dimer (black) and a monomer (gray) for the target site. The curves are obtained from $\langle \tau \rangle =\sqrt{\pi L_{\text{G}}/16k_{\mathrm{sl}}{k}_a}\left(\sqrt{P_d/P_c}+\sqrt{P_c/P_d}\right)$, which predicts an optimum at a binding ratio of one, P_d/P_c = 1 (see (4,34)). For larger binding ratios, TFs spend too much time exploring nearby sites with redundant one-dimensional diffusion, whereas TFs spend too much time unbound in solution when TF-DNA binding is weaker. Because dimers bind DNA more strongly than monomers, the binding ratio P_d/P_c of the dimer (indicated on the top x axis) is consistently larger than that of the monomers (bottom x axis). Hence, dimers and monomers cannot simultaneously operate in the search optimum.

At larger binding ratios, the local one-dimensional search becomes too redundant, whereas at smaller binding ratios TFs spend too large a fraction of their time in solution, not searching. However, the minima of the two search time curves do not coincide, because dimers bind DNA more tightly than monomers. Consequently the protein-DNA interaction cannot be simultaneously optimized for monomer and dimer search. We generally assume that the protein-DNA interaction is optimal for monomers, because single TFs are the basic functional unit for transcription control in bacteria (see below for further discussion). At this point in Fig. 4, the purely dimeric search time is roughly a factor-10 longer than the monomer search time. Returning to Fig. 3, this factor corresponds to the level of the plateau that is reached for very large ω in Fig. 3 C.

We now consider again the intermediate ω-range in Fig. 3 C. With increasing ω the monomer pathway eventually becomes slower than the dimer pathway, due to the increasing probability of missed encounters. At the same time, the dimerized state is increasingly stabilized. Upon dimerization of A and B in the background, it becomes more likely that this dimer localizes the target before it dissociates again into monomers. The increasing predominance of the faster dimer pathway explains the regime where the cooperative search time decreases with ω. It also explains why the kinetic monomer-dimer transition in Fig. 3 D occurs before the equilibrium monomer-dimer transition in Fig. 3 A: even when the dimer fraction has not reached 50%, the dimer pathway can be kinetically dominant. At very large ω, the monomer pathway is entirely negligible. The TFs form relatively stable dimers, either already in solution or when bound to nontarget sites, which subsequently search together for most of the time, and ultimately arrive at the target as a pair. This search mode is independent of the target binding energy and the cooperative search time then becomes independent of ω and equal to the pure dimer search time plotted in Fig. 4.

The cooperative search kinetics admits an analytical treatment, to quantitatively describe the kinetic competition between the monomer pathway and the dimer pathway. This description takes a coarse-grained view of the problem, with effective transition rates between only four states, as depicted in Fig. S1 in the Supporting Material. The initial state has both TFs A and B unbound in solution (state 2 in Fig. S1), from where the proteins either enter the dimer pathway by dimerizing (state 1) at rate r₂⁻ or one of them independently finds its target site on the DNA (state 3) at rate r₂⁺. From state 1, the dimer either locates its pair of target sites at rate r₁⁻ or reverts back to state 2 at the effective dissociation rate r₁⁺. Along the monomer pathway, from state 3, either the other TF locates its target as well (at rate r₃⁺), or the waiting TF leaves its target, leading back to state 2 at rate r₃⁻. In Section S3 in the Supporting Material, we express the six effective rate constants in terms of the parameters of the full model, and then use the mean first-passage time formalism to calculate the mean cooperative search time analytically. We have used this approach to obtain the curves in Fig. 3, C and D, which agree well with the simulation data.

So far, we have focused on the case of a single TF molecule of each type. We now turn to the general case where we have N_A molecules of type A and N_B molecules of type B. If we increase both molecule numbers simultaneously (N_A = N_B = N), mass action drives the monomer-dimer equilibrium toward the dimerized state. Fig. S2 A shows the probability for a molecule to be dimerized, P_dimer, as a function of ω, with the different curves corresponding to different N values. As expected, the dimerization threshold of the sigmoidal curves moves to smaller ω-values as N is increased. Note that although we have treated the case of exactly one molecule for N = 1, we keep the number of proteins constant only on average for N > 1, via the chemical potential in the grand canonical ensemble (see Section S1 in the Supporting Material for details). This choice is technically motivated, but is also biologically meaningful, because proteins are constantly produced and degraded in cells and their numbers can, at best, be constant on average.

Fig. S2 B displays the N-dependence of the fold-change ϕ. In contrast to Fig. 3 B, the ON-state level is now kept fixed at p_ab = 0.5 and instead the different curves are for different N values (the fold-change is defined here with respect to the state where N_A = N and N_B = 0). For ω below the dimerization threshold, the fold-change is independent of the molecule number N. However, as in Fig. 3 B, increasing ω does no longer raise the fold-change once the dimerization threshold is reached. As the dimerization threshold decreases with N, the fold-change saturates at smaller ω and the maximal ϕ decreases as $1/\sqrt{N}$.

The average time required for the parallel cooperative search with N_A = N_B = N molecules is shown in Fig. S2 C. As in Fig. 3, we have used the monomer search time as the reference timescale, but now scaled by N⁻¹, because the expected timescale for the parallel search of N monomers is 〈τ_M〉/N. Consequently, the fact that all curves fall on top of each other in the regimes of weak and very strong interaction shows that in these regimes the cooperative search time exhibits the simple 1/N scaling, which corresponds to a linear increase of the frequency at which the targets are visited by monomers (in the small ω regime) or by dimers (in the large ω regime). In the intermediate regime, we find a more complex dependence on N, indicated by the fact that the curves do not collapse. To understand this dependence, we extend our simplified analytical expression developed above. Under the conditions of interest here, the dimerization equilibrium P_dimer(ω) of Fig. S2 A is reached on a timescale much shorter than the cooperative search. As detailed in Section S3 in the Supporting Material, we can then approximate the search process as a parallel search of N ⋅ P_dimer dimers and N ⋅ (1 − P_dimer) monomers of each kind, resulting in

$$\langle \tau \left(\omega \right)\rangle =\frac{1}{N}\cdot {\left[\frac{P_{\mathrm{dimer}}\left(\omega \right)}{\langle {\tau }_D\rangle }+\frac{1-P_{\mathrm{dimer}}\left(\omega \right)}{\langle {\tau }_{A,B}\left(\omega \right)\rangle }\right]}^{-1}.$$ (4)

Here, 1/〈τ_A,B(ω)〉 is the independent search rate of the monomers, which indirectly depends on ω through the probability of missed encounters (see Section S3 in the Supporting Material), whereas the dimer search rate is 1/〈τ_D〉, as in Fig. 4. We used Eq. 4 to obtain the lines in Fig. S2 C, which display good agreement with the full simulation, showing that the analytical approximation yields a useful description of the cooperative search kinetics.

On a more qualitative level, Fig. S2 C shows how the peak in the search time at intermediate ω-values is affected by N. The peak shifts to smaller ω-values with larger N, and also becomes less pronounced. From Fig. S2 D, which shows the weight of the dimer pathway in the cooperative search process according to Eq. S26 in the Supporting Material, we see that the position of the peak remains determined by the switch from the monomeric to the dimeric search mode. The shifted switch to the dimeric search mode, which occurs at smaller ω for larger N, also explains the reduction in the peak height: The dimeric search mode takes over before the slowdown of the monomeric search mode becomes dramatic. However, even with hundreds of TF molecules of each species, we still find a peak in the cooperative search time, which divides the ω-values into three regimes, as discussed below.

Discussion

We studied the kinetics and the equilibrium statistics of cooperative transcription factor-DNA binding to specific target sites in the genomic background. For our analysis, we considered the dimensionless cooperativity ω as a parameter with a broad range of biochemically feasible values, and sought to identify functional tradeoffs associated with the choice of this value. We focused on the functional context of a signal integration scenario with AND-logic, but the results hold in a similar fashion for a signal transduction scenario (see Fig. 1). From this functional context, we derived the central assumption that the average activity of the regulated gene has an optimal level in the ON-state, such that there is a strong selection pressure to maintain this level fixed regardless of the ω-value. We satisfied this constraint by compensating changes in ω via the target site binding energy, which is programmable through the binding site sequence (10). Such a compensation has been observed in an analysis of combinatorial promoters, i.e., binding sites tend to deviate from the consensus motif when multiple TFs bind next to each other in the cis-regulatory region (35). It is also biologically plausible, as it does not interfere with the regulation of genes that are only regulated by one of the TFs or combinatorially with other TFs.

Given this functional setting, we determined which fold-change in the steady-state activity could be implemented at a given ω, and how the kinetic search time depends on ω. The fold-change quantifies the discrimination in the promoter output between the states where one or two input signals are present, whereas the search time is a lower limit to the response time of the regulatory system. The search process has contributions from a monomer and a dimer search pathway, the relative weights of which we determined, again as a function of ω. In the regime of weak protein-protein interactions, e.g., ω > 10³−10⁴, we found a tradeoff between the kinetics and the steady-state behavior, in the sense that a higher fold-change is associated with a slower response due to a longer assembly time for the protein-complex on the target site. This tradeoff is a consequence of gene activation via the monomer pathway, where individual TFs visit their targets independently and consecutively, possibly dissociating from the target before the cooperative partner arrives (i.e., missed encounters). In this regime, search time and fold-change both increase as ∼ω^1/2. At larger ω, heterodimers are more stable, increasing the probability that the target is located simultaneously by both proteins (dimer pathway). At the same time, the missed encounters further slow down the independent monomer search, to timescales larger than the dimeric search time. Thus, a transition occurs where the dimer pathway gains weight and the search time decreases again to settle at the purely dimeric search time.

Assumptions and limitations

We made a number of simplifying assumptions in our coarse-grained theoretical model. For instance, we assumed that the DNA-binding energy of the dimer is the sum of the binding energies of the monomers. While dimerizing, the monomers may undergo conformational changes that affect the DNA-binding strength (36), possibly speeding up the dimeric search. In that case, the peak of the cooperative search time as a function of ω can be even more pronounced than in our model. For simplicity, we assumed identical binding properties of the two TFs A and B; however, this assumption is without loss of generality and the extension to asymmetric cases is straightforward. We performed the analysis reported here under the assumption of a nonspecific background, although we have formulated our model and the theoretical methods to also cover the more general case of a heterogeneous DNA background.

A brief analysis of the heterogeneous case has shown that the most significant effect of the heterogeneous background is to slow down the search time in all regimes. For our model, we have also assumed that the cooperativity between the TFs is mediated by a direct interaction. Indirect cooperativity mediated, e.g., by DNA bending or looping has the same steady-state properties as direct cooperativity in the low ω regime. However, these indirect mechanisms lead to different steady-state behavior at large ω-values and to different kinetics. A detailed analysis of these mechanisms is beyond the scope of this study.

Biological ramifications and examples

A central and robust result of our theoretical study is that one can distinguish three qualitatively distinct regimes of TF-TF interaction strengths for transcription regulation:

• 1.Weak interactions, with a cooperativity ω < 10³−10⁴, suffice to implement regulation functions with moderate fold-changes, of ∼10-fold, in the transcription level. In this regime, the cooperative search time is only moderately elevated above the search time of a single TF (also of ∼10-fold). In bacteria, where the search time of a single TF molecule is ∼1 min (11), the parallel cooperative search of 10–100 copies of each TF would then still result in fast responses on the minute timescale. The principal advantage of this regime from a design point of view is that TFs with weak interactions are flexible components, which can be used to control different genes in different ways, alone or cooperatively in various combinations (37). Each TF then only needs to be separately optimized for monomeric search (via the nonspecific protein-DNA interaction), while cooperative regulation by pairs of TFs is still sufficiently fast.
• 2.Interactions of intermediate strength, with ω-values in the approximate range of ω ∼ 10⁴−10⁶, lead to cooperative search kinetics that are prohibitively slow, due to an excessive amount of missed encounters. Recent single-molecule experiments have been able to monitor the search process of a single TF in vivo (11). Our prediction of slow cooperative search kinetics could, in principle, be verified using two-color fluorescence methods. Alternatively, one could measure the transcriptional response time of a synthetically designed, cooperatively regulated gene with a rapid reporter. We also expect that TF-TF interactions within this intermediate regime are avoided by cells. A test of this implication of our study will require a large dataset quantifying a significant subset of the TF-TF interactions in a model organism. To our knowledge, a quantitative high-throughput assay for TF-TF interactions is not yet available and remains as an experimental challenge in the field. Instead, we discuss several specific biological examples below.
• 3.Strong interactions, with a cooperativity ω > 10⁶−10⁷, allow high fold-changes and a passable response time at the cost of losing combinatorial flexibility: Suppose that each TF signals a different environmental cue, and a set of genes needs to be activated whenever A is present, whereas another, more specialized group of genes is to be activated only if both signals are present. In this situation, a strong heterodimer would not lead to a favorable regulatory design, because the regulation of the unconditional genes by A would be strongly affected by the presence of B. In other words, the strong cooperativity can lead to undesired cross talk. Nevertheless, this regime of TF-TF interactions is biologically interesting: For instance, strong homodimers can exploit the cooperative stability mechanism to improve the robust function of regulatory circuits (38). Also, in cases where the combinatorial flexibility described above is not needed, strong heterodimers could be used to perform a very sharp and AND-like signal integration. This signal integration can be made very rapid by tuning the nonspecific protein-DNA interaction of the TFs into a weaker regime, such that the dimer DNA binding ratio P_d/P_c is closer to the optimal value 1 for search on the DNA. As Fig. 4 shows, this would lead to a concomitant decrease of the monomer-binding ratio. For TFs that work in this regime, we therefore expect that monomers spend <50% of their time bound on DNA. So far, the DNA binding ratios of transcription factors have not been assayed on a large scale. Such an experiment would yield interesting clues about the design and the mode of operation of these TFs.

Finally, we discuss biological examples. Currently, 383 operons in E. coli are known to be transcriptionally regulated by two or more TFs (see Section S4 in the Supporting Material). However, it is not known what fraction of these regulatory interactions involves cooperative protein-DNA binding. One well-studied case of codependent activation is the melAB promoter, where CRP and MelR bind cooperatively and activate transcription (19). The interaction of CRP and MelR occurs via a weak surface contact and the binding of either is found to be reduced if the binding of the partner is impeded. In the presence of both, the transcription rate is 10-fold increased (19). This case is a good example for our regime 1.

It is interesting to note that the binding sites of CRP and MelR in the melAB promoter display a relatively poor match to the consensus sequence, which is consistent with our assumption that the target binding energies are evolutionarily tuned. Also, CRP is a well-known global regulator that controls many other genes in different ways, and hence the combinatorial flexibility achieved with a small cooperativity ω appears to be amply exploited by E. coli. Other examples of prokaryotic coactivation are the ansB promoter, activated by CRP and FNR (15), and the activation of the mapEP promoter by CRP and MalT (18,39). More generally, the regime 1 corresponds to the regulated recruitment mechanism for transcription regulation (29), which appears to be widely used in eukaryotes. Indeed, the case of the melAB promoter described above has been described as a bacterial version of eukaryotic enhanceosomes (19). A prokaryotic example for regime 3 may be the RcsA/RcsB heterodimer that is required to activate capsule expression through the RcsF phosphorylation cascade (40). Interestingly, RcsB can also from homodimers and regulate the transcription of other genes by itself, suggesting that this TF may be optimized to always search and function as a dimer (homo- or heteromeric).

Conclusion

We reported a biophysical analysis of the design principles for TF-TF interactions. The exploration of our theoretical model leads us to two functionally favorable regimes for the cooperativity ω, corresponding to weak, gluelike promiscuous interactions and very strong heterodimerization, respectively. Cells appear to implement both favorable regimes, but in different biological contexts. On the other hand, our model predicts that the search kinetics will be prohibitively slow at intermediate ω-values, at least when the protein copy number is small as is typically the case for transcription factors. Hence, the intermediate ω-regime appears undesirable in this functional context. This prediction could be tested with experimental approaches from single-molecule biophysics. Currently, there are only limited biochemical data available for the cooperativity values involved in transcription regulation, typically from in vitro experiments with selected DNA-binding proteins. Once more data become available, it will be interesting to see whether the intermediate ω-regime is indeed avoided.