Inference of seed bank parameters in two wild tomato species using ecological and genetic data

Abstract

Seed and egg dormancy is a prevalent life-history trait in plants and invertebrates whose storage effect buffers against environmental variability, modulates species extinction in fragmented habitats, and increases genetic variation. Experimental evidence for reliable differences in dormancy over evolutionary scales (e.g., differences in seed banks between sister species) is scarce because complex ecological experiments in the field are needed to measure them. To cope with these difficulties, we developed an approximate Bayesian computation (ABC) framework that integrates ecological information on population census sizes in the priors of the parameters, along with a coalescent model accounting simultaneously for seed banks and spatial genetic structuring of populations. We collected SNP data at seven nuclear loci (over 300 SNPs) using a combination of three spatial sampling schemes: population, pooled, and species-wide samples. We provide evidence for the existence of a seed bank in two wild tomato species (Solanum chilense and Solanum peruvianum) found in western South America. Although accounting for uncertainties in ecological data, we infer for each species (i) the past demography and (ii) ecological parameters, such as the germination rate, migration rates, and minimum number of demes in the metapopulation. The inferred difference in germination rate between the two species may reflect divergent seed dormancy adaptations, in agreement with previous population genetic analyses and the ecology of these two sister species: Seeds spend, on average, a shorter time in the soil in the specialist species (S. chilense) than in the generalist species (S. peruvianum).

The effective size of a population or species (N_e) defines its evolutionary potential because it determines the rate at which adaptive substitutions appear and get fixed (1), as well as the vulnerability to loss of genetic diversity by genetic drift. A fundamental question in plant evolutionary biology, and of practical relevance for conservation biology, is to understand how the census size of a population above ground (N_cs) is affected by ecological disturbances and how this process, in turn, affects the N_e (2). Habitat loss and fragmentation attributable to human activities are indeed acute problems for conservation of spatially structured populations because they reduce deme sizes (N_e and N_cs) and gene flow among demes. The genetic diversity, reflected by the N_e, of many plant (and invertebrate) species, can be seen as an iceberg. The tip of the iceberg is composed of individuals observable above ground (N_cs), whereas the major part of the diversity is accounted for by among-population differences (3, 4) and seed banks (5–8).

Most, if not all, plant and animal species exist as spatially structured populations (metapopulations) with many demes linked by migration, which may be subjected to extinction/recolonization (9). Depending on extinction/recolonization rates and the type of group founding events (migrant vs. propagule pool), genetic differentiation among demes may generate a higher genetic diversity (N_e) for the metapopulation as a whole than predicted by the sum of all individuals across demes (10). The reproductive mode (seed or egg dormancy), which is often described as a bet-hedging strategy in plants (11), invertebrates (Daphnia and mosquitoes), and microorganisms (12) to buffer against environmental variability (6, 13), also generates an increase of the N_e compared with the N_cs in two ways. First, low germination rates in the banks promote the storage of genetic diversity and the increase of N_e compared with above-ground plant populations (6–8), although slowing down the rate of evolution (5) and coevolution (14). Second, seed banks counteract habitat fragmentation by buffering against the extinction of small and isolated populations, a phenomenon known as the temporal rescue effect (15).

Evidence for seed dormancy adaptation (11, 13) and for the influence of seed banks on plant evolution over evolutionary time scales (16) is scarce because of the complex ecological experiments in the field needed to measure it (11, 16) and the complex genetics of these traits (17, 18). Moreover, evidence for seed banks to increase the observed molecular diversity compared with expectations from the above-ground census size (15, 16) can be confounded by the spatial structuring of populations, where a significant part of the diversity may be attributable to population differentiation. Indeed, in a Wright–Fisher model of reproduction, both seed banks and spatial structure can be seen as a similar departure from random mating because there is separation of individuals into either different age classes (19) or different spatial demes (20). Developing an approximate Bayesian computation (ABC) method (21), which combines SNP data and ecological information, we demonstrate that it is possible to estimate the rate of germination and parameters of metapopulation structure (minimum number of demes and migration) jointly. Our study relies on computing the deme census size from ecological data. This value characterizes the expected genetic diversity per deme in absence of a seed bank, as well as the harmonic mean of the annual carrying capacity of the above-ground plant population (6).

The contribution of spatial structure to genetic diversity is studied using three types of sampling schemes, which allow us to infer the role of mutation, migration, and random genetic drift in shaping genetic diversity at different time and spatial scales (22). The different sampling schemes are defined as follows (22). A local population sample consists of several individuals per deme, the pooled sample combines all local population samples, and the species-wide sample is composed of a single individual per population, where many demes across the species range are sampled. First, the local population samples reflect the past history of the demes (3, 20) as well as local selective events, such as purifying selection (23). This short coalescent phase within demes integrating few migration events is called the “scattering phase” (20). Second, the major part of the metapopulation coalescent tree is contained in the so-called “collecting phase” (20). Species-wide events, such as size fluctuations, are thus expected to be reflected in the collecting phase (22). Finally, the pooled samples integrate both the collecting phase and the scattering phase of the metapopulation coalescent. As such, the difference between the species-wide and pooled samples indicates the relative weight of the scattering phase (short external branches in the tree) compared with the collecting phase (22).

We study two strictly outcrossing wild tomato species (Solanum chilense and Solanum peruvianum) found in western South America. They exhibit considerable molecular diversity despite their fragmented habitats (24) and differ in their ecological niches (25–27). S. chilense is found in dry to very dry habitats in southern Peru and northern Chile (25, 28–30), but S. peruvianum occurs in a variety of habitats, ranging from coastal plains with dry to mesic (lomas) environments (25, 26, 29, 31). There is empirical evidence for shorter germination rates under stressful conditions (temperatures below 15 °C) of S. chilense accessions compared with S. peruvianum (32, 33), and such traits are heritable and governed by common quantitative trait loci (QTL) in these species (18). These two sister species thus represent a good model to test if habitat diversity influences seed dormancy (i.e., different germination rates) in metapopulations with different spatial structuring.

Results and Discussion

Estimates of Deme Census Sizes and Number of Demes.

The ecological data were extracted from the database of the Tomato Genetics Resource Center (TGRC; http://tgrc.ucdavis.edu/) at the University of California, Davis. A total of 75 accessions of S. peruvianum and 107 accessions of S. chilense census sizes of above-ground populations are reported, based on over 5 decades of field work by C. M. Rick [e.g., Rick and Lamm (28)] and multiple investigators in Peru and Chile (30). This database provides a good description of the current range distributions of these species (25, 27). We assessed the mean census size per population (N_cs) for each species by fitting a negative exponential regression to the distribution of census sizes using R software (SI Appendix, Section 1 and Fig. S1). The precision for the reported census sizes was found to vary depending on year of sampling and size of the population (SI Appendix, Section 1). We took this uncertainty into account and computed N_cs to be between 44 and 185 for S. peruvianum and between 33 and 154 for S. chilense (SI Appendix, Table S1), where these values define priors on N_cs in the ABC analyses.

In addition, based on the spatial distribution of sampled accessions and ecological correlations with climatic data (25, 26), we calculated the total number of populations as 526 for S. peruvianum and 428 for S. chilense. These estimations of the range size (km²), potential niche breadth, and percentage of niche filling of each species are based on environmental variables (mean annual precipitation, mean annual temperature, precipitation during seasons, sun exposure, topsoil pH, and effective soil depth) best explaining each species’ distribution. These findings are in line with previous reports of a wider geographic and ecological range (26, 27, 29) and a larger effective population size (34) for S. peruvianum. Some demes might show high rates of extinction/recolonization or levels of geographic isolation, and thus may not contribute to the N_e of the metapopulation. The calculated ecological number of populations is then expected to represent an overestimation of the effective number of demes (9, 20).

Population Genetics Analyses.

We used sequences from seven loci with a total of 350–450 SNPs (24, 35) for three types of spatial sampling. First, 10–12 sequences per population previously obtained (24, 35) for each of three populations of both S. peruvianum (Tarapaca accession no. LA2744 from the TGRC, Nazca, Canta) and S. chilense (Tacna, Moquegua, Quicacha) are referred to as “local” samples (22) (details are provided in SI Appendix, Section 2 and Table S2). Second, we defined the combined set of these three samples as the “pooled” sample per species (22), which thus consists of 30–34 sequences. Third, we generated a unique set of sequences of one allele per accession at the same set of loci, the “species-wide” sample, for 14 and 10 accessions obtained from the TGRC and distributed uniformly over the range of S. peruvianum and S. chilense, respectively (list of accessions is provided in SI Appendix, Table S3).

The genetic diversity in the species-wide sample (θ_{w_sw} = 20.04 and 12.62) is smaller than that of the pooled sample (θ_{w_pooled} = 22.37 and 17.13, respectively, for each species) in both species, with S. peruvianum showing the higher genetic diversity (SI Appendix, Tables S5–S7). The average Tajima's D (36) of the species-wide sample, D_sw = −0.95 and −0.17, is more negative than that of the pooled sample, D_pooled = −0.91 and −0.04, in both species at synonymous sites (SI Appendix, Fig. S2 and Tables S5–S7) as expected from a previous theoretical study (22), although variability is found across loci (SI Appendix, Fig. S3). However, when using silent sites and all sites, the pooled and species-wide samples show lower Tajima's D values indicative of the action of purifying selection at intronic and nonsynonymous sites (SI Appendix, Figs. S2 and S3). Note that the strength of purifying selection is larger in S. chilense than in S. peruvianum as reflected by the differences in D_pooled between synonymous sites and all sites in each species (23). To avoid bias attributable to the action of purifying selection at these loci in our ABC inference, the following summary statistics were used: Tajima's D at synonymous sites [D_sw, D_pooled, and population sample (D_pop); values are provided in SI Appendix, Tables S5–S7], and the fixation index (F_ST), θ_w at all sites (θ_{w_sw} and θ_{w_pop}; values are provided in SI Appendix, Tables S5–S7). We also defined a previously undescribed statistic, ΔD = D_sw − D_pooled, which reflects the difference in the shape of the coalescent between these samples (length of scattering and collecting phase). For example, in a metapopulation with constant size, the ΔD value is expected to be negative and to increase (up to 0) with rising levels of gene flow (22).

Demographic Model for Each Species.

We used the model choice procedure of ABC (based on the best 1,000 simulations of 2,000,000 for each model) to decipher the species’ demographic history. Three possible models were tested under an island model of a metapopulation with a seed bank: a past species expansion, a constant species size, or a species decline (crash of species size). We computed the posterior probability for these three demographic scenarios assuming that each species is represented by an island model with a high number of demes, 428 in S. chilense and 526 in S. peruvianum, linked by migration rate κ (between each pair of demes). Each deme possesses a seed bank defined by germination rate b with a uniform prior between 0 and 1, and all demes have an identical census size, N_cs, defined by a uniform prior between 44 and 185 for S. peruvianum and a uniformed prior between 33 and 154 for S. chilense (other parameters are provided in SI Appendix, Table S8, and prior ranges are provided in SI Appendix, Table S9).

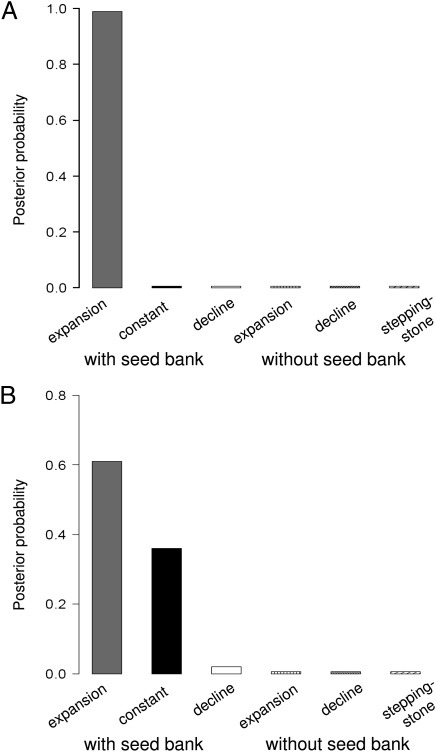
The D_pooled and D_sw values indicate a likely past demographic expansion in S. peruvianum [Bayes factor (BF) > 1,000, Fig. 1A] and possibly in S. chilense (Fig. 1B; BF = 1.7 for the model with expansion against constant size, BF = 30 for the model with expansion against decline). The possible past range expansion of S. chilense may be older or of smaller magnitude than that of S. peruvianum, explaining the higher value observed for D_sw. Note that the relatively small BF (37) supporting a weak past expansion in S. chilense contrasts with a previous estimation of a strong expansion (22). However, this latter inference was based on the frequency spectrum of silent sites (D_pooled at intronic and synonymous sites), a quantity shown to be affected by purifying selection (23).

Fig. 1.

Statistical evaluation of demographic scenarios indicated by the posterior probability for each model. Three types of past demographic events (constant population size, expansion, and decline) are tested with a seed bank, and two (expansion and decline) are tested without a seed bank under an island model of a metapopulation. The last model is a stepping-stone model with expansion. S. peruvianum (A) and S. chilense (B).

Evidence for Seed Banks.

Two alternative scenarios were evaluated to test for the existence of a seed bank in both species. First, we compared the best demographic scenario estimated above (Fig. 1) with a model without a seed bank with past expansion. The models without seed banks were examined with identical priors on N_cs per deme and a similar number of demes as above (526 and 428), and also with 1,000 demes. We tested the hypothesis that increasing the number of demes may generate additional overall genetic diversity in the metapopulation (20), compensating for the absence of a seed bank. Models with a seed bank were clearly chosen in each species (BF > 60 against alternative scenarios, Fig. 1). This demonstrates that increasing the number of demes to unrealistically high values (here, 1,000 being twice the number estimated from ecological data) does not generate the high levels of polymorphism observed in these species. As an extension, we also simulated a linear one-dimensional stepping-stone model with species expansion but without seed banks. This model had a symmetrical migration rate κ (between each pair of demes) and a similar number of demes as above (526 and 428), and sampled demes were uniformly distributed over the whole range. It is expected that a stepping-stone model may produce higher genetic differentiation among demes, and thus generate higher overall genetic diversity at the collecting phase level. This model was also clearly rejected (BF > 1,000 against this scenario in both species, Fig. 1), because both the species-wide and local diversity were too low or the F_ST was too high to explain the observed data.

The second alternative scenario was a model without a seed bank but assuming a large ancestral population shrinking at some time in the past with simultaneous population subdivision into 428 or 526 demes and 1,000 demes (mimicking habitat loss and fragmentation). This model was rejected by the model choice procedure in both species (BF for model with a seed bank >1,000 in S. peruvianum, Fig. 1A; BF = 215 in S. chilense, Fig. 1B), because even though it is possible to generate high genetic diversity (θ_{w_sw} and θ_{w_pop}), the Tajima's D for the species-wide sample (D_sw) is higher than that of the observed data (−0.95 in SI Appendix, Table S5a and −0.17 in SI Appendix, Table S5b) for most simulations. As a special case, however, running an additional 1,000,000 simulations, we found that a very recent crash less than 90 generations ago may generate very few datasets (less than 50) fitting our observed data. We explain this as follows: (i) ancestral diversity contained in a large panmictic population fragmented recently into 1,000 demes may explain the large current effective population size without seed banks, and (ii) the random process of coalescent simulations can generate very few datasets with negative D_sw because very recent demographic events have not yet left their signature at the DNA level (4). However, because the number of simulations fitting the observed data is small, a very recent crash without a seed bank may not be a likely scenario.

Inference of Species Germination Rates.

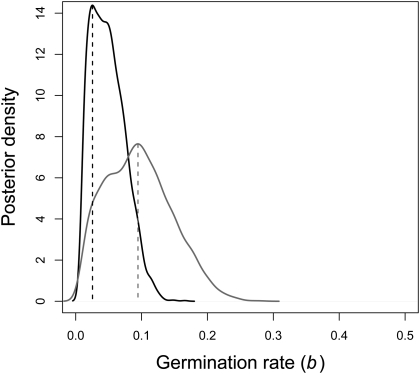
S. peruvianum is estimated to have a more pronounced effect of the seed bank, that is, a lower germination rate [b = 0.03, 95% confidence interval (CI): 0.011–0.103] than S. chilense for which b = 0.093 (95% CI: 0.016–0.2; Fig. 2; Kolmogorov–Smirnov test, P < 0.001). On average, seeds would spend 12 generations in the seed bank for S. peruvianum and 9 generations in the seed bank for S. chilense. Because these species are short-lived perennials, 1 generation lasts between 1 and 7 y (34). We also document the posterior density distributions for the migration rate, demographic parameters (time of expansion and expansion factor), and nuisance parameters N_cs and μ in SI Appendix, Table S10 and Figs. S4 and S5. S. peruvianum shows a signature of an at least sevenfold past expansion occurring at least 700,000 y ago, assuming 1 generation per year (lower bound of CI in SI Appendix, Fig. S4).

Fig. 2.

Posterior distributions of the germination rate (b) for each species. These curves represent the posterior densities of the germination rate obtained under the best demographic model by the ABC analysis for S. peruvianum (black) and S. chilense (gray). The mode of each posterior distribution is shown with a dashed line.

Influence of the Number of Demes on Our ABC Estimates.

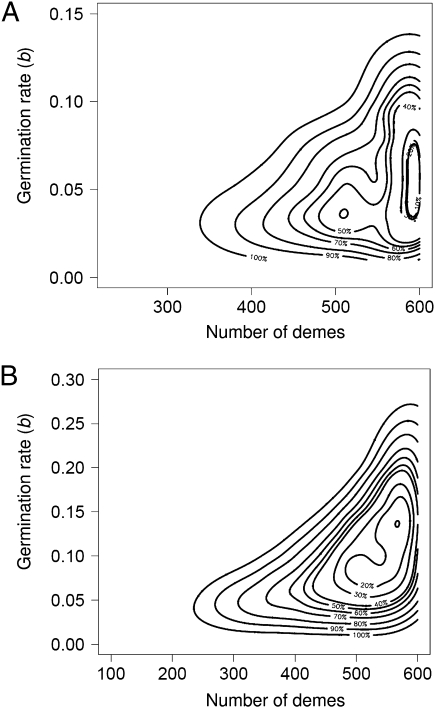
We studied how uncertainties in the effective number of demes may influence the estimates of the germination rate (b). Simulations were run varying the number of demes from 100 and 600 (overestimate from ecological data) for S. peruvianum and S. chilense (by steps of 100 and 2,000,000 simulations per number of demes). In other words, the choice of the number of demes suggests that the number of accessions sampled over 50 y at the TGRC (118 and 135) is a subset of at least 20% of all S. peruvianum populations and 25% of all S. chilense populations. We treated the number of demes as a parameter of the model and performed the ABC estimation procedure based on the best 2,500 datasets (joint posterior densities in Fig. 3). We show that a minimum number of 200–300 demes is necessary in both species (Fig. 3), meaning that small numbers of demes cannot explain the high observed genetic variability (θ_{w_sw} and θ_{w_pop}). By increasing the number of demes above 400 in S. peruvianum (Fig. 3A, 80% quantile) and above 300 in S. chilense (Fig. 3B, 80% quantile), a larger range of values for the germination rates is estimated. This is because increasing the number of demes generates higher genetic diversity in the metapopulation (20), and numerous combinations of migration rates and germination rates become likely to fit the observed data. Nonetheless, when accounting for uncertainties about the number of demes, the joint posterior distributions for germination rates are different between the two species (Hotelling T² test, P < 0.001; SI Appendix, Section 6) and the mode estimates for b are 0.058 in S. peruvianum (Fig. 3A) vs. 0.135 in S. chilense (Fig. 3B).

Fig. 3.

Bivariate density representation of the joint posterior distributions for the number of demes and the germination rate (b). The contour lines represent the quantiles of 2,500 simulated datasets for the two species under the chosen demographic scenario. S. peruvianum (A) and S. chilense (B).

Usefulness of Different Sampling Schemes.

We briefly summarize the respective contributions of genetic and ecological data in disentangling the effect of the seed bank, number of demes, and migration on the various model choices and parameter estimates. The observed high values of local diversity (θ_{w_pop}) in the three sampled populations per species compared with the low census sizes indicate the necessary existence of seed banks. The high local genetic diversity could not be obtained by just increasing the total number of demes in an island model or by considering a stepping-stone model because this would require levels of gene flow (κ) that were incompatible with observed F_ST values (correlation between κ and F_ST is shown in SI Appendix, Fig. S6A). The species-wide sample diversity (θ_{w_sw}) specifies the length of the collecting phase (20), a neutral coalescent phase that depends on the number of demes, migration among demes (κ), and germination rate (b). The shape of the coalescent tree of the collecting phase (here, D_sw) is indicative of the whole-species past demography (22) (correlation between expansion factor and D_sw in SI Appendix, Fig. S6A). Finally, the difference between the frequency spectra of the species-wide sample and pooled samples (in terms of D_sw and D_pooled) depends on the characteristics of the spatial structure (based on κ) and past demography of the species (22) (correlation between F_ST and ΔD is shown in SI Appendix, Fig. S6A). The difference in the level of genetic diversity (θ_W) and Tajima's D between the species-wide (θ_{w_sw}, D_sw) and pooled (θ_{w_pooled}, D_pooled) samples is a function of the degree of population structure [number of demes, migration, and mutation rates (38)] and old demographic events at the species level (22). Similarly, differences between local and pooled samples indicate local deme size and recent demographic events (39). Interestingly, the two sampling schemes (species-wide and pooled) show similar frequency spectra. This reveals that the three studied populations distributed over part of the range of each species (24, 35) accurately sample the collecting phase of the metapopulation tree. Note, however, that our metapopulation models are simple with regard to the spatial structure, assuming, for example, equal size for all demes or symmetrical migration rates in both the island and stepping-stone models. We performed a short simulation study to demonstrate that assuming an equal size, N_cs, for all demes in a metapopulation generates higher genetic diversity compared with a metapopulation with deme sizes being exponentially distributed with a similar mean N_cs (SI Appendix, Section 8). Varying deme sizes alone in a metapopulation is thus unlikely to produce the high observed genetic diversity without the need for seed banks. On the other hand, more complex models with variable migration rates might be able to generate additional genetic diversity. However, these models would have a large number of parameters that could not be estimated reliably with the current data under the ABC framework.

Bet-Hedging Strategies in Wild Tomato Species?

It has been suggested theoretically (6, 7, 13) and shown empirically (11) that adaptation for seed dormancy (variable germination rates) can be a bet-hedging strategy that serves to magnify the evolutionary effect of good years and to dampen the effect of bad years. Bet-hedging is defined here as a strategy in which adults release their offspring into several different environments, maximizing the chance that some will survive or find suitable habitats (13).

The lower germination rates in S. peruvianum may reflect a different adaptive strategy in response to more unstable environments compared with S. chilense (13). It has been shown that S. chilense has shorter dormancy in stress conditions (i.e., low temperatures), than S. peruvianum (32, 33), and variability for dormancy is a heritable trait in these plant species (18) as well as in others (17). Combining these results, we suggest that (i) S. peruvianum may occur in habitats that are more variable across years than those of S. chilense, although temporal variability of climatic conditions has not yet been included in ecological studies (25, 30), or that (ii) geographic variability of habitats may promote a longer seed dormancy in S. peruvianum as a generalist strategy to colonize different demes/habitats (13) and reduce risks for extinction following the temporal rescue effect (15). On the other hand, these two wild tomato species differ in their life cycle, with S. chilense being characterized by a generation time of 3 to 7 y (29, 30, 34) and S. peruvianum being characterized by a more variable generation time of 1 to 7 y (34). Because longer lived perennials are less prone to form seed banks than annual plants (40), part of the difference in germination rates between these two species might also be attributed to differences in generation time. In addition, strong differences in abiotic factors may explain part of the differences in germination rates between these two species. Note that the significant difference in estimates of b should be taken with caution, because the credibility intervals are found to overlap (Fig. 2).

S. chilense is a specialist species with a reduced range of habitats with regard to important abiotic stresses (e.g., cold, drought) (25–27). Shorter seed banks in S. chilense would decrease local and species effective population sizes (24, 34) and would potentially increase F_ST among populations (8), resulting in an enhanced potential for local adaptation at genes involved in abiotic stress tolerance, such as drought resistance in desert-like habitats (26, 29–31). As a result, such specialist species would evolve lower degrees of plasticity in coding sequences and for gene expression, reflected by higher rates of purifying selection (23). In contrast, S. peruvianum, which is found in a wide range of habitats, may show bet-hedging adaptation for seed banks with smaller germination rates, with seeds less prone to germinate under stress conditions (32, 33). Smaller germination rates would increase local (24) and species effective population sizes (24, 34) and decrease the potential for local adaptation. More effective seed banks slow down the rate of evolution (5, 7), potentially explaining the lack of evidence for genomic signatures of positive directional selection for abiotic stress tolerance in this species (26, 31). Conversely, small germination rates promote genetic diversity at host and parasite genes involved in coevolutionary interactions (14), making balancing selection at plant R-genes more likely to occur and to be observable in S. peruvianum (41).

Materials and Methods

DNA Sampling and Sequencing.

Seven unlinked nuclear loci used in this study (CT066, CT093, CT166, CT179, CT198, CT251, and CT268; SI Appendix, Table S4) are single-copy cDNA markers originally mapped by Tanksley et al. (42) in genomic regions with different estimated recombination rates (43). The gene products putatively perform key housekeeping functions, and purifying selection was thus suggested to drive their evolution; no locus, however, showed a signature of positive selection (23). PCR primers and PCR conditions followed those of the previous population genetic studies (24) of the same loci (details are provided in SI Appendix, Section 2); PCR primer information can be accessed at http://evol.bio.lmu.de/downloads.

Statistical Analyses.

To summarize the observed and simulated datasets, we computed the following statistics for both species: (i) the average value of θ_w (44) across loci and populations, called θ_{w_pop}; (ii) the average population sample Tajima's D (D_pop) across loci (36); (iii) the average F_ST value across populations [calculated as in the study by Hudson et al. (45) as a measure of migration across demes (38) based on the local population sample]; (iv) D_pooled, the average Tajima's D across loci for the pooled sample; (v) θ_{w_sw}, the average θ_w across loci at the species-wide level; and (vi) D_sw, the average Tajima's D across loci at the species-wide level. All statistics were computed using the Libsequence C++ library (46) for all sites (silent and synonymous sites), excluding gaps and multiple hits. Trial simulations revealed that the variance of these statistics across loci, and level of linkage disequilibrium, measured as the Z_ns statistic, were not informative.

Coalescent Model with Metapopulation and Demography.

Following previous studies on wild tomato species and their spatially structured habitats (24, 25, 35), we assumed that each species is composed of a large number, n_d, of effective demes [much larger than the number of sampled demes (20)] linked by migration of pollen with effective migration rate κ. Except when indicated, we used an island model without extinction/recolonization for simplicity, where all demes contribute equally to the migrant pool and all demes have the same size (N_cs). Each species, currently existing as a metapopulation, was assumed to be derived from a single ancestral panmictic population with size S_anc that split into n_d demes at time t_event in the past. The current metapopulation has n_d demes, each containing N_cs individuals, and its census size is S_current = N_cs × n_d. Three possible demographic scenarios were considered. First, expansion (up to 100-fold) of the species occurred if the ratio of the current to the ancestral census size (S_current/S_anc) was larger than 1. Second, the species size remained constant if the ratio S_current/S_anc was equal to 1. Third, the species experienced a population decline (up to 25-fold in magnitude) if the ratio S_current/S_anc was smaller than 1.

Coalescent Model with a Seed Bank.

The coalescent process with a seed bank was modeled within each of the n_d demes as a haploid Wright–Fisher dynamic (47) occurring in a population with constant census size N_cs. Seed germination was modeled as a memoryless process occurring at rate b per seed per generation (48). The germination probabilities followed a geometrical distribution (11) in which an individual plant above ground originated with the probability 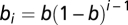from seeds produced at a given generation i (details are provided in SI Appendix, Section 3). The seeds remained in the soil for a maximum of m generations. Trial simulations revealed that it was not possible to estimate m independent of b if m is too small (m < 20). We fixed m = 40 based on information from the TGRC that seeds can be kept in the laboratory storage rooms for over 30–50 y and are still able to germinate. Additional ABC analyses revealed that our parameter estimates do not vary in the function of m when it is sufficiently large (m > 30).

It was shown that the rate of coalescence is decreased in a seed bank by a factor β₁², which is the probability that two lineages merge simultaneously in a single plant above ground (47). In addition, seed banks decrease the rates of mutation, recombination, and migration by a factor β₁ because these processes act only on single genealogical lineages in above-ground plants. Following the results by Kaj et al. (47), β₁ is defined as the inverse of the mean expected time that seeds spend in the soil (0 < β₁ < 1):

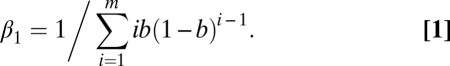Note that this equation assumes the sum of the germination probabilities over m generations is equal to 1 (47). The mutation rate is not thought to increase in the seed bank with the age of seeds (8, 15). The model parameters are provided in SI Appendix, Table S8. We implemented a modified version of Hudson's ms (49) to perform coalescent simulations with a metapopulation and seed bank, as well as a modified version of msABC (50) to perform ABC analyses with seed banks (software available at http://www.bio.lmu.de/˜pavlidis/home/?Software).

ABC.

Our ABC algorithm is composed of three steps: simulation of datasets, model choice, and parameter estimation. The simulation step consisted of simulating 2,000,000 datasets identical to the length of the loci, recombination rates, and sample sizes of our data for every evolutionary scenario (SI Appendix, Section 2). Recombination rate (r) was given as the local rate of crossing-over per site per generation as estimated by Stephan and Langley (43). Each evolutionary scenario was defined by a set of parameters (SI Appendix, Table S8) characterized by prior distributions (SI Appendix, Table S9 a and b), from which we sampled to perform coalescent-based simulations and computed summary statistics using the GSL C++ library and the Libsequence C++ library (46). A mutation rate of 5.1 × 10⁻⁹ was estimated at the same loci from divergence between the two species based on analyses of all sites (34). However, this value is likely to underestimate the neutral diversity because of the effect of purifying selection acting at these loci (23), and uncertainty is introduced by enlarging the uniform prior distribution for μ between 5 × 10⁻⁹ and 5 × 10⁻⁸ .

The model choice procedure is based on a weighted multinomial logistic regression (51) computed on the 1,000 simulations for which δ, the Euclidean distance between the observed summarized dataset and the simulated datasets, is smallest (21). BFs were calculated as the ratio of the posterior probabilities for the tested models (37).

For the parameter estimation procedure, we used the simulated 2,000,000 datasets under the best demographic model for each species (priors are provided in SI Appendix, Table S9). We applied a partial least-square (PLS) transformation to the simulated and observed sets of statistics (52, 53), which reduces the uninformative signal from the dataset and breaks down the correlations among the different summary statistics. The PLS latent components with 10,000 simulated datasets were constructed using the code available in the ABCtoolbox package (54). The best number of PLS components, four, was obtained by investigating the decrease of the root mean square error for every parameter as a function of the number of PLS components (53) (SI Appendix, Section 4). Finally, we estimated posterior distributions (mode and 95% credibility intervals) of each parameter by applying the locally weighted multivariate regression method (21) implemented in the ABCest program based on the 2,500 datasets closest to the observed data (55) (SI Appendix, Section 4).