A novel non-overlapping bi-clustering algorithm for network generation using living cell array data

Motivation

The living cell array quantifies the contribution of activated transcription factors upon the expression levels of their target genes. The direct manipulation of the regulatory mechanisms offers enormous possibilities for deciphering the machinery that activates and controls gene expression. We propose a novel bi-clustering algorithm for generating non-overlapping clusters of reporter genes and conditions and demonstrate how this information can be interpreted in order to assist in the construction of transcription factor interaction networks.

1 INTRODUCTION

One of the goals of molecular biology is deciphering the underlying mechanisms that give rise to the observed experimental responses to injury, disease or drug administration. In most long term compensatory responses, an organism responds to changes in its environment by altering its gene expression and therefore the relative levels of different proteins or enzymes which regulate key cellular processes. Therefore, understanding the underlying transcriptional regulation would give insights as to why organisms respond in the fashion that they do, and offer possible ways of altering the responses for a more desirable outcome.

The general mechanism by which transcriptional regulation occurs involves an incoming signal which activates a transcription factor through a mechanism such as phosphorylation or dimerization. This activated complex then translocates into the nucleus and binds to the promoter region of certain genes in the genome which then either activates or represses the transcription of a given gene. The complexity in the system arises from the fact that genes which are activated can themselves be transcription factors which in turn regulate other genes, or code for an enzyme which degrades the original signal.

The methods normally used for deciphering the underlying network architecture fall under three primary categories. The first category consists of predicting the overall network architecture either through computational means or through experimental data such as Chip-Chip experiments (Lee et al., 2002). These techniques attempt to decipher the network structure by first identifying the regulators and genes which they regulate. The second method for understanding transcriptional networks falls under the category of utilizing gene expression data to create a network where a link is drawn if two genes are co-expressed under the experimental conditions (D’Haeseleer et al., 2000). There exists a third technique with attempts to reconcile the results of these two techniques.

The strictly computational techniques focus upon the prediction of transcription factor binding sites and then using these predicted transcription factor binding interactions to generate a network (Pritsker et al., 2004). These techniques however suffer from the inaccuracies associated with computational predictions and therefore the network derived from the results can be questionable. Secondly, even if the predictions are accurate, what these techniques yield is a set of all possible connections, of which only a few may be active at a given time due to the complexities of transcription factor activation or through processes such as cooperative binding of transcription factors (Janson and Pettersson, 1990). Chip-Chip experiments on the other hand attempt to derive connections by identifying through fluorescence-labeled transcription factors which transcription factors bind to which genes, and constructing a network from this data (Lee et al., 2002). Such techniques have been successful in simple organisms such as yeast, but ambiguities in the promoter region of more complex species is problematic for this type of experiment. In mammalian systems, promoters that lie more than 5k away from the transcriptional start site may have an effect upon the transcription of the gene (Kirmizis and Farnham, 2004), and therefore the experiment may not have captured all relevant promoter regions. Additionally, it had been shown that transcription factors can bind in the coding region of a given gene in Chip-Chip experiments calling into question the process of immobilizing a given DNA strand as preparation for the binding (Wormald et al., 2006) and removing the contribution of in vivo DNA configuration on transcription factor binding.

Expression data can be used to build a network by making the assumption that genes which are co-expressed probably have a causal link between them. Techniques such as Boolean networks have been applied in the creation of such network but oftentimes offer contradictory network structures than the networks derived from the experimental methods (D’Haeseleer et al., 2000).

Attempts have been made to reconcile the two different regulatory structures as well as quantify the links between the regulators and the genes which they regulate. Methods such as Module Networks attempt to resolve the differences in the two networks (Segal et al., 2003). However, even with the reconciliation of two disparate solutions, there still exists a great deal of ambiguity in the results, i.e. the possibility that there exist multiple transcription factors which may be co-regulating a set of co-expressed genes. Techniques such as NCA which quantify the links given the structure have shown that multiple structures can reconstruct identical expression profiles (Brynildsen et al., 2006). This is a problem because multiple structures can be shown to have the exact same error in reconstructing the gene expression data.

The crux of the difficulty in obtaining these gene regulatory networks is the fact that individual contribution of a given transcription factor to the expression level of a given gene is unknown. This is because researchers are essentially solving an ill posed problem, which results in the fact that one is unable to determine the correctness of multiple structures. Essentially, researchers have been attempting to solve for more parameters than can be justified in the data. The living cell array (LCA) (King et al., 2007; Thompson et al., 2004; Wieder et al., 2005) simplifies the process of computationally determining the structure by allowing for the measurement of activated transcription factor activity and its effect upon the expression level of a gene. With information as to the overall expression, it becomes possible not only to identify the underlying transcriptional network, but also to quantify the links between the genes and their associated transcription factors.

1.1 Living cell array

The living cell array is a microfluidics device which allows the precise control of both molecular cellular signals as well as the seeding of cells from a certain population. The apparatus is more comprehensively described in the original paper (King et al., 2007). In essence, the LCA device contains hepatocytes which were transfected with a reporter gene that transcribes a fluorescent protein when activated by a given transcription factor.

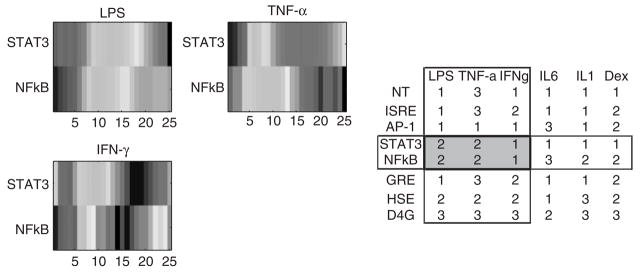
The promoter regions for these genes were constructed in such a manner where only its specific transcription factor will cause the activation. However, in spite of this design, it was found that there was significant cross talk, for instance the activation of the reporter gene for IL-6 (STAT3 promoter) being activated as well by TNF-α. The possibility of nonspecific binding of TNF-α that normally binds to the response element sequence GGGAATTTCC to the response element sequence for STAT3 (TTCCCGAA) was examined. While this is possible due to a common run of the short TTCC motif, this possibility seems to be unlikely.

An alternative explanation being explored is that the nonspecific activation of the reporter gene can occur via a secondary mechanism, i.e. the transcription of its associated transcription factor due to the effect of another transcription factor. To examine this possibility, a tri-clustering approach to determine which genes are co-expressed over a variety of conditions has been formulated. If the reporter gene is highly co-expressed over a range of different conditions, then it would suggest that there is a definite link between the two transcription factors in terms of their activation.

The tri-clustering formalism is an extension of the bi-clustering formalism except that one clusters over conditions, genes as well as time. For the purposes of deciphering the LCA, time can be treated independently and therefore a preprocessing clustering step can be performed to reduce the overall formulation into a bi-clustering problem.

Our attempt at handling data which can be tri-clustered is different from the TriCluster algorithm (Zhao and Zaki, 2005), in which the time vectors are all treated independently. For the LCA, the interest is which transcriptional events are tightly coupled and therefore have similar time expression profiles within the different conditions.

Given the artificial construction of the reporter genes, the direct effects of a given activator/transcription factor is clear. What is less clear are the effects of indirect activation (IDA). Under all of the different activation conditions, all of the reporter genes appear to be activated to a certain extent. The primary question is therefore, what the indirect links are. From the initial results obtained from the LCA (King et al., 2007), it would appear that under all of the conditions, there is significant activation of the reporter genes. It may be possible to isolate transcription factors which are tightly coupled, where the activation of one transcription factor causes the activation of a second transcription factor, or which are complementary, i.e. the activation of one system can be accomplished via the activation of any one in a set of transcription factors. This essentially allows for the identification of the mechanism behind the cross-talk and addresses issues such as why blocking a specific regulator does not always lead to the blocking of a given cellular response.

2 METHODS

2.1 Bi-clustering

Bi-clustering, or condition-specific clustering, attempts to isolate genes that are co-expressed under a specific set of conditions (Cheng and Church, 2000). Bi-clustering is nominally performed over a set of genes versus conditions with only a single value per condition. However, in the given dataset, each gene/condition combination is described as a time series. In bi-clustering, genes that have similar expression values under a given condition are considered as possible candidates to be clustered together for that specific condition. Given the temporal expression data, the temporal expression can be simplified into an integer, so that gene expression profiles with the same integer would have similar expression profiles. This could have been accomplished in a variety of ways from hashing-based methods (Lin et al., 2003), to standard clustering algorithms in which the cluster memberships are used to assign an integer denoting similarities in the expression profiles of different genes under a given condition.

For this problem, k-means clustering with a cosine similarity metric (Rahnenfuhrer et al., 2004) was selected. K-means was run with four clusters, the minimum number of clusters needed for consistent clusters over multiple runs. Therefore, the temporal expression profiles were converted into integers which indicate the similarity under a given condition of two or more genes.

Bi-clustering itself is NP-Hard (Jiang and Zhang, 2002), and therefore most of the algorithms which have been used for bi-clustering are heuristics. The most obvious problem with most of the techniques which are based upon heuristics is the fact that they do not solve the problem to global optimality. However, just as important is the inability for most of the heuristic-based methods to identify an arbitrary number of over-lapping bi-clusters. In most of the bi-clustering algorithms, finding multiple solutions involves removing a previously found bi-cluster from the dataset through techniques such as setting all of the values in a previous found bi-cluster to random numbers therefore breaking up any relationships within that cluster. There has been some work in finding overlapping clusters (Liu and Wang, 2007). However, such techniques are limited in the fact that one must determine before the structure of the overlap such as overlapping percentage as well as the number of possible overlapping structures within the data, something which is not known a priori.

The issue of overlapping bi-clusters is important because with non-overlapping bi-clusters, the networks which can be reconstructed from expression data will be a set of disjoint and independent networks. This contradicts with the general notion that transcriptional networks form highly interconnected networks (Jeong et al., 2000). Therefore, networks generated from the current algorithms cannot fully capture the level of interconnectedness present in transcriptional networks. The advantage of utilizing a math programming approach is that it is very easy to exclude previous solutions and re-solve the problem to find other bi-clusters which may overlap with a previous solution. Without overlapping bi-clusters, the overall network is then reduced to a set of independent cliques of which the most complex network which can be created is a feed forward network.

The biggest issue that complicates the search of overlapping clusters is illustrated in Figure 1. The primary problem is that after an optimal solution is found and that solution is rejected, there exists an overlapping cluster which is wholly a subset of the original solution. A mixed integer optimizations framework was selected due its ability to explicitly model constraints as well as solve the problem to global optimality, something which cannot be guaranteed with the standard heuristic-based method. In this mixed-integer framework, it is possible to eliminate a solution as well as all subsets of its solution through a modified system of integer cuts.

Fig. 1.

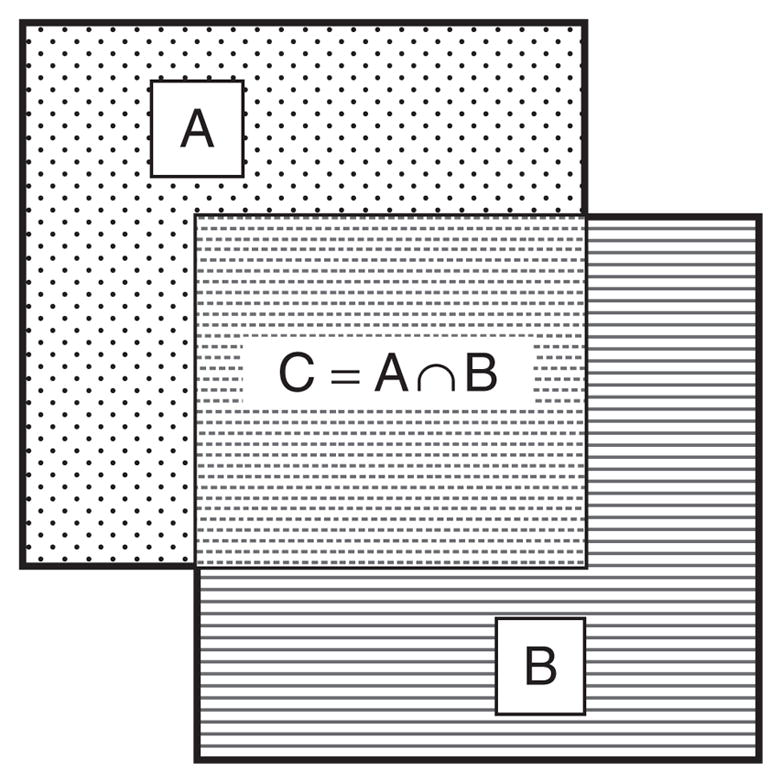
The problem of overlapping bi-clusters: given two bi-clusters, A and B, the intersection of the two bi-clusters, C should be eliminated.

The LCA experimental results had eight conditions two of which represented composite stimulus corresponding to inputs with multiple factors which were excluded. The overall goal of the LCA has been the generation of a network which can be used for the quantitative prediction of gene activity, and these conditions were excluded to be used as a testing set to determine how well our network can predict overall activity given an arbitrary input. At this point, the primary concern is whether a rational network can be generated, and the quantification of the network, i.e. determining the weight of the links that connect the individual nodes will be revisited at a later date.

One of the issues with using a formal mixed integer formulation is that it requires solving the full problem and not conducting an approximation. Therefore, the NP-hard issue still remains. The mixed integer formulation solves the problem efficiently through intelligent pruning of infeasible and sub-optimal solutions, but does not change the overall algorithmic complexity. In the current iteration of the LCA, there are six specific transcription factors being utilized under six different conditions, and therefore the computational complexity is not an issue. Even in the most comprehensive case for transcriptional regulation, the problem set is still relatively small, on the order of 200 transcription factor binding sites having been quantified (Harbison et al., 2004), and therefore still within the limits of solvability.

The mixed integer formulation is divided up into two portions, the bi-clustering formulation Equation (1), and the subset removal cuts Equation (2). The problem is solved parametrically for the number of genes starting from N genes and decreasing until the number of genes equals 2. The optimization criterion maximizes the number of conditions. With this formulation, it is not necessary to define constraints of what a good bi-cluster entails though such constraints could be formulated. We find this to be an artificial constraint, for there could exist two genes which are well correlated over a large number of different conditions, of which the implications would be just as important as a bi-cluster of 10 genes that were well correlated over fewer conditions.

$$\begin{array}{l}[({\lambda }_i+{\lambda }_j+{\mu }_k)-3]\times M\le ({\lambda }_i+{\mu }_k)\times D(i,k)-({\lambda }_j+{\mu }_k)\times D(j,k)\\ [3-({\lambda }_i+{\lambda }_j+{\mu }_k)]\times M\ge ({\lambda }_i+{\mu }_k)\times D(i,k)-({\lambda }_j+{\mu }_k)\times D(j,k)\end{array}$$ (1)

The bi-clustering portion described in Equation (1) requires the discretization of the signal. This works well for the time series data which is provided by the LCA. It essentially checks to see if two genes under a given condition have the same value with binary variables to indicate whether a given gene is included for the assessment. In Equation (1), D represents the integer transformed data, λ represents the genes selected within the bi-clusters where μ represents the conditions under which the genes are co-expressed. The indices i,j,k represent the index in the array for which the gene or condition exists. M represents a large number that functions to essentially eliminate the constraint when either of the two genes or conditions are not part of a given bi-cluster. In other words, genes i and j belong to bi-cluster k, i.e. λ_i=λ_j=μ_k=1, if and only if the symbolic representation of both genes are the same under condition k, i.e. D(i,k)=D(j,k). This is the only situation that would make Equation (1) feasible. If λ_i=λ_j=μ_k=1 whereas D(i,k) ≠ D(j,k) Equation (1) would be infeasible since the left-hand side of both inequalities will be zero, whereas the right-hand side is not. A schematic of how this assessment finds bi-clusters is shown in Figure 2. In Figure 2, there are two λ variables which denote the two genes which are being checked for co-expression whilst the μ represents the condition in which they are checked from. If two genes are part of a bi-cluster, then the value under the two different conditions ought to be identical.

Fig. 2.

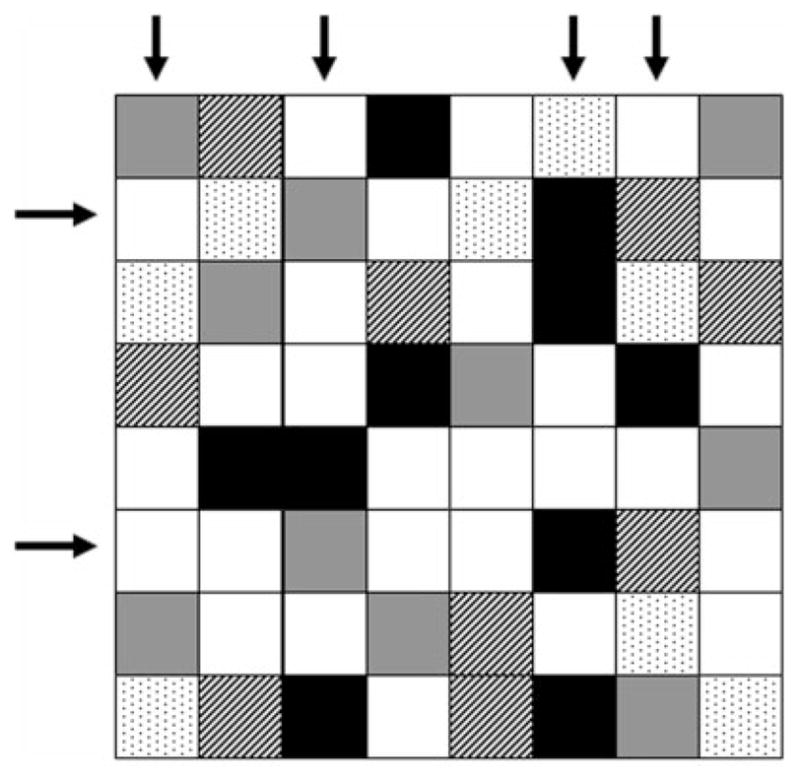
A schematic of how the formulation in Equation (1) works. Rows indicate genes and columns indicate conditions. Two genes (λ₂=1 and λ₆=1) are similarly expressed under four conditions (μ_k=1, k=1, 3, 6 and 7).

The problem with excluding subsets is simplified by the fact that the problem will be solved to optimality at every iteration with every iteration parametrically solving for different number of genes. The primary idea behind Equation (2) is that a new solution requires a condition to be included that was not in a previous solution. Equation (2) guarantees that each solution will not be a subset of a previously identified set of conditions. In Equation (2), ${\mu }_k^{\text{iter}}$ represents the previous solution and ${\mu }_k^{\text{citer}}$ represents the current solution which may or may not be excluded. Therefore, the bi-clusters are generated sequentially and the exclusion constraints of Equation (2) guarantee that the bi-cluster at iteration ‘citer’ is not a subset of the previous clusters ‘iter’.

$$\begin{array}{l}\sum _{Q(\text{iter})}{\mu }_k^{\text{iter}}-\sum _{P(\text{iter})}{\mu }_k^{\text{iter}}<\sum _k{\mu }_k^{\text{citer}}\forall \text{iter}<\text{citer}\\ P(\text{iter})=\{i\mid {\mu }_k^{\text{iter}}=1\}\\ Q(\text{iter})=\{i\mid {\mu }_k^{\text{iter}}=0\}\end{array}$$

Figure 3 illustrates how the subset removal cuts works. Equation (2) essentially forces the next possible solution to include a condition that was not included in a previous solution. If the current solution is a subset of any previous solution, then the following holds.

Fig. 3.

The solution for iterate (N–1) has five conditions, the next optimal solution has four. However, the solution which is wholly a subset of a previous solution should be excluded.

$$\sum _{Q(\text{iter})}{\mu }_k^{\text{iter}}=\sum _k{\mu }_k^{\text{citer}}\forall \text{iter}<\text{citer}$$

Given that the formulation solves for the maximum number of condition under which N genes is co-expressed, the exclusion only occurs for the set of conditions. The set of cuts can be limited to only the conditions rather than the genes because the problem is solved parametrically with the maximum number of genes being solved in the first iteration. This should give the smallest number of conditions which these genes are co-expressed under. Once the number of genes has been decreased, the set of conditions in which the genes are co-expressed ought to have at least one condition which was not present in the previous solution. Therefore, by solving it parametrically in N, it removes the complexity of requiring a subset excluding cut from requiring both the conditions as well as the set of genes. This greatly simplifies the formulation.

After the bi-clusters were generated, they were evaluated as to whether or not one of the condition/reporter interactions in that bi-cluster had a 2-fold change in the overall activity. The data was reported in fold change, and it was found that in the negative control case, the variability in the overall intensity differed by less than 2-fold. We opted to select bi-clusters which had at least one of the condition/ reporters show a two fold change instead of filtering out the gene/ condition combinations and then conduct the bi-clustering because it represented a compromise between focusing solely upon co-expression or the intensity values. The overall formulation is given in Equation (3) and is solved using the GAMS framework (Brooke et al., 2004) running CPLEX for the optimization.

$$\begin{array}{l}max\sum _k{\mu }_k^{\text{citer}}\\ \text{s}.\text{t}\sum _i{\lambda }_i^{\text{citer}}=N\\ [({\lambda }_i^{\text{citer}}+{\lambda }_j^{\text{citer}}+{\mu }_k^{\text{citer}})-3]\times M\le ({\lambda }_i^{\text{citer}}+{\mu }_k^{\text{citer}})\times D(i,k)-({\lambda }_j^{\text{citer}}+{\mu }_k^{\text{citer}})\times D(j,k)\\ [3-({\lambda }_i^{\text{citer}}+{\lambda }_j^{\text{citer}}+{\mu }_k^{\text{citer}})]\times M\ge ({\lambda }_i^{\text{citer}}+{\mu }_k^{\text{citer}})\times D(i,k)-({\lambda }_j^{\text{citer}}+{\mu }_k^{\text{citer}})\times D(j,k)\\ \sum _{Q(\text{iter})}{\mu }_k^{\text{citer}}-\sum _{P(\text{iter})}{\mu }_k^{\text{iter}}<\sum _k{\mu }_k^{\text{citer}}\forall \text{iter}<\text{citer}\\ P(\text{iter})=\{i\mid {\mu }_k^{\text{iter}}=1\}\\ Q(\text{iter})=\{i\mid {\mu }_k^{\text{iter}}=0\}\\ D(i,k)=\text{symbolic}\text{representation}\text{of}\text{gene}‘\text{i}’\text{in}\text{condition}‘k’\\ {\lambda }_i^{\text{citer}}=\{\begin{array}{ll}1,\hfill & \text{if}\text{gene}i\text{belongs}\text{to}\text{bicluster}‘\text{citer}’\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\\ P(\text{iter}),Q(\text{iter})=\text{denote}\text{the}\text{set}\text{of}\text{conditions}\text{that}\text{comprised}\text{previous}\text{biclusters}\end{array}$$

2.2 Network reconstruction

The primary purpose behind bi-clustering was to construct a network which gives insight as to the underlying mechanism which gave rise to the observed responses. Without any a priori information, a bi-partite network could be obtained in which links can be created from a regulator to a set of genes, if those regulators and genes are found in the same bi-cluster Figure 6. However, by incorporating additional information which is available due to the artificial construction of the reporter genes, one can generalize the bi-partite graph into a directed graph which gives insight as to the signaling cascade, specifically in this case, the induction of inflammatory/anti-inflammatory signals via external stimulus.

Fig. 6.

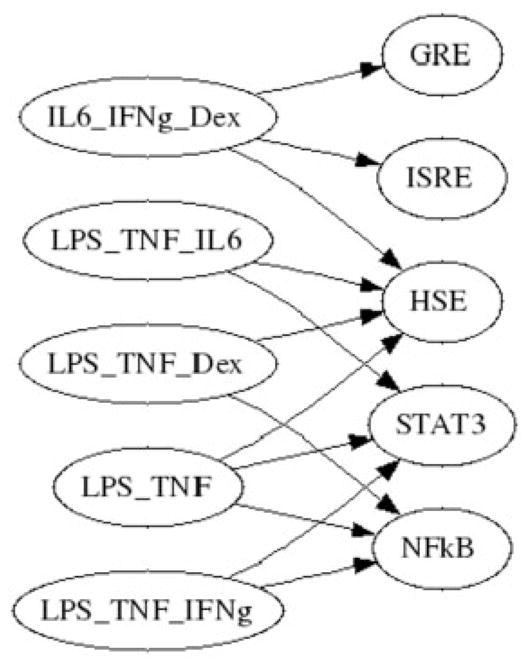
The bi-partite representation of the bi-clusters.

The specific piece of information which is utilized is the fact that the reporter genes can only be activated by their specific transcription factor, and therefore the only direct links that can be present in the graph is from a transcription factor to its specific reporter. These direct links are given in Table 1 of the original LCA manuscript (King et al., 2007). A schematic of the translation from the bi-partite graph in Figure 6 to a directed graph can be seen in Figure 4. One of the bi-clusters in Figure 6, encompasses the activation of STAT3, and NFκB via LPS, TNF-α and IFN-γ. Given the direct links of TNF-α to NFκB and IL6 to STAT3, the bi-cluster allows one to hypothesize that the activation of STAT3 given an input of TNF-α occurs indirectly as TNF-α activates the production NFκB, which thereby activates IL-6, and STAT3.

Fig. 4.

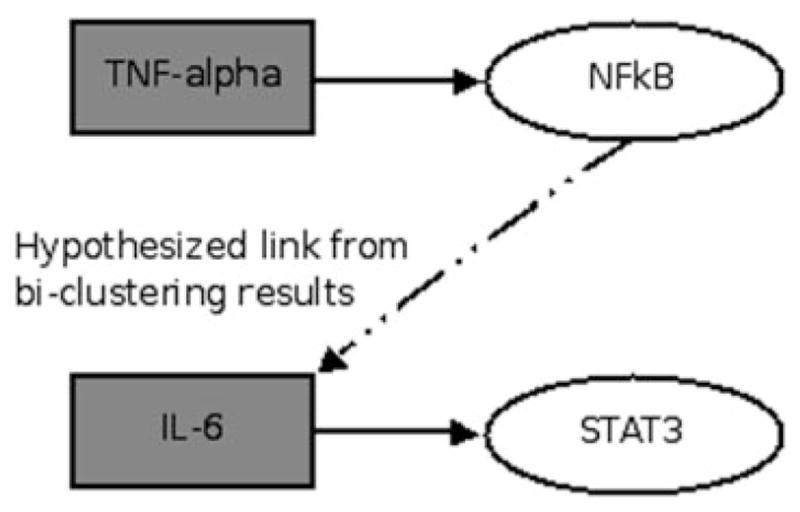
Directed graph network generation.

This secondary activation mechanism is necessary due to the construction of the reporter genes. The reporter STAT3 cannot be directly activated via TNF-α due to its construction, and therefore the induction of STAT3 must occur via a secondary activation of IL-6.

3 RESULTS

A representative bi-cluster is given in Figure 5. In general, the optimizations-based formulation of bi-clustering is well suited to process integer/discretized data, but is significantly affected by the initial clustering of time series.

Fig. 5.

A representative bi-cluster identified. The bi-clustering algorithm is highly dependent upon the initial time series clustering.

Without filtering for bi-clusters that showed greater than a 2-fold change, 98 different bi-clusters of which the minimum size were two reporters being co-expressed over two conditions were obtained. After the 2-fold filtering, five bi-clusters in which the minimum size was 2 × 3 (either two conditions and three reporters or vice versa) was obtained. The overall bipartite representation obtained from the bi-clustering is given in Figure 6, and the directed graph associated with the bipartite graph is given in Figure 7. The links for HSE and LPS were not included in Figure 7 due to the fact that they did not have specific molecular activators identified, and IL1→AP1 was excluded due to the fact that it was not part of a non-trivial bi-cluster which showed significant activation.

Fig. 7.

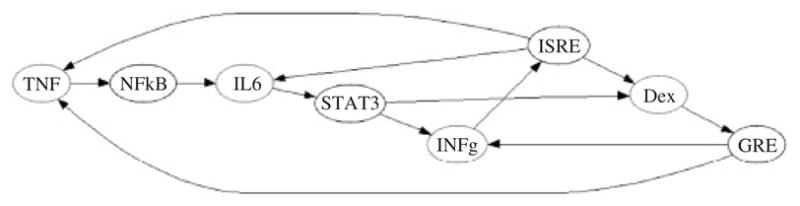
The directed graph version of the bi-clustering data with HSE and LPS removed (no specific activators). The condition specific activators (red) regulate only a single reporter gene (black). The indirect effects observed in the LCA have been identified as secondary effects. The IL1->AP1 link was not included because it was not found in a non-trivial bi-cluster.

From the bi-clustering result and the associated bipartite network, it was found that while HSE did not have a specific activator under the different experimental conditions; it showed significant co-expression and activation from a variety of different signaling factors. The activation of the heat shock element normally occurs in temperature above 35°, and yet it was activated under the administrations of Dexamethasone, IL-6 and Interferon Gamma. The possible transduction of the HSE by Interferon Gamma has been identified (Saile et al., 2004). The activation by Dexamethasone has been previously identified but is weak and like the other results involving Dexamethasone, this may be more of an artifact off the poor data obtained via the administration of Dexamethasone. However, perhaps as a reason for the poor results, the administration of Dexamethasone has been shown to either act as an antagonist for the binding of the heat shock element as well as increase the production of the heat shock protein. Therefore, the poor results obtained from the LCA may be indicative of more complex behavior, for which all of the variables have not been adequately controlled.

Incorporating the a priori information which comes from the construction of the LCA, the directed graph given in Figure 7 was obtained. The primary salient characteristic of this graph is the presence of loops such as those that involve IL6 IFN-γ, and IFN-γ and Dex. The presence of these loops gives a possible mechanism by which both IFN-γ and Dex are responsible for changing the way an organism responds to inflammatory cytokines, as well as suggesting that there may be a mechanism for inducing a tolerance phenomenon. This effect may be mediated through the transcription of the glucocorticosteroid receptor or the Interferon Gamma receptor which is present in the cell (Rakasz et al.,1993; Sanceau et al.,1992).

One of the concerns which we have with the results of both the bi-clustering as well as the network reconstruction is the effect of noisy data. One of the drawbacks of most clustering methods is that they oftentimes cluster all of the data without regard to data quality. Given the fact that our bi-clustering is highly dependent upon the initial clustering, any shortcomings due to noisy data would thereby be carried over to the generated network.

One of features which was noticed was the fact that the noise level was not consistent over the entire array with some transcription factors/reporters showing very consistent results while other transcription factors/reporters being very inconsistent. We hypothesize that one of the factors which affect the repeatability of a given experiment lies in the fact that there may exist complicated feedback loops that affect the transcription of receptors for a given signal, whereas those which show a greater repeatability between trials probably have a direct transcriptional link such as the link between TNF-α ->NFκB-> IL-6 and Stat 3.

4 DISCUSSION

It is arguable that bi-clustering may not be needed and that one could easily construct a network by utilizing only the 2-fold change criteria and creating a link between the response element and a given gene. Such a network has been constructed in Figure 8. It is notable that the TNF-α→NFκB→ IL-6→ STAT3 link still exists. However, what this network is not able to identify is the effect that Dex and IFN-γ have upon the overall system and leaving them as isolated interactions. This may be because given the current construction of the reporter genes, that the only significant change in activity is through activation, and therefore the effects of Dex and IFN-γ are not seen because they have a significant down-regulatory effect upon the other inflammatory cytokines such as IL6. The use of bi-clustering and the utilization of correlation have managed to deduce relationships that are not necessarily feed forward activations.

Fig. 8.

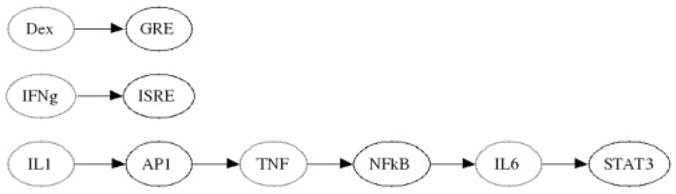
Network generated by looking only at significant activation. By ignoring the overall correlation between the different transcription factor activities, one is unable to obtain networks which include the effects of Dexamethasone and Interferon Gamma upon inflammatory cytokines, nor obtain any feedback loops that characterize the biological system.

One of the issues that was of concern was the effect of noise upon the overall quality of the experiments, namely the repeatability between trials as well as the overall effect it would have on the overall network. It has been shown that the presence of feedback loops themselves affect the noise propagation properties of a given transcriptional system (Dublanche et al., 2006), and that the effect is not entirely consistent. Normally, the hypothesis is that a negative feedback loop ought to dampen noise, and that a positive feedback loop would increase noise, however, it was found that the mere presence of loops has an indeterminate effect upon the noise characteristics. From this conclusion, we believe that the differences in the overall noise levels measured is evidence of the presence of loops, something which was not isolated in the network that only utilized up/down regulation.

Previously identified feedback loops such as those that involve IL6→TNF-α (Moeniralam et al., 1997), glucocorticosteorids→IL6 (Barber et al., 1993; Takeda et al., 1998) and IL6→IFN-γ (McLoughlin et al., 2003) are evident in Figure 7. Given that these loops have been previously identified in literature, we believe that the noise does not adversely affect the networks drawn via our bi-clustering methodology and serves as a confirmation of the fact that loops were isolated instead of independent feed-forward cliques. We make the additional hypothesis that the feedback loop IL6→TNF-α is mediated through the activity of IFN-γ which has not been directly established. However, it has been established that IFN-γ illustrates non-trivial effects on STAT3 and TNF-α (Kaur et al., 2003; Raponi et al.,1997) making it a possible candidate as the hub which mediates feedback activity. This hypothesis shows that the value of the LCA/bi-clustering lies not only in the validation of previously identified links, but also as a method for generating new testable hypotheses. Therefore, while not every gene shows a significant change in the activity, the use of correlation may still be able to identify the presence of other links besides feed forward loops and allows for a much more complete picture as to the overall regulatory pathway.

This may arise primarily due to the fact that the LCA in its current iteration is more sensitive to the up-regulation of a given factor rather than the down-regulation of a factor. Therefore, a network built in such a fashion may be more complete if the LCA was better able to handle the down-regulation aspect of transcriptional networks. However, by utilizing correlation, it is still possible to ascertain many of the down-regulatory aspects of gene regulation.

Additionally, we assert that a bi-clustering algorithm which was both globally optimal as well allowing for the arbitrary overlapping of bi-clusters is necessary. Additional bi-clustering was carried out utilizing BicAT (Barkow et al., 2006), which is a software package that has the options of running multiple clustering algorithms such as CC (Cheng and Church, 2000) and xMotifs (Murali and Kasif, 2003). In this evaluation it was found that the method by Cheng and Church was the only one that was able to select non-trivial bi-clusters. The failure of the other bi-clustering algorithms may be due to the structural constraints that are placed upon the data, something which may not be satisfied in the small dataset.

Combining the bi-clustering results as well as the network architecture obtained via the directed graph, it is possible to make hypotheses as to the overall mechanism behind the response to bacterial endotoxins. In the bi-clustering, it was found that LPS appears to regulate the activity of HSE, STAT3 and NFκB. Being that it regulate these reporter genes in similar fashion as both TNF-α as well as IL-6, it appears that the primary mode of LPS upon the hepatic system is through TNF-α for which there is some evidence in other tissues (Miller- Larsson et al.,1999). Additionally, the production of IL-6 increases with the administration of LPS (Muramami et al.,1993), though the mechanism by the activation of IL-6 is not clear. One of the possibility is that the induction of IL-6 through LPS occurs through the TNF-α mechanism given observation that TNF-α itself stimulates the production of IL-6 (King et al., 2007). However, it is also possible that IL-6 itself may be directly regulated via LPS. Evidence suggests the former due to the ability of TNF-α to stimulate IL-6, as well as the difficulty of distinguishing between the modes of activation for STAT3 given the administration of LPS, TNF-α or IL-6.

One of the ongoing challenges in this bi-clustering framework lies in the creation of more efficient formulations that allow one to tackle larger problems. The current formulation is sufficient in solving problems up to around 200 transcription factors which is around the number of transcription factors which have been previously identified (Harbison et al., 2004). However, improvements to the formulation that make it more efficient would allow one to tackle problems that involve other aspects of intracellular signaling. So while the scaling aspect of both the experimental components that comprise up of LCA as well as the algorithms behind the analysis are sufficient for transcriptional networks, and improvement in efficiency is still desired.

5 CONCLUSION/FUTURE WORK

From the initial prototype of the LCA, it is possible to obtain a regulatory network which has many of the features that have been experimentally observed. For the most part, while the network which has been identified via the LCA and bi-clustering appear to be well supported by experimental evidence, there are still issues that need to be worked out such as the large amount of error between replicates with a few of the reporters. It may be that this lack of repeatability suggests a more complex mechanism as previously proposed. However, this is still an issue that needs to be addressed.

One of the exciting things with the LCA which has not been directly addressed at this point is the possibility of whether the LCA would be able to predict the overall behavior of the system to a composite stimulus. In the original LCA experiment, there were conditions that represented the composite inputs of multiple factors such as IL-6, IL-1, TNF-α and Interferon Gamma. While it has not been done, it would be beneficial to test whether quantifying the identified network under the cases with a single stimulus would allow for the prediction of gene activation under a composite stimulus. If this were possible, then it would allow researcher to use the LCA to rapidly decipher the mechanism by which cells respond to external stimulus.