Evolutionary dynamics of feedback escape and the development of stem-cell–driven cancers

Abstract

Cancers are thought to arise in tissue stem cells, and similar to healthy tissue, are thought to be maintained by a small population of tumor stem or initiating cells, whereas the majority of tumor cells are more differentiated with limited replicative potential. Healthy tissue homeostasis is achieved by feedback loops, and particular importance has been attached to signals secreted from differentiated cells that inhibit stem-cell division and stem-cell self-renewal, as documented in the olfactory epithelium and other tissues. Therefore, a key event in carcinogenesis must be escape from these feedback loops, which is studied here using evolutionary computational models. We find that out of all potential evolutionary pathways, only one unique sequence of phenotypic transitions can lead to complete escape in stem-cell–driven tumors, even though the required mutations for these transitions are certainly tissue specific. This insight, supported by data, facilitates the search for driver mutations and for therapeutic targets. Different growth patterns can result from feedback escape, which we call “inhibited,” “uninhibited,” and “sigmoidal,” and which are found in published data. The finding of inhibited growth patterns in data indicates that besides architecture, the regulatory mechanisms of healthy tissue continue to operate to a degree in tumors.

Evidence suggests that tumors are maintained by a relatively small number of tumor stem cells or tumor initiating cells that have the potential to divide indefinitely (1–3). The rest of the tumor bulk is assumed to be made up of more differentiated cells that can only undergo a limited number of divisions (1, 4). This notion is supported by experiments where tumor cells are transplanted into immunodeficient mice, which show that a majority of cells fail to establish new tumors and only a small, defined subset of cells is capable of sustained proliferation (4–6). In these experiments, the subset of tumorigenic cells expressed markers that are also expressed in healthy tissue stem cells. Hence, these cells are thought to have certain stem characteristics that allow them to self-renew and regenerate the tumor.

Healthy human tissue is highly regulated to ensure homeostasis, with feedback loops playing a fundamental role in this regard. In particular, two types of feedback loops have been suggested to be crucial: Differentiated cells secrete factors that inhibit the division of stem cells. In addition, differentiated cells secrete factors that suppress self-renewal of stem cells and instead promote cell death following terminal differentiation (7–9). Strong evidence for these feedback mechanisms has been found in the olfactory epithelium (7, 8), but also in a variety of other tissues, including striated muscle, liver, bone, central nervous system, and hematopoietic system, among others (9–13).

Tumor formation occurs through a multistep process where cells sequentially accumulate random mutations and epigenetic changes. Different types of cancers (depending on the tissue of origin) tend to arise through different and specific mutational pathways of varying complexity (14, 15). Tumor initiation and progression can involve key events, such as the emergence of genetic instability that allows mutations to be accumulated faster, or the acquisition of the angiogenic phenotype that enables the formation of new blood supply, among other processes (16). Despite this great complexity and heterogeneity in the mechanism of tumor formation, there is ample evidence that escape from feedback regulation is a key ingredient in the formation of most, if not all, stem-cell-driven tumors (reviewed in ref. 14), and the corresponding evolutionary dynamics are the subject of this paper.

In a genetically heterogeneous population, the forces of selection may favor the outgrowth of individual cells with advantageous traits (notably those traits that favor proliferation) (17, 18). Within this framework of cancer as a product of somatic evolution, it is important to understand how mutants that originally appear in very small numbers are able to invade a cell population that is initially at dynamic equilibrium (such invasion analysis has been applied before to the dynamics of stem cells in niches; see ref. 19). In the context of tissue homeostasis controlled by feedback loops, the question becomes how and which phenotypical mutations that affect feedback control may lead to abnormal cellular growth and eventually cancer.

Using computational models that are applied to experimental data, we study the evolutionary dynamics of feedback escape as well as the resulting tumor growth laws. We find that escape from feedback-regulated tissue homeostasis can only occur via a unique sequence of phenotypic transitions, which we suggest to be common among stem-cell-driven tumors, and which is supported by published data. Different patterns of emerging tumor growth are predicted to occur, which can be successfully fit to a range of previously published experimental data that describe tumor growth dynamics in vitro and in vivo. Of particular interest are nonstandard growth patterns, both predicted by the model and found in published experimental data, which indicate that feedback regulatory mechanisms are still partly at work in growing tumors. This gives rise to the notion that tumors not only retain some of the architectural aspects of the underlying healthy tissue, but also some of the regulatory mechanisms.

Results and Discussion

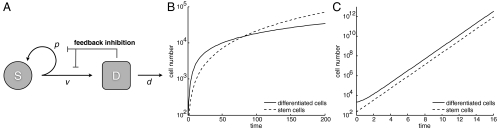
The dynamics of tissue regulation through feedback loops has been studied in several cell lineages including the hematopoietic system, the lymphocytic system, the olfactory epithelium, and the colon crypt (7, 20–22). To study the escape from feedback, we introduce a basic computational model of feedback-regulated tissue homeostasis that is based on previously published and experimentally validated work (7) (Fig. 1 A and B). This model, described by Eq. 1, takes into account two populations: stem cells, S, which have unlimited reproductive potential, and differentiated cells, D, that eventually die (this includes all cell populations with limited reproductive potential, such as transit cells):

[1]

Stem cells divide at a rate v; this results in either two daughter stem cells with probability p or two differentiated cells with probability 1 - p. Differentiated cells die at rate d. In accordance with data, we assume that differentiated cells secrete two types of feedback signals: One inhibits the rate of cell division, and the other reduces the probability of stem-cell self-renewal, leading to cell death via terminal differentiation. The rate of cell division and the probability of self-renewal are treated as general functions of the number of differentiated cells, v(D) and p(D), respectively. That is, we do not assume specific mathematical terms for these processes. This ensures that results are robust and are not dependent on particular and arbitrary mathematical expressions. We require, however, that both feedbacks be decreasing functions of the number of differentiated cells, D, and go to zero if D grows without bound. Also, 0.5 < p(0) ≤ 1, otherwise the only outcome is population extinction. Although asymmetric stem-cell divisions (giving rise to one stem and one differentiated cell) is a possibility, its introduction does not change any of our results. This issue, basic model properties, and the mathematical proofs are discussed in the SI Appendix.

Fig. 1.

Feedback-regulated tissue homeostasis and cell growth properties in the ordinary differential equations model. (A) Stem cells divide at a rate v producing either two stem cells with probability p or two differentiated cells with probability (1 - p). Differentiated cells die at a rate d and produce factors that inhibit self-renewal and division in stem cells. (B) Inhibited growth. If only differentiation feedback is lost, the population of stem cells and differentiated cells grows without bound at a slower than exponential rate. (B) Uninhibited growth. If both feedbacks are lost, stem cells and differentiated cells grow at a rate dominated by the same exponential. Time is expressed in units of 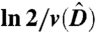, the expect duration of one cell cycle at equilibrium.

In this model, only loss of the differentiation feedback can lead to uncontrolled growth, two types of which are observed: If the division feedback is still intact, we observe relatively slow, subexponential, growth, which we call “inhibited growth” (Fig. 1 C and D). If the division feedback is also lost, we observe faster exponential growth, which we call “uninhibited growth.” We further observe that with uninhibited growth, the ratio of stem cells to differentiated cells always converges to a fixed percentage. With inhibited growth, however, stem cells make up an ever increasing fraction over time. The predicted importance of losing the differentiation feedback for carcinogenesis is in line with previous modeling approaches (20).

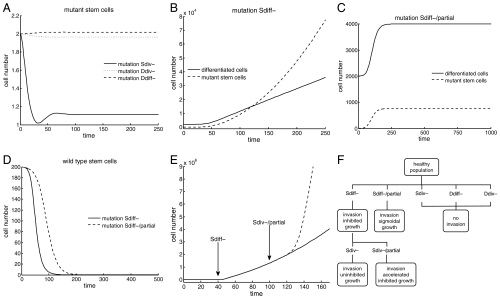
To study the evolutionary dynamics of feedback escape, we assume that the healthy cell population is near equilibrium, and investigate the growth of mutational phenotypes from low numbers. We denote mutations that lack production of feedback signals by differentiated cells with the prefix D and those that lack response by stem cells to these signals with the prefix S. Mutations that affect cell differentiation carry the suffix diff- and those affecting the division rate the suffix div-. The phenotypes considered are described as follows: (i) Type Ddiff- lacks production of differentiation-regulating signals by differentiated cells, (ii) type Sdiff- lacks the stem-cell response to the differentiation-regulating signals, (iii) type Ddiv- lacks production of division inhibiting signals by differentiated cells, and (iv) type Sdiv- lacks the stem-cell response to division inhibiting signals. The corresponding equations are given in the SI Appendix. The mutational steps, the nature and number of which are likely tissue dependent, are not modeled.

In a background of healthy tissue, types Ddiv-, Ddiff-, and Sdiv-, are not selected for; they are selectively neutral with respect to healthy cells, and are thus likely to go extinct in a stochastic setting (Fig. 2A). Only Sdiff- types, lacking a stem-cell response to the differentiation-regulating signals, can have a growth advantage in a background of healthy tissue, eventually taking over the entire population and growing uncontrolled according to the “inhibited” growth pattern (Fig. 2 B and D). Hence, this must be the first significant step toward malignancy. Only in these Sdiff- type mutants can the acquisition of the phenotype Sdiv- confer a selective advantage to the cells, which will grow exponentially according to the “uninhibited” growth pattern and eventually dominate the population. None of the other phenotypes enjoys a selective advantage in any setting. Hence, loss of feedback control in this system requires that mutants lose the ability to respond to, rather than produce, the signals. Importantly, this can only occur via a unique sequence of events, where first the response to differentiation, then to division feedback is lost (Fig. 2F). We suggest this to be a universal pathway of feedback escape among stem-cell–driven cancers, although the nature and number of mutation events to achieve this is certainly tissue specific.

Fig. 2.

Evolutionary dynamics of feedback loss in the ordinary differential equations model. The simulations begin at equilibrium with two stem cells carrying the specified mutation. (A) For populations near equilibrium mutations Sdiv-, Ddiv-, and Ddiff- do not confer any competitive advantages over their wild-type counterparts. If the mutation arises in a small number of cells, the steady-state number of mutant stem cells will be negligible. (B) Mutation Sdiff- results in inhibited growth in the number of mutant stem cells and differentiated cells. (C) Mutation Sdiff-/partial produces a finite increase in both the number of mutant stem cells and differentiated cells. (D) Mutations Sdiff- and Sdiff-/partial result in the extinction of the wild-type stem-cell population. (E) In a healthy population at equilibrium, a stem cell acquires mutation Sdiff- at the time indicated by the arrow (solid line); the subsequent appearance of mutation Sdiv-/partial in a Sdiff- cell produces an acceleration in the growth of the tumor (dashed line). (F) Tumor progression toward uninhibited growth follows a unique sequence of feedback inactivations: First, mutation Sdiff- must occur, followed by mutation Sdiv-.

We also consider mutations that confer only a partial loss of response to feedback signals. A mutation that only partially compromises the response to differentiation-regulating factors (denoted by Sdiff-/partial) will eventually take over the entire population, producing a third type of bounded “sigmoidal” growth pattern (Fig. 2 C and D). A mutation that produces a partial loss in the response to division rate factors (Sdiv-/partial) cannot invade a healthy cell population, but it will produce an acceleration in the growth rate of a tumor exhibiting inhibited growth (Fig. 2E).

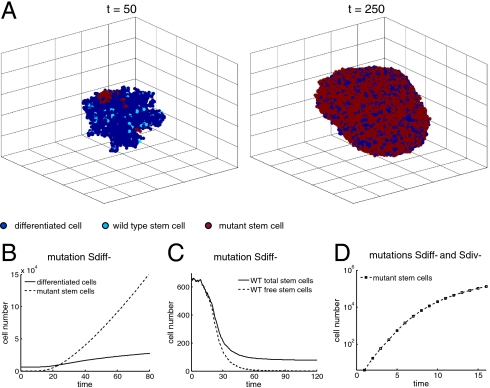
Next, we consider these dynamics in the context of a stochastic, three-dimensional rectangular lattice model corresponding to solid tumor growth with spatial structure. A lattice point can host at most one cell at any time. For a cell to divide, there must be a free lattice point adjacent to it to place the offspring. A stochastic simulation algorithm is used, where the probabilities of cell division, differentiation and death correspond to our previous nonspatial model. Our main results remain unchanged (Fig. 3). Again, we observe uninhibited tumor growth if both feedback loops are broken, and inhibited growth when only the differentiation feedback loop is broken. The percentage of stem cells increases progressively with inhibited growth, whereas it converges to a fixed percentage for uninhibited growth. However, in contrast to the nonspatial situation, the tumor growth rates are slower. Uninhibited growth is not characterized by exponential, but by cubic growth. Inhibited growth is characterized by subcubic growth. This difference is partly caused by surface growth dynamics in the three-dimensional model, a behavior observed in several types of solid tumors (23–25). Looking at the evolutionary dynamics, we find that feedback inactivation occurs via the same unique pathway as in the nonspatial model. More details are given in Materials and Methods.

Fig. 3.

Spatial model. (A) Spatial arrangement of the cell population at two different times. The simulation begins with a tissue at near equilibrium with two stem cells randomly selected to carry mutation Sdiff- at time t = 0. (B) The appearance of mutation Sdiff- results in the unlimited growth of the mutant stem cell and differentiated cell populations. (C) The number of wild-type stem cells decreases. Note that a small number of stem cells that are trapped—and thus unable to divide—lingers in the population for a long time. The number of wild-type stem cells, however, becomes a negligible percentage of the entire cell population. (D) Cell population with stem cells carrying mutations Sdiff- and Sdiv- (simulations start with a small number of stem cells carrying both mutations). Cell growth is much faster than if only mutation Sdiff- is present (note different scales in B and D); but, unlike the nonspatial model, the growth is not exponential. In B–D, results represent the average of 24 runs.

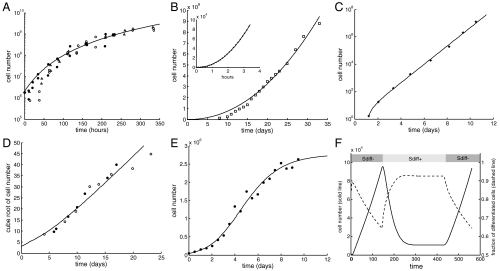
Performing extensive literature searches, we found that most growth patterns belong to one of the categories resulting from our models: the uninhibited pattern, which is exponential in the nonspatial system and cubic in the spatial system; the inhibited pattern, which is subexponential in the nonspatial system and subcubic in the spatial system; and the sigmoidal growth pattern. In the following examples, specific forms of the models were fitted to different types of published tumor growth data using least-squares procedures (for details see Materials and Methods and SI Appendix, Table S1). Among the estimated parameters, we focus on the relative magnitude of the differentiation (g) and division feedback (h). (i) Inhibited nonspatial growth is found in Ehrlich’s ascites tumor (26), where cells grow subexponentially and the best model fit yields parameters g = 0 and h > 0 (Fig. 4A). (ii) Inhibited spatial growth is found in A2780 human ovarian carcinoma growth in mice (27) (Fig. 4B). The data shows subcubic kinetics with a power law of 2.17 and no saturation, and is again well fitted with parameters g = 0 and h > 0. (iii) Uninhibited nonspatial growth is found in data from L1210 cells (28), a mouse lymphocytic leukemia, where cells grow exponentially and the best fit is characterized by g = 0 and h = 0 (Fig. 4C). (iv) Uninhibited spatial growth is found in data from spatial multicellular tumor spheroids of EMT6/Ro cells (29), derived from a mouse mammary tumor, which show cubic growth and are best fit with model parameters g = 0 and h = 0 (Fig. 4D). (v) A sigmoidal growth pattern, found in Jurkat cells (30) originating from a T cell human leukemia (Fig. 4E), is best fit if the differentiation feedback is only partially lost (g > 0).

Fig. 4.

Experimentally observed growth patterns and model fits. (A) Inhibited growth in the nonspatial model. Ehrlich’s ascites tumor (26) (three experiments shown: •, ▵, ○). (B) Inhibited growth in the spatial model. Main frame: (□) A2780 human ovarian carcinoma (27) and projection of the model using the function y = ax^b (solid line). (Inset) Simulation results (•) and projection of the model (simulations were not carried further in time do to computational constraints). (C) Uninhibited growth in the nonspatial model. (*) L1210 a mouse lymphocytic leukemia (28). (D) Uninhibited growth in the spatial model. Multicellular tumor spheroids of EMT6/Ro cells (29), a mouse mammary tumor (two experiments shown: ○, •). (E) Sigmoidal growth in the nonspatial model. (•) Jurkat T cell human leukemia (30). In A–E, the simulations are shown in solid lines; those corresponding to the stochastic spatial model represent the average of 24 runs. (F) Simulation of MYC regulation experiments (31–33). Upon activation of MYC (represented in the model by the Sdiff- phenotype) the cell population (solid line) exhibits sustained growth characterized by a reduction in the fraction of differentiated cells (dashed line). When MYC is subsequently inactivated (Sdiff+ phenotype) the fraction of differentiated cells increases while the cell population decreases to a lower-valued steady state; when MYC is reactivated the cell population rises again. See Results and Discussion.

We also sought to address model predictions about the order of phenotypic transitions and the central importance of the Sdiff- type with previously published data. A transgenic mouse model of hepatocellular carcinoma was developed, in which it is possible to regulate the expression of the human MYC oncogene in murine liver cells, suppressing it through doxycycline treatment (31–33). Although transgenic mice treated with doxycycline remained disease free, those with active MYC from the discontinuation of treatment developed malignant tumors that were locally invasive and able to metastasize. When MYC was subsequently inactivated, rapid tumor regression was observed that was associated with terminal differentiation into normal liver cells and apoptosis. Moreover, reactivation of MYC resulted in significant tumor regrowth and dedifferentiation. These observations validate key model predictions. MYC expression influences self-renewal and differentiation of cells, and thus influences the function p(D) in our model. Activation of MYC corresponds to corrupted differentiation feedback (i.e., to the Sdiff- phenotype in the model), whereas inhibition of MYC reverses this phenotype. The model predicts Sdiff- to be the initial and most crucial event in the evolution of feedback loss and uncontrolled growth. Even if cells have acquired other mutations that can also contribute to tumor progression, these mutations are predicted to only contribute to growth in cells that already have corrupted differentiation feedback. Hence, restoration of the differentiation feedback loop even in cells with further complex genetic alterations is predicted by the model to result in tumor regression and tissue dynamics that are characteristic of a healthy state. This same behavior is observed in the experiments where the macroscopic and malignant nature of the tumors indicate the presence of additional mutations, which are incapable of promoting growth in the absence of MYC (31). Fig. 4F shows a computer simulation that successfully recapitulates the dynamics observed in the MYC regulation experiments. Similar dynamics have been observed in the context of other tumors and/or oncogenes (e.g., Myc-induced hematopoietic tumors, breast cancers and osteogenic sarcoma, or Ras-induced melanomas), although details of the results can differ in various ways (e.g., treatment leading to complete extinction of the tumor) (31–33). Understanding the mechanisms that lead to differences in outcome will be important future work that can be aided by computational models, but is beyond the scope of the current paper.

In general, many key mutations in carcinogenesis disrupt negative feedback regulation of cell division patterns. Consider the protein transforming growth factor beta (TGF-β). This protein plays a key role in tissue homeostasis by inhibiting mitosis and promoting cell differentiation (16). Many types of cancers must circumvent TGF-β growth inhibition to be able to thrive. In these cancers, feedback escape is accomplished by inactivating the genes for the TGF-β receptors or through downstream alterations that disable the tumor-suppressive arm of the pathway (34–36). Half of all pancreatic carcinomas and more than a quarter of colon cancers carry mutations that make cells irresponsive to TGF-β signals that inhibit cell division and promote differentiation (37, 38). Mutations that affect TGF-β receptors also occur in gastric, biliary, pulmonary, ovarian, esophageal, and head and neck carcinomas (35). Another specific example of feedback escape in cancers is observed in glioblastomas that inactivate the bone morphogenetic protein 4 pathway (BMP4). There is strong evidence that glioblastomas are maintained by a small population of tumor initiating cells that have stem-cell characteristics (39). In humans, naturally occuring BMP4 induces glia stem cells to differentiate, inhibiting cell proliferation (40). The relationship between BMP4 and cancer is supported by evidence of epigenetic silencing of BMP4 receptors in glioblastomas (41), and by in vitro experiments that show that the addition of BMP4 causes a colony of glioblastoma multiforme cells to increase the fraction of differentiated cells and lose their tumorigenic capabilities (42). Finally, in colorecal cancer the initial mutational events are defined relatively well. They are the loss of the APC tumor suppressor gene and the concomitant activation of the Wnt cascade, followed by the activation of the K-Ras oncogene. Although both alterations lead to complex phenotypic changes, a common effect of both is that the cell division pattern is shifted away from differentiation and toward self-renewal, consistent with our model.

Conclusions

Using evolutionary computational models, we found that escape from feedback-regulated tissue homeostasis can only occur via a unique sequence of phenotypic transitions that we propose to be common among stem-cell–driven tumors, even if the nature and number of mutational events required to achieve this are certainly tissue specific. The resulting growth dynamics predicted by the model fall into three categories: uninhibited, sigmoidal, and inhibited. These can describe many experimental growth patterns found in the literature, which we demonstrated by fitting the model to five sets of published data. The finding of inhibited tumor growth patterns in the literature is of particular interest. Such a growth pattern, especially in the form of subcubic growth, could only be explained if the growing tumor is still partially subject to feedback regulation that has remained from the underlying tissue. This gives support to the notion that not only the tissue architecture, but also the regulatory mechanisms of the corresponding healthy tissue continue to operate to a certain degree in tumors, especially at early stages. A direct experimental test of this notion would be to identify and knock out the appropriate feedback loop in tumors characterized by inhibited growth, which should then result in uninhibited growth. The ability of our models to accurately describe the majority of tumor growth patterns found in the literature, and consistency of key model predictions with in vivo experimental data, provide confidence in the notion that feedback loss is a general requirement for cells to grow uncontrolled and develop into malignancies. This has practical implications for the search of mutations that give rise to specific cancers and provide targets for therapy.

Materials and Methods

Fitting Procedures.

Our modeling approach assumes general functions describing the feedbacks p(D) and v(D); however, data fitting algorithms require us to chose specific functional forms. In Fig. 4, we use Hill functions (2) to model feedback; these functions are good choices for the actions of secreted feedback factors, because they have been widely and successfully used to describe ligand-receptor interactions (43):

[2]

As a first step, we explored the possible values for the hill coefficients m and n. Using Matlab’s nonlinear optimization algorithm, the best fit for Fig. 4E resulted in no feedback on the replication rate (h = 0) and a hill coefficient on differentiation n = 0.5598. In Fig. 4A, the data was fitted assuming an inhibited growth pattern (g = 0), and the best fit resulted in m = 0.5348. In Fig. 4C, the best fit resulted in g = 0 and h = 0, making it impossible to extract any insights about m or n. Based on these results for the coefficients, and in an effort to reduce the number of free parameters, a value of m = n = 0.5 was used to produce all the fits in Fig. 4.

For data corresponding to the nonspatial model (Fig. 4 A, C, and E) least-squares solutions were calculated using Matlab’s nonlinear optimization algorithm. In the spatial model, computational constraints did not permit the use of search optimization algorithms based on the gradient of the target function. Thus, the strategy used was to first determine a search region in the parameter space and then generate random samples from this region. In Fig. 4B, the search region was found by creating a rectangular partition of the parameter space and computing the differences between the data and the model’s predictions evaluated at the vertices of the lattice; the region with the best agreement was then selected. In Fig. 4D, the nonspatial model was used as an approximation tool to establish the search region. In each case, once this search region was chosen, one hundred random parameter samples were generated, the average of 24 runs per sample was computed, and the best fit was selected.

Note that only under special circumstances does the Hill equation reflect a physically possible reaction scheme (44); hence, the values of the coefficients should not be used as an indication of the number of ligand biding sites. Moreover, the emphasis of this study is in the use of general feedback functions p(D) and v(D). This generality is one of its strengths, as more experimental work is still necessary to establish the details and thus the precise functional forms of the feedback mechanisms in specific tissues.

Algorithm for the Spatial Model.

In the spatial model, at any given time t, the system is described by a set of cells C(t), where each cell has two attributes: a position, given by a three-dimensional coordinate indicating its position in the lattice, and a type (the cell can be either a stem cell or a differentiated cell). Using Eq. 1 as the basis for the algorithm, the probability per unit of time that a particular differentiated cell dies in the next infinitesimal time interval δt is d; and the probability per unit of time that a particular stem cell with a free adjacent lattice point divides in the same time interval is v(D). Let F ≤ S be the number of stem cells that are able to divide and α, β, and γ be defined by: α = dD, β = Fv(D), and γ = α + β.

To implement the algorithm, first choose τ from the probability density function f(s) = γ exp(-sγ), and set the time of the next reaction to t + τ. Then, choose the type of reaction that occurs. The next reaction is either cell death with a probability α/γ, or cell division with a probability β/γ. If the next reaction is cell death, every differentiated cell has the same probability of being chosen; if it is cell division; every stem-cell that is able to define has the same probability of being selected. Finally, if cell division occurs, the probability that the cell divides into two stem cells is p(D), and the probability that it divides into two differentiated cells is 1 - p(D); the place where one of the offspring will reside is chosen at random, with each available adjacent position having an equal probability of hosting one of the daughter cells.