Fluid mechanics of nodal flow due to embryonic primary cilia

Abstract

Breaking of left–right symmetry is crucial in vertebrate development. The role of cilia-driven flow has been the subject of many recent publications, but the underlying mechanisms remain controversial. At approximately 8 days post-fertilization, after the establishment of the dorsal–ventral and anterior–posterior axes, a depressed structure is found on the ventral side of mouse embryos, termed the ventral node. Within the node, ‘whirling’ primary cilia, tilted towards the posterior, drive a flow implicated in the initial left–right signalling asymmetry. However, the underlying fluid mechanics have not been fully and correctly explained until recently and accurate characterization is required in determining how the flow triggers the downstream signalling cascades. Using the approximation of resistive force theory, we show how the flow is produced and calculate the optimal configuration to cause maximum flow, showing excellent agreement with in vitro measurements and numerical simulation, and paralleling recent analogue experiments. By calculating numerical solutions of the slender body theory equations, we present time-dependent physically based fluid dynamics simulations of particle pathlines in flows generated by large arrays of beating cilia, showing the far-field radial streamlines predicted by the theory.

1. Introduction

Left–right symmetry breaking in vertebrate development has been a subject of continuing interest and speculation (see Brown & Wolpert 1990). At 8 days post-fertilization, the developing mouse embryo exhibits a depression-like structure on its ventral side, at the end of the primitive streak, termed the ‘ventral node’, as shown in figure 1a. Sulik et al. (1994) discovered that the node contains a population of motile primary cilia that are 2–3 μm rod-like organelles. Unlike the propulsive cilia found in the airways or on micro-organisms, such as Paramecium, there is one primary cilium per cell that typically is not motile. Biologists remained sceptical about their motility, until Nonaka et al. (1998) showed that nodal cilia perform a ‘whirling’ motion (figures 1b and 2) that drives a flow directed towards the side conventionally termed the ‘left’. By studying knockout mice that do not assemble nodal cilia, evidence was produced to show that they are a vital part of left–right symmetry breaking. Subsequent experimental work demonstrated that artificial flow could correct the abnormal left–right development of mutants with immotile cilia (Nonaka et al. 2002). The nodal flow has also been found to be required for left–right symmetry breaking in zebrafish (Kawakami et al. 2005), and additionally has been observed in rabbit and medaka fish embryos (Okada et al. 2005). We note that while the role of left-specific genes, such as Nodal and Lefty2, appears to be evolutionarily conserved in vertebrates, the role of cilia in symmetry breaking is not universal, as can be seen from Xenopus and chick data (Mercola 2003; Tabin 2006). For a detailed review, see Hirokawa et al. (2006) and Raya & Izpisúa Belmonte (2006).

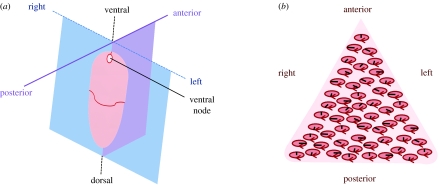
Figure 1.

(a) Diagram of the mouse embryo 8 days post-fertilization, showing with dorsal–ventral, anterior–posterior and left–right axes, the ventral node structure being indicated. Adapted from Nonaka et al. (2002). (b) Schematic of the node, containing an approximately triangular array of tilted, clockwise rotating cilia. The tilt results in the cilia paths appearing elliptical when viewed from above. The black lines depict instantaneous positions of cilia, and the ellipses and arrows depict the path of rotation.

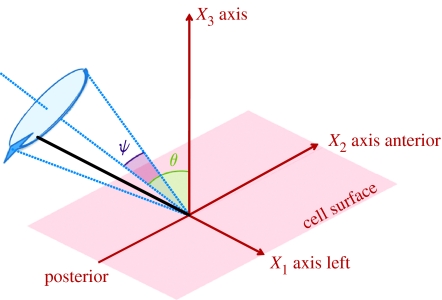
Figure 2.

The conical rotation model for an embryonic nodal cilium, with semi-cone angle ψ and posterior tilt θ. Positive X₁ corresponds to the ‘left’ of the node and negative X₁ to the ‘right’; positive X₂ corresponds to the anterior and negative X₂ to the posterior, as indicated.

A consensus has not been reached on the mechanism for how the nodal flow induces an asymmetric signal that ultimately results in asymmetric regions of left-specific gene expression (Tabin 2006). The main theories involve asymmetric bending of mechanosensory cilia on opposite sides of the node (McGrath et al. 2003; Tabin & Vogan 2003) or the directional transport of (i) morphogen proteins (Nonaka et al. 1998) or (ii) nodal vesicular parcels (NVPs) that are vesicles containing sonic hedgehog (SHH) and retinoic acid (RA; Tanaka et al. 2005). It was also not immediately obvious how whirling cilia could produce such a directional flow. The rotating motion appears to result from bending of the cilium close to its base. Although the base of the cilium is fixed and the cilium does not rotate about its centreline, the direction of bending near the base rotates continuously. As noted by both Nonaka et al. (2005) and Okada et al. (2005), the majority of cilia are not tilted to the degree that they make contact with the node floor. Consequently, the distal portion of the cilium traverses a nearly conical surface. These studies also reported a deviation from a perfect cone as the cilia are slightly bent due to viscous resistance.

A vital step forward was the paper of Cartwright et al. (2004), which used a theoretical model of point rotations to show how an array of cilia with axes of rotation tilted towards the posterior could establish directional flow. Their prediction of a ‘posterior tilt’ was confirmed experimentally by Nonaka et al. (2005) and Okada et al. (2005). An additional recent publication (Cartwright et al. 2007) has developed the time-averaged analysis further, using computational fluid dynamics modelling to include the effect of the cell surface and also the upper membrane that is removed in experiments. This allows the assessment of the effect of the upper membrane. However, considering only the time-averaged flow field, with velocity boundary conditions imposed on the conical envelopes of the cilia, leads to incorrect conclusions for the movement of particles near the ciliated surface: their results show a steady rightward flow near the cell surface from which the cilia protrude. Smith et al. (2007) showed how time-dependent fluid dynamic simulation predicts that particles released near the cell surface in fact are transported to the left.

Other models have been presented by a number of groups, including the phenomenological model of Buceta et al. (2005), which failed to incorporate correctly the influence of cell surface interactions, invoking inappropriate and unsubstantiated mechanisms postulating differences in velocity or shape between effective and recovery strokes. This led to the incorrect conclusion (Raya & Izpisúa Belmonte 2006) that one mechanism by which cilia produce a ‘robust’ flow field is by beating faster during the effective stroke. Since the Stokes flow equations governing fluid mechanics in this regime have no explicit time dependence, this cannot be the case. Discussion of the interaction between the posterior tilt and the cell surface boundary has been given by Brokaw (2005), and our recent work (Smith et al. 2007) shows how the effect of the cell surface can be efficiently and explicitly included in a simulation.

In this article, we use a simpler approach to the fluid mechanics of the nodal flow, using the classic Gray & Hancock (1955) approximation, modified to account for the surface effect. This leads to an analytical solution for the optimal configuration for the production of directional flow by a whirling rod, which agrees closely with numerical simulation results based on our previous detailed treatment (Smith et al. 2007) and with observations on nodal cilia and an experimental model. Finally, we present new calculations of particle pathlines due to larger arrays for cilia using the simulation technique of Smith et al. (2007).

2. Generation of leftward flow by rotating nodal cilia

Figure 1a depicts schematically the location of the ventral node that may be 20–50 μm in width in the mouse, and figure 1b shows an array of rotating cilia with axes of rotation tilted towards the posterior part of the node structure. The view is from the posterior, looking at the ventral surface of the embryo, so that the l.h.s. of the embryo is on the r.h.s. of the figure. Figure 2 depicts a ‘conical rotation’ model of a single whirling cilium that will be used for the optimal transport calculation.

Motile cilia beat in the very low Reynolds number regime, in which viscous forces dominate, and so must perform a time-irreversible motion in order to produce a net positive flow. This is achieved not by a change in speed during leftward and rightward strokes, but rather by the combination of the posterior tilt in the axis of rotation and the cell surface boundary. In this section, we briefly review how this effect may be modelled using the fundamental singularities of Stokes flow (see also the electronic supplementary material).

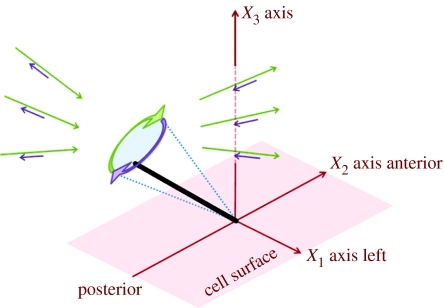
Analysis of the fluid flow produced by the movement of cilia protruding from a surface must take into account the effect of the ‘no-slip’ condition on the cell surface—both forces and torques applied to the fluid near a boundary result in ‘straining’ far-field flows. Figure 3 depicts the stronger leftward far-fields (thin green arrows) and weaker rightward far-fields (purple arrows) that result from leftward and rightward motions of the cilium, respectively. The straining far-field effect can be accounted for using the image systems derived by Blake (1971) and Blake & Chwang (1974). The first accurate analysis was carried out by Blake (1974) on the movement of ciliated micro-organisms such as Paramecium. These cilia execute a three-dimensional pattern with an effective stroke during which the nearly straight cilium swings through an arc while extended from the surface. This is followed by a recovery stroke during which the cilium swings back while remaining close to the surface. There is a similarity to the simple circling movements of a tilted nodal cilium. However, during the recovery stroke of Paramecium cilia, and many other ‘9+2’ cilia, a propagated bend of the cilium causes its movement to become tangential, rather than normal, and this reduces the force applied to the fluid.

Figure 3.

Schematic showing the near-field and far-field fluid flow due to whirling cilium motion, modelled as a tilted rotating rod. The near-field is rotational, while the far-field is a ‘stresslet’ straining flow. The leftward movement of the cilium (thick green arrow) causes a long range leftward stresslet flow (thin green arrows), while the rightward movement of the cilium (thick purple arrow) causes a long range rightward stresslet flow (thin purple arrows). Owing to the posterior tilt, the rightward movement occurs closer to the cell surface than the leftward movement, so that the rightward flow velocity is smaller than the leftward flow velocity due to viscous interaction with the surface. Hence, there is an overall leftward flow in the far-field.

The ciliary beat produces a flow due to differences between the motion produced by the cilium during the effective stroke in one direction and the recovery stroke in the opposite direction. In 9+2 cilia, this difference results from both effects: the difficulty in moving fluid close to the surface, and the change in shape that reduces the force applied to the fluid during the recovery stroke. There is no evidence that nodal cilia exploit the latter effect to gain a propulsive advantage. Nor do nodal cilia constitute a closely packed array that would be able to exploit energetic advantages from metachronal coordination, unlike the 9+2-type system modelled by Gueron & Levit-Gurevich (1999). Nodal cilia appear to rely entirely on the interaction between the cell surface and a simple circling motion around a tilted axis. This was discussed qualitatively by Brokaw (2005), Nonaka et al. (2005) and Okada et al. (2005), and has since been given a detailed theoretical basis in the analysis of Smith et al. (2007).

To model the fluid mechanics mathematically, one may replace the cilium with a line of point forces. A point force is the mathematical idealization of a finite force concentrated to a point of fluid. The point-force solution of the Stokes flow equations is known as the Stokeslet and the associated fluid velocity decays with the inverse of distance in an infinite fluid. This technique was pioneered by Hancock (1953) and formed the basis for work on ciliary propulsion (Blake 1972; Blake & Sleigh 1974; Sleigh et al. 1988), recent high-accuracy modelling (Smith et al. 2007) and the efficient hydrodynamic–internal mechanics simulations of Gueron & Levit-Gurevich (1999, 2001) via the Lighthill–Gueron–Liron theorem (Gueron & Liron 1992). The Stokeslet singularity can be differentiated to give a higher order singularity termed a Stokes doublet, which can be broken down into the antisymmetric rotlet and symmetric stresslet components (Blake & Chwang 1974). The rotlet is the flow produced by a point torque, while the stresslet is the flow produced by a point straining of the fluid; in these cases the velocity decays with the inverse square of distance. The rotlet singularity alone was used by Cartwright et al. (2004) to model the time-averaged effect of a field of rotating cilia. However, their model neglected the influence of the image systems due to the cell surface. The Stokeslet and associated image system form the basis of precise modelling of how the three-dimensional unsteady flow varies over the course of a cilium beat (Smith et al. 2007). The approach is exploited below in the calculation of the optimal angular configuration for fluid advection.

3. Optimal advection

A question that arises, and has been explored experimentally by Nonaka et al. (2005), is: what is the optimal angular configuration of a conically rotating cilium to generate maximum fluid advection? Figure 2 illustrates a simplified conical rotation model with tilt angle θ and the semi-cone angle ψ, as defined by Nonaka et al. Using a hydrodynamically accurate experimental model with wire ‘cilia’, Nonaka et al. observed that a combined angle of θ+ψ=90°, with the cilium almost in contact with the lower surface during the rightward stroke, gives optimal advection (as also observed experimentally by Okada et al. 2005), and that ψ=60° resulted in slightly better advection than ψ=45°. Below, we show how a classic analytic technique can be used to predict the optimal configuration for the experimental study of Nonaka et al.

The technique, first pioneered by Gray & Hancock (1955) in the modelling of flagella, is to model the force per unit length as being proportional to the relative velocity of the body and the fluid, with ‘resistance coefficients’ C_N in the normal and C_T in the tangential directions. For a segment of a slender body translating with velocity components V_N and V_T in the normal and tangential directions, the force components per unit length are C_NV_N and C_TV_T, respectively. Slender body theory, part of a wider class of ‘singularity methods’, models the flow field around a slender body such as a cilium by a line distribution of point forces. However, since the line distribution lies on the inside of the cilium, a finite flow velocity is obtained outside the cilium. Below, we briefly outline how the theory can be used to derive an estimate for the volume flow rate due to a tilted rotating cilium, from which we calculate the optimal angular configuration. Further details are given in the electronic supplementary material.

The rigid cilium can be represented parametrically by the vector X=(X₁, X₂, X₃) as functions of arc length s and time t, where 0<s<L and t>0, with L being the cilium length

$$X_1=s\text{sin}\psi \text{cos}\omega t,$$ (3.1)

$$X_2=-s\text{sin}\psi \text{sin}\omega t\text{cos}\theta -s\text{cos}\psi \text{sin}\theta ,$$ (3.2)

$$X_3=-s\text{sin}\psi \text{sin}\omega t\text{sin}\theta +s\text{cos}\psi \text{cos}\theta ,$$ (3.3)

where ω is the angular frequency of rotation. Note that 0<θ+ψ<90°, and for zero tilt (θ=0) points of the cilium will perform circular orbits at constant height.

A point force F, a distance h from and parallel to a surface, in a fluid of viscosity μ, is known to produce a volume flow rate of q=Fh/πμ in the direction in which it acts, and a volume flow rate of zero in other directions (see Liron (1978) and the electronic supplementary material). The volume flow rate in the X₁ direction due to a force distribution f=(f₁, f₂, f₃) along 0<s<L is given by

$${\int }_0^L\frac{X_3(s,t)}{\pi \mu }{f}_1(s,t)\text{d}s,$$ (3.4)

where we have used h=X₃ and F=f₁ ds. The factor X₃ in the integrand accounts for the boundary effect. To calculate f₁(s, t), we use Gray & Hancock (1955) theory as formulated by Blake (1972)

$$f_j=C_{\text{T}}\left(\gamma {\delta }_{jk}-(\gamma -1)\frac{\partial X_j}{\partial s}\frac{\partial X_k}{\partial s}\right)\frac{\partial X_k}{\partial t},$$ (3.5)

with the summation convention for repeated indices, the symbol δ_jk denoting the Kronecker delta tensor and γ=C_N/C_T. The factor in parentheses accounts for the fact that the normal and tangential components of the force on the slender body result from different resistance coefficients.

Using equations (3.1)–(3.3), we calculate the partial derivatives in (3.5) to substitute for f₁(s, t) in (3.4). We then integrate over one beat cycle 0<t<T and obtain the mean volume flow rate Q in the ‘leftward’ direction

$$Q=(1/6\pi \mu )C_{\text{N}}\omega L^3{\text{sin}}^2\psi \text{sin}\theta .$$ (3.6)

Because the motion of the rotating cilium is only in the direction normal to its centreline axis, Q depends only on C_N, in contrast to 9+2 cilia where the tangential motion of the recovery stroke would require inclusion of a tangential resistance coefficient C_T. Note also that, since C_N is proportional to viscosity, the viscosity dependence in Q cancels out—the flow is determined entirely by the cilium motion with no dependence on the viscosity value, for a given beat pattern.

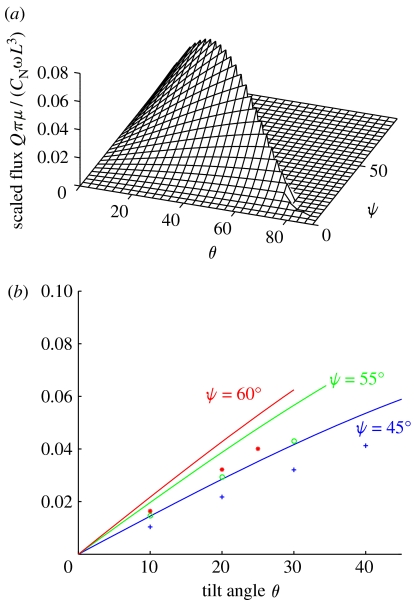
The volume flow rate Q is optimized by the following: the combined angle θ+ψ=90° because Q is a non-decreasing function for the range of θ and ψ considered, so that the maximum lies on the boundary, and the semi-cone angle ψ=arctan(√2)=54.7°, so that the tilt angle θ is approximately 35° (shown in figure 4). We note for a conically rotating cilium in situ that the model is not valid for θ+ψ precisely equal to 90° because this would imply the cilium being in direct contact with the surface. Hence, the prediction for the optimal configuration is one in which θ+ψ is close to 90°, but conical beating is not disrupted by the torques associated with the cilium coming into contact with the surface.

Figure 4.

(a) The optimization of the analytic estimate for scaled volume flow rate Qπμ/C_NωL³, showing that the maximum value is given by θ+ψ=90° and ψ=54.7°. (b) The analytic estimate of scaled volume flow rate Qπμ/C_NωL³ (solid lines) and numerical calculations (points), plotted against tilt angle θ for fixed values of semi-cone angle ψ, in the manner of the flow velocity results presented by Nonaka et al. (2005). For the analytic estimate, the largest values always occur when θ+ψ=90°. The simulation results are given for θ+ψ up to 85°, so that the cilium does not approach the cell surface boundary too closely. While there is no precise agreement between the magnitude of the analytic and numerical curves, both sets of results show identical trends, with the optimal volume flow rate being achieved for ψ∼55°.

The precise value of C_N does not affect our conclusion regarding optimal advection; however, for the purpose of comparing with simulation results, we employ the value used by Gueron & Liron (1992)

$$C_{\text{N}}=\frac{8\pi \mu }{1+2\text{log}(2q/a)},$$ (3.7)

where a is the cilium width; L is the length; and q is a length scale O(L(L/a)^1/2). The precise values of q and a have a relatively weak effect on C_N; we choose the values q=0.6 μm and a=0.1 μm. This leads to the estimate C_N=1.34πμ.

Figure 4b shows the variation in Qπμ/(C_NωL³) against tilt angle θ for both the estimate (3.6) and for numerical simulations, for three fixed values of semi-cone angle ψ: 45° and 60° (for comparison with the experimental measurements of Nonaka et al. 2005) and the approximate optimal value of 55°. The analytic values are given up to θ+ψ=90°, while the numerical simulations are given up to θ+ψ=85°, so that the cilium does not come into close contact with the surface. Although there is not exact agreement in the magnitude of Q, as would be expected since resistive force theory is only an approximation, both analytic and numerical results give excellent agreement regarding the optimal values for both the individual and combined angles. In vivo observations suggest that the tilt angle in mouse, rabbit and medaka fish embryos is θ∼40° (Okada et al. 2005) while Nonaka et al. (2005) reported approximately 27° in the mouse. While our model has assumed the cilia transverse a perfect cone, and thus neglects the slight cilium bending due to viscous resistance (Okada et al. 2005), one should note the correspondence between the in vivo observations and our optimal prediction of θ∼35° with θ+ψ∼90°.

4. Conversion of the nodal flow to left–right asymmetry

The process by which nodal flow may be converted to asymmetric gene expression has been the subject of speculation and investigation since the work of Nonaka et al. (1998). The most recent discovery concerns NVPs (Tanaka et al. 2005; Raya & Izpisúa Belmonte 2006)—micron-sized membrane-enclosed vesicles that contain RA and SHH morphogen proteins. The break-up of these objects has been modelled recently by Cartwright et al. (2007).

Brownian motion will affect the path of an individual micron-sized particle. The diffusion coefficient of a 1 μm particle is estimated to be approximately D=0.2 μm² s⁻¹ using the Einstein–Stokes relation, so that particles may cross pathlines over the time scales associated with motion around and over cilia, which may affect their eventual location. However, as observed by Okada et al. (1999), advection is the dominant effect in the node, the Peclet number associated with length scale l=10 μm and velocity u=1 μm s⁻¹ being ul/D=20; hence to model the motion of ensembles of particles, it is appropriate to simulate pathlines due to advection only. The simulation model using slender body theory presented by Smith et al. (2007) yields quantitative predictions of particle advection in the unsteady, three-dimensional flow field induced by the whirling cilia, approximated as rigid body structures, with very modest computational requirements. This initial study revealed a number of features of the flow field as follows:

1. All particles sufficiently far from the envelopes of cilia were drawn to the left, no matter how near the nodal floor. The ‘mainstream’ flow due to a small array of three cilia was predicted to be approximately 1 μm s⁻¹. At 4 μm from the nodal floor there was a continuous layer of transport, as observed experimentally.

2. Particles may be trapped in vortices near the envelopes of cilia. Some particles will make a number of orbits and then continue moving to the left, as observed experimentally. Particles starting nearby may eventually follow very different paths, suggesting limited ‘chaotic’ mixing.

3. There is no rightward flow close to the boundary.

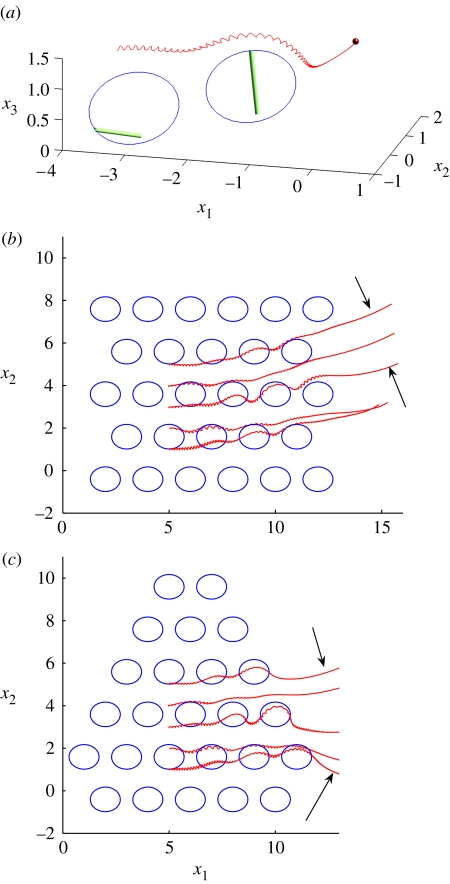
In this section, we present new simulation results for larger arrays of cilia, again representing them as whirling rigid bodies. The physical parameters used were 3 μm for the cilium length and 10 Hz for the cilia frequency. Figure 5a shows an example particle pathline predicted by fluid dynamic simulation of two whirling cilia, each with tilt angle 35° and semi-cone angle 45°. The particle starts at height 1.2L, and is then swept over both cilia to the left. Particle pathlines may become rather complicated, as discussed by Smith et al. (2007), with particles being ‘trapped’ by cilia or performing several orbits before escaping. This is highly dependent on the starting positions and spacing of cilia.

Figure 5.

Simulation results obtained with the model and method of Smith et al. (2007). Particle paths are shown due to flow driven by conically rotating cilia beating with tilt angle θ=35° and semi-cone angle ψ=45°. (a) Advection by two cilia of a particle starting at height 1.2L, where L is cilium length. (b,c) Transport of five particles starting at height 1.2L by approximately rectangular and triangular arrays of cilia (the paths traced by the cilia tips are depicted by ellipses). Note the radial streamlines due to the far-field flow, once the particles leave the array (indicated by arrows).

Figure 5b,c shows particle transport by larger arrays of cilia than have previously been considered taking rectangular and triangular shapes, respectively. Using the above physical parameters, particle pathlines sweep across the middle of the relatively dense rectangular array with a velocity of approximately 4 μm s⁻¹. Okada et al. (2005) observed flow rates of 1–3 μm s⁻¹ in the mouse node. An array of several hundred cilia would not result in significantly greater transport due to the rapid decay of influence of the cilium far-fields, which is as the inverse square of distance. Increasing the cilium spacing by 50%, however, significantly affects the transport velocity, reducing it by approximately 50%. The particle transport speeds due to these larger arrays are greater than the 1 μm s⁻¹ value given in Smith et al. (2007), which was computed for flow due to three cilia only. The approximately rectangular and triangular arrays produce similar particle pathlines, and in both cases the stresslet far-field is evident, as particles leave the array exhibiting radial pathlines.

5. Discussion

We have shown how the fundamental mechanics of low Reynolds number flow are essential in explaining the generation of directional transport by nodal cilia. Consideration of the flow produced by the point-force singularity and associated image systems led to predictions of the optimal configuration for fluid advection, and formed the basis for accurate simulation of particle transport in the unsteady flow field. Numerical simulation techniques based on singularity modelling form the basis for accurate and highly efficient calculation of particle pathlines due to multiple cilia, taking account of the time-dependent nature of the flow field, as well as demonstrating the presence of radial streamlines.

Because the nodal cilium is tilted posteriorly and rotated clockwise, the cell surface boundary that has been incorporated into our analysis via image systems shields the fluid from the effect of the cilium during its rightward motion. No alteration in the cilium shape or radius during the beat cycle is required, nor is the cilium slenderness ratio violated, in contrast to recent modelling in the literature. Future extension of this work to incorporate a closed nodal volume is under development, using a hybrid technique that combines slender body modelling with a boundary integral representation of the no-slip surfaces bounding the fluid volume. Consideration of the effect of diffusion in the slower flowing regions of the periphery of the node, and the associated break-up of NVPs, will be an important aspect of these models. This more complete modelling of flow in the nodal volume is expected to be valuable in unravelling the relationships between nodal flow and signal transduction that are crucial for the proper development of the asymmetry of the embryo.

Supplementary Material

The volume flow rate due to a conically rotating tilted cilium protruding from a surface

The mathematical details of the calculation of the configuration for optimum fluid transport by a tilted, conically rotating nodal cilium