Abstract
Motivation: Pairwise protein sequence alignments are generally evaluated using scores defined as the sum of substitution scores for aligning amino acids to one another, and gap scores for aligning runs of amino acids in one sequence to null characters inserted into the other. Protein profiles may be abstracted from multiple alignments of protein sequences, and substitution and gap scores have been generalized to the alignment of such profiles either to single sequences or to other profiles. Although there is widespread agreement on the general form substitution scores should take for profile-sequence alignment, little consensus has been reached on how best to construct profile–profile substitution scores, and a large number of these scoring systems have been proposed. Here, we assess a variety of such substitution scores. For this evaluation, given a gold standard set of multiple alignments, we calculate the probability that a profile column yields a higher substitution score when aligned to a related than to an unrelated column. We also generalize this measure to sets of two or three adjacent columns. This simple approach has the advantages that it does not depend primarily upon the gold-standard alignment columns with the weakest empirical support, and that it does not need to fit gap and offset costs for use with each substitution score studied.
Results: A simple symmetrization of mean profile-sequence scores usually performed the best. These were followed closely by several specific scoring systems constructed using a variety of rationales.
Contact: altschul@ncbi.nlm.nih.gov
Supplementary Information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Protein sequence comparison is fundamental to computational molecular biology. Early work in this field focussed on pairwise sequence alignment, and was then inevitably extended to multiple alignment. Approaches to multiple alignment that generalize dynamic programming to more than two dimensions (Altschul and Lipman, 1989; Carrillo and Lipman, 1988; Lipman et al., 1989; Murata et al., 1985; Sankoff, 1975; Sankoff and Cedergren, 1983) are necessarily confined to a small number of sequences, and have therefore found limited applications. Most multiple alignment algorithms proceed, in either a progressive or iterative manner, by performing pairwise alignments either between single sequences and multiple alignments or between two multiple alignments (Bacon and Anderson, 1986; Berger and Munson, 1991; Edgar, 2004a; Feng and Doolittle, 1987; Notredame et al., 2000; Papadopoulos and Agarwala, 2007; Taylor, 1987; Thompson et al., 1994a). Closely related subfields concern the extraction of protein ‘profiles’, or position-specific score matrices, from multiple alignments and their comparison either to single sequences (Altschul et al., 1997; Gribskov et al., 1987; Patthy, 1987; Taylor, 1986) or to one another (Altschul et al., 2010; Edgar, 2004b; Edgar and Sjölander, 2003, 2004; Heger and Holm, 2001, 2003; Marti-Renom et al., 2004; Mittelman et al., 2003; Ohlson et al., 2004; von Öhsen and Zimmer, 2001; Panchenko, 2003; Pietrokovski, 1996; Rychlewski et al., 2000; Sadreyev and Grishin, 2003; Söding, 2005; Tomii and Akiyama, 2004; Wang and Dunbrack, 2004; Yona and Levitt, 2002).
Central to any protein alignment method is the scoring system; it uses to distinguish among the exponentially large number of alternative alignments. For pairwise sequence comparison, alignment scores are usually constructed as the sum of ‘substitution scores’ for aligning pairs of letters, and ‘gap scores’ for aligning runs of letters in one sequence to null characters inserted into the other. In the context of ungapped local alignment, an analytic statistical theory (Altschul, 1991; Dembo et al., 1994; Karlin and Altschul, 1990) characterizes all substitution scores as log-odds scores, and most popular pairwise substitution scores have been explicitly constructed using the log-odds formalism (Dayhoff et al., 1978; Henikoff and Henikoff, 1992; Schwartz and Dayhoff, 1978). Similarly, most extensions of substitution scores to profile-sequence comparison now involve log-odds scores as well, mediated by position-specific amino acid frequencies estimated from a multiple alignment column (Altschul et al., 1997; Brown et al., 1993; Sjölander et al., 1996; Tatusov et al., 1994). However, for profile–profile comparison, there is no consensus on how the alignment of positions or columns from two profiles should be scored, and a large variety of such substitution scores have been proposed.
There have abeen a variety of comparative evaluations of profile–profile scoring systems (Edgar, 2004b; Edgar and Sjölander, 2004; Marti-Renom et al., 2004; Mittelman et al., 2003; Ohlson et al., 2004; Panchenko, 2003; Pietrokovski, 1996; Wang and Dunbrack, 2004), some quite systematic and comprehensive. Most of these studies have assessed scoring systems by how well they were able to distinguish by score alignments of related and unrelated profiles, or by how accurately they were able to align related profiles. Several studies (Edgar and Sjölander, 2004; Marti-Renom et al., 2004; Ohlson et al., 2004; Wang and Dunbrack, 2004) faced the issue of how to choose profile–profile gap scores to use in conjunction with the various substitution scores considered. In addition, they had to ‘offset’ raw substitution scores so they could be used with equal footing in a local alignment algorithm. They addressed this problem by attempting to optimize, for each scoring system, gap and offset score parameters over a multidimensional space.
Here, we take up again the question of comparing profile–profile substitution scores, but propose a new evaluation methodology that avoids the question of how best to select gap and offset parameters. In brief, given a ‘gold standard’ multiple alignment, we first choose two subsets of sequences from the alignment, and construct a profile from each aligned set. We then simply calculate the probability that a column from one of the profiles has a higher substitution score when aligned to the correct column of the other profile than when aligned to an incorrect column. We generalize this measure by considering two or three adjacent columns from one profile aligned to adjacent columns of the other. We argue below that these measures of scoring system quality are appropriate, and have several advantages to previous measures. Our approach is related to one suggested by Edgar (2004b), but differs in several ways, e.g. in that it does not compare column–column scores from different profile pairs.
As described below, our approach requires a set of accurate multiple alignments involving fairly large numbers of distantly related proteins. Several multiple alignments sets have been developed for evaluating multiple alignment methodologies, but not all are well suited to our approach, often because their alignments involve too few sequences, or sequences that are on average too closely related. Accordingly, we based our evaluation set of multiple alignments upon a standard database, but supplemented it with carefully curated multiple alignments from several recent publications.
We applied our measures of alignment quality to 39 profile–profile substitution scoring systems, most of which have previously been proposed in the literature. Although no single scoring system emerged as best in all our tests, variations on the approach of constructing scores as an average of profile-sequence scores (Heger and Holm, 2003; Mittelman et al., 2003; Panchenko, 2003; Sadreyev and Grishin, 2003) consistently outperformed most others. Fairly close behind were ‘BILD scores’, constructed as a generalization to multiple alignments of pairwise log-odds scores (Altschul et al., 2010), a weighted and symmetrized form of relative entropy-based scores (Yona and Levitt, 2002) and ‘co-emission’-based scores (Söding, 2005). Incorporating any of these substitution scores into a profile–profile or a multiple alignment program will generally require the introduction of gap scores and perhaps of offset scores. Our evaluation method purposely avoids the consideration of such scores, and the best way to define them may depend upon the substitution scores with which they will be used.
2 METHODS
2.1 Gold standard alignment set
In order to evaluate profile–profile scoring systems, we require a set of accurate multiple alignments to serve as a ‘gold standard’. A variety of multiple alignment datasets have been developed for the explicit purpose of evaluating multiple alignment methods. Recently, Edgar (2010) analyzed several such sets (Edgar, 2004a; Raghava et al., 2003; Thompson et al., 1999; van Walle et al., 2004), and found them flawed by a variety of measures. Nevertheless, we require some alignments as a basis for analysis, and so began with OXBench (Raghava et al., 2003), the dataset that appeared most reliable by Edgar's measures.
Our approach requires relatively large alignments, ideally containing over 25 sequences, of distantly related sequences. Only 11 OXBench alignments were suitable, so we supplemented these with 14 additional, carefully constructed multiple alignments from recently published papers (Zhang and Aravind, 2010; Zhang et al., 2011). The resulting alignment set is summarized in Supplementary Table S1; it has 25 alignments from 8 superfamilies, each alignment containing from 27 to 122 sequences. As described below, these large multiple alignments may be used to generate many distinct pairs of profiles, already in putatively proper alignment.
Profile–profile alignment methods generally are used to compare profiles that are constructed from multiple alignments whose constituent sequences are more closely related within an alignment than between them. To construct pairs of profiles with this property, we proceed as follows. From a given gold standard multiple alignment, we choose at random a pair of sequences S1 and S2 to act as seeds for two profiles. We then choose at random a new sequence from the multiple alignment, determine with which of S1 and S2 (to both of which it is already aligned) it shares greater percent identity, and add it to the profile seeded by that sequence. We repeat this process until the two profiles have in aggregate N sequences, with N equal to 10 or 20. If one of the profiles so constructed has <3 sequences, we start over. Finally, the pair of profiles is assigned to a bin, depending on the mean percent identity between all sequences from one profile and all those from the other. Our bins cover the percent identity ranges 5–10, 10–15, 15–20, 20–25, 25–30 and 30–35; any pair of profiles that falls into none of these bins is discarded.
Given the size of our original alignments, we are able to generate a very large number of effectively distinct pairs of aligned profiles. We therefore populate our bins evenly, and with equal representation from each superfamily and, subordinately, from each constituent family. The only hindrance is that certain of our alignments lend themselves to generating profile pairs only for a subrange of percent identities, as detailed in Supplementary Table S1. When populating bins outside their effective range, these alignments are ignored.
2.2 Quality measures for profile–profile substitution scores
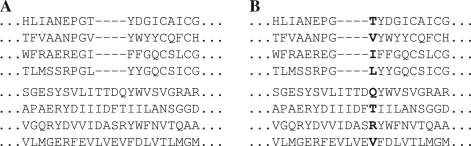
Our measures of substitution score quality are calculated on pairs of profiles that are putatively accurately aligned. For a given column of one profile, we calculate the percent probability π1 that its substitution score, when aligned to the correct column of the other profile, is greater than when aligned to an incorrect column; ties register as half a success. Averaging π1 over all columns of both profiles yields our quality measure Π1. For profile–profile as for sequence–sequence alignment, perhaps the simplest error involves the misalignment of a single column, which leads to the slight misplacement of a gap, as illustrated in Figure 1. The measure Π1 can be seen to bear directly on the probability of such a simple alignment error arising.
Fig. 1.
Two profile–profile alignments. (A) A putatively correct alignment. (B) One column misaligned.
Slightly larger errors in gap placement can correspond to the misalignment of two or more adjacent columns. An error of this sort, however, cannot always be explained as multiple single-column misalignment errors, and may require the scores of the misaligned columns to be considered together. Accordingly, we can extend the measure Π1 to Πn by determining, for two related profiles, the mean percent probability that the aggregate score of n adjacent columns from one profile is greater when properly than when improperly aligned to n adjacent columns from the other. In this article, we will consider only the measures Π1, Π2 and Π3.
Measuring substitution score quality in this way avoids using the scores actually to construct by dynamic programming new profile–profile alignments, and may therefore be considered somewhat indirect. Nevertheless, our approach has several distinct advantages. The location of gaps in an accurate alignment of two profiles effectively limits realignment-based measures to evaluating scores on a very small number of column pairs. In contrast, our measures treat all profile positions equivalently, and gather information from them all. Furthermore, it has recently been argued that none of the collections of multiple alignments used as gold standards for evaluating multiple alignment programs, or sometimes for evaluating profile–profile scoring systems, is very reliable (Edgar, 2010). A problem with constructing a new alignment B from sequences contained in a gold standard alignment A, and then comparing B to A, is that the two alignments are most likely to differ precisely in the columns of A that are least reliably aligned, whereas no information is gained from the majority of A's columns that are relatively easy to align, and therefore most likely to be accurate.
An additional problem with realignment-based measures for evaluating substitution scores is that they generally require gap and offset scores to be specified for each scoring system. This entails optimizing at least three independent parameters (Edgar and Sjölander, 2004; Marti-Renom et al., 2004; Ohlson et al., 2004; Wang and Dunbrack, 2004), which is time consuming and, because inevitably non-optimal, introduces noise into the analysis. More importantly, as discussed below, the best form for gap scores to take varies with the substitution scores employed (Altschul, 1989), so choosing a particular form for gap scores is likely to bias one's conclusions. This article proceeds on the assumption that it is reasonable to analyze substitution scores independently of gap and offset scores. Once a particular set of substitution scores has been selected, gap and offset scores may then be optimized in the chosen context.
2.3 General issues for profile–profile scoring systems
2.3.1 Sequence weights and independent observations
Profile–profile substitution scores depend at root upon the counts of amino acids observed in the two multiple alignment columns implicitly being aligned. However, the sequences comprising a multiple alignment generally cannot be viewed as independent observations from a protein family, but may have a complex structure of correlations arising from phylogenetic relationships. Accordingly, it is often advisable to downweight the amino acid counts derived from closely related and thus highly correlated sequences, and a large number of methods for doing this have been proposed (Altschul et al., 1989; Bailey and Gribskov, 1996; Eddy et al., 1995; Gerstein et al., 1994; Gotoh, 1995; Henikoff and Henikoff, 1994; Krogh and Mitchison, 1995; Sander and Schneider, 1991; Sibbald and Argos, 1990; Sunyaev et al., 1999; Thompson et al., 1994b; Vingron and Sibbald, 1993). Relatedly, it is also sometimes useful to estimate the number of effectively independent observations a column represents (Altschul et al., 1997, 2009; Brown et al., 1997; Sunyaev et al., 1999; Wang and Dunbrack, 2004), which is generally smaller than the actual number of residues it aligns. Using these methods, the data in a profile column can be summarized by an ‘effective’ amino acid frequency vector 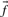 (perhaps extended to include the null character as a twenty-first letter), and an ‘effective’ number of observations c. One may, of course, forgo any weighting methods in generating these column statistics. In either case, it will sometimes be useful to refer to the ‘observed’ amino acid count vector
(perhaps extended to include the null character as a twenty-first letter), and an ‘effective’ number of observations c. One may, of course, forgo any weighting methods in generating these column statistics. In either case, it will sometimes be useful to refer to the ‘observed’ amino acid count vector 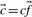 . In this article, when sequence weighting is performed, we used the method of Sunyaev et al. (1999) with a modification described in Altschul et al. (2009) for estimating the effective number of independent observations.
. In this article, when sequence weighting is performed, we used the method of Sunyaev et al. (1999) with a modification described in Altschul et al. (2009) for estimating the effective number of independent observations.
2.3.2 Predicted frequencies
Before comparing a column, summarized by c and 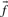 , to another, it may be useful to estimate the unobserved amino acid frequencies
, to another, it may be useful to estimate the unobserved amino acid frequencies 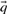 thought to characterize the column. When c is large
thought to characterize the column. When c is large  should approach
should approach 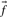 , but when c is small this will generally be a poor approximation: it is clearly wrong to infer zero probability for an amino acid to appear in an alignment position just because it is not observed in a small sample. Two methods for inferring
, but when c is small this will generally be a poor approximation: it is clearly wrong to infer zero probability for an amino acid to appear in an alignment position just because it is not observed in a small sample. Two methods for inferring  from c and
from c and 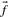 have gained widespread use. The ‘Dirichlet mixture method’ (Brown et al., 1993; Sjölander et al., 1996) is rigorously Bayesian. It assumes a Dirichlet mixture prior on the space of amino acid frequency vectors, and obtains
have gained widespread use. The ‘Dirichlet mixture method’ (Brown et al., 1993; Sjölander et al., 1996) is rigorously Bayesian. It assumes a Dirichlet mixture prior on the space of amino acid frequency vectors, and obtains 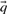 by integration over the posterior distribution implied by the data from a column. The alternative ‘data-dependent pseudocount method’ (Altschul et al., 1997; Tatusov et al., 1994) calculates
by integration over the posterior distribution implied by the data from a column. The alternative ‘data-dependent pseudocount method’ (Altschul et al., 1997; Tatusov et al., 1994) calculates 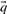 by adding ‘pseudocounts’ to the observed amino counts
by adding ‘pseudocounts’ to the observed amino counts  ; these pseudocounts are derived from
; these pseudocounts are derived from  and a specified pairwise amino acid substitution matrix. One motivation for this method is the desire for the target frequencies
and a specified pairwise amino acid substitution matrix. One motivation for this method is the desire for the target frequencies 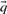 to approach those implicit in the specified matrix (Altschul, 1991; Karlin and Altschul, 1990) as c approaches 1. Both methods imply that
to approach those implicit in the specified matrix (Altschul, 1991; Karlin and Altschul, 1990) as c approaches 1. Both methods imply that  approaches
approaches 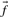 as c grows large.
as c grows large.
Many of the profile–profile substitution scores we will consider are defined using predicted frequencies 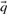 for the profile columns aligned. In order not to confound an analysis of the quality of substitution scores with the method used for deriving
for the profile columns aligned. In order not to confound an analysis of the quality of substitution scores with the method used for deriving 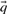 from
from 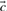 , we employ the Dirichlet mixture method throughout. This choice is preferred because the Dirichlet mixture method is integral to the BILD-based scores (Altschul et al., 2010) that we will consider. We use the ‘recode3’ Dirichlet mixture priors developed at the University of California at Santa Cruz (Supplementary Table S2a; http://compbio.soe.ucsc.edu/dirichlets/index.html), but make no claim that these are superior to other possible priors.
, we employ the Dirichlet mixture method throughout. This choice is preferred because the Dirichlet mixture method is integral to the BILD-based scores (Altschul et al., 2010) that we will consider. We use the ‘recode3’ Dirichlet mixture priors developed at the University of California at Santa Cruz (Supplementary Table S2a; http://compbio.soe.ucsc.edu/dirichlets/index.html), but make no claim that these are superior to other possible priors.
2.3.3 Gap scores
Profile–profile alignment scoring systems in general must deal with two distinct issues arising from gaps. The first is that a profile column itself may be constructed from a multiple alignment that contains gaps in the corresponding position. Should the frequency of gaps in this position be estimated explicitly? If so, how should such gap frequencies be considered when defining substitution scores for aligning two profile columns? As will be evident, some of the profile–profile substitution scores considered below have natural (although not necessarily optimal) generalizations to deal with gap frequencies, while others do not. The second issue is that the alignment of two profiles may introduce gaps, aligning columns of one profile with gap columns inserted into the other. How such gaps should be scored will depend upon the profile–profile substitution scores adopted, and also upon the way in which gap frequencies are treated by such substitution scores.
Because the gap-scoring problems for profile–profile alignment are multifarious and likely not subject to a uniform optimal treatment (Altschul, 1989), we here attempt to sidestep the issues involved as much as possible. We ignore gaps within a column for all profile–profile substitution scores. To minimize the effect upon our results, we confine our analysis primarily to profile columns derived from alignment positions containing relatively few gaps. Also, our quality measures for substitution scores avoid any need to specify gap scores for profile–profile alignment.
2.4 Profile–profile substitution scores
The substitution scoring systems we consider largely subsume those analyzed by Edgar and Sjölander (2004); Edgar (2004b); Marti-Renom et al. (2004); Mittelman et al. (2003); Ohlson et al. (2004); Pietrokovski (1996); Panchenko (2003); Wang and Dunbrack (2004). We do not, however, consider scores that are rounding variants of others, or that are asymmetric under exchange of the aligned columns, but we do analyze several scores considered in none of these papers.
Many substitution scores make use either of the observed frequencies 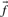 associated with the columns compared, or the predicted frequencies
associated with the columns compared, or the predicted frequencies 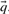 . In addition, some substitution scores use the odds ratio vectors
. In addition, some substitution scores use the odds ratio vectors 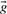 or
or  , defined by gi=fi/pi and ri=qi/pi, where
, defined by gi=fi/pi and ri=qi/pi, where 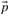 is the vector of background amino acid frequencies. Yet others use the log-odds score vector
is the vector of background amino acid frequencies. Yet others use the log-odds score vector  defined by si=log ri; a corresponding score vector cannot be derived from
defined by si=log ri; a corresponding score vector cannot be derived from 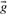 , because some of
, because some of 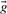 's components may be zero.
's components may be zero.
Certain profile–profile scores are defined using a standard pairwise substitution score matrix. Such a matrix S has implicit amino acid pair target frequencies Q (Altschul, 1991; Karlin and Altschul, 1990), which may also be expressed as amino acid pair odds ratios R. In short, Ri,j=Qi,j/(pipj) and 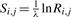 , where λ is a scale factor. In this study, we will use the BLOSUM-62 matrix (Henikoff and Henikoff, 1992), and its associated target frequencies and odds ratios, whenever such a matrix is called for.
, where λ is a scale factor. In this study, we will use the BLOSUM-62 matrix (Henikoff and Henikoff, 1992), and its associated target frequencies and odds ratios, whenever such a matrix is called for.
We use the convention that larger substitution scores are better. However, some scoring systems are based on distances, with smaller distances preferred, so for these the substitution score needs to be the negative distance. In practice, an offset is usually added for constructing local alignments, but because we do not use the scores here for this purpose, we have no need for such offsets.
We summarize below the 39 substitution scores we consider. Where these substitution scores have been analyzed by one of Edgar and Sjölander (2004); Edgar (2004b); Mittelman et al. (2003); Marti-Renom et al. (2004); Ohlson et al. (2004); Pietrokovski (1996); Panchenko (2003); Wang and Dunbrack (2004), Supplementary Table S3 lists the corresponding names those papers employ. Also, if a score was not introduced in one of these articles, the table cites the paper where it was first proposed, as best as we have been able to determine.
2.4.1 Euclidean-distance based scores
Intuitively, one prefers to align columns with similar letter frequencies, so one may base a scoring system on a ‘distance’ between two column-derived vectors. An obvious candidate is the Euclidean distance between vectors 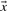 and
and 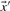 :
:
| (1) |
For aligning two profile columns, the vector 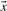 used in Equation (1) may be taken, variously, to be the
used in Equation (1) may be taken, variously, to be the 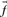 ,
, 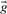 ,
, 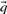 ,
,  or
or  derived from the first column, and
derived from the first column, and 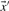 the corresponding vector from the second. We call the five resulting scores, defined as the negative of Equation (1), Euclid-f, Euclid-g, Euclid-q, Euclid-r and Euclid-s.
the corresponding vector from the second. We call the five resulting scores, defined as the negative of Equation (1), Euclid-f, Euclid-g, Euclid-q, Euclid-r and Euclid-s.
2.4.2 Dot-product based scores
The dot product of two vectors 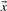 and
and 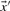 is defined as
is defined as
| (2) |
Because the dot product of two vectors of fixed magnitude increases as the angle between the vectors decreases, it has been seen as a promising basis for profile–profile substitution scores. Basing 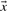 and
and 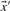 in Equation (2) on the various profile-column vectors we have defined yields the five scores dot-f, dot-g, dot-q, dot-r and dot-s. In addition, when
in Equation (2) on the various profile-column vectors we have defined yields the five scores dot-f, dot-g, dot-q, dot-r and dot-s. In addition, when 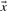 and
and 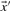 are odds ratios, it has been suggested that a substitution score is better defined as the log of the dot product (Madera et al., 2004), yielding in our notation the two additional scores ldot-g and ldot-r. Although such a monotonic transformation is invisible to our Π1 measure of score quality, it can make a difference when the scores for aligned column pairs are added. Finally, Söding (2005) has proposed a profile–profile scoring system that, in essence, is the log of
are odds ratios, it has been suggested that a substitution score is better defined as the log of the dot product (Madera et al., 2004), yielding in our notation the two additional scores ldot-g and ldot-r. Although such a monotonic transformation is invisible to our Π1 measure of score quality, it can make a difference when the scores for aligned column pairs are added. Finally, Söding (2005) has proposed a profile–profile scoring system that, in essence, is the log of 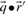 or
or 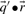 ; we call this score ldot-qr.
; we call this score ldot-qr.
2.4.3 Pearson-correlation based scores
The Pearson correlation of two vectors 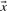 and
and 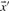 is defined as
is defined as
| (3) |
where  and
and 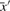 are, respectively, the means of the components of
are, respectively, the means of the components of  and
and 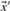 . Basing
. Basing 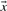 and
and 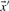 on our various profile-column vectors yields the five scores corr-f, corr-g, corr-q, corr-r and corr-s. It has also been suggested (Pietrokovski, 1996) that one replace the components of the vectors
on our various profile-column vectors yields the five scores corr-f, corr-g, corr-q, corr-r and corr-s. It has also been suggested (Pietrokovski, 1996) that one replace the components of the vectors  and
and 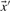 by their numerical ranks within these vectors (i.e. replacing the largest xi by 1, etc.) to yield
by their numerical ranks within these vectors (i.e. replacing the largest xi by 1, etc.) to yield 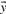 and
and 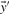 , and then calculate the Pearson correlation of these new vectors. Doing so yields the four scores we call rank-f, rank-g, rank-q and rank-r; because logarithms are monotonic, rank-s is identical to rank-r.
, and then calculate the Pearson correlation of these new vectors. Doing so yields the four scores we call rank-f, rank-g, rank-q and rank-r; because logarithms are monotonic, rank-s is identical to rank-r.
2.4.4 Pairwise-substitution-matrix based scores
Given a pairwise substitution score matrix S and two probability vectors 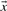 and
and 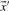 , one can calculate the average score:
, one can calculate the average score:
| (4) |
Depending upon whether the observed or predicted frequencies are used for 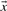 and
and 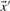 , we call the two resulting scores aS-f and aS-q. The former is closely related to what are frequently called ‘SP’ or ‘Sum-of-Pairs’ scores for multiple alignments (Bacon and Anderson, 1986). A variation on this idea averages the target frequencies Q or odds ratios R implied by S and then takes the logarithm of this average (von Öhsen and Zimmer, 2001). We call the resulting scores laQ-f, laQ-q, laR-f and laR-q.
, we call the two resulting scores aS-f and aS-q. The former is closely related to what are frequently called ‘SP’ or ‘Sum-of-Pairs’ scores for multiple alignments (Bacon and Anderson, 1986). A variation on this idea averages the target frequencies Q or odds ratios R implied by S and then takes the logarithm of this average (von Öhsen and Zimmer, 2001). We call the resulting scores laQ-f, laQ-q, laR-f and laR-q.
2.4.5 Relative-entropy based scores
The relative entropy (Cover and Thomas, 1991) of two probability vectors 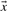 and
and 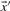 is defined as
is defined as
| (5) |
By continuity, H may be extended to the case where some xi are zero by simply omitting the corresponding terms. However, if any x′i vanishes while xi remains positive, H is undefined. Although H is asymmetric, it may be symmetrized (Lin, 1991) using the definition
| (6) |
With predicted frequencies  and
and 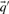 substituted for
substituted for 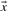 and
and 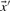 , the negative of this expression yields a score we call sre-q (Sjölander, 1998). In general, no corresponding score using observed frequencies is valid, because one H term or both may be undefined.
, the negative of this expression yields a score we call sre-q (Sjölander, 1998). In general, no corresponding score using observed frequencies is valid, because one H term or both may be undefined.
An alternative symmetrization of relative entropy is the Jensen–Shannon divergence (Lin, 1991), defined as
| (7) |
where 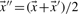 . The negative of this expression may be used with either observed or predicted frequencies to yield the two scores we call JS-f and JS-q, respectively. Yona and Levitt (2002) argued that columns with amino acid frequencies far from the background frequencies
. The negative of this expression may be used with either observed or predicted frequencies to yield the two scores we call JS-f and JS-q, respectively. Yona and Levitt (2002) argued that columns with amino acid frequencies far from the background frequencies 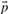 should have greater weight than those with frequencies near
should have greater weight than those with frequencies near 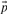 , and therefore defined a score
, and therefore defined a score
| (8) |
Depending upon whether observed of predicted frequencies are used for 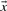 and
and 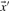 , we call the resulting scores YL-f and YL-q.
, we call the resulting scores YL-f and YL-q.
2.4.6 Profile-sequence based scores
Over the years a number of methods have been proposed for generating profile-sequence substitution scores, but a consensus has formed on the best general strategy. From a multiple alignment column with observed counts  , one estimates amino acid frequencies
, one estimates amino acid frequencies  , from which odds ratios
, from which odds ratios  and log-odds scores
and log-odds scores  are derived. The score for aligning the profile column to a particular amino acid then reduces to selecting the appropriate component of
are derived. The score for aligning the profile column to a particular amino acid then reduces to selecting the appropriate component of  . If instead one wishes to align the profile column to that from another profile, one possible generalization is to use the observed frequencies
. If instead one wishes to align the profile column to that from another profile, one possible generalization is to use the observed frequencies 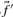 from the second profile column to calculate a weighted average
from the second profile column to calculate a weighted average 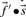 of profile-sequence scores (Heger and Holm, 2001).
of profile-sequence scores (Heger and Holm, 2001).
An immediate conceptual difficulty is that it is unclear why one profile column should be used to generate the scores and the other to average them. It is simple, however, to symmetrize this approach and define the score 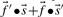 (Mittelman et al., 2003), which we call sdot-fs. Variations on this idea replace the observed frequencies
(Mittelman et al., 2003), which we call sdot-fs. Variations on this idea replace the observed frequencies 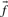 and
and 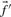 with either the observed counts or the predicted frequencies, to yield respectively the scores sdot-cs and sdot-qs (Heger and Holm, 2003; Mittelman et al., 2003; Panchenko, 2003).
with either the observed counts or the predicted frequencies, to yield respectively the scores sdot-cs and sdot-qs (Heger and Holm, 2003; Mittelman et al., 2003; Panchenko, 2003).
A modification of sdot-cs, implemented in the program Compass (Sadreyev and Grishin, 2003), and which we call comp-cs, is
| (9) |
A motivation for this definition is that it reduces to the standard profile-sequence substitution score when one of the columns consists of a single observation. We will also consider the scoring system comp-fs, with the same limiting property, in which the count vectors in Equation (9) are replaced by observed frequency vectors. For either comp-cs or comp-fs, when both c and c′ are 1 the substitution score may be defined using a standard pairwise score matrix.
As described above, we here calculate 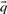 and
and 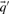 and the resulting
and the resulting  and
and 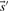 using the Dirichlet mixture method in lieu of the data-dependent pseudocount method employed by PSI-BLAST (Altschul et al., 1997) and in Sadreyev and Grishin (2003); Wang and Dunbrack (2004).
using the Dirichlet mixture method in lieu of the data-dependent pseudocount method employed by PSI-BLAST (Altschul et al., 1997) and in Sadreyev and Grishin (2003); Wang and Dunbrack (2004).
2.4.7 BILD scores
Altschul et al. (2010) recently proposed a generalization of pairwise log-odds substitution scores to profile–profile alignments. Specifically, they assumed an M-component Dirichlet mixture prior, with mixture parameters (mi; i=1,2,…,M) and Dirichlet parameters (αi,j; i=1,2,…,M; j=1,2,…,20). Then the probability of observing a specific column with count vector  is given by
is given by
| (10) |
where αi≡∑jαi,j and Γ(·) is the Gamma function. The BILD score for aligning two columns with count vectors  and
and  is then
is then
| (11) |
3 RESULTS
We evaluated the profile–profile substitution scores described above on profile pairs generated as described in Section 2. Specifying either 10 or 20 aggregate sequences, we generated 2400 aligned profile pairs 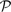 and
and 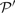 for each mean percent identity bin. For each pair, we calculated the quality scores Π1, Π2 and Π3 defined above, either using sequence weights or not. We omitted, however, from this calculation any columns of
for each mean percent identity bin. For each pair, we calculated the quality scores Π1, Π2 and Π3 defined above, either using sequence weights or not. We omitted, however, from this calculation any columns of 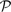 or
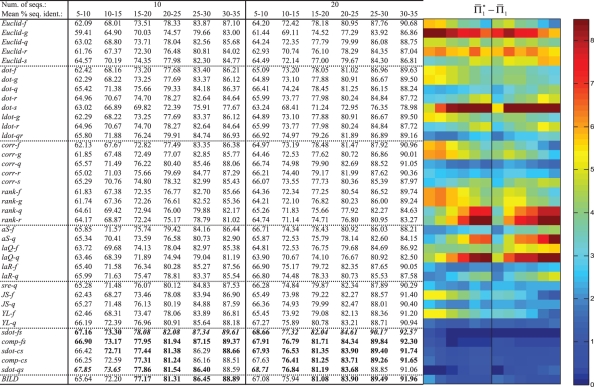
or 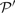 containing over 25% gap characters. For each substitution score, the mean values of Π1, using weights, are shown in Figure 2. These values are significant to approximately the first digit past the decimal. In each column, the largest
containing over 25% gap characters. For each substitution score, the mean values of Π1, using weights, are shown in Figure 2. These values are significant to approximately the first digit past the decimal. In each column, the largest 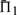 is italicized, and all
is italicized, and all 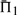 that differ by <1% (in absolute rather than relative value) are shown in bold. In addition, for ease of interpretation, the differences between each value of
that differ by <1% (in absolute rather than relative value) are shown in bold. In addition, for ease of interpretation, the differences between each value of 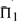 and the maximum in its column are represented in a color panel to the right of the table of numbers. We discuss below several broad features of Figure 2, and the relationship of its data to those that result when various parameters of our analysis are varied.
and the maximum in its column are represented in a color panel to the right of the table of numbers. We discuss below several broad features of Figure 2, and the relationship of its data to those that result when various parameters of our analysis are varied.
Fig. 2.
Scoring system quality. Scoring systems are assessed using the measure 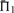 on 2400 weighted profile pairs for each column. The color panel shows the difference between the maximum value in each column,
on 2400 weighted profile pairs for each column. The color panel shows the difference between the maximum value in each column, 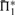 , and individual values of
, and individual values of 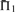 . Some differences exceed the upper limit of the color scale.
. Some differences exceed the upper limit of the color scale.
For each score, the values of 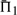 increase both with the mean percent identity between profiles, and with their aggregate number of sequences. This is fully expected, as both changes should render it easier to align the profile columns correctly.
increase both with the mean percent identity between profiles, and with their aggregate number of sequences. This is fully expected, as both changes should render it easier to align the profile columns correctly.
The performances of certain pairs of scores, i.e. (dot-g and ldot-g) and (dot-r and ldot-r), are indistinguishable by 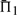 . Brief consideration reveals that this will be true of any scores that may be mapped to one another by a monotonic function. Nevertheless, we continue to consider both scores from each pair because the quality measures
. Brief consideration reveals that this will be true of any scores that may be mapped to one another by a monotonic function. Nevertheless, we continue to consider both scores from each pair because the quality measures 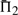 and
and 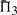 do in fact distinguish them.
do in fact distinguish them.
We now turn to examining the relative performance of the 39 substitution scores. Several scores, namely Euclid-g, Euclid-r, dot-s, rank-q, rank-r, aS-q and laQ-q, do quite poorly—more than 5 percentage points worse than the best score—in most or all columns of Figure 2. The score sdot-fs (Mittelman et al., 2003), a simple average of profile-sequence scores, outperforms all others in 75% of the columns, and is second best to the related sdot-qs in the remaining 25%. The ideas of using observed counts (sdot-cs) or predicted frequencies (sdot-qs) in place of the observed frequencies to calculate this average do not, in general, yield an improvement, nor does the idea of giving extra weight to the profile-sequence scores derived from the larger profile (comp-fs; comp-cs). After sdot-fs and closely related scores, BILD scores (Altschul et al., 2010) usually perform second best, and YL-q scores (Yona and Levitt, 2002) third; both almost always yield a 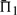 within 2 percentage points of the best.
within 2 percentage points of the best.
In 47.9% of the cases shown in Figure 2, employing sequence weights yields a worse value for 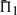 than does leaving the profile data unweighted. The differences between the values of
than does leaving the profile data unweighted. The differences between the values of 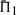 when weights are employed and when they are not is shown in Supplementary Figure S1. It is somewhat surprising that weights degrade performance so often. Of course, for the alignments used to generate the test set, some care has been taken to eliminate redundancy. Thus, sequence weighting is less likely to be of value for our than for more general profile pairs. Nevertheless, Supplementary Figure S1 shows clearly that the weights we have employed (Altschul et al., 2009; Sunyaev et al., 1999) tend to improve most scoring systems' performances at low mean sequence identity (5–15%), but to hurt them at moderate identity (25–35%), and this effect is more pronounced the more sequences the profiles contain. Also, it is evident that these weights are substantially better adapted to certain profile–profile scoring systems than to others. The use of weights or not does not alter in any substantive way our conclusions concerning which profile–profile scoring systems are best. However, that weighting degrades so many of the
when weights are employed and when they are not is shown in Supplementary Figure S1. It is somewhat surprising that weights degrade performance so often. Of course, for the alignments used to generate the test set, some care has been taken to eliminate redundancy. Thus, sequence weighting is less likely to be of value for our than for more general profile pairs. Nevertheless, Supplementary Figure S1 shows clearly that the weights we have employed (Altschul et al., 2009; Sunyaev et al., 1999) tend to improve most scoring systems' performances at low mean sequence identity (5–15%), but to hurt them at moderate identity (25–35%), and this effect is more pronounced the more sequences the profiles contain. Also, it is evident that these weights are substantially better adapted to certain profile–profile scoring systems than to others. The use of weights or not does not alter in any substantive way our conclusions concerning which profile–profile scoring systems are best. However, that weighting degrades so many of the 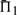 , some very significantly, implies that much remains unknown about the proper construction of sequence weights, at least for use with profile–profile substitution scores. Pursuing such an analysis further is beyond the scope of this article.
, some very significantly, implies that much remains unknown about the proper construction of sequence weights, at least for use with profile–profile substitution scores. Pursuing such an analysis further is beyond the scope of this article.
It is advisable to consider quality measures based upon multiple columns, so we have performed experiments similar to those described above for 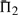 and
and 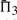 . The results are given in Supplementary Figures S2 and S3. We observe, first, that by these measures, a monotonic function applied to a scoring system now affects its quality, because the magnitude of the scores becomes relevant once they are added. As a result, dot-g becomes distinguishable from ldot-g, and dot-r from ldot-r. Second, as more adjacent columns are considered, it becomes easier to distinguish correct from incorrect alignments. For alignment pairs containing 20 total sequence, with 30–35% mean sequence identity, the best scoring system has a >99% chance, and almost every other scoring system a > 94% chance, of assigning the correct alignment of three adjacent columns a better score than an incorrect alignment. We could extend our measure to four or more adjacent columns, but such an analysis eventually becomes irrelevant. There are a few minor differences between the one-, two- and three-column results. The basic finding stands that sdot-fs and related scores in general perform best. The relatively poor performance of BILD scores at low mean sequence identity is more apparent, but as we will see below, this deficit may be mitigated by using different Dirichlet mixture priors. Also, for Π2 and Π3, the performance of ldot-qr scores (Söding, 2005) rises to among the best.
. The results are given in Supplementary Figures S2 and S3. We observe, first, that by these measures, a monotonic function applied to a scoring system now affects its quality, because the magnitude of the scores becomes relevant once they are added. As a result, dot-g becomes distinguishable from ldot-g, and dot-r from ldot-r. Second, as more adjacent columns are considered, it becomes easier to distinguish correct from incorrect alignments. For alignment pairs containing 20 total sequence, with 30–35% mean sequence identity, the best scoring system has a >99% chance, and almost every other scoring system a > 94% chance, of assigning the correct alignment of three adjacent columns a better score than an incorrect alignment. We could extend our measure to four or more adjacent columns, but such an analysis eventually becomes irrelevant. There are a few minor differences between the one-, two- and three-column results. The basic finding stands that sdot-fs and related scores in general perform best. The relatively poor performance of BILD scores at low mean sequence identity is more apparent, but as we will see below, this deficit may be mitigated by using different Dirichlet mixture priors. Also, for Π2 and Π3, the performance of ldot-qr scores (Söding, 2005) rises to among the best.
One may construct predicted frequencies 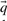 for an alignment column using a variety of priors for the Dirichlet mixture method, as well as by using the alternative data-dependent pseudocount method (Altschul et al., 1997; Tatusov et al., 1994) with a standard pairwise substitution matrix. To study whether our results are sensitive to these variations, we reran our experiments for the quality measure
for an alignment column using a variety of priors for the Dirichlet mixture method, as well as by using the alternative data-dependent pseudocount method (Altschul et al., 1997; Tatusov et al., 1994) with a standard pairwise substitution matrix. To study whether our results are sensitive to these variations, we reran our experiments for the quality measure 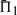 with sequence weights, but using ‘recode4’, ‘recode5’ and ‘fournier’ Dirichlet mixture priors (Supplementary Tables S2b, S2c, S2d; http://compbio.soe.ucsc.edu/dirichlets/index.html) in the place of ‘recode3’, as well as using the data-dependent pseudocount method in conjunction with the BLOSUM-62 substitution matrix (Henikoff and Henikoff, 1992). We compare the results to those using ‘recode3’ in Supplementary Figure S4. Many of the scoring systems we have studied make no use of predicted frequencies, so these are omitted from the comparison. Also, as discussed above, BILD scores can be used only with the Dirichlet mixture method. As can be seen, different Dirichlet priors may be optimal for different scoring systems. For example, ‘recode4’ priors yield the best average results for YL-q, ‘recode3’ for sdot-fs and ‘fournier’ for BILD. Furthermore, the data-dependent pseudocount method yields better results than does the Dirichlet mixture method for most scoring systems, but not for sdot-fs and most related scores. Nevertheless, even when each scoring system is paired with its optimal method for estimating
with sequence weights, but using ‘recode4’, ‘recode5’ and ‘fournier’ Dirichlet mixture priors (Supplementary Tables S2b, S2c, S2d; http://compbio.soe.ucsc.edu/dirichlets/index.html) in the place of ‘recode3’, as well as using the data-dependent pseudocount method in conjunction with the BLOSUM-62 substitution matrix (Henikoff and Henikoff, 1992). We compare the results to those using ‘recode3’ in Supplementary Figure S4. Many of the scoring systems we have studied make no use of predicted frequencies, so these are omitted from the comparison. Also, as discussed above, BILD scores can be used only with the Dirichlet mixture method. As can be seen, different Dirichlet priors may be optimal for different scoring systems. For example, ‘recode4’ priors yield the best average results for YL-q, ‘recode3’ for sdot-fs and ‘fournier’ for BILD. Furthermore, the data-dependent pseudocount method yields better results than does the Dirichlet mixture method for most scoring systems, but not for sdot-fs and most related scores. Nevertheless, even when each scoring system is paired with its optimal method for estimating 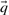 , our basic conclusions still hold.
, our basic conclusions still hold.
4 CONCLUSION
In this article, we have addressed the isolated question of how best to define substitution scores for profile–profile comparison. Using gold standard multiple alignment datasets, we constructed pairs of profiles with known alignment. We then measured the quality of a scoring system by the probability with which it rated properly aligned columns better than improperly aligned ones. This evaluation method has several advantages, as described above.
Our results suggest that among the wide variety of substitution scores considered, the best are variations on sequence-profile based scores, most notably sdot-fs (Mittelman et al., 2003), followed fairly closely by BILD (Altschul et al., 2010), YL-q (Yona and Levitt, 2002) and ldot-qr (Söding, 2005) scores. BILD scores have various attractive theoretical features; for example, they yield a consistent measure of multiple alignment similarity, and may help define the proper boundaries of a homologous domains (Altschul et al., 2010). Although BILD scores may be preferred for these reasons, this study suggests that other scores may be somewhat superior for the simple purpose of profile–profile comparison.
To the extent that previous studies have been able to distinguish among the scoring systems they considered, their results are broadly consistent with ours. For example, Mittelman et al. (2003) took an evaluation approach different than ours, but one that also avoided defining gap and offset scores. They found that, among those scores they considered, the best were YL-q (Yona and Levitt, 2002), and several sequence profile-based scores, probably led by comp-cs (Sadreyev and Grishin, 2003). BILD and ldot-qr scores, of course, had yet to be defined. Several studies that required the fitting of gap and offset costs (Edgar and Sjölander, 2004; Wang and Dunbrack, 2004) were unable to demonstrate much significant difference among most of the scores they considered.
Because of this article's focus, it is silent upon the questions of how best to weight correlated sequences within a multiple alignment when constructing a profile, and on how best to define gap and offset scores for use with the recommended substitution scores. Any fully functional profile–profile alignment program needs to address these questions. It is hoped, however, that by restricting the variety of substitution scores that are best considered, it will be easier to take up these additional issues.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Drs Dapeng Zhang and L. Aravind for helpful conversations.
Funding: Intramural Research Programs of the National Library of Medicine and the Center for Information Technology at the National Institutes of Health.
Conflict of Interest: none declared.
REFERENCES
- Altschul S.F. Gap costs for multiple sequence alignment. J. Theor. Biol. 1989;138:297–309. doi: 10.1016/s0022-5193(89)80196-1. [DOI] [PubMed] [Google Scholar]
- Altschul S.F. Amino acid substitution matrices from an information theoretic perspective. J. Mol. Biol. 1991;219:555–565. doi: 10.1016/0022-2836(91)90193-A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S.F., Lipman D.J. Trees, stars, and multiple biological sequence alignment. SIAM J. Appl. Math. 1989;49:197–209. [Google Scholar]
- Altschul S.F., et al. Weights for data related by a tree. J. Mol. Biol. 1989;207:647–653. doi: 10.1016/0022-2836(89)90234-9. [DOI] [PubMed] [Google Scholar]
- Altschul S.F., et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S.F., et al. PSI-BLAST pseudocounts and the minimum description length principle. Nucleic Acids Res. 2009;37:815–824. doi: 10.1093/nar/gkn981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S.F., et al. The construction and use of log-odds substitution scores for multiple sequence alignment. PLoS Comput. Biol. 2010;6:e1000852. doi: 10.1371/journal.pcbi.1000852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacon D.J., Anderson W.F. Multiple sequence alignment. J. Mol. Biol. 1986;191:153–161. doi: 10.1016/0022-2836(86)90252-4. [DOI] [PubMed] [Google Scholar]
- Bailey T.L., Gribskov M. The megaprior heuristic for discovering protein sequence patterns. In: States D.J., et al., editors. Proceedings of the Fourth Intenational Conference Intelligent Systems for Molecular Biology. Menlo Park, CA: AAAI Press; 1996. pp. 15–24. [PubMed] [Google Scholar]
- Berger M.P., Munson P.J. A novel randomized iterative strategy for aligning multiple protein sequences. Comput. Appl. Biosci. 1991;7:479–484. doi: 10.1093/bioinformatics/7.4.479. [DOI] [PubMed] [Google Scholar]
- Brown M., et al. Using Dirichlet mixture priors to derive hidden Markov models for protein families. In: Hunter L., et al., editors. Proceedings of the First International Conference Intelligent Systems for Molecular Biology. Menlo Park, CA: AAAI Press; 1993. pp. 47–55. [PubMed] [Google Scholar]
- Brown D.P., et al. Automated protein subfamily identification and classification. PLoS Comput. Biol. 1997;3:e160. doi: 10.1371/journal.pcbi.0030160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrillo H., Lipman D. The multiple sequence alignment problem in biology. SIAM J. Appl. Math. 1988;48:1073–1082. [Google Scholar]
- Cover T.M., Thomas J.A. Elements of Information Theory. New York, NY: Wiley; 1991. [Google Scholar]
- Dayhoff M.O., et al. A model of evolutionary change in proteins. In: Dayhoff M.O., editor. Atlas of Protein Sequence and Structure. Vol. 5. Washington, DC: 1978. pp. 345–352. Suppl. 3. Natl. Biomed. Res. Found. [Google Scholar]
- Dembo A., et al. Limit distribution of maximal non-aligned two-sequence segmental score. Ann. Prob. 1994;22:2022–2039. [Google Scholar]
- Eddy S.R., et al. Maximum discrimination hidden Markov models of sequence consensus. J. Comput. Biol. 1995;2:9–23. doi: 10.1089/cmb.1995.2.9. [DOI] [PubMed] [Google Scholar]
- Edgar R.C. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004a;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar R.C. MUSCLE: a multiple sequence alignment method with reduced time and space complexity. BMC Bioinformatics. 2004b;5:113. doi: 10.1186/1471-2105-5-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar R.C. Quality measures for protein alignment benchmarks. Nucleic Acids Res. 2010;38:2145–2153. doi: 10.1093/nar/gkp1196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar R.C., Sjölander K. SATCHMO: sequence alignment and tree construction using hidden Markov models. Bioinformatics. 2003;19:1404–1411. doi: 10.1093/bioinformatics/btg158. [DOI] [PubMed] [Google Scholar]
- Edgar R.C., Sjölander K. A comparison of scoring functions for protein sequence profile alignment. Bioinformatics. 2004;20:1301–1308. doi: 10.1093/bioinformatics/bth090. [DOI] [PubMed] [Google Scholar]
- Feng D., Doolittle R.F. Progressive sequence alignment as a prerequisite to correct phylogenetic trees. J. Mol. Evol. 1987;25:351–360. doi: 10.1007/BF02603120. [DOI] [PubMed] [Google Scholar]
- Gerstein M., et al. Volume changes in protein evolution. Appendix: a method to weight protein sequences to correct for unequal representation. J. Mol. Biol. 1994;236:1067–1078. doi: 10.1016/0022-2836(94)90012-4. [DOI] [PubMed] [Google Scholar]
- Gotoh O. A weighting system and algorithm for aligning many phylogenetically related sequences. Comput. Appl. Biosci. 1995;11:543–551. doi: 10.1093/bioinformatics/11.5.543. [DOI] [PubMed] [Google Scholar]
- Gribskov M., et al. Profile analysis: detection of distantly related proteins. Proc. Natl Acad. Sci. USA. 1987;84:4355–4358. doi: 10.1073/pnas.84.13.4355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heger A., Holm L. Picasso: generating a covering set of protein family profiles. Bioinformatics. 2001;17:272–279. doi: 10.1093/bioinformatics/17.3.272. [DOI] [PubMed] [Google Scholar]
- Heger A., Holm L. Exhaustive enumeration of protein domain families. J. Mol. Biol. 2003;328:749–767. doi: 10.1016/s0022-2836(03)00269-9. [DOI] [PubMed] [Google Scholar]
- Henikoff S., Henikoff J.G. Amino acid substitution matrices from protein blocks. Proc. Natl Acad. Sci. USA. 1992;89:10915–10919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henikoff S., Henikoff J.G. Position-based sequence weights. J. Mol. Biol. 1994;243:574–578. doi: 10.1016/0022-2836(94)90032-9. [DOI] [PubMed] [Google Scholar]
- Karlin S., Altschul S.F. Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proc. Natl Acad. Sci. USA. 1990;87:2264–2268. doi: 10.1073/pnas.87.6.2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krogh A., Mitchison G. Maximum entropy weighting of aligned sequences of protein or DNA. In: Rawlings C., et al., editors. Proceedings of the Third International Conference Intelligent Systems for Molecular Biology. Menlo Park, CA: AAAI Press; 1995. pp. 215–221. [PubMed] [Google Scholar]
- Lin J. Divergence measures based on the Shannon entropy. IEEE Trans. Informat. Theory. 1991;37:145–151. [Google Scholar]
- Lipman D.J., et al. A tool for multiple sequence alignment. Proc. Natl Acad. Sci. USA. 1989;86:4412–4415. doi: 10.1073/pnas.86.12.4412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madera M., et al. The SUPERFAMILY database in 2004: additions and improvements. Nucleic Acids Res. 2004;32:D235–D239. doi: 10.1093/nar/gkh117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marti-Renom M.A., et al. Alignment of protein sequences by their profiles. Protein Sci. 2004;13:1071–1087. doi: 10.1110/ps.03379804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittelman D., et al. Probabilisitic scoring measures for profile-profile comparison yield more accurate short seed alignments. Bioinformatics. 2003;19:1531–1539. doi: 10.1093/bioinformatics/btg185. [DOI] [PubMed] [Google Scholar]
- Murata M., et al. Simultaneous comparison of three protein sequences. Proc. Natl Acad. Sci. USA. 1985;82:3073–3077. doi: 10.1073/pnas.82.10.3073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Notredame C., et al. T-Coffee: a novel method for fast and accurate multiple sequence alignment. J. Mol. Biol. 2000;302:205–217. doi: 10.1006/jmbi.2000.4042. [DOI] [PubMed] [Google Scholar]
- Ohlson T., et al. Profile-profile methods provide improved fold-recognition: a study of different profile-profile alignment methods. Proteins. 2004;57:188–197. doi: 10.1002/prot.20184. [DOI] [PubMed] [Google Scholar]
- von Öhsen N., Zimmer R. Improving profile-profile alignments by log average scoring. In: Gascuel O., Moret B.M.E, editors. Proceedings of the First International Workshop on Algorithms in Bioinformatics. London, UK: Springer; 2001. pp. 11–26. [Google Scholar]
- Panchenko A.R. Finding weak similarities between proteins by sequence profile comparison. Nucleic Acids Res. 2003;31:683–689. doi: 10.1093/nar/gkg154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papadopoulos J.S., Agarwala R. COBALT: constraint-based alignment tool for multiple protein sequences. Bioinformatics. 2007;23:1073–1079. doi: 10.1093/bioinformatics/btm076. [DOI] [PubMed] [Google Scholar]
- Patthy L. Detecting homology of distantly related proteins with consensus sequences. J. Mol. Biol. 1987;198:567–577. doi: 10.1016/0022-2836(87)90200-2. [DOI] [PubMed] [Google Scholar]
- Pietrokovski S. Searching databases of conserved sequence regions by aligning protein multiple-alignments. Nucleic Acids Res. 1996;24:3836–3845. doi: 10.1093/nar/24.19.3836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raghava G.P., et al. OXBench: a benchmark for evaluation of protein multiple sequence alignment accuracy. BMC Bioinformatics. 2003;4:47. doi: 10.1186/1471-2105-4-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rychlewski L., et al. Comparison of sequence profiles. Strategies for structural predictions using sequence information. Protein Sci. 2000;9:232–241. doi: 10.1110/ps.9.2.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadreyev R., Grishin N. COMPASS: a tool for comparison of multiple protein alignments with assessment of statistical significance. J. Mol. Biol. 2003;326:317–336. doi: 10.1016/s0022-2836(02)01371-2. [DOI] [PubMed] [Google Scholar]
- Sander C., Schneider R. Database of homology-derived protein structures and the structural meaning of sequence alignment. Proteins. 1991;9:56–68. doi: 10.1002/prot.340090107. [DOI] [PubMed] [Google Scholar]
- Sankoff D. Minimal mutation trees of sequences. SIAM J. Appl. Math. 1975;28:35–42. [Google Scholar]
- Sankoff D., Cedergren R.J. Simultaneous comparison of three or more sequences related by a tree. In: Sankoff D., Kruskal J.B., editors. Time Warps, String Edits and Macromolecules: The Theory and Practice of Sequence Comparison. Reading, MA: Addison-Wesley; 1983. pp. 253–263. [Google Scholar]
- Schwartz R.M., Dayhoff M.O. Matrices for detecting distant relationships. In: Dayhoff M.O., editor. Atlas of Protein Sequence and Structure. Vol. 5. Washington, DC: 1978. pp. 353–358. Suppl. 3. Natl. Biomed. Res. Found. [Google Scholar]
- Sibbald P.R., Argos P. Weighting aligned protein or nucleic acid sequences to correct for unequal representation. J. Mol. Biol. 1990;216:813–818. doi: 10.1016/S0022-2836(99)80003-5. [DOI] [PubMed] [Google Scholar]
- Sjölander K., et al. Dirichlet mixtures: a method for improved detection of weak but significant protein sequence homology. Comput. Appl. Biosci. 1996;12:327–345. doi: 10.1093/bioinformatics/12.4.327. [DOI] [PubMed] [Google Scholar]
- Sjölander K. Phylogenetic inference in protein superfamilies: analysis of SH2 domains. In: Glasgow J., et al., editors. Proceedings of the Sixth International Conference Intelligent Systems of Molecular Biology. Menlo Park, CA: AAAI Press; 1998. pp. 165–174. [PubMed] [Google Scholar]
- Söding J. Protein homology detection by HMM-HMM comparison. Bioinformatics. 2005;21:951–960. doi: 10.1093/bioinformatics/bti125. [DOI] [PubMed] [Google Scholar]
- Sunyaev S.R., et al. PSIC: profile extraction from sequence alignments with position-specific counts of independent observations. Protein Eng. 1999;12:387–394. doi: 10.1093/protein/12.5.387. [DOI] [PubMed] [Google Scholar]
- Tatusov R.L., et al. Detection of conserved segments in proteins: Iterative scanning of sequence databases with alignment blocks. Proc. Natl Acad. Sci. USA. 1994;91:12091–12095. doi: 10.1073/pnas.91.25.12091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor W.R. Identification of protein sequence homology by consensus template alignment. J. Mol. Biol. 1986;188:233–258. doi: 10.1016/0022-2836(86)90308-6. [DOI] [PubMed] [Google Scholar]
- Taylor W.R. Multiple sequence alignment by a pairwise algorithm. Comput. Appl. Biosci. 1987;3:81–87. doi: 10.1093/bioinformatics/3.2.81. [DOI] [PubMed] [Google Scholar]
- Thompson J.D., et al. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994a;22:4673–4680. doi: 10.1093/nar/22.22.4673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson J.D., et al. Improved sensitivity of profile searches through the use of sequence weights and gap excision. Comput. Appl. Biosci. 1994b;10:19–29. doi: 10.1093/bioinformatics/10.1.19. [DOI] [PubMed] [Google Scholar]
- Thompson J.D., et al. BAliBASE: a benchmark alignment database for the evaluation of multiple alignment programs. Bioinformatics. 1999;15:87–88. doi: 10.1093/bioinformatics/15.1.87. [DOI] [PubMed] [Google Scholar]
- Tomii K., Akiyama Y. FORTE: a profile-profile comparison tool for protein fold recognition. Bioinformatics. 2004;20:594–595. doi: 10.1093/bioinformatics/btg474. [DOI] [PubMed] [Google Scholar]
- Vingron M., Sibbald P.R. Weighting in sequence space: a comparison of methods in terms of generalized sequences. Proc. Natl Acad. Sci. USA. 1993;90:8777–8781. doi: 10.1073/pnas.90.19.8777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Walle I., et al. SABmark - a benchmark for sequence alignment that covers the entire known fold space. Bioinformatics. 2004;21:1267–1268. doi: 10.1093/bioinformatics/bth493. [DOI] [PubMed] [Google Scholar]
- Wang G., Dunbrack R.L. Scoring profile-to-profile sequence alignments. Protein Sci. 2004;13:1612–1626. doi: 10.1110/ps.03601504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yona G., Levitt M. Within the twilight zone: a sensitive profile-profile comparison tool based on information theory. J. Mol. Biol. 2002;315:1257–1275. doi: 10.1006/jmbi.2001.5293. [DOI] [PubMed] [Google Scholar]
- Zhang D., Aravind L. Identification of novel families and classification of the C2 domain superfamily elucidate the origin and evolution of membrane targeting activities in eukaryotes. Gene. 2010;469:18–30. doi: 10.1016/j.gene.2010.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D., et al. A novel immunity system for bacterial nucleic acid degrading toxins and its recruitment in various eukaryotic and DNA viral systems. Nucleic Acids Res. 2011;39:4532–4552. doi: 10.1093/nar/gkr036. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.