Self-assembly of soft-matter quasicrystals and their approximants

Abstract

The surprising recent discoveries of quasicrystals and their approximants in soft-matter systems poses the intriguing possibility that these structures can be realized in a broad range of nanoscale and microscale assemblies. It has been theorized that soft-matter quasicrystals and approximants are largely entropically stabilized, but the thermodynamic mechanism underlying their formation remains elusive. Here, we use computer simulation and free-energy calculations to demonstrate a simple design heuristic for assembling quasicrystals and approximants in soft-matter systems. Our study builds on previous simulation studies of the self-assembly of dodecagonal quasicrystals and approximants in minimal systems of spherical particles with complex, highly specific interaction potentials. We demonstrate an alternative entropy-based approach for assembling dodecagonal quasicrystals and approximants based solely on particle functionalization and shape, thereby recasting the interaction-potential-based assembly strategy in terms of simpler-to-achieve bonded and excluded-volume interactions. Here, spherical building blocks are functionalized with mobile surface entities to encourage the formation of structures with low surface contact area, including non-close-packed and polytetrahedral structures. The building blocks also possess shape polydispersity, where a subset of the building blocks deviate from the ideal spherical shape, discouraging the formation of close-packed crystals. We show that three different model systems with both of these features—mobile surface entities and shape polydispersity—consistently assemble quasicrystals and/or approximants. We argue that this design strategy can be widely exploited to assemble quasicrystals and approximants on the nanoscale and microscale. In addition, our results further elucidate the formation of soft-matter quasicrystals in experiment.

Until fairly recently, quasicrystals and their approximants have been observed only in atomistic systems. Over the past decade, there have been sporadic reports of quasicrystals and approximants in nanometer and micron-scale systems. Examples include holographically trapped (1) and laser-field-induced (2, 3) quasicrystalline materials made of micron-sized spheres, self-assembled quasicrystals and approximants formed by spherical dendrimer micelles (4, 5), phase-separated star-triblock copolymers (6), binary nanoparticle superlattices (7), spherical micelles of phase-separated block copolymers (8, 9), and simulations of hard tetrahedra (10). These reports pose an intriguing possibility that these structures might be assembled in a broad range of systems. In one such system, spherical dendrimeric micelles functionalized with alkyl tails form a dodecagonal (12-fold) quasicrystal (DQC), as well as other non-close-packed structures such as the body-centered cubic (bcc) and A15 crystals (11). In similar systems, various types of block copolymer micelles arrange into quasicrystals with 12-fold, and possibly 18-fold, symmetry (9), as well as various periodic approximants (8).

The dendrimer and block copolymer micelle systems in particular all share an important common feature: Their constituent micelles exhibit a soft “squishy corona” in which terminal groups avoid each other to minimize steric interactions. It has been predicted that this mechanism causes the system to adopt structures that minimize surface contact area between neighboring micelles (12, 13). The structure that minimizes surface contact area, known as the Weaire–Phelan or A15 structure (14), is structurally similar to a DQC, but, because DQCs do not minimize surface contact area, other factors must contribute to their stability. It has been suggested that entanglement of terminal groups may give rise to three-body entropic effects that favor quasicrystals in systems of monodisperse micelles (15, 16). In all these micellar systems, entropic effects appear to play a predominant role in stabilizing the quasicrystals and approximants, potentially distinguishing them from many of their atomistic counterparts in which strong attractive interactions are present.

Computer simulation studies of self-assembly have demonstrated that quasicrystals can be assembled by an inverse-design mechanism. In particular, pair potentials can be designed to make close packing unfavorable, causing such systems to instead form quasicrystals and approximants (17–19). These complex interaction potentials have yet to be realized in experimental systems on the microscale or nanoscale, but we propose that a similar effect can be achieved via shape polydispersity, where a subset of the micelles deviate from the ideal spherical shape. Shape polydispersity arises naturally in many micelle-forming systems, and, in general, particle shape is a tunable parameter in many microscale and nanoscale systems (20).

In this article, we introduce a design strategy based on the ideas described above to direct the self-assembly of three-dimensional DQCs and/or their periodic approximants in systems of (approximately) spherical micelles or similarly shaped particles. We study different types of nanoscale/microscale building blocks with features that promote structures with low surface contact area and suppress close packing. Structures with low surface contact area are promoted by functionalizing spherical building blocks with mobile entities connected to their surface, similar to functionalized spherical dendrimers (5). Close packing is suppressed by incorporating shape polydispersity into the system in the form of particle asphericity. Both features are relatively common aspects of soft matter and related systems and should be achievable experimentally; a schematic of our strategy is shown in Fig. 1A. Applying this strategy in computer simulations, we show three key results. (i) We verify the theoretical predictions that interactions between terminal coatings can drive the system to form surface-area minimizing structures (12, 13). (ii) We demonstrate that shape polydispersity can be used to suppress the formation of close-packed structures. (iii) We show that three different simulated micellar systems that possess both of these characteristics reproducibly form DQCs and/or approximants. These models—a simplified model of a spherical micelle (MSM) and two micelle-forming systems composed of tethered nanosphere (TNS) building blocks (21–24)—represent the only simulated micellar systems currently known to form 3D quasicrystals or approximants through self-assembly. Because the models are closely related to experimental systems known to form DQCs and/or approximants (4, 5, 8, 9), our results may provide pertinent insight regarding their formation. In the future, the assembly strategy that we employ may serve as a heuristic for expanding the range of systems that assemble DQCs and approximants.

Fig. 1.

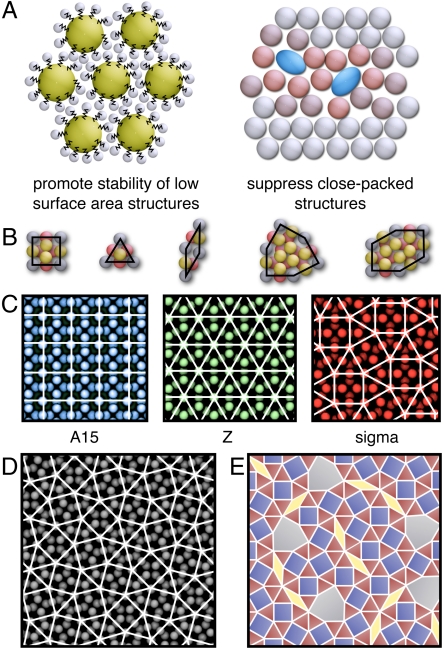
Assembly strategy and structure of the DQCs and approximants. (A) Schematic of the proposed two-part strategy that uses functionalization and shape to form DQCs. Particle functionalization (Left) promotes the formation of structures with low surface contact area, and asphericity (Right) inhibits the formation of close-packed structures. Particles colored red in the asphericity schematic (Right) are meant to highlight where the crystal is disrupted by the presence of aspherical particles (blue). (B) Valid tiles for the DQC. The DQC and approximants can be described as a periodic stacking of plane-filling arrangements of tiles in the z direction (out of the page). The gray particles at the nodes of the tiles form layers at z = 1/4 and z = 3/4 and sit at the centers of 12-member rings. The yellow particles and red particles form layers at z = 0 and z = 1/2, respectively. In the DQC, the gray particles form a dodecagonal layer with 12-fold symmetry, and the yellow and red particles form hexagonal layers rotated by 30° to obtain 12-fold symmetry. (C) Three common DQC approximants. (D) A higher-order approximant generated through the inflation method (see text). (E) A representative DQC random tiling of squares, triangles, rhombs, and shields, adapted from ref. 36.

DQCs and Approximants

We first introduce definitions and terminology that will facilitate our discussions in subsequent sections. A crystal is defined as a structure with long-range positional order, as identified, for example, by the presence of Bragg peaks in the diffraction pattern (25). A quasicrystal is a quasi-periodic crystal; that is, a crystal that lacks periodicity (26), but still exhibits diffraction peaks. Quasicrystals sometimes (but need not) exhibit rotational symmetries that are incompatible with periodicity. Several types of quasicrystals have been observed in experiment, but in this article we focus on DQCs in particular because those are, to date, the most commonly reported type of quasicrystal in soft-matter systems. DQCs are characterized by their long-range dodecagonal rotational symmetry.

DQCs are polytetrahedral structures (27) of the Frank–Kasper (FK) type (28). For the class of FK structures considered here, ordered structures are distinguished by their “tiling” pattern, constructed by connecting the centers of neighboring 12-member rings of particles (see Fig. 1 B–E). The structures are layered, and, whether periodic or aperiodic in the plane, they repeat periodically in the direction orthogonal to the plane (into the page in Fig. 1). There are five valid tiles that can be arranged to form structures with complete 12-member rings without disorder. These tiles take the shape of a square, a triangle, a rhomb, a shield, and an asymmetric hexagon (18), and are illustrated in Fig. 1B. Periodic arrangements of these tiles result in periodic crystals, sometimes known as “approximants,” that are indistinguishable from DQCs locally (29). Three common approximants, known as the A15, Z, and sigma structures, are shown in Fig. 1C. Increasingly complex approximants, such as the structure depicted in Fig. 1D, can be constructed by inflation, whereby tiles are sequentially replaced with smaller subtiles (30, 31).

In addition to periodic arrangements, nonperiodic arrangements of tiles that fill the plane can also be constructed, resulting in quasicrystals. Various methods can be used to construct the tilings; methods such as inflation (31), projection (30), or matching rules (32, 33) produce deterministic quasicrystals, whereas random tilings (34) give rise to a range of similar quasicrystals with the tiles reshuffled locally, characterized by local phason fluctuations. Imperfect quasicrystals of either type may also exhibit global phason strain whereby particular tiles or orientations of tiles occur more or less frequently that in the ideal case, giving rise to shifts and broadening of the diffraction peaks (35). Deterministic quasicrystals are thought to be energetically stabilized, whereas random-tiling quasicrystals are thought to be entropically stabilized (34). Fig. 1E shows a typical random-tiling DQC (36) that we envision might form in soft-matter systems, which are often stabilized by entropy. The structure is composed mostly of squares and triangles, and is locally similar to the sigma approximant. The sigma approximant is the thermodynamically stable state for many systems that form DQCs, and the two structures often arise in nearby regions of parameter space (4, 5, 7). The experimental protocol may dictate whether a metastable DQC or a stable sigma approximant is obtained. In the case of the simulations we perform on model micelles, we are limited to relatively small, finite size simulations, as discussed subsequently. As such our systems are typically too small to unambiguously distinguish between quasicrystals and approximants, or identify phason strain. With this caveat in mind, we refer to our assembled structures as quasicrystals if they are composed of valid tiles for the DQC, exhibit strong peaks in the diffraction pattern, and are not periodic (aside from the trivial periodicity imposed by the periodic boundary conditions on the scale of the sample).

Simulation Results

We begin by performing molecular dynamics simulations (37) of a simplified MSM that considers only excluded volume interactions between terminal groups on the micelle surface (Fig. 2A). Unlike the truly minimal “fuzzy sphere” micelle model of ref. 12 that treats intermicelle interactions with an effective pair potential, our model treats these excluded volume interactions explicitly through mobile spheres attached to the micelle surface. This allows us to (i) study the self-assembly of the micelles and (ii) directly measure the relative effect of entropy and energy in driving the stabilization of assembled phases. The MSM consists of a noninteracting rigid scaffolding with 42 points on the surface of a sphere, given by the vertex points of a two-frequency icosahedral geodesic with diameter = 5.27σ. With this diameter, the average spacing between surface points is 1.5σ. Each surface point anchors a small spherical particle with diameter σ. The particles and surface points are attached by harmonic springs of stiffness k that control the degree of surface particle mobility. Surface particle mobility increases as k decreases, creating a larger, “squishier” outer corona. Decreasing k can also be interpreted as increasing the radius of gyration of the surface coating, if we consider the spheres to be dumbbell polymers anchored to the surface (38). Excluded volume interactions between the surface spheres are modeled by the purely repulsive Weeks–Chandler–Andersen (WCA) potential (39) (see SI Text). Roughly speaking, the MSM can represent many different nanoscopic objects, including core-satellite nanoparticles (40–42), where nanospheres are functionalized with an outer coating of smaller nanospheres; spherical micelles composed of dendrimers (5, 12, 13) where the outermost layer of the dendrimer “tree” is functionalized with oligomers or polymers; spherical block copolymer micelles (8, 9) that possess an outer corona of polymers; or spherical micelles created from amphiphilic tethered nanoparticles (21–23), as we discuss later.

Fig. 2.

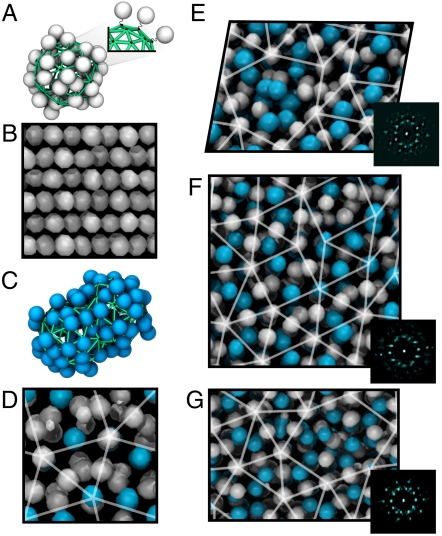
MSM systems. (A) MSM monomer (white) extracted from a simulation. (B) Sixty MSMs at k = 5 with f_dimer = 0 (no dimers) in a bcc configuration. (C) MSM dimer (cyan) extracted from a simulation. (D) Sixty MSMs with k = 5 and f_dimer ≈ 0.24 in a sigma structure. (E–G) Systems with 360 MSMs and (E) k = 4 and f_dimer ≈ 0.39, (F) k = 4.75 and f_dimer ≈ 0.37, and (G) k = 5 and f_dimer ≈ 0.36. In all cases, we plot time-averaged density isosurfaces of the centers of mass of the micelles/dimers, rather than the micelles themselves, to remove thermal noise and produce a clearer image (see SI Text). Systems are viewed along the pseudo-12-fold-symmetry axis, as calculated using the diffraction pattern, shown to the right of each panel. In all cases, systems are colored-coded with monomer centroids shown in white/gray and dimer centroids shown in cyan. Note, Eappears as a parallelogram because of the projection; all simulation boxes are square or rectangular cuboids. Additional views of various self-assembled structures are included in the SI Text.

In the absence of shape polydispersity, the MSMs tend to form close-packed [face-centered cubic (fcc) or hexagonally close packed (hcp)] arrangements for k > 5 (lower surface particle mobility) and bcc structures for k ≤ 5 (higher surface particle mobility); structures are identified using the algorithms described in ref. 43. These results support the conjecture that increasing surface particle mobility drives the system toward structures with lower surface contact area (such as bcc), as we discuss in detail in the following section. At these state points, sphere packing constraints favor the bcc structure over the surface-contact-area-minimizing A15 structure. A bcc-ordered structure of 60 MSMs is shown in Fig. 2B for k = 5.

We find a more dramatic change in the structural arrangement of the MSMs when shape polydispersity is incorporated into the system in the form of aspherical “dimer” micelles (see Fig. 2C). We allow dimers to form in an unbiased manner by exploiting the fact that at low k, surface particles are only loosely bound to the surface sites on the scaffold, allowing the MSMs to overlap; some of the MSMs become locked together into dimers when k is increased. By slowly increasing from a highly disordered state at k = 2, we create systems with dimer fraction in the range 0.20 ≤ f_dimer < 0.40, consisting of dimers with an average aspect ratio of approximately 1.45∶1. This procedure roughly mimics the process by which micelles are formed in amphiphilic soft-matter systems, such as the tethered nanoparticle models that we discuss later. In such systems, spherical micelles assemble from a disordered mixture of individual building blocks as the system temperature is reduced (22, 44) (see SI Text). In the MSM system, increasing k has a similar effect to decreasing the temperature.

We find that systems with a mixture of spherical and dimer MSMs consistently form FK structures (28). Fig. 2D shows a typical sigma approximant formed by 60 MSMs at k = 5 with f_dimer = 0.24; sigma structures were reproducibly observed in over 25 independent simulations where k was slowly increased from 2 to 5. This approximant closely matches the expected result for 60 particles interacting via the Dzugutov or Lennard–Jones–Gauss pair potentials at densities that yield DQCs for larger systems. The formation of the sigma structure is also consistent with the observed experimental behavior of spherical dendrimer (4) and block copolymer micelles (8). Three representative independent simulations, each composed of 360 MSMs in rectangular boxes with aspect ratio 1.28∶1.28∶1.00, are presented in Fig. 2 E–G. Fig. 2 E–G show systems at k = 4, 4.75, and 5, with f_dimer = 0.39, 0.37, and 0.36, respectively. In all cases, we observe finite-size DQCs that exhibit long-range rotational order of the MSM center of mass but no periodicity aside from the trivial periodicity imposed by the boundary conditions. Our simulations are limited to smaller system sizes than typical point-particle models (17, 19) because we must resolve timescales corresponding to the microscopic motions of the surface particles that comprise the MSM, rather than the MSM centroid. Nevertheless, the finite structures depicted in Fig. 2 E–G exhibit local indicators of DQC ordering. The systems form unique tilings with different configurations rather than any particular approximant. The systems also contain the entire range of valid tiles, rather than containing squares and triangles exclusively like the sigma phase, which often competes with DQCs for stability. Because DQCs grow more easily than approximants (45), it is possible that the DQC-like tilings are thermodynamically metastable relative to a stable approximant. The structures do not rearrange or undergo phason flips after solidification during the timescale of our simulations.

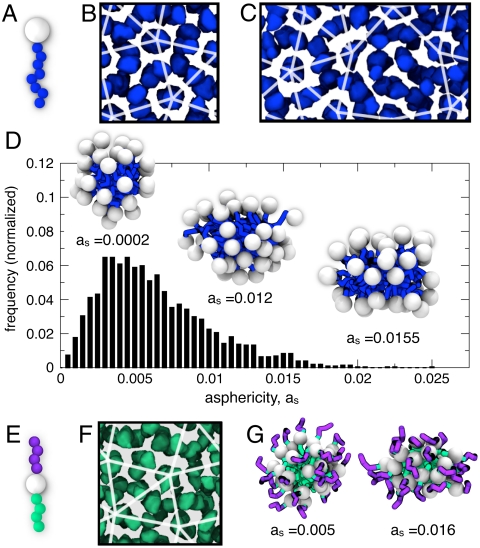
We can further test our proposed strategy in systems where we do not have explicit control over surface particle mobility or shape polydispersity, but where these two key features instead emerge naturally as a result of phase separation. We consider two model TNS systems, mono-TNS (21, 22) and di-TNS (21, 23, 24), both of which form roughly spherical micelles with mobile surface entities. Schematics of the building blocks are shown in Fig. 3 A and E, respectively, and the micelles they form are shown in Fig. 3 D and G, respectively. The mono-TNS micelles have an outer shell of mobile nanospheres that closely match the MSM model, whereas the di-TNS micelles have a shell of short polymers, more closely resembling the spherical micelles formed by block copolymers (8, 46, 47) and functionalized dendrimers (5, 12, 13). These models are computationally expensive, and thus only relatively small systems in terms of the number of micelles are explored. Fig. 3B depicts density isosurfaces (48) of the aggregating tethers for a system of 2,500 mono-TNS building blocks that assemble into approximately 60 spherical micelles arranged in a sigma approximant. Fig. 3C depicts isosurfaces for a system of 5,000 mono-TNSs that self-assemble into approximately 120 spherical micelles arranged in an FK structure containing squares, triangles, shields, and rhombs. The increasing complexity of the tiling arrangement with system size indicates that the TNS system may form a higher-order approximant or a DQC in the infinite limit. The mono-TNS micelles naturally exhibit shape polydispersity. Fig. 3D shows a histogram of the asphericity, a_s, computed from the principle radii of gyration (44) of the micelles, with representative micelles at various values of a_s depicted in the Inset. For reference, a_s = 0 corresponds to an ideal sphere, and a_s = 0.02 corresponds to the MSM dimer with aspect ratio 1.45∶1 shown in Fig. 2C. Fig. 3F shows a sigma structure formed from 2,000 di-TNS building blocks that self-assemble into approximately 60 micelles. The distribution of a_s for the di-TNS (plotted in SI Text) is similar to that for the mono-TNS system. Two representative di-TNS micelles at low and high a_s are depicted in Fig. 3G. Overall, FK structures self-assembled from TNS building blocks were reproducibly observed in 20 independent simulations. Whether these systems form DQCs in the infinite limit remains an open question that should be explored in the future as computational power increases.

Fig. 3.

TNS systems. (A) Schematic of a mono-TNS building block, where the eight tether beads (blue) of size σ aggregate and self-assemble spherical micelles with a soft core surrounded by relatively hard “satellite” nanoparticles (white) of size 2.5σ that act as mobile surface entities. (B) A simulation snapshot of approximately 60 micelles formed by mono-TNS that arrange into a sigma approximant, and (C) approximately 120 mono-TNS micelles that form a DQC-like structure; for both systems, ϕ = 0.275 and T = 1.1. (D) Histogram of asphericity, a_s, of the mono-TNS micelles in the sigma phase. (E) Schematic of the di-TNS building block, where the four beads in the tether (green) each of size σ aggregate and nanoparticles (white) of size 2σ are also attractive; four bead tethers (purple) of bead size σ that do not aggregate coat the outside of the micelle. (F) Approximately 60 di-TNS micelles arranged in a sigma approximant at ϕ = 0.2 and T = 1.2. (G) Representative di-TNS micelles with different a_s. In all cases, for clarity, we show density isosurfaces of the aggregating polymer tethers (i.e., the micelle core); additional views of the structures are included in the SI Text.

Free-Energy Calculations

Having explored the self-assembly of the three micelle models, we now perform free-energy calculations to investigate the thermodynamic basis underlying both aspects of our strategy for DQC-like structure stabilization. The first aspect, the functionalization of particles with mobile surface entities, is inspired by the observation that soft-matter systems with relatively soft intermicelle interactions often form non-close-packed structures, as described in the Introduction. For example, spherical dendrimeric micelles functionalized with alkyl tails to create a “squishy corona” are known to form non-close-packed structures such as the bcc and A15 crystals (11). Ziherl and Kamien proposed that the formation of the bcc and A15 structures is related to the Kelvin problem, which involves finding the space-filling arrangement of cells that minimizes surface contact area (12, 13). In this picture, the dendrimeric micelles adopt structures with low surface contact area in order to reduce steric interactions between terminal polymer groups. The bcc and A15 crystals both exhibit low surface contact area, with A15 representing the current best-known solution to the Kelvin problem (14). It has been suggested (5) that this mechanism may also stabilize the dendrimer DQC observed in experiments (5). However, because minimizing surface area alone favors the A15 structure rather than the DQC, other factors must be important as well.

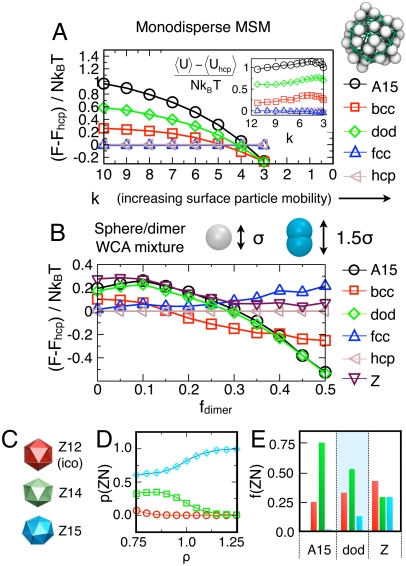
We calculate the Helmholtz free energy, F (49, 50), as a function of the surface particle mobility k for a system of monodisperse MSMs (i.e., without dimers); see SI Text for more information. The value of F in Fig. 4A is shown relative to the value for the hcp crystal, taken as a convenient reference state. Fig. 4A illustrates that as k decreases (i.e., surface particle mobility increases), F decreases more rapidly for the A15, dodecagonal approximant (dod), and bcc structures than for the fcc and hcp structures. Here, the value for the dod curve is the average of the sigma phase and several higher-order square-triangle approximants to the DQC (31), all of which have nearly identical free energies. For low k, bcc appears to be the stable state, consistent with our MSM simulation results. For very low k (k < 3) the system becomes disordered. The change in F as a function of k is the strongest for the A15 structure, which minimizes surface contact area, followed by the dod and bcc structures, respectively. We note that the dod structure has a lower free energy than the A15 structure over the entire range; however, at sufficiently low k, the difference in free energy between bcc, A15, and dod is indistinguishable. The change in F with k is entropically driven; the difference in average potential energy 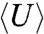changes little, and does not decrease with F (Fig. 4A, Inset). This serves as a direct verification of the predictions of Ziherl and Kamien (12, 13). Note that the Z structure (Fig. 1C) is omitted because it is not stable in the parameter range under consideration. Although the trends in entropy are as we expect, we find surface particle mobility alone is not sufficient to stabilize DQCs or approximants for the state points and model under consideration. Thus, as our self-assembly simulations previously showed, a second mechanism is needed to form DQC structures for this model.

Fig. 4.

(A) Helmholtz free energy per micelle, F, as a function of surface particle mobility (controlled by the spring stiffness k) for monodisperse MSMs. The Inset shows the potential energy per micelle U. (B) F as a function of f_dimer for the WCA sphere/dimer mixture. For parts A and B, the energies and free energies are reported with respect to the hcp crystal for convenience. For all datapoints, error bars are smaller than the data labels. (C) Depiction of three different FK polyhedra. (D) Probability of observing dimers at the center of Z12, Z14, and Z15 structures in the dod phase as a function of number density, ρ. (E) Fraction of Z12, Z14, and Z15 local structures in A15, sigma and Z structures. Note, D and E) are color coded following the convention in C.

The thermodynamic basis underlying the second aspect of our strategy—shape polydispersity—can be understood in the context of previous studies of both quasicrystal formation and sphere packing. Systems of particles with short-ranged, spherically symmetric interaction potentials, such as hard spheres or particles with short-ranged van der Waals interactions, modeled by the Lennard–Jones (LJ) potential, tend to form close-packed crystals in the solid phase (e.g., fcc and/or hcp). Although these systems tend to locally favor polytetrahedral structures (51), close-packed structures maximize the overall packing density and hence maximize the entropy, and also often exhibit low potential energy. Specialized interparticle potentials, such as the Dzugutov (17) and Lennard-Jones-Gauss (19) potentials, have been contrived with features that help drive systems away from close-packed structures. Like the standard LJ potential, the Dzugutov and Lennard-Jones-Gauss potentials have an attractive well that encourages local polytetrahedral ordering. However, these specialized potentials include an additional relative energy penalty for adopting the characteristic interatomic spacings associated with close packing, ultimately driving the system to form alternative structures, such as bcc crystals, as well as DQCs and their approximants under certain conditions (18, 19). We propose, as our previous MSM simulations show, that shape polydispersity can have a similar effect, driving the system away from close packing. However, in contrast to the energetic repulsion of the Dzugutov potential, the destabilizing effect, in this case, is entropic.

To explicitly quantify the effect of shape polydispersity, we perform free-energy calculations (52–56) for binary mixtures of soft spheres and short, pill-shaped dimers, with particle interactions modeled by the WCA potential (see SI Text). The dimers are modeled by a rigid body of length 1.5σ consisting of two overlapping soft spheres 0.5σ apart (see Fig. 4B), resulting in an aspect ratio of 1.5∶1, similar to the aspect ratio observed in the simulation of MSMs. Fig. 4B shows the Helmholtz free energy, F, as a function of the dimer fraction, f_dimer, for several structures at a representative state point with number density ρ = 0.9 and T = 0.25. The free energy is computed based on the standard Einstein crystal thermodynamic integration (TI) method (54, 55), with an additional alchemical (56) TI step to compute the free energy required to transform a given fraction of spheres into dimers (see SI Text). As f_dimer increases, the A15 and dod structures become increasingly stable relative to close-packed crystals, and, to a lesser extent, the bcc crystal. We note that the dod phase has a lower value of F than the A15 structure for all state points, although the difference becomes minimal for high dimer fraction.

This difference in stability between the FK phases (A15 and dod) and standard crystals can be traced to the tendency for dimers to adopt larger, more aspherical neighbor shells, which are present in FK structures but not fcc, hcp, or bcc crystals. The first neighbor shells of particles in FK structures form different types of polyhedra, which may be icosahedral (coordination number 12), or take on higher coordination numbers Z, such as Z13, Z14, or Z15 depicted in Fig. 4C. In Fig. 4D, we plot the probability of observing dimers in Z12, Z14, and Z15 configurations for the dod structure where we fix particle centroids but allow dimers to rotate and swap positions with monomers. We observe that dimers strongly favor Z15 coordination shells because these are the largest and thus most accommodating. Dimers sit in Z14 arrangements as a second-best option and almost never occupy Z12 structures, which are the smallest. We can gain additional insight by examining the relative fraction of Z12, Z14, and Z15 within the three approximant structures, as shown in Fig. 4E. Although the free energy of the A15 and dod phases are similar, the A15 phase does not possess any Z15 arrangements, whereas the dod phase has an appreciable fraction (approximately 0.13). This difference may account for the widespread formation of dod rather than the A15 structures in our three simulation models. We note that although the Z phase has the largest fraction of Z15 coordinations, it also possesses the largest fraction of the less favorable Z12 coordinations, which may partially account for its relative instability for this density and dimer size.

We observe that for f_dimer > 0.4, A15 and dod are more stable than fcc, hcp, and bcc crystals. This implies that mixtures of spherical and pill-shaped colloids might produce DQCs or approximants. However, because many dimers are required to destabilize crystal structures, in practice, these mixtures may remain liquid-like, phase separate, or form other ordered structures not considered here. Along this same line, it is possible that, in specific cases, systems may form DQCs or other FK structures based on mobile surface particles alone; the entropic effect may be stronger for terminal groups that are longer or more complex than the one-bead model tested here; however, it seems likely that the A15 structure would still demonstrate the strongest entropic response because of the minimal surface-area mechanism (12–14). Because asphericity is common in many micellar systems that also have soft coronas, such as the previously discussed TNS micelles, it may not be possible to completely separate these two aspects. Our results suggest that even moderate levels of asphericity may enhance the relative stability and/or range of stability of DQCs and approximants for systems with squishy surface coatings.

Conclusions

Our results demonstrate a two-part, experimentally feasible assembly strategy for forming 3D DQCs and their approximants that can potentially be realized for a wide variety of systems. We have introduced three models that form DQCs and/or approximants, including a simplified MSM and two tethered nanoparticle models that resemble micelle-forming systems of dendrimers (4, 5) and block copolymers (8, 9, 46). Our study lends strong numerical evidence in support of the explanation for the stability of the A15 structure in systems of dendrimer micelles (12, 13) and its subsequent adoption to help explain the formation of the spherical dendrimer DQC (5, 15, 16). Our results imply that shape polydispersity, in addition to surface particle mobility, is likely to play a role in stabilizing DQCs and approximants in micellar systems observed in experiment. In the future, our assembly strategy may be employed to facilitate the design of systems that can form DQCs at the nanoscale and microscale, including dendrimers (4, 5, 11), surfactants, block copolymers (8, 9, 46), and core-satellite nanoparticles (40–42). Our results also suggest that mixtures of spheres and dimers (57–59) might, even without surface particle mobility, stabilize DQCs or approximants under certain conditions, possibly providing a trivial design rule for forming these structures. In addition to the implications regarding DQC assembly, our results illustrate a powerful design approach for assembling structures by controlling particle shape and functionality to mimic the key features of pair potentials (20). This paves the way for future studies based on mapping complex interaction potentials to packing models, which can potentially render currently unrealizable systems experimentally feasible, or expand the breadth of unique structures to more general classes of systems.

Materials and Methods

A full description of the simulation and free-energy methodologies is included in the SI Text.