Abstract
Interactions between individuals that are guided by simple rules can generate swarming behavior. Swarming behavior has been observed in many groups of organisms, including humans, and recent research has revealed that plants also demonstrate social behavior based on mutual interaction with other individuals. However, this behavior has not previously been analyzed in the context of swarming. Here, we show that roots can be influenced by their neighbors to induce a tendency to align the directions of their growth. In the apparently noisy patterns formed by growing roots, episodic alignments are observed as the roots grow close to each other. These events are incompatible with the statistics of purely random growth. We present experimental results and a theoretical model that describes the growth of maize roots in terms of swarming.
Introduction
To exploit soil resources optimally, plants have developed intricate root systems that are characterized by complex patterns and based on the coordinated group behavior of the growing root apices [1]–[3]. The communication channels among different root apices of the same plant depend on both fast electrical [4], [5] and slower hydraulic and chemical signals [6], [7]. In addition, secreted chemicals and released volatiles allow rapid communication among individual roots of the same plant and among roots of different plants. It has been shown that plants can distinguish between self and non-self roots [8]–[11] and that the sensory information collected by one plant is shared with neighboring plants [12], [13] to optimize territorial activities [10]–[13], including competitive behaviors [14] and symbioses with fungi and bacteria [1], [2], [6], [7]. Growing roots are well known to generate electric fields around their extending apices where their magnitude is maximum. Such fields are changing when roots are subject to gravitational stimuli [15] and are tightly linked with the polar transport of auxin, which controls root growth, tropism and root navigation [16]. Moreover, they affect protein distributions, conformations and activities and play an important role in regulating endocytosis and cytoskeleton [17]. On the other hand, it has been shown that external electric fields influence growing roots [18], for instance through the electrotropism phenomenon [19]–[21]. Recently, these evidences have led to the hypothesis that swarm intelligence might not be restricted to animals and that other complex systems involving mutual interactions, such as plant roots, could also be accurately described in terms of swarming [22]. Swarming refers to a situation in which individuals of a group of animals create a spatiotemporal order characterized by the alignment of directions and maintenance of equal speeds and distances. The emergence of swarming has been observed in many biological systems, such as fishes [23], bees [24], birds [25], bacteria [26] and insects [27]–[29], and in many human activities, including the correlated movements of pedestrians [30] and traffic [31] (for a recent review of swarm intelligence in animals and humans, see [32]). Such order may emerge from simple rules based on mostly local protocols [33]. One approach to modelling collective motion in biological systems uses self-propelled particles, i.e., particles that make decisions according to certain rules. A simple model proposed by Vicsek et al. [34] to describe such particles focused mainly on the emergence of directional alignment. Further studies have considered phase transitions in collective motions [35], adaptive velocities models [36] and network topologies [31]. A more biologically realistic approach to modelling swarming behavior considers local repulsion, alignment and attractive tendencies based on the relative positions and orientations of individuals [25], [37], [38]. Recent studies [39]–[41] have demonstrated that by considering only three laws of repulsion, attraction and heading alignment, it is possible to generate behavioral patterns very similar to those of real swarms. Thus far, questions of plant behavior have never been considered in terms of swarming. Here, we present experiments that demonstrate the existence of guided interaction in plant groups, providing evidence for swarming behavior in growing roots. Although chemical substances could play a role in the observed swarm-like root behavior, the ability of root apices of generating and detecting electric fields represents a further and more plausible mechanism. In addition, we propose a theoretical model based on the dynamics of self-propelled particles affected by forces of repulsion and attraction that depend on the positions and orientations of individuals growing in a given area. To distinguish observed root patterns from random root growth, we used an algorithm to generate random growth, which we compare to the experimental data.
Results
Characteristics of growing roots
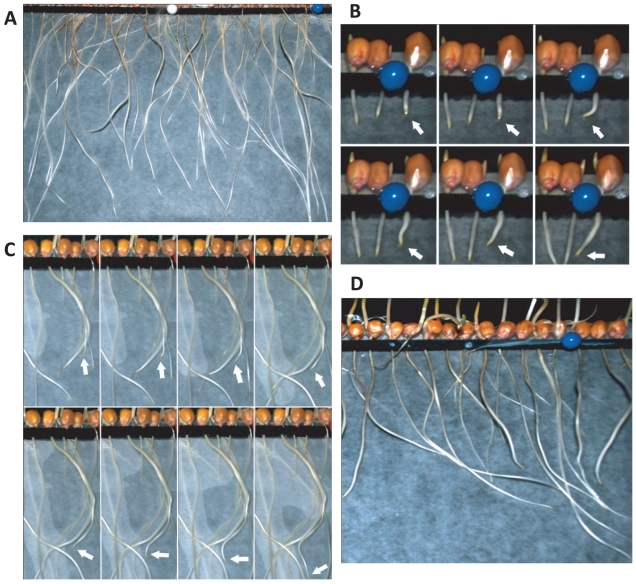
Fig. 1 A shows the growth of maize roots over time, displaying the roots' complex trajectories. The separation between the seeds is approximately 
cm. The direction of growth is controlled by the root apex, as shown in Fig. 1 B (see also Video S1 and S2). There are two types of interaction between the roots: alignments based on distance and repulsions. The crossing of roots is also occasionally observed, which could be interpreted as attraction followed by repulsion or as no interaction. The adjustment of the direction of growth (alignment) is often based on distance, as shown in Fig. 1 C. This dependence of growth on mutual distance indicates the existence of a form of signaling, possibly mediated by chemical substances. Another important feature of the growing roots is their collective behavior. In Fig. 1 D, a group of roots are shown to have chosen the same direction of growth, forming a type of cluster. It should be noted that water was homogenously distributed, and the experimental setup was well protected from the external environment to avoid localized stimuli.
Figure 1. Experimental growth of maize roots.
A. An image showing root growth in one of 10 experiments. B. Decision-making by the root apex: the movement of the root in the two opposite directions before committing to a growth direction. C. The alignment of one root with others based on distance, i.e., without physically contacting neighbors. D. An example of collective behavior: a group of roots chooses the same growth direction.
The random-growth model
We generated random growing paths by considering an assembly of independent particles separated initially by distance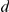 
with associated velocity vectors; there were no forces from the neighbors. At each time step, the particle positions are updated according to 
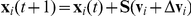, where we considered a unitary time step. The velocities 
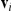have absolute value 
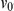, and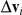 
is a stochastic term consisting of random numbers distributed uniformly in the interval 
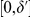. The direction of growth is determined by the matrix 
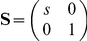, where 
is a two-valued variable where the values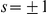 
are selected randomly with probability 
(
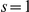for growth to the right and 
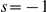for growth to the left). The introduction of 
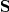to the model was made in order to direct the growth in a downward direction (more precisely, to restrict movements to the east-south and west-south directions).
Model of non-random growth
In the model of non-random growth, we consider the root apex or tip as a moving particle, and we treat the length of the root as the temporal history of the particle. Each particle is described by a velocity vector, the orientation of which denotes the direction in which the root apex moves. We assume that each seed produces only one main root and no collateral roots. This simplification is reasonable because the main root provides the longest and clearest history of interaction with its neighbors. The roots can interact with their neighbors at any point along their lengths. We assume that each root grows at a slightly different speed, giving rise to different root lengths. While this feature is clearly observed in experiments, thus motivating its inclusion in the theoretical model, we remark that this is not crucial in determining the growing-roots patterns. We have introduced the variation in speeds in accordance to experimental data which revealed that the variability in root lengths is always observed. Moreover, each plant is assumed to interact with neighboring plants causing spatial attraction or repulsion depending on the individual root responses. As mentioned before electric fields may be a possible mechanism of such interaction. These attractive and repulsive forces become effective when a certain distance separates the roots and leads them to grow closer or far away to together. As two roots approach each other, the mechanisms of direction adjustment (alignment) would switch on. The root apices adjust their direction as they detect their neighbors within a certain radius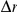 
. The roots are constrained to grow on a two-dimensional surface, so no-flux boundary conditions are considered. The time evolution of each root apex's vector marks the growing path of the root on the surface. The simulations were performed in a rectangular cell of horizontal length 
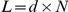, where 
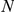is the number of seeds and 
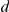is the spatial separation between two adjacent seeds. The vertical size is marked by the longest root, 
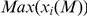, where 
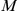is the last time value. The spatiotemporal history of the moving particle marks the shape of the whole root. The position of the 
th root apex is updated according to
 |
(1) |
where we considered a unitary time step. Because roots grow at slightly different speeds, instead of an equal velocity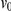 
for all particles, we consider different velocities for each root. More precisely, the velocities 
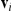have the absolute value 
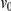, and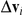 
is the fluctuation term composed of random numbers distributed uniformly in the interval 
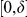. The angle 
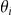with respect to the horizontal direction is updated according to 
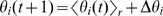, where 
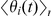denotes the average direction of the growing root apices within a radius 
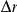surrounding root apex 
. The average direction is defined as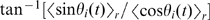 
. Small noisy fluctuations 
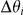in the angle are considered to incorporate the effects of varying environmental conditions on the roots' decision-making. The fluctuations are modelled as random numbers chosen with a uniform probability from the interval 
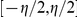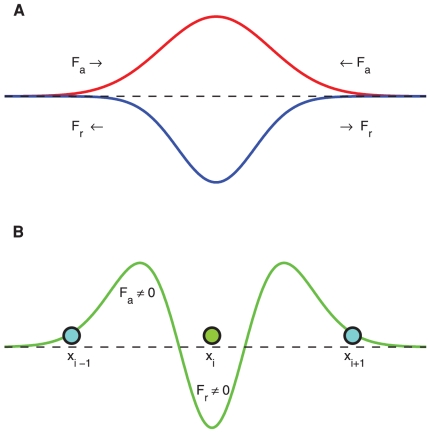
. The forces produced by the root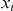 
that act on the neighbors are schematically presented in Fig. 2. We assume a Gaussian dependence of the force magnitude as a function of the distance, so they become stronger as the distance between the roots diminishes. The attractive and repulsive forces produced by the root 
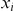and acting on the root 
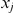(corresponding to the profiles in Fig. 2 A) are defined as:
 |
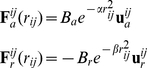(2) |
where parameters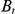 
, 
, 
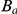and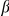 
are constant, with additional constraint 
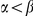. The total force acting on the root 
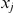, which models the root decision making on how to interact with a given neighbor, is then 
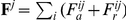. In Fig. 2 B we show that the force generated by the root situated in between the two neighbors defines two regions, i) where only the repulsive force is present and ii) where only the attractive force is present. When more roots are situated in a certain spatial region they all contribute in determining the resultant force acting on a particular neighboring root. For the sake of simplicity, we assume that the forces 
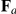and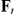 
act only in the horizontal directions. The action of the gravitational force is modelled by assuming that when the critical value 
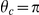of the angle is reached, the root apex starts to adjust its direction according to 
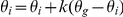, where 
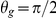and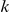 
is a constant parameter. In other words, the root apex is pushed to align with the direction of the gravitational force. The growing paths of the roots are adequately modelled by adjusting the system parameters.
Figure 2. Forces acting on the roots.
A. The force of attraction,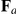 
, and the force of repulsion, 
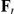. B. The effective force associated with each root being a sum of profiles shown in A. Filled circles indicate the position of roots.
Data analysis from the experiments, the non-random model and the model of random growth
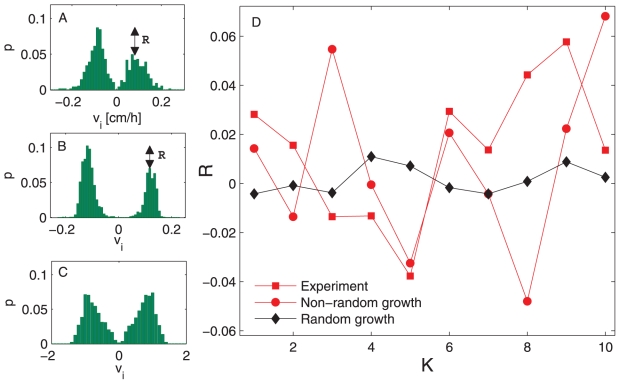
We calculate the velocity vectors associated with root growth rate and direction for 10 experiments and analogously for 10 realizations of the numerical experiments. In numerical simulations, approximately the same number of seeds and temporal data points are considered as in the experiment. The sample growing paths from the experiment, the model of non-random growth and the model of random growth are shown in Fig. 3 A, B and C, respectively. The probability distributions of the velocities are bimodal, revealing the growth direction: negative velocities denote roots growing to the right, and positive velocities denote roots growing to the left (all roots also grew downward). In the case of non-random growing (both in the model and experiment) the distributions tend to be asymmetric (see Fig. 4 A and B, respectively), meanwhile in the case of random growing the bimodal distribution is symmetric (see Fig. 4 C). We define a symmetry indicator of the binomial distribution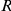 
, as the difference 
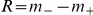, where 
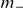and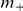 
are the local maxima of the left- and right-hand sides of the distribution, respectively. When 
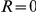, as is the case of a random-growth model, this corresponds to zero mean velocity vector (
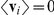). On the other side, when 
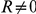, the corresponding mean velocities have non zero values (
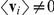). We plotted the indicator 
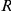for the results from the experiment and the models of non-random and random growth in Fig. 4 D. The observed asymmetries in distributions, with 
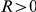or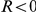 
for various experiments, give an indication of episodic alignments of the directions of neighboring root apices. When plotting the mean probabilities 
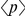for all experiments, we notice large fluctuations in the heights of these distributions (Fig. S1 A). The same phenomenon is observed in the model based on attractive and repulsive forces (Fig. S1 B). In contrast, in the random-growth model, we observe homogenous distributions for all directions and small fluctuations in the distribution heights (Fig. S1 C). The consequences of such asymmetry are also observed in the distributions of the horizontal distances of the root apices from their seeds, defined as 
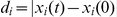. We report the probability distributions of these distances and their means in Fig. S2. The mean values of the probabilities of 
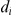are associated with higher standard deviations in the experiment (Fig. S2 A) and the model of non-random growth (Fig. S2 B), whereas the probabilities remain fixed and have relatively small standard deviations in the model of random growth (Fig. S2 C). This pattern indicates that the root apices grow in response to their neighbors rather than randomly.
Figure 3. Growing root paths marked by data from the: A. experiment; B. non-random model; and C. model of random growth.
The parameter values used in B are: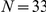 
, 
, 
, 
, 
, 
, 
, 
, 
, 
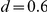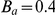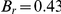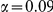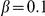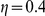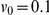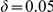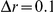and 
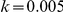. The parameter values used in C are: 
, 
, 
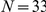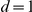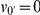and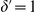 
.
Figure 4. The binomial distributions and the indicator of direction of the growing roots .
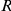. The sample bimodal distribution calculated from the: A. experiment; B. non-random model; and C. model of random growth. Double arrows mark the difference between maxima of bimodal distributions. This difference defines the value of 
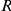. D. The indicator of direction of the growing roots, 
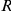, exhibits high variations in the case of non-random growth, both in experiments and numerical simulations, and low variations in the case of random-growth model. The parameter values used in B and C are as in Fig. 3 B and C, respectively. 
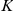stands for experiment number.
Indicator for velocity correlations
As described in the previous paragraph, the asymmetry in the heights of the bimodal distributions may indicate the existence of a preferred direction of growth or episodic alignments of directions between neighboring roots. To investigate, we calculated the spatial correlations between velocity vectors as a function of the distances between the roots. More precisely, we defined a radius 
and the radial area from 
to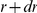 
and then calculated the mean of the absolute value of the velocity differences in the circular area enclosed in the interval 
, 
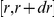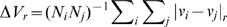, where 
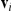is the velocity of the reference particle (all points along the root body are considered) and 
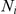is the total number of the reference particles. 
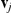and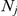 
describe the velocities of all particles within the radius 
and their total number, respectively. We then calculated the mean absolute velocity differences of the particles which could be found within a given radius 
around the reference particle 
, 
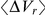, over all experiments and normalized it by the overall mean velocity 
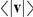, which gave a dimensionless description of the velocity correlations, defined as follows:
 |
(3) |
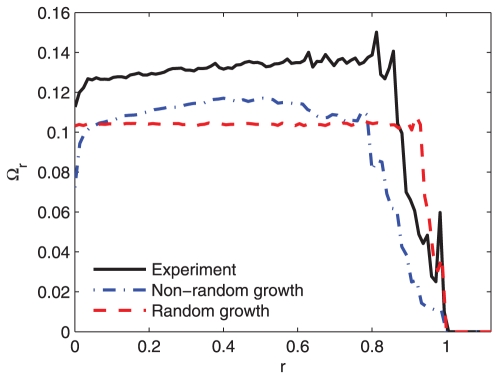
This dimensionless indicator was used to compare the correlations in directions of growing in the experiment and the numerical simulations of random and non-random growth. The indicator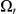 
was calculated for all three cases, and its dependence on 
plotted in Fig. 5. The curves from the experiment (solid line) and the non-random growth model (dotted-dashed line) exhibit a positive slope, indicating the presence of correlations in the velocities at small values of 
. For the random-growth model (dashed line), the slope is equal to zero; the particle motion is random and does not depend on the velocities of its neighbors.
Figure 5. Velocity correlation indicator .
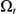of the experiment (solid line), model of non-random growth (dotted-dashed line) and model of random growth (dashed line). The value of radius 
was normalized in all cases to equal 
at the system size. The curve obtained from a random growth model differs essentially from the curves obtained from experiment and the non-random growth model. The parameter values used in numerical simulations of non-random growth model are as in Fig. 3 B, meanwhile for the random growth model are: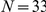 
, 
, 
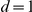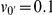and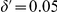 
.
Discussion
In the non-random model, the mean probability distribution of the velocities tends very slowly to a symmetric shape, and large fluctuations in the differences between the heights of the bimodal peaks are observed between individual experiments. In the random-growth model, different patterns are observed. The effect of noise makes the distributions symmetrical, and consequently, the fluctuations in the differences of the heights of the bimodal distributions are smaller. However, when interactive forces are present, the distributions become asymmetric and the fluctuations larger. These fluctuations arise from the alignment of growing roots and some type of synchronization of growth directions. The results of the experiment and non-random model differ qualitatively from those of the random-growth model, and the experimental results differ slightly from the predictions of the non-random model. This difference may be related to the fact that the non-random model considers only a few of the most essential ingredients that contribute to non-random growth. Other elements which have been neglected for the sake of simplicity contribute to root interactions and behavior: for instance, inhomogeneities in water distribution, initial distances between the seeds, or angle of the support on which the roots are growing. Despite these facts the proposed model allowed us to qualitatively reproduce the observed growing root patterns by making use of few basic ingredients.
Concerning the swarming behavior in roots, one of the advantages could be the efficient chemical modification of the soil in their vicinity. This would allow the maintenance of specific root micro-niche which is optimal for their physiological performances, in particular, the extraction of the essential nutrients from the soil and the defense against pathogens.
In conclusion, the experiments revealed that the qualitative features of root growth are well explained by a model of swarm behavior. The main insight gained in this study is that the root apices act as decision-making centers, giving rise to correlations in the growth patterns. We have identified a few key ingredients allowing us to explain and reproduce qualitatively the observed phenomenology, in particular, the angle adjustment and the attractive and repulsive interactions. Repulsive forces have been considered in the description of the polymer brushes [42] displaying similar patterns. However, in this case the brushes never intersect and the alignments are absent. In contrast, roots display both alignments and intersections between them, thus motivating the further inclusion in our model of the attractive force and angle adjustment.
Materials and Methods
Maize seeds were germinated at 24
C and allowed to grow for 4 days before being used in the experiments. The seeds were placed in a dark room on top of a plain supporting table fixed at approximately 75 degrees from horizontal. Water was homogenously distributed at the bottom of the supporting table and wicked up by the paper covering the table. Cameras were programmed to take photos every 30 minutes for 7 days on average. Images were processed with Tracker 4.0 software from the Open Source Physics collection, and data were processed by using routines written in MATLAB.
Supporting Information
Probability distribution of the velocities of growing roots. A. Experiment, B. non-random growth model and C. random-growth model. The parameter values used in B are: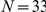 
, 
, 
, 
, 
, 
, 
, 
, 
, 
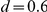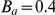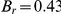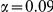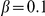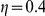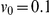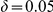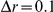and 
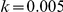. The parameter values used in C are: 
, 
, 
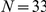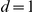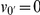and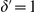 
. The three panels from the left show the representative distributions observed in single experiments and numerical realizations. The right panels show the averaged probability distributions.
(EPS)
Probability distributions of the distances of the root apices from their seeds:
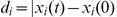. A. Experiment, B. non-random growth model and C. random-growth model. The parameter values in B and C are as in Fig. S1. The three panels from the left show the representative distributions observed in single experiments and numerical realizations. The right panels show the averaged probability distributions.
(EPS)
Experiment with a growing group of maize roots.
(MOV)
Experiment with a single growing maize root.
(MOV)
Acknowledgments
MC wishes to thank T. Vicsek for his hospitality at Eötvös Loránd University.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: Financial sources that have supported the work: Marie Curie European Reintegration Grant (N. 239324) within the 7th European Community Framework Program. URL: http://cordis.europa.eu/fp7/dc/index.cfm. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Baluska F, Mancuso S, Volkmann D, Barlow PW. Root apex transition zone: a signalling - response nexus in the root. Trends Plant Sci. 2010;15:402–408. doi: 10.1016/j.tplants.2010.04.007. [DOI] [PubMed] [Google Scholar]
- 2.Hodges A. Root decisions. Plant Cell Environ. 2009;32:628–640. doi: 10.1111/j.1365-3040.2008.01891.x. [DOI] [PubMed] [Google Scholar]
- 3.Baluska F, Mancuso S, Volkmann D, Barlow PW. Root apices as plant command centres: the unique ‘brain-like’ status of the root apex transition zone. Biologia. 2004;59:9–17. [Google Scholar]
- 4.Collings DA, White RG, Overall RL. Ionic current changes associated with the gravityinduced bending response in roots of Zea mays L. Plant Physiol. 1992;100:1417–1426. doi: 10.1104/pp.100.3.1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Masi E, Ciszak M, Stefano G, Renna L, Azzarello E, et al. Spatio-temporal dynamics of the electrical network activity in the root apex. Proc Natl Acad Sci USA. 2009;106:4048–4053. doi: 10.1073/pnas.0804640106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brenner ED, Stahlberg R, Mancuso S, Vivanco J, Baluska F, et al. Plant neurobiology: an integrated view of plant signaling. Trends Plant Sci. 2006;11:413–419. doi: 10.1016/j.tplants.2006.06.009. [DOI] [PubMed] [Google Scholar]
- 7.Baluska F, Mancuso S, Volkmann D, Barlow PW. The ‘root-brain’ hypothesis of Charles and Francis Darwin: Revival after more than 125 years. Plant Signal Behav. 2009;4:1121–1127. doi: 10.4161/psb.4.12.10574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Trewavas A. What is plant behaviour? Plant Cell Environ. 2009;32:606–616. doi: 10.1111/j.1365-3040.2009.01929.x. [DOI] [PubMed] [Google Scholar]
- 9.Callaway RM, Mahall BE. Family roots. Nature. 2007;448:145–147. doi: 10.1038/448145a. [DOI] [PubMed] [Google Scholar]
- 10.Gruntman M, Novoplansky A. Physiologically mediated self/non-self discrimination. Proc Natl Acad Sci USA. 2004;101:3863–3867. doi: 10.1073/pnas.0306604101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Biedrzycki ML, Jilany TA, Dudley SA, Bais HP. Root exudates mediate kin recognition in plants. Commun Integr Biol. 2010;3:28–35. doi: 10.4161/cib.3.1.10118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schenk HJ, Seabloom EW. Baluska F, Ninkovic V, editors. Evolutionary ecology of plant signals and toxins: a conceptual framework. Plant Communication from an Ecological Perspective. 2010. pp. 1–19. Springer-Verlag, Berlin.
- 13.Heil M, Karban R. Explaining evolution of plant communication by airborne signals. Trends Ecol Evol. 2010;25:137–144. doi: 10.1016/j.tree.2009.09.010. [DOI] [PubMed] [Google Scholar]
- 14.Novoplansky A. Picking battles wisely: plant behavior under competition. Plant Cell Environ. 2009;32:726–741. doi: 10.1111/j.1365-3040.2009.01979.x. [DOI] [PubMed] [Google Scholar]
- 15.Behrens HM, Weisenseel MH, Sievers A. Rapid changes in the pattern of electric current around the root tip of Lepidium sativum L. following gravistimulation. Plant Physiol. 1982;70:1079–1083. doi: 10.1104/pp.70.4.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Goldsworthy A, Rathore KS. The electrical control of growth in plant tissue cultures: the polar transport of auxin. J Exp Bot. 1985;36:1134–1141. [Google Scholar]
- 17.Antov Y, Barbul A, Korenstein R. Electroendocytosis: stimulation of adsorptive and fluidphase uptake by pulsed low electric fields. Exp Cell Res. 2004;297:348–362. doi: 10.1016/j.yexcr.2004.03.027. [DOI] [PubMed] [Google Scholar]
- 18.Wawrecki W, Zagorska-Marek B. Influence of a weak DC electric field on root meristem architecture. Ann Bot. 2007;100:791–796. doi: 10.1093/aob/mcm164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Morris DA. The influence of small direct electric currents on the transport of auxin in intact plants. Planta. 1980;150:431–434. doi: 10.1007/BF00390181. [DOI] [PubMed] [Google Scholar]
- 20.Ishikawa H, Evans ML. Electrotropism of maize roots. Role of the root cap and relationship to gravitropism. Plant Physiol. 1990;94:913–918. doi: 10.1104/pp.94.3.913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stenz HG, Weisenseel MH. Electrotropism of maize (Zea mays l.) roots. Plant Physiol. 1993;101:1107–1111. doi: 10.1104/pp.101.3.1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Baluska F, Lev-Yadun S, Mancuso S. Swarm intelligence in plant roots. Trends in Ecology and Evolution. 2010;25:682–683. doi: 10.1016/j.tree.2010.09.003. [DOI] [PubMed] [Google Scholar]
- 23.Parrish JK, Edelstein-Keshet L. Complexity, pattern, and evolutionary trade-offs in animal aggregation. Science. 1999;284:99–101. doi: 10.1126/science.284.5411.99. [DOI] [PubMed] [Google Scholar]
- 24.Visscher PK. Animal behaviour: How self-organization evolves. Nature. 2003;421:799–800. doi: 10.1038/421799a. [DOI] [PubMed] [Google Scholar]
- 25.Cavagna A, Cimarelli A, Giardina I, Parisi G, Santagati R, et al. Scale-free correlations in starling flocks. Proc Natl Acad Sci USA. 2010;107:11865–11870. doi: 10.1073/pnas.1005766107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Atkinson S, Williams P. Quorum sensing and social networking in the microbial world. J R Soc Interface. 2009;6:959–978. doi: 10.1098/rsif.2009.0203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Holldobler B, Wilson EO. The superorganism: the beauty, elegance, and strangeness of insect societies. New York: W.W. Norton & Company; 2009. [Google Scholar]
- 28.Rauch EM, Millonas MM, Chialvo DR. Pattern formation and functionality in swarm models. Phys Lett A. 1995;207:185–193. [Google Scholar]
- 29.Gadagkar R. The social biology of Ropalidia marginata: toward understanding the evolution of eusociality. Cambridge, MA: Harvard University Press; 2001. [Google Scholar]
- 30.Helbing D, Keltsch J, Molnár P. Modelling the evolution of human trail systems. Nature. 1997;387:47–50. doi: 10.1038/40353. [DOI] [PubMed] [Google Scholar]
- 31.Nagel K. Particle hopping models and traffic flow theory. Phys Rev E. 1996;53:4655–4672. doi: 10.1103/physreve.53.4655. [DOI] [PubMed] [Google Scholar]
- 32.Krause J, Ruxton GD, Krause S. Swarm intelligence in animals and humans. Trends Ecol Evol. 2009;25:28–34. doi: 10.1016/j.tree.2009.06.016. [DOI] [PubMed] [Google Scholar]
- 33.Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
- 34.Vicsek T, Czir'ok A, Ben-Jacob E, Cohen I, Shochet O. Novel type of phase transition in a system of self-driven particles. Phys Rev Lett. 1995;75:1226–1229. doi: 10.1103/PhysRevLett.75.1226. [DOI] [PubMed] [Google Scholar]
- 35.Bussemaker HJ, Deutsch A, Geigant E. Mean-field analysis of a dynamical phase transition in a cellular automaton model for collective motion. Phys Rev Lett. 1997;78:5018–5021. [Google Scholar]
- 36.Li W, Wang X. Adaptive velocity strategy for swarm aggregation. Phys Rev E. 2007;75:021917(1–7). doi: 10.1103/PhysRevE.75.021917. [DOI] [PubMed] [Google Scholar]
- 37.Aoki I. A simulation study on the schooling mechanism in fish. Bull Jap Soc Sci Fish. 1982;48:1081–1088. [Google Scholar]
- 38.Huth A, Wissel C. The simulation of the movement of fish schools. J Theor Biol. 1992;156:365–385. [Google Scholar]
- 39.Couzin ID, Krause J, James R, Ruxton GD, Franks NR. Collective memory and spatial sorting in animal groups. J Theor Biol. 2002;218:1–11. doi: 10.1006/jtbi.2002.3065. [DOI] [PubMed] [Google Scholar]
- 40.Couzin ID, Krause J, Franks NR, Levin SA. Effective leadership and decision-making in animal groups on the move. Nature. 2005;433:513–516. doi: 10.1038/nature03236. [DOI] [PubMed] [Google Scholar]
- 41.Couzin ID. Collective minds. Nature. 2007;445:715–715. doi: 10.1038/445715a. [DOI] [PubMed] [Google Scholar]
- 42.Milner ST. Polymer brushes. Science. 1991;251:905–914. doi: 10.1126/science.251.4996.905. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
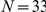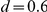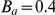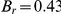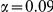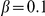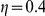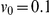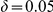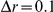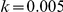Probability distribution of the velocities of growing roots. A. Experiment, B. non-random growth model and C. random-growth model. The parameter values used in B are: , , , , , , , , , and . The parameter values used in C are: 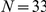, , 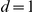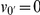and 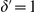. The three panels from the left show the representative distributions observed in single experiments and numerical realizations. The right panels show the averaged probability distributions.
(EPS)
Probability distributions of the distances of the root apices from their seeds:
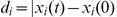. A. Experiment, B. non-random growth model and C. random-growth model. The parameter values in B and C are as in Fig. S1. The three panels from the left show the representative distributions observed in single experiments and numerical realizations. The right panels show the averaged probability distributions.
(EPS)
Experiment with a growing group of maize roots.
(MOV)
Experiment with a single growing maize root.
(MOV)