Worm-Like Ising Model for Protein Mechanical Unfolding under the Effect of Osmolytes

Abstract

We show via single-molecule mechanical unfolding experiments that the osmolyte glycerol stabilizes the native state of the human cardiac I27 titin module against unfolding without shifting its unfolding transition state on the mechanical reaction coordinate. Taken together with similar findings on the immunoglobulin-binding domain of streptococcal protein G (GB1), these experimental results suggest that osmolytes act on proteins through a common mechanism that does not entail a shift of their unfolding transition state. We investigate the above common mechanism via an Ising-like model for protein mechanical unfolding that adds worm-like-chain behavior to a recent generalization of the Wako-Saitô-Muñoz-Eaton model with support for group-transfer free energies. The thermodynamics of the model are exactly solvable, while protein kinetics under mechanical tension can be simulated via Monte Carlo algorithms. Notably, our force-clamp and velocity-clamp simulations exhibit no shift in the position of the unfolding transition state of GB1 and I27 under the effect of various osmolytes. The excellent agreement between experiment and simulation strongly suggests that osmolytes do not assume a structural role at the mechanical unfolding transition state of proteins, acting instead by adjusting the solvent quality for the protein chain analyte.

Introduction

Throughout the course of evolution, nature has successfully modulated protein stability using organic osmolytes, which are small molecules that shift the native-unfolded thermodynamic balance by changing the solvent quality for the protein chain. This thermodynamic description is commonly referred to as the “osmolyte effect” (1). Even though the thermodynamic model of the osmolyte effect is now widely accepted, the molecular details of the mechanism by which osmolytes influence protein kinetics and transition states are still not completely understood.

Mechanistic information about the role of osmolytes in protein folding and unfolding processes may be obtained by projecting protein transition states onto a geometrically relevant reaction coordinate. Single-molecule force spectroscopy (SMFS) has become the technique of choice for geometrical mapping of protein energy landscapes (2). From protein mechanical unfolding experiments, SMFS readily provides not only the distance between the native state and the mechanical unfolding transition state, commonly referred to as the unfolding distance Δx_u, but also an estimate of the spontaneous unfolding rate k_u(0) of the protein (3).

A previous SMFS study of mechanical unfolding of protein ubiquitin reported that the presence of glycerol as a cosolvent in aqueous solution leads to an increase of the protein's unfolding distance (4). Other SMFS studies reported that glycerol (5), ethylene glycol, and propylene glycol (6) increase the unfolding distance of the I27 titin module of the human muscle. Based on the Ansatz that the unfolding distance of proteins may be determined by the bridging length of solvent molecules at the unfolding transition state (7, 8), the mentioned SMFS studies concluded that small osmolyte molecules bridge the critical β-strands of proteins under mechanical tension, leaving their distinct signature on their unfolding distance. In particular, because osmolyte molecules are larger than water molecules, the small osmolytes were reported to increase the unfolding distance of proteins by amounts that correlate with their molecular size. It should be noted, however, that larger osmolytes such as sorbitol and sucrose were instead found to leave the unfolding distance of I27 unchanged, indicating their inability to partake in solvent bridging (6).

We challenge the above view that small osmolytes increase the unfolding distance of proteins and bridge their critical β-strands in the unfolding transition state through the following experimental and theoretical considerations.

Experimentally, we show herein that, contrary to what was reported in Dougan et al. (5), glycerol does not change the unfolding distance of I27. It should be noted that recent studies by us and others have also shown that the small osmolytes dimethylsulfoxide (DMSO) (9), glycerol (10), and guanidinium chloride (GndCl) (11) do not change the unfolding distance of streptococcal protein G (GB1). Taken together, these experimental results challenge the view that small osmolytes increase the unfolding distance of proteins.

Theoretically, we have recently shown that an Ising-like model with support for the osmolyte effect does not exhibit any movement of the unfolding transition state of GB1 in the presence of glycerol 30% v/v, when projected thermodynamically onto a commonly used nonmechanical reaction coordinate (10). Herein we show that the same lack of movement holds for various concentrations of DMSO and GndCl, indicating that osmolytes may not generally produce significant movements of the unfolding transition states of proteins. Furthermore, we expand the mentioned thermodynamic analysis with mechanical unfolding simulations based on the worm-like-chain (WLC) force-distance relation (12, 13), showing that our Ising-like model exhibits no significant change in the unfolding distance of GB1 and I27 under the effect of various concentrations of DMSO, glycerol, and GndCl, in excellent agreement with the experimental results presented herein and those of Aioanei et al. (9, 10) and Cao and Li (11). Note that our Ising-like model lacks the expressive power to account for any possible structural role of osmolytes at the unfolding transition state of proteins, while still being able to explain the mentioned experimental data. Therefore, our mechanical unfolding simulations challenge the view that osmolyte-bridging may be a general phenomenon in nature, because a structural role of osmolytes at the unfolding transition state is not necessary to explain the aforementioned experimental results.

In the next two sections we give a general overview of the protein mechanical unfolding model we propose together with a short overview of how the model supports the osmolyte effect.

Ising-Like Protein Models with Exactly Solvable Thermodynamics

A recent model for protein mechanical unfolding (14, 15, 16), which we shall refer to as the IPZ model (based on the initials of the authors), was built as a generalization of the Ising-like Wako-Saitô-Muñoz-Eaton (WSME) protein model (17, 18, 19, 20, 21, 22). Like the WSME model that it extends, the IPZ model has exactly solvable thermodynamics (23, 24) and it has been employed to investigate protein folding/unfolding kinetics and trajectories by simulating protein refolding under force-clamp conditions (25) and protein mechanical unfolding either in the force-clamp (15, 25, 26), force-ramp (14, 15), or velocity-clamp (26, 27) modes.

The IPZ model takes into account the entropic elasticity of the protein chain by allowing every WSME state to behave similarly to a freely jointed chain, with the angle between consecutive segments being taken from a finite set, usually being either zero or π-radians (15). Such an approach comes, however, with two limitations:

• 1.The experimentally observed behavior of unfolded protein chains does not show significant deviations from the ideal behavior of a worm-like chain under mechanical tension. Indeed, lock-in force spectroscopy with a resolution of 400 fN has failed to find any such deviations down to a force of 1.7 pN (28). Therefore, the WLC force-distance formula is extensively used in the analysis of velocity-clamp experiments performed with either the AFM (29) or optical-tweezers (30, 31). Rather than aiming at approximating the WLC entropic elasticity, the IPZ model (14, 15, 16) tries to approximate the entropic elasticity of the freely jointed chain, which differs significantly at high forces (2).
• 2.The IPZ model has more states than the WSME model, which may make it more difficult to obtain statistically representative sets of trajectories during Monte Carlo simulations, or to compute exactly the kinetics of small protein domains (19, 20). Indeed, for a protein with N peptide bonds, we computed that the IPZ model has 2 × 3^N states when only two possible angle values are allowed, while the WSME model has the lower number of 2^N states. It should be noted, however, that this shortcoming may be somewhat mitigated by the fact that the partition sum over the extra microscopic degrees of freedom introduced by the IPZ model (relative to the WSME model) can be computed analytically (15), and through the local equilibrium approach for kinetic simulations (16, 32).

We address both limitations by introducing an Ising model for proteins under mechanical tension that dictates that for every WSME state, the end-to-end extension of the protein chain is given by the WLC average force-distance relation. For any fixed stretching force, the number of states of the model is the same as that of the WSME model. In brief, a protein state consists of a set of contiguous native stretches of the peptide chain, contributing to the contour length with the distance in the native structure of the protein between the start and end of the stretch. Our worm-like Ising protein model maintains exactly solvable thermodynamics and, in the absence of a stretching force, it reduces trivially to the WSME-like model it extends.

Incorporating the Osmolyte Effect into the Protein Model

The osmolyte effect has been dissected into groupwise free energy contributions, with the protein backbone making up most of the protein's free energy of transfer to osmolyte-containing solutions (1). Making use of the group transfer free energies of amino-acid backbone units and side chains, a recent extension of the WSME model for the osmolyte effect enabled the thermodynamic projection of the protein energy landscape in the presence of osmolytes onto reaction coordinates commonly employed to monitor protein folding and unfolding (10).

However, a purely thermodynamic theory cannot directly explain the results of SMFS experiments in osmolyte-containing solutions, for which a kinetic theory of protein mechanical unfolding in the presence of osmolytes is needed instead. In this work we address the effect of osmolytes on GB1 (Protein Data Bank (PDB) (33) code 1PGA (34), Fig. 1 A) and I27 (PDB code 1TIT (35), Fig. 1 B) both at the thermodynamic and kinetic levels. Thermodynamically, we extend the previous equilibrium analysis of the osmolyte effect projected onto the reaction coordinate represented by the weighted number of native contacts (10) to a larger range of osmolytes and osmolyte concentrations for GB1, and we also apply it to I27 in the presence of glycerol 30% v/v. Kinetically, we use our worm-like Ising model to investigate protein mechanical unfolding in the presence of osmolytes by simulating the mechanical unfolding of GB1 and I27 under force-clamp and velocity-clamp conditions. We compare the mechanical unfolding kinetics as predicted by the worm-like Ising protein model in the presence of varying concentrations of osmolytes, namely DMSO, glycerol, and GndCl, to experimental SMFS data obtained in similar solvent conditions.

Figure 1.

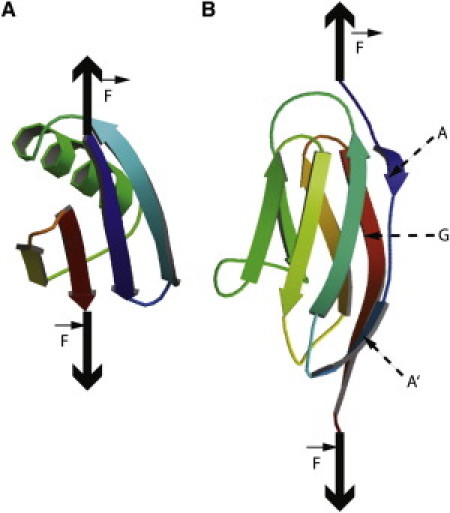
(A) Native structure of GB1 (PDB code 1PGA). (B) The native structure of I27(PDB code 1TIT) showing the A, A′, and G strands.

Theory

The original WSME formulation

According to the WSME model (17, 18, 19, 21, 23), a protein N + 1 amino-acids-long is described as a chain of N peptide bonds. The state of the protein is captured by the vector $\overrightarrow{m}$, where the i^th peptide bond is represented by the binary variable m_i that has only two possible values: 1 for a native peptide bond, and 0 for a nonnative peptide bond. The effective free energy of the system reads as

$$H_{WSME}\left(\overrightarrow{m}\right)=1\text{K}\times k_{\text{B}}\epsilon \sum _{1\le i<j\le N}{h}_{ij}\prod _{k=i}^j{m}_k-k_{\text{B}}T\sum _{i=1}^N{q}_i\left(1-m_i\right),$$ (1)

where 1 K is one Kelvin, k_B is Boltzmann's constant, T is the temperature, ε is a dimensionless enthalpic scale, and h_ij ≤ 0 are dimensionless numbers representing the relative strength of the contact between the i^th and the j + 1^th amino acids and q_i > 0 represents the entropic cost of ordering bond i. The contact strength h_ij is commonly defined as 0 if j = i + 1, and –⌈c_ij/5⌉ if j > i + 1 where c_ij is the number of pairs of atoms, the first atom of the pair belonging to amino acid i and the second atom of the pair belonging to amino acid j + 1, that in the native state are closer than 0.4 nm and ⌈·⌉ is the ceiling function (14, 15). The thermodynamics of the WSME model can be exactly computed via the transfer-matrix approach (23) (see also Section S1.1 in the Supporting Material for zero osmolyte concentration).

The fraction of folded molecules is estimated as

$$p_f\left(T\right)=\frac{\left[\alpha \left(T\right)-\alpha (\infty )\right]}{\left[\alpha \left(0\right)-\alpha (\infty )\right]},$$ (2)

where α(T) is the thermodynamic average of the number of native peptide bonds at temperature T. At zero temperature we have α(0) = N, whereas at infinite temperature the exact expression for the mentioned thermodynamic average (36) reads as

$$\alpha (\infty )=\stackrel{N}{\sum _{i=1}}{\left[1+\text{exp}\left(q_i\right)\right]}^{-1}.$$ (3)

Assuming the entropic costs q_i are known, the parameter ε in Eq. 1 can be fitted by imposing the known value of the folded fraction p_f(T) at a certain temperature.

Adding the osmolyte effect to the WSME model

Tanford's transfer model has proved very successful at predicting osmolyte-induced energetics of protein stability (37). In particular, the procedure of scaling group transfer free energies by the accessible surface area has previously proved accurate at interpreting the thermodynamics of the osmolyte effect (37, 38, 39). We describe next how the osmolyte effect has been incorporated into the WSME model by applying the transfer model to every WSME state (10).

A native stretch is defined as a sequence of consecutive amino acids connected by native bonds and delimited by two nonnative bonds. More formally, the stretch delimited by bonds i and j is said to be native if S_ij = 1, where

$$S_{ij}=\left(1-m_i\right)\left(1-m_j\right)\prod _{k=i+1}^{j-1}{m}_k,$$ (4)

with 0 ≤ i ≤ j ≤ N + 1 and taking m₀ = m_N+1 = 0. In the limiting case of j – i = 1 the stretch reduces to one amino acid (14, 15).

Accordingly, we consider each native stretch to have the exact same structure as in the native state of the full protein. To the effective free energy of Eq. 1, we add a term representing the free energy of transfer M_ij of the native stretch delimited by peptide bonds i and j, in isolation, relative to the denatured state,

$$H_O\left(\overrightarrow{m}\right)=H_{WSME}+\sum _{0\le i\le j-2\le N-1}{S}_{ij}{M}_{ij},$$ (5)

with M_ij taken as

$$M_{ij}=\sum _{i<k\le j}\left[\frac{\Delta g_{bb,R\left[k\right]}^{ref}\left(A_{bb,k}^{den}-A_{bb,k}^{ij}\right)}{A_{bb,R\left[k\right]}^{ref}}+\frac{\Delta g_{sc,R\left[k\right]}^{ref}\left(A_{sc,k}^{den}-A_{sc,k}^{ij}\right)}{A_{sc,R\left[k\right]}^{ref}}\right].$$ (6)

Here, R[k] denotes the amino acid at position k of the protein chain, $g_{bb,R\left[k\right]}^{ref}$ is the free energy of transfer of amino acid R[k] in the reference state (which is determined by the type of experimental or theoretical data available; see Section S2.1 in the Supporting Material), $A_{bb,k}^{den}$ is the accessible surface area of the backbone unit at position k of the protein chain in the denatured state, $A_{bb,k}^{ij}$ is the accessible surface area of the backbone unit at position k of the protein chain in the isolated native stretch from peptide bond i to peptide bond j, $A_{bb,R\left[k\right]}^{ref}$ is the accessible surface area of the backbone of amino acid R[k] in the reference state, and finally $g_{sc,R\left[k\right]}^{ref}$, $A_{sc,k}^{den}$, $A_{sc,k}^{ij}$, and $A_{sc,R\left[k\right]}^{ref}$ are defined similarly to the last four mentioned quantities, with the only difference that they refer to side chains rather than the backbone.

The thermodynamics of Eq. 5 are solved as described in Section S1.1 in the Supporting Material.

The worm-like Ising model for proteins under mechanical tension

Let us represent the amino acid k by its nitrogen, α-carbon, and carbon of the carbonyl group as a three-long N_k – C_α,k – C_k sequence. For 0 ≤ i ≤ j ≤ N we define the length l_ij of the native stretch delimited by peptide bonds i and j as the distance between the midpoint of the C_i and N_i+1 atoms and the midpoint of the C_j and N_j+1 atoms, making the convention that C₀ = N₁ and N_N+2 = C_N+1 (14, 15). Although the extensibility of native stretches is not taken into account (25), to get better agreement with the experimental contour-length increments upon unfolding of individual protein modules in characteristic velocity-clamp sawtooth patterns, we fix l_i,i+1 = 0.4 nm (40, 41).

We define the contour length of a WSME state $\overrightarrow{m}$ as the sum of the lengths of its native stretches

$$L\left(\overrightarrow{m}\right)=\sum _{0\le i<j\le N+1}{S}_{ij}{l}_{ij}\left(\overrightarrow{m}\right).$$ (7)

To introduce mechanical tension into the model, we add to the effective free energy H_O (or H_WSME in the absence of osmolytes) a potential energy function that depends on the end-to-end extension x. For a given contour length L and an acting force f, we fix the end-to-end extension x according to the WLC force-distance interpolation relation (12, 13)

$$F_{WLC}\left(\frac{x}{L}\right)=k_{B}T{\left(4p_l\right)}^{-1}\left[{\left(1-\frac{x}{L}\right)}^{-2}+4\frac{x}{L}-1\right],$$ (8)

where p_l is the persistence length, assumed to be constant all throughout. Therefore, the end-to-end extension becomes $x\left(L,f\right)=F_{WLC}^{-1}\left(f\right)L$.

The force-clamp potential energy takes the form

$$V\left(L,f\right)=-\xi x\left(L,f\right)f=-\xi F_{WLC}^{-1}\left(f\right)Lf,$$

where ξ is a dimensionless scaling factor that is computed by imposing that the folded fraction has a known value at a given temperature and force combination.

The velocity-clamp potential energy takes the form

$$V\left(L,t\right)=\xi \frac{\kappa }{2}{\left[vt-x\left(\kappa ,L,vt\right)\right]}^2,$$

where v is the constant velocity of the cantilever, κ is the cantilever spring constant, and x(κ,L,z) is the unique root in the interval $\left[0,L\right)\cap \left[0,z\right]$ of the equation

$$F_{WLC}\left(\frac{x\left(\kappa ,L,z\right)}{L}\right)=\kappa \left(z-x\left(\kappa ,L,z\right)\right).$$ (9)

The thermodynamics of the model, in the presence of a constant stretching force, are solved as described in Section S1.2 in the Supporting Material.

Materials and Methods

Materials and methods herein employed are described in Section S2 in the Supporting Material.

Results and Discussion

Our SMFS experiments show that glycerol 30% v/v does not change the unfolding distance of I27

The presence of glycerol at a concentration of 30% v/v consistently shifted the unfolding force distribution of I27 to higher forces, as seen in Fig. 2. Upon extracting the unfolding kinetics of I27 (as described in Section S2.9 in the Supporting Material) we found that glycerol reduces the spontaneous unfolding rate k_u(0) of protein I27 without changing the distance Δx_u = 0.25 nm between the ground state and the transition state along the reaction coordinate. The height of the unfolding activation barrier of I27 was increased in the presence of glycerol 30% v/v by ΔΔG_u = 1.36 ± 0.06 k_BT.

Figure 2.

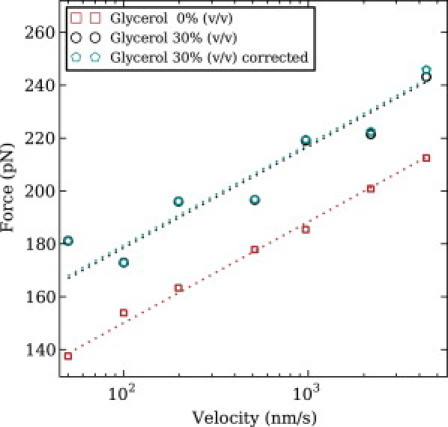
Average unfolding force of I27 at various pulling speeds increases in the presence of glycerol 30% v/v, and increases again slightly when adjusting for the viscous drag-force on the cantilever. As a guide to the eye, we fitted a dashed line to the average unfolding forces in each condition with a fixed slope of k_BT/(Δx_u log₁₀ (e)), where e is Euler's constant and Δx_u = 0.25 nm. The formula for the eye-guide fixed slope has been inspired from the so-called standard method of kinetic parameter estimation, and it was not used for the statistical estimation of the kinetic parameters that we report, which was performed instead via maximum-likelihood estimation (see Section S2.9 in the Supporting Material).

Thermodynamics

We projected the free energy landscapes of GB1 and I27 onto the nonmechanical reaction coordinate given by the weighted number of native contacts (see Section S1.1 in the Supporting Material). The chosen reaction coordinate allowed us to identify the unfolding transition state of GB1 in the absence of osmolytes and in the presence of 1), DMSO 30%, 20% and 10% v/v; 2), glycerol 30% v/v; and finally 3), GndCl 2.25 and 1 M. In all the mentioned conditions, the unfolding transition barrier was located at the same position of 381 weighted native contacts. GB1, in the presence of higher DMSO concentrations, as well as I27 in the absence of osmolytes and in the presence of glycerol 30% v/v, did not exhibit an easily identifiable unfolding transition state on the chosen reaction coordinate. A full discussion of the thermodynamic projection analysis can be found in Section S3.1 in the Supporting Material.

Kinetics

For protecting osmolytes, it holds in Eq. 6 that $\Delta g_{bb,R\left[k\right]}^{ref}>0$. Therefore, they disfavor microscopic states that are more exposed to solvent, thus slowing the transitions going from more native-like to more unfolded states (according to Eq. S15 in the Supporting Material) and, overall, slowing down the unfolding kinetics. Conversely, for denaturing osmolytes, it holds that $\Delta g_{bb,R\left[k\right]}^{ref}<0$. Therefore, they favor the microscopic states that are more exposed to solvent, speeding up the transition rates going from more native-like to more unfolded states and, overall, speeding up the unfolding kinetics. The simulation results presented next are consistent with this view, and additionally they offer insights into the effect of osmolytes on the unfolding distance of the studied proteins.

Force-clamp

We performed force-clamp simulations of mechanical unfolding of GB1 with constant forces from 0 pN to 500 pN, inclusive, with a step size of 5 pN, in the absence of osmolytes and in the presence of 1), DMSO 50%, 40%, 30%, 20% and 10% v/v; 2), glycerol 30% v/v; and 3), GndCl 2.25 and 1 M. We found that in each solvent condition the logarithm of the force-dependent unfolding rate grows approximately linearly with force. Previous works of mechanical unfolding via WSME-like models have fitted the Bell model only on ranges of forces selected to maximize the quality of the fit (14, 15, 25, 26). Because we need to compare the fitted values between different solvent conditions, to remove any bias in the selection of the fitting force ranges we adopted the simple approach of fitting over the full set of forces, even if that results in somewhat lower quality fits, as can be seen in Fig. 3.

Figure 3.

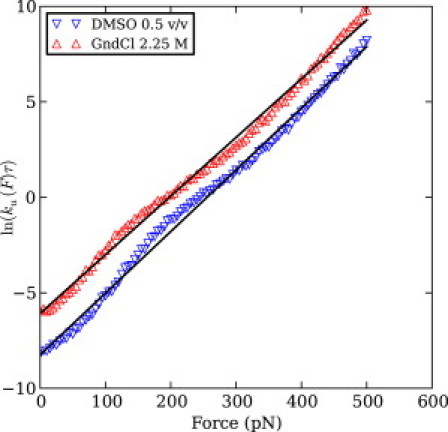
(Color online) Logarithm of the unfolding rate of GB1 as a function of the stretching force in two solvent conditions, namely the most destabilizing one and the most stabilizing one, selected such as to reduce visual clutter. (Points) Inverse of the average unfolding time from at least 125 trajectories. (Lines) Fit of Bell's model via Eq. S17 in the Supporting Material.

Fitting Bell's model given by Eq. S17 in the Supporting Material to the force-dependent unfolding rates resulted in negligible variation of the unfolding distance Δx_u among the different solvent conditions, as seen in Table S2 in the Supporting Material. Moreover, the unfolding distance in all conditions was close to the experimentally measured value of 0.165–0.17 nm (9, 10, 11). The unfolding barrier height changes are also in qualitative agreement with the activation barrier changes inferred from the SMFS experiments, which are indicated in the last column of Table S1.

For the force-clamp simulations of mechanical unfolding of I27, we used constant forces from 0 pN to 200 pN, inclusive, with a step size of 5 pN, in the absence of osmolytes and in the presence of 30% glycerol v/v. We found that, in either solvent condition, the logarithm of the force-dependent unfolding rate shows two approximately linearly regimes with respect to force. Therefore we fitted Bell's model over each linear regime, as seen in Fig. 4, selecting the crossover point between the two regimes by minimizing the total squared fitting error.

Figure 4.

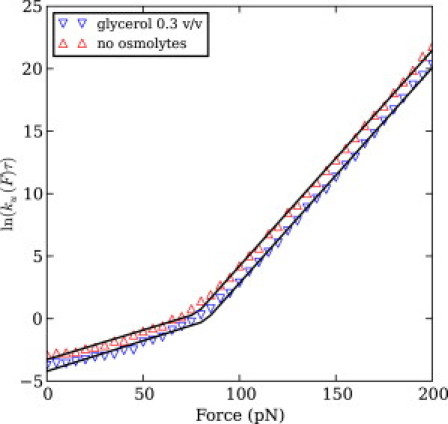
(Color online) Logarithm of the unfolding rate of I27 as a function of the stretching force in two different solvent conditions. Each point represents the inverse of the average unfolding time from at least 125 trajectories. (Lines) Fit of Bell's model via Eq. S17 in the Supporting Material over two different linear regimes, selected for each solvent condition so as to minimize the total squared error. In the absence of osmolytes, the crossing point was found to be 80 pN, whereas in the presence of glycerol 30% v/v the crossing point was found to be 85 pN.

For each of the two linear regimes, the unfolding distance showed only negligible variation between the two conditions, while the free energy changes are in qualitative agreement with the experimentally inferred activation barrier change, as can be seen in Table S3.

Velocity-Clamp

We performed velocity-clamp simulations of mechanical unfolding of (GB1)₈ with a cantilever of spring constant 0.06 N/m and velocities of 50.1, 100, 198, 513, 969, 2180, and 4360 nm/s, matching the spring stiffness and pulling velocities of some previous SMFS velocity-clamp experiments with (GB1)₈ in the presence of osmolytes (9, 10). Because (as described in Section S2.3.1 in the Supporting Material) knowledge of the product vτ is required for velocity-clamp simulations, we estimated τ by confronting the average unfolding time from 1000 simulated force-clamp mechanical unfolding traces at zero force with the experimentally inferred zero-force mean unfolding time of GB1 (9), obtaining the approximate value τ = 0.039 s.

The simulated force-distance traces exhibited the characteristic WLC sawtooth pattern, as seen in Fig. 5. In each condition, the average unfolding forces, shown in Fig. 6, increased with increasing pulling velocities, as expected from Bell's model. Moreover, average unfolding forces increased with increasing DMSO concentration and they decreased with increasing GndCl concentration. The unfolding forces were, however, generally higher than the experimental ones (see Table S4), for reasons explained below.

Figure 5.

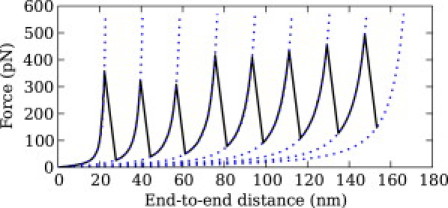
Simulated velocity-clamp curve of (GB1)₈. The velocity was 969 nm/s, the cantilever spring constant was 0.06 N/m, and the solvent had a GndCl concentration of 2.25 M.

Figure 6.

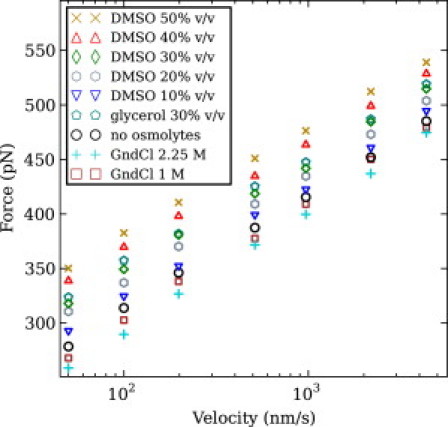
(Color online) Average unfolding force versus pulling velocity in different solvent conditions for protein (GB1)₈. (Points) Average unfolding force from at least 125 trajectories.

For each solvent condition, we performed maximum-likelihood estimation of the unfolding kinetic parameters by using all velocities simultaneously (3), with the results being summarized in Table S5. The unfolding activation barrier changes from velocity-clamp simulations are in good agreement with those from force-clamp simulations indicated in Table S2 and the experimental ones indicated in the last column of Table S1. The unfolding distance, estimated from velocity-clamp simulations, is smaller than the one estimated from force-clamp simulations and from SMFS experiments, resulting in unfolding forces much higher than the experimental SMFS ones at the same velocities. However, the unfolding distance from velocity-clamp simulations still shows only negligible variation between the different solvent conditions.

For the velocity-clamp mechanical unfolding simulations of I27, we used a single I27 module, in the absence and presence of glycerol 30% v/v. The simulated force-distance traces exhibited the characteristic WLC pattern, as seen in Fig. 7.

Figure 7.

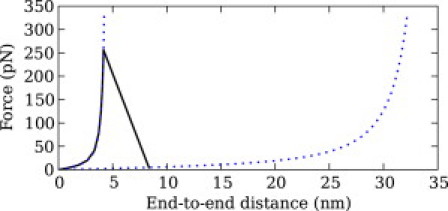
Simulated velocity-clamp curve of I27. The velocity was 50.1 nm/s, the cantilever spring constant was 0.06 N/m, and the solvent was free of osmolytes.

The I27 velocity-clamp simulations showed that the presence of glycerol 30% v/v increases the average unfolding forces of I27 (see Fig. 8), without causing any significant movement of the unfolding transition state, producing but a deceleration of its spontaneous unfolding kinetics (see Table S6). The unfolding forces from the simulation were also compatible with the range of unfolding forces from the SMFS experiments, as seen in Fig. 2 and Fig. 8.

Figure 8.

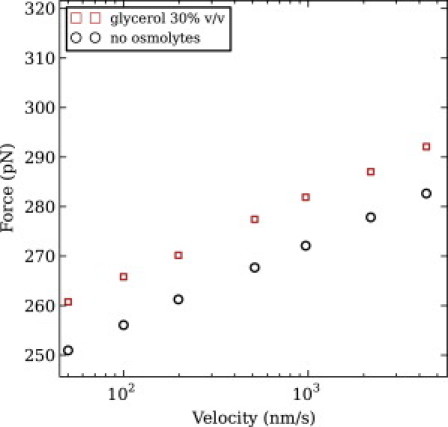
Average unfolding force versus pulling velocity in different solvent conditions for protein I27. (Points) Average unfolding force from at least 1000 trajectories.

Conclusion

We showed experimentally that contrary to what has been previously reported, glycerol does not increase the unfolding distance of I27. In light of previous similar findings with GB1 in the presence of DMSO, glycerol, and GndCl, taken together these results suggest that there is a general mechanism through which osmolytes affect the mechanical stability of proteins that does not affect their unfolding distance.

To understand whether the above general mechanism is based on osmolytes adjusting the solvation quality for the protein chain, as suggested by the thermodynamic description of the osmolyte effect, we developed an Ising-like model for protein mechanical unfolding that incorporates the transfer free energy of various conformations of the protein chain. Notably, our Ising-like model is endowed with exactly solvable thermodynamics and it satisfies the WLC force-distance relation, which is a common fingerprint of mechanical unfolding experiments.

When applied to the mechanical unfolding of GB1 and I27 in osmolyte-containing solutions, our model correctly predicts that osmolytes do not change their unfolding distance. This level of agreement validates our approach for building a microscopic model of protein mechanical unfolding in the presence of osmolytes, and it strongly suggests that osmolytes may not play a structural role at the unfolding transition state of proteins, contrary to what has been previously suggested.

Editor: Peter Hinterdorfer.