Inference for discretely observed stochastic kinetic networks with applications to epidemic modeling

Abstract

We present a new method for Bayesian Markov Chain Monte Carlo–based inference in certain types of stochastic models, suitable for modeling noisy epidemic data. We apply the so-called uniformization representation of a Markov process, in order to efficiently generate appropriate conditional distributions in the Gibbs sampler algorithm. The approach is shown to work well in various data-poor settings, that is, when only partial information about the epidemic process is available, as illustrated on the synthetic data from SIR-type epidemics and the Center for Disease Control and Prevention data from the onset of the H1N1 pandemic in the United States.

1. INTRODUCTION

Historically, infectious disease spread through populations has been modeled using the deterministic dynamics of ordinary differential equations (ODEs). Such ODE models have the advantage of simplicity, as they rely on the appropriate law of large numbers (see, e.g. Andersson and Britton, 2000a, Chapter 5) to describe longitudinally the average epidemic trends in the population. However, the disease propagation is an inherently stochastic phenomenon, and stochastic models are needed to properly capture the transmission dynamics (see, e.g. Keeling and others, 2001,). The aims of this paper were to introduce a rigorous Bayesian inference method for partially and discretely observed stochastic kinetic models and to explore its applicability to some contemporary epidemic data. The need for accurate modeling of the epidemic process is becoming increasingly apparent as the financial consequences of infectious disease outbreaks are growing, 3 important recent examples being the 2001 foot and mouth disease outbreak in the UK, the severe acute respiratory syndrome epidemic in the spring of 2003, and the worldwide A/H1N1 (swine flu) pandemic of 2009 (see, e.g. Keeling and others, 2001, Lipsitch and others, 2003, Balcan and others, 2009).

In this paper, we present a general inference method for the so-called Markovian stochastic kinetic network (SKN) models described in Chapters 5 and 9 of Andersson and Britton (2000a). For readers convenience, a brief description of SKNs is provided in Section A of the supplementary material (available at Biostatistics online). The inference method utilizes modern Bayesian techniques via the usual Markov Chain Monte Carlo (MCMC), extending some of the earlier work in this area. In particular, it is partially based on the ideas of Gibson and Renshaw (1998), who presented a first statistical analysis of a SIR-type model based on MCMC methods, as well as on O'Neill and Roberts (1999). Although we concentrate on Markovian models, this setting may be in fact extended, in a manner similar to Streftaris and Gibson (2004). The main methodological contributions of the current paper are presented in Sections 2 and 3. In Section 4, we use our approach to analyze the data, by now famous, from the early stages of the US H1N1 pandemic of 2009. In Section 5, we give a brief summary of the paper's main points and offer some concluding remarks. Additional simulation studies and discussions are provided in the papers' supplementary material available at Biostatistics online.

1.1. Example: SIRS epidemic model

As an introductory example, consider the “endemic” modification of the classical SIR model of Kendal and McKendrick (cf., e.g. Chapter 1 of Andersson and Britton, 2000a). The classical SIR model assumes a fixed population size (M) with 3 time-varying species: susceptible (x), infective (y), and removed (z, dead or recovered), such that for any t ≥ 0, we have x(t) + y(t) + z(t) = M. In the SIRS model, in addition to the usual SIR interactions, we assume an additional one, converting removed back into susceptibles. The general deterministic law of mass action model (see Section A of the supplementary material (available at Biostatistics online) for details) specializes then to the following ODE system

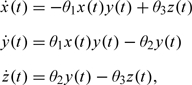(1.1)

with the initial conditions x(0) = M − 1, y(0) = 1, and z(0) = 0.

The above ODE represents one of the simplest classical models of an endemic disease spread within fixed-size population (M), and its various variants seem to be still in use for some simple epidemics (e.g. certain sexually transmitted diseases, cf. Kouyos and others, 2010). Note that from the above model, it follows that, for example the SIRS epidemic threshold function (cf. also Andersson and Britton, 2000a, Chapter 5) is given by R₀(t) = θ₁x(t)/θ₂.

Using the biochemical notational convention (see Section A of the supplementary material available at Biostatistics online), the SKN for the above SIRS model is given by

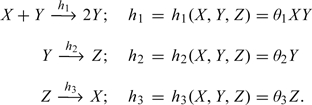(1.2)

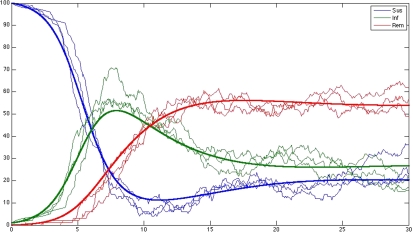
Note that R₀(t) is now stochastic and its distribution is, in general, not tractable but may be simulated from (1.2), for a given vector of constants θ = (θ₁,…,θ₃). In Figure 1, we present the simulated (via the Gillespie algorithm, as given in Gibson and Bruck, 2000) realizations of 3 stochastic trajectories for the SIRS network (1.2) as compared to the deterministic trajectories obtained from (1.1) with M = 101 and θ = (0.01,0.2,0.1).

Fig. 1.

ODE and SKN trajectories for SIRS model species (susceptibles, infectives, and removed, respectively, top, middle, and bottom curve at the origin) with total population size M = 100.

2. STATISTICAL INFERENCE

The SKN inferential procedure for the case when the entire single trajectory X is observed is rather straightforward (Boys and others, 2008). For completeness, we review it briefly in Section B of the supplementary material available at Biostatistics online. Due to the form of the likelihood function derived there, a family of independent gamma distributions is seen as a natural set of conjugate priors, that is θ_s∼Γ(a_s,b_s), s = 1,…,v. Under this family of priors the application of Bayes' theorem produces posterior gamma distributions (given the trajectory X = x) which retain independence, that is

(2.1)

Note that the maximum aposteriori (MAP) estimator is simply the mode of the posterior distribution, that is the adjusted maximum likelihood estimator (MLE). In particular, in case of “uninformative and improper” priors with a_s = 1 and b_s = 0, MLE and MAP estimators coincide.

2.1. MCMC—Gibbs sampler

In practice, information about the entire trajectory X is rarely available. Typically, the data are only collected as species counts at some fixed set of time points (e.g. daily or weekly) with no information in-between. This results in incomplete trajectory information, say, X_obs. There may be also other complications associated with data collection, for instance, some of the species may not be observable, or their counts may be obtained with large errors. Both these situations may be handled in our current framework.

Within our Bayesian inferential framework, the focus is on the posterior distribution of both model parameters and the missing parts of the trajectories, to be denoted (θ,X|X_obs). There are several ways of obtaining this distribution, typically within the realm of various MCMC methods utilizing versions of the Metropolis–Hastings algorithm (MHA; see, e.g. Chapter 11 in Andersson and Britton, 2000a,). For instance, Boys and others (2008) proposed to use the nested Metropolis–Hastings–Gibbs sampler approach which, in order to properly sample the hidden trajectory, calls first for sampling from certain approximate process within the Gibbs sampler, and then for correcting the result via the Metropolis–Hastings step. The method was seen to work well for some simple SKNs, like, the stochastic Lotka–Volterra model.

In the current paper, we propose a different way of tackling the problem of trajectory sampling. It does not require MHA, but rather takes advantage of the relation (2.1) and the ability to generate SKN conditionally on the partially observed trajectory. The lack of an algorithm for the latter has been a major obstacle in building effective Gibbs samplers in settings similar to ours (Boys and Giles, 2007). However, as it turns out, an elegantly simple solution is available with the help of the “uniformization” technique (Hobolth and Stone, 2009) applied to sequential path generation, conditional on the observed states. Similar ideas were applied recently in a somewhat different context of codon substitution analysis (Rodrigue and others, 2008). Details are deferred to Section 3 below.

Assuming, for the time being, that we have a way of sampling the hidden process, the following procedure approximately samples the required posterior distribution.

ALGORITHM 1

(Gibbs sampler for partially observed SKN)

1. Initialize the algorithm with a valid sample path, given observed data X_obs.

2. Sample θ's from their full gamma conditionals, given the current path, via (2.1).

3. Sample paths space (hidden events and times), given observed data X_obs and θ's, via the “uniformization” method described below.

4. Repeat steps 2–3 until convergence occurs.

3. UNIFORMIZATION AND PATH SAMPLING

We now present a method for sampling the conditional process (X|θ,X_obs) on the bounded interval (0,T]. First, we need to introduce the so-called uniformization procedure for SKN (see, e.g. Hobolth and Stone 2009 and references therein).

Let Q = [q_ij] be the infinitesimal generator of a Markov process {X(t)} evolving in time 0 < t < T < ∞ over state space S. Each off-diagonal entry in Q specifies the instantaneous rate of transition from one state to another, and the diagonal entries are set so the sum of each row equals zero (i.e. q_ii = − ∑_i≠jq_ij). For any infinitesimal increment Δt, P(X(t + Δt) = j|X(t) = i) = q_ijΔt + o(Δt),P(X(t + Δt) = i|X(t) = i) = 1 − ∑_j≠iq_ijΔt + o(Δt). By truncating the state space of the original process by time T < ∞, we may assume that the dimension of Q is bounded with high probability. (In particular, with probability 1 when the system is closed, that is the total size of the population is constant). Under this assumption, consider the Poisson process {N(t)} on (0,T] with rate μ such that

(3.1)

and recall from basic theory that {N(t)} is defined as a counting process satisfying P(N(t + Δt) − N(t) = 1|N(t) = k) = μΔt + o(Δt), for any integer k ≥ 0.

The uniformization procedure transforms the process defined by Q into a process allowing for virtual events or self-transitions (from the state i to i). This is done by first defining the discrete time Markov chain {Z_n} with state space S and transition probability matrix R where

(3.2)

and I is the identity matrix. One can now easily argue that on the trajectories on which X(t) is uniformly bounded (note that this is true with arbitrarily high probability on a bounded time interval) we have X(t) = Z_N(t) in distribution. Indeed, note that, for the trajectories for which (3.1) holds, both processes have the same generators, since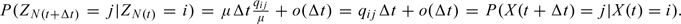

3.1. Sampling hidden trajectories under constraints

With the uniformization procedure in hand, we may now describe the method for exact sampling of the hidden path of the process {X(t)}, conditional on the observed values and under the constraint (3.1). Due to the assumed Markov property, the hidden trajectories in-between observations are independent of each other (see, e.g. formula (5) in Boys and others 2008), and therefore, it suffices to consider a sampling scheme for a single time interval between any 2 adjacent observed values, say, X(0) = i and X(t) = j. The overall method for sampling the hidden process {X(s)} for 0 < s < t can be summarized as a 3-stage progressive demarginalization: (i) sample the number of events (including virtual ones) marginalized over their nature and timing; (ii) sample the nature of events in order, marginalized over their exact timing; and (iii) sample the timing of events (Fearnhead and Sherlock, 2006). Note that in view of our definition of the chain {Z_N(t)}, we have

(3.3)

as well as

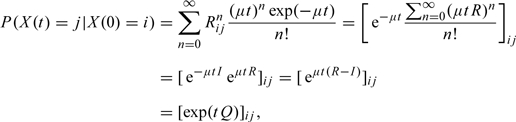where the last identity follows from (3.2). In view of (3.3) and (3.4), we may first sample the number of hidden events (including virtual ones) between (0,t) using the fact that

(3.5)

The sampling from (3.5) may be done easily via the usual method of inversion of the distribution function (see, e.g. Gibson and Bruck, 2000,). Having sampled the number of events n, we now wish to sample the specific series of events, say s₀ = X(0) = i,s₁,s₂,…,s_n = X(t) = j, leading from i to j. This is done sequentially as follows. The state s₁ is sampled from 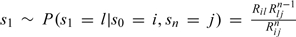Subsequently, the state s₂ is sampled from 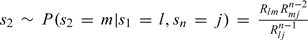and so on, until n events are sampled. Note that the second factor in the numerator in the above formulas ensures that the state sampled will not trap the trajectory into a state s_k which could not lead to s_n = j in n events. Finally, having sampled the sequence of events, sampling of their timings can be done simply by drawing n independent identically distributed uniform U(0,t) variables (cf. e.g. Durrett, 1999, Chapter 3, Theorem 5.1). After removing the virtual events, one obtains the trajectory of the desired process (X|θ,X_obs) on (0,T], conditional on (3.1).

3.2. Partially observed species

In the sampling algorithm above, we have assumed that the entire vector X(t) is available at all the points of observation. However, in practice, this is often not the case. For instance, in the SIRS model, one might consider removed as relatively easy to observe and count, but not necessarily infectives or susceptibles. In general, suppose we have X(t) = (X^o(t),X^u(t)) where X^o(t) and X^u(t) are, respectively, observed and unobserved parts of the vector X(t) and assume we observe at n time points X^o(t_k) = j_k^o, k = 0…,n. Since the state space for the underlying discrete Markov chain (3.3) is finite and P(X(t) = j^o|X(0) = i,N(t) = n) = ∑_j^uR_i,(j^o,j^u)ⁿ, the algorithm from the previous section may be modified in an obvious way to sample the additional space of missing components, via an extra layer of de-marginalization in parts (i) and (ii). However, such modification will necessarily increase (typically, by an order of magnitude) the computational overhead, and, therefore, the following approximate algorithm may be often more useful (see Section C of the supplementary material (available at Biostatistics online) for some numerical examples).

In order to approximately identify the unobserved species X^u(t), we maximize the joined probability

(3.6)

and take the maximizer (j₀^u,…,j_n^u)^* as the imputed trajectory. To this end, we apply the Bellman dynamic optimization principle (BOP, cf. e.g. Bellman and Dreyfus 1959) in the following way. Denote δ_k(j) = max_{j0^u,…,jk − 1^u}P(X^o(t₀) = j₀^o,…,X^o(t_k) = j_k^o,X^u(t₀) = j₀^u,…,X^u(t_k) = j) for k = 1…,n. The Markov property of the complete chain X(t_i) = (X^o(t_i),X^u(t_i)), i = 0…,n, yields the decomposition

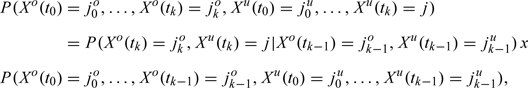which implies the following BOP recursion for k = 1,…,n

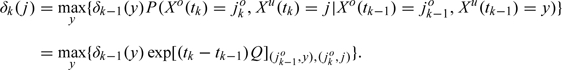The above leads to the following simple algorithm for finding the maximizing path (j₀^u,…,j_n^u)^* in (3.6), reminiscent of the “Viterbi path” method, a popular tool in the hidden Markov models theory (see, e.g. Koski 2001, Chapter 14)

ALGORITHM 2

(BOP-based imputation for partially observed species)2

1. Given j^o at t = 0, initialize δ₀(j).

2. For k = 1,…,n compute δ_k(j) via (3.7) for all j s.t. δ_{k − 1}(j) > 0 and store the associated maximizer y_j,k^*.

3. Take (j_n^u)^* = argmax_jδ_n(j), and recursively backtrack (j_{k − 1}^u)^* = y_(jk^u)^*,k^* for k = n,…,1.

4. EXAMPLES

We illustrate the performance of the Gibbs sampler algorithm described in Section 2.1, with and without data imputation via Algorithm 2 from the previous section, using 2 examples: simulated data from the SIRS model and real data obtained from the Center for Disease Control and Prevention (CDC) database tracking the onset of the 2009 H1N1 pandemic in the United States.

4.1. Analysis of synthetic data from SIRS model

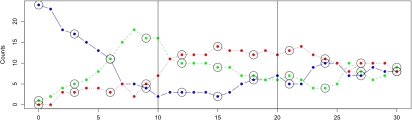
As the first example, we consider some synthetic data generated from the SIRS model (1.1). In the simulation, in order to make the stochastic effects more pronounced, we took a smaller population size than that depicted in Figure 1, with M = 25 and the initial number of infectives equal to 1 (Y(0) = 1) and set θ = (0.02,0.2,0.1). As readily seen in the trajectory data plot of Figure 2, this SKN model fluctuates much more heavily than the one depicted in Figure 1, where M = 100.

Fig. 2.

Datapoints along the trajectories for susceptibles, infectives, and removed (top, middle, and bottom curve at the origin, respectively) in the SIRS model. Vertical lines indicate the data batches used for the 3 first dense grid scenarios (m = 1) reported on in Table 1. Circled values mark the data set used in fourth (sparse grid) scenario when m = 3.

In order to assess the proposed method's performance, we have simulated a single trajectory for the SKN corresponding to the SIRS model given by (1.2) with T = 30, and, in various scenarios, collected model species counts at the equidistant time intervals of length m = 1,2,3 (thus generating between 10 and 30 observed data points). The trajectory data are presented in Figure 2. More extensive comparative analysis for other trajectories, with different values of M and with partially observed species only, are given in Section C of the supplementary material (available at Biostatistics online). Overall, we did not notice much dependence of the inference results on the particular trajectory selected. For the simulated data, in order to illustrate the effects of trajectory undersampling and varying sample sizes, we have divided the longitudinal observations into 3 batches of consecutive time points (10 time points in each batch, marked by the vertical lines in Figure 2). We then ran the Metropolis-Hestings step (MH) and uniformization Gibbs samplers based on 5 data scenarios: (i) data from batch 1 only (first 10 observation points), (ii) data from batches 1 and 2 (first 20 points), (iii) data from all batches combined (all 30 points from the trajectory included), as well as (iv) data from all batches in 2-unit intervals (15 points, m = 2) and (v) data from all batches in 3-unit intervals (10 points, m = 3). The observation batches are depicted in Figure 2, and the corresponding numerical results of the Gibbs sampler algorithm (Algorithm 1 in Section 2) are summarized in Table 1. For comparison, we have also provided the results of the same data analysis performed using the Gibbs sampler with nested MH, as described in Boys and others (2008) and implemented in their “StochInf” software. In both cases, the values are based on the 5000 steps of the Gibbs samplers after 1000 burn-in period, with the samplers convergence assessed via the usual Gelman–Rubin statistic (Gelman and Rubin, 1992). The noninformative proper priors (a_s = 0.1 and b_s = 0.1) were used for all θs, in which case the posterior means of the marginals approximately coincided with the MLEs. Note that the posterior marginal gamma distributions of θ could be estimated, after the usual thinning procedure (cf., e.g. O'Neill, 2002), by the sample from the converged Gibbs sampler. The examples of such estimates with some further discussions are presented in Section C of the supplementary material available at Biostatistics online.

Table 1.

Posterior means (standard deviations) of the SIRS model parameters with M = 25 for the uniformization Gibbs sampler (U) and the Gibbs sampler with nested MH for different data collection scenarios and interval lengths (m)

	Sampler type
First 10 points (m = 1)	U	0.0133 (0.0053)	0.1405 (0.0807)	0.0135 (0.0427)
	MH	0.0113 (0.0046)	0.1135 (0.0653)	0.0007 (0.0066)
First 20 points (m = 1)	U	0.018 (0.0039)	0.1443 (0.0415)	0.0662 (0.0379)
	MH	0.0179 (0.0037)	0.1388 (0.0403)	0.061 (0.0364)
All 30 points (m = 1)	U	0.0197 (0.0039)	0.1902 (0.0392)	0.1059 (0.0322)
	MH	0.0199 (0.0039)	0.1885 (0.0394)	0.1059 (0.0318)
Sparse 10 points (m = 3)	U	0.0178 (0.0041)	0.1762 (0.0433)	0.112 (0.0355)
	MH	0.0562 (0.0134)	0.546 (0.1362)	0.3424 (0.1129)
Sparse 15 points (m = 2)	U	0.0197 (0.0043)	0.1863 (0.0426)	0.1119 (0.0354)
	MH	0.04 (0.0088)	0.3698 (0.085)	0.2364 (0.0695)
True values		0.02	0.2	0.1

The numerical values of the estimates for both Gibbs samplers in each data scenario are listed in the 3 last columns of Table 1. As we may readily see, increasing the number of samples and the trajectory length T generally decreases biases and standard errors of the Bayesian estimates, suggesting the consistency of both sampler algorithms when using the sufficiently dense regular grid over large T. However, we also note the significant downward bias in the posterior mean estimates based on the data from the first batch only. This behavior illustrates the problem of possible temporal bias caused by a too short sampling interval, a phenomenon not uncommon in longitudinal analysis with dependent data (Andersson and Britton, 2000b). As to comparing the 2 samplers' performance, note that whereas for the dense grid scenarios (m = 1), both seem to produce very similar results, the slower convergence of the MHA-based Gibbs sampler is clearly visible for sparse data (m = 2,3), where a much larger number of hidden reactions needs to be sampled in-between observations. More details on this convergence rate comparison, along with further examples, are provided in Section C of the supplementary material available at Biostatistics online.

4.2. Analysis of data from H1N1 pandemic

In order to illustrate the method in a more realistic setting, we have also analyzed data from the recent influenza A/H1N1 pandemic. For the benefit of the journal readership, we briefly recall some basic facts. Influenza A/H1N1 virus is a subtype of influenza “A” virus, and in 2009 was the most common worldwide cause of human influenza (flu). In April 2009, an outbreak of influenza-like illness occurred in Mexico, and the US CDC reported several cases of novel A/H1N1 influenza, dubbed the “swine flu” by the media, in the southwestern United States. By April 24, 2009, it became clear that the outbreak in Mexico and the confirmed cases of influenza A in the southwestern United States were related (Lipsitch and others, 2009) and caused by a novel A/H1N1 influenza strain, at which time a national-level daily monitoring of A/H1N1 cases was undertaken. The disease was seen to spread very rapidly, with the number of confirmed cases in the United States rising from 20 on April 26 to 4298 on May 14 (Garske and others, 2009).

In view of the great interest in modeling spread of H1N1, in addition to analyzing the synthetic data from the SIRS model (1.1), we have also applied our inferential method to a simplified stochastic model of A/H1N1 influenza early pandemic, using the data collected by the CDC and available through the resources on their website http://www.cdc.gov/h1n1flu/. The specific data set we have used consists of daily counts of confirmed new A/H1N1 influenza cases in the US population, dating from April 26, 2009 until May 14, 2009, at which date the nationwide tracking of individual influenza cases was suspended. The data set is presented for reference in Table 2.

Table 2.

Daily counts of the confirmed number of H1N1 cases in the continental United States from April 26, 2009 until May 14, 2009

Day	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
Count	20	40	64	91	109	141	160	226	279	403	642	896	1639	2254	2532	2600	3009	3352	4298

Due to a large number of susceptibles at the early stages of H1N1, the simplified (local) SIRS model may be used as an approximation of the epidemic data presented in Table 2. This simplified model assumes that the susceptible population is approximately constant as compared to infectives, that is the increase in the number of infections (and removals) does not, in any meaningful way, change the number of susceptibles in the population. Whereas the actual counts of infectives are unknown, the daily data in Table 2 may be considered as the counts of “symptomatic” infectives. The simplified SIRS model considers therefore the interactions between 2 infective species types: the “latent” (active) and the “symptomatic” (quarantined). Comparing with (1.2), the former plays the role of an “infective” (Y) and the latter is the surrogate for a “removed” (Z). Denoting thus for simplicity, these species by Y,Z, respectively, the model then becomes

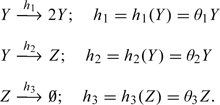(4.1)

Assuming that the process which generated the count data in Table 2 may be approximated by the above SKN, the inferential problem for θ = (θ₁,θ₂,θ₃) is seen as the partially observed species problem (Section 3.2) amenable to the analysis via Algorithm 1 of Section 2, with the unobserved {X^u(t_i) = Y_i}_{i = 1}¹⁹ values imputed via BOP (Algorithm 2 of Section 3). Note that θ₂ may be now interpreted as the rate of H1N1 latency (the serial interval), and θ₃ as the rate of recovery. The basic reproduction number (or the epidemic threshold, see Section 1) is in this case R₀ = θ₁/θ₂.

In our analysis, we first preprocessed the data in Table 2 via local

“exponential smoothing,” rounding to the nearest integer values. We then assumed that such preprocessed data were approximately free of miscounts. For better numerical stability in calculating the generator matrix Q (see, Section 3), we also found it convenient to rescale the time unit so as to have a priori θ₃∼Γ(16,16), that is to assume that the prior recovery rate follows gamma distribution with unit mean and standard deviation of 1/4. This simplification allowed us to express the remaining parameters in relation to the average a priori recovery rate from the A/H1N1 virus (which is assumed to be known).

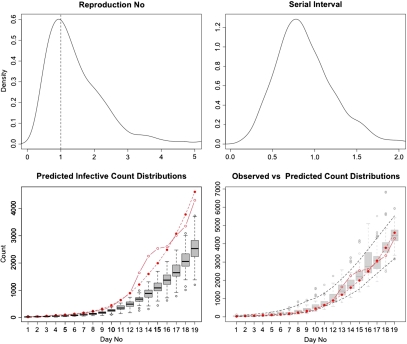
As in the previous example, the data analysis was performed based on 5000 iterations of the Gibbs sampler (excluding the 1000 iterations burn-in period), with the posterior values of the estimates found as independent gamma variates with means and standard deviations SD(θ) = (1.97,1.29,0.36). The results of the analysis based on the posterior distributions are presented in Figure 3. The 2 top panels show the posterior distributions of the reproduction number R₀ = θ₁/θ₂ (left) as well as the recovery rate θ₃ (right). The 2 bottom panels summarize the cross-sectional and the longitudinal stochastic trajectory analysis. The bottom-left panel presents the posterior daily cross-sectional distributions of the “latent” infectives, as obtained from Algorithm 2, overlaid with the raw and the smoothed “symptomatic” infective counts {Z_i} presented as solid-dot and dash-dot lines. The bottom-right panel presents the goodness of fit analysis, comparing the raw-observed and the smoothed-observed counts of “symptomatic” infectives with their cross-sectional distributions obtained by simulating the posterior model (4.1). The longitudinal, model predicted 95% credibility envelopes are also drawn. As we may readily see, the model seems to fit reasonably well, showing good agreement between the observed data (marked by the dots) and the prediction 95% credibility envelopes (marked by the dashed lines). We note that, as expected (see, e.g Balcan and others 2009), with the increase in the number of infectives, the uncertainty in the model prediction of the absolute species counts also increases. It is important to note that the analysis presented here is very different from simply fitting the exponential curve to data in Table 2, in which case, in general, neither the counts of cross-sectional distributions nor the credibility bounds or probability of the disease persistence would be available. From our analysis, it follows in particular (see the top-left panel distribution of reproductive number) that there was about 30% chance of the epidemic dying out in its early stages (as represented by the density mass left of the vertical line drawn at one).

Fig. 3.

Results of the H1N1 model analysis. Top panel left: the posterior distribution of the reproduction number R₀ = θ₁/θ₂. Top panel right: the posterior distribution of θ₃ or the rate of conversion from “latent” to “symptomatic” infectives (the serial interval). Bottom panel left: model predicted posterior cross-sectional distributions of the time-specific counts of “latent” infectives (bar plots) along with observed and smoothed counts (bullets) of H1N1 cases in the continental United States during the onset of the epidemic. Bottom panel right: goodness of fit analysis. The comparison of the observed data with the model predicted 95% posterior credibility bounds (dashed lines) along with the cross-sectional distributions of the observed counts generated from the model with estimated parameters.

5. SUMMARY AND CONCLUSIONS

Stochastic epidemic modeling techniques are increasingly relevant in epidemiology due to their potential for more accurate predictions of epidemic trends, as illustrated here with the H1N1 data. The need for developing reliable and efficient statistical methods for data fitting in such cases is very obvious, and a current paper makes a step toward addressing it. Historically, infectious disease spread through population has been modeled using the deterministic dynamics of the ODEs, but such deterministic approximation may often be too simplistic, particularly in the early stages of epidemics or when studying the effects of defensive actions, like vaccinations or quarantines. The stochastic versions of the classical ODE epidemic models are appealing, but they are computationally more demanding than their deterministic counterparts and also considerably more difficult to fit to the experimental data. In this paper, we have focused on a particular class of stochastic models, referred to as the SKNs. As we have shown herein, SKNs may be used to obtain stochastic versions of the classical SIR epidemic models as well as some new ones, like, the early H1N1 epidemic. In case of the completely observed trajectory, the statistical inference for SKN's parameters is seen to be straightforward. In most cases, the complete trajectory is not available however, and the missing data need to be reconstructed given the available information, typically via the familiar Gibbs sampler procedures. Whereas the Gibbs sampler methods were applied to this problem before, in most circumstances they had to resort to techniques unreliable in data-poor settings, like the Metropolis–Hastings-within-Gibbs sampler. As we have illustrated, if at least some longitudinal data from the model variables are available, the so-called uniformization method may be applied instead, in order to obtain the correct samples of the hidden trajectories (i.e. the unobserved states of the process). The resulting sampling method, conditionally on the parameters, uses no MCMC approximation. This allows one to build a very efficient Gibbs sampler, which produces reliable rate estimates, even for systems with relatively large stochastic noise (e.g. small population epidemics). Moreover, as also illustrated, the uniformization-based approach naturally and efficiently incorporates the Bellman dynamical optimization principle into the sampling algorithm, which makes it also applicable to data with only partially observed species.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

The research was partially supported by the US National Science Foundation under grants DMS-0840695 and DMS-0941113 and US National Institutes of Health under grant R01-DE19243.