Spatial organization of the extracellular matrix regulates cell–cell junction positioning

Abstract

The organization of cells into epithelium depends on cell interaction with both the extracellular matrix (ECM) and adjacent cells. The role of cell–cell adhesion in the regulation of epithelial topology is well-described. ECM is better known to promote cell migration and provide a structural scaffold for cell anchoring, but its contribution to multicellular morphogenesis is less well-understood. We developed a minimal model system to investigate how ECM affects the spatial organization of intercellular junctions. Fibronectin micropatterns were used to constrain the location of cell–ECM adhesion. We found that ECM affects the degree of stability of intercellular junction positioning and the magnitude of intra- and intercellular forces. Intercellular junctions were permanently displaced, and experienced large perpendicular tensional forces as long as they were positioned close to ECM. They remained stable solely in regions deprived of ECM, where they were submitted to lower tensional forces. The heterogeneity of the spatial organization of ECM induced anisotropic distribution of mechanical constraints in cells, which seemed to adapt their position to minimize both intra- and intercellular forces. These results uncover a morphogenetic role for ECM in the mechanical regulation of cells and intercellular junction positioning.

Epithelial sheets lie on a layer of extracellular matrix (ECM), the so-called basement membrane. In such epithelia, cells establish integrin-based adhesions on the basal part of the cell in contact with ECM, and cadherin-based intercellular adhesions on the apical part of contacting lateral domains, away from contact with ECM. The two adhesion systems display nonoverlapping spatial distributions. Both cell–cell and cell–ECM adhesions are required to establish proper epithelium morphology (1). They both participate in mechano-transduction of external physical cues into intracellular signaling (2). The biochemical nature of adhesion molecules engaged in intercellular adhesion, the energy of the interaction, as well as the mechanical tension developed along intercellular junctions have been shown to govern epithelial cell shape and orient intercellular junctions in various systems (3–6). However, whereas the contribution of cell–cell adhesion to epithelial topology has been the focus of many studies, much less attention has been paid to the role of ECM. ECM is a dynamic scaffold that is actively remodeled during morphogenesis, where it plays major roles in stimulating and guiding cell migration as well as orienting stem cell fate (7, 8). ECM is also known to impart morphoregulatory signals to epithelia, and thereby regulates tissue morphogenesis (8, 9). However, the mechanism by which ECM guides cell positioning at the single-cell scale is still not known. ECM geometry has been shown to regulate intracellular architecture (10) and provide spatial information for cell polarization (1, 11, 12), but how it regulates cell positioning and thereby spatially organizes multicellular architectures remained to be investigated.

Results

Intercellular Junctions Are Stabilized in Regions Deprived of ECM.

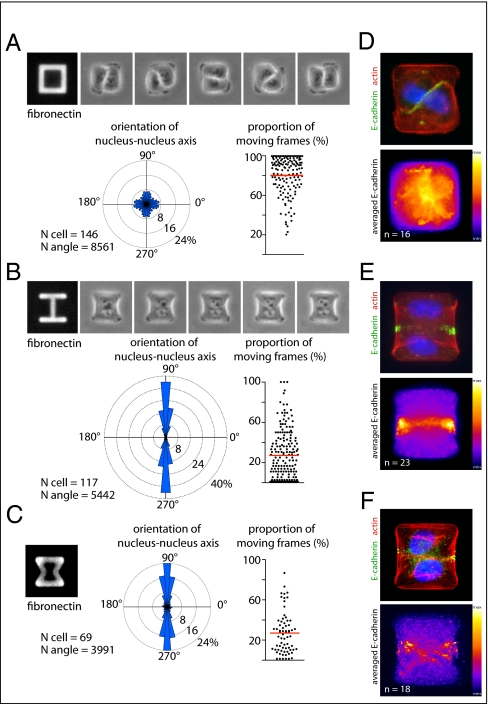
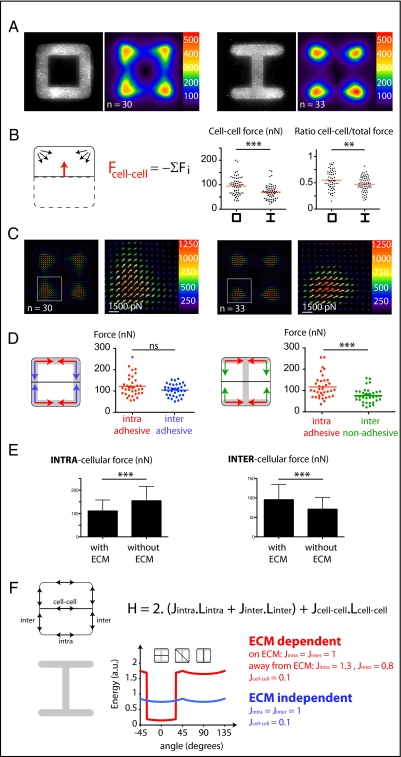
The effect of the spatial distribution of ECM on the localization of MCF10A intercellular junctions was investigated by controlling the location of ECM with fibronectin micropatterns (13, 14) (SI Methods). To provide a maximum degree of freedom to the intercellular junction and to minimize the number of parameters participating in its positioning, we focused our analysis on cell doublets, formed by daughter cells after mitosis. The positioning of cells, as revealed by the spatial coordinates of their nucleus, was recorded by time-lapse microscopy during a complete cell cycle and automatically quantified (Fig. S1, Movie S1, and SI Methods). We measured the angular distribution of the nucleus–nucleus axis as well as the proportion of time during which cells were moving. As expected from previous work (15), cells were almost randomly positioned and turned steadily around each other on [square]-shaped micropatterns (Fig. 1A and Movie S2). Under such conditions, ECM is present all along the contour of the cell doublet and provides a continuous peripheral track for cell movement. Because in epithelia, cadherins tend to flow from the ECM-rich basal pole to the ECM-free apical pole (16), we tested whether the absence of ECM could stabilize the intercellular junction and interfere with cell movement. [H]-shaped micropatterns were designed to provide two large regions devoid of ECM. In striking contrast to their behavior on [square], a large proportion of cell doublets on [H] did not move at all, resulting in highly stable configurations in which cells were positioned on each side of the gap (Fig. 1B and Movie S3). We further tested whether the nuclear axis was perpendicular to the intercellular junction by staining E-cadherin on fixed cells. We confirmed that the intercellular junctions were positioned over the gap where ECM was absent (Fig. 1 D and E).

Fig. 1.

The cell–cell junction is stabilized in regions deprived of ECM. (A–C) Time-lapse acquisition in phase contrast of an MCF10A cell doublet on a [square]- (A) or [H]-shaped micropattern (B). Time frame is 15 min. Automated movie analysis of Hoechst-stained cells (Fig. S1) provided the angular distribution of the nucleus–nucleus axis orientation and quantification of cell-doublet movements on [square]- (A), [H]- (B), and [hourglass]-shaped micropatterns (C). (D–F) Examples of immunofluorescent stainings of E-cadherin on cell doublets (Upper) and averaged staining over several images (Lower) on [square] (A), [H] (B), and [hourglass] (C). Micropattern width is 35 μm.

On [H], the absence of ECM was probably not the only factor contributing to cell-doublet stabilization. The presence of the large gap and the absence of a continuous peripheral track along the cell-doublet contour may also have physically separated cells and prevented cell movement. [Hourglass]-shaped micropatterns were designed to provide both a continuous peripheral track for cell movement and two regions along the cell-doublet contour in which ECM was absent (Fig. 1C). Thereby we could test the specific effect of ECM on intercellular junction positioning under conditions where migration was not impaired. Analysis of both nucleus position and junction position confirmed that cell doublets tend to stabilize their positions in configurations where their intercellular junction lies above regions deprived of ECM (Fig. 1 C and F). Under these conditions, the central part of the junction lies above ECM. However, cadherins tend to concentrate at the extremity of the junction (17), where most of the intercellular force is applied (18), and we could show that it is indeed the absence of ECM at the extremity and not in the central part of the junction that stabilizes junction displacements (Fig. S2). Notably, these orientations of cell doublets did not merely result from the orientation of the mother cell division but instead implied an active repositioning mechanism of the intercellular junction in response to ECM geometry (Fig. S3).

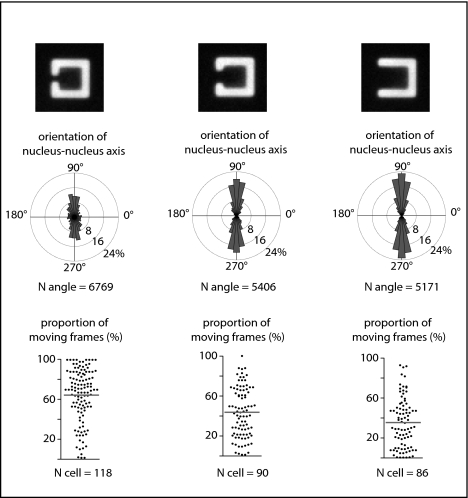
If epithelial cells actively tend to form their intercellular junction away from ECM, the geometry of ECM and the size of ECM-deprived regions should directly regulate the degree of stability of the intercellular junction positioning. We tested this hypothesis by varying the size of the gap in [C]-shaped micropatterns (Fig. 2). As the gap size increased from 7 to 20 μm, the proportion of cells with the intercellular junction positioned over the gap increased progressively, whereas the proportion of cell movement gradually decreased (Fig. 2).

Fig. 2.

The distance from ECM regulates the stability of intercellular junction position. Analyses of cell-doublet positioning from time-lapse acquisition (Fig. S1) provided angular distributions of nucleus–nucleus axis orientations as well as the distributions of the proportion of moving frames in [gapped-square] shapes with gap sizes of 7, 14, and 20 μm (from left to right). Micropattern width is 35 μm.

Intercellular Junctions Are Destabilized by the Presence of ECM.

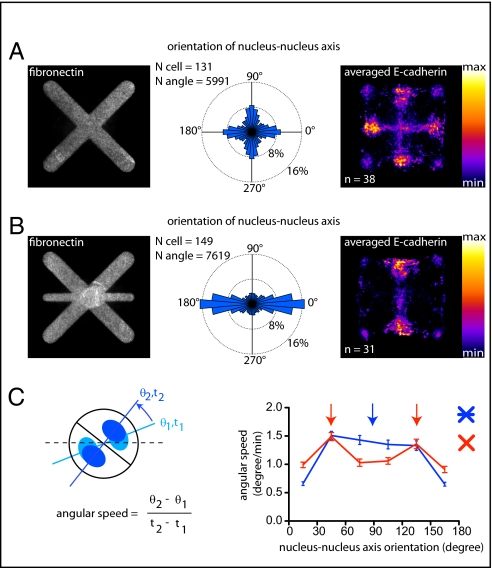
To further confirm whether ECM promotes intercellular junction displacement, we tested a complementary approach in which ECM was added along a stable intercellular junction position. To that end, we first designed a micropattern geometry in which cell doublets could adopt two stable configurations. On [cross], the intercellular junction was positioned along the midlines, either horizontally or vertically, within the two large regions devoid of ECM (Fig. 3A). Cell-doublet angular speed was high when the intercellular junction passed over ECM-rich diagonals. It slowed down when the junction passed over ECM-free midlines (Fig. 3C). When ECM was introduced along the horizontal midline, the cell–cell junction was no longer slowed down along this axis, and cell doublets could not adopt the corresponding orientation anymore (Fig. 3 B and C).

Fig. 3.

Contact with ECM destabilizes the cell–cell junction. (A and B) Analyses of cell-doublet positioning from time-lapse acquisition (Center) (Fig. S1) and averaged staining of E-cadherin over several cells (Right) on [cross]- (A) and [cross+bar]-shaped micropatterns (B). Micropattern width is 35 μm. (C) Quantification of averaged angular rotation speed of cell doublets with respect to axis orientation. Arrows indicate cell acceleration when the junction passes over ECM along diagonals on [cross] (red arrows), and along diagonals and horizontal bars on [cross+bar] (blue arrow).

From these experiments, we concluded that the proximity of cell–cell adhesion sites with ECM promotes the displacement of the intercellular junction, whereas the distance between cell adhesion sites and ECM stabilizes it.

Regulation of Tensional Forces Is Implicated in Intercellular Junction Guidance by ECM.

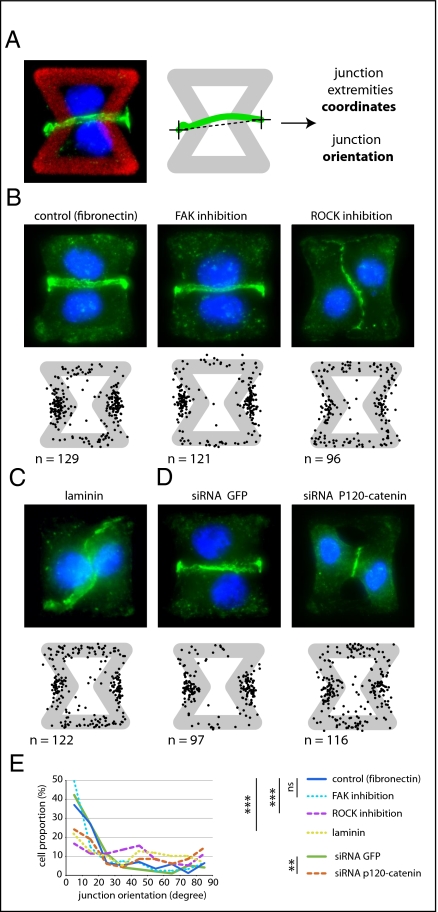
To further investigate the molecular mechanism governing intercellular junction positioning in response to ECM geometry, we inactivated some of the signaling pathways specifically associated with cell adhesion and modified the formation or maturation of cell–cell and cell–ECM adhesion constituents. We tested the effects of these treatments on cell doublets plated on the [hourglass], because this geometry guides intercellular junction positioning without impairing cell migration. We quantified the orientation of the intercellular junction and the precise positions of its extremities on fixed cells stained for α-catenin (Fig. 4A). Under control conditions, most intercellular junction extremities were positioned in the region deprived of ECM, on both sides of the narrow part of the [hourglass] (Fig. 4B and Fig. S4). This phenotype was not significantly perturbed by the inhibition of FAK, ERK, JNK, Rac, or Src, which are the main kinases conveying biochemical signaling from cell adhesions (19) (Fig. 4B and Fig. S4). However, intercellular junction position and orientation were strongly perturbed by the inactivation of cell contraction using either Rho kinase inhibition or myosin II inhibition (Fig. 4 B and E and Fig. S4). Down-regulation of focal adhesion proteins, on which traction forces are applied, impaired cell spreading and precluded the analysis of their specific contribution to intercellular junction positioning. However, cell spreading on laminin, which is known to engage a distinct subset of integrins than fibronectin (20), significantly perturbed junction positioning (Fig. 4 C and E and Fig. S4) and thereby showed that this positioning was directly regulated by the nature of the cell–ECM interactions. We then tried to perturb the assembly of junctional complexes that are able to transfer the forces applied on ECM to the adjacent cells. Down-regulation of p120-catenin by siRNA treatment is known to affect intercellular junction turnover and actin dynamics (21). It significantly perturbed junction positioning (Fig. 4 D and E and Fig. S4). These results suggested that the production of mechanical forces on intercellular junctions was responsible for junction positioning away from ECM.

Fig. 4.

Cell contractility regulates intercellular junction positioning. (A) Immunostaining of α-catenin on cell doublets plated on [hourglass] (Left) (α-catenin in green, DNA in blue) allowed the detection and measurement of intercellular junction positions (Right). (B–D) The positions of junction extremities (black dots) were measured on cells treated for 6 h with PF-573228 (1 μM) to inactivate FAK or Y27632 (5 μM) to inactivate ROCK (B), cells plated on laminin-coated micropatterns (C), or cells pretransfected with siRNA against GFP or p120-catenin (D). Images are examples of treated cells (α-catenin in green, DNA in blue). More representative stainings are shown in Fig. S4. Micropattern width is 35 μm. (E) Curves indicate the proportion of junctions for each angular sector with the same set of data as in B and C. Differences between the two curves were compared using the Kolmogorov–Smirnov test; **, 0.5% and ***, 0.1% error probability in the rejection of the hypothesis that the two distributions are identical; ns indicates that the probability would be higher than 5%.

Intercellular Tension Is Reduced in Regions Deprived of ECM.

To measure intercellular tensional forces, we grafted ECM micropatterns on soft polyacrylamide gels (22) (SI Methods). Deformations of polyacrylamide gels were used to measure the forces exerted by cell doublets on the substrate (23–25) (Fig. 5A) and indirectly derive the forces they exert on each other (26) (SI Methods). The analysis of force balance in cell doublets on [square] and [H] revealed that intercellular forces were significantly reduced when intercellular junction extremities lay above ECM gaps (Fig. 5B). Because intercellular tension reduction on [H] could result from a decrease in global traction force rather than a specific decrease of the intercellular force, we calculated the ratio between the intercellular force and the total traction force. Like the intercellular force, this ratio was lower when the junction was stabilized over ECM gaps (Fig. 5B). To further explain how large traction forces on sites flanking ECM gaps could be associated with reduced levels of intercellular forces over such gaps, we analyzed force orientations depending on the presence or absence of ECM at the extremities of the junction (Fig. 5 C and D). Traction forces at cell apices were decomposed into a component perpendicular to the junction, considered as contributing mainly to intercellular forces, and a component parallel to the junction, considered as contributing mainly to intracellular forces (Fig. 5D). This component of the traction perpendicular to the junction was a good approximation of the global cell–cell force (Fig. S5). On [square], intercellular forces along ECM-rich edges were equivalent to intracellular forces. However, on [H], intercellular forces along ECM-free edges were almost half the strength of intracellular forces (Fig. 5D). We further compared the intra- and intercellular forces on various micropattern shapes (Fig. S6) and found that the presence of ECM had an opposite effect on each: It reduced intracellular forces but increased intercellular forces (Fig. 5E).

Fig. 5.

Junction positioning away from ECM is associated with relaxation of intercellular forces. (A) Fibronectin micropatterns with [square] and [H] shapes on polyacrylamide gels and traction maps, averaged over several cells, on the corresponding geometries. The color code indicates the local traction in Pascal. (B) Cell–cell force measurement. The mechanical balance in each cell imposes that the force exerted between cells counterbalances the sum of traction forces exerted on the substrate. Cell–cell force was measured and compared between cells plated on [square] and [H]. Each dot corresponds to a measure on a single cell. The ratio between the intercellular force and the total traction force (sum of all force magnitude over the micropattern) was calculated and plotted to confirm the specific reduction of cell–cell forces on [H]. (C) Traction force fields averaged over several cells plated on [square] (Left) and [H] (Right). Magnifications correspond to the white square regions on global maps. Arrows indicate force orientation; color and length both represent local force magnitude in pN. (D) Decomposition of traction forces into “intra” forces oriented toward intracellular space and “inter” forces oriented toward the intercellular junction. These forces were noted “adhesive” or “nonadhesive” whether they were oriented along a cell edge in contact or not with ECM. The absence of ECM is associated with relaxed intercellular forces. (E) Force measurements along cell edges on various micropattern shapes ([square], [X], and [H]; Fig. S6) were combined depending on their orientation (intra or inter) and the presence of ECM along their length (with or without ECM). These graphs represent three separate experiments and 100 cells per condition. The presence of ECM showed opposite effects on intra- and intercellular tension. All statistical comparisons were Student's t tests, **P < 0.01, ***P < 0.001, ns, P > 0.05 (F) Physical modeling. The various orientations of the intercellular junction can be described by a simple energy function H taking into account the length L and the tension J along all edges of the cell doublets. The two curves correspond to numerical simulations of the energy function for various junction orientations when the tension depends (red) or not (blue) on the local presence of ECM. A favored orientation (junction orientation at 0°), corresponding to experimental observations, only occurs when tension depends on ECM.

Overall Tension Minimization Accounts for Cell Positioning.

To test whether the regulation of intra- and intercellular forces in response to the presence of ECM could account for the favored cell positioning we observed, we performed numerical simulations to take into account all cortical forces and compare the energetic costs of all cell positions. We used a well-established physical model of the energy associated with the development of cortical forces (4, 27) and applied it to the simplified case of cells having a fixed area (28) (Fig. 5F and SI Methods). Numerical simulations showed that when tension was considered to be independent of the presence of ECM, all cell orientations had approximately the same energetic cost. However, when we incorporated into the model the relative differences of tension we measured in response to the presence of ECM, the tension along cell edges became anisotropic, and the configurations associated with the lower total energy actually corresponded to those we observed experimentally (Fig. 5F and Fig. S7). This suggested that cell positioning could actually result from minimization of global tension in response to ECM geometry.

Discussion

Here we described the development of an experimental system to study multicellular morphogenesis. Although this system partly lacks some of the physiological characteristics found in situ in animal systems (3) and in vitro in 3D cyst formation (29, 30), it offers the possibility of quantifying cell movement and accurately measuring the spatial distribution of forces in a large number of reproducible assays. In addition, the fine manipulation of ECM geometry allows precise control of the degree of freedom for cell movements. Thus, although spatially confined, multiple cells can reveal their natural self-assembly process.

ECM has been shown to guide tissue morphogenesis by modulating cell–cell interactions (31, 32). The biochemical, structural, and mechanical interactions between cell–ECM and cell–cell adhesions have been well-characterized (2, 33, 34). However, how these interactions translate into spatial organization of multicellular arrangements remained to be clarified. Our results suggest that intercellular junction positioning away from ECM did not result from the action of a single ECM signal. Indeed, most of the main signaling pathways associated with cell–ECM adhesion could be impaired individually without affecting junction position, at least in the range of inhibitor concentration and the time window we tested. Neither did it result from oriented cell divisions. Instead, it appeared to stem from ECM-regulated production of intra- and intercellular forces and overall minimization of global tension.

We found that the contact of intercellular junctions with ECM caused the displacement of the cell–cell junction and the production of large perpendicular tensional forces and constant motion of the cells. In support of these findings, work from others has shown that cell adhesion to ECM alters cell–cell adhesion and promotes the development of large tensional forces responsible for junction disruption and subsequent cell migration (35, 36). In addition, we found that when cells place their intercellular junction on ECM-deprived regions, intra- and intercellular tension gets reduced and cell position is stabilized (Fig. 6). How cell interaction with ECM regulates inter- and intracellular forces in an opposed way remains to be elucidated. We suspect this involves complex interplays between the growth and dynamics of several types of actin-based structures formed in proximity to cell–ECM and cell–cell contacts.

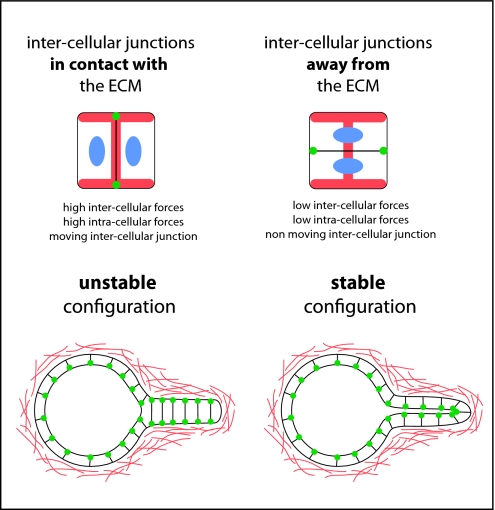
Fig. 6.

Summary and illustration. On micropatterns, cells develop elevated intra- and intercellular tension when the intercellular junction is in contact with ECM (Left) and reduced tension when it is far from ECM (Right). In situ, as shown here in the case of tubulogenesis, this mechanism would promote the relocalization of junctions away from ECM and the formation of multilayered structures of opposed polarities. ECM is shown in red, intercellular junction complexes are in green, and nuclei are in blue.

Anisotropic distribution of forces along the cell periphery has been shown to regulate cell shape, junction remodeling, and cell spatial repositioning within tissues (3). Our results suggest that ECM could participate in similar morphogenetic processes. In response to heterogeneous distribution of ECM, cell doublets developed anisotropic force fields and adopted stable positions along the axis of low tension. According to this mechanism, cells tend to stabilize the position of their intercellular junctions away from ECM. This could account for many important processes during epithelium morphogenesis (Fig. 6). For example, during tubulogenesis, cells first form a single-file chain of cells. This stage, during which cell–cell junctions are close to ECM, is only transient. Cells reorganize and move their junctions away from ECM to form a multilayered cord with a central lumen (30, 37). During this transformation, intracellular forces that were developed across the ECM gap get relocalized along ECM fibers, whereas intercellular forces undergo the opposite reorientation. According to the mechanism we describe, this transformation would be favored by the relaxation of both intra- and intercellular tensions (Fig. 6).

Although much attention has been paid to the role of cell–cell interaction in the shaping of epithelia, our results suggest that we should also consider the organizing role of ECM, which, far from being a mere supporting scaffold, plays an instructive role in regulating mechanical forces and orienting multicellular assembly.

Methods

Cell Culture.

The culture of mammary epithelial cells MCF10A was described previously (38). Cells were seeded on patterned substrates at a density of 8 × 10⁴/cm². Cells not attaching to the adhesive region on the substrate were washed away 1 h after seeding. After cell spreading on micropatterns, Hoechst 33342 was added at 5 ng/mL to label the nucleus during time-lapse acquisition.

Chemical Inhibitors.

Chemical inhibitors were added 24 h after cell plating on micropatterns at the following concentrations: PF573228, 1 μM (FAK inhibition); PD98059, 2 μM (ERK1 inhibition); SP600125, 1.8 μM (JNK inhibition); SU6656, 5 μM (Src inhibition); NCS23766, 5 μM (Rac inhibition); Y27632, 5 μM (ROCK inhibition); blebbistatin, 15 μM (myosin II inactivation); ML7, 5 μM (MLCK inhibition). Cells were fixed 6 h later.

Micropatterning.

Glass coverslip micropatterning has been described elsewhere (14). Micropatterned polyacrylamide gels were made as previously described (22) (SI Methods).

Immunofluorescent Staining.

Thirty hours after plating cells on a micropatterned coverslip, cells were either extracted in cytoskeleton buffer containing 0.5% Triton X-100 and fixed in 4% paraformaldehyde or fixed in methanol at −20 °C. Fixed cells were incubated with a 1:200 dilution of anti-α-catenin (B52975; Calbiochem) or a 1:50 dilution of anti-E-cadherin (sc8426; Santa Cruz Biotechnology) for 1 h, and then incubated with corresponding secondary antibodies and FITC-phalloidin (Invitrogen) at 1 μg/mL for 30 min.

Traction Force Microscopy.

Images of fluorescent beads with and without cell doublets were first aligned to correct experimental drift using the ImageJ plugin “align slices in stack.” The displacement field was subsequently calculated by a custom-written particle image velocimetry (PIV) program implemented as an ImageJ (http://rsb.info.nih.gov/ij) plugin. The PIV was performed through an iterative scheme. In each iteration, the displacement was calculated by the normalized correlation coefficient algorithm, so that an individual interrogation window was compared with a larger searching window. The next iteration takes into account the displacement field measured previously, so that a false correlation peak due to insufficient image features is avoided. The normalized cross-correlation also allowed us to define an arbitrary threshold to filter out low correlation values due to insufficient beads presented in the window. The resulting final grid size for the displacement field was 1.63 × 1.63 μm, with six beads per interrogation window on average. The erroneous displacement vectors due to insufficient beads present in the window were filtered out by their low correlation value and replaced by the median value from the neighboring vectors.

With the displacement field obtained from the PIV analysis, the traction force field was reconstructed by the Fourier transform traction cytometry (FTTC) method with regularized scheme (25) on the same grid (1.63 × 1.63 μm) without further interpolation or remapping. The regularization parameter was set at 9 × 10⁻¹⁰ for all traction force reconstructions. The FTTC code was also written in Java as an ImageJ plugin, so that the whole traction force microscopy procedure from PIV to force calculation could be performed with ImageJ. The entire package of traction force microscopy software is available at https://sites.google.com/site/qingzongtseng/tfm.