Evolution of functional specialization and division of labor

Abstract

Division of labor among functionally specialized modules occurs at all levels of biological organization in both animals and plants. Well-known examples include the evolution of specialized enzymes after gene duplication, the evolution of specialized cell types, limb diversification in arthropods, and the evolution of specialized colony members in many taxa of marine invertebrates and social insects. Here, we identify conditions favoring the evolution of division of labor by means of a general mathematical model. Our starting point is the assumption that modules contribute to two different biological tasks and that the potential of modules to contribute to these tasks is traded off. Our results are phrased in terms of properties of performance functions that map the phenotype of modules to measures of performance. We show that division of labor is favored by three factors: positional effects that predispose modules for one of the tasks, accelerating performance functions, and synergistic interactions between modules. If modules can be lost or damaged, selection for robustness can counteract selection for functional specialization. To illustrate our theory we apply it to the evolution of specialized enzymes coded by duplicated genes.

All organisms face different tasks during their life, like the acquisition of food, locomotion, reproduction and repair, to name a few. In organisms with a modular structure often different tasks are executed by specific modules that are specialized for their task, a phenomenon we call division of labor or functional specialization. Division of labor can be found at all levels of biological organization. For instance, for many genes it is believed that they originated from a duplication event (1, 2). If the original gene coded for an unspecific enzyme while some time after duplication each copy of the gene codes for a more specific enzyme, division of labor has evolved. Another example is the evolution of novel cell types that goes hand in hand with division of labor (3–6). A particular well-studied instance of division of labor at the cellular level is the transition from undifferentiated multicellular organisms to organisms with germ–soma differentiation in the green algae volvocaceae (7, 8). Another example of cell differentiation, this time from multicellular cyanobacteria, is the differentiation into carbon-fixating vegetative cells and nitrogen-fixating heterocysts (9, 10). There is also the suggestion that division of labor is a common feature in bacterial populations (11). At higher levels of organization, division of labor can be found in teeth (12) and arthropod limbs (13). Also some instances of left–right asymmetry (14) in bilateral organisms such as asymmetric chelipeds in fiddler craps can be classified as division of labor. Division of labor can also be found in colonial organisms. It is present in eusocial insects (15–18) and many groups of aquatic invertebrates, e.g., in colonial cnidaria (19–22) and bryozoa and thaliacea (23). Another intriguing example for division of labor is heteranthery in plants where some species with nectarless flowers produce two types of anthers: feeding anthers and pollination anthers (24, 25). The evolution of division of labor has also been linked to major transitions in evolution (26) and it is this aspect of division of labor that has received the lion's share of attention by theoreticians (15, 27–35). These transitions are the change from unicellular to multicellular organization with germ–soma differentiation and the emergence of group living. Central to both these transitions and accordingly to the accompanying modeling effort is the potential for genetic conflict and cheating (36).

For each level of organization also examples can be found where functional specialization is not pronounced or even absent. In these cases modules are involved in several tasks and show characteristics that allow them to be classified as generalist modules. For instance, ant colonies typically have to execute between 20 and 40 different tasks, depending on the size of the colony. However, of 263 ant genera only 20% consist of morphologically differentiated worker castes (15). The highest number of such physical castes is three, which is realized in only three genera. In addition to physical castes, ants (and many social bees and wasps) go through ontogenetic stages in which individuals fulfill different tasks, but the total number of temporal and physical castes rarely seems to exceed six (15). Similarly, it has been noted that polymorphisms are conspicuously absent from some taxa of colonial marine invertebrates (23) and that limb differentiation in crustaceans consistently increased over geological time but never reached the highest possible complexity indexes (37). It is furthermore clear that many genes and cells fulfill a multitude of tasks.

This comparison of modules that either have or have not evolved functional specialization is evidence that division of labor is not an inevitable outcome of evolution, raising the question: What limits the evolution of specialized modules? Whether division of labor can evolve will at least partly depend on system-specific factors such as the availability of genetic variation and thus on developmental constraints, on possible costs for maintaining differentiated developmental pathways, and, in the case of colonial organisms, on possible conflicts between individual colony members over reproduction. In this article we propose, however, that there are also necessary conditions that have to be fulfilled for division of labor to evolve that are not system specific. More specifically, we derive conditions that constitute minimal requirements and have to be fulfilled by any system for division of labor to be favored by selection.

Our results are derived from a minimal set of assumptions that presumably are fulfilled in many biological systems: (i) Ancestral modules were identical in form and function to each other and these undifferentiated modules contributed to two tasks, (ii) fitness increases with increasing levels of performance in both tasks, and (iii) functional constraints result in a trade-off: modules that are well adapted to contribute to one task can contribute less to the other task and vice versa. We phrase our result in terms of properties of functions that map traits to functional performance. More specifically, we show that the evolution of division of labor is favored by three factors: (a) positional effects (the contribution of different modules to the different tasks depends on their position within the organism), (b) accelerating performance functions, and (c) synergistic interactions between modules. Furthermore, we show that selection for functional robustness can counteract selection for division of labor. Although our framework is very general and not geared toward any specific system, concrete predictions can be generated when the relevant functions are derived from mechanistic considerations in a specific system. This point is illustrated by applying our framework to the evolution of specialized enzymes coded by duplicated genes.

Model and Results

We consider an organism that contains n different modules at some level of its organization that contribute to two tasks. For example, in many arthropods iterated body segments carry appendages that are involved in multiple functions such as foraging and locomotion (13, 37) or walking and burst swimming (38). Another example fitting within our framework, and one that we explore in some depth later, is pairs of duplicated genes coding for bifunctional gene products.

We assume that performance in both tasks is connected by a trade-off; i.e., the performance of a given module cannot be maximized for both tasks simultaneously. With n modules, evolution is then naturally constrained to move on an n-dimensional trade-off manifold. To see this, assume first that phenotypic variation occurs only at a single module (all other modules are fixed at a particular phenotype). We can map all states (genotypes) of this module to a 2D space by assigning them performance values for each task. Due to the trade-off, adaptive evolution in this module will reach a state where a further increase in the performance for one task can be achieved only at the cost of a reduced performance in the other task. The set of states with this property forms a one-dimensional boundary in the 2D space of performances. This boundary is often referred to as trade-off curve (39). Once it is reached, any further (nondeleterious) evolutionary change can occur only along this curve. For a single variable module, we can parameterize the position on the trade-off curve by a scalar θ. For n variable modules, the corresponding trade-off manifold can be parameterized by an n-dimensional vector (θ₁, … , θ_n), where θ_i corresponds to variation in the ith module. From now on, we refer to θ_i as the trait value of the ith module. Because different parameterizations correspond to different scalings of the underlying traits, results do not depend on the chosen parameterization. In Application: Specialization of Duplicated Genes we give an explicit example of such a parameterization.

In our model we can distinguish assumptions affecting the phenotype and assumptions affecting fitness. These are now described in turn. Performance in the two tasks, measured at the level of the whole individual, is denoted by F₁ and F₂ or, stressing the dependence of performance on the traits, by F₁(θ₁, … , θ_n) and F₂(θ₁, … , θ_n). The assumption that evolution is constrained by trade-offs implies

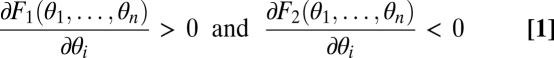for i ∈ {1, … , n}, where the choice that F₁ is increasing in its arguments while F₂ is decreasing in its arguments is made without loss of generality. Fitness of a phenotype is denoted by ρ(F₁, F₂) or, more precisely, by ρ(F₁(θ₁, … , θ_n), F₂(θ₁, … , θ_n)). The only assumption we make with respect to fitness is that it is an increasing function of performance in both tasks:

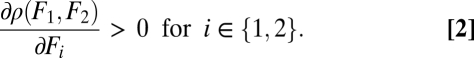Our framework is very general in the sense that we not have to choose a specific measure of fitness. In particular, our theory is independent of a change in fitness scale (sensu ref. 40).

We first derive the theory for two modules and later extend it to n modules. We envisage a scenario where, ancestrally, the two modules have identical characteristics. These phenotypes are described by vectors (θ₁, θ₂) with θ₁ = θ = θ₂. Throughout, we refer to the one-dimensional trait space defined by θ₁ = θ₂ as constrained trait space. This constrained trait space corresponds to the thick shaded curve in Fig. 1 and to the diagonal line in the contour plots of the fitness landscape shown in Fig. 2. All phenotypes characterized by (θ₁, θ₂) with θ₁ ≠ θ₂ show some degree of functional specialization. Central to our theory are values θ* that are maxima of the fitness function in the constrained trait space and hence characterized by

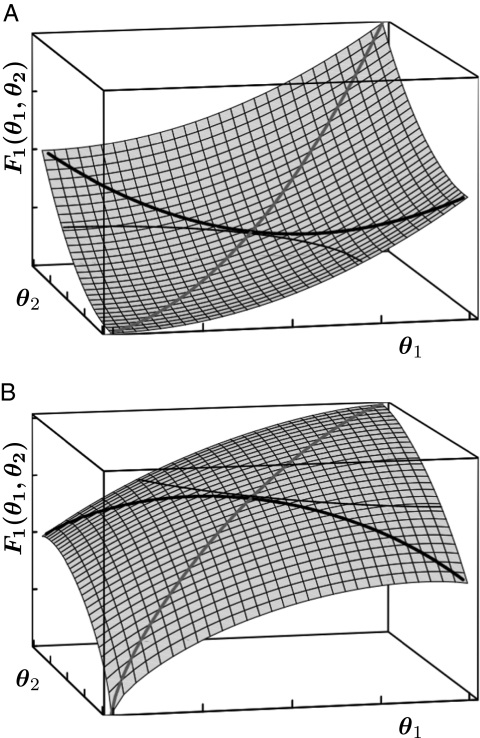
Fig. 1.

Convex (A) and concave (B) performance landscape for the first task. Performance 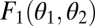, plotted on the z axis, is a monotonically increasing function of the trait values of the two modules, θ₁ and θ₂, plotted on the x and y axes, respectively. Shaded lines show performance along the constrained trait space defined by 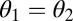. Thick solid lines show performance along a straight line orthogonal to the constrained trait space. Another possibility to visualize the curvature of performance landscapes is by means of contour lines or iso-performance curves. An iso-performance curve consists of all combinations 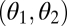that result in the same level of performance 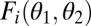. Iso-performance curves are shown as thin solid lines and are useful in Fig. 2 and Fig. S1. Importantly, for F₁ iso-performance curves are concave if and only if the thick solid line is convex (A) and convex if and only if the thick solid line is concave (B). For F₂ this relationship is reversed. Note that with nonequivalent modules it is also possible that a performance landscape is convex along one axis and concave along the other.

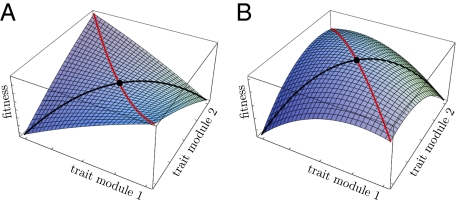
Fig. 2.

Fitness landscape for the case of two equivalent modules (A–C) and two nonequivalent modules (D–F). Contours of the fitness landscape are indicated by shading with lighter shades indicating higher fitness. Solid circles indicate the location of fitness maxima 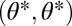in the constrained trait. The expected direction of the evolutionary dynamics is indicated by arrows. The solid and dashed curves depict iso-performance curves of the underlying performance functions F₁ and F₂, respectively, as introduced in the Fig. 1 legend. (A) Iso-performance curves are convex for F₁ and concave for F₂, indicating that functional differentiation decreases performance in both tasks. Thus, the point 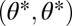is a fitness maximum. (B) Iso-performance curves are concave for F₁ and convex for F₂, indicating that functional differentiation increases performance in both tasks. Thus, the point is a saddle point of the fitness landscape. (C) Iso-performance curves are concave for both F₁ and F₂, indicating that functional differentiation increases performance for task 1 and decreases performance for task 2. In this particular example the increase in performance in task 1 is sufficiently large to outweigh the decrease in performance in task 2 such that the point is still a saddle point of the fitness landscape. For plots D, E, and F it is assumed that module 1 has an intrinsic advantage in contributing to task 2 whereas module 2 has an intrinsic advantage in contributing to task 1. Each plot in the lower row is a perturbation of the corresponding plot in the upper row. In D nonequivalence of modules moves the fitness maximum above the diagonal whereas in E and F nonequivalence moves the saddle point below the diagonal. In both cases, selection favors specialization of module 1 for task 1 and of module 2 for task 2. Note that extrema of the fitness landscape correspond to points 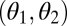where iso-performance curves for F₁ and F₂ are tangent to each other. Plots show the function 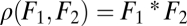with F₁ and F₂ defined in Eq. S2 in SI Text A with 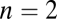and .

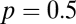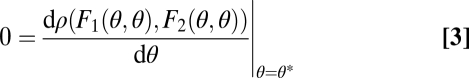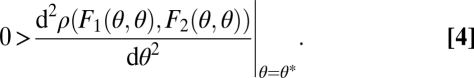Evolution of undifferentiated modules, that is, evolution in the constrained trait space, approaches such points θ*. In the unconstrained, 2D trait space this point is written as (θ*, θ*), indicated by the solid circles in Fig. 2.

The purpose of this article is to determine conditions under which functionally differentiated phenotypes (θ₁, θ₂) with θ₁ ≠ θ₂ exist that have a higher fitness than the phenotype (θ*, θ*). Whether such phenotypes can exist depends on whether functionally differentiated phenotypes perform better in the two tasks than the undifferentiated phenotype (θ*, θ*). It is therefore no surprise that our main results can be phrased largely in terms of curvature properties of the performance functions F_i(θ₁, θ₂). In the continuation of our argument we distinguish two scenarios, corresponding to equivalent and nonequivalent modules.

Equivalent Modules.

We call two modules equivalent with respect to the ith task if F_i(θ₁, θ₂) is symmetric, i.e., if F_i(θ₁, θ₂) = F_i(θ₂, θ₁). In this case the contribution of a module to a task depends only on its phenotype and not on its location within the organism, that is, not on its label 1 or 2. Examples are organisms that are rotational symmetric and transregulated duplicated genes. A consequence of equivalence is that graphs of the performance functions F₁ and F₂ and the fitness function ρ are symmetrical around the constrained trait space (i.e., mirror symmetric around the 45° line in Figs. 1 and 2 A–C). It follows that in the case of equivalent modules the point (θ*, θ*) can generically be only a fitness maximum or a minimum in the direction orthogonal to the constrained trait space (Fig. 2 A–C). In the first case, (θ*, θ*) is a fitness maximum in the unconstrained 2D trait space whereas in the second case it is a saddle point of the fitness landscape. By evaluating the Hessian matrix of the functions F₁(θ₁, θ₂) and F₂(θ₁, θ₂) in the direction of the vector (1, −1), it is now straightforward to show that the curvature of the performance landscape for the ith task in the direction orthogonal to the constrained trait space at the point (θ*, θ*) is given by

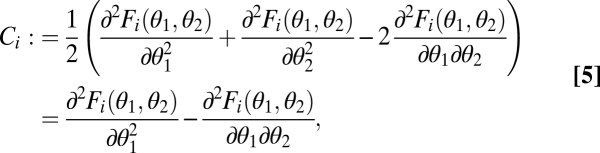where all derivatives are evaluated at the point (θ*, θ*). The simplification leading to the second equality results from the fact that for equivalent modules 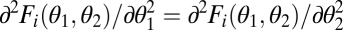. If C_i > 0, then performance of phenotypes with differentiated modules lying on the line orthogonal to the constrained trait space exceeds performance of the undifferentiated phenotype (θ*, θ*) (Fig. 1A). These phenotypes, characterized by trait vectors (θ₁, θ₂) = (θ* + Δ, θ* − Δ), are represented by the thick black line in Fig. 1. In contrast, if C_i < 0, then performance has a maximum at the point (θ*, θ*) in the direction orthogonal to the constrained trait space (Fig. 1B).

On the basis of these curvature properties we show in Appendix: Saddle Points of the Fitness Landscape that the point (θ*, θ*) is a saddle point of the fitness landscape if and only if

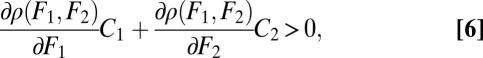where again all derivatives are evaluated at the point (θ*, θ*). Condition Eq. 6 can be phrased verbally as follows: Functional specialization is favored by natural selection if the sum of the effects of specialization on performance in the two tasks, weighted by the effect of a change in performance on fitness, is positive. Remember that by assumption Eq. 2 the weighting terms ∂ρ(F₁, F₂)/∂F_i are positive. It should be noted that if functional differentiation is favored in the case of equivalent modules, due to the symmetry no prediction can be made about which module specializes on which function (Fig. 2B).

Two cases can be distinguished under which condition Eq. 6 is fulfilled. First, if functional specialization increases performance in both tasks, thus if C₁ > 0 and C₂ > 0, then both terms on the left-hand side of condition Eq. 6 are positive (Fig. 2B). In this case functional specialization is unambiguously advantageous. Second, if functional differentiation increases performance in one task, say task 1 (C₁ > 0), while it decreases performance in task 2 (C₂ < 0), then the situation is more complicated. Condition Eq. 6 is then fulfilled if 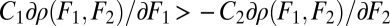, that is, if either the gain in performance due to functional specialization in task 1 is sufficiently large or a change in performance in task 1 has a large effect compared with the effect of a change in performance in task 2 (Fig. 2C).

The definition of C_i shows that for the case of equivalent modules two factors favorable for functional specialization exist:

• i) Accelerating performance functions: We say that a performance function is accelerating if the performance landscape is convex along the trait axes [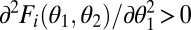; Fig. 1A] and saturating if the performance landscape is concave along the trait axes [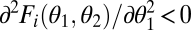; Fig. 1B]. With accelerating performance functions, the gain in performance through increased specialization of one module exceeds the loss due to decreased specialization of the other module, resulting in increased performance at the level of the whole organism.

• ii) Synergistic interactions between modules: Modules interact with each other when performance in a task cannot be expressed as the sum of their separate contributions. We say that modules interact synergistically when the joint contribution of two differentiated modules to performance exceeds the sum of their separate contributions. From Eq. 5 it is clear that this case corresponds to a negative mixed derivative 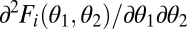. Conversely, modules interact antagonistically when the joint contribution of two differentiated modules to performance is less than the sum of their separate contributions, corresponding to a positive mixed derivative.

Nonequivalent Modules.

If the two modules are not equivalent with respect to a task, then the effect of a change in a module on performance depends on the module, for instance because of its position within the organism. An example is serial modules such as limbs in arthropods. Limbs at anterior segments are likely to have a higher contribution to food processing than limbs at more posterior segments even if limbs are not differentiated yet. Another example is teeth, where anterior ones will be more efficient at cutting than posterior ones. We refer to such asymmetries as positional effects.

If the two modules are nonequivalent with respect to the ith task, thus if 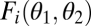is not symmetric with respect to its arguments, then the performance landscape for the ith task is not mirror symmetric with respect to the 45° line. Then, generically, also the fitness landscape lacks this mirror symmetry. As a consequence, with nonequivalent modules the point 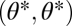is not an extremum in the extended trait space and thus neither a maximum nor a saddle point of the fitness landscape (Fig. 2 D–F). Instead, the fitness landscape is increasing in one direction along the line that passes orthogonally through the point 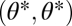and directional selection at the point 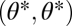favors functional specialization. More precisely, in Appendix: Saddle Points of the Fitness Landscape we show that phenotypes 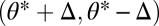, with Δ small and positive, are favored if

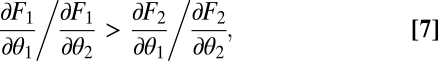where all derivatives are evaluated at the point 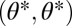, whereas phenotypes 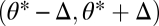are favored if inequality Eq. 7 is reversed. Thus, in contrast to the case of equivalent modules, with nonequivalent modules specialization away from the constrained trait space is possible only to one side (compare Fig. 2B with 2 D–F). Condition Eq. 7 makes intuitive sense. If the contribution of module 1 to task 1 exceeds the contribution of module 2, then the left-hand side of inequality Eq. 7 exceeds one. On the other hand, if the contribution of module 2 to task 2 exceeds the contribution of module 1, then the right-hand side of inequality Eq. 7 is less than one. In this case one expects module 1 to specialize on task 1 whereas module 2 specializes on task 2.

Importantly, with nonequivalent modules functional specialization is favored regardless of the curvature of the performance landscapes described by C_i. However, this curvature determines the degree to which functional specialization is favored. When C₁ and C₂ are negative, then nonequivalence constitutes a perturbation of a fitness landscape that has a maximum at 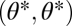. In other words, the maximum moves slightly off-diagonal (compare Fig. 2A with 2D). On the other hand, when C₁ and C₂ are positive, then nonequivalence constitutes a perturbation of a fitness landscape that has a saddle point at 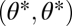. In this case, the saddle point moves slightly off-diagonal (compare Fig. 2B with 2E). In the first case, functional specialization is favored only to a limited degree whereas in the second case it is favored to a larger degree (compare Fig. 2D with 2E).

So far the starting point of our considerations was a phenotype 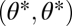that fulfills Eqs. 3 and 4, i.e., that is a maximum of the fitness function in the constrained trait space. This assumption can be justified because specialization requires the developmental decoupling of modules. Initially serially homologous modules will have high genetic correlations and thus the selection response along the constrained space is going to be much higher than the selection response orthogonal to it. In this case the population is thus expected to reach the fitness optimum of the constrained space first before selection for specialization is likely to be effective. However, in other cases, for example with duplicated genes, the decoupling is a by-product of the duplication, and independent evolution in the two modules is actually the default scenario. What are the conditions for functional specialization in this more general scenario? Whenever a phenotype 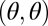is not at a maximum in the constrained trait space, phenotypes 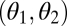exist in its neighborhood with 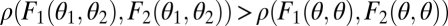. However, only in the neighborhood of a point 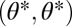that is not a maximum in the direction of the vector 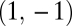(i.e., that is either a saddle point or a point that is not a critical point in the unconstrained trait space) is invasion of such mutants not merely a short excursion away from the constrained trait space but the start of functional specialization. These considerations justify the focus on points .

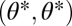Application: Specialization of Duplicated Genes

In this section, we apply our framework to a specific example: specialization of duplicated genes. This application allows us to incorporate system-specific mechanistic details in the formulation of the performance functions, which, in turn, results in some surprisingly concrete predictions. However, it should be clear that we do not aim at developing a full-fledged theory for specialization of duplicated genes but merely illustrate how our framework can be applied to concrete examples.

For a long time, the predominant hypothesis for the evolution of new function in duplicated genes was due to Ohno (1). His model, called neofunctionalization, assumes that duplication results in a redundant copy of a gene. This copy is freed from purifying selection. In most cases, mutations will deteriorate the sequence, resulting in a loss of function. Occasionally, however, mutation may result in a gene coding for a new function. This new sequence would then be under positive selection. With accumulating molecular data the importance of neofunctionalization has been questioned to the extent that some researchers believe that new functions rarely, if ever, evolve according to Ohno's model (2, 41–43). In the meantime, a suite of alternative models explaining the fixation, maintenance, and specialization of gene duplicates has been developed (see ref. 44 for a recent review). One of these alternatives, proposed by Hughes (2, 41), fits squarely within our framework but has, according to Innan and Kondrashov (44), never been explored formally. Hughes’ verbal model is based on the observation that some gene products serve two functions that cannot be independently improved (45, 46). If such a bifunctional gene becomes duplicated, the duplicate can become either lost or fixed where fixation can occur either by drift or due to positive selection because of a dosage effect. If in the unduplicated gene neither function could be improved without deteriorating the other function, each copy of the fixed duplicates can then specialize on a different function. This latter step earned this model the name escape from adaptive conflict (47). Here, we use our framework to investigate this idea more formally.

We consider a gene coding for an unspecific enzyme that binds to and converts two different substrates. The affinity of the enzyme to the different substrates is determined by structural features. Selection acts to maximize the affinities for both substrates but ultimately has to run into a constraint where an increase in affinity for one enzyme comes at the expense of a decrease in affinity for the other substrate. If we denote the affinity of the enzyme for the ith substrate by a_i, we can then write one affinity as a function of the other one: 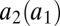with 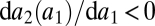. Thus, we can characterize the gene by the affinity of the corresponding enzyme to substrate 1, which is more accessible to measurements than the structural features of the enzyme that determine the affinities. If the gene becomes duplicated, we have to extend our notation to be able to distinguish between enzymes coded by the two loci. The affinity of the enzyme coded by the ith locus for the jth substrate is denoted by 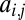. Performance is defined as the total amount of substrate converted and denote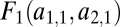d and 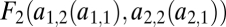for substrates 1 and 2, respectively. After duplication the two loci are identical, and thus equivalent, and characterized by 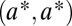, where the asterisk indicates that we assume that 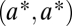corresponds to a maximum of the constrained trait space. We seek the condition for this point to be a saddle point of the fitness function .

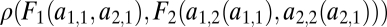In SI Text C we show that condition Eq. 6 for the example of duplicated genes equals

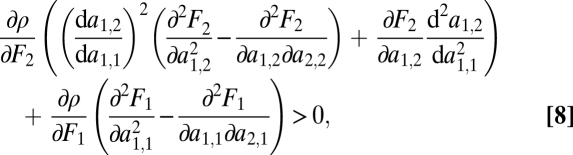where all derivatives are evaluated at a point 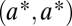. Note that this inequality does not show the same pleasing symmetry as condition Eq. 6. The more complex form of the left-hand side of condition Eq. 8 is due to the manner in which we introduced the trade-off: 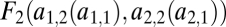is not directly a function of 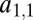and 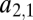but via the functions 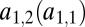and 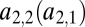. Keeping in mind that 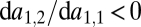, we can draw the following conclusions:

• i) A saturating response of the amount of converted substrate to an increase in substrate affinity disfavors specialization, whereas an accelerating response favors specialization.

• ii) Synergistic interactions between the gene products coded by different loci favor specialization.

• iii) A convex trade-off 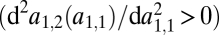between the affinities to the two substrates favors specialization, whereas a concave trade-off 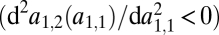disfavors specialization.

In the following we show how information about these functional properties could be derived from mechanistic considerations. It is widely acknowledged that substrate conversion by enzymes can be approximated by Michaelis–Menten kinetics. Then the speed of the substrate conversion, at quasi-steady state, is described by

where 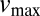denotes the maximum conversion rate, 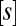the substrate concentration, and 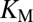the Michaelis–Menten constant. At 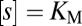, the reaction reaches its half-maximum speed 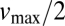. By deriving the Michaelis–Menten kinetics from an explicit model one can show that 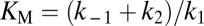, where k₁ is the speed with which enzyme–substrate complexes are formed whereas 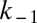and k₂ are the decay constants for this complex, either to substrate and enzyme or to converted substrate and enzyme, respectively (48). Eq. 9 can be rewritten as

where 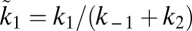. Obviously, v is a saturating function of 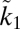and therefore of k₁. The total amount of converted substrate, F_i, is proportional to the speed with which the substrate is produced. If we now identify the affinity a with the constant k₁, the double derivatives 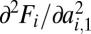in condition Eq. 8 are negative. In other words, negative curvature of the performance function is a mechanistic consequence of Michaelis–Menten kinetics and disfavors functional specialization. Hence, functional specialization of duplicated multifunctional enzymes is far from a forgone conclusion and we have to investigate other potential factors that could explain it.

Interactions between gene products coded by different loci can emerge when enzymes are dimers or multimers. For example, consider a dimeric enzyme and let us assume that before gene duplication such dimers are formed by two proteins coded by the same gene; i.e., the enzyme is a homodimer. After gene duplication dimers can form from pairs of proteins that are both coded by the original locus, both coded by the new locus, or from pairs where one protein is coded by the original locus and the other by the new locus. If the two loci accumulate different mutations, the latter enzymes become heterodimers. If heterodimers perform, averaged over the two different substrates, better than each homodimer, then specialization of duplicated loci is favored by selection. In the terminology of our model, interactions between the two loci occur through the formation of heterodimers. If these heterodimers perform better than homodimers, then the interaction between loci is synergistic and functional specialization is adaptive. In SI Text C we formalize this verbal argument and show that the strength of the selective force due to heterodimers increases with the frequency with which they are formed.

The third factor affecting condition Eq. 8, trade-off curvature, is basically unknown. Thus, whereas Michaelis–Menten kinetics is a ubiquitous mechanism disfavoring specialization, synergistic interactions between loci are a mechanism that might allow specialization despite constraints imposed by Michaelis–Menten kinetics, although only under rather special conditions. On the basis of these findings one might conclude that the conditions for specialization of duplicated genes are only rarely met. However, so far we have assumed that duplicated genes are equivalent. This need not to be the case. Often genes with multiple functions will execute these functions in different tissues or at different times. If the two copies of a duplicated gene differ in their regulatory regions, either because of mutations or because of the duplication event itself, positional effects are present. Then changes in the coding region of a gene specializing it for one function are always favored if these changes occur in the copy that expresses the gene preferentially in the appropriate location or at the appropriate time. Thus, the scope for specialization between duplicated genes can become much wider if differences between their regulatory regions exist. This latter idea is closely related to the duplication–degeneration–complementation model suggested by Force and colleagues (42). These authors argue that duplicated genes are easily maintained if degenerative mutations affect complementary regulatory regions. Our model suggests that under such conditions duplicated genes not only are maintained but also become specialized for alternative tasks.

Many Modules

Many examples given in the introductory section of this paper are about organisms that consist of many modules, posing the question of how our results are affected if more than two modules are involved in the execution of two tasks. Answering this question in full generality is complex, because we then would have to deal with an n-dimensional trait space, n being the number of modules. Here we make the simplifying assumption that the n modules of an organism fall into two groups with modules within the same group being characterized by the same trait value θ. This assumption is justified if the developmental program for the modules contains switches that allow only for discrete alternatives. Revisiting our introductory example, this means that m pairs of appendages in a shrimp are specialized on walking whereas the remaining pairs are specialized on burst swimming. We note that our approach is conservative in the sense that it is possible that an undifferentiated organism resides at a saddle point of the fitness landscape when each module is allowed to change independently whereas it resides at a maximum under the constraint that modules within each group are identical.

For n equivalent modules we show in SI Text A that condition Eq. 6 remains necessary and sufficient for the existence of a saddle point. The difference is that in the case of n modules the allocation of modules to the different tasks, determined by m and n, imposes a constraint on the variation in θ₁ and θ₂ for specialization to evolve. Consider an organism with n modules, m of which are characterized by 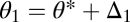and by 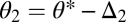with Δ₁ and Δ₂ small and positive. In SI Text A we show that if condition Eq. 6 is just barely fulfilled, then Δ₁ and Δ₂ have to be related according to

for specialization to be favored. This result can also be interpreted the other way around: If phenotypic variation occurs mainly in the direction given by Δ₁ and Δ₂, then the allocation of modules to the different tasks has to be such that Eq. 11 is fulfilled. This result implies that the number of modules specializing on each task has to compensate for the degree of specialization: If one group is highly specialized for one task while the other group is only weakly specialized for the other task, the second group should comprise more modules than the the first one (Fig. S1). This finding is relevant when in the initial phase of specialization the phenotypes of the different modules cannot evolve independently but are positively correlated due to shared developmental pathways. Then 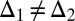and therefore the two groups of modules are expected to differ in size, a phenomenon that indeed seems common in nature.

In SI Text A we also prove that as the left-hand side of condition Eq. 6 increases, the constraint given by Eq. 11 becomes more relaxed. In other words, as the inequality in condition Eq. 6 becomes more pronounced, functional specialization is favored for a wider array of values m, Δ₁, and Δ₂. Furthermore, as the inequality in condition Eq. 6 becomes more pronounced, the direction of fastest fitness increase becomes increasingly tilted in the direction where both types of modules become specialized to a similar degree, i.e., in the direction of the vector 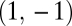(SI Text A). This result is true regardless of the frequency of the two types of modules. Similarly, as the inequality in condition Eq. 6 becomes more pronounced, the optimal allocation of modules to the different tasks approaches 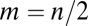regardless of the direction of functional specialization given by Δ₁ and Δ₂. Finally, for the case of n nonequivalent modules we prove in SI Text B that condition Eq. 7 remains unchanged.

In cases with more than two modules, functional differentiation can result in very different spatial configurations. For instance, in cyanobacteria nitrogen-fixating heterocysts and photosynthesizing cells are evenly distributed within an individual. Intuitively the reason is clear: Each heterocyst has to supply a certain number of neighboring photosynthesizing cells with nitrogen and a homogeneous distribution maximizes the efficiency of diffusion as a transport mechanism whereas aggregated heterocysts would be ineffective in providing all photosynthesizing cells with nitrogen. On the other hand, specialized tissues and organs are examples where differentiated cells are aggregated. This type of pattern formation can be understood within our framework by realizing that the strength of interactions between modules in many cases depends on their distance. In cyanobacteria, heterocysts and photosynthesizing cells exchange metabolites and due to diffusion synergistic interactions exist between neighboring cells. These interactions favor a mosaic of cell types. In contrast, we hypothesize that the evolution of aggregations of specialized cells results from interactions that are antagonistic between neighboring cells. With such interactions a group of cells specializing for the same task performs better than would be expected on the basis of the sum of their separate contributions.

Functional Specialization and Environmental Robustness

During the lifespan of an organism modules can be damaged due to various causes. For instance, one paralog of a duplicated gene can become functionless due to a somatic mutation, and appendages of an arthropod can be lost or damaged in a predator attack. If modules are highly differentiated, damage to one module can result in a drastic decrease in performance in the task it was specialized for and a high level of performance cannot be robustly maintained. If fitness becomes drastically reduced as soon as an organism cannot execute both tasks reasonably well, then it is clear that selection for robustness, i.e., a reliable ability to perform both tasks, disfavors functional specialization. This is, for instance, the case when performance in the two tasks affects fitness multiplicatively, e.g., when performance in one task affects survival whereas performance in the other task affects reproduction. If either survival or reproduction is drastically reduced, the same holds true for fitness.

The just described scenario is not the only possibility by which selection for robustness can disfavor functional specialization. By means of a simple example we show how selection for robustness can act in a scenario where fitness does not hinge on the reliable execution of both tasks. Specifically, we consider the case that the two performances can compensate each other in their effect on fitness. Mathematically, this means that fitness depends additively on performance in the two tasks. For simplicity, we consider the case of two equivalent modules that become damaged with the same constant probability per unit of time. This probability is sufficiently low such that we can neglect the possibility that both modules become damaged. All individuals have the same life span that we scale to one. If we assume that offspring are produced continuously throughout life and that reproduction is proportional to the sum of the performance in both tasks at the moment of reproduction, then the expected fitness can be written as

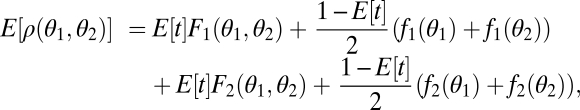where 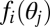denotes performance of an organism with only one module intact and the other functionless and 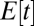is the expected time where a module becomes damaged. The curvature of the average performance landscape orthogonal to the constrained trait space at 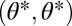equals

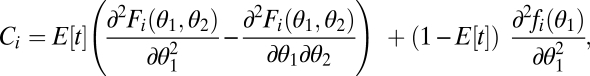where all derivatives are evaluated at 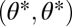. The first term accounts for the time before one of the modules was damaged and the second term accounts for the time with only one intact module. Consider the case that performance functions are saturating but that in an intact organism condition Eq. 6 is nevertheless fulfilled due to synergistic effects between modules. If the risk of damage is sufficiently high such that the life span as an intact organism is sufficiently short, then C_i can become negative and condition Eq. 6 is not fulfilled anymore.

Discussion

We present a unifying perspective for the evolution of functional specialization of repeated modules. Such functional specialization, also known as division of labor, is present over a wide range of organismal complexity from molecules to organisms organized in colonies. A distinctive feature of our mathematical framework is its generality because it is based on few mild assumptions: A set of ancestrally undifferentiated modules contributes to two tasks, fitness is increasing with increasing levels of performance in each task, and specialization of modules is constrained by a trade-off; i.e., a module with characteristics suitable for one task can contribute only little to the other task.

Our results are largely phrased in terms of functions that map traits to performance whereas the map from performance to fitness plays a minor role. We consider this aspect of our approach particularly important because detailed knowledge of fitness landscapes is generally very hard to come by or requires a suite of extra assumptions whereas the map from traits to performance can sometimes be measured directly or deduced from mechanistic considerations. The important but also very natural assumption we make about fitness is that it is monotonically increasing with performance in both tasks. For simplicity of the presentation we phrased our results in terms of fitness that is density and frequency independent. If this independence is not given, all that is required is to confirm by means of an invasion analysis (49, 50) that the point 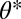is an attractor of the evolutionary dynamics in the constrained trait space.

We identify the following properties of performance functions that favor functional differentiation. First, if modules are differently predisposed to contribute to a task due to their position within the organism, then specialization of modules, at least partially, is always favored by selection. We refer to this phenomenon as positional effects. In the absence of positional effects, functional specialization is selectively favored whenever condition Eq. 6 is fulfilled. Specifically, functional specialization is favored by the following two features. (i) Accelerating performance functions: When performance is an accelerating function of the degree of specialization, then the gain in performance due to specialization of a module for one task exceeds the loss in performance due to specialization of another module for the other task. As a consequence, performance increases when half the modules specialize for one task while the remaining modules specialize for the other task. This mechanism has indeed been proposed as the driving force for germ–soma differentiation in Volvox by Michod and coworkers (27, 28). (ii) Synergistic interactions between modules: In this case the performance of an organism consisting of differentiated modules exceeds the performance that could be expected on the basis of the sum of the separate contributions from all modules. This last result can also be phrased the other way around: Functional specialization is favored if the performance of an organism with undifferentiated modules is less than what could be expected on the basis of the sum of the separate contributions from all modules. In other words, interference between identical modules performing the same task favors functional specialization.

Because our conditions are only necessary for functional specialization to be favored, and generally not sufficient, we suggest that it is useful to take the opposite perspective: When none of the above conditions is fulfilled, the evolution of specialization cannot be expected to be caused by natural selection. From this perspective, the absence of positional effects, as for example in rotational symmetric organisms, saturating performance functions, and antagonistic interactions between modules can all prevent the emergence of division of labor. As a further factor that can counteract the emergence of division of labor we identify selection for environmental robustness. We show that if modules can become damaged, then organisms with differentiated modules can have a lower performance when averaged over their life time than organisms with undifferentiated modules.

Given the generality of our approach it is inevitable that our conditions are only necessary but not sufficient for division of labor to evolve by natural selection. Constraints at various levels can frustrate the emergence of differentiated modules even in the presence of positional effects or if condition Eq. 6 is fulfilled. For instance, costs for maintaining differentiated developmental pathways are not included in our theory. If such costs exist, the conditions for the emergence of division of labor will be more stringent. Furthermore, it is clear that functional specialization can evolve only if the strictly positive correlation between modules—which we assumed as the ancestral state—can be broken. In some cases a positive correlation can be broken easily. An example we considered is the evolutionary fate of duplicated genes that should be completely uncorrelated. In other cases, independent changes between modules require the evolution of independent developmental programs and empirical evidence exists that this process is possible. For instance, it has been shown that antagonistic selection of correlated, serially homologous traits can lead to complementary changes in trait size (51, 52). In addition, recent QTL mapping studies have shown that in intercrosses of inbred mouse strains there is ample genetic variation for trait correlation, so-called relationship QTL (53). Hence, for quantitative traits it may be easy to change genetic correlations (54). Several authors even suggested that segmented body plans are successful exactly because they facilitate the evolution of independent developmental pathways between modules (55, 56). To conclude our discussion of constraints we note that it has been suggested that “evolution is best viewed as a history of organisms finding devious routes for getting around constraints” (ref. 57, p. 282), suggesting that long-term evolution might indeed be governed by the conditions identified in this article.

The theory presented here is best understood as a formal framework for the analysis of specific, mechanistic models. The results presented above, in particular condition Eq. 6, provide criteria for the analysis of a large set of specific models. Hence, these results are more a guide for the analysis of mechanistic models rather than a model itself. To illustrate this point, we apply our framework to the evolution of the coding region of multifunctional duplicated genes. We thereby formalize a verbal model introduced by Hughes (2, 41), who suggests that specialization of duplicated genes with multiple functions can be driven by what has been called “escape from adaptive conflict.” By applying our framework we identify Michaelis–Menten enzyme kinetics as a factor acting against specialization of multifunctional enzymes coded by duplicated genes. If specialization is observed nevertheless, we predict that other forces favoring specialization have to be in place. Candidates are synergistic interactions between gene products coded by the duplicated loci or positional effects due to differences in the regulatory regions of the duplicated genes and both possibilities are explored in some detail in Application: Specialization of Duplicated Genes. In conclusion, although our framework is very general and derived from few mild assumptions, surprisingly specific predictions emerge when applied to concrete examples.

Some existing models about the evolution of division of labor can be understood within our framework. For instance, Michod and coworkers (27, 28) and Gavrilets (31) investigated the evolution of germ–soma differentiation in multicellular organisms by means of mathematical models. In an undifferentiated multicellular organism all cells contribute to survival and reproduction, two tasks that are likely to be traded off. Both Michod and Gavrilets find that germ–soma differentiation can evolve when the trade-off curve that relates survival to reproduction is convex. This finding is related to our results in the following way. Let θ denote the proportion of energy a cell allocates to functions improving its survival. The trade-off results form the fact that such a cell can allocate only the remaining fraction, 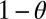, to reproduction. 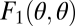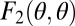Let and denote a colony's survival and reproduction, respectively. It is then easy to show that if both F₁ and F₂ are accelerating functions, i.e., they are convex, then also the curve one obtains when plotting F₁ against F₂ for different values of θ is convex. Thus, in the absence of interactions between cells and positional effects, the findings of Michod and Gavrilets are driven by the remaining factor, accelerating performance functions.

In the remainder of the Discussion we relate our results to the evolution of organismal complexity. Complexity is often defined as the number of independent parameters necessary to describe an organism's morphology (58–61). According to this definition, functional specialization then clearly corresponds to an increase in complexity because once 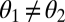, two parameters instead of one are necessary to describe the phenotype of the two modules. Carroll (56) and Wainwright (38) speculate that segmentation in metazoans has been favored because it more easily allows one to increase complexity and explore new dimensions of morpho-space.

It has been repeatedly reported that over the tree of life organismal complexity is positively correlated with size, in particular with cell number (5, 62) and colony size (15, 63). Our model shows that a priori module number has no influence on the strength of selection for functional specialization because condition Eq. 6 is independent of n. Thus, a positive size–complexity relationship requires that module size or module number is correlated with one or more of the factors favoring functional specialization. For instance, a positive size–complexity relationship could result from an intrinsically higher robustness of larger organisms (15). If large modules are less prone to damage or if, in the case of many modules, the risk decreases that all modules specialized for a certain task are damaged or lost, then selection for robustness becomes a weaker force counteracting selection for division of labor. Furthermore, it seems feasible that increased body size amplifies the strength of positional effects resulting in increased levels of differentiation. It is an interesting idea that the evolution of functional specialization could be a self-reinforcing process: Increased levels of functional specialization in one type of module could create positional effects that then favor functional differentiation in another type of module. Last but not least, body size and module number can also affect the magnitude of the derivatives featured in condition Eq. 6 as for example argued by Michod and coworkers (28, 29).

In a recent book on the evolution of complexity McShea and Brandon (64) argue that increase in body plan complexity is the prediction of a zero-force law, meaning that complexity in terms of the number of differentiated parts increases in evolution unless special constraints apply. The argument is that small changes will inevitably arise, leading to more and more differences between parts of the organism. Here we discuss this idea in the light of our model. We first observe that a zero-force perspective has to accommodate the fact that organisms are under selection as soon as there is heritable variation and reproduction, and both are boundary conditions of organismal existence. Our model suggests that functional specialization can be understood from an adaptationist point of view, i.e., in terms of fitness maximization. On the basis of this perspective, our model predicts that stable heritable differentiation will occur only if performance as a function of traits fulfills certain conditions. If condition Eq. 6 is not fulfilled and in the absence of positional effects, natural selection will actively maintain uniformity among modules regardless of random variation in their phenotype. Thus, even under very general conditions, as long as selection is acting on the parts of an organism and there are trade-offs regarding the performance of different functions, an increase in complexity is not inevitable. This could be one reason why there are still relatively simple organisms in the world, for instance undifferentiated colonies of protozoans, or metazoans with few or without any internal organs.

Appendix: Saddle Points of the Fitness Landscape

In this Appendix we derive the conditions under which functional specialization is favored for the case of two modules, first for equivalent modules and then for nonequivalent modules. The derivation of the general case of n modules can be found in SI Text A and B.

For the case of equivalent modules the fitness landscape is symmetric with respect to mirroring across the line 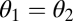representing the constrained trait space. Thus, the point 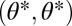is an extremum of the fitness landscape and its shape locally around the point 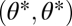can be described by the Hessian matrix 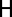of the fitness function ρ with entries 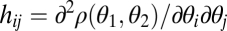for 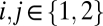and with all partial derivatives evaluated at 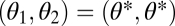. For equivalent modules 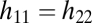. Then, because the Hessian matrix is also symmetric, both diagonal entries and both off-diagonal entries are equal to each other and the eigenvectors of the Hessian matrix equal 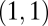and 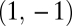. The assumption that the point 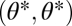is a maximum in the constrained trait space means that the eigenvalue corresponding to is negative. The point is a maximum of the fitness landscape if also the eigenvalue corresponding to the eigenvector 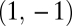is negative. Conversely, the point 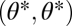is a saddle point of the fitness landscape if the eigenvalue corresponding to the eigenvector 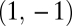is positive.

The curvature of the fitness landscape in the direction of the vector 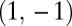and thus the eigenvalue corresponding to this vector equal 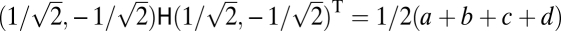with

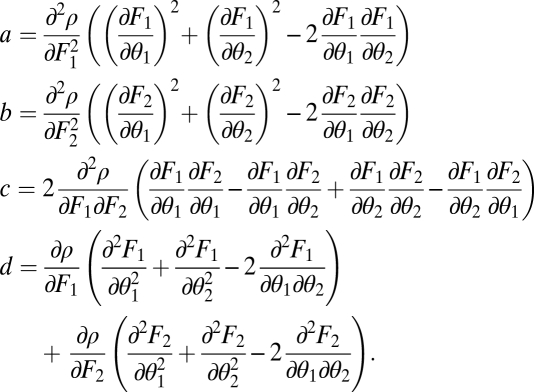Using that for equivalent modules , , , 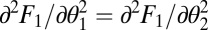and 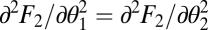, the expression 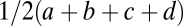simplifies to the left-hand side of condition Eq. 6.

For the case that modules are nonequivalent we calculate the gradient of the fitness function at 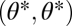: 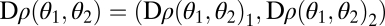with

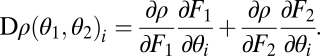The derivative in the direction of the constrained trait space equals 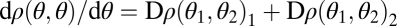and because we have 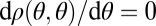at , it follows that

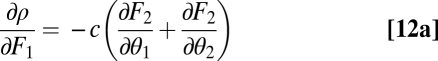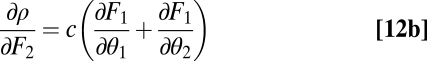for some positive constant c. Inserting Eq. 12a and Eq. 12b into 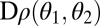gives 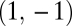as a gradient at the point 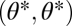. The derivative in the direction of the gradient equals

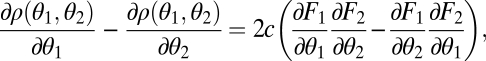leading to condition Eq. 7.