Significance levels for studies with correlated test statistics

Abstract

When testing large numbers of null hypotheses, one needs to assess the evidence against the global null hypothesis that none of the hypotheses is false. Such evidence typically is based on the test statistic of the largest magnitude, whose statistical significance is evaluated by permuting the sample units to simulate its null distribution. Efron (2007) has noted that correlation among the test statistics can induce substantial interstudy variation in the shapes of their histograms, which may cause misleading tail counts. Here, we show that permutation-based estimates of the overall significance level also can be misleading when the test statistics are correlated. We propose that such estimates be conditioned on a simple measure of the spread of the observed histogram, and we provide a method for obtaining conditional significance levels. We justify this conditioning using the conditionality principle described by Cox and Hinkley (1974). Application of the method to gene expression data illustrates the circumstances when conditional significance levels are needed.

1. INTRODUCTION

Many studies involve testing large numbers of hypotheses. For example, we may be interested in whether the expression levels of a large number M of genes are similar in 2 types of cancer tissue or whether genotypes of M genetic markers are similar in individuals with and without a given disease. To address such questions, investigators obtain random samples from the 2 populations and form M test statistics T₁,…,T_M evaluating the differences. An important analytic starting point is assessment of the overall evidence against the global null hypothesis H₀ of no differences between the 2 populations, that is, that none of the M null hypotheses is false. Such evidence, when present, motivates the search for specific attributes that differ in the populations. Even if such evidence is absent, the study can provide important leads for investigation in other studies. Ultimately, however, one is unlikely to declare that the populations differ in any specific attributes unless evidence against H₀ has been observed in several independent studies.

There are several strategies for testing H₀ (see Westfall and Young, 1993, for a review). Here, we shall work with the test statistic having largest magnitude. For analytic convenience, we first convert each test statistic to a z-value:

(1.1)

where Φ is the standard normal cumulative distribution function (cdf) and Ψ is a putative null marginal cdf for each statistic. Under H₀, each Z_m has a standard normal marginal distribution. Let X = max_m|Z_m|. If the M statistics were independent, the overall p-value associated with the observed value X = x would be P_x = 1 − [1 − 2Φ( − x)]^M∼2MΦ( − x), where the approximation holds for large x. When the test statistics are correlated, we can estimate P_x by simulating the global null distribution of X. This is done by permuting the sample units many times. In each permutation, we compute M test statistics and record the value of the one with largest magnitude. We estimate P_x as the proportion of all permutations whose maximum test statistic exceeds the observed value x.

However, there is a potential problem with using P_x as a measure of overall significance. Specifically, the shape of the histogram of values Z_m varies across studies with correlated tests more than it does across studies with independent tests (Owen, 2005, Efron, 2007). The larger variation among histograms of correlated statistics can cause misleading tail counts, and some adjustment is needed to avoid erroneous inferences.

Here, we describe those situations when histogram variability can produce misleading values for an overall significance level. We begin with a more formal description of the problem and our proposal for addressing it. We then review a conditionality principle that describes the circumstances when conditional significance levels are more appropriate than unconditional ones. We present a simple, permutation-based method for estimating the difference between conditional and unconditional significance levels, while also estimating the variance of C (and its covariance with tail counts) for comparison with expected values. The investigator can then consider whether conditional p-values would substantially alter the interpretation of results and report them when appropriate. We also derive approximations that elucidate the 2 key factors determining the need for conditional significance levels. The first factor is the average of the squared correlation coefficients for all pairs of distinct test statistics. The second factor is the magnitude x of the maximum test statistic. Finally, we illustrate the method by application to gene expression data.

2. THE PROBLEM

Consider the sample histograms of data from several studies, each producing M test statistics, Z₁,…,Z_M, with each Z_m having a standard Gaussian marginal distribution. If the Z_m are independent, the histograms vary across studies in predictable ways. For example, we can calculate various moments of the distribution of a histogram's “central proportion” C, that is, the proportion of test statistics Z_m with absolute value less than 1: C = #{Z_m:|Z_m| < 1}/M. The expected value of C is Φ(1) − Φ( − 1) = 0.6827, and its variance is 0.6827(1 − 0.6827)/M = 0.2166/M. However, correlation among the test statistics increases the variability of the sample histograms (Efron, 2007). For instance, with M = 2000 test statistics, the standard deviation of C increases from 0.01 under independence to about 0.08 when the average squared correlation coefficient between pairs of test statistics is 0.05. Of particular importance, extreme values of the test statistics can be more variable than appreciated in the presence of correlation, which can complicate interpretation of results from any given study. Because a permutation-based estimate of the overall p-value P_x does not account for the excess variability, significance levels assigned to an observed value X = x can be misleading.

2.1. Conditioning on the central proportion C

We propose assessing the variability of X via that of C and, when the variability is large, reducing it by conditioning on the observed value C = c. That is, we replace the permutation-based unconditional p-value P_x by the conditional p-value

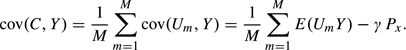Here, Y = 1 if X > x and Y = 0 otherwise.

This variance-reducing tactic is familiar to statisticians. Our statistic of interest Y is correlated with another statistic C that is not of interest. (C is not of interest because the test statistics between ±1 are unlikely to represent hypotheses that are false and thus “interesting.”) Moreover, the variance of C is greater than expected under standard assumptions, such as independence of the test statistics. This is precisely the setup for the conditionality principle described by Cox and Hinkley (1974). The principle states that when C has large variance and is strongly correlated with Y, inferences based on Y should be drawn as if C were fixed at its observed value. Other values that C might have taken are irrelevant to the data at hand.

2.2. Example illustrating the conditionality principle

Suppose we randomly choose a coin from a bag containing 90% nickels and 10% quarters. We flip our chosen coin and then use the outcome (heads or tails) to select one of 2 hypotheses. The first hypo- thesis states that the nickels are biased toward heads, while the second hypothesis states that the quarters are so biased. Columns 1 and 2 of Table 1 show the probabilities of heads specified by the 2 hypotheses for each of the 2 choices of coin. The unconditional probability of heads is 0.9(0.8) + 0.1(0.1) = 0.73 according to hypothesis 1 and 0.9(0.1) + 0.1(0.8) = 0.17 according to hypothesis 2. Suppose we choose a quarter, flip it, and get heads. If we ignore the coin type chosen, the probabilities in column 3 would prompt us to favor hypothesis 1. But if we condition on the fact that we chose a quarter, we would favor hypothesis 2. Thus, directly conflicting evidence is provided if we do not condition on the type of coin chosen.

Table 1.

Probability of heads when flipping a randomly selected coin, under 2 hypotheses

Hypothesis	Heads probability
	Conditional on coin type†		Unconditional
	Nickel	Quarter
Nickels biased toward heads	0.80	0.10	0.73
Quarters biased toward heads	0.10	0.80	0.17

^†Coin is selected from a bag containing 90% nickels and 10% quarters.

In this example, there is a strong association between the heads/tails outcome of interest and the choice C of coin, and this choice varies from one experiment to another. The likelihood of substantial differences between conditional and unconditional inferences increases with the strength of dependence between the outcome of interest and the coin selection C, and it increases with the variance of C. The example shows that if the covariance between an extreme-value statistic and an appropriately chosen conditioning statistic C is sufficiently large, and if C is sufficiently variable, then different conclusions about H₀ may be drawn, depending on whether or not we condition on C.

2.3. When are conditional p-values needed?

The most straightforward way to evaluate the need for conditional p-values is to estimate both conditional and unconditional p-values and compare them. This can be done by repeatedly permuting the sample units and generating M test statistics for each permutation. The unconditional p-value is estimated as the proportion of permutations whose maximal test statistic exceeds x. In principle, the conditional p-value could be estimated by restricting the permutations to those whose C-value lies in a small interval around the observed value C = c and basing the p-value estimate only on the permutation outcomes within that small subset. For example, for a study comparing the M attributes of 2 samples of N₁ and N₂ units, the rth of the R permutations would involve the following steps: (i) randomly select a subset of N₁ of all the units, call it sample 1, and call the remaining N₂ units sample 2; (ii) compute the M test statistics comparing the 2 samples; and (iii) flag the permutation if the magnitude of any test statistic exceeds x. Repeating these 3 steps R times, we estimate the unconditional overall p-value as 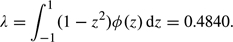_x = # {flagged permutations}/R. In addition, we might estimate the conditional overall p-value, given conditioning statistic C = c, as

(2.1)

where δ is a small positive number.

A limitation of the latter estimate is the large number of permutations needed to achieve adequate precision, particularly when the observed c falls in the tail of the distribution of C, a circumstance yielding the largest potential difference between conditional and unconditional p-values. Instead, we propose inferring p_x(c) by regression smoothing. Specifically, let Y_r = 1 if the test statistic of largest magnitude in the rth permuted data set is flagged, with Y_r = 0 otherwise. We fit to the points {(Y_r,C_r),r = 1,…,R} the logistic regression model logit[Pr(Y_r = 1|C_r)] = α + βC_r to obtain fitted parameter values 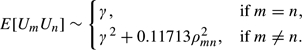and 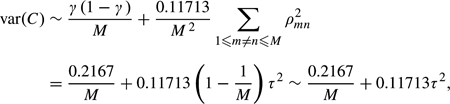. We then use these to estimate the conditional p-value given the observed C = c as

(2.2)

If the 2 p-values 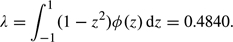_x and 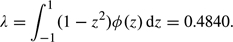_x(c) differ appreciably, then the conditionality principle indicates that the latter is a better summary of the evidence against H₀. This regression smoothing borrows strength from the full ensemble of R permutations instead of just those with C close to c. It is similar in flavor to the regression smoothing of Efron (2007) when inferring the false discovery rate and the extreme-value smoothing of Dudbridge and Koeleman (2004). Using simulated data sets (not shown), we have found that the smoothed conditional p-values (2.2) agree closely with those obtained from extensive permutations using (2.1), for a wide range of values of C and X.

The permutations also can provide a fuller picture of the need for conditioning, by providing empirical estimates of the moments var(C) and cov(C,Y). The extent to which these empirical moments exceed their expected values under the independence assumption indicates the need for conditioning. We show in the Appendix that when all pairs of test statistics have bivariate Gaussian distributions, both these moments have approximate representations in terms of the mean of the squared correlation coefficients for all pairs of test statistics,

Specifically,

(2.3)

and

(2.4)

These approximations hold for small values of τ² and large values of x. Expressions (2.3) and (2.4) show that potential differences between conditional and unconditional significance levels increase with the correlation measure τ² and the threshold value x.

3. APPLICATION TO GENE EXPRESSION DATA

Here, we apply the method to expression levels of M = 3226 genes in the breast cancers of 15 patients with pathogenic mutations of the tumor-suppressor genes BRCA1 (N₁ = 7) or BRCA2 (N₂ = 8), as described by Hedenfalk and others (2001) and analyzed by Efron and Tibshirani (2002) and Efron (2007). The study goal was to identify genes that are differentially expressed in the 2 cancer groups. An important first step toward this goal is to determine whether the data provide evidence against the global null hypothesis that none of the genes are differentially expressed. In this example, each individual's expression levels for different genes are likely to be correlated. The test statistic for the mth gene is the usual 2-sample t-statistic

where g_mi is the log-expression level of gene m in the cancer of individual i and 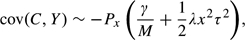_m1 and 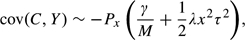_m2 are the means in individuals with BRCA1 and BRCA2 mutations, respectively. (The t-distribution assumes that the individual expression levels have lognormal marginal distributions.) We work with the transformed statistics (1.1), where Ψ is the cdf for the t-distribution on N₁ + N₂ − 2 = 13 degrees of freedom.

As shown in Table 2, X = max_{1 ≤ m ≤ 3226}|Z_m| = 4.70 and C = 0.4817. Because this value of C is less than its expected value 0.6827, the histogram of test statistics Z_m is wider than expected under the assumption of independence. Thus, unconditional overall p-values are likely to be less than conditional ones. To obtain the latter, we considered the R = 15!/(7!8!) = 6435 ways of randomly assigning 7 and 8 BRCA1 and BRCA2 labels, respectively, to the 15 patients. We computed the corresponding set of 3226 transformed t-statistics and, for each, its central proportion C_r and a variable Y_r indicating whether its largest test statistic exceeded 4.70,r = 1,…,6435. We then used the regression smoothing of (2.2) to estimate the conditional overall p-value given C = 0.4817. The fitted parameters were 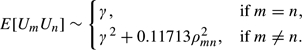= 3.139 and 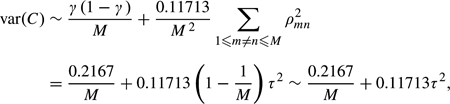= −12.681. The unconditional overall p-value, given by the proportion of permutations r with X_r > 4.70, was P_x = P_4.70 = 0.006. In contrast, the conditional p-value was 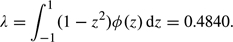_x(c) = 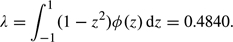_4.70(0.4817) = 0.049. Table 2 gives some insight into the reasons for such a large difference. Shown are the permutation-based value of var(C) and the estimated mean squared test correlation τ² obtained from (2.3). Also shown is the permutation-based value of cov(C,Y) and its bivariate Gaussian approximation (2.4). The table includes for comparison the values expected if the 3266 test statistics were independent. The correlations among gene expression levels increase var(C) about 60-fold and increase the magnitude of cov(C,Y) about 200-fold.

Table 2.

Effect on overall p-value of correlation among test statistics comparing expression of 3226 genes in 2 samples of cancer tissue^†

Unconditional p-value‡Px, x = 4.70	0.006
Conditional p-value‡px(c), c = 0.4817	0.049
var(C)
Independence	6.71 × 10−5
Permutation based‡	4.04 × 10−3
Average squared correlation τ2§	3.36 × 10−2
cov(C, Y)¶
Independence	− 1.76 × 10−6
Permutation based‡	− 3.87 × 10−4
Theoretical‖	− 9.70 × 10−4

^†Seven BRCA1 cancers and 8 BRCA2 cancers from Hedenfalk and others (2001).

^‡Based on 15!/(7!8!) = 6435 permutations.

^§From formula (2.3).

^¶Y = 1 if maximum test statistic exceeds 4.70, Y = 0 otherwise.

^‖From formula (2.4).

The conditional p-value of 0.049 provides only borderline evidence against the global null hypothesis that none of the genes are differentially expressed, contrary to the interpretation of Hedenfalk and others (2001). These conclusions are consistent with those of Efron (2007), who worked with the proportion of false discoveries in these data. Thus, as illustrated by the coin-tossing example of the previous section, conditional and unconditional inferences can be substantially different; when this occurs the conditional ones are more reliable.

4. DISCUSSION

Owen (2005) and Efron (2007) have warned that when the test statistics for a large collection of null hypotheses are correlated, their histogram can be highly variable. This variability can lead to misleading inferences from a single study. This is particularly problematic if the study is large and costly so that replication is difficult. The conditionality principle states that in this situation, inferences conditioned on statistics that capture this variability are more appropriate than unconditional inferences.

Efron (2007) has suggested ways to implement this conditioning when estimating tail probabilities and false discovery rates. The general approach involves defining a statistic X on which inferences are based and then conditioning X on the observed value of a summary statistic C for the histogram spread. Here, we have used this approach to estimate overall significance levels, with X taken as the test statistic with maximum magnitude and C taken as the central proportion of the test statistics. We have focused on overall significance levels to simplify the presentation. However, the proposed permutation-based conditional procedure applies to a large class of inferential problems, such as estimating null tail probabilities, adjusted p-values for subsets of hypotheses of interest, and false discovery rates.

While we have used the central proportion as the conditioning statistic, other choices are possible. However, care is needed in choosing this statistic. In general, the set of M test statistics will be a mixture of 2 unobserved subsets: (i) the test statistics representing the true null hypotheses and (ii) the “nonnull” test statistics representing the false ones. The summary statistic should account for a large fraction of the variability of the histogram of null test statistics and conditioning on it should reduce much of the variability of X. But to avoid power loss by “overconditioning,” the summary statistic should be independent of the nonnull statistics.

FUNDING

National Institutes of Health (R01 CA94069); National Institute of Mental Health (R01 MH61675, K24 MH64197).

APPENDIX

To prove (2.3) and (2.4), we use the following lemma, which follows from straightforward differentiation.

LEMMA The standard bivariate Gaussian distribution can be expanded in powers of the correlation coefficient ρ:

(A.1)

Here, ϕ(z) denotes the standard univariate Gaussian density.

Proof of approximations (2.3) and (2.4).

To prove (2.3), we introduce the indicator variable U_m = 1 if |Z_m| < 1, with U_m = 0 otherwise, m = 1,…,M. Thus, E[U_m] = γ = ∫ _{− 1}¹ϕ(z)dz = 0.6827, and C = (∑_{m = 1}^MU_m)/M has variance

(A.2)

Our goal is to approximate the expectations E[U_mU_n]. We need to only consider pairs m≠n since E[U_m²] = γ. We assume that under H₀, the test statistics Z_m and Z_n have the bivariate Gaussian distribution f(z_m,z_n;ρ_mn) of (A.1). Then, using the lemma and neglecting terms of order ρ_mn³, we have

(A.3)

where

(A.4)

Thus,

(A.5)

Substituting (A.5) into (A.2) gives

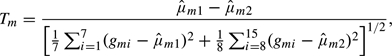(A.6)

which proves (2.3).

To prove (2.4), we rewrite it as

(A.7)

where λ is given by (A.4). Since C = (∑_{m = 1}^MU_m)/M, we have

(A.8)

But

(A.9)

The first factor in the nth summand of (A.9) is

(A.10)

For large x, the second factor is approximately

Substituting these 2 expressions into (A.9) gives

(A.11)

where

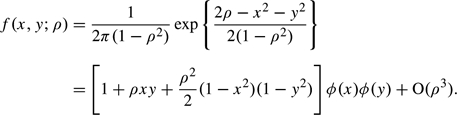(A.12)

Substituting the expansion (A.1) for the integrand in (A.12) and integrating and ignoring terms of order ρ_mn³ give

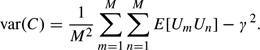(A.13)

Here, we have used the fact that ∫_x^∞(1 − u²)ϕ(u)du = − xϕ(x) and that for large values of x, Φ( − x) can be approximated by ϕ(x)/x. Substituting (A.13) into (A.11) gives

(A.14)

Finally, substituting (A.14) into (A.8) gives (A.7).   □