Chemical and Mechanical Impact of Silica Nanoparticles on the Phase Transition Behavior of Phospholipid Membranes in Theory and Experiment

Abstract

The interaction of nanoparticles (NPs) with lipid membranes is an integral step in the interaction of NPs and living cells. During particle uptake, the membrane has to bend. Due to the nature of their phase diagram, the modulus of compression of these membranes can vary by more than one order of magnitude, and thus both the thermodynamic and mechanical aspects of the membrane have to be considered simultaneously. We demonstrate that silica NPs have at least two independent effects on the phase transition of phospholipid membranes: 1), a chemical effect resulting from the finite instability of the NPs in water; and 2), a mechanical effect that originates from a bending of the lipid membrane around the NPs. Here, we report on recent experiments that allowed us to clearly distinguish both effects, and present a thermodynamic model that includes the elastic energy of the membranes and correctly predicts our findings both quantitatively and qualitatively.

Introduction

The increasing number and variety of artificially produced nanometer-scale particles calls for a thorough understanding of the influence of such nanoparticles (NPs) on biological material. In particular, many research teams are focusing on the uptake of NPs in human cells and its consequences (1,2). Silica NPs occur in exhaust emissions and are also added to food, textiles, and construction materials to improve their properties (3). Moreover, they are even considered for use in drug delivery (4). The uptake of NPs by living cells has recently become the subject of risk assessments because it correlates with cytotoxicity (5). In this context, it was shown that clathrin-dependent endocytosis is the most important pathway for the cellular uptake of silica NPs (6). For a detailed understanding of endocytotic mechanisms, it is helpful to study the mechanical properties of pure lipid membranes, which have been shown to be suitable model systems for cell membranes (7). However, one has to bear in mind that the elastic properties of the lipid membrane depend on its thermodynamic state and can vary substantially. Especially during the transition from the gel to the fluid phase, the bending modulus changes by at least one order of magnitude (8,9).

It has been demonstrated that this phase transition can trigger a variety of morphological transitions even in the absence of membrane proteins. Tube formation, fission, budding, and the expulsion of entire vesicles have been reported (10–13). Therefore, the thermodynamic state of the membrane must be considered as an important factor in the transport mechanisms of cells. The lipid phase transition can be conveniently monitored by differential scanning calorimetry (DSC), which allows one to detect even minor changes in the membrane properties (14). In 1992, Naumann et al. (15) showed that 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) bilayers on a spherical particle support (R ≈ 300 nm) melted cooperatively but exhibited a suppressed pretransition. Using particles of two different sizes (R ≈ 30 nm and R ≈ 300 nm), Brumm et al. (16) further showed that the transition temperature of supported membranes is related to their curvature, i.e., the radius of the particles. Finally, for vesicles with diameters <100 nm, Ahmed and Wunder (17) applied the same concept to analyze the influence of differences in the curvatures of the inner and outer leaflets on the transition melting temperature T_m.

Here, we employ DSC to characterize the impact of the same NPs that have been shown to be cytotoxic for human endothelial cells (5) on different phospholipid membranes. We investigate spherical supported vesicles (SSVs) in terms of their transition temperature and find significantly different dependencies on the membrane curvature for different lipid chain lengths. To explain our experimental findings, we present a thermomechanical model that includes the bending energy of the bilayer in the thermodynamic potential. In addition, we report a chemically induced depression of T_m that is triggered by the release of small amounts of silicic acid (SA) from the NPs.

Materials and Methods

For the experiments, we used silica particles with the following diameters: d = 16 ± 2 nm, 18 ± 2 nm, 85 ± 4 nm, 212 ± 25 nm, 305 ± 35 nm, and 348 ± 40 nm. All NPs used were synthesized and analyzed as described previously in detail by Blechinger et al. (6). 1,2-Ditridecanoyl-sn-glycero-3-phosphocholine (13:0PC), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (14:0PC), 1,2-dipentadecanoyl-sn-glycero-3-phosphocholine (15:0PC), DPPC (16:0PC), and 1,2-diarachidoyl-sn-glycero-3-phosphocholine (20:0PC), dissolved in chloroform, were obtained from Avanti Polar Lipids (Alabaster, AL) and used without further purification.

Suspensions of vesicles and NPs were prepared by rehydrating a dried lipid film with a dispersion of NPs in ultrapure water (18.2 MΩcm; Pure Aqua, Tuttlingen, Germany). The final lipid concentration was 1 mg/ml. To prepare multilamellar vesicles (MLVs), the sample was heated above the main phase transition temperature T_m for 60 min and vortexed several times. Afterward, the solution was either sonicated above T_m for 30 min or directly loaded into the calorimeter. The pure NP dispersions as well as the SSV containing sonicated samples were analyzed regarding their colloidal stability. A dynamic light scattering analysis showed that the hydrodynamic radius of such samples did not change significantly over typical experimental timescales (i.e., several hours; see Supporting Material). Furthermore, observations of different dried samples by scanning electron microscopy/transmission electron microscopy showed no signs of large agglomerates.

The measurements were carried out with a Microcal VPDSC differential scanning calorimeter (18) at a scan rate of 17 K/h. The reference sample was ultrapure water. The supernatant of centrifuged NP dispersions was analyzed by electrospray ionization mass spectrometry (Thermo Finnigan LTQ FT, resolution 100.000 at m/z = 400, up to 2000 u, 4 kV, heating capillary temperature 250°C) to quantify the most frequent oligomers of SA released from the NPs.

Results and Discussion

Chemical impact of silica NPs on T_m

When NPs were added to a suspension of MLVs, both the main transition and the pretransition peaks shifted toward lower temperatures (see Fig. 1 A). To quantify this effect, we analyzed the peak position of the main transition (T_m) as a function of particle concentration and size (Fig. 1 B). The mass concentration c_m was chosen so as to keep the total NP surface area per sample in the same range for all NP sizes. Thus, c_m covered a wider range for the larger NPs (Fig. 1 B).

Figure 1.

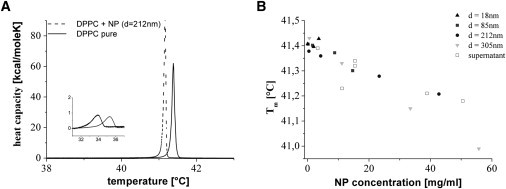
Melting-point depression due to NPs. (A) Heat capacity profile of an MLV sample (DPPC, 1.34 mM; solid line, without NPs; dashed line, with NPs). Inset: Pretransition region. (B) T_m is plotted against the final mass concentration of added NPs. Different-shaped, solid symbols indicate different-sized particles. The open rectangles show the T_m for NP-free samples containing only the supernatant of a centrifuged particle dispersion.

Our experiments revealed the following trend: independently of particle size, the temperature shift of the main transition exhibits a linear dependence on the total amount of added NP mass, which indicates an effect that is not related to the total particle surface. We then repeated the measurements, substituting the particles with the supernatants of the centrifuged NP dispersions of adequate particle concentration (10,000 × g, 3–300 min, depending on NP size). Fig. 1 B shows that the temperature shift of the NP-free samples is equal to the corresponding NP-containing samples. Therefore, the shift in T_m with increasing concentration is not due to the physical presence of the NPs but to substances dissolved from the NPs. This is confirmed by the fact that an increase in incubation time of washed NPs led to an increasing shift in T_m as well. Alexander et al. (19) reported that silica always partially dissolves in aqueous solutions, forming SA oligomers. According to Eq. 42 of Rimstidt and Barnes (20), 95% of the equilibrium concentration of silica in water should be reached within 9 h in the case of the NPs used here. The equilibrium concentration of SA is in the range of 150 ppm (19,21). The electrospray ionization mass spectra showed that tetramers (m/z = 274.8809) and pentamers (m/z = 370.8693) are the most frequent oligomers in our NP dispersions (data not shown).

To confirm that SA is indeed the origin of the decrease in T_m, we added a freshly prepared and oversaturated SA solution to the MLV samples. A linear decrease in T_m, as presented in Fig. 2, was found.

Figure 2.

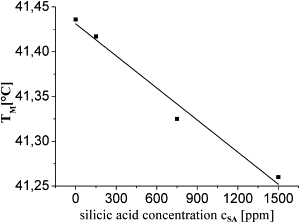
SA causes a melting-point depression. T_m of DPPC MLV samples in the presence of SA. A clear linear dependence on the SA concentration can be observed.

Regarding the hydrophilic character of SA (22), we expect that headgroup effects cause the observed melting-point depression. One possible explanation could be an altered solvation of both lipid phases in an SA solution compared with water.

Disregarding the specific nature of the SA-lipid interaction, we assume that the solute SA influences the chemical potentials of gel phase μ_gel and fluid phase μ_fluid

$${\mathit{\mu }}_i\left(T\right)={\mathit{\mu }}_i^w\left(T\right)+\Delta {\mathit{\mu }}_i^{tr}\left(T\right),$$ (1)

where ${\mathit{\mu }}_i^w$ denotes the standard chemical potential of the corresponding lipid phase in water, and ${\mathit{\mu }}_i^{tr}$ is the free energy associated with a transfer of the phase from water to the solution.

Along these lines, Chapman et al. (23) derived that for the shift of the transition temperature ΔT_m,

$$\Delta T_m=\left[-\frac{R{T}_m^2}{\Delta H\left(T_m\right)}\right]\mathit{\alpha }{c}_{SA}=\mathrm{:}A{c}_{SA},$$ (2)

where R is the gas constant, T_m is the melting temperature of the lipid in pure water, ΔH (T_m) is the change in the system's enthalpy at T_m, and c_SA is the concentration of the solute SA. For low concentrations c_SA and small temperature changes, α is a constant that depends on the strength of the interaction of the solute with both phases, i.e., the values of ${\mathit{\mu }}_{gel}^{tr}\left(T_m\right)$ and ${\mathit{\mu }}_{fluid}^{tr}\left(T_m\right)$.

It is noteworthy that Eq. 2 should be true for a direct interaction between lipid phases and solute, as well as for indirect influences of, e.g., solvation effects. Our measurements with oversaturated SA suggest a proportionality constant of A = 0.119 mK/ppm (see Fig. 2).

We emphasize that silica NPs release small amounts of SA that can significantly influence the thermodynamic properties of lipid membranes. The concentration of dissolved SA seems to be approximately proportional to the mass concentration of NPs in the dispersion, and does not depend on their size (Fig. 1 B). Future studies should take this effect into account, regardless of the curvature-induced effect explained in the following section.

Preparation of spherical solid-supported phospholipid bilayers

Storage of the samples for 1 wk after preparation led to the occurrence of an additional peak in the DSC profile at a temperature T_s (see Fig. 3). After sonication, this additional peak became more pronounced than the original one at T_m, indicating an increasing portion of the lipids undergoing the transition at T_s after this step. Some samples were centrifuged after sonication at 10,000 × g for 15–60 min. Before the centrifugation step was repeated, the supernatant was replaced with ultrapure water. In the inset of Fig. 3, the ratios of the transition enthalpies of the additional (ΔH_s) and main (ΔH) transitions are shown before and after centrifugation. Although this ratio was only ∼0.01 for the untreated sample, it increased to 1 after the first centrifugation step and to 2.2 after the second step. This clearly indicates that the additional peak at T_s has its origin in lipids that are attached to the NPs.

Figure 3.

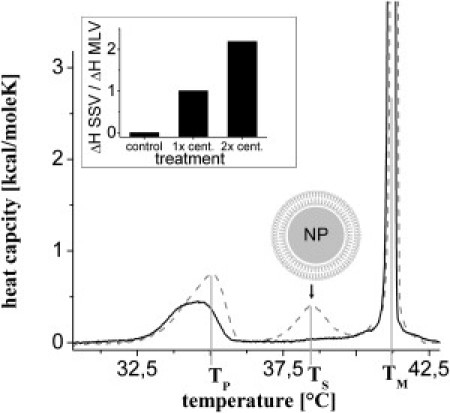
Solid support leads to an additional peak in the heat capacity profile. Heat capacity profile of a DPPC MLV sample directly after addition of NPs (solid line) and after 1 wk of storage at 4°C (dashed line). An additional peak appears (arrow), indicating the existence of a solid-supported lipid population. The pretransition temperature T_p and main transition temperatures T_s and T_m for SSVs and free MLVs are indicated by vertical lines. Inset: The ratio of the enthalpies of the peak at T_s and T_m was determined before and after one or two centrifugation steps. With each centrifugation step, a more pronounced peak at T_s verifies the assumption of a solid-supported lipid population.

This observation and conclusion are consistent with the findings of Naumann et al. (15) and Bayerl and Bloom (24), who coated NPs with lipid membranes and reported comparable shifts in T_m. Furthermore, in 1996, Brumm et al. (16) showed some differences in the curvature dependence between 14:0PC and 18:0PC; however, these authors did not perform a systematic study of the influence of NP size.

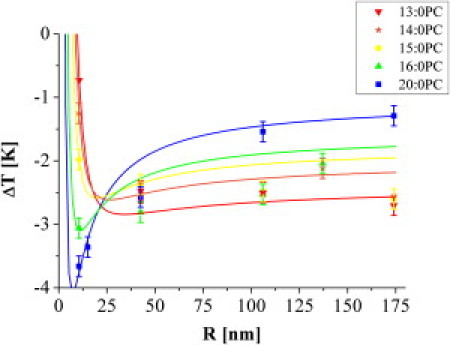
Hence, we analyzed the heat capacity profile of the supported membrane population for both NPs of different diameters (20–348 nm) and lipids with different chain lengths (13–20 carbon atoms) but identical headgroups. To account for the abovementioned chemical melting-point depression, we analyzed the difference ΔT: = T_s − T_m between the transition temperatures of free and supported lipids (see Fig. 4 A). Assuming that the above chemical effect is of the same order for both experiments, it should cancel out.

Figure 4.

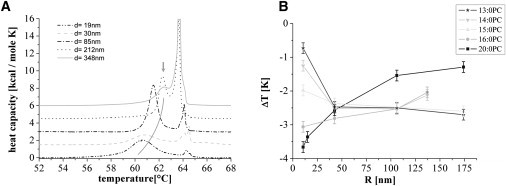
Effect of NP size and chain length. (A) Heat capacity profiles of 20:0PC MLV samples with silica NPs of different diameters between 19 nm and 348 nm (the baselines are shifted in the vertical direction for clarity). The gray line (arrow) indicates the shift in T_s. (B) The difference ΔT between T_m and T_s is plotted versus the NP diameter for different lipid chain lengths. The curvature dependence differs significantly.

All measurements show the same tendency, namely, a shift of T_m toward lower temperatures for the solid-supported case. The heat capacity profiles for 20:0PC are shown in Fig. 4 A for different NP sizes. The expected broadening (15) of the SSV due to decreasing cooperativity with increasing membrane curvature was observed but not analyzed further.

Fig. 4 B shows ΔT for different lipids and NP diameters. Whereas ΔT decreases with decreasing NP diameter for 13:0PC, 14:0PC, and 15:0PC, it increases for 16:0PC and 20:0PC. For all lipids except 20:0PC, the limit for a flat support of zero curvature is roughly ΔT = −2.5 K.

To summarize, our results consist of three main observations: 1), for all lipids and NP sizes, T_s shifts toward lower temperatures, with ΔT ranging between −0.5 K and −4 K; 2), the curvature dependence changes its sign for increasing chain length; and 3), for all lipids, ΔT shows a saturation behavior with decreasing curvature.

Theory

Bending contribution to ΔT

In the case of SSVs, the vesicles spread on and covered the NPs or parts of them, and thus experienced a curved substrate. Below, we derive an analytical expression for the expected change in phase transition temperature T_m based on the mechanical and calorimetric properties of the system. We therefore integrate the bending energy of the membrane in a Landau-type potential. No new or additional model assumptions are introduced; instead, we combine existing theories to provide a coherent explanation of our results.

Contributions to the Landau potential

In the Landau theory, a first-order phase transition is represented by the relative evolution of the double-well potential of the form shown in Fig. 5 (25,26):

$$\mathit{\Phi }\left(P,T,\mathit{\Pi },\mathit{\eta }\right)={\mathit{\Phi }}_0+A{\mathit{\eta }}^2+B{\mathit{\eta }}^4+C{\mathit{\eta }}^6,$$ (3)

where η is the order parameter and A(T,p,Π), B(p,Π), and C(p,Π) are functions of the thermodynamic variables temperature T, bulk pressure p, and lateral pressure Π, respectively.

Figure 5.

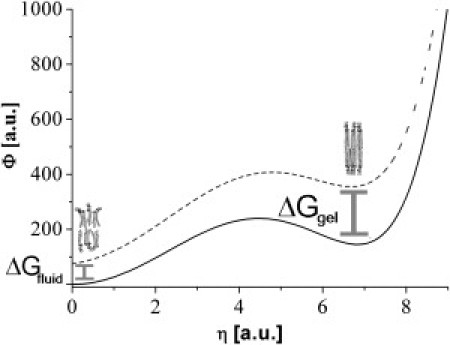
Landau representation of the thermodynamic potential. The presence of the solid support (NP) can be represented as an additional thermodynamic force (mechanical stress) on the membrane that causes a relative shift (dashed line) of the lower symmetry versus the higher symmetry phase minimum.

It is convenient and common to consider only the evolution of the potential minima in η with temperature. These minima are commonly identified with the Gibbs free-energy potentials for the gel phase and fluid phase (27,28), as indicated in Fig. 6.

Figure 6.

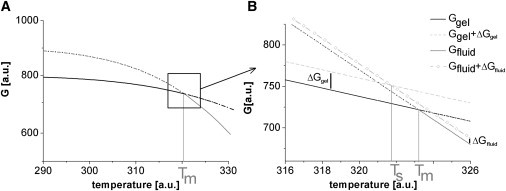
Minimum of Gibbs free-energy representation of the main transition. (A) The phase transition takes place at the intersection (T_m) of the potentials of both phases (black line, gel phase; gray line, fluid phase). (B) Linear approximation of G near T_m. The dark line is the Gibbs free energy G of the gel phase without solid support G_gel, the dashed line is G_gel(T) shifted by the contribution ΔG_gel due to the support, the gray solid line is the potential of the fluid phase ΔG_fluid(T), and the dashed-dotted line is ΔG_fluid(T) shifted by the contribution ΔG_fluid due to the support. The resulting phase transition is now taking place at a lower temperature T_s at the intersection of the dashed and dashed-dotted lines.

In the absence of any solid support, the two potentials intersect at the phase transition temperature T_m (see Fig. 6). The additional energies ΔG_gel and ΔG_fluid (see Fig. 5) in the presence of the support shifts the intersection toward lower temperatures T_s. For the transition temperature T_s now holds:

$$G_{gel}\left(T_S\right)+\Delta G_{gel}=G_{fluid}\left(T_S\right)+\Delta G_{fluid}.$$ (4)

Assuming the pressure p to be constant and ${\partial }^2\mathit{\pi /}\partial {\mathit{T}}^2\approx 0$, as shown previously (29), G_gel(T) and G_fluid(T) can be approximated by a first-order Taylor series near the transition point T_m:

$$G_{gel}\left(T_m\right)+\frac{\partial G_{gel}}{\partial T}\left|T_m\left(T_s-T_m\right)+\Delta G_{gel}=G_{gel}\left(T_m\right)+\frac{\partial G_{fluid}}{\partial \mathit{T}}\right|T_m\left(T_s-T_m\right)+\Delta G_{fluid}$$ (5)

and consequently

$$\Delta T\mathrm{:}=T_s-T_m=-\frac{\Delta G_{gel}-\Delta G_{fluid}}{\left(\frac{\partial G_{gel}}{\partial T}|T_m-\frac{\partial G_{fluid}}{\partial T}|T_m\right)}=:-\frac{\Delta G_{gel}-\Delta G_{fluid}}{\Delta \left(\frac{\partial G}{\partial T}\right)}.$$ (6)

This general analytical expression relates the contribution of the solid support to the free energy ΔG_gel/fluid with the shift of the transition temperature ΔT.

Δ $\partial G/\partial T$ from the heat capacity profile

Δ $\partial G/\partial T$ can be extracted from the experimental DSC data, recalling the relation between the thermodynamic potential G and the heat capacity c_p as its susceptibility:

$$-T\frac{{\partial }^{2}G}{\partial T^2}{|}_p=T\frac{\partial S}{\partial T}{|}_p=c_p$$ (7)

In agreement with the linear approximation that was described above, we have to integrate over ${\partial }^{2}G/\partial {\mathit{T}}^2$ (respectively c_p) in the transition region to get Δ $\partial G/\partial T$:

$$\Delta \frac{\mathbf{\partial }\mathit{G}}{\mathbf{\partial }\mathit{T}}={\int }_{{\mathit{T}}_{\mathbf{1}}}^{{\mathit{T}}_{\mathbf{2}}}\frac{{\partial }^{2}G}{\partial T^2}dT=-{\int }_{{\mathit{T}}_{\mathbf{1}}}^{{\mathit{T}}_{\mathbf{2}}}\frac{{\mathit{c}}_{\mathit{p}}}{\mathit{T}}\mathbf{dT}\approx -\frac{\Delta \text{H}}{T_m}$$ (8)

The last approximation introduces the transition enthalpy ΔH and holds for sharp transitions for which a constant temperature T_m can safely be assumed.

Mechanical contributions to ΔG

In the case of SSVs, we consider two main contributions to ΔG: 1), a curvature-dependent one caused by the bending of the membrane; and 2), a curvature-independent one due to the bare presence of the substrate (planar limit). The latter, constant contribution to ΔG can be caused by various interactions between lipids and support, for example by electrostatic forces.

To describe the mechanical contribution due to curvature, we use the well-known expression for the bending energy E_bend of a membrane (30). For the curvature-independent contribution, we add an additional constant G_s:

$$\Delta \text{G}=E_{bend}+G_s\approx \frac{1}{2}{\left(\frac{2}{R}-\frac{1}{R_0}\right)}^2\mathit{\kappa }{A}_{mem}+\frac{1}{R^2}{\mathit{\kappa }}_G{A}_{mem}+G_s,$$ (9)

where A_mem is the area of one lipid molecule, $c_0:=1/R_0$ is the spontaneous curvature, κ is the bending modulus, and κ_G is the modulus of Gaussian curvature. In the case of a chemically symmetric bilayer, the spontaneous curvature is caused by the asymmetry of the environment due to the NP and a thin layer of water inside and the bulk water outside the vesicle. The bending radius R is simply determined by the radius R of the particle.

Due to the higher flexibility of lipid membranes in the fluid phase, we assume a stronger contribution of the mechanical bending energy to Φ for the low symmetric gel phase (Fig. 5.). Therefore, we neglect the bending energy contribution to ΔG_fluid. The final expression for the temperature shift ΔT can then be found by combining Eqs. 6, 8, and 9:

$$\begin{array}{l}\Delta T=-T_m\frac{\frac{1}{2}{\left(\frac{2}{R}-\frac{1}{R_0}\right)}^2\mathit{\kappa }{A}_{mem}+\frac{1}{R^2}{\mathit{\kappa }}_G{A}_{mem}+G_{Sgel}-G_{Sfluid}}{\Delta \mathit{H}}\underline{\underline{\text{def}}}\\ =-T_m\frac{\frac{1}{2}{\left(\frac{2}{R}-\frac{1}{R_0}\right)}^2\mathit{\kappa }{A}_{mem}+\frac{1}{R^2}{\mathit{\kappa }}_G{A}_{mem}+\Delta G_s}{\Delta H},\end{array}$$ (10)

where κ and κ_G are the mechanical parameters for the gel phase and ΔG_s: = G_Sgel − G_Sfluid.

This expression explicitly relates the shift ΔT of the main phase transition temperature with the mechanical and calorimetric properties of the membrane, and predicts trends that can be compared with the experiments.

Discussion

In Fig. 7 we show that our thermodynamic model can well explain the observed trends of the temperature shift for different lipid chain lengths. Equation 10 was fitted to the data points of Fig. 4 B. T_m and ΔH were taken from the heat capacity profiles, and k was set to 2.5 10⁻¹⁸J for 16:0PC and estimated according to κ = 2.5 10⁻¹⁸J(h/16)³ for the other lipids, where h is the number of carbon atoms of the hydrophobic chains of the lipids (31,32). Furthermore, A_mem was set as 0.5 nm² and R is the radius of the NPs. Thus there are three unknown parameters: ΔG_s, κ_G, and $1/R_0$. We will show that κ_G turns out to be the crucial parameter.

Figure 7.

One-parameter fit of the model (Eq. 10) to the data points of Fig. 4B (ΔG_s = 140 J/mol, R₀ = −250 nm).

Initially we perform a three-parameter fit (ΔG_s, R₀, and κ_G free) to obtain a first estimate of the magnitude of the free parameters (Fig. S3 a). Because ΔG_s denotes a mainly headgroup-associated energy contribution, it is reasonable to consider ΔG_s as constant. Consistent fits are achieved for ΔG_s = constant = 150 J/mol. The two-parameter fit with fixed ΔG_s still shows good qualitative and quantitative agreement between the theory (Eq. 10) and experiments (Fig. S3 b). The values for R₀ and κ_G are comparable to those of the three-parameter fit mentioned before (Fig. S3 c).

Because the fit parameters affect each other, we also compare the aforesaid results with a one-parameter fit by additionally keeping R₀ fixed (ΔG_s = 140 J/mol, R₀ = −250 nm). We still achieve very good agreement between the measurements and the analytical curves from Eq. 10 (Fig. 7).

For all fits. the ratio z: = κ_G/κ is a critical parameter, which turns out to be roughly −2 for all experiments. Independently of ΔG_s and R₀, any substantial deviation from −2 would predict transition temperature shifts ΔT more than an order of magnitude larger than the ones observed. Our model therefore delivers the ratio z as predicted by Helfrich (33) for the transition regime from the lamellar to the vesicular phase.

Finally, we note that in fits with R₀ as a free parameter and fixed z, a contradiction with earlier theoretical work (33,34) appears. Instead of a decrease in the spontaneous curvature 1/R₀ with increasing h, as theoretically predicted, the fit indicates an increase. We hope that a more thorough understanding of ΔG_s, as well as better models and more information than is currently available for R₀, will improve the model in the near future. Along the same lines, a refined model would account for more subtle differences in bending energy between fluid and gel phases, and consider variations in A_mem.

Conclusion

In summary, our in-depth theoretical and experimental studies of the NP-membrane interaction show that silica NPs are able to influence the thermodynamic state of lipid membranes via at least two different mechanisms. First, we clearly identified a melting-point depression caused by SA released from the NPs in aqueous solution, which highlights the need for a thorough analysis of the chemical stability of NPs before studies on their interaction with biological matter. Even minute amounts of soluble substances can significantly change the thermodynamic properties of lipid membranes. Apart from this chemical aspect, we also found a size-dependent impact of silica NPs on the thermodynamic properties of phospholipid membranes mediated by the bending energy of the membrane. We propose an analytical expression that describes the shift in T_s of solid-supported lipid bilayers by means of thermodynamic and mechanical considerations. Together with further experimental data, this could offer a way to estimate the modulus of Gaussian curvature of lipid membranes, a parameter that is very difficult to access otherwise. Finally, we note that previous studies have shown that ion permeability, morphological changes, and adhesion phenomena can be controlled by a shift in the thermodynamic state of the lipid membranes (11,12,27,35). A comparison between these data and the shift in state by NPs observed here demonstrates that, in principle, NPs are capable of inducing such phenomena. We believe that similar changes in membrane state may be induced in the membranes of cells. In experiments conducted in collaboration with Bauer et al. (5), we showed that the same NPs studied here increase their toxicity with total surface area and not simply with mass, which clearly exemplifies the role of NP-cell membrane contact. It will be interesting to determine the extent to which this contact modifies the thermodynamic state of the cell membrane.