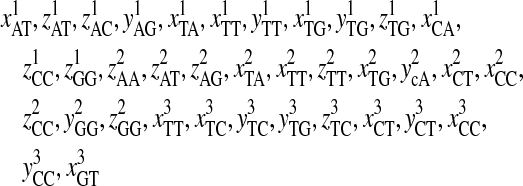Abstract
With the ever-increasing pace of genome sequencing, there is a great need for fast and accurate computational tools to automatically identify genes in these genomes. Although great progress has been made in the development of gene-finding algorithms during the past decades, there is still room for further improvement. In particular, the issue of recognizing short exons in eukaryotes is still not solved satisfactorily. This article is devoted to assessing various linear and kernel-based classification algorithms and selecting the best combination of Z-curve features for further improvement of the issue. Eight state-of-the-art linear and kernel-based supervised pattern recognition techniques were used to identify the short (21–192 bp) coding sequences of human genes. By measuring the prediction accuracy, the tradeoff between sensitivity and specificity and the time consumption, partial least squares (PLS) and kernel partial least squares (KPLS) algorithms were verified to be the most optimal linear and kernel-based classifiers, respectively. A surprising result was that, by making good use of the interpretability of the PLS and the Z-curve methods, 93 Z-curve features were proved to be the best selective combination. Using them, the average recognition accuracy was improved as high as 7.7% by means of KPLS when compared with what was obtained by the Fisher discriminant analysis using 189 Z-curve variables (Gao and Zhang, 2004). The used codes are freely available from the following approaches (implemented in MATLAB and supported on Linux and MS Windows): (1) SVM: http://www.support-vector-machines.org/SVM_soft.html. (2) GP: http://www.gaussianprocess.org. (3) KPLS and KFDA: Taylor, J.S., and Cristianini, N. 2004. Kernel Methods for Pattern Analysis. Cambridge University Press, Cambridge, UK. (4) PLS: Wise, B.M., and Gallagher, N.B. 2011. PLS-Toolbox for use with MATLAB: ver 1.5.2. Eigenvector Technologies, Manson, WA. Supplementary Material for this article is available at www.liebertonline.com/cmb.
Key words: classifiers, feature selection, human gene, short coding sequence, Z-curve
1. Introduction
With the explosive development of synthetic biology and genome-sequencing projects, there is an urgent need for developing gene prediction and genome annotation methods. A variety of gene-finding algorithms have been improved significantly, and many algorithms have been developed, such as GeneMark (Besemer and Borodovsky, 2005; Borodovsky and McIninch, 1993), GeneID (Guigo et al., 1992), MZEF (Zhang, 1997a, Zhang, 2000), Genscan (Burge and Karlin, 1997), GeneMark.hmm (Lukashin and Borodovsky, 1998), and many others (Salzberg et al., 1998). At the core of most of these gene-finding algorithms are coding measures (feature extraction) (Gao and Zhang, 2004) and classifiers.
For a given window of sequence, feature extractions calculate a scalar or a vector intended to measure the “codingness” of the sequence. The extracted features can be applied to both supervised and unsupervised learning algorithms as the input variables. Many new methods have been researched in recent years (Gao and Zhang, 2004; Bernal et al., 2007; Liu and Yu, 2005; Saeys et al., 2007; Varshavsky et al., 2006). Saeys et al. (2007) used complementary sequence features and compared them with several models in coding protein prediction (CPP) of animals, plants, Fungi, and Apicomplexa. Gao and Zhang (2004) evaluated 19 feature extraction algorithms, such as the methods of Markov models with orders of 1–5, codon usage, hexamer usage, codon preference, amino acid usage, codon prototype, Fourier transform, and eight Z-curve methods with various numbers of parameters. Consequently, considering both the recognition accuracy and the computational simplicity, they showed appreciation for an analysis on short human sequences using the Z-curve methods.
Although the recognition of short coding sequences is considered an important issue (Catherine et al., 2002; Gotoh, 2008), up to now a large-scale analysis of the problem has not been performed. Hence, in this study, we have focused on the problem of supervised classifier assessment and feature selection for the identification of short coding sequences, where the class labels are known beforehand. Our aim is twofold: First, to find the best data-driven classifiers, various state-of-the-art algorithms have been extensively assessed according to the accuracy as well as tradeoff between sensitivity/specificity and the time requirements. Second, from the interpretability of the PLS technique and the Z-curve methods, the best combination of features has been selected for improving recognition accuracy and for further understanding of short exons. These works are promising for accelerating the development of gene-finding algorithms.
2. Databases and Methods
2.1. Databases
For comparison, we chose the same databases used by Gao and Zhang (2004). The databases consisted of dataset-1 and dataset-2, which contained two subsets (i.e., coding and noncoding fragments of the human DNA sequences, respectively). The coding fragments were used as positive samples, whereas the noncoding fragments were used as negative samples. Each subset of dataset-1 included 4,000 sequences with length longer than 210 bp. The coding sequences were extracted from the file 4813_Hum_CDS.fa (available at http://www.fruitfly.org/seq_tools/datasets/Human/coding_data/4813_hum_CDS.fa). The coding fragments with various window lengths were extracted from the beginning of the sequences. However, the coding fragments with various window lengths in dataset-2 were extracted from the short exons matched with known mRNAs. These exons were derived from the Exon-Intron Database (EID), which is based on GenBank (release 112) (Saxonov et al., 2000). The exons were divided into nine classes according to their length: 21–30, 30–42, 42–63, 63–87, 87–108, 108–129, 129–162, 162–192, and >192 bp. These nine classes of dataset-2 consisted of 206, 343, 977, 1840, 1865, 1937, 2538, 1590, and 2484 exons, respectively. The noncoding sequences were extracted from the files in the directory intron_v105 at the aforementioned website, including complete intron sequences of 462 human genes. The noncoding fragments used as negative samples of these two datasets were randomly extracted from the intron files with length longer than 200 bp. For the detailed procedure to construct the databases, see Gao and Zhang [2004].
2.2. The Z-curve methods
Considering the superiority of the Z-curve methods in feature extraction problems of short exons, they were adopted to extract features as the input variables of the classifiers.
Z-curve
The Z-curve is a powerful tool for visualizing and analyzing DNA sequences (Zhang and Zhang, 1991; Zhang, 1997b). For convenience, the phase-specific mononucleotide Z-curve parameters are briefly introduced here. The derivations of other parameters such as phase-specific/phase-independent di-nucleotides and tri-nucleotides parameters were illustrated in detail by Gao and Zhang (2004).
The Z-curve parameters for frequencies of phase-specific mononucleotides (3 × 3 = 9)
The frequencies of the bases A, C, G, and T occurring in an open reading frame (ORF) or a fragment of DNA sequence at the first, second, and third codon positions are denoted by ai, ci, gi, and ti, where i = 1, 2, 3, respectively. Based on the Z-curve methods, ai, ci, gi, and ti are mapped onto a point Pi in a three-dimensional space Vi, where i = 1, 2, 3, which are denoted by xi, yi, zi (Gao and Zhang, 2004).
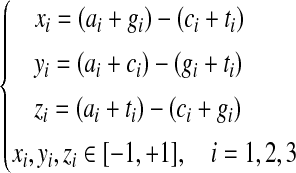 |
(1) |
By a selective combination of n variables or features derived from the Z-curve methods, an ORF or a fragment of DNA sequence can be represented by a scalar or a vector in an n-dimensional space V. In our study, n = 69, 93, 93′, 189, 252. For more details, see Gao and Zhang (2004) and the Supplementary Material (which is available at www.liebertonline.com/cmb).
2.3. Supervised classification methods
Although there are many pattern recognition algorithms, here we assess only supervised pattern recognition algorithms. The four linear classifiers used in our case are Fisher discriminant analysis (FDA), least squares (LS), partial least squares (PLS), and ridge regression (RR). For reference, the FDA used by Gao and Zhang (2004) must be included; LS, the most fundamental linear algorithm, was selected. Being a typical space compression technique, PLS was reasonably selected. Then RR was included as an example of the commonly used regularization methods for ill-posed problems. FDA defines the separation, in which the points are maximally separated in the sense that the ratio of between-classes variances to within-classes variances is maximized (Zhang and Wang, 2000; Mika, 2002). “Least squares” means that the overall solution minimizes the sum of the squares of the errors between observed values and the fitted values provided by a model. Instead of finding hyperplanes of maximum variance between the input variables and the labels, PLS creates orthogonal latent variables (LVs) that are linear combinations of the original variables. Thus, by the projection of the PLS algorithm, the n-dimensional X-space is compressed into the v-dimensional LV-space (v << n in common cases) to remove the noise and the multi-colinearity of the original variables (Geladi and Kowalski, 1986; Hoskuldsson, 1988). Ridge regression technique is the most commonly used method of regularization of ill-posed problems. To give preference to a particular solution with desirable properties, the regularization term is included in the objective function of RR. This regularization improves the conditioning of the problem, thus enabling a numerical solution (Hoerl, 1962; Hoerl and Kennard, 1970; Ghosh, 2003).
The four kernel-based classifiers were kernel fisher discriminant analysis (KFDA), kernel partial least squares (KPLS), support vector machine (SVM), and Gaussian process (GP). Among nonlinear supervised pattern recognition algorithms, up to now, SVM and neural networks are most widely used algorithms. Due to the limited space and the bad prediction performance, neural networks were not included. Unlike other learning algorithms, SVM is a structural risk minimization principle-based classification algorithm. Moreover, the use of a kernel in the SVM can be interpreted as an embedding of the input space into a high-dimensional feature space, where the classification is carried out without explicitly using this feature space (Vapnik, 1995; Cortes and Vapnik, 1995). KFDA and KPLS are kernel-based generalized algorithms of FDA and PLS, respectively (Taylor and Cristianini, 2004). For comparison with PLS, FDA, and SVM, they were selected for the current study. Gaussian Process (GP) is the comparatively newer method and can optimize parameters automatically; thus, it was selected to provide information for biologists. For GP, the training set Z is assumed to be drawn i.i.d. from an unknown, but fixed, joint probability distribution p(x, l). Following a Bayesian approach, the prediction of a label for a new observation xnew is obtained by computing the posterior probability distribution over labels and selecting the label that has the highest probability (Rasmussen and Williams, 2006; Williams and Barber, 1998).
For more detailed mathematical descriptions of the aforementioned eight classifiers, please refer to the Supplementary Material (which is available at www.liebertonline.com/cmb).
2.4. The performance of various classifiers
To evaluate the performance of an algorithm, we used the same measurements used by Gao and Zhang (2004). The sensitivity Sn is the proportion of coding sequences that have been correctly predicted as coding, Sn = TP/(TP + FN). The specificity Sp is the proportion of noncoding sequences that have been correctly predicted as noncoding, Sp = TN/(TN + FP). TP, TN, FP, and FN are fractions of true positive, true negative, false positive, and false negative predictions, respectively. The accuracy a is defined as the average of Sn and Sp. Thus, the goal in this study was to maximize the prediction accuracy a of the testing set as well as make a good tradeoff between Sn and Sp.
The cross-validation tests were adopted to ensure the validation of the results. For dataset-1, twofold cross-validation test was performed 10 times. The coding and the noncoding sequences were randomly divided into two identical parts: parts 1 and 2. Part 1 was taken as the training set, and part 2 was taken as the testing set. The sensitivity, the specificity, and the accuracy of the algorithms based on part 2 were calculated. This random division procedure was repeated 10 times for the sequences with various window lengths. Accounting for the comparatively smaller size of dataset-2, a 10-fold cross-validation procedure was performed, in which dataset-2 was divided into 10 parts and tested on the 10 different one-tenths, while trained on the remaining nine-tenths.
3. Results and Discussion
3.1. Comparison of the four classic linear classifiers
3.1.1. Comparing the prediction accuracy of the four classic linear classifiers
Owing to computational simplicity, linear classifiers are still widely used methods. Moreover, owing to their interpretability, they are always used to find key variables in pattern recognition. In the current study, FDA was evaluated as a baseline classifier to be compared with other linear classifiers. As exemplified by Gao and Zhang (2004), good results were achieved with FDA using 69 and 189 Z-curve variables. Therefore, in this article, we used their results as a reference. In addition, to find the optimal combination of features, all 252 Z-curve variables (the variable description is available in Table S1, Supplementary Material, which is available at www.liebertonline.com/cmb) were used together to carry out pattern analysis to evaluate their contributions fairly. As the Z-curve methods could extract features of any length fragments, the fragments with 30- and 21-bp length were also included to investigate the performance of linear classifiers. The exon prediction results using different linear classifiers for fragments with lengths of 192, 42, 30, and 21 bp of dataset-2 are listed in Table 1. Due to limited space, fragments with other lengths of dataset-2 and the corresponding results of dataset-1 are listed in Tables S2 and S3 (Supplementary Material is available at www.liebertonline.com/cmb)
Table 1.
Prediction Results of Dataset-2 Using Various Linear Classifiers
| |
|
Number of Z curve variables |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |
|
69 |
189 |
252 |
|||||||||
| Length | Classifiers |  |
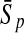 |
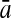 |
Std | 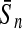 |
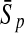 |
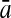 |
Std | 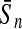 |
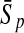 |
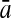 |
Std |
| 192 bp | FDA | 96.36 | 96.74 | 96.55 | / | 96.09 | 96.99 | 96.54 | / | 88.93 | 85.41 | 87.17 | 0.47 |
| PLS | 98.52 | 95.49 | 97.01 | 0.89 | 98.40 | 96.23 | 97.31 | 0.90 | 98.64 | 96.39 | 97.52 | 0.90 | |
| LS | 98.23 | 95.16 | 96.70 | 0.89 | 98.32 | 95.65 | 96.98 | 0.90 | 91.43 | 89.38 | 90.4 | 1.19 | |
| RR | 98.23 | 95.12 | 96.68 | 0.89 | 98.52 | 95.57 | 97.05 | 0.90 | 98.56 | 96.02 | 97.29 | 0.90 | |
| 42 bp | FDA | 90.84 | 80.74 | 80.79 | 80.18 | 81.50 | 80.84 | 77.31 | 73.39 | 75.35 | 0.56 | ||
| PLS | 87.61 | 78.75 | 83.18 | 0.70 | 87.82 | 81.95 | 84.88 | 0.75 | 88.44 | 82.46 | 85.45 | 0.78 | |
| LS | 87.20 | 76.38 | 81.79 | 0.71 | 85.65 | 78.54 | 82.10 | 0.77 | 82.67 | 77.00 | 79.83 | 1.09 | |
| RR | 89.78 | 74.22 | 82.00 | 0.69 | 89.78 | 74.53 | 82.15 | 0.72 | 89.78 | 75.66 | 82.72 | 0.74 | |
| 30 bp | FDA | 82.83 | 68.17 | 75.50 | 77.26 | 71.10 | 74.18 | 73.74 | 67.00 | 70.37 | 0.41 | ||
| PLS | 82.83 | 73.16 | 77.99 | 0.65 | 81.07 | 74.33 | 77.70 | 0.84 | 81.36 | 76.38 | 78.87 | 0.79 | |
| LS | 81.95 | 69.93 | 75.94 | 0.68 | 71.98 | 69.64 | 70.81 | 0.84 | 71.40 | 64.95 | 68.17 | 1.19 | |
| RR | 87.81 | 60.55 | 74.18 | 0.59 | 82.53 | 62.90 | 72.72 | 0.70 | 78.43 | 65.53 | 71.98 | 0.75 | |
| 21 bp | FDA | 71.29 | 71.78 | 71.53 | 68.81 | 69.80 | 69.30 | 63.86 | 62.87 | 63.37 | 0.28 | ||
| PLS | 74.26 | 79.70 | 76.98 | 0.64 | 76.73 | 79.70 | 77.22 | 0.82 | 78.71 | 79.70 | 79.21 | 0.79 | |
| LS | 73.28 | 71.29 | 72.28 | 0.71 | 71.78 | 69.80 | 70.79 | 1.04 | 70.30 | 66.34 | 68.32 | 1.41 | |
| RR | 80.20 | 55.94 | 68.07 | 0.57 | 80.69 | 64.36 | 72.52 | 0.75 | 75.74 | 71.78 | 73.76 | 0.92 | |
The average accuracies of PLS models, which were the best ones among the algorithms evaluated here, are shown in boldface. The results of FDA calculated by Gao and Zhang (2004) are shown in italics. Std, standard deviations of prediction results; FDA, Fisher discriminant analysis; LS, least squares; PLS, partial least squares; RR, ridge regression.
The real lengths of the exons of dataset-1 were found to be longer than 210-bp, and the fragments were extracted from their beginning. In other words, only a part of the sequence information was used in pattern recognition. Using the 69 and the 189 Z-curve variables, the prediction performances of the linear classifiers were quite similar to each other. Only by using all 252 Z-curve variables were the accuracies of PLS of different length fragments slightly better than that of other methods, as shown in Table S3 (Supplementary Material is available at www.liebertonline.com/cmb). On the other hand, the coding fragments with various lengths in dataset-2 were extracted from the short exons of CDSs. For example, the 63-bp fragments were extracted from the exons of size 63–87 bp. The results in Tables 1 and S2 showed that the accuracy of PLS was higher than that of other classifiers, regardless of the length class and the Z-curve variables. Additionally, for a given set of the Z-curve variables, the shorter the fragment, the larger the difference between the PLS performance and that of others. Furthermore, the highest accuracy was achieved unexceptionally by PLS using the 252 Z-curve variables.
According to the definition of the phase-independent and the phase-specific mononucleotide variables of the Z-curve methods, the following equation could be deduced (Zhang and Zhang, 1991).
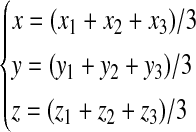 |
(2) |
A similar linear relationship between the phase-independent and the phase-specific di-nucleotides/tri-nucleotides variables of the Z-curve methods can be deduced easily. In other words, there are strong multi-collinear relationships among the 252 Z-curve variables.
It is well known that the multi-colinearity among variables is the main factor limiting the performance of ordinary data-driven techniques, namely, FDA and LS. However, PLS could overcome this interference by extracting an appropriate number of orthogonal latent variables from the original data space. Meanwhile, the idea behind ridge regression (RR) is at the heart of the “bias-variance tradeoff” issue. It is an illustration of the fact that a biased estimator may outperform an unbiased estimator, provided its variance is small enough (Hoerl, 1962; Hoerl and Kennard, 1970; Ghosh, 2003). Consequently, in this case, the prediction results of PLS and RR turned out to be more accurate than those of LS and FDA.
It is worthwhile pointing out that the basic methodology of the PLS modeling procedure is that the weights used to determine the linear combinations of the original variables are proportional to the maximum covariance among input variables and labels (Helland, 1988; Wold et al., 1999; Burnham et al., 1999). Comparing the results across different combinations of the Z-curve variables and different lengths of fragments, the PLS was found to perform consistently extremely well.
3.1.2. The PLS-based feature selection of Z-curve variables
Apart from feature extraction, in pattern recognition, feature selection, also known as variable selection, is another important aspect for improving the recognition results. Although the prediction accuracies of linear supervised classification algorithms are usually lower than that of nonlinear classifiers, but benefiting from the comparatively simple methodologies, they have satisfactory interpretability of their models which could be used for feature selection.
To select a proper set of features, the contribution of each Z-curve variable to pattern recognition models must be estimated quantitatively. For univariate regression problem, the value of the regression coefficient of each variable is the reasonable quantitative measurement of its contribution. Considering the predominant performance, the regression coefficients of PLS model were selected to estimate the contributions of Z-curve variables.
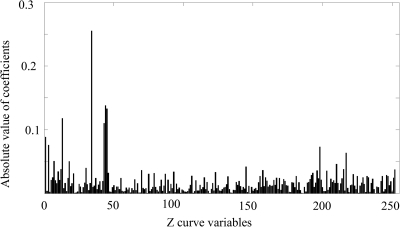
The absolute values of regression coefficients corresponding to the 252 Z-curve variables in the PLS model of dataset-2 are shown in Figure 1 and Figures S1–S3 (Supplementary Material is available at www.liebertonline.com/cmb). According to the results shown in these figures, it is clear that irrespective of the length of the fragments, only a few variables' regression coefficients are remarkably larger than the others. Consequently, 93′ Z-curve variables (denoted as 93′ to differentiate from the 93 Z-curve variables used by Gao and Zhang [2004]) were chosen by means of the feature selection power of PLS algorithm. The descriptions of the 93′ Z-curve variables are shown in Table 2. The prediction results of the two datasets using PLS and the 93′ Z-curve variables are listed in Tables 3 and S4, respectively. It is obvious that the performance of the PLS classifier is improved by the selected 93′ Z-curve variables.
FIG. 1.
The absolute values of regression coefficients of the 252 Z-curve variables in the PLS model (fragments with 192-bp length of dataset-2). In order to identify key variables that characterize different patterns, the contribution of each variable to pattern recognition models is necessary to estimate quantitatively. And for univariate regression problems, the regression coefficient of each variable is the reasonable quantitative measurement. According to the results, it is clear that only a few variables' coefficients are remarkably larger than other variables'.
Table 2.
Descriptions of the Selected 93′ Z-Curve Variables
| Variables | Descriptions | |
|---|---|---|
| x1, y1, z1, x2, y2, z2, x3, y3, z3, | Phase-specific parameters of mononucleotide | |
 |
Phase-specific parameters of di-nucleotides | |
|
Phase-specific parameters of tri-nucleotides | |
| x, y, z | Phase-independent parameters of mononucleotide | |
| xA, yA, zA, xT, yT, zT, xC, yC, yG | Phase-independent parameters of di-nucleotide | |
| xAT, zAT, yAG, xTA, zTA, xTT, yTT, zTT, xCA, xCT, zCT, xCC, zCC, xCG, yCG, zGA, xGT, xGC, yGC, zGC, yGG, zGG | Phase-independent parameters of tri-nucleotide |
Table 3.
Prediction Results of Dataset-2 Using 93′ Z-Curve Variables by Means of the PLS Method
| |
|
Fragment length (bp) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variables | Results (%) | 192 | 162 | 129 | 108 | 87 | 63 | 42 | 30 | 21 |
| 252 | 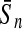 |
98.64 | 98.97 | 96.85 | 96.94 | 93.51 | 90.26 | 88.44 | 81.94 | 80.20 |
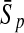 |
96.39 | 95.51 | 94.86 | 92.33 | 90.26 | 86.93 | 82.46 | 74.62 | 76.24 | |
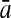 |
97.52 | 97.24 | 95.85 | 94.63 | 91.88 | 89.62 | 85.45 | 78.28 | 78.22 | |
| 93′ | 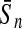 |
98.85 | 98.97 | 97.41 | 97.20 | 93.56 | 91.77 | 88.64 | 84.59 | 84.16 |
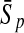 |
96.72 | 96.34 | 94.42 | 92.48 | 90.42 | 85.80 | 81.02 | 76.38 | 79.21 | |
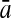 |
97.78 | 97.65 | 95.91 | 94.84 | 91.99 | 88.78 | 84.83 | 80.48 | 81.68 | |
From the descriptions of the Z-curve variables, we could see that the frequencies of “TT,” “TG,” and “GG” di-nucleotides were much more important than those of other di-nucleotides. Additionally, the most important variable was the phase-specific parameter of tri-nucleotides transformed from the Z-curve methods:
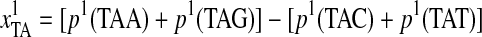 , where “TAA (ochre)”/“TAG (amber)” are both stop codons and “TAC”/“TAT” are both Tyrosine codons. Thus,
, where “TAA (ochre)”/“TAG (amber)” are both stop codons and “TAC”/“TAT” are both Tyrosine codons. Thus, 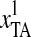 means the difference between the frequencies of stop codons and Tyrosine codons. Meanwhile, “TGT” and “TGC” are both Cysteine codons, “TGA (opal)” is the stop codon, and “TGG” is the Tryptophan codon. Hence, the definitions of the first, sixth, seventh, and twelfth Z-curve variables indicated that the frequencies of the three kinds of stop codons, Tyrosine codons, and Cysteine codons were the key features for discriminating coding and noncoding gene sequences.
means the difference between the frequencies of stop codons and Tyrosine codons. Meanwhile, “TGT” and “TGC” are both Cysteine codons, “TGA (opal)” is the stop codon, and “TGG” is the Tryptophan codon. Hence, the definitions of the first, sixth, seventh, and twelfth Z-curve variables indicated that the frequencies of the three kinds of stop codons, Tyrosine codons, and Cysteine codons were the key features for discriminating coding and noncoding gene sequences.
3.2. Comparison of the four kernel-based classifiers
The performance of the kernel-based classifiers was evaluated by prediction accuracy, tradeoff between sensitivity and specificity, time requirements, etc. There are multiple widely used kernels for SVM, KPLS, and other kernel based methods such as linear, quad, and sigmoid kernels. But according to our practice, the prediction performance of the rbf kernel was much higher than that of other kernels. Thus, due to the limited space and for fair comparison, we used the rbf kernel for SVM, KPLS, and KFDA.
The prediction results of the two datasets using different sets of the Z-curve variables and the four kernel-based classifiers are listed in Tables S5 and S6 (Supplementary Material is available at www.liebertonline.com/cmb):
⋄ Comparing the accuracies of the kernel-based classifiers:
The results listed in Tables S5 and S6 show that, for each length class, the highest accuracy was almost achieved by KPLS model using the 93′ Z-curve variables. The results prove that the 93′ Z-curve variables are the optimal features for recognition of short exons.
The highest accuracies calculated by the four kernel-based classifiers are shown in Table 4. It shows that, for shorter fragments, the accuracy superiority of KPLS was much more remarkable over other kernel-based classifiers. For example, for 42-bp fragments of dataset-2, the highest prediction accuracy obtained by KPLS was 88.54%, which was 0.77% higher than that of SVM, 2.58% higher than that of GP, and 1.55% higher than that of KFDA; for 30-bp fragments of dataset-2, the highest accuracy obtained by KPLS was 85.61%, which was 1.61% higher than that of SVM, 8.64% higher than that of GP, and 7.03% higher than that of KFDA.
Table 4.
Best Prediction Results of FDA, PLS, and the Four Kernel-Based Classifiers
| |
|
Dataset-1 results (%) |
Dataset-2 results (%) |
||||
|---|---|---|---|---|---|---|---|
| |
|
Length of fragments |
Length of fragments |
||||
| Classifiers | Results (%) | 192 bp | 42 bp | 30 bp | 192 bp | 42 bp | 30 bp |
| FDA | 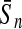 |
96.28 | 82.99 | 82.82 | 96.36 | 80.18 | 82.83 |
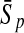 |
96.20 | 83.83 | 77.94 | 96.74 | 81.50 | 68.17 | |
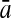 |
96.24 | 83.41 | 80.38 | 96.55 | 80.84 | 75.50 | |
| PLS | 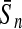 |
98.40 | 86.59 | 82.91 | 98.85 | 88.44 | 84.59 |
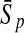 |
95.27 | 81.18 | 79.48 | 96.72 | 82.46 | 76.38 | |
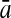 |
96.83 | 83.89 | 81.19 | 97.78 | 85.45 | 80.48 | |
| KPLS | 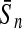 |
98.36 | 87.09 | 84.99 | 99.50 | 89.78 | 86.64 |
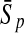 |
97.98 | 86.08 | 81.67 | 98.52 | 87.30 | 84.59 | |
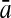 |
98.16 | 86.59 | 83.33 | 99.01 | 88.54 | 85.61 | |
| SVM | 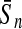 |
96.86 | 85.84 | 83.25 | 98.65 | 89.26 | 87.52 |
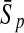 |
97.16 | 85.78 | 81.94 | 98.63 | 86.27 | 80.48 | |
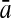 |
97.51 | 85.81 | 82.59 | 98.64 | 87.77 | 84.00 | |
| GP | 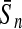 |
97.88 | 86.58 | 83.74 | 98.89 | 88.75 | 80.48 |
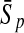 |
97.67 | 82.80 | 79.91 | 97.13 | 83.18 | 73.45 | |
 |
97.78 | 84.69 | 81.82 | 98.01 | 85.96 | 76.97 | |
| KFDA | 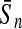 |
96.50 | 84.74 | 87.88 | 96.43 | 90.19 | 77.55 |
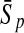 |
96.32 | 86.62 | 76.64 | 99.22 | 83.80 | 79.60 | |
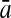 |
96.43 | 85.68 | 82.26 | 97.82 | 86.99 | 78.58 | |
For comparison, the results obtained by Gao and Zhang (2004) with FDA and the best results of the four linear classifiers that were achieved by the PLS method are shown. The results of FDA calculated by Gao and Zhang (2004) are shown in italics. The average accuracies, which were the best ones among the algorithms evaluated here, are shown in boldface. FDA, Fisher discriminant analysis; PLS, partial least squares; KFDA, kernel Fisher discriminant analysis; KPLS, kernel partial least squares; SVM, support vector machine; GP, Gaussian process.
⋄ Comparing the accuracies of linear and kernel-based classifiers:
Because of limited space, only the best results of the four linear classifiers which were achieved by PLS method are shown in Table 4. For comparison, the results obtained by Gao and Zhang (2004) with FDA are also shown. It is obvious that the shorter the fragment, the higher the superiority of KPLS. In particular, using KPLS and the 93′ Z-curve variables, the prediction accuracy for 42-bp fragments of dataset-2 was improved as high as 7.7% compared with the results obtained by Gao and Zhang (2004) using FDA.
On the other hand, for other kernel-based classifiers, there existed some cases in which the prediction accuracies were not higher than that of PLS.
⋄ Comparing the tradeoff between sensitivity and specificity of kernel-based classifiers:
One thing to be noted is that comparing classifiers only based on accuracy often does not provide a fair comparison. A better solution to this problem is to compare the classifiers both by the average accuracy of prediction and by the tradeoff between sensitivity and specificity. More attention should be paid when recognizing short coding sequence. Similar to PLS, KPLS can also avoid over-/under-study, and can overcome multi-colinearity of variables by selecting an appropriate number of latent variables (Rosipal and Trejo, 2001; Rosipal, 2003). Thus, KPLS is capable of making good tradeoff between Sn and Sp by the optimization of the number of LVs. For instance, by taking the results of 30 bp shown in Table 4, the differences between Sn and Sp of the four kernel-based algorithms were 2.05% (KPLS), 7.04% (SVM), 7.03% (GP), and 2.05% (KFDA). The results made it clear that considering both the accuracy and the tradeoff between Sn and Sp, the performance of KPLS was better than that of KFDA, GP, and SVM.
⋄ Comparing the time requirements of kernel-based classifiers:
Through the so-called kernel trick mapping, it is “only” necessary to handle an m × m (m is the number of observations) kernel matrix, and the kernel-based technique limitations are much more related to the number of observations than to the number of variables (Cortes and Vapnik, 1995). However, the CPU time of calculating the inner product of the 93′ variables is much shorter than that of the 189 or 252 variables. For example, when using the KPLS method as a classifier, for 2000 positive samples and 2000 negative samples, the computing time of one operation of the 93′ variables was 1839.4 s, of the 189 variables was 3359.9 s, and of the 252 variables was 4300.5 s. (All algorithms were operated in MATLAB R2009a; the operation system was a 64-bit Windows 7, and the personal computer had Intel Core 2 Quad processor Q8200 2.33 GHz with 8-GB memory.)
To find the optimum parameters, it is necessary to run the program dozens of times for each set of data. The computing time could be expanded to be a heavy load when using 189/252 variables. Thus, accounting for both the prediction performance and the time consumption, KPLS with the 93′ Z-curve variables was the best choice for short exon recognition. The corresponding results of fragments with various window lengths of dataset-1 and dataset-2 are listed in Table S7 (Supplementary Material is available at www.liebertonline.com/cmb).
In summary, for short coding sequence recognition, PLS can be used to obtain the necessary knowledge and preliminary results as soon as possible, and then KPLS becomes the first choice for further research.
4. Conclusion
This study did not aim to add another algorithm to the existing collection of supervised classification tools. Our approach was to facilitate the selection of more sophisticated methods and highlight optimum combinations of Z-curve parameters for successful implementation of classification-based studies. Based on the databases constructed here and with considerations of accuracy as well as the tradeoff between sensitivity/specificity and computing time, PLS and KPLS were recommended as linear and kernel-based classifiers for recognizing short coding sequences of human genes.
Other main conclusions drawn from our analyses were that the 93′ Z-curve variables were verified to be the best features for short exon recognition. With the use of these 93′ variables, the performances of the classifiers were improved remarkably without increasing computing time. According to the mechanism of the Z-curve methods of the 93′ variables, the frequencies of three kinds of stop codons, Tyrosine codons, Cysteine codons, and “TT”/“TG”/“GG” di-nucleotides, were found to be the most essential peculiarities for distinguishing short coding and noncoding gene sequences.
Supplementary Material
Acknowledgments
We are grateful to Dr. Feng Gao, the Department of Physics, Tianjin University, China, for providing the data. This work was supported in part by the National Natural Science Foundation of China (grant 31000592) and the Doctoral Fund of the Ministry of Education of China (grant 200800561005).
Disclosure Statement
No competing financial interests exist.
References
- Bernal A. Crammer K. Hatzigeorgiou A., et al. Global discriminative learning for higher-accuracy computational gene prediction. PLoS Comput Biol. 2007;3:e54. doi: 10.1371/journal.pcbi.0030054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besemer J. Borodovsky M. GeneMark: web software for gene finding in prokaryotes, eukaryotes and viruses. Nucleic Acids Res. 2005;33:W451–W454. doi: 10.1093/nar/gki487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borodovsky M. McIninch J. Genmark: parallel gene recognition for both DNA strands. Comput. Chem. 1993;17:123–133. [Google Scholar]
- Burge C. Karlin S. Prediction of complete gene structures in human genomic DNA. J. Mol. Biol. 1997;268:78–94. doi: 10.1006/jmbi.1997.0951. [DOI] [PubMed] [Google Scholar]
- Burnham A.J. MacGregor J.F. Viveris R. Latent variable multivariate regression modeling. Chemometrics Intell. Lab. Syst. 1999;48:167–180. [Google Scholar]
- Catherine M. Marie-France S. Thomas S., et al. Current methods of gene prediction, their strengths and weaknesses. Nucleic Acids Res. 2002;30:4103–4117. doi: 10.1093/nar/gkf543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortes C. Vapnik V. Support-vector networks. Mach. Lear. 1995;20:273–297. [Google Scholar]
- Gao F. Zhang C.T. Comparison of various algorithms for recognizing short coding sequences of human genes. Bioinformatics. 2004;20:673–681. doi: 10.1093/bioinformatics/btg467. [DOI] [PubMed] [Google Scholar]
- Geladi P. Kowalski B.R. Partial least squares regression: a tutorial. Anal. Chem. Acta. 1986;185:1–17. [Google Scholar]
- Ghosh D. Penalized discriminant methods for the classification of tumors from gene expression data. Biometrics. 2003;59:992–1000. doi: 10.1111/j.0006-341x.2003.00114.x. [DOI] [PubMed] [Google Scholar]
- Gotoh O. Direct mapping and alignment of protein sequences onto genomic sequence. Bioinformatics. 2008;24:2438–2444. doi: 10.1093/bioinformatics/btn460. [DOI] [PubMed] [Google Scholar]
- Guigo R. Knudsen S. Drake N., et al. Prediction of gene structure. J. Mol. Biol. 1992;226:141–157. doi: 10.1016/0022-2836(92)90130-c. [DOI] [PubMed] [Google Scholar]
- Helland I.S. On structure of partial least squares regression. Commun. Stat. Elements Simul. Comput. 1988;17:581–607. [Google Scholar]
- Hoerl A.E. Application of ridge analysis to regression problems. Chem. Eng. Prog. 1962;58:54–59. [Google Scholar]
- Hoerl A.E. Kennard R. Ridge regression: biased estimation for nonorthogonal problems. Technometrics. 1970;12:55–67. [Google Scholar]
- Hoskuldsson A. PLS regression methods. J. Chemometrics. 1988;2:211–228. [Google Scholar]
- Liu H. Yu L. Toward integrating feature selection algorithms for classification and clustering. IEEE TKDE. 2005;17:491–502. [Google Scholar]
- Lukashin A.V. Borodovsky M. GeneMark.hmm: new solutions for gene finding. Nucleic Acids Res. 1998;26:1107–1115. doi: 10.1093/nar/26.4.1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mika S. Kernel Fisher discriminants [Ph.D. dissertation] University of Technology; Berlin, Germany: 2002. [Google Scholar]
- Rasmussen C.E. Williams C.K.I. Gaussian Processes for Machine Learning. MIT Press; Cambridge, MA: 2006. [Google Scholar]
- Rosipal R. Kernel partial least squares for nonlinear regression and discrimination. Neural Netw. World. 2003;13:291–300. [Google Scholar]
- Rosipal R. Trejo L.J. Kernel partial least squares regression in reproducing kernel hilbert space. J. Mach. Learn. Res. 2001;2:97–123. [Google Scholar]
- Saeys Y. Rouze P. Van de Peer Y. In search of the small ones: improved prediction of short exons in vertebrates, plants, fungi and protists. Bioinformatics. 2007;23:414–420. doi: 10.1093/bioinformatics/btl639. [DOI] [PubMed] [Google Scholar]
- Salzberg S. Delcher A.L. Fasman K.H., et al. A decision tree system for finding genes in DNA. J. Comput. Biol. 1998;5:667–680. doi: 10.1089/cmb.1998.5.667. [DOI] [PubMed] [Google Scholar]
- Saxonov S. Daizadeh I. Fedorov A., et al. EID: the Exon-Intron Database—an exhaustive database of protein-coding intron-containing genes. Nucleic Acids Res. 2000;28:185–190. doi: 10.1093/nar/28.1.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor J.S. Cristianini N. Kernel Methods for Pattern Analysis. Cambridge University Press; Cambridge, UK: 2004. [Google Scholar]
- Vapnik V. The Nature of Statistical Learning Theory. Springer-Verlag; New York: 1995. [Google Scholar]
- Varshavsky R., et al. Novel unsupervised feature filtering of biological data. Bioinformatics. 2006;22:e507–e513. doi: 10.1093/bioinformatics/btl214. [DOI] [PubMed] [Google Scholar]
- Williams C.K.I. Barber D. Bayesian classification with Gaussian processes. IEEE Trans. Pattern Anal. 1998;20:1342–1351. [Google Scholar]
- Wold S. Sjostrom M. Eriksson L. PLS in chemistry, 2006–2020. In: Schleyer P.V.R., et al., editors. The Encyclopedia of Computational Chemistry. Wiley; Chichester, UK: 1999. [Google Scholar]
- Zhang C.T. A symmetrical theory of DNA sequences and its applications. J. Theor. Biol. 1997b;187:297–306. doi: 10.1006/jtbi.1997.0401. [DOI] [PubMed] [Google Scholar]
- Zhang C.T. Wang J. Recognition of protein coding genes in the yeast genome at better than 95% accuracy based on the Z curve. Nucleic Acids Res. 2000;28:2804–2814. doi: 10.1093/nar/28.14.2804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C.T. Zhang R. Analysis of distribution of bases in the coding sequences by a diagrammatic technique. Nucleic Acids Res. 1991;19:6313–6317. doi: 10.1093/nar/19.22.6313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang M.Q. Identification of protein coding regions in the human genome by quadratic discriminant analysis. Proc. Natl. Acad. Sci. USA. 1997a;94:565–568. doi: 10.1073/pnas.94.2.565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang M.Q. Discriminant analysis and its application in DNA sequence motif recognition. Brief. Bioinform. 2000;1:331–342. doi: 10.1093/bib/1.4.331. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.