Abstract
A novel isothermal titration calorimetry (ITC) method was applied to investigate RNA helical packing driven by the GAAA tetraloop–receptor interaction in magnesium and potassium solutions. Both the kinetics and thermodynamics were obtained in individual ITC experiments, and analysis of the kinetic data over a range of temperatures provided Arrhenius activation energies (ΔH‡) and Eyring transition state entropies (ΔS‡). The resulting rich dataset reveals strongly contrasting kinetic and thermodynamic profiles for this RNA folding system when stabilized by potassium versus magnesium. In potassium, association is highly exothermic (ΔH25°C = −41.6 ± 1.2 kcal/mol in 150 mM KCl) and the transition state is enthalpically barrierless (ΔH‡ = −0.6 ± 0.5). These parameters are sigificantly positively shifted in magnesium (ΔH25°C = −20.5 ± 2.1 kcal/mol, ΔH‡ = 7.3 ± 2.2 kcal/mol in 0.5 mM MgCl2). Mixed salt solutions approximating physiological conditions exhibit an intermediate thermodynamic character. The cation-dependent thermodynamic landscape may reflect either a salt-dependent unbound receptor conformation, or alternatively and more generally, it may reflect a small per-cation enthalpic penalty associated with folding-coupled magnesium uptake.
INTRODUCTION
Proper tertiary folding of RNA is crucial to its array of enzymatic and regulatory functions (1). Due to the significant increase in anionic charge density and structure-dependent apposition of phosphate oxygens that accompany RNA tertiary folding, metal ions play a significant and nuanced role in the folding equilibrium. Beginning with the seminal series of tRNA folding studies (2–8), the highly stabilizing role of the divalent cation magnesium (Mg2+) has been an experimental focal point. Misra and Draper (9) demonstrated that Mg2+ can confer this stability to folded tRNA entirely through diffuse (hydrated) ion accumulation, consistent with the fact that tRNA can fold in magnesium salt or monovalent salt alone (2). For some other RNA structures, magnesium is directly coordinated and essential for folding (10,11); in principle, intermediate hydration states are also possible although the prevalence and thermodynamic stability afforded by these types of ions is not well understood. Such molecular considerations may underlie the systematic underestimation of magnesium accumulation by Poisson–Boltzmann theory (12). As theoretical work continues in this area (13–15), additional complementary experiments studying this crucial component of RNA stability are also necessary.
In addition to the nature of association (11) and the change in charge density accompanying RNA folding (16), the quantitative role of magnesium depends strongly on the concentration and identity of other metal ions (17). This is an important consideration given in vivo free potassium (K+) concentrations near 150 mM. The Tetrahymena thermophila Group I self-splicing intron provides an excellent case study. For the P4–P6 domain of this ribozyme, the GAAA tetraloop–receptor tertiary interaction can form in solutions containing either MgCl2 or monovalent salt (NaCl) alone (18–20), but formation of the A-rich bulge tertiary contact requires magnesium (20). While the uptake of Mg2+ and Na+ is tied to tertiary folding, and addition of either improves folding stability via a reduced entropic penalty, in some concentration regimes when both ions are present they act competitively (21). Interestingly, salt-dependent differences in RNA folding kinetics have also been observed. For example, at salt concentrations that elicit similar overall folding stabilities, intron folding is faster when driven by monovalent cations than when driven by a multivalent cation such as magnesium (22–24). The underlying thermodynamic composition of these findings is not yet understood.
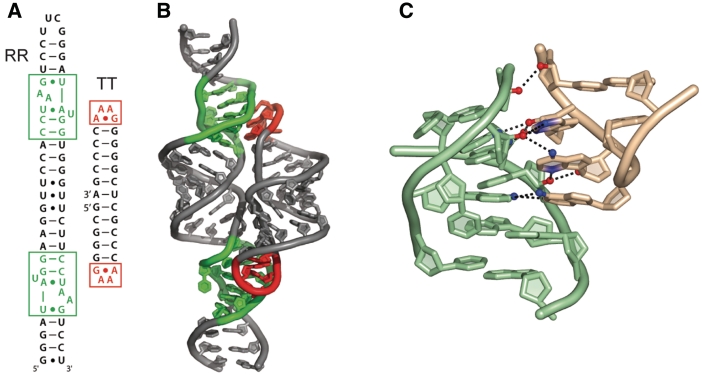
The ubiquitous GAAA tetraloop receptor mediates helical packing (25) in Groups I and II self-splicing introns (26–28) and RNase P (29,30). In this work we examine a bimolecular helical packing event driven by this interaction (Figure 1) (31), in solutions containing either one of the physiologically dominant cations, K+ or Mg2+. This domain separation strategy has proven successful in determining RNA folding principles (32–35) and allows access to the rich thermodynamic information provided by calorimetry. The approach involves two helical RNA molecules, one containing two tetraloop receptor motifs phased by one helical turn (termed RR) and another containing two cognate GAAA tetraloops (TT). The helices therefore assemble in parallel into a well-defined structure mediated solely by the tetraloop–receptor interaction (Figure 1), as demonstrated by our previous thermodynamic investigation (32) and excellent agreement with single molecule fluorescence resonance energy transfer (FRET) studies of tethered tetraloop receptors (36). We have also solved the nuclear magnetic resonance structure of this interaction, which within experimental error is superimposable with previous crystal structures (18,28,37).
Figure 1.
Structure of the TT–RR system. Red/salmon: tetraloop; green/mint: receptor. (A) Secondary structure of dual receptor (RR) and dual tetraloop (TT) constructs employed in this study. (B) Cartoon model of TT–RR complex. (C) Close-up view of tetraloop–receptor interaction, structurally stabilized by stacking of the tetraloop 5′ adenine on the 3′ adenine of the receptor AA platform, in addition to 10 intermolecular hydrogen bonds (PDB code 1HR2).
Mg2+ accumulation in the tetraloop–receptor contact is entirely or largely diffuse (10,11) in character (18,28). Thus a direct comparison of folding in MgCl2 and KCl can potentially uncover core energetic differences in Mg2+ and K+ accumulation. Here, by application of a novel titration calorimetry approach, we characterize the thermodynamic and kinetic landscape of tetraloop–receptor mediated helical packing interaction when stabilized by either K+ or Mg2+. We find that the thermodynamic and kinetic profiles for tetraloop–receptor association are indeed significantly dependent on the identity of the cation, such that the transition state enthalpy barrier is on average 9 kcal/mol larger and the overall binding enthalpy is 19 kcal/mol less exothermic in MgCl2 relative to the values in KCl.
MATERIALS AND METHODS
Preparative methods
TT and RR RNA were prepared by in vitro transcription and quantitated as described previously (32,37). All samples were prepared for calorimetry by extensive dialysis. Magnesium solutions contained 20 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) and MgCl2 at the stated concentration; potassium solutions contained 20 mM HEPES, 1 mM ethylenediaminetetraacetic acid, and the stated KCl concentration. Both solutions were titrated to pH 7.0 at room temperature before dialysis.
ITC thermodynamics analysis
Binding data were analyzed as described previously. A small fraction of TT misfolds during preparation (32). This is accounted for using a TT ‘activity’ term in the binding data and in [RNA]free determinations used in kinetics analysis below; the fraction of active TT in the experiments herein ranged from 0.75–1.0. Error estimates throughout this work reflect a potential uncertainty in the active TT concentration of ±10%. As per standard protocol, the first data point is removed from analysis due to syringe dead volume complications.
ITC kinetics analysis
Following baseline subtraction and deconvolution [(38), Supplementary Data], an injection power trace reflects the real-time derivative of the negative of heat evolution within the calorimeter cell, and subsequent integration results in the negative of the corresponding heat evolution as a function of time (Qev). Qev for each injection is approximately described as the time-dependent concentration of new complex formed [C*(t)] scaled by the binding enthalpy and the sample cell volume (V0 = 1.42 ml).
| (1) |
The equilibrium involves three species, so knowledge of the total TT and RR concentrations reduces the description of all solution concentrations to a single degree of freedom, which can be defined in terms of the displacement from equilibrium, λ. Here we define λ as the difference between the equilibrium concentration [C]eq and the current concentration [C]. The reaction rate can then be written
| (2) |
Assuming only that Kd = koff/kon, Equation (3) is the resulting most general expression for λ, which cannot be expressed analytically.
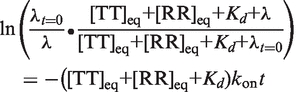 |
(3) |
Here λt=0 is the displacement from equilibrium following addition of RNA. More precisely in the case of an ITC experiment, it is the displacement at a theoretical time point following the injection period but preceding formation of any new complexes. λt=0 also reflects concentration changes caused by the addition of titrant and by the dilution of all species due to the injection volume (λt=0 = [C]eq−[C]t=0+, where [C]t=0+ is the starting [C] after accounting for the injection-caused dilution). Equation (3) shows that in the most general case, determination of λ(t) requires prior knowledge of kon, Ka (i.e. koff), and the total starting concentrations. In our application, the latter two terms are known: the total RNA concentrations are defined for each injection by the experimental setup, and Ka is obtained directly in the same experiment or through an extrapolation from higher temperature according to the van't Hoff equation.
Because λ cannot be determined analytically, its numerical solution from Equation (3) is wrapped within a least squares procedure for determining kon. The predicted heat evolution function is given by
| (4) |
where λt=0 is a known quantity defined by the Ka and the RNA concentrations and λ is a function of kon. Data were fit to a time regime starting at the minimum in the raw power trace (to exclude the injection period from analysis), and the final fitted time point never exceeded 10 times a prior-estimated half-time (to avoid over-weighting the baseline). Only injections from the first half of a titration were analyzed because signal-to-noise decreases significantly for subsequent injections.
Kinetic data fitting may be performed by integrating the post-deconvolution power trace to obtain Qev for least squares minimization with target Equation (4). Alternatively, Equations (3) and (4) can be differentiated for comparison with the deconvolved power trace (Edc). We implemented the latter approach here (Figure 2).
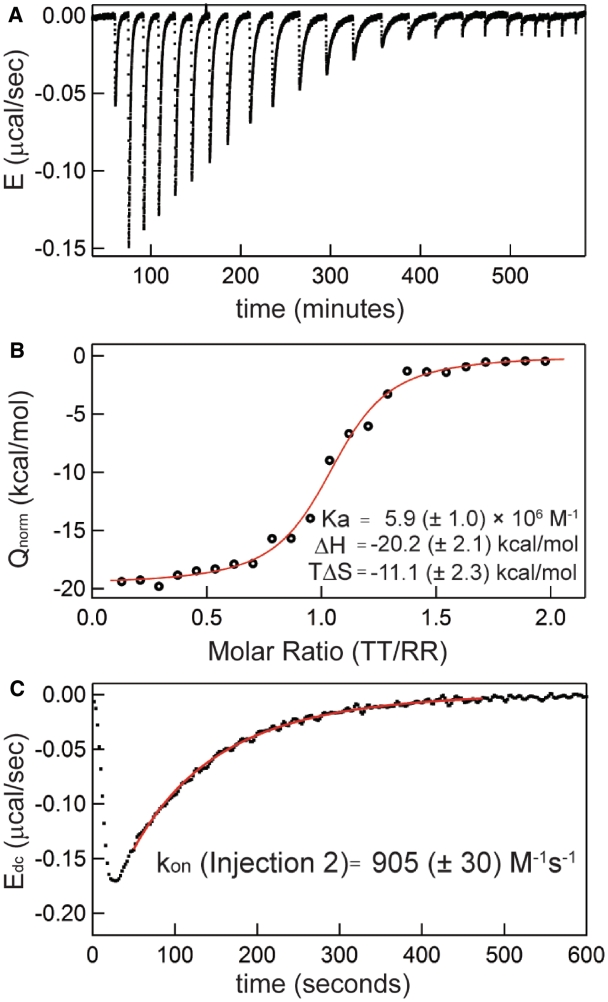
Figure 2.
Extraction of both thermodynamic and kinetic parameters from a single binding titration. Forward titration with titrant [TT] = 229 µM, starting cell [RR] = 10 µM, using 5 µL injections, at 20°C in 0.5 mM MgCl2 solution. (A) Raw power trace following baseline subtraction to present excess power [E = (∂Q/∂t)]. (B) Binding curve following integration of each peak to plot the concentration-normalized heat evolved (Qnorm) against the current molar ratio. Best fit parameters for the displayed dataset are listed. (C) Injection Peak 2 following deconvolution (Edc); best-fit curve and resulting kon value for the peak using fit methodology as described in ‘Materials and Methods’ section are provided.
All experiments were performed on a GE Healthcare Microcal VP-ITC, using a feedback setting of ‘high’, a stirring rate of 307 rpm, and an injection rate of 0.5 µL/sec. The feedback setting was chosen to maximize the instrument response rate constant; the latter two settings have little effect on the instrument response time. The slow kinetics are also not complicated by any RNA dilution effect (Supplementary Figure S1).
Error analysis
A weighted average kon was determined for each titration experiment from the population of individual injection measurements. The underlying error in these individual determinations is a combination of random noise, baseline drift and uncertainty in the instrumental rate constant (kITC). The true uncertainty also contains contributions from uncertainty in Ka and in the RNA concentrations. All of these error sources were incorporated into both kon and koff measurements through error propagation as described in Supplementary Data. Higher order analysis of data, such as measurement of slope values to determine ΔH‡, used a ‘nested’ bootstrap approach to properly estimate error (Supplementary Data). All data processing and analysis routines were implemented and performed using the high-level programming language in Igor Pro 6.
RESULTS
Extraction of thermodynamic and kinetic parameters from a single ITC experiment
Figure 2 shows a typical ITC experiment in which both thermodynamic and kinetic measurements are obtained. The experiment depicted is a titration in which TT RNA is serially injected into a cell initially containing 10 µM RR. The data demonstrate exothermic binding as a series of TT injection-induced negative deflections in the compensatory power trace followed by a slow decay back to the relative baseline value of 0.0 µW (Figure 2A). Integration of each peak yields the heat evolved by binding, which is plotted against the corresponding molar ratio ([TT]/[RR]) for each injection to generate an ITC binding isotherm (Figure 2B). The binding enthalpy (ΔH) and binding constant (Ka) are determined through least squares fits to these binding data (‘Materials and Methods’ section).
A typical titration microcalorimeter power compensation trace can be viewed as the convolution of a binding-generated ‘impulse’ heat evolution function with the calorimeter ‘response’ function. Using a Laplace Transform approach with an instrumental time constant of 12.5 s, the heat evolution function is recovered (deconvolved) for each injection [(38), Supplementary Data]. A representative deconvolved peak and the associated least squares-minimized kinetics curve are displayed in Figure 2C. This fitting procedure in general requires knowledge of the equilibrium RNA concentrations (‘Materials and Methods’ section); in Figure 2, these values were obtained from the total RNA concentrations and the measured binding constant (Figure 2B). Below, the thermodynamic results from this study are analyzed first, then the corresponding kinetic data are considered.
Comparison of the thermodynamics of tetraloop–receptor association in KCl and MgCl2
Analysis of TT–RR binding data reveals strikingly different thermodynamic profiles for this helical packing event in MgCl2 and KCl solutions (Figure 3). Representative experiments performed at 20°C in either 0.5 mM MgCl2 or 150 mM KCl demonstrate that, while binding is enthalpy-driven in both salts, in KCl it is significantly more exothermic (for these conditions, on average ΔΔH = −21.7 (±3.7) kcal/mol) and less favorable entropically (Δ(−TΔS) = +22.4 (±3.8) kcal/mol) (Figure 3A). The differences in these terms represent contributions to ΔG that are nearly three times greater than the overall stabilities.
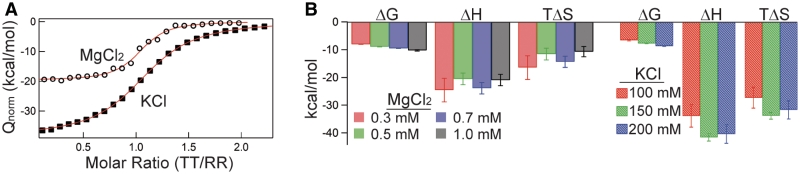
Figure 3.
Thermodynamics of TT–RR binding in MgCl2 and KCl solutions. (A) Representative titration comparison in conditions eliciting comparable complex stabilities. Open circles, 0.5 mM MgCl2, 20°C, titrant [TT] = 229 µM, starting cell [RR] = 10 µM. Solid squares, 150 mM KCl, 20°C, titrant [TT] = 145 µM, starting cell [RR] = 10 µM. (B) Left, linear fit-determined maximum likelihood ΔG25C, ΔH25C and TΔS25C in 0.3 (red), 0.5 (green), 0.7 (blue) and 1.0 mM (black) MgCl2. Right, ΔG25C, ΔH25C and TΔS25C in 100 (red), 150 (green) and 200 (blue) mM KCl.
To more fully describe the folding landscapes in MgCl2 and KCl, we performed calorimetry experiments in a range of salt concentrations and temperatures (Tables 1 and 2). In aggregate the thermodynamic data are highly self-consistent. Ka increases as a function of added MgCl2 or KCl, and it decreases with increasing temperature.
Table 1.
Thermodynamic and kinetic parameters for TT–RR binding in Mg2+
| Temp. (°C) | Ka (M−1) × 105 | ΔG°obs (kcal/mol) | ΔH°obs (kcal/mol) | TΔS°obs (kcal/mol) | kon (M−1s−1) | koff (s−1) × 10−5 |
|---|---|---|---|---|---|---|
| 0.3 mM MgCl2 | ||||||
| 10 | –a | –a | −20.5 (±3.3) | –a | 200 (±80) | 3.2 (±1.3) |
| 20 | 18 (±5) | −8.4 (±0.4) | −21.9 (±5.0) | −13.6 (±5.2) | 270 (±60) | 13 (±10) |
| 30 | 5.6 (±1.3) | −8.0 (±0.3) | −26.9 (±4.2) | −19.0 (±4.0) | 510 (±210) | 87 (±13) |
| 0.5 mM MgCl2 | ||||||
| 2 | – | – | −20.7 (±4.1) | – | 310 (±180) | 0.4 (±0.5) |
| 5 | – | – | −19.6 (±2.1) | – | 420 (±60) | 1.0 (±0.1) |
| 10 | – | – | −17.8 (±2.7) | – | 600 (±140) | 3.3 (±0.7) |
| 15 | – | – | −19.6 (±3.9) | – | 630 (±410) | 6.4 (±6.2) |
| 20 | 64 (±7) | −9.1 (±0.2) | −18.9 (±2.0) | −9.8 (±2.0) | 940 (±80) | 16 (±4) |
| 30 | 24 (±1) | −8.9 (±0.1) | −23.2 (±1.9) | −14.3 (±1.9) | 1530 (±120) | 62 (±7) |
| 0.7 mM MgCl2 | ||||||
| 10 | – | – | −20.5 (±3.0) | – | 1240 (±30) | 1.7 (±0.1) |
| 20 | 160 (± 4) | −9.7 (±0.1) | −24.8 (±3.2) | −15.1 (±3.2) | 2360 (±60) | 14 (±1) |
| 30 | 56 (± 2) | −9.4 (±0.1) | −22.4 (±3.1) | −13.1 (±3.1) | 3130 (±550) | 58 (±8) |
| 1.0 mM MgCl2 | ||||||
| 5 | – | – | −19.4 (±3.0) | – | 1690 (±270) | 0.7 (±0.1) |
| 10 | – | – | −18.4 (±2.2) | – | 2230 (±210) | 2.2 (±0.2) |
| 15 | – | – | −18.9 (±3.7) | – | 3180 (±630) | 6.7 (±1.3) |
| 20 | – | – | −19.5 (±2.3) | – | 3950 (±540) | 15 (±2) |
| 25 | – | – | −23.6 (±4.7) | – | 5660 (±4890) | 57 (±42) |
| 30 | – | – | −21.3 (±2.1) | – | 5800 (±580) | 68 (±6) |
| 35 | 55 (±7) | −9.5 (±0.2) | −23.9 (±3.0) | −14.3 (±3.1) | 6810 (±1510) | 120 (±20) |
| 40 | 23 (±5) | −9.1 (±0.3) | −26.7 (±3.7) | −17.5 (±3.8) | 7840 (±2060) | 310 (±50) |
| 45 | 9.9 (±2.1) | −8.7 (±0.3) | −28.6 (±5.5) | −19.9 (±5.8) | – | – |
– not determined because ITC c-value greater than 200
–a not determined because post-injection decay too slow to accurately integrate throughout titration
Table 2.
Thermodynamic and kinetic parameters for TT–RR binding in K+
| Temp. (°C) | Ka (M−1) × 105 | ΔG°obs (kcal/mol) | ΔH°obs (kcal/mol) | TΔS°obs (kcal/mol) | kon (M−1s−1) | koff (s−1) × 10−5 |
|---|---|---|---|---|---|---|
| 100 mM KCl | ||||||
| 5 | 52 (±3) | −8.5 (±0.1) | −35.1 (±3.8) | −26.6 (±3.8) | 550 (±60) | 10 (±1) |
| 15 | 5.9 (±0.7) | −7.6 (±0.2) | −34.9 (±2.8) | −27.3 (±2.8) | 530 (±90) | 95 (±14) |
| 150 mM KCl | ||||||
| 5 | – | – | −39.4 (±1.5) | – | 2290 (±200) | 3.9 (±0.3) |
| 10 | – | – | −38.7 (±1.6) | – | 2250 (±80) | 12 (±1) |
| 15 | 58 (±4) | −8.9 (±0.1) | −40.4 (±2.6) | −31.5 (±2.6) | 2300 (±70) | 38 (±8) |
| 20 | 18 (±1) | −8.4 (±0.1) | −40.6 (±1.7) | −32.2 (±1.8) | 2200 (±60) | 110 (±20) |
| 25 | 4.7 (±0.2) | −7.7 (±0.1) | −41.8 (±1.9) | −34.1 (±1.9) | 2190 (±90) | 440 (±30) |
| 200 mM KCl | ||||||
| 5 | – | – | −37.9 (±5.2) | − | 6080 (±200) | 3.2 (±0.3) |
| 10 | – | – | −37.1 (±3.3) | – | 6060 (±460) | 9.5 (±0.7) |
| 20 | 76 (±3) | −9.2 (±0.1) | −40.0 (±4.2) | −30.8 (±4.1) | 5680 (±1040) | 76 (±16) |
| 25 | 27 (±5) | −8.8 (±0.2) | −46.3 (±4.8) | −37.4 (±4.8) | 6170 (±370) | 180 (±50) |
| 30 | 9.4 (±6.9) | −8.3 (±0.1) | −43.9 (±4.2) | −35.7 (±4.3) | 5810 (±650) | 650 (±90) |
– not determined because ITC c-value greater than 200.
Figure 3B plots the thermodynamics for TT–RR binding across the full set of examined salt conditions at a common temperature (25°C); the values are also listed in Table 3. The significant discrepancy in MgCl2 and KCl thermodynamic profiles persists across the examined salt concentrations. ΔH25C is bounded by −24.6 and −20.5 kcal/mol in the ensemble of MgCl2 solutions; in KCl the minimum and maximum values are −41.6 and −34.0, respectively. Contrastingly, TΔS25C ranges from −16.5 to −10.7 kcal/mol in MgCl2 while it is much more unfavorable in KCl solutions, ranging from −27.4 to −33.8 kcal/mol.
Table 3.
Average Thermodynamic parameters
| Salt | Temp (°C) | ΔG25C (kcal/mol) | ΔH25C (kcal/mol) | TΔS25C (kcal/mol) | ΔCp (kcal/mol/K) | ΔHVH (kcal/mol) |
|---|---|---|---|---|---|---|
| 0.3 mM MgCl2 | 10–30 | −8.1 (±0.1) | −24.6 (±4.3) | −16.5 (±4.4) | −0.21 (±0.15) | −24.2 (±0.6) |
| 0.5 mM MgCl2 | 2–30 | −9.0 (±0.1) | −20.5 (±2.1) | −11.6 (±2.1) | −0.12 (±0.10) | −17.4 (±2.9) |
| 0.7 mM MgCl2 | 10–30 | −9.5 (±0.1) | −23.9 (±2.0) | −14.4 (±2.0) | −0.17 (±0.06) | −17.8 (±1.0) |
| 1.0 mM MgCl2 | 5–45 | −10.2 (±0.2) | −20.9 (±2.1) | −10.7 (±2.3) | −0.11 (±0.05) | −31.0 (±6.7)a |
| −0.57 (±0.29)a | ||||||
| 100 mM KCl | 5–15 | −6.6 (±0.3) | −34.0 (±4.1) | −27.4 (±4.5) | 0.11 (±0.31) | −36.4 (±3.8) |
| 150 mM KCl | 5–25 | −7.8 (±0.1) | −41.6 (±1.3) | −33.8 (±1.4) | −0.13 (±0.07) | −42.4 (±2.5) |
| 200 mM KCl | 5–30 | −8.8 (±0.1) | −40.4 (±3.3) | −31.7 (±3.3) | −0.16 (±0.10) | −37.6 (±3.5) |
aDetermined from 30–45°C; all other values determined using temperatures ≤30°C.
These 25°C thermodynamic quantities are maximum likelihood (i.e. ‘optimized’) values from the full set of measurements across a range of experimental temperatures. ΔH25C values were calculated for each salt condition from linear fits of individual ΔH measurements plotted against the experimental temperature. The average slopes from these measurements are also given in Table 3 as the heat capacity change (ΔCp = ∂ΔH/∂t). For data collected in 1.0 mM MgCl2, the fit excluded data above 30°C, where the binding enthalpy displays a statistically significant change in slope (Supplementary Figure S2). This observation corroborates our previous hypothesis that the free receptor exists in a temperature-dependent conformation (32). In other words, the enthalpy becomes increasingly temperature dependent at temperatures where the melting intermediate becomes significantly populated. While the shift in ΔCp may begin between 20 and 30°C (Tables 1 and 2, Supplementary Figure S2), overall the ΔCp is small and negative for the full set of experiments conducted below 30°C. The average ΔCp below 30°C are similar in MgCl2 and KCl solutions: bootstrap analysis yields −0.14 (±0.02) kcal/mol/K in MgCl2 versus −0.04 (±0.08) kcal/mol/K in KCl. The weighted average ΔCp for a single tetraloop–receptor interaction is therefore −0.06 (±0.02) kcal/mol/K. This value is not far from that predicted by a coarse-grained surface area burial calculation (−0.002 kcal/mol/K) (39).
The free energy at 25°C (ΔG25C) in Table 3 is also a maximum likelihood value (interpolated in 5 of the 7 salt conditions) determined from Ka (ΔG°=−RTlnKa) according to its temperature dependence using the van't Hoff equation.
| (5) |
The van't Hoff enthalpies (ΔHVH) determined from Equation (5) agree well with the ΔH25C values (Table 3). Only in 1.0 mM MgCl2 is there a noticeable discrepancy between ΔH25C and ΔHVH, because Ka measurements in 1.0 mM MgCl2 were performed across the temperature range 30–45°C, where ΔH is significantly more exothermic than it is from 10 to 30°C. The overall strong agreement shown in Table 3 corroborates homogeneous, one-to-one binding and underscores the robustness of van't Hoff equation-based extrapolations of Ka for kinetics analysis (below).
The 25°C entropy contribution (TΔS25C) in Table 3 was calculated according to the Gibbs equation using ΔG25C and ΔH25C. TΔS25C is large and negative in all cases, indicating an unfavorable contribution. Parameter uncertainty and the relatively small number of salt concentrations examined in this study do not allow an unambiguous determination of whether the [salt]-dependence of the stability is largely entropically or enthalpically based, but additional data show it to be largely entropic as expected (16,40,41) (Supplementary Figure S3).
Comparison of the kinetics of tetraloop–receptor association in KCl and MgCl2
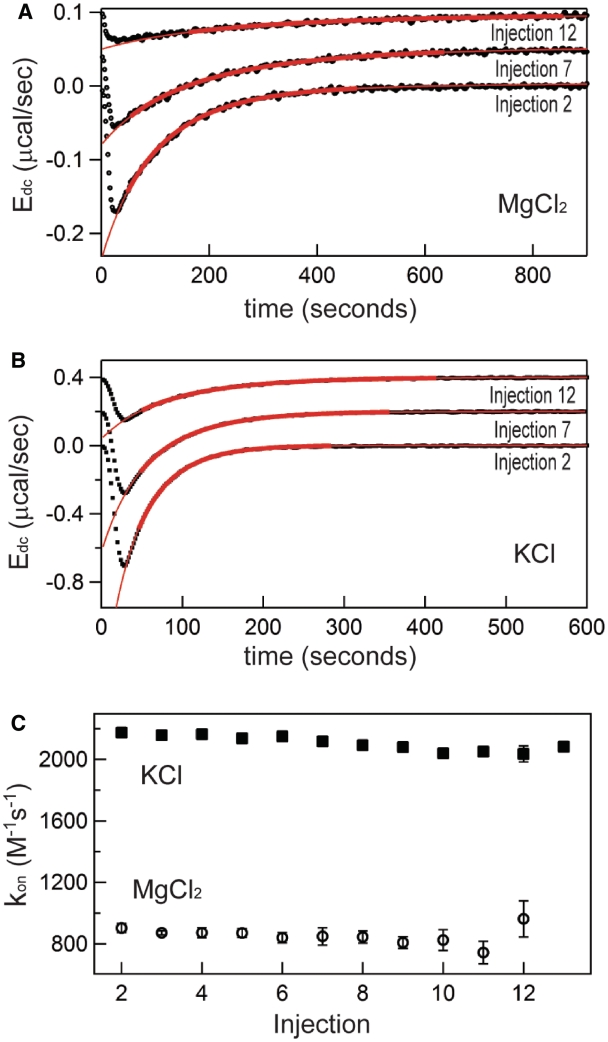
Representative kinetic analyses of the titrations in Figures 2 and 3 are displayed in Figure 4. Figure 4A plots the deconvolved power trace and respective fitted curves for injections 2, 7 and 12 from the representative titration collected in 0.5 mM MgCl2, 20°C, and a similar sampling of peaks and fits from the 150 mM KCl, 20°C dataset is displayed in Panel B. The resulting forward rate constants, kon, are plotted for each injection from the first half of each titration (all injections such that [TT]total > [RR]total) in Figure 4C. As is visible in the raw data (Figure 2A), the observed rate of association decreases appreciably with each subsequent injection over the course of the first half of the titration, reflecting the decreasing concentration of unbound RR. Because kon is a microscopic rate constant, it is independent of the RNA concentration (Figure 4C); the weighted-average kon for these experiments are 860 (±50) M−1 s−1 in MgCl2 and 2180 (±240) M−1 s−1 in KCl. The faster association of TT–RR in KCl versus MgCl2 solution at ambient temperatures and respective salt concentrations eliciting similar stabilities is consistent with extant RNA folding literature (22–24).
Figure 4.
Representative kinetics (kon) measurements from titrations in either 0.5 mM MgCl2 or 150 mM KCl at 20°C (titrations are the same as those in Figures 2 and 3). (A) Selected deconvolved energies (Edc) and fits for peaks 2, 7 and 12 for titration performed in 0.5 mM MgCl2, 20°C. Bold red lines represent target function description of the data using best-fit parameters over the time range used in fitting; extrapolations of these functions are displayed in thin red lines. Peaks 7 and 12 are arbitrarily offset from 0 to aid visualization. (B) Representative peaks and fit functions for titration in 150 mM KCl, 20°C. (C) Corresponding complete population of kon values from sampled titrations. Solid squares, KCl data; Open circles, MgCl2 data.
The bimolecular kinetics equation applied to obtain kon requires knowledge of Ka (‘Materials and Methods’ section). For many conditions in this work, the binding strength is in an optimal window, so Ka can be obtained with high precision and the measured value can be directly inserted into the kinetic analysis. However, in many of the low temperature experiments, the binding constant is greater than 2 × 107 M−1 (i.e. c > 200), so in these cases Ka was determined by van't Hoff extrapolation. Note that for these roughly stoichiometric binding scenarios, error in Ka only weakly influences kon (‘Materials and Methods’ section). koff was subsequently calculated according to the assumption of a single step mechanism, i.e. koff = kon/Ka. kon and koff measurements for all conditions are listed alongside the aforementioned thermodynamic results in Tables 1 and 2. The rate constants observed in this work are consistent with those obtained by Downey et al. (19), using a tethered tetraloop–receptor construct (Supplementary Data).
Analysis of the temperature dependence of kon and koff using the Eyring equation allows a thermodynamic characterization of the transition state.
| (6) |
The slope in a plot of ln(k) against the inverse temperature reveals the transition state enthalpy (ΔH‡) in the slope and a term containing the transition state entropy (ΔS‡) in the y-intercept. The so-called pre-exponential term (α) (42) is necessary to recover ΔS‡ and has been discussed in the context of RNA folding elsewhere (43,44); here we simply assume a value within the range of possible values for macromolecular folding (43–46), as our intention is merely to provide ΔS‡ values for comparison among salt conditions. Because turnover probability is a fundamental property of the transition state, it is almost certainly not influenced by salt type or concentration, thus application of a single α-value to all conditions is the only requirement for rigorous comparative analysis. Additionally, the logarithmic relationship between ΔS‡ and α means the likely maximum error in TΔS‡ is no more than a few kcal/mol.
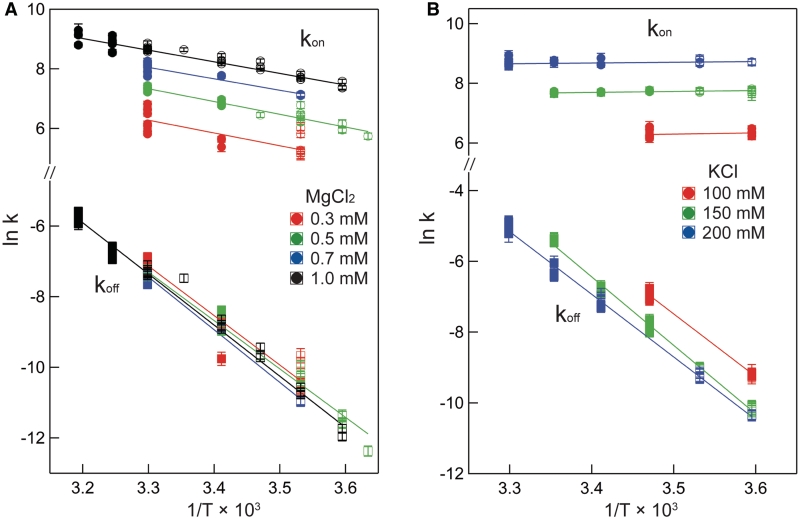
Figure 5 plots the logarithms of kon and koff against inverse temperature for all of the experiments in this work. In MgCl2 (Figure 5A), the slopes (−ΔH‡/R) for each salt concentration and both reaction directions are negative, indicating that ΔH‡ is large and positive for both association and dissociation. The full set of transition state theory thermodynamic quantities are listed in Table 4. 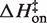 is on average 8.1 (±0.5) kcal/mol in MgCl2 solutions. This is consistent with a previous measurement, which used an oligonucleotide linker to monitor intra-construct tetraloop–receptor association via FRET, and determined an upper limit
is on average 8.1 (±0.5) kcal/mol in MgCl2 solutions. This is consistent with a previous measurement, which used an oligonucleotide linker to monitor intra-construct tetraloop–receptor association via FRET, and determined an upper limit 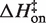 of 12.7 kcal/mol in 10 mM MgCl2 (19). Using the aforementioned α-value, the average entropy contribution to forming the transition state (TΔS‡on) from the unbound starting state is small and slightly favorable: 2.4 (±0.5) kcal/mol. For dissociation (koff), the slopes are significantly steeper than the association plots, indicating even larger values for
of 12.7 kcal/mol in 10 mM MgCl2 (19). Using the aforementioned α-value, the average entropy contribution to forming the transition state (TΔS‡on) from the unbound starting state is small and slightly favorable: 2.4 (±0.5) kcal/mol. For dissociation (koff), the slopes are significantly steeper than the association plots, indicating even larger values for 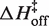 . The difference in association and dissociation transition state enthalpies is consistent with the binding exothermicity (Table 3). Also notable in Figure 5A is the difference between the [MgCl2]-dependence of the association and dissociation profiles. In plots of kon there exists a significant and systematic trend in the rate constants measured at a common temperature, manifested as a horizontal offset. However, for koff the temperature-dependent plots are nearly collinear. This behavior reflects a much more significant [MgCl2]-dependence in kon than in koff.
. The difference in association and dissociation transition state enthalpies is consistent with the binding exothermicity (Table 3). Also notable in Figure 5A is the difference between the [MgCl2]-dependence of the association and dissociation profiles. In plots of kon there exists a significant and systematic trend in the rate constants measured at a common temperature, manifested as a horizontal offset. However, for koff the temperature-dependent plots are nearly collinear. This behavior reflects a much more significant [MgCl2]-dependence in kon than in koff.
Figure 5.
Eyring plot of both association (kon) and dissociation (koff) rate constants measured in MgCl2 and KCl solutions. Each symbol represents the average rate constant measurement from a single titration, and error bars represent the measurement's true uncertainty as described in Supplementary Material. Circles, kon; squares, koff. For both rate constants, closed symbols reflect data that were obtained from titrations where Ka was measured directly (1 × 105 M−1 < Ka < 2 × 107 M−1), while for open symbols, Ka > 2 × 107 M−1. Lines were generated using best-fit regression parameters. (A) MgCl2 data, (B) KCl data. Y- and X-axis scaling are identical in the two panels.
Table 4.
Average kinetic parameters
| Salt | Temp (°C) | kon,25C (M−1s−1) |
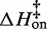 (kcal/mol) (kcal/mol) |
aTΔS‡on,25C (kcal/mol) | koff,25C (s−1) |
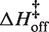 (kcal/mol) (kcal/mol) |
aTΔS‡off,25C (kcal/mol) |
|---|---|---|---|---|---|---|---|
| 0.3 mM MgCl2 | 10–30 | 380 (±140) | 6.3 (±1.4) | −0.5 (±1.5) | 3.3 (±1.8) × 10−4 | 25.8 (±6.0) | 10.7 (±6.4) |
| 0.5 mM MgCl2 | 2–30 | 1160 (±100) | 7.3 (±2.4) | 1.2 (±2.4) | 3.3 (±0.6) × 10−4 | 26.9 (±2.4) | 11.9 (±2.5) |
| 0.7 mM MgCl2 | 10–30 | 2770 (±140) | 8.7 (±0.7) | 3.1 (±0.7) | 2.8 (±0.3) × 10−4 | 30.3 (±1.7) | 15.1 (±1.9) |
| 1.0 mM MgCl2 | 5–40 | 4840 (±630) | 7.8 (±1.1) | 2.5 (±1.1) | 3.1 (±0.5) × 10−4 | 28.8 (±1.8) | 13.8 (±1.8) |
| 100 mM KCl | 5–15 | 510 (±100) | −1.0 (±1.4) | −7.5 (±1.5) | 7.6 (±2.0) × 10−3 | 35.4 (±2.3) | 22.3 (±2.4) |
| 150 mM KCl | 5–25 | 2200 (±50) | −0.4 (±0.6) | −6.2 (±0.6) | 3.9 (±0.5) × 10−3 | 38.6 (±1.1) | 25.0 (±1.2) |
| 200 mM KCl | 5–30 | 5770 (±270) | −0.5 (±0.4) | −5.6 (±0.4) | 2.2 (±0.2) × 10−3 | 35.3 (±1.4) | 21.5 (±1.5) |
aDetermined using pre-exponential term α = 1 × 1010 s−1 (for comparison, application of α = 6 × 1012 s−1 would decrease all TΔS‡ by ~3.8 kcal/mol).
Eyring plots obtained in KCl are displayed in Figure 5B. The data bear a strong resemblance to MgCl2 data with one particularly striking difference: the temperature-dependence of kon is almost entirely absent and is in fact slightly in the opposite direction as the MgCl2 data for all KCl solutions, indicating that 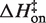 is slightly negative. Thus, the cation identity-based difference in
is slightly negative. Thus, the cation identity-based difference in 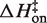 parallels the observed difference in ΔH for the equilibrium binding process (Figure 3 and Table 3). The average
parallels the observed difference in ΔH for the equilibrium binding process (Figure 3 and Table 3). The average 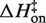 value in KCl is −0.5 (±0.3) kcal/mol in KCl, a slightly favorable contribution that is much less than the unfavorable average value of 8.1 (±0.5) in MgCl2. TΔS‡on is similarly reduced in KCl to an unfavorable average value of −5.9 (±0.3) kcal/mol, contrasting with the transition state entropy term in MgCl2.
value in KCl is −0.5 (±0.3) kcal/mol in KCl, a slightly favorable contribution that is much less than the unfavorable average value of 8.1 (±0.5) in MgCl2. TΔS‡on is similarly reduced in KCl to an unfavorable average value of −5.9 (±0.3) kcal/mol, contrasting with the transition state entropy term in MgCl2.
Trends in the salt concentration dependence of binding and rate constants are listed in Table 5, according to the log–log slope, using the molal salt activity (asalt) as the dependent variable. These dependences report the change in the salt preferential interaction coefficient (ΔΓsalt) for a process (16,34), which conveys the net cation uptake into the RNA coulombic atmosphere. The salt activity dependence for the equilibrium binding event, ∂lnKa/∂ln(asalt) is 6.2 (±0.5) in KCl and 2.8 (±0.1) in MgCl2. This approximately 2-fold difference is consistent with the cation valences.
Table 5.
Salt activity dependence decomposition, ΔΓsalt
| Salt | 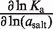 |
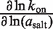 |
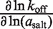 |
|---|---|---|---|
| MgCl2 | 2.8 (±0.1) | 2.2 (±0.2) | −0.1 (±0.3) |
| KCl | 6.2 (±0.5) | 3.8 (±0.2) | −2.0 (±0.4) |
In MgCl2, the [salt]-dependence of the binding constant is almost entirely explained through the on-rate. The dependence of kon (∂lnkon/∂ln(aMgCl2)) accounts for most of the dependence of Ka on aMgCl2, whereas the off-rate exhibits a negligible aMgCl2-dependence (Table 5). In KCl the situation is slightly more balanced: the kon aKCl-dependence is 61% as large as ∂lnKa/∂ln(aKCl), while the relative magnitude of the reverse rate constant quantity is approximately half as large.
DISCUSSION
TT–RR association in the context of RNA folding
As generally observed for RNA folding, tetraloop–receptor driven helical packing exhibits highly salt-dependent behavior (20,47,48) and is enthalpy-driven (2,4,49–55). The results here demonstrate that the exothermicity can be extremely solution dependent, with the association enthalpy varying by as much as 20 kcal/mol. Additional data indicate that it is the balance of Mg2+ and K+ concentrations that is most relevant to the thermodynamic structure of the folding landscape (17) (Supplementary Figures S4 and S5). Mikulecky et al. (54) also observed a significantly less negative enthalpy for folding the hammerhead ribozyme in a solution containing added MgCl2, with a ΔΔH of 24 kcal/mol in solutions containing 100 mM NaCl and either 0 or 10 mM MgCl2.
Kinetic studies of RNA folding have generally observed a (large) positive activation enthalpy (3–5,44,47,56–63), and these studies were almost all conducted in solutions containing millimolar concentrations of MgCl2. Interestingly though, Cole and Crothers (3) identified a tRNA tertiary structure transition with ΔH‡ ~0 kcal/mol for formation in a solution lacking MgCl2 (4). Here we observe a large positive 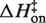 in MgCl2 solutions but a lower, near-zero enthalpic barrier in KCl solutions. The tRNA result and the [MgCl2]-dependent hammerhead ribozyme ΔH suggests potential generality to these findings.
in MgCl2 solutions but a lower, near-zero enthalpic barrier in KCl solutions. The tRNA result and the [MgCl2]-dependent hammerhead ribozyme ΔH suggests potential generality to these findings.
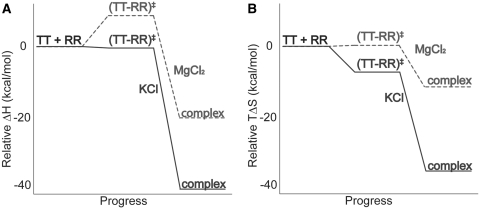
Figure 6 summarizes the thermodynamic reaction coordinate profiles for TT–RR binding in solutions containing either MgCl2 or KCl, using representative conditions (0.5 mM MgCl2 or 150 mM KCl). A sizeable enthalpic barrier to association in MgCl2 of 7.3 kcal/mol contrasts with the slightly negative 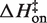 of −0.6 kcal/mol in KCl (Figure 6A). The overall binding process is 21.7 kcal/mol more exothermic in KCl. Thus both steps in the reaction, formation of the transition state from the unbound state and conversion to the bound state from the transition state, are more favorable enthalpically in KCl than in MgCl2 (by 7.9 and 13.8 kcal/mol, respectively). The entropic contribution to binding (TΔS) is essentially the reverse energetically of the enthalpic diagram (Figure 6B). In other words, formation of the transition state and subsequent conversion to the bound state are each more entropically opposed in KCl than in MgCl2. The reason for the stepwise disparity cannot be resolved from our data; it may relate to the bivalent construct design if the folding pathway traverses two similar activation barriers on the way to the final bound state.
of −0.6 kcal/mol in KCl (Figure 6A). The overall binding process is 21.7 kcal/mol more exothermic in KCl. Thus both steps in the reaction, formation of the transition state from the unbound state and conversion to the bound state from the transition state, are more favorable enthalpically in KCl than in MgCl2 (by 7.9 and 13.8 kcal/mol, respectively). The entropic contribution to binding (TΔS) is essentially the reverse energetically of the enthalpic diagram (Figure 6B). In other words, formation of the transition state and subsequent conversion to the bound state are each more entropically opposed in KCl than in MgCl2. The reason for the stepwise disparity cannot be resolved from our data; it may relate to the bivalent construct design if the folding pathway traverses two similar activation barriers on the way to the final bound state.
Figure 6.
(A) Enthalpic (ΔH) and (B) entropic (TΔS) contributions to the free energy of TT–RR association in KCl (solid line) and MgCl2 (dashed line) solutions, relative to the starting state. The schemes represent values in 150 mM KCl or 0.5 mM MgCl2 at 25°C.
The data suggest that the transition state is relatively compact; in other words, the transition state is at least a partially associated TT–RR complex. In both MgCl2 and KCl, the forward rate constant [salt]-dependence, ∂lnkon/∂ln(asalt) constitutes most of the asalt-dependence of the overall association process, ∂lnKa/∂ln(asalt) (Table 5). This result is in line with the analogous process of double helix formation (64), and suggests the charge density of the rate-limiting transition state is most similar to that of the final bound state. The [salt]-dependence breakdown for TT–RR is also similar to that previously identified by Nesbitt and co-workers using a tethered tetraloop–receptor design. They found ∂lnkon/∂ln[MgCl2] = 0.49 to be approximately 2/3 of the overall ∂lnKa/∂ln[MgCl2] = 0.74 (65). This agreement suggests that a compact transition state is not specific to the bimolecular design in our study.
While the evidence points to a compact transition state, it may not involve tertiary contacts. Previous investigations of RNA folding identified an ‘early’ transition state; i.e. a state lacking specific stabilizing tertiary contacts (43,44,66). Bokinsky et al. (66) went on to also characterize the [salt]-dependence of hairpin ribozyme folding. As is true here for tetraloop–receptor mediated helical packing, the [salt]-dependence of hairpin ribozyme folding is almost entirely in the forward direction in MgCl2. Moreover, in the monovalent salt NaCl, the hairpin ribozyme [salt]-dependence is more balanced between the forward and reverse rate constants, further paralleling our TT–RR association data. Bokinsky et al. concluded that the transition state is compact yet early, and further hypothesized that in monovalent salt, the transition state may be slightly less compact than in MgCl2. This interpretation is consistent with the data herein for tetraloop–receptor mediated helical packing.
Potential explanations for cation-dependent ΔH and ΔH‡
We consider two conceptual explanations for the cation-dependent TT–RR binding profile highlighted by Figure 6. Either there is a cation-dependent difference in the RNA structure that influences the thermodynamics of folding, or the explanation lies in the difference in the thermodynamics of potassium and magnesium ion uptake that occurs concomitant with tetraloop–receptor association. The difference is not directly related to the potassium ‘binding’ site (28,34,67) (Supplementary Table S2 and Figure S6). In the discussion below we focus on the cation-dependence in enthalpy terms because entropy terms are strongly [salt]-dependent, whereas ΔH is only weakly [salt]-dependent in these physiological salt concentration regimes (16,40) (Supplementary Figure S3).
In terms of structural explanations, we think the most likely interpretation invokes a salt-dependent unbound receptor conformation. For example, if a free receptor conformation such as that previously observed (68) were stabilized by magnesium, the unbound state would be enthalpically stabilized and a corresponding penalty for obligate disruption of this structure would be observed in forming the transition state and final bound state in MgCl2, but not in KCl. There is some precedence for this functional behavior as kinetic traps in large RNA folding are more prevalent in solutions containing Mg2+ and little or no monovalent salt (22,48,57). The effect here does not appear to be related to a structural effect induced by some level of ‘ionic strength’, however (Supplementary Figure S4).
Alternatively and potentially of more generality, cation hydration may explain the divergent thermodynamic profiles in KCl and MgCl2. Formation of the transition or bound state from the unbound state requires an uptake of cations due to the increased charge density (Table 5). Thus it may be that the uptake of diffuse monovalent and divalent cations by the tetraloop–receptor contact in particular, or in folded RNA structures in general, occurs with different thermodynamic signatures. Most simply, partial dehydration of one or more Mg2+ accumulated in the local domain of the RNA might incur an additional enthalpic penalty concomitant with formation of both the transition state and final bound state. Given a Mg2+ dehydration enthalpy of ~450 kcal/mol, even a slight disturbance in an outer hydration shell could explain this difference (69).
We favor this ion hydration hypothesis because it is consistent with an early but compact transition state. There is evidence that Mg2+ accumulation by nucleic acids is accompanied by partial dehydration and is partially non-coulombic in nature (70,71), and replacement of sodium with magnesium in the local domain of polyU or polyA-polyU may be accompanied by a slightly positive ΔH (72). On the other hand, low-resolution data argue against a difference in ΔH for magnesium and monovalent cation accumulation near RNA (2,6).
The magnitude and generality of the phenomenon observed here may of course depend on RNA structural details. A slight variation on (or addition to) the ion hydration hypothesis focuses on differences in how cations affect RNA hydration. Magnesium, more than a monovalent cation, preferentially accumulates in the most electronegative regions of nucleic acids (9,73). Thus relative to K+, complexation in the presence of Mg2+ is accompanied by a disproportionate release of RNA hydrating waters from these regions; if these water molecules possess a significantly favorable solvating enthalpy term, then their displacement will be observed as a positive ΔH contribution. Accumulation of Mg2+ may therefore displace a larger quantity of such highly enthalpically stabilized hydrating waters from the RNA than does K+. As above this would yield the observed behavior that magnesium-driven RNA folding is associated with a larger enthalpic penalty.
Overall the data provide new insight into RNA folding in a physiological, mixed salt solution. Preliminary data suggest tertiary folding in physiological conditions may exhibit a balance of K+ and Mg2+ stabilization (Supplemental Figure S5). One consequence of this finding would be that RNA folding in vivo does not exhibit the extreme temperature dependence in the rate of folding predicted by most in vitro studies, which have been conducted in solutions dominated by MgCl2.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR online.
FUNDING
University of Wisconsin–Madison and (grants BIR-9512577) (NSF) and (S10 RR13790) (NIH); NSF (grant MCB-0445613 to S.E.B.). Funding for open access charge: University of Wisconsin, Madison Vilas Associate Award to S.E.B.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We would like to thank Dr Julie Fiore, Dr Darrell McCaslin and the UW Biophysics Instrument Facility for helpful discussions and calorimeter maintenance. Thanks also to M. Thomas Record and Lauren Michael for manuscript comments. Data were obtained at the University of Wisconsin–Madison Biophysics Instrumentation Facility, which was established with support from the University of Wisconsin–Madison and grants BIR-9512577 (NSF) and S10 RR13790 (NIH). Kirk Vander Meulen performed the experiments, data analysis and manuscript preparation. Sam Butcher assisted in manuscript preparation and data analysis.
REFERENCES
- 1.Chu VB, Herschlag D. Unwinding RNA's secrets: advances in the biology, physics, and modeling of complex RNAs. Curr. Opin. Struc. Biol. 2008;18:305–314. doi: 10.1016/j.sbi.2008.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Privalov PL, Filimonov VV. Thermodynamic analysis of transfer-RNA unfolding. J. Mol. Biol. 1978;122:447–464. doi: 10.1016/0022-2836(78)90421-7. [DOI] [PubMed] [Google Scholar]
- 3.Cole PE, Crothers DM. Conformational changes of transfer ribonucleic acid. Relaxation kinetics of the early melting transition of methionine transfer ribonucleic acid (Escherichia coli) Biochemistry. 1972;11:4368–4374. doi: 10.1021/bi00773a025. [DOI] [PubMed] [Google Scholar]
- 4.Crothers DM, Cole PE, Hilbers CW, Shulman RG. Molecular mechanism of thermal unfolding of Escherichia-Coli formylmethionine transfer-RNA. J. Mol. Biol. 1974;87:63–88. doi: 10.1016/0022-2836(74)90560-9. [DOI] [PubMed] [Google Scholar]
- 5.Lynch DC, Schimmel PR. Cooperative binding of magnesium to transfer ribonucleic-acid studied by a fluorescent-probe. Biochemistry. 1974;13:1841–1852. doi: 10.1021/bi00706a012. [DOI] [PubMed] [Google Scholar]
- 6.Rialdi G, Biltonen R, Levy J. Thermodynamic studies of transfer ribonucleic-acids .1. Magnesium binding to yeast phenylalanine transfer ribonucleic-acid. Biochemistry. 1972;11:2472–2479. doi: 10.1021/bi00763a014. [DOI] [PubMed] [Google Scholar]
- 7.Lindahl T, Adams A, Fresco JR. Renaturation of transfer ribonucleic acids through site binding of magnesium. Proc. Natl Acad. Sci. USA. 1966;55:941–948. doi: 10.1073/pnas.55.4.941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stein A, Crothers DM. Conformational changes of transfer RNA. The role of magnesium(II) Biochemistry. 1976;15:160–168. doi: 10.1021/bi00646a025. [DOI] [PubMed] [Google Scholar]
- 9.Misra VK, Draper DE. Mg2+ binding to tRNA revisited: the nonlinear Poisson–Boltzmann model. J. Mol. Biol. 2000;299:813–825. doi: 10.1006/jmbi.2000.3769. [DOI] [PubMed] [Google Scholar]
- 10.Grilley D, Soto AM, Draper DE. Mg2+-RNA interaction free energies and their relationship to the folding of RNA tertiary structures. Proc. Natl Acad. Sci. USA. 2006;103:14003–14008. doi: 10.1073/pnas.0606409103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Misra VK, Draper DE. A thermodynamic framework for Mg2+ binding to RNA. Proc. Natl Acad. Sci. USA. 2001;98:12456–12461. doi: 10.1073/pnas.221234598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Soto AM, Misra V, Draper DE. Tertiary structure of an RNA pseudoknot is stabilized by “diffuse” Mg2+ ions. Biochemistry. 2007;46:2973–2983. doi: 10.1021/bi0616753. [DOI] [PubMed] [Google Scholar]
- 13.Tan ZJ, Chen SJ. Predicting ion binding properties for RNA tertiary structures. Biophy. J. 2010;99:1565–1576. doi: 10.1016/j.bpj.2010.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bai Y, Greenfeld M, Travers KJ, Chu VB, Lipfert J, Doniach S, Herschlag D. Quantitative and comprehensive decomposition of the ion atmosphere around nucleic acids. J. Am. Chem. Soc. 2007;129:14981–14988. doi: 10.1021/ja075020g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kirmizialtin S, Elber R. Computational exploration of mobile ion distributions around RNA duplex. J. Phys. Chem. B. 2010;114:8207–8220. doi: 10.1021/jp911992t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Record MT, Zhang WT, Anderson CF. Analysis of effects of salts and uncharged solutes on protein and nucleic acid equilibria and processes: A practical guide to recognizing and interpreting polyelectrolyte effects, Hofmeister effects, and osmotic effects of salts. Adv. Protein Chem. 1998;51:281–353. doi: 10.1016/s0065-3233(08)60655-5. [DOI] [PubMed] [Google Scholar]
- 17.Shiman R, Draper DE. Stabilization of RNA tertiary structure by monovalent cations. J. Mol. Biol. 2000;302:79–91. doi: 10.1006/jmbi.2000.4031. [DOI] [PubMed] [Google Scholar]
- 18.Davis JH, Foster TR, Tonelli M, Butcher SE. Role of metal ions in the tetraloop-receptor complex as analyzed by NMR. RNA. 2007;13:76–86. doi: 10.1261/rna.268307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Downey CD, Fiore JL, Stoddard CD, Hodak JH, Nesbitt DJ, Pardi A. Metal ion dependence, thermodynamics, and kinetics for intramolecular docking of a GAAA tetraloop and receptor connected by a flexible linker. Biochemistry. 2006;45:3664–3673. doi: 10.1021/bi0520941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Takamoto K, He Q, Morris S, Chance MR, Brenowitz M. Monovalent cations mediate formation of native tertiary structure of the Tetrahymena thermophila ribozyme. Nat. Struct. Biol. 2002;9:928–933. doi: 10.1038/nsb871. [DOI] [PubMed] [Google Scholar]
- 21.Uchida T, He Q, Ralston CY, Brenowitz M, Chance MR. Linkage of monovalent and divalent ion binding in the folding of the P4-P6 domain of the Tetrahymena ribozyme. Biochemistry. 2002;41:5799–5806. doi: 10.1021/bi020042v. [DOI] [PubMed] [Google Scholar]
- 22.Heilman-Miller SL, Pan J, Thirumalai D, Woodson SA. Role of counterion condensation in folding of the Tetrahymena ribozyme II. Counterion-dependence of folding kinetics. J. Mol. Biol. 2001;309:57–68. doi: 10.1006/jmbi.2001.4660. [DOI] [PubMed] [Google Scholar]
- 23.Shcherbakova I, Gupta S, Chance MR, Brenowitz M. Monovalent ion-mediated folding of the Tetrahymena thermophila ribozyme. J. Mol. Biol. 2004;342:1431–1442. doi: 10.1016/j.jmb.2004.07.092. [DOI] [PubMed] [Google Scholar]
- 24.Sclavi B, Sullivan M, Chance MR, Brenowitz M, Woodson SA. RNA folding at millisecond intervals by synchrotron hydroxyl radical footprinting. Science. 1998;279:1940–1943. doi: 10.1126/science.279.5358.1940. [DOI] [PubMed] [Google Scholar]
- 25.Laederach A, Chan JM, Schwartzman A, Willgohs E, Altman RB. Coplanar and coaxial orientations of RNA bases and helices. RNA. 2007;13:643–650. doi: 10.1261/rna.381407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Costa M, Michel F. Frequent use of the same tertiary motif by self-folding RNAs. EMBO J. 1995;14:1276–1285. doi: 10.1002/j.1460-2075.1995.tb07111.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Toor N, Keating KS, Taylor SD, Pyle AM. Crystal structure of a self-spliced group II intron. Science. 2008;320:77–82. doi: 10.1126/science.1153803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cate JH, Gooding AR, Podell E, Zhou KH, Golden BL, Kundrot CE, Cech TR, Doudna JA. Crystal structure of a group I ribozyme domain: principles of RNA packing. Science. 1996;273:1678–1685. doi: 10.1126/science.273.5282.1678. [DOI] [PubMed] [Google Scholar]
- 29.Tanner MA, Cech TR. An important RNA tertiary interaction of group I and group II introns is implicated in gram-positive RNase P RNAs. RNA. 1995;1:349–350. [PMC free article] [PubMed] [Google Scholar]
- 30.Krasilnikov AS, Yang XJ, Pan T, Mondragon A. Crystal structure of the specificity domain of ribonuclease P. Nature. 2003;421:760–764. doi: 10.1038/nature01386. [DOI] [PubMed] [Google Scholar]
- 31.Jaeger L, Westhof E, Leontis NB. TectoRNA: modular assembly units for the construction of RNA nano-objects. Nucleic Acids Res. 2001;29:455–463. doi: 10.1093/nar/29.2.455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vander Meulen KA, Davis JH, Foster TR, Record MT, Jr, Butcher SE. Thermodynamics and folding pathway of tetraloop receptor-mediated RNA helical packing. J. Mol. Biol. 2008;384:702–717. doi: 10.1016/j.jmb.2008.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Geary C, Chworos A, Jaeger L. Promoting RNA helical stacking via A-minor junctions. Nucleic Acids Res. 2011;39:1066–1080. doi: 10.1093/nar/gkq748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lambert D, Leipply D, Shiman R, Draper DE. The influence of monovalent cation size on the stability of RNA tertiary structures. J. Mol. Biol. 2009;390:791–804. doi: 10.1016/j.jmb.2009.04.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Geary C, Baudrey S, Jaeger L. Comprehensive features of natural and in vitro selected GNRA tetraloop-binding receptors. Nucleic Acids Res. 2008;36:1138–1152. doi: 10.1093/nar/gkm1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fiore JL, Kraemer B, Koberling F, Edmann R, Nesbitt DJ. Enthalpy-driven RNA folding: single-molecule thermodynamics of tetraloop-receptor tertiary interaction. Biochemistry. 2009;48:2550–2558. doi: 10.1021/bi8019788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Davis JH, Tonelli M, Scott LG, Jaeger L, Williamson JR, Butcher SE. RNA helical packing in solution: NMR structure of a 30 kDa GAAA tetraloop-receptor complex. J. Mol. Biol. 2005;351:371–382. doi: 10.1016/j.jmb.2005.05.069. [DOI] [PubMed] [Google Scholar]
- 38.Mayorga OL, Freire E. Dynamic analysis of differential scanning calorimetry data. Biophys. Chem. 1987;27:87–96. doi: 10.1016/0301-4622(87)80049-2. [DOI] [PubMed] [Google Scholar]
- 39.Spolar RS, Ha JH, Record MT. Hydrophobic effect in protein folding and other noncovalent processes involving proteins. Proc. Natl Acad. Sci. USA. 1989;86:8382–8385. doi: 10.1073/pnas.86.21.8382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mascotti DP, Lohman TM. Thermodynamics of single-stranded RNA and DNA interactions with oligolysines containing tryptophan - effects of base composition. Biochemistry. 1993;32:10568–10579. doi: 10.1021/bi00091a006. [DOI] [PubMed] [Google Scholar]
- 41.Vander Meulen KA, Saecker RM, Record MT. Formation of a wrapped DNA-protein interface: Experimental characterization and analysis of the large contributions of ions and water to the thermodynamics of binding IHF to H ' DNA. J. Mol. Biol. 2008;377:9–27. doi: 10.1016/j.jmb.2007.11.104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kramers HA. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7:284–304. [Google Scholar]
- 43.Silverman SK, Cech TR. An early transition state for folding of the P4-P6 RNA domain. RNA. 2001;7:161–166. doi: 10.1017/s1355838201001716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bartley LE, Zhuang X, Das R, Chu S, Herschlag D. Exploration of the transition state for tertiary structure formation between an RNA helix and a large structured RNA. J. Mol. Biol. 2003;328:1011–1026. doi: 10.1016/s0022-2836(03)00272-9. [DOI] [PubMed] [Google Scholar]
- 45.Kubelka J, Hofrichter J, Eaton WA. The protein folding ‘speed limit’. Curr. Opin. Struct. Biol. 2004;14:76–88. doi: 10.1016/j.sbi.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 46.Dill KA, Chan HS. From levinthal to pathways to funnels. Nat. Struct. Biol. 1997;4:10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 47.Silverman SK, Deras ML, Woodson SA, Scaringe SA, Cech TR. Multiple folding pathways for the P4-P6 RNA domain. Biochemistry. 2000;39:12465–12475. doi: 10.1021/bi000828y. [DOI] [PubMed] [Google Scholar]
- 48.Russell R, Zhuang XW, Babcock HP, Millett IS, Doniach S, Chu S, Herschlag D. Exploring the folding landscape of a structured RNA. Proc. Natl Acad. Sci. USA. 2002;99:155–160. doi: 10.1073/pnas.221593598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gluick TC, Draper DE. Thermodynamics of folding a pseudoknotted messenger-RNA fragment. J. Mol. Biol. 1994;241:246–262. doi: 10.1006/jmbi.1994.1493. [DOI] [PubMed] [Google Scholar]
- 50.Laing LG, Draper DE. Thermodynamics of RNA folding in a conserved ribosomal-RNA domain. J. Mol. Biol. 1994;237:560–576. doi: 10.1006/jmbi.1994.1255. [DOI] [PubMed] [Google Scholar]
- 51.Fang XW, Golden BL, Littrell K, Shelton V, Thiyagarajan P, Pan T, Sosnick TR. The thermodynamic origin of the stability of a thermophilic ribozyme. Proc. Natl Acad. Sci. USA. 2001;98:4355–4360. doi: 10.1073/pnas.071050698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Klostermeier D, Millar DP. Helical junctions as determinants for RNA folding: Origin of tertiary structure stability of the hairpin ribozyme. Biochemistry. 2000;39:12970–12978. doi: 10.1021/bi0014103. [DOI] [PubMed] [Google Scholar]
- 53.Banerjee AR, Jaeger JA, Turner DH. Thermal unfolding of a group-I ribozyme - the low-temperature transition is primarily disruption of tertiary structure. Biochemistry. 1993;32:153–163. doi: 10.1021/bi00052a021. [DOI] [PubMed] [Google Scholar]
- 54.Mikulecky PJ, Takach JC, Feig AL. Entropy-driven folding of an RNA helical junction: An isothermal titration calorimetric analysis of the hammerhead ribozyme. Biochemistry. 2004;43:5870–5881. doi: 10.1021/bi0360657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Szewczak AA, Podell ER, Bevilacqua PC, Cech TR. Thermodynamic stability of the P4-P6 domain RNA tertiary structure measured by temperature gradient gel electrophoresis. Biochemistry. 1998;37:11162–11170. doi: 10.1021/bi980633e. [DOI] [PubMed] [Google Scholar]
- 56.Fang XW, Pan T, Sosnick TR. Mg2+-dependent folding of a large ribozyme without kinetic traps. Nat. Struct. Biol. 1999;6:1091–1095. doi: 10.1038/70016. [DOI] [PubMed] [Google Scholar]
- 57.Pan T, Sosnick TR. Intermediates and kinetic traps in the folding of a large ribozyme revealed by circular dichroism and UV absorbance spectroscopies and catalytic activity. Nat. Struct. Biol. 1997;4:931–938. doi: 10.1038/nsb1197-931. [DOI] [PubMed] [Google Scholar]
- 58.Zarrinkar PP, Williamson JR. Kinetic intermediates in RNA folding. Science. 1994;265:918–924. doi: 10.1126/science.8052848. [DOI] [PubMed] [Google Scholar]
- 59.Downs WD, Cech TR. Kinetic pathway for folding of the tetrahymena ribozyme revealed by three UV-inducible crosslinks. RNA. 1996;2:718–732. [PMC free article] [PubMed] [Google Scholar]
- 60.Gluick TC, Gerstner RB, Draper DE. Effects of Mg2+, K+, and H+ on an equilibrium between alternative conformations of an RNA pseudoknot. J. Mol. Biol. 1997;270:451–463. doi: 10.1006/jmbi.1997.1119. [DOI] [PubMed] [Google Scholar]
- 61.Kao TH, Crothers DM. A proton-coupled conformational switch of Escherichia coli 5S ribosomal RNA. Proc. Natl Acad. Sci. USA. 1980;77:3360–3364. doi: 10.1073/pnas.77.6.3360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lang K, Rieder R, Micura R. Ligand-induced folding of the thiM TPP riboswitch investigated by a structure-based fluorescence spectroscopic approach. Nucleic Acids Res. 2007;35:5370–5378. doi: 10.1093/nar/gkm580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wickiser JK, Cheah MT, Breaker RR, Crothers DM. The kinetics of ligand binding by an adenine-sensing riboswitch. Biochemistry. 2005;44:13404–13414. doi: 10.1021/bi051008u. [DOI] [PubMed] [Google Scholar]
- 64.Porschke D, Uhlenbeck OC, Martin FH. Thermodynamics and kinetics of helix-coil transition of oligomers containing GC base pairs. Biopolymers. 1973;12:1313–1335. [Google Scholar]
- 65.Hodak JH, Downey CD, Fiore JL, Pardi A, Nesbitt DJ. Docking kinetics and equilibrium of a GAAA tetraloop-receptor motif probed by single-molecule FRET. Proc. Natl Acad. Sci. USA. 2005;102:10505–10510. doi: 10.1073/pnas.0408645102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Bokinsky G, Rueda D, Misra VK, Rhodes MM, Gordus A, Babcock HP, Walter NG, Zhuang XW. Single-molecule transition-state analysis of RNA folding. Proc. Natl Acad. Sci. USA. 2003;100:9302–9307. doi: 10.1073/pnas.1133280100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Basu S, Rambo RP, Strauss-Soukup J, Cate JH, Ferre-D'Amare AR, Strobel SA, Doudna JA. A specific monovalent metal ion integral to the AA platform of the RNA tetraloop receptor. Nat. Struct. Biol. 1998;5:986–992. doi: 10.1038/2960. [DOI] [PubMed] [Google Scholar]
- 68.Butcher SE, Dieckmann T, Feigon J. Solution structure of the conserved 16 S-like ribosomal RNA UGAA tetraloop. J. Mol. Biol. 1997;268:348–358. doi: 10.1006/jmbi.1997.0964. [DOI] [PubMed] [Google Scholar]
- 69.Markham GD, Glusker JP, Bock CW. The arrangement of first- and second-sphere water molecules in divalent magnesium complexes: results from molecular orbital and density functional theory and from structural crystallography. J. Phys. Chem. B. 2002;106:5118–5134. doi: 10.1021/ic020602e. [DOI] [PubMed] [Google Scholar]
- 70.Kankia BI, Marky LA. DNA, RNA, and DNA/RNA oligomer duplexes: A comparative study of their stability, heat, hydration, and Mg2+ binding properties. J. Phys. Chem. B. 1999;103:8759–8767. [Google Scholar]
- 71.Paulsen MD, Anderson CF, Record MT. Counterion exchange-reactions on DNA - Monte-Carlo and Poisson–Boltzmann analysis. Biopolymers. 1988;27:1249–1265. doi: 10.1002/bip.360270806. [DOI] [PubMed] [Google Scholar]
- 72.Krakauer H. Calorimetric investigation of heats of binding of Mg++ to Poly a, to Poly U, and to their complexes. Biopolymers. 1972;11:811–828. doi: 10.1002/bip.1972.360110406. [DOI] [PubMed] [Google Scholar]
- 73.Braunlin WH, Anderson CF, Record MT. Na-23-Nmr investigations of counterion exchange-reactions of helical DNA. Biopolymers. 1986;25:205–214. doi: 10.1002/bip.360250114. [DOI] [PubMed] [Google Scholar]
- 74.Record MT, Jr, Anderson CF, Lohman TM. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening, and ion effects on water activity. Q. Rev. Biophys. 1978;11:103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.