Dynamic Retrospective Filtering of Physiological Noise in BOLD fMRI: DRIFTER

Abstract

In this article we introduce the DRIFTER algorithm, which is a new model based Bayesian method for retrospective elimination of physiological noise from functional magnetic resonance imaging (fMRI) data. In the method, we first estimate the frequency trajectories of the physiological signals with the interacting multiple models (IMM) filter algorithm. The frequency trajectories can be estimated from external reference signals, or if the temporal resolution is high enough, from the fMRI data. The estimated frequency trajectories are then used in a state space model in combination of a Kalman filter (KF) and Rauch-Tung-Striebel (RTS) smoother, which separates the signal into an activation related cleaned signal, physiological noise, and white measurement noise components. Using experimental data, we show that the method outperforms the RETROICOR algorithm if the shape and amplitude of the physiological signals change over time.

1. Introduction

The methodology of functional Magnetic Resonance Imaging (fMRI, Ogawa et al., 1990; Belliveau et al., 1991; Kwong et al., 1992) is rapidly evolving and as the spatial resolution, sampling frequency and signal-to-noise-ratio (SNR) of fMRI increases, the accurate treatment of various noise sources in measurements becomes more and more important. In addition to thermal and other random noises, which can be modeled as white noise, there exists several non-white noise sources as well (Lund et al., 2006). One of the most significant non-white factors is physiological noise, which mainly consists of vascular fluctuations and quasi-periodic oscillations caused by cardiac and respiratory activity (Krüger and Glover, 2001). At 3 T, in gray matter, the cardiac and respiratory noise account for a bit over 30% of the total standard deviation. At higher fields the physiological noise is likely to be more dominant (Krüger and Glover, 2001).

There exists several approaches to suppress cardiac, respiration and related physiological noise from fMRI measurements. If the temporal resolution of the fMRI time series is high enough, it is possible to design notch filters, which remove the frequency bands corresponding to cardiac pulsation, respiration and their harmonics (Biswal et al., 1996). However, this approach cannot cope with spectral aliasing, and it assumes stationarity of the signal, which is not a valid assumption if the frequency of the cardiac activity or respiration changes.

One widely used approach to physiological noise elimination is RETROICOR (Glover et al., 2000), which is based on fitting a low-order Fourier basis to the data and eliminating the components corresponding to the cardiac activity and respiration together with their harmonics. The phases of the cardiac and respiratory cycles are estimated from reference signals by peak-detection and histogram based methods, respectively (Glover et al., 2000). Unlike the notch filtering approach, RETROICOR is able to cope well with spectral aliasing and time-varying frequencies.

Other image-based physiological noise reduction approaches include adaptive filtering (Deckers et al., 2006), Principal Component Analysis (PCA) and Independent Component Analysis (ICA, Thomas et al., 2002), and IMPACT (Chuang and Chen, 2001). It is also possible to do retrospective noise reduction in k-space (Hu et al., 1995; Le and Hu, 1996; Frank et al., 2001) or to utilize the phase information (Cheng and Li, 2010).

Due to the typical 2–4 second time resolution of echo planar imaging (EPI) based fMRI, the physiological signals are heavily aliased in the data and thus the methods have to be able to cope with the aliasing. In image-based retrospective methods this usually means using reference signals or taking the timings of individual slices into account (Frank et al., 2001). In recent fast acquisition methods such as Inverse Imaging (InI, Lin et al., 2006, 2008) the sampling rates can reach 10 Hz (0.1 s), which enables possibility to eliminate physiological noises even without reference signals (Lin et al., 2011).

In this article, we introduce the DRIFTER algorithm, which is a Bayesian method for physiological noise modeling and removal allowing accurate dynamical tracking of the variations in the cardiac and respiratory frequencies by using Interacting Multiple Models (IMM), Kalman Filter (KF) and Rauch-Tung-Striebel (RTS) smoother algorithms (Bar-Shalom et al., 2001; Grewal and Andrews, 2001). Due to the model based approach DRIFTER is not limited by the Nyquist frequency, and can remove physiological noises also from long TR fMRI data, provided that the frequency trajectories are estimated from a more densely sampled signal. The frequency trajectories can be either estimated from reference signals, or if the time resolution allows, directly from the fMRI signal. The estimated frequency trajectory is used for accurate model based separation of the spatio-temporal fMRI signal into activation, physiological noise and white noise components using Kalman filter and RTS smoother algorithms. We test the performance of the method with simulated data and fMRI data, and compare it to the RETROICOR method.

2. Models and methods

2.1. Kalman filtering, RTS smoothing and IMM

The Kalman filter and Rauch-Tung-Striebel smoother (see, e.g., Grewal and Andrews, 2001) are algorithms, which can be used for computing the exact Bayesian posterior distributions of the state in discrete-time linear Gaussian state space models of the form:

$$\begin{array}{l}\overrightarrow{x}(t_{k+1})=A_k\overrightarrow{x}(t_k)+\overrightarrow{q}(t_k)\\ \overrightarrow{y}(t_k)=H_k\overrightarrow{x}(t_k)+\overrightarrow{\epsilon }(t_k),\end{array}$$ (1)

where x⃗(t_k) ∈ ℝⁿ is the state at time t_k, where k = 0, 1, 2,…, y⃗(t_k) ∈ ℝ^d is the measurement at time t_k, q⃗ (t_k) ~ N(0, Q_k) is the Gaussian process noise, and ε⃗ (t_k) ~ N(0, Σ_k) is the Gaussian measurement noise. Matrix A_k is the state transition matrix and H_k is the measurement model matrix. In this context, state refers to the minimum set of variables, which represents the configuration of the system at any given time.

Note that we can also handle continuous dynamic models (stochastic differential equations, see, Øksendal, 2003) of the following form using the Kalman filter and RTS smoother:

$$\frac{d\overrightarrow{x}(t)}{dt}=F\overrightarrow{x}(t)+L\overrightarrow{\xi }(t),$$ (2)

where ξ⃗(t) is a white noise process with a given spectral density matrix W. If we define Δt_k = t_k+1 − t_k then the (weak) solution to this continuous-time stochastic differential equation can be expressed as

$$\overrightarrow{x}(t_{k+1})=exp(\mathrm{\Delta }{t}_{k}F)\overrightarrow{x}(t_k)+{\int }_{t_k}^{t_{k+1}}exp((t_{k+1}-s)F)L\overrightarrow{\xi }(s)ds.$$ (3)

The second integral¹ above is just a Gaussian random variable with covariance

$$Q_k={\int }_0^{\mathrm{\Delta }{t}_k}exp((\mathrm{\Delta }{t}_k-\tau )F)LW{L}^{T}exp{((\mathrm{\Delta }{t}_k-\tau )F)}^{T}d\tau .$$ (4)

Thus if we define A_k = exp(Δt_k F), then the model becomes equivalent to the discrete-time model in Equations (1).

The Interacting Multiple Models (IMM) algorithm (Bar-Shalom et al., 2001) can be used for computing posterior distributions of switching linear state space models, where the model matrices depend on an additional latent variable θ_k:

$$\begin{array}{l}\overrightarrow{x}(t_{k+1})=A_k({\theta }_k)\overrightarrow{x}(t_k)+\overrightarrow{q}(t_k)\\ \overrightarrow{y}(t_k)=H_k({\theta }_k)\overrightarrow{x}(t_k)+\overrightarrow{\epsilon }(t_k).\end{array}$$ (5)

This variable takes values in a finite set θ_k ∈ Ω = {θ⁽¹⁾,…, θ^(S)} and its dynamics are modeled with a Markov chain with a transition matrix Π:

$$P({\theta }_k^{(i)}\mid {\theta }_{k-1}^{(j)})={\mathrm{\Pi }}_{ij}.$$ (6)

The IMM algorithm provides the efficient means for computing an S-component Gaussian mixture approximation to the joint posterior distribution of the latent variables and states.

2.2. Modeling quasi-periodic signals with noisy resonators

As well known, band-limited zero-mean periodic signals with period frequency f can be approximated to an arbitrary precision with truncated Fourier series:

$$c(t)\approx \sum _{n=1}^N{a}_{n}cos(2\pi nft)+b_{n}sin(2\pi nft).$$ (7)

Here we are interested in modeling quasi-periodic signals, where the frequency f(t) is a function of time. Substituting this into the Fourier series gives

$$c(t)\approx \sum _{n=1}^N{a}_{n}cos(2\pi nf(t)t)+b_{n}sin(2\pi nf(t)t).$$ (8)

This model now has the serious problem that it is very sensitive to changes in frequency. When t is large, even a tiny change in the frequency causes a large change in signal c(t). Also when the frequency suddenly changes (i.e., when f(t) has a discontinuity), the signal c(t) has a discontinuity. One way to circumvent this is to use the phase of the signal instead of the frequency, that is, $\phi (t)={\int }_0^{t}2\pi f(t)dt$. For example RETROICOR (Glover et al., 2000) estimates the signal phase from the reference signals and never explicitly works with frequencies. This indeed solves the problem of time-varying frequencies, but there is another problem: if the coefficients a_n and b_n are assumed to be constant in time, this implies that the amplitude of the phenomenon is assumed to be constant, which is a quite unrealistic assumption in real data.

Our approach is based on the observation that the Fourier series (7) can also be represented in an alternative form by observing that the following differential equation (oscillator)

$$\frac{d^2{c}_n(t)}{{dt}^2}=-{(2\pi nf)}^2{c}_n(t),$$ (9)

has the solution

$$c_n(t)=a_{n}cos(2\pi nft)+b_{n}sin(2\pi nft),$$ (10)

where the constants a_n and b_n are set by the initial conditions of the differential equation. We can now replace the constant frequency with a time varying one, which leads to the following differential equation model for the nth harmonic:

$$\frac{d^2{c}_n(t)}{{dt}^2}=-{(2\pi nf(t))}^2{c}_n(t).$$ (11)

Unlike the extended Fourier series (8), this signal has the pleasant property that it is continuous even when frequency has discontinuities. Note that in the case of time-varying frequency, the solution to this differential equation is not given by the n’th term in the Fourier series (8).

Another source of aperiodicity in the signal are the small changes in the shape of the signal, which correspond to changes in amplitudes and phases in the harmonics. These changes can be modeled by adding a white noise component ξ_n(t) with spectral density q_n to the differential equation of each harmonic component:

$$\frac{d^2{c}_n(t)}{{dt}^2}=-{(2\pi nf(t))}^2{c}_n(t)+{\xi }_n(t).$$ (12)

This equation could now be written in stochastic differential equation form (cf. Eq. (2)) as follows:

$$\frac{d}{dt}\left(\begin{array}{c}{c}_n(t)\\ \frac{{dc}_n(t)}{dt}\end{array}\right)=\left(\begin{array}{cc}0& 1\\ -{(2\pi nf(t))}^2& 0\end{array}\right)\left(\begin{array}{c}{c}_n(t)\\ \frac{{dc}_n(t)}{dt}\end{array}\right)+\left(\begin{array}{c}0\\ 1\end{array}\right){\xi }_n(t).$$ (13)

This model has the disadvantage that its discretized version does not preserve the norm of the signal and thus when the frequency changes, the amplitude changes as well. A better state space model in this sense is

$$\frac{d}{dt}\left(\begin{array}{c}{c}_n(t)\\ \frac{d{\stackrel{\sim }{c}}_n(t)}{dt}\end{array}\right)=\left(\begin{array}{cc}0& -2\pi nf(t)\\ -2\pi nf(t)& 0\end{array}\right)\left(\begin{array}{c}{c}_n(t)\\ \frac{d{\stackrel{\sim }{c}}_n(t)}{dt}\end{array}\right)+\left(\begin{array}{c}0\\ 1\end{array}\right){\stackrel{\sim }{\xi }}_n(t),$$ (14)

where the signal derivative and noise have been rescaled by dividing with 2π n f(t). However, this model is no longer an exact state space representation of (13), because in general, there should be a term depending on the derivative of the frequency as well. But it is safe to leave it out, because we are modeling our frequency trajectory as a piecewise constant signal, and because we have a noise term, which is able to account for the potential modeling error.

The full quasi-periodic signal then has the representation

$$c(t)=\sum _{n=1}^N{c}_n(t).$$ (15)

The model can also be represented in canonical state space form by defining the state and vector of noises respectively as

$$\begin{array}{l}\overrightarrow{x}={(\begin{array}{ccccccc}{c}_1& d{\stackrel{\sim }{c}}_1/dt& c_2& d{\stackrel{\sim }{c}}_2/dt& \cdots & c_N& d{\stackrel{\sim }{c}}_N/dt\end{array})}^T\\ \overrightarrow{\xi }={(\begin{array}{cccc}{\xi }_1& {\xi }_2& \cdots & {\xi }_N\end{array})}^T.\end{array}$$ (16)

If we now define

$$G(f)=\left(\begin{array}{cc}0& 2\pi f\\ -2\pi f& 0\end{array}\right)$$ (17a)

$$F_o(f)=\text{blockdiag}(G(f),G(2f),\dots ,G(Nf)),$$ (17b)

then the stochastic state space model for the quasi-periodic signal can be written as follows:

$$\frac{d\overrightarrow{x}(t)}{dt}=F_o(f(t))\overrightarrow{x}(t)+L\overrightarrow{\xi }(t)$$ (18a)

$$c(t)=H\overrightarrow{x}(t),$$ (18b)

where the matrix L has elements L_2n,n = 1 for n = 1,…, N, and all other are zero, and H = (1 0 1 0 ···1 0). When the frequency trajectory f(t) is known, the model above is a time-varying linear state space model, which is directly suitable for Kalman filters. With unknown f(t) we can use the IMM algorithm for inferring the state and frequency trajectories as will be shown in the next section.

2.3. Processing of physiological reference signals

Assume that we have some reference sensor, which measures the cardiac cycle such as an ECG sensor or pulse oximeter. The cardiac signal can now be modeled with the quasi-periodic signal model described in the previous section.

To account for the possible drifting of the reference signal, we include a time-varying bias b(t), and model it using a Wiener velocity model:

$$\frac{d^{2}b(t)}{{dt}^2}={\xi }_b(t),$$ (19)

where ξ_b(t) is a white noise process with spectral density q_b. If we define the joint state consisting of the bias and a quasi-periodic signal with N_rc harmonics as

$${\overrightarrow{x}}_{rc}={(\begin{array}{ccccccc}b& db/dt& c_1& d{\stackrel{\sim }{c}}_1/dt& \cdots & c_{N_{rc}}& d{\stackrel{\sim }{c}}_{N_{rc}}/dt\end{array})}^T,$$ (20)

then the measured reference cardiac signal y_rc, which is sampled at times t_k can be written in form

$$\begin{array}{l}\frac{d{\overrightarrow{x}}_{rc}(t)}{dt}=F_{rc}(f_c(t)){\overrightarrow{x}}_{rc}(t)+L_{rc}{\stackrel{\sim }{\xi }}_{rc}(t)\\ y_{rc}(t_k)=H_{rc}{\overrightarrow{x}}_{rc}(t_k)+{\epsilon }_{rc}(t_k),\end{array}$$ (21)

where ε_rc(t_k) is a Gaussian measurement noise (residual noise) with zero mean and variance s², which accounts for the physical noise, uncertainties and the differences between the model and the reality. The matrices L_rc and H_rc are defined in analogous manner as in Equations (18).

If the frequency f_c(t) is constant between the measurements, say, has value f_c(t_k) on the interval t ∈ [t_k, t_k+1), then we can use the discretization procedure presented in Section 2.1 to convert the dynamic model into the form

$${\overrightarrow{x}}_{rc}(t_{k+1})=A_{rc}(f_c(t_k)){\overrightarrow{x}}_{rc}(t_k)+{\overrightarrow{q}}_{rc}(t_k),$$ (22)

where q⃗_rc(t_k) ~ N(0, Q_rc(f_c(t_k))). Because the frequency trajectory f_c(t) is unknown, we shall model it as a stochastic process as well. We assume that the frequency is constant between the measurements and that it can only take values from a given discrete set $f_c\in \{f_c^{(1)},\dots ,f_c^{(M_c)}\}$. If we model the time behavior of the discrete set of frequencies as a Markov chain, we obtain a switching linear state space model as in Equations (5) and (6), where the latent variable is the frequency. Thus we can use the IMM algorithm for inferring the state and frequency trajectories from the measurements.

The respiratory reference signal and its frequency trajectory f_r(t) can be modeled in a completely analogous manner as the cardiac signal. Obviously, the discrete set of frequencies needs to be different and the spectral densities of the noises need to be set to differ from the cardiac case.

2.4. Models for physiological and activation related brain signals in fMRI

From the reference signal analysis described in the previous section, we obtain estimates of the cardiac frequency trajectory f_c(t) and respiratory frequency trajectory f_r(t). We also get estimates of all the harmonic components of the signals, but because the harmonic decomposition of the cardiac and respiration signals as seen in the fMRI signal are likely to be completely different from what is seen in the reference signals, we only use the frequency trajectories at this stage. We assume that the delays between the reference signals and brain are short enough such that the instantaneous frequencies of cardiac and respiration signals are the same in the reference signals and in the brain.

The fMRI data is a four-dimensional signal, where we have separate time series for each voxel in 3D space. At this stage we do not make assumptions about the spatial structure of the signal or noise and treat all the voxel time series independently. We assume that the measured signal consists of the following components:

1. The cardiac signal is modeled as a zero mean quasi-periodic signal with the given frequency trajectory f_c(t) as estimated from the reference signal. Thus the model has similar form as Equation (18a), where the cardiac state x⃗_c contains the states of the N_c harmonics.

2. The respiratory signal is modeled in analogous manner as the cardiac signal, but with different frequency trajectory f_r(t) and number of harmonics N_r.

3. The activation related brain signal is assumed to be smooth and it is modeled using the Wiener velocity model in Equation (19). Note that if there are other slowly varying signal components, such as the scanner drift, they become parts of this component and should be later removed with appropriate filtering (e.g., high-pass filtering).

4. The measurement noise is assumed to be additive spatially and temporally independent Gaussian noise with zero mean and standard deviation s.

We can now define the state of a single voxel as concatenation of the states of cardiac, respiration and activation related brain signals. The full brain state is different in each spatial location r⃗ and thus it has the form x⃗(t, r⃗). The full model for the dynamics of the state and the corresponding measurements can be expressed as

$$\begin{array}{l}\frac{\partial \overrightarrow{x}(t,\overrightarrow{r})}{\partial t}=F\overrightarrow{x}(t,\overrightarrow{r})+L\overrightarrow{\xi }(t,\overrightarrow{r})\\ y(t_k,\overrightarrow{r})=H\overrightarrow{x}(t_k,\overrightarrow{r})+\epsilon (t_k,\overrightarrow{r}),\end{array}$$ (23)

where ε(t_k, r⃗) is a spatially white zero mean Gaussian sequence with standard deviation s, which models the measurement noise in fMRI images. The white noises ξ⃗(t, r⃗) are assumed to be independent in each voxel and have a joint spectral density W, which is independent of the position r⃗.

The discretization procedure presented in Section 2.1 now results in a model of the form

$$\begin{array}{l}\overrightarrow{x}(t_{k+1},\overrightarrow{r})=A_k\overrightarrow{x}(t_k,\overrightarrow{r})+\overrightarrow{q}(t_k,\overrightarrow{r})\\ y(t_k,\overrightarrow{r})=H\overrightarrow{x}(t_k,\overrightarrow{r})+\epsilon (t_k,\overrightarrow{r}),\end{array}$$ (24)

where q⃗(t_k, r⃗) ~ N(0, Q_k). The state transition matrix A_k and the process noise covariance Q_k are independent of the position r⃗ as well. This model is now of the form, which is suitable for Kalman filter and RTS smoother.

2.5. Efficient implementation of Kalman filter and RTS smoother for separation of fMRI signals

Because the processes are assumed to be independent in each voxel, the estimation of the state from the fMRI data amounts to running independent Kalman filters and RTS smoothers (Grewal and Andrews, 2001) for each voxel. The computations of the filters and smoothers can be significantly reduced by noticing that if the initial covariances of the voxel signals are independent of the voxel position, the state covariances, innovation covariances, and gains become independent of the voxel position as well. Thus we need to compute the covariances and gains only once per measurement time, not for each voxel separately.

The filter and smoother means depend on the measurements and consequently on the positions, and for this reason we still need to evaluate mean prediction, update and smoothing equations for each voxel separately. However, they are simple matrix expressions without any matrix inversions and thus light to evaluate. As the equations are independent in each voxel, they can very easily be computed in parallel.

3. Materials and benchmarking

3.1. Simulated data

For testing the overall behavior of the method we generated a simple artificial data. Because all methods work quite well with constant amplitude periodic signals, we concentrated on the less ideal cases. The simulated data involves frequency changes, amplitude changes, and stimulus-related drifting of the signal.

To further test the performance of the method in known conditions, we generated fMRI-like artificial data. The goal was to include all the main effects in the real data to the simulated data. Simulated fMRI and external reference data were generated as a superposition of three different oscillating shapes. The shapes were a ‘smiley face’ and the letters ‘A’ and ‘B’, which can be seen in Figure 1. The face shape represents the underlying noise-free hemodynamical signal and it is slowly oscillating with a frequency around 0.03 Hz and a relative amplitude of 40 points. The letters are representing the cardiac and respiratory signals with relative maximum amplitudes of 20 points each, alternating over time. Their frequency trajectories are drawn randomly so that they alter smoothly over time in a range of 60–120 bpm and 10–70 cpm, respectively. The phases of the signals are non-homogeneously spatially distributed so that each waveform spreads from the center towards the edges. Each observation is disturbed by independent Gaussian normal noise with a relative standard deviation of 5 points. Ten independent Monte Carlo simulations were performed to set up the datasets.

Figure 1.

The amplitude components in the artificial data are shown on the upper row. The lower row shows a noisy observation frame and the corresponding DRIFTER reconstruction.

3.2. Empirical data

Empirical fMRI data and anatomical images for one volunteer were obtained with a 3.0 T scanner (Signa HDxt; General Electric) located at Advanced Magnetic Imaging Centre of Aalto University School of Science using both 8-channel (MRI Devices Corporation) and 16-channel (MR Instruments, Inc.) receive-only head coils. The visual stimuli were presented with a 3-micromirror data projector (Christie X3; Christie Digital Systems) using the Presentation software (Neurobehavioral Systems). For the functional imaging, the major parameters were two different repetition times (TR), 100 ms and 1800 ms; echo time (TE), 20 ms; flip angle (FA), 60°; field-of-view (FOV), 20 cm; and matrix size, 64 × 64. In the data sets with TR 100 ms, only two slices were acquired with a spacing of 5 mm and slice thickness of 5 mm, due to limited time for data acquisition when using an extremely short TR. In the data sets with TR 1800 ms, 29 slices were acquired with a slice thickness of 3 mm and spacing 1 mm.

The stimuli consisted of 50 achromatic photographs of familiar objects presented in the center of the visual field of the volunteer at a distance of 37 cm from the eyes. The stimulus condition was contrasted with fixation alone. The runs, each roughly 120 (runs 1–8) or 240 (runs 9–12) seconds in length, comprised of similar blocks (~15 s of stimulus-on and ~7 s of stimulus-off). During the EPI-runs, the heart and respiratory signals were acquired time-locked to the fMRI data using the scanner integrated peripheral pulse measure and respiratory belt, respectively. The sampling frequency of the physiological signals was 1 kHz. The measurements conformed to the guidelines of the Declaration of Helsinki, and the research was approved by the ethical committee in the Hospital District of Helsinki and Uusimaa.

The data consists of 12 runs altogether, where session 1 (runs 1–4) was acquired with the 16-channel coil and sessions 2 and 3 (runs 5–12) with the 8-channel coil. The amount of variation is physiological noise signals varied in the runs. The runs are summarized in Table 1. In runs 9 and 10 the subject was instructed to start breathing heavily during the run while staying as still as possible. This was to include more extreme data into the analysis. The fMRI data was used without any additional preprocessing.

Table 1.

The properties of the 12 runs of fMRI data.

Run	TR (ms)	Coil Channels	Noise Fluctuations
1–4	100	16	Moderate
5–8	100	8	Moderate
9	1800	8	Strong
10	100	8	Strong
11	1800	8	Low
12	100	8	Low

The number of harmonics were 3 and 4 for cardiac- and respiration induced noise in both DRIFTER and RETROICOR. The IMM algorithm was initialized with 60, 61,…, 120 bpm and 10, 11, …, 70 cpm for the cardiac and respiration frequencies, respectively.

3.3. RMSE and SNR based benchmarking

We test the performance of the proposed DRIFTER method by comparing it to the well-known RETROICOR method due to Glover et al. (2000). There is a slight interpretation difference in the estimation results of RETROICOR and DRIFTER, because RETROICOR estimates the physiological noise signals and then subtracts them from the measured signal. DRIFTER in turn estimates the cleaned activation related brain signal directly and thus also filters out the measurement noise. For fair comparison, we also test DRIFTER in a RETROICOR-compatible mode (DRIFTER(x + ε), see below), where we only subtract the estimated physiological noises from the measured signal and retain the measurement noise part. The estimation results itself are not affected, but only the interpretation of which part of the results is noise and which part is signal.

The tested methods can be summarized as follows:

• True: The true signal characteristics (available only in the simulated case). The SNR is calculated as the ratio of the standard deviations of the activation and measurement noise signals.

• Uncorrected: The result of using the plain measured signal without any corrections. The SNR is calculated as the ratio of standard deviations of observed and measurement noise signals.

• RETROICOR: The result of RETROICOR. The SNR is calculated as the ratio of the standard deviations of the RETROICOR result and measurement noise signals.

• DRIFTER(x + ε): The result of DRIFTER in the RETROICOR-compatible mode, when we only subtract the estimated physiological noises from the signal and retain the measurement noise. The SNR is calculated from the standard deviations of the estimation result and measurement noise.

• DRIFTER(x): The result of DRIFTER when we estimate the activation related brain signal directly, that is, also filter out the measurement noise. The SNR is calculated from the standard deviations of the estimation result and residual noise (i.e. the estimation error).

The methods are numerically benchmarked in terms of the following values:

• Root mean squared errors (RMSE) of the estimates with respect to the true signals (available only for simulated data).

• Signal-to-noise ratios (SNR) averaged over the voxels. Here the SNR in a single voxel is defined by the ratio SNR = σ_s/σ_n, where s stands for the part interpreted as signal and n is the noise part.

• Normalized standard deviations of the components² σ_x, σ_n, σ_c, and σ_r averaged over the voxels, denoting the cleaned signal, unexplained noise, cardiac and respiration component standard deviations, respectively. The normalization was done by dividing signals with the voxel standard deviation σ_y before averaging.

In the empirical data there is no real signal to compare to, so we estimated the noise variance ${\sigma }_n^2$ required in the SNR calculations by studying the parts of the data between the activations, where it can be supposed that the brain signal has minimal contribution. To diminish the post-stimulus effects of the hemodynamic responses to the estimate, a two-second period of adaption was excluded after the end of each stimulus block. However, the hemodynamic response remains non-zero also after this adaptation period (cf. Handwerker et al., 2004) and this needs to be accounted for. To diminish the contribution of the remaining activation and other remaining slow drifting in the signal (such as scanner drift), we applied a windowed de-trending smoother to the signal before estimating the noise variance. Because this simple de-trending only removes the slowly varying part of the signal, the remaining faster post-stimulus undershoot effects still have a small contribution to the estimate. This may cause slight overestimation of noise variance and consequently underestimation of SNRs. In the case of long TR, the filtering can over-fit to the signal, which in turn can cause slight underestimation of the noise variance. In any case, the comparison of the methods is fair, because same noise estimation is used with all the methods.

3.4. SPM based statistical analysis

We also perform general linear model (GLM) analysis using the Statistical Parametric Mapping software (‘SPM8’, Friston et al., 2007) in MATLAB using the classical GLM approach³. The design matrix of the experimental design is constructed using the stimulus timing from the experiments, with an epoch design. As the convolution kernel function the default ‘canonical HRF’ approach is used, and the activations are separately studied. A default high-pass filter with cutoff 128 seconds is applied during the analysis. No spatial pre-processing (referred in SPM to as realignment, normalization, and smoothing) is performed.

4. Results

4.1. Results with simulated data

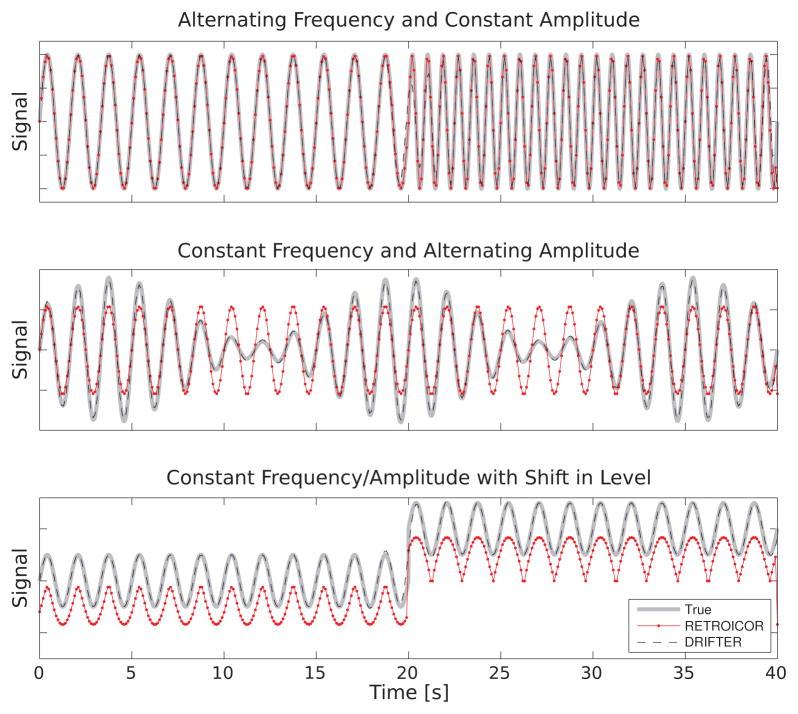
Figure 2 shows the performance of the RETROICOR method and the proposed DRIFTER method in tracking simulated signals with changing frequency, changing amplitude, and DC-level shift. Both methods can cope with time-varying frequency quite well. Because such effects seem to have a stronger presence in respiration signals than in cardiac signals, we used the respiration reference signal processing algorithm of RETROICOR (Eq. 3 in Glover et al., 2000). Normally, the RETROICOR algorithm only computes the phases and does not provide the direct means to reconstruct the reference signal, but for visualization purposes we have done the Fourier reconstruction to the RETROICOR signal in the same way as is normally done for the fMRI data itself.

Figure 2.

Four simple examples using one fundamental oscillator and no harmonics. In each case the true signal sampled at 1 kHz is shown in gray, and both the RETROICOR and DRIFTER estimates sampled at 10 Hz (TR=100 ms).

The case of varying amplitude reveals one shortcoming of RETROICOR: because it uses a global Fourier series, the amplitude changes cannot be taken into account and therefore the signal reconstruction has wrong amplitude. Another shortcoming is revealed by the signal drifting: there is no mechanism in RETROICOR to track the DC-level change in the signal and thus the RETROICOR fit is seriously distracted by the level change in the reference. The DRIFTER method is able to track the time varying amplitudes and level changes very well.

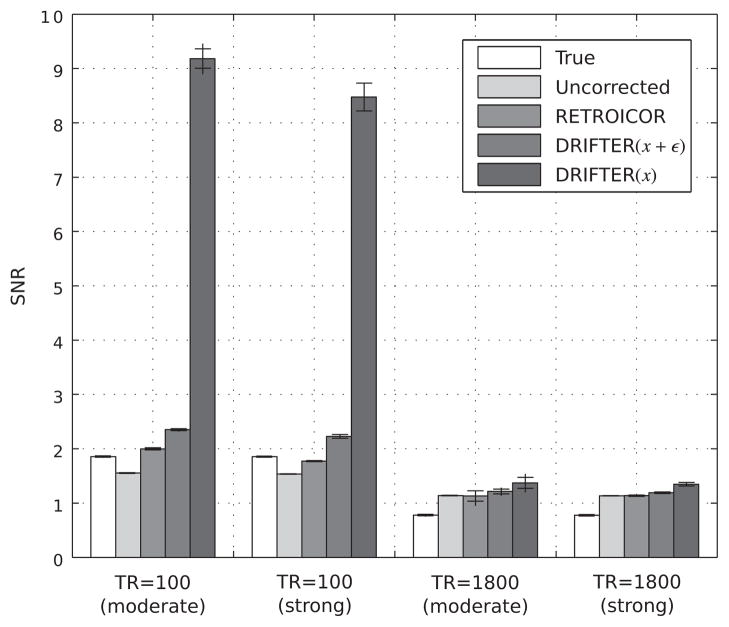
Table 2 and Figure 3 show the results from the simulated fMRI-like data with repetition times 100 ms and 1800 ms with moderate and strong fluctuations in frequency and amplitude. The RMSE values show that the uncorrected signal suffers from bad divergence from the actual signal. By applying RETROICOR or DRIFTER(x + ε) to the data, the RMSE levels fall considerably. In the case of short repetition times (100 ms) DRIFTER(x + ε) performs on average clearly better than RETROICOR. With the longer repetition time (1800 ms) the difference between the methods is smaller than with shorter repetition time. In most cases, the results of DRIFTER(x) are better than of other methods, but when interpreting the results, one has to remember that DRIFTER(x) is the only method where the measurement noise is also filtered out.

Table 2.

Results from the simulation study. Root mean square errors (RMSE), signal-to-noise ratios (SNR), and the normalized standard deviations of the signal components averaged over 10 independent simulations.

Method	RMSE	SNR	σx	σn	σc	σr	σε
TR=100 ms (moderate fluctuations)
True	—	1.86	0.53	0.44	0.27	0.19	0.44
Uncorrected	14.28	1.55	1.00	0.74	—	—	—
RETROICOR	5.95	2.00	0.80	0.47	0.29	0.19	—
DRIFTER(x + ε)	4.67	2.35	0.75	0.40	0.34	0.24	—
DRIFTER(x)	1.06	9.18	0.57	0.09	0.34	0.24	0.39
TR=1800 ms (moderate fluctuations)
True	—	0.78	0.34	0.56	0.32	0.21	0.56
Uncorrected	14.11	1.14	1.00	0.90	—	—	—
RETROICOR	7.43	1.13	0.73	0.66	0.48	0.30	—
DRIFTER(x + ε)	8.16	1.21	0.76	0.64	0.46	0.36	—
DRIFTER(x)	6.52	1.37	0.63	0.49	0.46	0.36	0.29
TR=100 ms (strong fluctuations)
True	—	1.85	0.51	0.43	0.28	0.19	0.43
Uncorrected	16.77	1.54	1.00	0.75	—	—	—
RETROICOR	7.82	1.77	0.81	0.52	0.28	0.18	—
DRIFTER(x + ε)	5.00	2.23	0.74	0.40	0.34	0.24	—
DRIFTER(x)	1.20	8.47	0.55	0.09	0.34	0.24	0.39
TR=1800 ms (strong fluctuations)
True	—	0.78	0.32	0.55	0.31	0.21	0.55
Uncorrected	15.89	1.14	1.00	0.90	—	—	—
RETROICOR	11.74	1.14	0.85	0.76	0.38	0.25	—
DRIFTER(x + ε)	11.07	1.19	0.80	0.69	0.31	0.31	—
DRIFTER(x)	7.38	1.35	0.62	0.47	0.31	0.31	0.37

Figure 3.

The signal-to-noise ratios for each batch of simulated data with error bars illustrating the minimum, maximum and mean standard deviation of the results over 10 independent simulations.

The SNR results for the methods are consistent with the RMSE results. Theoretically, the SNRs of all the methods should match the ‘True’ SNR except for DRIFTER(x), where the elimination of measurement noise increases the SNR significantly. It can be seen that the SNR values of RETROICOR and DRIFTER(x + ε) are often higher than the true values, which means that some of the noise has been interpreted as part of the actual signal. This effect is stronger with shorter TRs and with the DRIFTER method.

The dynamical properties in DRIFTER have an influence on the accuracy of the noise component standard deviation estimates σ_c, σ_r and σ₃, which are also shown in Table 2. DRIFTER can be seen to have the tendency to overestimate the amplitudes of the reference signals.

4.2. Results with empirical data

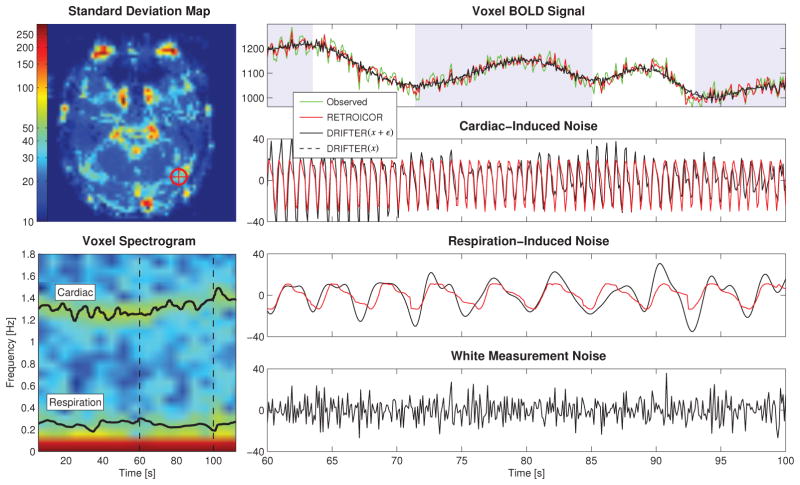
Figure 4 features results based on run 1 (see Table 1), where the noise fluctuations are moderate. One voxel from the high-order object-sensitive cortex (marked by a cross), with confirmed activation using a GLM study, was chosen for further analysis. A spectrogram of the voxel time series shows that the IMM estimates of the frequency trajectories match the frequencies of the periodic effects in the time series.

Figure 4.

Part of the time series data of one voxel in run 1 from the high-order object-sensitive cortex with moderate fluctuations in both respiration and heart beat rate. The spectrogram of the voxel is shown together with frequency trajectories estimated from external data. The noisy observations are shown with no correction. The shaded background signals stimulus-on.

An extract of the voxel time series over a time span of 40 s shows the signal component estimates. Both RETROICOR and DRIFTER return similar estimates for both cardiac- and respiration induced noise components. The cleaned activation related brain signal estimates by RETROICOR and DRIFTER(x + ε) resemble each other, whereas DRIFTER(x) returns a smooth estimate with all noise contribution removed. Please note that although we here talk about activation related signal, the slowly varying signal in Figure 4 (and Fig. 5) actually also contains the scanner drift, which will later be removed with a high pass filter in SPM.

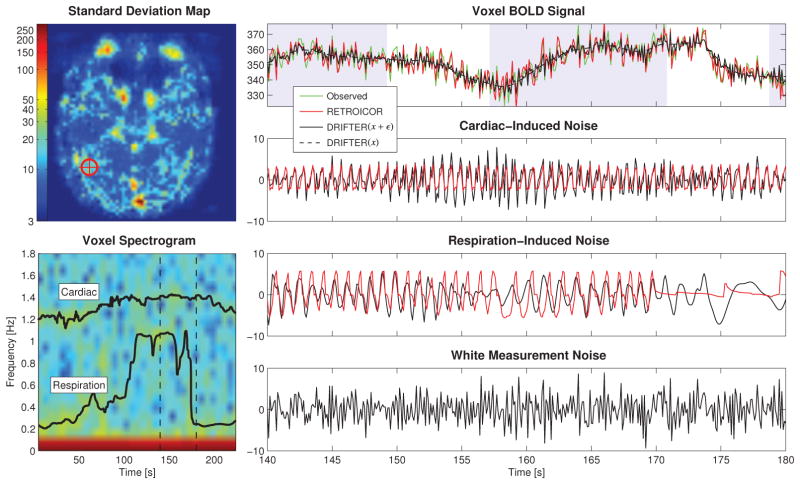
Figure 5.

Part of the time series data of one voxel in run 10 from the high-order object-sensitive cortex with strong fluctuations in both respiration and heart beat rate induced by the subject breathing heavily during the run. The spectrogram of the voxel is shown together with frequency trajectories estimated from external data. The noisy observations are shown with no correction. The shaded background signals stimulus-on.

Opposed to the ideal case of well-behaved data, we also study a similar figure with strong fluctuations in both signal amplitude and frequency (run 10). This is visualized in Figure 5 similarly as earlier, with a standard deviation map and component-wise voxel time series. The difference in the scales of the time series data in Figure 4 and 5 is due to the fact that measurements were made on different days and with different coils.

The fluctuations in the respiration frequency strongly affect the estimation results. This can be seen in the both cardiac- and respiration-induced noise components. RETROICOR has problems with amplitude tracking as anticipated in the section with simulated data, and finally degenerates to a line when the frequency suddenly drops. The phase–amplitude interlocking in RETROICOR proves problematic in the cardiac component as the amplitude is not able to change. The cleaned activation related brain signal shows significantly lower variation in both DRIFTER(x + ε) and DRIFTER(x).

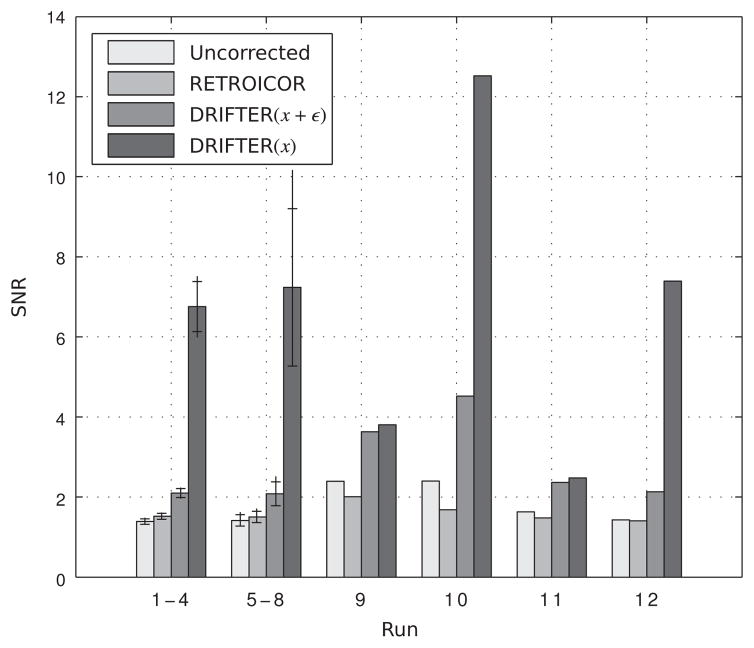
Similarly as for the simulated data, we calculated SNR values and component standard deviation estimates for the empirical data. The SNR values are visualized as a bar chart in Figure 6. For runs 1–4 and 5–8 the mean performance is visualized together with minima and maxima. These results show some improvement in SNR when using RETROICOR and clear advantage when using DRIFTER. In the four remaining runs of data the spread is stronger. RETROICOR suffers from the problem that it too often loses the track of the signal and is performing badly on average. DRIFTER shows improvement in SNR in all cases, even though the difference between DRIFTER(x + ε) and DRIFTER(x) being smaller with longer TR (in runs 9 and 11).

Figure 6.

The signal-to-noise ratios in experimental fMRI data for each run and each method. The average performance is shown for runs 1–4 and 5–8 with error bars illustrating the minimum, maximum and mean standard deviation of the results.

Table 3 shows average signal standard deviations σ_y and normalized standard deviations of the signal components. By comparing the physiological noise component standard deviations (σ_c for cardiac, σ_r for respiratory) it can be noticed that DRIFTER estimates are on average 1.51- and 1.25-fold compared to the RETROICOR estimates. Consequently the cleaned BOLD signal standard deviation estimate σ_x is on average 13% less in DRIFTER.

Table 3.

Results for the empirical data. Average signal standard deviations σ_y, and normalized standard deviations σ_i of the signal components, where the is stand for cleaned BOLD signal x, unexplained noise n, cardiac-induced noise c, respiration-induced noise r, and the white measurement noise estimate ε.

Run	σy	Uncorrected		RETROICOR				DRIFTER(x + ε)				DRIFTER(x)
		σx	σn	σx	σn	σc	σr	σx	σn	σc	σr	σx	σn	σc	σr	σε
1	35.21	1.00	0.77	0.90	0.63	0.25	0.29	0.75	0.39	0.37	0.37	0.63	0.10	0.37	0.37	0.37
2	30.69	1.00	0.76	0.91	0.63	0.26	0.25	0.76	0.39	0.37	0.35	0.64	0.10	0.37	0.35	0.38
3	36.65	1.00	0.71	0.92	0.61	0.24	0.24	0.79	0.39	0.35	0.33	0.68	0.10	0.35	0.33	0.37
4	31.03	1.00	0.78	0.90	0.66	0.27	0.26	0.75	0.41	0.38	0.36	0.62	0.11	0.38	0.36	0.39
5	7.89	1.00	0.76	0.92	0.66	0.24	0.25	0.77	0.41	0.37	0.34	0.63	0.10	0.37	0.34	0.40
6	7.35	1.00	0.78	0.92	0.67	0.24	0.23	0.76	0.43	0.37	0.34	0.62	0.11	0.37	0.34	0.41
7	7.30	1.00	0.77	0.93	0.68	0.23	0.23	0.77	0.44	0.36	0.34	0.62	0.11	0.36	0.34	0.42
8	8.78	1.00	0.66	0.95	0.59	0.20	0.19	0.83	0.37	0.32	0.28	0.73	0.08	0.32	0.28	0.36
9	65.79	1.00	0.45	0.95	0.49	0.12	0.28	0.94	0.28	0.19	0.17	0.94	0.27	0.19	0.17	0.04
10	16.09	1.00	0.50	0.92	0.58	0.11	0.35	0.88	0.26	0.22	0.26	0.84	0.08	0.22	0.26	0.24
11	29.82	1.00	0.64	0.93	0.65	0.30	0.29	0.84	0.38	0.33	0.31	0.83	0.36	0.33	0.31	0.06
12	8.54	1.00	0.74	0.93	0.69	0.23	0.24	0.78	0.41	0.37	0.31	0.65	0.09	0.37	0.31	0.40

The SPM based statistical analysis was run on four differently treated sets of fMRI acquisitions from runs 1–4 and 5–8. The tested methods were: No correction, physiological noise removal using RETROICOR, physiological noise removal using DRIFTER(x + ε), and physiological and measurement noise removal using DRIFTER(x). We chose an active set of voxels from the visual cortex for analysis by studying activations in SPM and used the data from sessions 1 (runs 1–4) and 2 (runs 5–8), where the condition for successive blocks alternated between rest and visual stimulation, starting from rest. Due to T1 effects the first four seconds of scans were discarded.

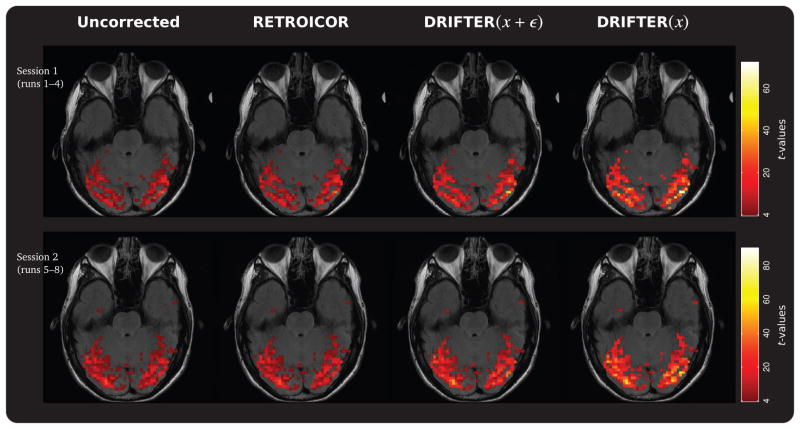
Using a critical threshold of p = 0.05, the numbers of activated voxels for which the null hypothesis of stimulus related correlation could not be rejected were 344/391, 411/439, 583/616, and 1000/920, for each method and the two sessions respectively. The intersection of these activated voxels sets contained 344 and 391 voxels. By comparing the relative change in the t-statistic in these voxels against the statistics in the results for uncorrected noise, average 1.21/1.12-, 1.71/1.65-, and 2.65/2.50-fold increases in t-statistics were documented. These t-statistics maps are shown in Figure 7 for one slice.

Figure 7.

Statistical parametric mapping (SPM) t-statistics maps acquired using a GLM analysis setup. The results visualize the results from using no correction of physiological noise and three different correction methods. Only the activated voxels returned by all methods are shown. Compared to the uncorrected data average 16%, 68%, and 157% improvement rates in t-values were documented for the correction methods.

5. Discussion

5.1. Interpretation of experimental results

The simulated and experimental fMRI results clearly point out the main difference between the RETROICOR and DRIFTER methods: the dynamic nature of DRIFTER makes it able to adapt to changes in both shape and amplitude in periodic noise signals, without requiring these effects to be present in the reference signal. The proposed method was also shown to be able to track varying frequency and ignore level changes in reference signals, whereas RETROICOR has often problems with keeping track of rapidly varying signals, especially in the case of time-varying amplitudes. This same problem can be expected to be present in all image-based methods that use low-order Fourier series fitting (including the methods in Chuang and Chen, 2001; Hu et al., 1995; Le and Hu, 1996; Frank et al., 2001).

Artifacts in the reference signals, such as drifting, amplitude changes (deep breaths) and sudden frequency changes, can be to some extent dealt with by preprocessing the references. However, as was shown, the IMM based method in DRIFTER copes well with these problems, and it is able to track the frequency of the desired phenomenon within a given frequency band with confidence. The IMM based approach was more robust and required less preprocessing than the peak-detection and histogram-based methods in RETROICOR.

The dynamic nature of DRIFTER sometimes causes slight overestimation of the amplitudes of reference signals in fMRI data. This is because the model allows rapid changes, which makes it harder to distinguish between the rapidly varying physiological noises and white measurement noise. However, this effect can be dealt with by setting the parameters of the method into values that best model the situation. When the physiological signal fluctuations are smaller, we can use smaller process noises for the signals.

We have used the DRIFTER method in two different modes of operation: in DRIFTER(x) we eliminated not only the physiological noise, but also the measurement noise from the signals, and in DRIFTER(x+ε) we retained the measurement noise as is done in RETROICOR. The former method clearly increases the SNR of the result significantly, because of the removal of one more noise component. But the difficulty is to know if this ‘measurement noise’ is really noise at all or should it be regarded as part of the activation signal. If the activation related brain signal really is such a smooth function that our model assumes, the correct approach would be to eliminate the measurement noise as well, as has been done in DRIFTER(x).

The practical advantages of the DRIFTER method were presented using GLM analysis in the SPM software. The results in Figure 7 showed difference in the statistical significance of the linear model results.

5.2. Extensions and future work

It would also be possible to estimate the frequencies of the cardiac and respiration signals with IMM directly from the fMRI measurements, for example, from the average of voxels in each 3D image or from some suitably chosen active region. In practice, due to the sampling theorem by Nyquist and Shannon (see, e.g., Oppenheim et al., 1999), it is only possible if the sampling frequency is at least twice the fundamental frequencies of the signals. That is, to reconstruct a typical 72 bpm cardiac signal this way, TR should be less than roughly 400 ms. Note that the theorem only applies to continuous spectrum signals (cf. Candès and Wakin, 2008) and thus is a limitation only on the frequency estimation stage. In the Kalman filter and RTS smoother based fMRI signal separation the Nyquist frequency is not a limitation. The spatial correlation of the physiological signals could also be used for reconstructing the cardiac and respiratory signals from multi-slice EPI data, even in the case of long TR, in a similar way as was done by Frank et al. (2001).

Here we have assumed that we first collect a batch of data and then estimate the frequencies and eliminate the noises. But the present methodology would fit to real-time operation as well, because the Kalman filter and IMM filter algorithms were originally designed for real time operation. The statistically optimal non-delay real time operation can be done by running the IMM filter and Kalman filter continuously with real time data and using their estimates directly without a backward pass. If we do afford some delay, we could use so called fixed-lag smoothers (see, e.g., Grewal and Andrews, 2001) for improving the estimates.

The model constructed in this paper only consists of a smooth activation related brain signal (that also accounts for other slow phenomena, such as scanner drift), cardiac and respiration related physiological noises and white measurement noise. But there exists other kinds of physiological noises as well (Krüger and Glover, 2001; Wise et al., 2004; Birn et al., 2006; Shmueli et al., 2007), and these could be included into the model as additional oscillators or as other kinds of stochastic state space models. Instead of using a high-pass filter based preprocessing and a Wiener velocity model (which has 1/f² spectrum), we could use a separate long-term model for the slow signal drift (say, a model with approximately 1/f spectrum) and a smooth but a bit quicker varying activation signal on top of that. We could also use a more elaborate model for the brain activation, which would account for the known or estimated shape of the hemodynamic response (Buxton et al., 1998; Friston et al., 1998, 2000; Havlicek et al., 2011). In the case of nonlinear hemodynamic models, for the separation of the signal components, we could utilize non-linear Kalman filters and RTS smoothers (see, e.g., Bar-Shalom et al., 2001; Grewal and Andrews, 2001) or more recently developed sigma-point and Gaussian integration based methods (Julier et al., 2000; Ito and Xiong, 2000; Arasaratnam and Haykin, 2009; Särkkä, 2008; Särkkä and Hartikainen, 2010).

Here we have not used any parameter estimation methods for determining the best parameter values, because all the parameters have a clear physical meaning. However, it would be quite easy to use a generic parameter estimation method on top of the present state space model framework. In the Wiener velocity model the process noise parameter defines the diffusion constant of the derivative and thus ‘stiffness’ of the signal, and it can be set to a value, which best models the brain activation that we are expecting. In a fast event-related design we might use a higher process noise parameter in the Wiener velocity model than in a relatively slowly varying block design. The process noises in the resonators define how much the signal harmonics differ from perfect sinusoids. When setting the values of the process noises, one should favor larger values to lower values, to avoid too stiff models. The measurement noise variance is really the variance of the near-white component that we interpret as the noise.

In the fMRI signal model presented in Section 2.4 we assumed that the signals in each voxel are independent. However, this is not the case in reality and it might be beneficial to model interactions between the voxels as well. Especially the respiration signal is highly correlated, because the signal is quite constant in the whole brain (Glover et al., 2000). There is also significant spatial structure in the cardiac signal (Dagli et al., 1999; Glover et al., 2000). The interaction model could be implemented by replacing the matrix F in the Equation (23) with a suitable linear operator such as differential operator, which acts on the spatial variable r⃗. The resulting model could then be estimated using infinite-dimensional versions of the Kalman filter and RTS smoother (see, e.g., Omatu and Seinfeld, 1989; Cressie and Wikle, 2002; Kaipio and Somersalo, 2005). Although, the resulting algorithm might be overly complex for physiological noise elimination alone, it might be beneficial when combined with inversion based fMRI methods (cf. Lin et al., 2006, 2008).

6. Conclusion

In this paper we have introduced the DRIFTER algorithm, which is a new image-based Bayesian method for retrospective elimination of physiological noise from fMRI measurements. The method uses a stochastic state space model and the interacting multiple models (IMM) algorithm for estimating the frequency trajectories of cardiac and respiration from reference signals, or if the time resolution allows, from the fMRI signal itself. The estimated frequency trajectories are then used as known frequencies in a stochastic state space model, which consists of a slowly varying activation related brain signal model and stochastic oscillator models for the physiological signals and their harmonics. The separation of the fMRI voxel signals into activation related brain signals and physiological noises is done using Kalman filter and Rauch-Tung-Striebel smoother algorithms. Due to the model based approach, the separation operation is not limited by the Nyquist-Shannon theorem and can be used with relatively long TRs, provided that frequency trajectories of the physiological signals are estimated from more densely sampled signals. The performance of the method was compared to RETROICOR and the experimental result show that the new DRIFTER method is able to cope with sudden changes in physiological signals better than RETROICOR.

Highlights.

• New Bayesian method for removing physiological noise from fMRI data

• Cardiac and respiration frequencies from reference signals with the IMM algorithm

• Possible to estimate the frequencies from fMRI data if time-resolution allows

• Separation of fMRI into activation and noise with Kalman filtering and RTS smoothing

• Outperforms the RETROICOR method when physiological signals change much over time