Finessing the fracture energy barrier in ballistic seed dispersal

Abstract

Fracture is a highly dissipative process in which much of the stored elastic energy is consumed in the creation of new surfaces. Surprisingly, many plants use fracture to launch their seeds despite its seemingly prohibitive energy cost. Here we use Impatiens glandulifera as model case to study the impact of fracture on a plant’s throwing capacity. I. glandulifera launches its seeds with speeds up to 4 m/s using cracks to trigger an explosive release of stored elastic energy. We find that the seed pod is optimally designed to minimize the cost of fracture. These characteristics may account for its success at invading Europe and North America.

Explosive dehiscence is a common seed dispersal strategy in plants (1). The mechanism is analogous to a catapult (2): stored elastic energy is rapidly released and converted into kinetic energy of the seeds. Unlike in the catapult however, there is no equivalent in the plant kingdom of a mechanical latch to trigger the energy release and plants instead resort to physically breaking the bonds that sequester the elastic energy. For explosive dehiscence the bond breaking is accomplished by a fast moving crack. However, cracks consume energy and should thus significantly degrade the efficient use of stored energy. Here we investigate the energy balance in the fracture mediated seed dispersal of Impatiens glandulifera Royle, one of the most invasive nonnative plant species in Europe (3–5) and North America (6, 7). We find that the construction of the seed pod is a marvel of natural design that achieves a highly efficient energy transfer by exploiting the fleetness of fracture, finessing the fracture energy cost, and coordinating the simultaneous fracture of its five seams.

The seedpod of I. glandulifera, shown in Fig. 1A, consists of 5–10 seeds held within a shell comprised of five elongated segments or valves (8). The relaxed shape of a single valve is curled, as shown in Fig. 1B. When the seedpod is whole, the valves are held straight in a state of tension by a membrane connecting adjacent valves. Seed ejection proceeds as shown in Fig. 1D: a single seam cracks, minute contractions of the pod split the reaming seams (not visible in Fig. 1B), and now fully freed the valves contract and accelerate the payload.

Fig. 1.

(A) Impatiens glandulifera seedpod with two seams indicated and top/bottom convention marked. (B) An unconstrained pod valve. The relaxed state is curled. (C) Top and side view of a valve glued to a glass slide. Each valve is approximately 20 mm long, and consists of a rigid section approximately 15 mm long with a triangular cross-section which widens and thickens along the length and a thin-walled and floppy 5 mm long membrane. The (red) dashed line demarcates the boundary between the floppy and the rigid parts. The scale bar corresponds to 5.6 mm. (D) Photographic sequence of the pod opening extracted from a high speed video. From left to right t = 0; 263; 789; 1,578; 2,104 μs. (see also Movie S1). Note that only the upper rigid section curls and accelerates the load.

During the ejection sequence, the mechanical energy stored in the valves in the form of elastic potential energy U_e is released. Some of this energy pays for the fracture energy U_f, some is transferred to the kinetic energy of the seeds K_s and valves K_v, and the remainder D is lost due to dissipative processes. From energy conservation U_e = U_f + K_s + K_v + D.

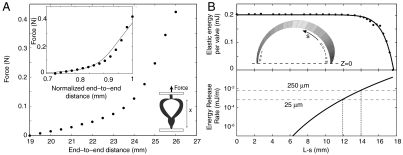
We measured the force needed to stretch a seed pod from a fully open state to a closed state (see e.g., Fig. 2) and calculated U_e from the area under the force-separation curve. We obtain a value U_e = 0.9 ± 0.2 mJ . We determined the kinetic energy K_s of the seeds using high speed video to measure the speed of the seeds. We ignore the rotational kinetic energy due to its smallness (see ref. 9). The mean mass of a seed m was measured to be 19.9 mg (N = 7), the mean speed of the seeds u was measured to be 3 ± 1 m/s (N = 4). The kinetic energy of the seeds 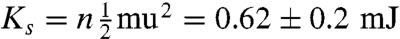, where n = 7 is the mean number of seeds per pod. Kinetic energy imparted to the valves is difficult to quantify due to their odd shape and motion of the valves (see Movie S1). An estimate based on the mass of the five valves (0.1 mg) and the speed of the seeds (because part of the valve must be moving at least as fast the seed) gives a value of 0.4 mJ. Thus, almost all the stored energy is converted into kinetic energy. Interestingly, similar measurements on Impatiens capensis show much lower conversion efficiency (9); we revisit this difference below.

Fig. 2.

(A) Force vs. displacement for a 26 mm long seedpod pulled from a relaxed state to its original length. Bottom right inset: cartoon of force-displacement apparatus showing a pod in an almost fully relaxed state. Top inset: Same data as in main figure but with the end-to-end distance normalized by the length. The solid line shows the result of a finite element calculation for the same geometry with a Mooney-Rivlin constitutive relation. (B) Results of finite element calculation. Elastic energy per valve (top) and energy release rate (bottom) for a seedpod (17.5 mm rigid section length) with a crack of length L - s extending from the stem downward. When the pod is fully sealed the elastic energy is 0.2 mJ per valve. As the crack extends virtually no energy is released until the crack is longer than 12 mm. Conversely, the pod is able to maintain its structural integrity even if the seams are split along 70% of their length. The energy release rates were calculated by differentiating the fit to the data for the elastic energy per valve (shown as solid line in top). Dashed lines shown the threshold value for unstable crack growth for a seam with 25 μm and 250 μm thickness. Inset: finite element model with arc length s shown as the distance from the bottom. The z = 0 plane is impenetrable and represents a neighboring valve.

Given that almost all the stored energy is transferred into kinetic energy, the fracture energy must be small. Estimating the fracture energy, however, leads to the opposite conclusion. We assume that the material is brittle (see ref. 2). The fracture energy is proportional to the new surface area created by a crack and a material dependent constant Γ with units of energy per unit area. The total fracture energy for the seed pod U_f = 5 × 2ΓtL where t and L are the seam thickness and length; the factor for five corresponds to the number of seams. A conservative estimate for Γ is 10 J/m², the fracture energy of wood along its grain (10) and to the best our knowledge the lowest value for plant matter in the published literature. With L = 2.5 cm and t = 300 μm from measurement, and thus U_f ≈ 0.6 mJ. Clearly something is wrong in this estimate because U_f is not small compared to U_e in contradiction to our measurements. One possible resolution of this paradox is that the estimate for Γ is too high. However, that possibility is unlikely because even the most brittle materials (e.g., glass) have Γ ≈ 3 J/m²,. Below we show that the problem lies in the assumption that the entire length of the pod must be fractured by the elastic fields.

In order to reconcile the difference between the measured and estimated fracture energy, we examined the mechanics of a single valve using a finite element model (11) with the actual geometry of a valve and a nonlinear stress-strain law selected to match the measured elastic response of a valve. The result of these calculations show that only 30% of seam’s length is needed to keep the pod closed, and thus the pod is highly resistant to cracks. The latter can be quantified via Griffith’s criteria: a crack will lengthen if the elastic energy per unit area gained by an advancing crack is sufficient to pay the energetic cost of creating two new crack faces (12). Fig. 2 shows a plot of calculated from the finite element model. is essentially zero for the first 70% of the seam, and therefore up to 70% of the seam can be cracked without precipitating a release of the stored energy.

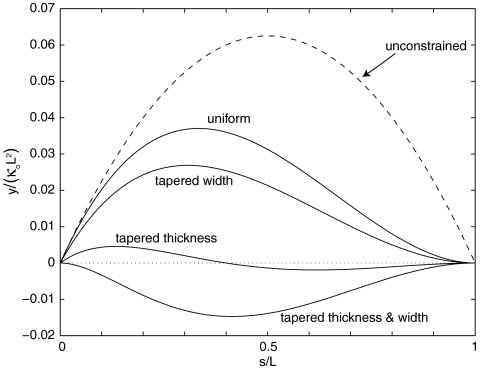
While the finite element calculation shows that the seed pod is highly resistant to cracking, it does not show why this is the case. A simpler model, based on the elastica approximation (13), reveals a crucial dependence on the shape of the valve. We considered valves with triangular cross-sections and varying tapers from none (i.e., uniform thickness and width) to the actual taper of I. glandulifera’s valves (i.e., linearly increasing thickness and width; see Fig. 1B). The model gives the shape of the valve when its end are held flush to its neighbor. These data are plotted in Fig. 3. For the case of uniform thickness and of a tapered width, the entire length (except the ends) of the valve is separated from its neighbor. In contrast, as shown in when the thickness is tapered, the valve is forced up against its neighbor because to relax towards its natural (positive) curvature would introduce a more costly (negative) curvature (see Fig. 4). Thus, the resistance to cracking is due to tapered cross-section of the valves and furthermore the valve is tapered no more than needed to achieve this characteristic.

Fig. 3.

Results of elastica computation for beams of varying cross section. The dashed curve shows the relaxed state of the beam. The solid curves show the shape of the beam for various tapers for the boundary conditions y = 0 at s = 0 and dy/ds = 0 at s = L corresponding physically to the attachment of the valve to its neighbor at a point (at s = 0) and along a line (at s = L). The result for the uniform and tapered width cases indicate that the beginning part of the valve will relax towards its preferred curvature κ_o. Conversely, the beam crosses the y = 0 plane for both cases in which the thickness is tapered. This result occurs because it is energetically favorable to allow the thicker portions of the beam relax towards the preferred curvature and use the thinner portions to satisfy the y = 0 boundary condition. However, in a pod the valve would be prevented from crossing the y = 0 plane by its neighbor, and thus the valve will do the next best thing which is to press flat against its neighbor.

Fig. 4.

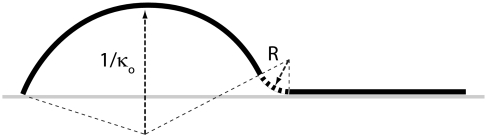
Illustration of negative curvature (indicated by dashed segment) produced when part of the pod relaxes to its natural curvature κ_o while maintaining the boundary conditions dictated by bonding to neighboring valves. In the absence of a taper the decrease in energy from the relaxed portion outweighs the increase due to the negatively curved portion. With a taper in the thickness of the valve the energy balance is reversed: the energy increase due to the negatively curved segment outweighs the energy decrease due to relaxed segment because the negative curvature is on a thicker—and thus more rigid—segment.

In comparison to I. glandulifera, I. capensis is not as energy efficient (14), it has a smaller throwing range (8,15), and it is less invasive (16). These differences are explained by the elastica model. I. capensis’s valves are almost uniform in thickness and width. The absence of a taper means that the seams cannot be precracked as in I. glandulifera because any precracking causes the pod to open up. Thus, I. capensis must pay the full cost of fracturing the seams at the time of launch which leads to a highly inefficient transfer of potential to kinetic energy.

These computational results are consistent with our observations of crack propagation in I. glandulifera seed pods. We applied pressure on the stem of immature seed pods with intact seams. High speed video recordings show that the crack creeps along the seam and only when it exceeds approximately 80% of the seam’s length will the crack accelerate to full speed and proceed without further external forcing (see Movie S2).

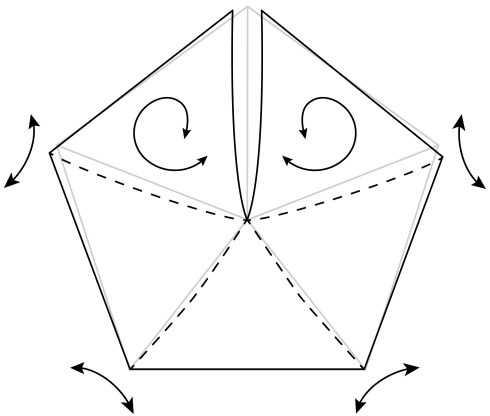
So far we have only considered the mechanics of a single valve. For an efficient use of the stored energy all five valves must be free from each other which can only occur if all five seams are cracked simultaneously. Our video recording (see Movie S3) show that this is indeed the case: all the seams open within 250 μs, which is short compared to the 3 ms time scale on which the pod fully relaxes and accelerates the seeds. How is such fine tuned synchronization achieved? In short, through the mechanical coupling of the valves. As the valves on either side of the crack begin to relax they open outwards pivoting about the seam with adjacent valve, as illustrated in Fig. 5. The rotation about these uncracked seams drives a mode I crack through the thickness of the seam. We constructed a mechanical model of the pod (see Figs. S1, S2) which duplicates this behavior. In the paper model, the only way bend the valves is to first unroll the pod along its longitudinal axis; conversely, bending the valves causes the pod to unroll.

Fig. 5.

Schematic illustrating the coupling between valves as viewed down the symmetry axis of the pod. When the bond between adjacent valves cracks, the valves begin to curl which in turn causes all the valves to rotate about the unbroken seams. The original uncracked arrangement of valves is shown in light gray. The mechanical model constructed from paper is given in Fig. S1 and its mechanical response to bending is given in Fig. S2.

Our analysis reveals a more detailed sequence of events for seed ejection. First, long before the triggering event cracks creep down all five seams. This process costs about 0.5 mJ irrespective of how it is done. Beyond demonstrating that the energy does not come from the elastic fields, this study does not address this mechanism. With 80% of the seams cut the pod is primed for triggering by an external event. The cascade begins when one of the seams is driven past the threshold for crack growth. The seam begins to open, triggering the remaining seams to fracture. Finally, with all five valves free, the seeds are accelerated by the relaxation of the tension in the valves. The temporal separation of the fracturing process from the acceleration phase are crucial to achieving an explosive release. Because only a small fragment of the seam remains intact at the release event, the seed pod achieves an efficient transfer of elastic to kinetic energy, wasting little energy on cracking the seams.

Materials and Methods

Seed Collection.

We measured the quantities K_s and U_e for seed pods obtained from I. glandulifera growing wild around Bristol, United Kingdom. Our experiments were performed within a couple of hours of when the pod was picked.

Force Measurement.

Aluminum blocks with holes machined to accommodate the ends of the seed pod were attached to the pod with cyanoacrylate. The lower block was fixed to a balance and the upper block was attached to a translation stage with a micrometer actuator. With two ends now fixed, the seams of the pod were cut with a knife. The upper block was translated downward until the interior components were accessible; these were then removed. The upper block was then moved yet closer until the force measured zero. Thereafter, the force on the lower block and the separation of the blocks was measured as the upper block was translated upwards.

Finite Element Calculation.

The cross section was triangular with a base and height that increased linearly over the first 70% of the length and then decreased over the remaining 30% to the initial size consistent with the shape shown in Fig. 1C. The shape was curved such that the inner edges formed a half circle of length L. The deformations were calculated using ALGOR mechanical event simulator with a Mooney-Rivlin constitutive relation with energy density Π = C₁λ₁ + C₂λ₂ where λ₁ and λ₁ are the first and second invariants of the deformation tensor (17), and C₁ = 4.0 × 10⁷ dynes/cm² and C₂ = 1.3 × 10⁷ dynes/cm². The calculation started from the relaxed state with both ends on the model on the z = 0 plane as shown in Fig. 2. s is the arc length measured from the bottom. We calculated the energy needed to move the outer edge of the model down to the z = 0 plane along a segment [0,s]. From the finite element model we calculate the energy needed to bring edges together of length s. This calculation is physically equivalent to measuring the stored energy when adjacent valves are bonded along the bottom s of their length.

Elastica.

The energy of a valve is given by:

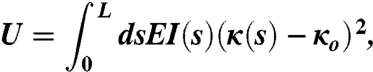[1]

where E is the elastic modulus, κ is the curvature, κ_o is the natural curvature, 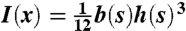is the moment of inertia where b is the width of the valve and h is the thickness of the valve, and s is the arc length measured from the top. The shape of the valve is codified in b and h. Both h and b increase approximately linearly along the length of the valve (see Fig. 1), and therefore I = I_o(1 + s/L)^α . The case α = 0 corresponds to a beam with constant height and width, α = 1 to a constant height and linear increase of width, α = 3 to constant width and linear increase of height, and α = 4 to a linear increase in both the height and the width (i.e., the actual geometry of the valve). We define y(s) to be the defection of the beam. With the approximation κ ≈ d²y/ds², U was minimized to obtain the equation:

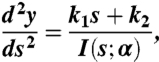where k₁ and k₂ are integration constants to be determined by the boundary conditions. Boundary conditions were simply supported at s = 0 (i.e., y(0) = 0 and 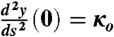) and forced to lie flat at s = L (i.e., y(L) = 0 and 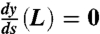). The elastica model allows the material to pass thru y = 0. Nonetheless, the requirement that the y = 0 plane be inpenetrable can be obtained by requiring that y(L - ε) = 0. The solution is unchanged except that L is renomalized to L - ε. Iterating this procedure will generate the solution y(x) = 0 for all x