Theory of Free Energy and Entropy in Noncovalent Binding

1. Introduction

Noncovalent binding provides an invisible wiring diagram for biomolecular pathways and is the essence of host-guest and supramolecular chemistry. Decades of theoretical and experimental studies provide insight into the determinants of binding affinity and specificity. The many practical applications of targeted molecules have also motivated the development of computational tools for molecular design aimed at drug-discovery¹ and, to a lesser extent, the design of low molecular weight receptors.^2–6 Nonetheless, there remain unresolved questions and challenges. The rules of thumb for maximizing binding affinity are unreliable, and there is still a need for accurate methods of predicting binding affinities for a range of systems.

Many researchers are now renewing progress in this area by delving deeper into the physical chemistry and modeling of noncovalent binding.^1,7 Important themes today include the use of more refined models of interatomic energies,^8–12 computational^13–23 and experimental^24–34 characterization of configurational entropy changes on binding, enhanced techniques for sampling molecular conformations and extracting free energies from simulations,^35–43 and the exploitation of advances in computer hardware.^44–53

Such efforts require both a quantitative understanding of interactions at the atomic level and a means of mapping of these interactions to macroscopically observable binding affinities. Statistical thermodynamics provides the required mapping, and the theoretical underpinnings of binding thermodynamics appear to be well established.^14,54–56 Nonetheless, analyses of binding, both experimental and theoretical, still frequently employ non-rigorous frameworks which can lead to puzzling or contradictory results. This holds especially in relation to entropy changes on binding, which can be both subtle and controversial. For example, although the change in translational entropy when biomolecules associate has been discussed in the literature for over 50 years, it remains a subject of active discussion.^{15,18,56–71}

This review of the theory of free energy and entropy in noncovalent binding aims to support the development of well-founded models of binding and the meaningful interpretation of experimental data. We begin with a rigorous but hopefully accessible discussion of the statistical thermodynamics of binding, taking an approach that differs from and elaborates on prior presentations; background material and detailed derivations are provided in Supporting Information. Then we use this framework to provide new analyses of topics of long-standing interest and current relevance. These include the changes in translational and other entropy components on binding; the implications of correlation for entropy; multivalency (avidity) and the relationship between bimolecular and intramolecular binding; and the applicability of additivity in the interpretation of binding free energies.

Several caveats should be noted. First, we focus on general concepts rather than specific systems or computational methods, the latter having been recently reviewed.^1,7 Second, our formulation of binding thermodynamics is based on classical statistical mechanics, although occasional reference is made to quantum mechanics when the connection is of particular interest. Finally, we have not attempted to be exhaustive in citing the literature but hope to have provided enough references to offer a useful entry.

2. Free Energy, Partition Function, and Entropy

This section provides the groundwork for our treatment of binding thermodynamics by introducing and analyzing two central concepts, the free energy and its entropy component. Section 1 of Supporting Information provides background material and further details.

The free energy can be calculated from a microscopic description of the system in question. The Helmholtz free energy, F, which is particularly useful for the condition of constant volume, is given by

$$F=-k_{\text{B}}\mathit{T}ln\mathit{Q}$$ (2.1)

where k_B is Boltzmann’s constant and T is absolute temperature. If the coordinates (and perhaps momenta) of the system are collectively denoted as x and its energy function is E(x), then the partition function, Q, is given by the configurational integral

$$Q=\mathcal{N}\int d{\mathbf{x}e}^{-\beta E(\mathbf{x})}$$ (2.2)

where β = (k_BT)⁻¹ and the constant N is inserted to render Q unitless; its particular value does not have any significance here. The average energy of the system is

$$\langle E\rangle =\int d\mathbf{x}E(\mathbf{x})\rho (\mathbf{x})$$ (2.3)

in which ρ(x), the equilibrium probability density in x, is

$$\rho (\mathbf{x})=\frac{e^{-\beta E(\mathbf{x})}}{\int d{\mathbf{x}e}^{-\beta E(\mathbf{x})}}$$ (2.4)

As shown in Section 1 of Supporting Information, the entropy is

$$S=\frac{-F+\langle E\rangle }{T}$$ (2.5a)

$$=-k_{\text{B}}\int d\mathbf{x}\rho (\mathbf{x})ln\rho (\mathbf{x})+k_{\mathbf{B}}ln\mathcal{N}$$ (2.5b)

The entropy given by eq 2.5b will be referred to as the configurational entropy. The constant term, k_BlnN, serves to cancel the units of ρ(x) inside the logarithm and does not have any consequence when differences in entropy are calculated.

The following subsections introduce ideas that provide a basis for the theory of binding and its analysis in Sections 3–8.

2.1 Entropy for Single and Multiple Energy Wells

The entropy can be viewed as a measure of uncertainty, and, for an energy function with multiple energy wells, there are two different sources of uncertainty. One arises from motions within a single well, the other from transitions between the different energy wells. The configurational entropy may be decomposed into two parts, one corresponding to each source of uncertainty, as now illustrated for a one-dimensional system with coordinate x.

To start, let us consider the case where the energy has a single minimum, located at x = x₀. When only a small region around the energy minimum makes a significant contribution to the configurational integral, a harmonic approximation may be made,

$$E(x)\approx E_0+{(x-x_0)}^2/2$$ (2.6)

where k is the curvature of the energy function at x = x₀. The partition function is then

$$Q=\mathcal{N}{\left(\frac{2\pi }{\beta k}\right)}^{1/2}{e}^{-\beta E_0}$$ (2.7)

and the free energy is

$$F=E_0-k_{\text{B}}Tln\left[\mathcal{N}{\left(\frac{2\pi }{\beta k}\right)}^{1/2}\right]$$ (2.8)

The average energy and entropy are given by

$$\langle E\rangle =E_0+\frac{k_{\text{B}}T}{2}$$ (2.9a)

$$S=k_{\text{B}}ln{\left(\frac{2\pi }{\beta k}\right)}^{1/2}+\frac{k_{\text{B}}}{2}+k_{\text{B}}ln\mathcal{N}$$ (2.9b)

As the curvature, k, decreases, the energy well becomes broader, the system explores a broader range of positions, and the entropy increases.

When the energy function E(x) has multiple local minima, we can break the configurational integral of eq 2.2 into pieces, each covering an energy well, i^16,72–74

$$Q=\sum _i{Q}_i$$ (2.10a)

$$Q_i=\mathcal{N}{\int }_{i}dx{e}^{-\beta E(x)}$$ (2.10b)

The subscript “i” in eq 2.10b signifies that the integration is restricted to energy well i. Within each energy well, one can normalize the probability density ρ(x),

$${\rho }_i(x)\equiv \rho (x)/p_i,x\in \text{well}i$$ (2.11)

where p_i = Q_i/Q is the probability of finding the system in energy well i. The average energy 〈E〉 and the entropy S can be obtained from ρ(x) according to eqs 2.3 and 2.5b, respectively. For each well, one can obtain the corresponding quantities 〈E〉_i and S_i from ρ_i(x).

We now establish relations of 〈E〉 and S with 〈E〉_i and S_i. By breaking the integral of eq 2.3 into individual wells and writing ρ(x) as p_iρ_i(x), one can easily verify that

$$\langle E\rangle =\sum _i{p}_i{\langle E\rangle }_i$$ (2.12)

while eq 2.5b becomes^75,76

$$S=\sum _i{p}_i{S}_i-k_{\text{B}}\sum _i{p}_{i}ln{p}_i$$ (2.13)

Note that, whereas the average energy (eq 2.12) is simply a weighted average of the energy associated with each well, the entropy (eq 2.13) includes a second term which is akin to the entropy of mixing. Intuitively, eq 2.13 states that the total configurational entropy is the weighted average of the entropies S_i of the individual wells plus the entropy associated with the distribution of the system across the energy wells i. This observation is just a molecular instance of the more general composition law of entropy.⁷⁷ In the present context, the two terms of the configurational entropy are often referred to, respectively, as the vibrational and conformational entropies.^75,78 It is worth noting that the same expression would be obtained if we partitioned configuration space in some other manner; in the mathematical sense at least, there is nothing special about a partitioning into energy wells.

2.2 Uncorrelated vs. Correlated Coordinates

The degree of correlation among different coordinates significantly affects the magnitude of the entropy. Correlation means that knowing the value of one coordinate reduces the uncertainty regarding the value of another coordinate. Therefore, in general, correlation reduces the entropy.

We denote the components of x as x₁, x₂, … If each coordinate contributes an additive term to the energy, so that E(x) = E₁(x₁) + E₂(x₂) + …, then motions along the coordinates are uncorrelated with each other, and the partition function of the multidimensional system is the product of the partition functions associated with individual coordinates:

$$Q={\mathcal{N}}_1\int {dx}_1{e}^{-\beta E_1(x_1)}\times {\mathcal{N}}_2\int {dx}_2{e}^{-\beta E_2(x_2)}\times \cdots$$ (2.14)

As a result, the joint probability density is given by the product of the one-dimensional marginals:

$$\rho (x_1,x_2,\dots )=\rho (x_1)\rho (x_2)\dots$$ (2.15)

Correspondingly the free energy, average energy, and entropy can be written as sums of contributions from each coordinate. In particular,

$$S=\sum _i{S}_i$$ (2.16a)

where

$$S_i=-k_{\text{B}}\int {dx}_i\rho (x_i)ln\rho (x_i)+k_{\text{B}}ln{\mathcal{N}}_i$$ (2.16b)

The concept of uncorrelated coordinates can be generalized to a situation in which x₁, x₂, …, each refer to nonoverlapping groups of coordinates, rather than to individual coordinates.

An important example of uncorrelated coordinates is presented by the total energy of a classical system, which is the sum of the potential energy and the kinetic energy. The additivity of these two forms of energy means that they contribute multiplicative factors to the full partition function, one depending only on spatial coordinates and the other depending only on momenta, which together completely specify the state of a classical system in phase space. This result has important consequences, which are further discussed in the next subsection. Here we illustrate the separability of potential energy and kinetic energy for the case of a one-dimensional harmonic oscillator. The total energy for this system is

$$E(x,p)=E_0+k{(x-x_0)}^2/2+p^2/2m$$

where p is momentum and m is mass. The partition function

$$Q=\mathcal{N}\int \mathit{dxd}p{e}^{-\beta E(x,p)}$$

can be evaluated by integrating over x and p separately. The integral over x is given by eq 2.7, and the integral over p gives (2πm/β)^1/2, so the full partition function is

$$Q=\mathcal{N}\frac{2\pi }{\beta \omega }{e}^{-\beta E_0}$$ (2.17)

where ω = (k/m)^1/2 is the angular frequency. When this classical expression is derived as the high-temperature limit of a quantum treatment, one finds the multiplicative constant N to be 1/h, the inverse of Planck’s constant. For the more general case of a polyatomic molecule, each atom, by its motion in three dimensions, contributes a factor (1/h)³ to the multiplicative constant N.

Now let us examine the more common situation in which E(x) is not given by E₁(x₁) + E₂(x₂) + …, so that motions along the different coordinates of the system do correlate. In this case, the entropy of the system is no longer equal to the sum of the contributions from the marginal entropies, as in eq 2.16a for the uncorrelated case. In fact, as proven in Section 1 of Supporting Information, the actual entropy of any system is always less than or equal to the sum of the marginal entropies, and the equality holds only when the coordinates are uncorrelated. In the proof, we derive the following result for the entropy of a system with two coordinates, x₁ and x₂:

$$S=-k_{\text{B}}\int {dx}_1\rho (x_1)ln\rho (x_1)-k_{\text{B}}\int {dx}_1\rho (x_1)\int {dx}_2\rho (x_2\mid x_1)ln\rho (x_2\mid x_1)+k_{\text{B}}ln\mathcal{N}$$ (2.18)

The first term gives S₁ (cf. 2.16b). However, unless x₁ and x₂ are uncorrelated, the second term cannot be reduced to S₂. Nonetheless, one can still refer to this term as the entropy associated with x₂ in the following sense. The quantity −k_B ∫dx₂ ρ(x₂|x₁ )ln ρ(x₂|x₁) constitutes the entropy due to motion along x₂ for a given value of x₁; the second term is just this entropy averaged over the equilibrium distribution of x₁. We will return to this interpretation of the second term in Subsection 2.4. In eq 2.18, x₁ and x₂ have been set up in different roles: x₁ is kept as an “explicit” coordinate for detailed attention, whereas x₂ is treated as a “bath” or “implicit” coordinate which is readied for suppression through an approximate or mean-field model. Note that, from a mathematical standpoint, either variable can be chosen as explicit; i.e., an equally valid formulation for S is obtained when x₁ and x₂ are interchanged in eq 2.18.

The difference, I₁₂ ≡ S₁ + S₂ − S, known as the pairwise mutual information, provides a measure of the degree of correlation between two coordinates.^79–81 This concept generalizes to systems with more than two coordinates in two ways. First, the pairwise mutual information also can be applied when x₁ and x₂ are not single coordinates, but rather nonoverlapping subsets of coordinates. For example, x₁ might represent the coordinates of a receptor and x₂ those of its ligand. In addition, one can define higher order mutual information terms.^79–81 For example, the entropy of a system with three coordinates, x₁, x₂, and x₃, can be written as

$$S=\sum _{i=1}^3{S}_i-\sum _{j>i}^3{I}_{ij}+I_{123}$$ (2.19)

where I₁₂₃ is the third-order mutual information.

2.3 The Molecular Partition Function: Rigid vs. Flexible Formulations

In order to formulate the statistical thermodynamics of noncovalent binding, we need expressions for the partition functions of the free receptor and ligand, which are in general flexible, polyatomic molecules, and their bound complex. This subsection reviews and analyzes two approaches to writing these molecular partition functions.

2.3.1 Rigid Rotor, Harmonic Oscillator Approximation

The first approach is to use the rigid rotor, harmonic oscillator (RRHO) approximation.^82,83 This approximation was first formulated in order to make a quantum mechanical treatment of molecular motions mathematically tractable.^84,85 Treating a molecule as essentially rigid, so that its internal motions comprise only vibrations of small amplitude, allows one to approximate the energy contributions—both kinetic and potential—of its translational, rotational and vibrational motions as uncoupled from each other. This allows the partition function to be factorized, as discussed in Subsection 2.2. Overall translation of the molecule contributes a factor

$$Q_{\text{t}}=V{\left(\frac{2\pi m}{\beta h^2}\right)}^{\frac{3}{2}}$$ (2.20a)

to the full partition function of the molecule, where the molecular mass m appears because of the contribution of the kinetic energy of overall translation. This expression is the classical approximation to the quantum mechanical sum over states. For future reference, we note that Q_t leads to an expression for translational entropy known as the Sackur-Tetrode equation (Subsection 5.3). The assumption of rigidity in the RRHO treatment allows the moments of inertia to be approximated as constants so that the rotational contribution to the partition function can be written as

$$Q_{\text{r}}=8{\pi }^2{\left(\frac{2\pi }{\beta h^2}\right)}^{\frac{3}{2}}{(I_1{I}_2{I}_3)}^{\frac{1}{2}}$$ (2.20b)

where I₁, I₂, and I₃ are the molecule’s three principal moments of inertia, and we have again used the classical approximation. Finally, a quantum mechanical treatment of the internal vibrations, each with angular frequency ω_i, contributes a factor

$$Q_{\text{vib}}=e^{-\beta E_0}\prod _i\frac{e^{-\beta h{\omega }_i/4\pi }}{1-e^{-\beta h{\omega }_i/2\pi }}$$ (2.20c)

The full partition function of the molecule then takes on the familiar form

$$Q=Q_{\text{t}}{Q}_{\text{r}}{Q}_{\text{vib}}$$ (2.21)

2.3.2 Flexible Molecule Approach

The second approach to formulating the molecular partition function is not new, but we are not aware of a term for it in the literature. In order to distinguish it from the RRHO approximation, we call it the flexible molecule (FM) approach. The FM approach relies upon classical statistical thermodynamics, which is routinely and appropriately used for Monte Carlo and molecular dynamics simulations of biomolecular systems. In the classical approximation, the kinetic energy of each atom makes a fixed contribution to the partition function that is independent of conformation and potential energy. In particular, these kinetic energy contributions to the partition function do not change when two molecules bind to form a noncovalent complex, so they do not affect the binding free energy. This means that classical calculations of the binding constant can completely neglect kinetic energy, and hence that any correctly formulated classical treatment of binding yields results that are independent of the masses of the atoms. By the same token, each atom contributes a factor (1/h)³ to the multiplicative constant N in the partition function (Subsection 2.2), so the binding free energy is also independent of N and hence of Planck’s constant h. As a corollary, any dependence on mass or Planck’s constant of a quantum mechanical expression for the free energy or entropy of binding should disappear when β → 0, since in such a limit the quantum result must reduce to classical statistical mechanics. This cancellation is demonstrated below for the classical limit of the RRHO treatment.

When the kinetic energy contribution to the partition is omitted, as allowed by classical statistical thermodynamics, what is left is the configurational integral over spatial coordinates. There is no longer any need to consider the coupled kinetic energies of overall rotation and conformational change, and the approximation of fixed moments of inertia becomes unnecessary so the unrealistic rigid rotor approximation can be eliminated. It is still convenient to separate the n spatial coordinates of the molecule into 3 coordinates for overall translation, 3 more for overall rotation, and 3n – 6 internal coordinates. Overall translation contributes a factor of V, the total volume, to the configuration integral, and overall rotation contributes a factor of 8π². The internal contribution can be written as

$$Q_{\text{in}}=\int d\mathbf{x}J(\mathbf{x})e^{-\beta E(\mathbf{x})}$$ (2.22)

where x now refers to internal coordinates, and J(x) is a Jacobian factor whose form depends upon the choice of internal coordinates.^86–90 The multiplicative constant N is omitted, since, as noted above, its presence has no consequence on the final result for the binding free energy ΔG_b. The partition function of the molecule is now

$$Q=8{\pi }^{2}V\int d\mathbf{x}J(\mathbf{x})e^{-\beta E(\mathbf{x})}$$ (2.23)

Note that relying on the classical approximation from the outset allows us to consider conformational variations of any amplitude and form, so that the FM approach is not restricted to the small amplitude, vibrational model of internal motion in the RRHO treatment, and hence is far more suitable for flexible biomolecules. For this reason, and because of its simplicity, the developments in this paper rely on the FM approach except as otherwise noted.

2.4 Solvation and a Temperature-Dependent Energy Function

In a fully microscopic description of a system, the potential energy is completely determined by the coordinates. However, it is often useful to consider only a subset of coordinates explicitly and model the rest of them implicitly. In particular, for a molecule in solution phase, one may treat the coordinates of the solute molecule explicitly but the coordinates of the solvent implicitly. This treatment is rigorous when the energy function of the explicit coordinates is replaced by a potential of mean force that includes one contribution from the internal energy of the solute and another from the net effect of the solvent on the conformational energetics of the solute.⁵⁵ If the solute coordinates are denoted by x, one may write the potential of mean force, W(x), as

$$W(\mathbf{x})=U(\mathbf{x})+V_{\text{solv}}(\mathbf{x})$$ (2.24)

where U(x) is the internal potential energy obtained as if the molecule were in vacuum, and V_solv(x) is the solvation free energy. Because the latter accounts implicitly for the thermal motions of solvent molecules, it depends on temperature.

When the system composed of a single solute molecule surrounded by the solvent is described by the potential of mean force, W(x), the entropy is given by

$$S=\frac{-F+\langle W\rangle }{T}-\langle {\left(\frac{\partial W}{\partial T}\right)}_V\rangle$$ (2.25)

as shown Supporting Information. Here, the second term arises from the temperature dependence of W, specifically its solvation free energy term in eq 2.24, and the notation ( )_V indicates a partial derivative taken at constant volume. The two terms of eq 2.25 are referred to as configurational entropy and solvation entropy, respectively,⁴ where the configurational entropy results from motions of the solute molecule and the solvation entropy results from motions of the solvent molecules. It may be unexpected that this separation can be effected, given that solute and solvent motions are correlated with each other, so it is worth noting that the precise meaning of this decomposition is conveyed by eq 2.18, if x₁ and x₂ are taken to represent solute and solvent degrees of freedom, respectively. (See Supporting Information for further details.)

3. Binding Free Energy and Binding Constant

Suppose that two molecules, A and B, can bind to form a complex C. Now consider a system consisting of the three species of solute molecules present at concentrations C_α, α = A, B, and C. (The solvent is treated implicitly.) We assume that the only significant interactions are between the binding molecules when complexed. In Section 2 of Supporting Information we derive the change in Gibbs free energy when one A molecule and one B molecule bind to form a single complex under constant pressure, a typical experimental condition. The result is

$$\mathrm{\Delta }{G}_{\text{b}}={\mu }_{\text{C}}-{\mu }_{\text{A}}-{\mu }_{\text{B}}$$ (3.1a)

$$=-k_{\text{B}}Tln\frac{C_{\text{A}}{C}_{\text{B}}{K}_{\text{a}}}{C_{\text{C}}}$$ (3.1b)

where μ_α is the chemical potential of molecule α and K_a is the binding constant defined as⁸²

$$K_{\text{a}}\equiv \frac{Q_{\text{C}}/V}{(Q_{\text{A}}/V)(Q_{\text{B}}/V)}$$ (3.2)

Intuitively, dividing each molecular partition function by V removes the factor of V present in each partition function (see eqs. 2.20a and 2.23) to yield volume-independent quantities. The significance of K_a is that it determines the concentrations of the three species of molecules when the binding reaction reaches equilibrium, where the binding free energy is 0. The resulting equilibrium concentrations satisfy

$$\frac{{(C_{\text{C}})}_{\text{eq}}}{{(C_{\text{A}})}_{\text{eq}}{(C_{\text{B}})}_{\text{eq}}}=K_{\text{a}}$$ (3.3)

Experimentalists often use the dissociation constant, which is simply the inverse of K_a.

When the three species of molecules are all present at a “standard” concentration C^∘, normally 1 M, the standard binding free energy is

$$\mathrm{\Delta }{G}_{\text{b}}^{\circ }=-k_{\text{B}}Tln(C^{\circ }{K}_{\text{a}})$$ (3.4)

In using this equation to convert a measured K_a to the standard free energy of binding, if K_a is given in M⁻¹, then C^∘ is to be assigned a numerical value of 1 M. If K_a is given in other units, then C^∘ must be adjusted accordingly; for example, if K_a is in nM⁻¹, then C^∘ must be assigned a numerical value of 10⁹ nM. The standard binding free energy and the binding constant provide, on different scales, equivalent measures of binding affinity.

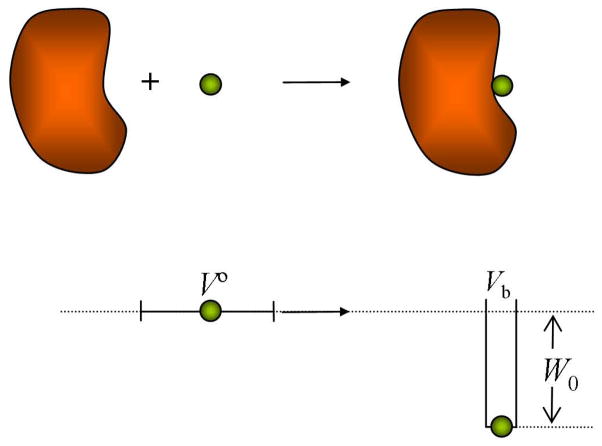
A fact often overlooked in the literature is that the value of $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ depends on the choice of the standard concentration. The inverse of the standard concentration may be thought of as a standard volume V^∘, which is the average volume occupied by a single molecule at standard concentration. When C^∘ = 1 M, then V^∘ = 1661 ų. It can be shown that $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ is also the free energy difference between two states illustrated in Figure 1 (for the case of a square-well binding interaction). In the initial state the ligand is allowed to translate within the volume V^∘ and freely rotate, but the receptor is fixed in a particular position and orientation; no restriction is placed on internal motions of either molecule, but there is no interaction between them. In the final state the receptor is still fixed in its position and orientation, and the ligand now moves in the binding site of the receptor and interacts with it. Clearly, the equilibrium between these two states, and hence $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$, is affected by the initial volume, V^∘, available to the ligand. The role of C^∘ may be further clarified by considering a room-temperature simulation of one molecule each of A and B in a cubic box of volume V. If the equilibrium probability of finding the molecules bound is p, then C_C = p/V, and C_A = C_B = (1 − p)/V, so, from eqs 3.3 and 3.4, K_a = pV/(1 − p)² and $\mathrm{\Delta }{G}_{\text{b}}^{\circ }=-k_{\text{B}}Tln(C^{\circ }V)-k_{\text{B}}Tln[p/{(1-p)}^2]$. If, for example, V = 10⁶ ų, the first term in $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ here will be −3.8 kcal/mol at room temperature.

Figure 1.

An interpretation of the standard binding free energy. Upon binding, the volume available to the ligand is changed from V^∘ to V_b. At the same time, the ligand gains interaction energy W₀.

Let us now illustrate the calculation of the binding constant for three examples of increasing complexity.

3.1 Binding of Two Atoms to form a Diatomic Complex

Arguably the simplest binding model is the formation of a diatomic molecule from two atoms. Here we consider the molecule to be held together by a harmonic potential (cf. eq 2.6)

$$E(r)=E_0+k{(r-r_0)}^2/2$$ (3.5)

where r is the interatomic distance.

3.1.1 Classical Rigid Rotor/Harmonic Oscillator Treatment

As discussed in Subsection 2.3, the molecular partition function in the RRHO treatment includes both potential and kinetic energy contributions. Before binding, each atom has only translational degrees of freedom, so their partition functions are given by eq 2.20a as

$$Q_{\alpha }=V{\left(\frac{2\pi m_{\alpha }}{\beta h^2}\right)}^{\frac{3}{2}}$$ (3.6a)

where α = A or B, and m_α is the mass of the subscripted atom. After binding, the diatomic molecule has three translational degrees of freedom, two rotational degrees of freedom, and one vibrational degree of freedom. Here we use the high-temperature, or classical, limit (eq 2.17) of the quantum treatment for vibration (eq 2.20c). The partition function of the complex, C, is

$$Q_{\text{C}}=\left[V{\left(\frac{2\pi m_{\text{C}}}{\beta h^2}\right)}^{\frac{3}{2}}\right]\left[\frac{8{\pi }^{2}I}{\beta h^2}\right]\left[\frac{2\pi }{\beta h\omega }{e}^{-\beta E_0}\right]$$ (3.6b)

where m_C = m_A + m_B is the mass of the diatomic molecule; I = mr₀² is the moment of inertia about the center of mass, where m ≡m_Am_B/m_C is the reduced mass; and ω = (k/m)^1/2 is the angular frequency of the interatomic vibration. Inserting eqs 3.6a and 3.6b into eq 3.2, we find

$$K_{\text{a}}=4\pi {r_0}^2{\left(\frac{2\pi }{\beta k}\right)}^{\frac{1}{2}}{e}^{-\beta E_0}$$ (3.7)

Thus, as anticipated in Subsection 2.3, the final classical result for K_a is independent of masses and Planck’s constant, even though factors of mass and Planck’s constant appear in the individual terms of the RRHO treatment. Note that the pre-exponential factor is the volume effectively accessible to one atom when the other is treated as fixed (see eq II.14a of Supporting Information and cf. eq 3.14b below).

3.1.2 Flexible Molecule Treatment

The FM approach to the molecular partition function (Subsection 2.3.2) excludes kinetic energy from the outset, because the contributions of kinetic energy to the partition functions will cancel in the final result. In the present case, the atoms prior to binding have only translational degrees of freedom, so Q_A = Q_B = V. After binding, the diatomic complex has overall translation and interatomic relative motion. The partition function is

$$Q_{\text{C}}=V\int dr4\pi r^2{e}^{-\beta E(r)}$$ (3.8)

where we have used spherical coordinates to represent the relative separation and integrated out the polar and azimuthal angles to yield the factor 4π. From these partition functions, we find the binding constant to be

$$K_{\text{a}}=\int dr4\pi r^2{e}^{-\beta E(r)}$$ (3.9)

If we now assume that the force constant, k, is great enough that r deviates minimally from r₀, we recover the expression of eq 3.7.

3.2 Binding of a Polyatomic Receptor with a Monatomic Ligand

Consider the binding of a monatomic ligand (e.g., a simple ion), B, to a polyatomic receptor, A. The ligand has only translational degrees of freedom, so Q_B = V. The partition function of the receptor, according to eq 2.23, is given by

$$Q_{\text{A}}=8{\pi }^{2}V\int {d\mathbf{x}}_{\text{A}}{J}_{\text{A}}({\mathbf{x}}_{\text{A}})e^{-\beta E_{\text{A}}({\mathbf{x}}_{\text{A}})}$$ (3.10a)

where x_A represents the internal coordinates of the receptor and E_A(x_A) is its energy, which is understood to represent the potential of mean force with the solvent degrees of freedom averaged out. For the complex, the set of internal coordinates, x_C, consists of all the internal coordinates of molecule A, along with the separation, r, of the ligand from molecule A: x_C = (x_A, r). Similar to eq 3.10a, we find the partition function of the complex to be

$$Q_{\text{C}}=8{\pi }^{2}V\int {d\mathbf{x}}_{\text{C}}{J}_{\text{A}}({\mathbf{x}}_{\text{A}})e^{-\beta E_{\text{C}}({\mathbf{x}}_{\text{C}})}$$ (3.10b)

However, we have to stipulate that the integration is restricted to the region of configurational space where the complex is deemed formed,^55,91,92 as further discussed in Subsection 3.3. For example, the complex cannot be considered as formed in a configuration with r = ∞. The energy of the complex can be written in the form

$$E_{\text{C}}({\mathbf{x}}_{\text{C}})=E_{\text{A}}({\mathbf{x}}_{\text{A}})+w({\mathbf{x}}_{\text{C}})$$ (3.11)

where the second term, which represents the energy arising from receptor-ligand interactions, vanishes at r = ∞.

With the partition functions for the receptor, ligand, and complex, the binding constant is found as

$$K_a=\frac{\int {d\mathbf{x}}_{\text{C}}{J}_{\text{A}}({\mathbf{x}}_{\text{A}})e^{-\beta E_{\text{C}}({\mathbf{x}}_{\text{C}})}}{\int {d\mathbf{x}}_{\text{A}}{J}_{\text{A}}({\mathbf{x}}_{\text{A}})e^{-\beta E_{\text{A}}({\mathbf{x}}_{\text{A}})}}=\frac{\int {d\mathbf{x}}_{\text{A}}d\mathbf{r}{J}_{\text{A}}({\mathbf{x}}_{\text{A}})e^{-\beta E_{\text{C}}({\mathbf{x}}_{\text{A}},\mathbf{r})}}{\int {d\mathbf{x}}_{\text{A}}{J}_{\text{A}}({\mathbf{x}}_{\text{A}})e^{-\beta E_{\text{A}}({\mathbf{x}}_{\text{A}})}}$$ (3.12)

We now define a potential of mean force in r:

$$e^{-\beta W(\mathbf{r})}\equiv \frac{\int {d\mathbf{x}}_{\text{A}}{J}_{\text{A}}({\mathbf{x}}_{\text{A}})e^{-\beta E_{\text{C}}({\mathbf{x}}_{\text{A}},\mathbf{r})}}{\int {d\mathbf{x}}_{\text{A}}{J}_{\text{A}}({\mathbf{x}}_{\text{A}})e^{-\beta E_{\text{A}}({\mathbf{x}}_{\text{A}})}}$$ (3.13a)

$$={\langle e^{-\beta (E_{\text{C}}({\mathbf{x}}_{\text{A}},\mathbf{r})-E_{\text{A}}({\mathbf{x}}_{\text{A}}))}\rangle }_{\text{A}}={\langle e^{-\beta w({\mathbf{x}}_{\text{A}},\mathbf{r})}\rangle }_{\text{A}}$$ (3.13b)

where <…>_A represents an average over the equilibrium distribution of the internal coordinates of molecule A, computed as if the ligand were absent. Eq 3.13a expresses W(r) in terms of the ratio of two configurational integrals, one for the bound state in which the ligand is at a relative separation r from the receptor and the other for the unbound state in which is ligand is at infinite separation. The potential of mean force W(r) can thus been seen as the change in free energy when the ligand is brought from infinite separation to a separation r from the receptor. In terms of W(r), the binding constant can now be written as

$$K_{\text{a}}={\int }_{\text{b}}d\mathbf{r}{e}^{-\beta W(\mathbf{r})}$$ (3.14a)

where the subscript “b” signifies that the integration is restricted to the region where the ligand is deemed bound. This result can be compared with eq 3.9. Here W(r) plays the role of the potential energy arising from the interaction between the receptor and ligand.

Usually the ligand is found in one distinct binding site. A simple illustration is provided by a square well form of the potential of mean force W(r), which takes a value W₀ when the ligand is in a binding region of volume V_b and value 0 elsewhere (see Figure 1). Then

$$K_{\text{a}}=V_{\text{b}}{e}^{-\beta W_0}$$ (3.14b)

3.3 A General Expression for K_a

More generally, the ligand also has internal coordinates, so a complete specification of the complex requires not only the relative separation r between the ligand and the receptor but also their relative orientation ω, along with coordinates specifying the conformation of the ligand. As in eq 3.13, one can again define a potential of mean force W(r, ω), whereby the binding constant can be expressed as

$$K_{\text{a}}={(8{\pi }^2)}^{-1}{\int }_{\text{b}}d\mathbf{r}d\mathbf{\omega }J(\mathbf{\omega })e^{-\beta W(\mathbf{r},\mathbf{\omega })}$$ (3.15)

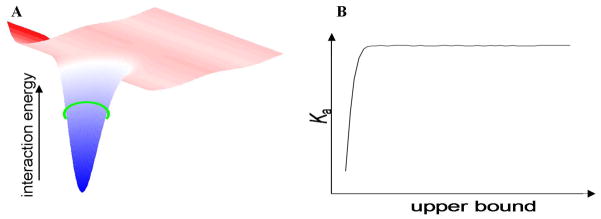
Details of the derivation can be found in Section 3 of Supporting Information. A practical issue in the calculation of K_a via eq 3.15 is the specification of the region of integration (as indicated by the subscript “b”) for the complex.^55,93 In order to be considered as a separate species in a thermodynamic sense, the complex must be dominated by well localized configurations with very low values of W(r, ω) (Figure 2A), which make the overwhelming contributions to K_a. As long as the specified region of integration covers these configurations, an unequivocal value for K_a will be obtained (Figure 2B).^55,91,92

Figure 2.

(A) Diagram of a receptor-ligand potential of mean force W(r, ω), shown as an energy surface in two dimensions with the bound state defined by the deep energy well. The boundary of the bound state can be specified by an upper bound, indicated by a green ring, of W(r, ω) so long as the well is only big enough to hold a single ligand at a time.⁹¹ (B) Sketch of the binding constant associated with the energy well in (A) as a function of the upper bound of W(r, ω). The binding constant is seen to be virtually independent of the upper bound so long as the lowest energy configurations are included.

4. Enthalpy-Entropy Decomposition of Binding Free Energy

The “standard” binding entropy under constant pressure is

$$\mathrm{\Delta }{S}_{\text{b}}^{\circ }=k_{\text{B}}ln(C^{\circ }{K}_{\text{a}})+k_{\text{B}}T{\left(\frac{\partial ln{K}_{\text{a}}}{\partial T}\right)}_P$$ (4.1)

in which we have neglected a small term arising from the fact that, under constant pressure, the volume and hence the concentration vary with temperature (Section 2 of Supporting Information). Note that the binding entropy inherits the dependence of the binding free energy on the standard concentration.

The binding enthalpy is

$$\mathrm{\Delta }{H}_{\text{b}}=-k_{\text{B}}{T}^2{\left(\frac{\partial ln{K}_{\text{a}}}{\partial T}\right)}_P$$ (4.2)

which has no dependence on concentration. Thus, changing the arbitrarily selected value of C^∘ shifts both the standard free energy and the standard entropy of binding, but does not affect the enthalpy change.

Binding is sometimes referred to as enthalpy-driven or entropy-driven, depending on the signs and magnitudes of ΔH_b and $\mathrm{\Delta }{S}_{\text{b}}^{\circ }$. However, this distinction is not especially meaningful because it is based on the incorrect assumption that the zero value of $\mathrm{\Delta }{S}_{\text{b}}^{\circ }$ has physical significance. In reality, as just noted, the value of $\mathrm{\Delta }{S}_{\text{b}}^{\circ }$ depends on the choice of the standard concentration, whose conventional value of 1 M is arbitrary and historical in nature. In fact, there is no special physical significance to a zero value of either $\mathrm{\Delta }{S}_{\text{b}}^{\circ }$ or $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$. This point does not bear on the phenomenon of entropy-enthalpy compensation, however, because changing C^∘ shifts all values of $\mathrm{\Delta }{S}_{\text{b}}^{\circ }$ by a constant and therefore does not influence any correlation that may exist between $\mathrm{\Delta }{S}_{\text{b}}^{\circ }$ and ΔH_b.

The example of a monatomic ligand binding a polyatomic receptor provides insight into the entropy component of the binding free energy. First let us specialize to the square-well potential of mean force, with the further assumption that the well depth W₀ and the volume, V_b, of the binding region are both temperature independent. Inserting eq 3.14b in eq 4.1, we find

$$\mathrm{\Delta }{S}_{\text{b}}^{\circ }=k_{B}ln(C^{\circ }{V}_{\text{b}}{e}^{-\beta W_0})+\frac{1}{T}{W}_0$$ (4.3a)

$$=k_{\text{B}}ln(C^{\circ }{V}_{\text{b}})=k_{\text{B}}ln\left(\frac{V_{\text{b}}}{V^{\circ }}\right)$$ (4.3b)

which can be viewed as the entropy change when the volume available to the ligand changes on binding from the standard volume V^∘ to the volume accessible to the ligand after binding, V_b (Figure 1). The result in this case can be identified as the change in translational entropy.

Now consider a general form of W(r). Using eq 3.14a, we have

$$\mathrm{\Delta }{S}_{\text{b}}^{\circ }=k_{\text{B}}ln(C^{\circ }{K}_{\text{a}})+k_{\text{B}}T\frac{{\int }_{\text{b}}d\mathbf{r}{\left(\frac{\partial e^{-\beta W(\mathbf{r})}}{\partial T}\right)}_P}{{\int }_{\text{b}}d\mathbf{r}{e}^{-\beta W(\mathbf{r})}}$$ (4.4a)

$$=k_{\text{B}}ln(C^{\circ }{K}_{\text{a}})+\frac{1}{T}{\langle W(\mathbf{r})\rangle }_{\text{b}}-{\langle {\left(\frac{\partial W(\mathbf{r})}{\partial T}\right)}_P\rangle }_{\text{b}}$$ (4.4b)

The last result is formally similar to eq 2.25. By comparing against eq 4.3a, we can still identify the first two terms of eq 4.4b as the change in translational entropy:

$$\mathrm{\Delta }{S}_{\text{t}}^{\circ }=k_{\text{B}}ln(C^{\circ }{K}_{\text{a}})+\frac{1}{T}{\langle W(\mathbf{r})\rangle }_{\text{b}}$$ (4.5)

The binding entropy can now be written as

$$\mathrm{\Delta }{S}_{\text{b}}^{\circ }=\mathrm{\Delta }{S}_{\text{t}}^{\circ }-{\langle {\left(\frac{\partial W(\mathbf{r})}{\partial T}\right)}_P\rangle }_{\text{b}}$$ (4.4c)

By further equating $\mathrm{\Delta }{S}_{\text{t}}^{\circ }$ to k_Bln(V_b/V^∘), one can interpret the V_b thus obtained as the effective volume accessible to the ligand in the bound state. (A calculation of V_b is illustrated in Subsection 2.2 of Supporting Information.) For the present case of a monatomic ligand, the change in translational entropy apparently corresponds to what has been termed the “association entropy”.⁹⁴ The second term in eq 4.4c contains entropy contributions from internal motions and solvation.

Eq 4.5 for the change in translational entropy can also be applied to a flexible, polyatomic ligand, when averaging is taken not only over receptor and solvent degrees of freedom but also over the internal and rotational coordinates of the ligand to arrive at a potential of mean force, W̄(r), which still depends only on the relative separation r⁵⁵ (see eq III.6 of Supporting Information). Subtleties in the calculation of the change in translational entropy will be discussed in Subsection 5.3.

Rearranging eq 4.5, we find that the binding free energy can be written as

$$\begin{array}{l}\mathrm{\Delta }{G}_{\text{b}}^{\circ }=-k_{\text{B}}Tln(C^{\circ }{K}_{\text{a}})={\langle W(\mathbf{r})\rangle }_{\text{b}}-T\mathrm{\Delta }{S}_{\text{t}}^{\circ }\\ ={\langle W(\mathbf{r})\rangle }_{\text{b}}-k_{\text{B}}Tln\left(\frac{V_{\text{b}}}{V^{\circ }}\right)\end{array}$$ (4.6)

There is an intuitively helpful analogy here between the first term and the enthalpy change on binding, and between the second term and the entropy change on binding, and this analogy would become an identity if W(r) were temperature independent. It is sometimes hypothesized that the binding free energy can be modeled as the result of additive contributions from the chemical groups making up a compound. There may indeed be cases where the average receptor-ligand potential of mean force, 〈W (r)〉_b, can be approximated in the group-additive form,

$${\langle W(\mathbf{r})\rangle }_{\text{b}}=\sum _i{\langle W_i(\mathbf{r})\rangle }_{\text{b}}$$ (4.7)

where i refers to different groups of the compound, and 〈W_i (r)〉_b is the contribution of group i to 〈W (r)〉_b. On the other hand, it is not clear that the translational entropy term of the standard binding free energy in eq 4.6 can be accurately modeled as additive in nature. Section 8 returns to this issue of group-additivity.

5. Changes in Configurational Entropy upon Binding

As the discussion in Sections 2 and 4 indicates, the change in entropy upon binding can be decomposed into a part associated with changes in solute motions, the configurational entropy, and a part associated with changes in solvent motions, the solvent entropy.⁷⁶ This decomposition can be understood as an application of eq 2.18 in which x₁ and x₂ stand for the solute and solvent degrees of freedom, respectively. The solvent part of the entropy change relates to the temperature-dependence of the difference in solvation free energy between the bound and unbound states (Subsection 2.4), and has contributions from hydrophobic and electrostatic interactions between the receptor and ligand. The configurational entropy relates to the changes in mobility of the receptor and ligand upon binding and can be estimated through evaluation of the first term in eq 2.18 by various means, including the quasi-harmonic approximation in Cartesian^95–98 or torsional³⁷ coordinates, scanning methods,²¹ the M2 method,^16,76 the mutual information expansion,⁸¹ the nearest-neighbor method,⁹⁹ or a combined mutual information/nearest neighbor approach.¹⁰⁰

We now address the experimental evaluation of configurational entropy and the further decomposition of configurational entropy into translational, rotational, and internal parts, with particular attention to the long-standing issue of changes in translational entropy on binding.

5.1 Experimental Determination of Configurational Entropy Changes

The total change in entropy on binding can be determined experimentally by measuring K_a at different temperatures and then computing the enthalpy and entropy components of the binding free energy by taking temperature derivatives. Alternatively, isothermal titration calorimetry can be used to measure the binding free energy via the equilibrium constant and the binding enthalpy via heat release, and from these the binding entropy can be computed. However, neither approach can separate the configurational and solvation parts of the binding entropy.

Elegant neutron-scattering methods have been used to probe differences in the vibrational density of states before and after enzyme-inhibitor binding, yielding an estimated 4 kcal/mol configurational entropy change that, somewhat surprisingly, favors binding.³³ It is worth noting that density of states measurements were done only for the free and complexed protein, so the configurational entropy associated with the free ligand was not subtracted from the final result. As a consequence, the experiment may not report on the full change in configurational entropy upon binding, and accounting for the free ligand might reverse the sign of the final result. Interestingly, a follow-up computational study³⁴ suggests that the measured entropy change is an average over proteins trapped in different local energy wells due to the low temperature at which the experiment was done. The reported penalty thus appears to represent a change in vibrational entropy without a contribution from the conformational entropy, in the sense of eq 2.13.

NMR relaxation data are uniquely able to provide structurally correlated information about the configurational entropy change upon binding.^25–32 The NMR order parameter S² of a bond vector n, often that of a backbone amide N-H bond, is a measure of the extent of orientational fluctuation of n. The order parameter is defined as¹⁰¹

$${\mathcal{S}}^2=\frac{4\pi }{5}\sum _{m=-2}^2{\mid \int d\mathbf{n}\rho (\mathbf{n})Y_{2m}(\mathbf{n})\mid }^2$$ (5.1a)

where ρ(n) is the probability density of n. The entropy associated with the orientational motion of n can be written as (cf. eq 2.5b)

$$S_{\text{om}}=-k_{\text{B}}\int d\mathbf{n}\rho (\mathbf{n})ln\rho (\mathbf{n})$$ (5.1b)

It is clear that S² and S_om are related. For the diffusion-in-a-cone model of orientational motion, in which the polar angle of n is restricted to between 0 and an upper limit θ₀, both S² and S_om can be easily obtained. Using cosθ₀ as an intermediate variable to relate S_om directly to S², one finds^102,103

$$S_{\text{om}}=k_{\text{B}}ln\{\pi [3-{(1+8{\mathcal{S}}^2)}^{1/2}]\}$$ (5.1c)

The order parameters of backbone amides and side-chain methyls of a protein can be determined before and after ligand binding. These results can be converted into entropic contributions by a relation like eq 5.1c and summed over individual residues, to yield information on the change in configurational entropy of the protein upon binding. Such studies yield unique and valuable insight into the contribution of conformational fluctuations to the binding affinity, but the numerical results should be interpreted with caution.²⁷ First, a model for bond orientational motion other than diffusion-in-a-cone will yield a different relation between S_om and S². Second, summing the contributions of individual bond-vectors effectively makes the assumption that that their motions are independent; in reality motions of neighboring bonds can be highly correlated, and the numerical consequences of such correlations for the entropy (see Subsection 2.2.2) are still uncertain. At least one study has argued that the entropic consequences of pairwise correlations are minor, although correlations expected to be large due to short-ranged chain connectivity were not assessed.¹⁰⁴ Finally, order parameters are sensitive only to a subset of motions, both in timescale (picoseconds to nanoseconds) and in type (motions that affect bond orientations), so some important coordinates, such as translation of a bound ligand relative to the receptor, may not be captured. It is worth mentioning recent work¹⁰⁵ directed at clarifying the connections between bond vector fluctuations and conformational distributions, as such connections can help interpret order parameters in terms of well-defined coordinate fluctuations.

5.2 Decomposition of Configurational Entropy

The coordinates of a molecule or complex with n atoms can be broken into a set of 3 translational coordinates; a set of 3 rotational coordinates; and a set of 3n – 6 internal coordinates. Following eq 2.19, the configurational entropy can be written as

$$S=S_{\text{t}}+S_{\text{r}}+S_{\text{in}}-I_{\text{t},\text{r}}-I_{\text{t},\text{in}}-I_{\text{r},\text{in}}+I_{\text{t},\text{i},\text{in}}$$ (5.2)

where S_t, for example, is the entropy associated with the marginal probability density of the translational coordinates, I_{t, r} is the mutual information measuring correlation between translational and rotational motion, and I_{t, r, in} measures the third order correlation among all three sets of coordinates. Each of these groups of coordinates can be further decomposed, and such decomposition would reveal additional correlations among, for example, the three translational coordinates. The changes of individual entropy terms, S_in, S_r, and, especially, S_t, on binding have been the subject of considerable discussion in the literature (e.g., Refs. 14,18,58–61,67,70,106–108). However, little attention has been given to the mutual information terms, i.e., to the entropic consequences of correlation, even though the mutual information terms can be similar in magnitude to the individual terms, as, indeed, suggested by a recent study.^76,109

5.3 Changes in Translational Entropy on Binding

The change in S_t on binding has been addressed with particular vigor in the theoretical literature, as noted in the Introduction. This is, perhaps, appropriate, given that the essence of binding is that two molecules which initially move about independently become attached to one another and then translate together. The present section uses the theoretical framework presented in the preceding sections to analyze various views of translational entropy from a consistent standpoint.

5.3.1 Sensitivity of the Translational Entropy to Coordinate System

As discussed in Section 4, the change in translational entropy can be separated formally from other entropy contributions arising from the motions of the solutes and the solvent. It is a subtle but important conceptual point that the change in translational entropy defined in this way depends on the coordinate system chosen to define the position and orientation of the ligand with respect to the receptor.⁵⁵ There are multiple different and yet correct ways to define this coordinate system. For example, r might be a vector from the center of mass of the receptor to the monatomic ligand,¹⁵ or it could equally well be a vector from any atom of the receptor to the ligand (e.g., Ref. 81). Any such definition of r can be used as the translational part of a fully consistent coordinate system for the ligand relative to the receptor, yet each will, in general, lead to a different change in translational entropy upon binding. For example, if r is the vector from an atom in the receptor’s binding site to the ligand, then the ligand will be found to have low translational entropy after binding. In contrast, if r is chosen to be the vector from a receptor atom that is very mobile relative to the binding site, then the ligand may be found to have relatively high translational entropy after binding. Similar considerations apply if one turns the system around and regards the receptor as a polyatomic ligand and the ligand as a small receptor.

Furthermore, different coordinate systems will correspond to different degrees of correlation, and hence different mutual information terms between translational and other coordinates (eq 5.2). For example, defining the ligand’s position with respect to a mobile atom far from the binding site, is likely to generate large mutual information between ligand translation and the internal degrees of freedom of the receptor. A lower mutual information is likely if the ligand is defined relative to an atom in the binding site. The latter definition is also more intuitively appealing, and one’s intuitive choice of a reasonable coordinate system tends to be one that minimizes mutual information.

Of course, the choice of coordinate system cannot affect the total change in configurational entropy on binding; it can only affect the partitioning of the change in configurational entropy among the translational, rotational, internal and mutual information parts (eq 5.2). (It is worth remarking that a correct and complete treatment of these coordinate system issues can become quite complicated, requiring careful attention to Jacobian contributions, as previously emphasized.^89,90) One may legitimately conclude, therefore, that the change in translational entropy upon binding in general is not in itself a well-defined physical quantity. It is best understood as one part of the larger picture of entropy changes on binding.

5.3.2 The Sackur-Tetrode Approach to Translational Entropy

An alternative treatment of the change in translational entropy on binding is based on the Sackur-Tetrode equation, which derives from the RRHO approximation (see, e.g., Ref. 107). In the RRHO approach to binding thermodynamics, the receptor, ligand, and the complex have partition functions given by eq 2.21. Effectively each species is treated as an ideal gas, a view that is justified by the McMillan-Mayer solution theory.¹¹⁰ Inserting eq 2.21 in eq I.35 of Supporting Information yields the entropy per reactant or product molecule at, for convenience, the standard concentration, C^∘:

$$S_{\text{RRHO}}^{\circ }=S_{\text{RRHO},\text{t}}^{\circ }+S_{\text{RRHO},\text{r}}+S_{\text{RRHO},\text{vib}}$$ (5.3a)

where

$$S_{\text{RRHO},\text{t}}^{\circ }=k_{\text{B}}ln\left[{\left(\frac{2\pi m}{\beta h^2}\right)}^{\frac{3}{2}}\frac{e^{\frac{5}{2}}}{C^{\circ }}\right]$$ (5.3b)

$$S_{\text{RRHO},\text{r}}=k_{\text{B}}ln\left[8{\pi }^2{\left(\frac{2\pi e}{\beta h^2}\right)}^{\frac{3}{2}}{(I_1{I}_2{I}_3)}^{\frac{1}{2}}\right]$$ (5.3c)

$$S_{\text{RRHO},\text{vib}}=k_{\text{B}}\sum _i\left[\frac{\beta h{\omega }_i}{2\pi }{\left(e^{\frac{\beta h{\omega }_i}{2\pi }}-1\right)}^{-1}-ln\left(1-e^{-\frac{\beta h{\omega }_i}{2\pi }}\right)\right]$$ (5.3d)

Eq 5.3b for the translational part is called the Sackur-Tetrode equation. The standard binding entropy is finally calculated as

$$\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }=\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }(\text{C})-\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }(\text{A})-\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }(\text{B})$$ (5.4)

where A, B, and C refer to the receptor, ligand, and complex, respectively.

The translational part, $\mathrm{\Delta }{S}_{\text{RRHO},\text{t}}^{\circ }$, of this calculation is sometimes referred to as the change in translational entropy on binding. However, $\mathrm{\Delta }{S}_{\text{RRHO},\text{t}}^{\circ }$ is different from $\mathrm{\Delta }{S}_{\text{t}}^{\circ }$ introduced by eq 4.5. It is straightforwardly shown that $\mathrm{\Delta }{S}_{\text{RRHO},\text{t}}^{\circ }$ is given by $-S_{\text{RRHO},\text{t}}^{\circ }$ with m set to the reduced mass m_Am_B/m_C. Therefore $\mathrm{\Delta }{S}_{\text{RRHO},\text{t}}^{\circ }$ depends on the molecular masses, whereas $\mathrm{\Delta }{S}_{\text{t}}^{\circ }$ has no mass dependence. In this connection we note that ΔS_{RRHO, r} and ΔS_{RRHO, vib}, the rotational and vibrational parts of $\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }$, are also mass-dependent. It turns out that the mass-dependence of ΔS_{RRHO, r} and ΔS_{RRHO, vib} leads to near-complete cancellation of the mass-dependence of $\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }$ as a whole when the quantum expression for the vibrational entropy is used, and to apparently complete cancellation when the classical expression is used.

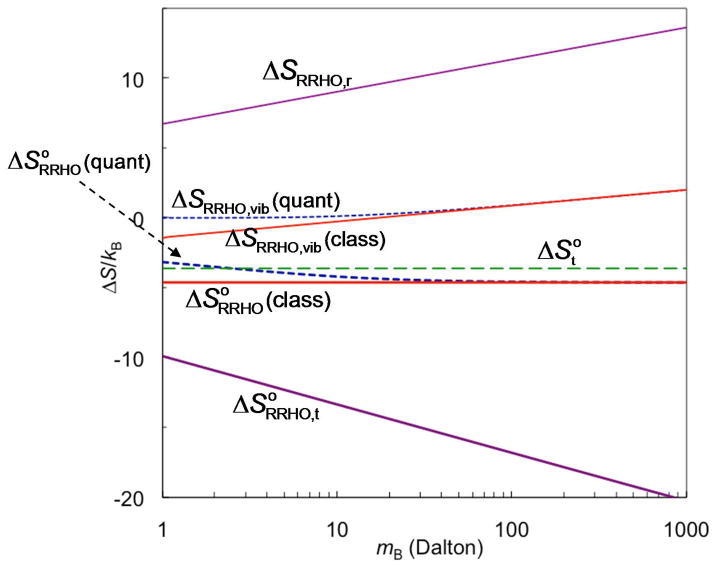
The last observation is illustrated in Figure 3, which graphs $\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }$ and its components $\mathrm{\Delta }{S}_{\text{RRHO},\text{t}}^{\circ }$, ΔS_{RRHO, r}, and ΔS_{RRHO, vib} for the binding of two atoms to form a diatomic complex held together by a harmonic bond (eq 3.5), as a function of atomic mass. (See Subsection 2.2 of Supporting Information.) For ΔS_{RRHO, vib} both the quantum mechanical result, from eq 5.3d, and the classical approximation, obtained by taking the β → 0 limit, are shown. It is clear that, although the separate entropy terms from the RRHO treatment – translational, rotational, and vibrational – all depend upon mass, the total entropy change, $\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }$, is independent of mass for the classical approximation, and, in the quantum mechanical case, becomes dependent on mass only when the atoms are very light. The mass independence of the classical approximation for $\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }$ is expected, since the binding constant in this case, given by eq 3.7b, is independent of mass.

Figure 3.

The entropy of binding and its parts for a diatomic binding model according to the RRHO approximation. The entropy of binding in the FM approach is also shown for comparison. As also labeled in the figure, from top to bottom on the left axis the graphs are: ΔS_{RRHO, r}; ΔS_{RRHO, vib} in the quantum and classical formulations, respectively; $\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }$ in the quantum formulation; $\mathrm{\Delta }{S}_{\text{t}}^{\circ };\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }$ in the classical formulation; and $\mathrm{\Delta }{S}_{\text{RRHO},\text{t}}^{\circ }$. The results are derived in Subsection 2.2 of Supporting Information.

For the diatomic binding model, we show in Subsection 2.2 of Supporting Information that $\mathrm{\Delta }{S}_{\text{t}}^{\circ }$ is the total binding entropy calculated by the FM approach and that it differs from the RRHO counterpart, i.e., the classical approximation for $\mathrm{\Delta }{S}_{\text{RRHO}}^{\circ }$, by a small amount, −k_B. For comparison, we also graph $\mathrm{\Delta }{S}_{\text{t}}^{\circ }$ in Figure 3. It is clear that $\mathrm{\Delta }{S}_{\text{t}}^{\circ }$ differs substantially from $\mathrm{\Delta }{S}_{\text{RRHO},\text{t}}^{\circ }$. Thus, while the two approaches basically agree on the change in total entropy, they differ sharply on the change in translational entropy. Closer inspection reveals that that these are really two very different definitions of the change in translational entropy. In the RRHO approach, the motions of the bound ligand are not considered to include any translational component; instead, all the entropy associated with its motions is ascribed to the vibrational entropy of the complex, as previously emphasized,⁵⁹ and thus does not appear as a component of the translational entropy after binding. In contrast, the definition of $\mathrm{\Delta }{S}_{\text{t}}^{\circ }$ from the FM approach considers the ligand to retain translational entropy after binding due to its motions in the binding site of the receptor. It should be emphasized that the difference between $\mathrm{\Delta }{S}_{\text{RRHO},\text{t}}^{\circ }$ and $\mathrm{\Delta }{S}_{\text{t}}^{\circ }$ does not reflect a deficiency in either expression. Instead, these are two different and equally valid definitions of the change in translational entropy on binding. That said, it is worth noting that the assumption of rigidity in treating overall rotation means that the RRHO treatment is not well suited for studying highly flexible molecules.

Sometimes $\mathrm{\Delta }{S}_{\text{RRHO},\text{t}}^{\circ }$ and ΔS_{RRHO, r} are combined with other contributions to empirically construct the binding free energy. We note that, if these other contributions do not depend on mass and Planck’s constant in a way that makes the binding free energy as a whole independent of mass and Planck’s constant as β → 0, then such constructions must be internally inconsistent.

5.3.3 Free Volume Theories of Translational Entropy

It has been argued that the loss of translational entropy on binding can be markedly overestimated by approaches like those just discussed because, even in their unbound state, molecules A and B are caged by solvent molecules so the “free volume” accessible to them before binding, V_f, is much smaller than the system volume, V, or the standard volume, V^∘, which appear in the expressions above.⁶⁴ Accordingly, the effective concentration, C = 1/V_f, has been inserted into the Sackur-Tetrode equation to compute the translational entropy.⁶⁴ (It is not clear why similar arguments have not been applied to the rotational entropy, too, since rotational motion is subject to similar solvent-caging.) This reasoning appears problematic, however, because molecules A and B are restricted to their solvent cages only on a very short time scale. Over the time scale of typical binding measurements, molecules A and B roam the entire system volume. After binding, they still roam the entire volume, but the translational range of molecule B relative to A (or vice versa) is greatly reduced, as discussed above, so there is a substantial loss of translational freedom and entropy. Put differently, A and B still roam the entire volume after binding, but now their motions are highly correlated, and the translational correlation lowers the entropy due to a large mutual information term (Subsection 2.2.2). The free volume approach appears to ignore this part of the translational entropy loss.

Another part of the reasoning in support of the free volume viewpoint has been that the drop in entropy when a monatomic gas dissolves in water results from its becoming translationally caged by water molecules. Even if one adopted this view, there would still be an additional translational entropy loss if the gas atom were then to bind another molecule in solution, due again to an increase in correlation. It is this binding entropy, not the solvation entropy, that is the topic of the present discussion.

An alternative development of the free volume theory has been used to argue that the change in translational entropy on binding is given by

$$\mathrm{\Delta }{S}_{\text{t},\text{free}\text{vol}}^{\circ }=k_{\text{B}}ln(C^{\circ }{V}_{\text{f},\text{bound}})-k_{\text{B}}ln(C_{\text{solvent}}{V}_{\text{f},\text{solvent}})-k_{\text{B}}$$ (5.5)

(eq 6 in Ref. 64). Here C_solvent is the molarity of the solvent (55 M for water), and V_{f, solvent} and V_{f, bound} represent the free volume accessible to the ligand in solvent versus the binding site. This expression has been rearranged from the original to highlight its similarity to eq 4.3b. In fact, if V_{f, bound} is considered equivalent to V_b, then the differences between eq 5.5 and eq 4.3b cancel for the relative change in translational entropy on binding to two different receptors by the same ligand. Thus, the two equations appear to reflect similar theoretical approaches. On the other hand, it is difficult to determine whether or when the second term in eq 5.5 is correct, especially because, as discussed above, a formula for the change in translational entropy should be considered in the context of a theory for the total change in entropy, and we are not aware of such a context for eq 5.5. It is also unclear whether problems surrounding the so-called communal entropy in this free volume theory, which were highlighted by Kirkwood,¹¹¹ have been fully resolved.

6. Relation between Intermolecular and Intramolecular Binding

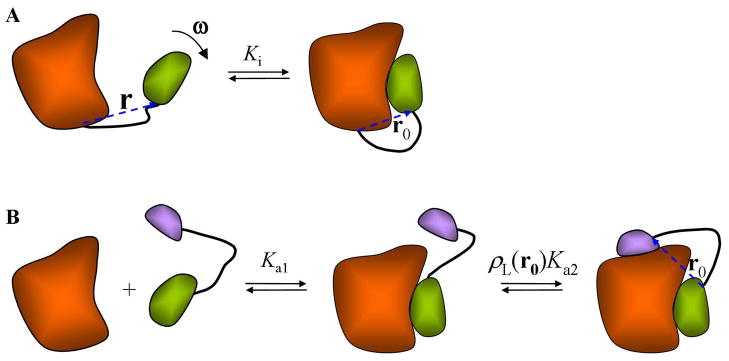
When the ligand is tethered to the receptor, binding becomes intramolecular (Figure 4A). For example, SH3 domains sometimes are found tethered to their proline-rich ligands. The intramolecular binding constant is given by

Figure 4.

(A) A receptor (orange) and ligand (green) connected by a linker (black), showing the position vector, r, relating the ligand to the receptor, and the orientation of the ligand in space ω. In the bound state r takes the value r₀. (B) Binding of a bivalent ligand can be viewed as the sequential binding of the first fragment followed by intramolecular binding of the second.

$$K_{\text{i}}\equiv \frac{{(C_{\text{C}})}_{\text{eq}}}{{(C_{\text{A}})}_{\text{eq}}}$$ (6.1)

where C_C and C_A now signify, respectively, the concentrations of the receptor with the tethered ligand in and out of the binding site. Their ratio is determined by the relative probabilities of the single receptor-tether-ligand molecule in two conformations, and is unaffected by its total concentration. This marks an important departure from intermolecular binding, where the concentration ratio of bound and free receptors depend on the concentration of the ligand (see eq 3.3). The concentration independence of intramolecular binding may partly account for the gene fusion of proteins which function in the bound form.

Intuitively, one may assume that the role of a flexible tether is to fix the ligand at an effective concentration, C_{B, eff}. Comparison between eqs 6.1 and 3.3 then leads to

$$K_{\text{i}}=K_{\text{a}}{C}_{\text{B},\text{eff}}$$ (6.2a)

A formal derivation shows that the effective concentration is given by the probability density, ρ_L(r), of the end-to-end vector r of the linker:¹¹²

$$K_{\text{i}}=K_{\text{a}}{\rho }_{\text{L}}({\mathbf{r}}_0)$$ (6.2b)

where r₀ is the end-to-end vector when the ligand is bound to the receptor (Figure 4A). (See Section 4 of Supporting Information). Values of the effective concentration as given by ρ_L(r₀) for flexible peptide linkers are typically found in the mM range.^112,113 Therefore, tethering the ligand to its receptor achieves the same effect as having the ligand present at a fixed concentration of ~ 1 mM. Intramolecular ligand binding plays prominent roles in regulation of enzyme activities,¹¹³ and tethering by disulfide bond formation has been used as a technique for identifying weak binding ligands.¹¹⁴ Inasmuch as ligand binding can shift the folding-unfolding equilibrium of a protein toward the folded state, intramolecular ligand binding can also increase the stability of a folded protein.¹¹³

Tamura and Privalov⁶⁵ measured the difference in binding entropies, $\mathrm{\Delta }{S}_{\text{b}}^{\circ }-\mathrm{\Delta }{S}_{\text{i}}$, between a dimeric protein and a cross-linked variant, and, like Page and Jencks,¹¹⁵ attributed the binding-entropy difference to the loss of translational/rotational entropy. Karplus and Janin⁶⁸ correctly pointed out that there is no relation between the two entropy changes.

We now use eq 6.2b to analyze $\mathrm{\Delta }{S}_{\text{b}}^{\circ }-\mathrm{\Delta }{S}_{\text{i}}$ in more detail. Neglecting the temperature dependence of the probability density ρ_L(r₀), we find that

$$\mathrm{\Delta }{S}_{\text{i}}=\mathrm{\Delta }{S}_{\text{b}}^{\circ }+k_{\text{B}}ln[V^{\circ }{\rho }_{\text{L}}({\mathbf{r}}_0)]$$ (6.3a)

or, equivalently

$$\mathrm{\Delta }{S}_{\text{b}}^{\circ }-\mathrm{\Delta }{S}_{\text{i}}=-k_{\text{B}}ln[V^{\circ }{\rho }_{\text{L}}({\mathbf{r}}_0)]$$ (6.3b)

The right-hand side of eq 6.3b can be recognized as the entropy change of the ligand when its concentration is changed from the standard concentration, 1/V^∘, to the effective concentration, ρ_L(r₀). In essence, there is a difference in ligand concentration in the unbound state between intermolecular and intramolecular binding: it is the standard concentration in the former case but the effective concentration in the latter case. The difference between the intermolecular and intramolecular binding entropies is a reflection of the difference in ligand concentration before binding. When ρ_L(r₀) was predicted from a polymer model and used in eq 6.3, experimental results for $\mathrm{\Delta }{S}_{\text{b}}^{\circ }-\mathrm{\Delta }{S}_{\text{i}}$ were reasonably reproduced.¹¹⁶

7. Multivalent Binding

High affinities can be achieved by multivalent binding, where the receptor has multiple binding sites and the ligand consists of multiple linked fragments, each with affinity to one site. When two fragments that target neighboring nonoverlapping sites on a receptor are tethered to each other, the binding constant (K_1–2) of the resulting bivalent ligand can be related to the binding constants (K_a1 and K_a2) of the fragments. The binding can be envisioned to occur stepwise: the first fragment followed by the second fragment (Figure 4B). Upon binding, the first fragment effectively becomes part of the receptor; the binding of the second fragment can then be considered intramolecular. Combining the two steps and using eq 6.2b, we have

$$K_{1-2}=K_{\text{a}1}{K}_{\text{a}2}{\rho }_{\text{L}}({\mathbf{r}}_0)$$ (7.1)

When K_a1ρ_L(r₀) and K_a2ρ_L(r₀) are greater than 1, the affinity of the bivalent ligand will be higher than that of either of the two fragments by itself. (Note that K_1–2 is the binding constant for simultaneous association of both fragments with their respective sites. If it happened that ρ_L(r₀) and hence K_1–2 were extremely small, then the dominant bound species would consist of the two singly bound fragments.) As noted in the preceding section, typical values of ρ_L(r₀) are around 1 mM, so that the affinity of the bivalent ligand is expected to be greater than that of one individual fragment when the fragmental binding constants are greater than ~10³ M⁻¹. Fragments with such a modest affinity are relatively easy to find, so covalent linkage between fragments can provide a simple strategy for achieving high affinity. This strategy has found significant successes in practice.^117,118 Moreover, the scheme can be easily extended to treat more than two linked fragments, with each additional fragment providing extra affinity enhancement. For example, a designed trivalent ligand was able to increase the affinity from 10⁶ M⁻¹ to 3 × 10¹⁶ M⁻¹.¹¹⁹ Multivalent ligands provide a trivial example of the fact that K_a does not have an upper limit so long as one places no upper limit on the sizes of the ligand and receptor.

Despite an early warning by Jencks,¹²⁰ it is still a common mistake to expect that K_1–2 equals the product K_a1K_a2, or equivalently, that the binding free energy of a bivalent ligand equals the sum of the binding free energies of the two fragments. A simple indication of the fallacy of this expectation is the mismatch in units, M⁻¹ for K_1–2 vs. M⁻² for K_a1K_a2. Eq 7.1 lays the foundation for the relation between the binding free energy of the bivalent liagnd and those of its fragments. In terms of standard binding free energy, this equation becomes

$$\mathrm{\Delta }{G}_{1-2}^{\circ }=\mathrm{\Delta }{G}_1^{\circ }+\mathrm{\Delta }{G}_2^{\circ }-k_{\text{B}}Tln[V^{\circ }{\rho }_{\text{L}}({\mathbf{r}}_0)]$$ (7.2)

The first two terms are the additive contributions of the two fragments. The third term, which has already appeared as entropy in eq 6.3b, accounts for the fact that, after the first fragment has bound, the unbound second fragment is present at the effective concentration, not the standard concentration.

In the same the paper, Jencks also proposed that $\mathrm{\Delta }{G}_{1-2}^{\circ }-\mathrm{\Delta }{G}_1^{\circ }$ provides an estimate for the interaction energy of the second fragment with the receptor. We can assess Jencks’s proposition for the case where the second fragment is a monatomic ligand and the linker is fully flexible. For this case, eqs 7.1 and 3.14b yield $\mathrm{\Delta }{G}_{1-2}^{\circ }-\mathrm{\Delta }{G}_1^{\circ }={\langle W_2(\mathbf{r})\rangle }_{\text{b}2}-k_{\text{B}}Tln[{\rho }_{\text{L}}({\mathbf{r}}_0)V_{\text{b}2}]$. Thus, there are actually two contributions to $\mathrm{\Delta }{G}_{1-2}^{\circ }-\mathrm{\Delta }{G}_1^{\circ }$. One, consistent with Jencks’s view, is the interaction energy, 〈W₂ (r)〈_b2. The second, −k_BTln[ρ_L(r₀)V_b2], arises from the fact that the linker end-to-end vector r can explore all the allowed space in the unbound state but is restricted to the volume V_b2 available to the monatomic ligand while bound. This second term is essentially the loss in translational entropy of the monatomic ligand on binding, conditional upon the fact that it is attached to the already bound first fragment via a flexible linker. However, Jencks’s proposition does appear to be valid for the special case in which the monatomic ligand is attached to the first fragment via a linker whose conformation and orientation relative to the first fragment are rigidly fixed, because in this case, $\mathrm{\Delta }{G}_{1-2}^{\circ }-\mathrm{\Delta }{G}_1^{\circ }=W_2({\mathbf{r}}_0)$ (eq IV.5d of Supporting Information). This quantity measures the free energy arising from the interaction of the ligand with the receptor while rigidly held at r₀ by the linker. In short, there is an entropy cost associated with restricting the second fragment to its binding site; this is minimized when a suitable rigid linker is used.

8. Ligand Efficiency and Additivity Analysis of Binding Free Energy

There is general expectation that the binding affinity can increase as more functional groups are added to a ligand, and this expectation is met, at least to some extent, by experimental studies.^121,122 On the other hand, the finite size of the protein target sets some upper limit on the molecular weight for a ligand that is to become a drug, so it can be important to gain as much affinity as possible with a small ligand. Accordingly, the ratio of $-\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ to n_ha, the number of heavy atoms in the ligand, has been proposed as a figure of merit termed the ligand efficiency.¹²³ It is worth noting that this quantity depends upon the choice of standard concentration in a nontrivial fashion, as now discussed.

According to eq 4.6, $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ consists of two terms, one arising from receptor-ligand interactions and the other from the change in available volume from V^∘ to V_b. A typical binding constant of 10⁹ M⁻¹ corresponds to a binding free energy $\mathrm{\Delta }{G}_{\text{b}}^{\circ }=-12.3\text{kcal}/\text{mol}$ at room temperature. There are no rules for the magnitude of V_b, but for the sake of argument let us assume a value ~ 1 ų. The corresponding translational entropy term has a value of 4.4 kcal/mol, so the interaction energy term must have a value of −16.7 kcal/mol. This simple calculation shows that the interaction energy term dominates the translational entropy term. This dominance helps account for the near-zero y-intercepts in graphs of $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ vs n_ha for different ligands.^121,122 For example, a correlation analysis by Wells and McClendon¹²² showed that the binding free energies of 13 ligands targeting different receptors closely followed the relation $-\mathrm{\Delta }{G}_{\text{b}}^{\circ }=0.24n_{\text{ha}}$. According to this relation, ligands with 34, 51, and 68 heavy atoms would have binding constants of 10⁶, 10⁹, and 10¹² M⁻¹, respectively, and these ligands all have ligand efficiency of 0.24. Now, consider what would happen if the standard concentration were 1 nM. First, the value of $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ corresponding to K_a = 10⁹ M⁻¹ would be exactly 0, and the translational entropy term would have the same magnitude as the interaction energy term. Second, for the ligands listed above with 34, 51, and 68 heavy atoms and corresponding binding constants of 10⁶, 10⁹, and 10¹² M⁻¹, the values of $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ would be −4.1, 0, and 4.1 kcal/mol, respectively. The ligand efficiency, $-\mathrm{\Delta }{G}_{\text{b}}^{\circ }/n_{\text{ha}}$, would therefore have widely disparate values, −0.12, 0, and 0.06, and might no longer be perceived as a useful metric.

A fundamental issue with the definition of ligand efficiency is that the change in translational entropy on binding, and consequently the binding free energy as a whole, are not group additive. This problem is significantly lessened when we focus on differences in binding free energy among similar ligands for the same receptor, since then we will benefit from the cancellation of the dependence on the standard concentration, and at least partial cancellation of the translational entropy in the bound state. Consider the case where an additional atom, forming significant favorable interactions with the receptor, is rigidly attached to an existing ligand. The motion of the original ligand within its binding site is assumed to be unperturbed by the added atom. Then, as concluded in the last paragraph of the preceding section, the added atom only contributes to the interaction energy term. Calculations of mutation effects in toy models of protein-protein binding support the dominance of the interaction energy term in the contribution of an additional group bonded to a ligand which already has significant affinity.⁹² One may thus conclude that an additive model is much more likely to be successful when applied to relative binding free energies than total binding free energies.^124,125

Finally, we comment on the practice of discussing the energetic contributions of individual chemical groups in the context of the total binding free energy, as sometimes done in studies of mutational effects on protein-protein binding affinity. To illustrate, suppose that two proteins form a complex with a binding constant of 10⁹ M⁻¹, which, as mentioned above, corresponds to $\mathrm{\Delta }{G}_{\text{b}}^{\circ }=-12.3\text{kcal}/\text{mol}$ at room temperature. Now a point mutation from arginine to alanine is made on one of the proteins. As a result, the binding constant is reduced to 10⁷ M⁻¹, or equivalently, the binding free energy is raised by ΔΔG_b = 2.7 kcal/mol. It may then be claimed that the arginine residue contributes $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{b}}/(-\mathrm{\Delta }{G}_{\text{b}}^{\circ })=2.7/12.7=22\%$ of the binding free energy. This view is problematic in two respects. First, as the preceding discussion makes clear, the bulk of the 2.7 kcal/mol contribution of arginine is to the interaction energy term; the mutant likely pays a translational entropy cost similar to that of the wild-type protein. Thus, the presence of the essentially constant translational entropy term in the denominator, $-\mathrm{\Delta }{G}_{\text{b}}^{\circ }$, masks any simple interpretation of the ratio $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{b}}/(-\mathrm{\Delta }{G}_{\text{b}}^{\circ })$. Second, because the value of $-\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ depends on the choice of the standard concentration, the value of $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{b}}/(-\mathrm{\Delta }{G}_{\text{b}}^{\circ })$ also depends on this completely arbitrary quantity. For example, if the standard concentration were 1 nM, $\mathrm{\Delta }{G}_{\text{b}}^{\circ }$ would be 0, and it would then certainly not be sensible to assign any meaning to the ratio $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{b}}/(-\mathrm{\Delta }{G}_{\text{b}}^{\circ })$.

9. Concluding Remarks

The theory of noncovalent binding has been formulated and interpreted in a number of different ways in the literature, some more faithful than others to the underlying statistical thermodynamics. We have sought here to provide a unified, rigorous review of this material that addresses not only simple, bimolecular binding but also intramolecular and multivalent binding; to generate insight through simple examples; and to bring out important physical implications of the mathematical formulas. Central observations include the following:

1. Because the RRHO approximation treats molecules as rigid, it is not well suited to the partition functions of flexible biomolecules and offers no advantage relative to the FM approach except when a quantum mechanical treatment of vibrational motion is needed.

2. Although the individual terms of the RRHO approximation have contributions from mass and Planck’s constant, in the classical limit these contributions cancel in the free energy and entropy of binding.

3. There is no physical significance to a zero value of binding free energy or its entropy component, because these quantities depend upon the standard concentration, C^∘, whose value is established by culture rather than physics.

4. There are two distinct definitions of the change in translational entropy upon binding. In the FM approach, the ligand retains some translational freedom after binding, and the change in translational entropy is related to the volume effectively accessible to it in the bound state, relative to the standard volume 1/C^∘. In the RRHO, or Sackur-Tetrode, approach, the ligand has no translational motion of its own after binding; only the complex as a whole is considered to translate. Both definitions are legitimate, so long as they are used consistently within the theoretical frameworks from which they derive.

5. Although entropy is a property of the whole system, it may be partitioned in useful and rigorous ways. For example, partitioning entropy into contributions from different degrees of freedom via conditional probability distributions enables one to define the configurational and solvation entropies, while partitioning into contributions from different regions of configurational space via the composition law of entropy enables one to define vibrational and conformational entropies.

6. Mutual information terms usefully quantify the entropic consequences of correlation.

7. When bimolecular binding is made intramolecular through the introduction of a flexible linker between receptor and ligand, the change in the entropy of binding is determined by the statistical properties of the linker. When a new group is linked to an existing ligand to create a bivalent ligand, there is an entropy cost associated with restricting the new group to its binding site, which can be minimized by a suitably chosen rigid linker.

8. While the partitioning of the binding enthalpy into contributions of chemical groups seems justified, a similar partitioning of the binding entropy is problematic, because of the latter’s dependences on the standard concentration and on correlated motions (e.g., overall translation). Consequently, analyses of ligand affinities based on group additivity of the total (as opposed to relative) binding entropy or binding free energy can be misleading.

We hope the present work will be found useful, especially to theorists formulating new methods of computing binding thermodynamics, and to experimentalists deriving insight from thermodynamic and structural data.