Accelerating Membrane Insertion of Peripheral Proteins with a Novel Membrane Mimetic Model

Abstract

Characterizing atomic details of membrane binding of peripheral membrane proteins by molecular dynamics (MD) has been significantly hindered by the slow dynamics of membrane reorganization associated with the phenomena. To expedite lateral diffusion of lipid molecules without sacrificing the atomic details of such interactions, we have developed a novel membrane representation, to our knowledge, termed the highly mobile membrane-mimetic (HMMM) model to study binding and insertion of various molecular species into the membrane. The HMMM model takes advantage of an organic solvent layer to represent the hydrophobic core of the membrane and short-tailed phospholipids for the headgroup region. We demonstrate that using these components, bilayer structures are formed spontaneously and rapidly, regardless of the initial position and orientation of the lipids. In the HMMM membrane, lipid molecules exhibit one to two orders of magnitude enhancement in lateral diffusion. At the same time, the membrane atomic density profile of the headgroup region produced by the HMMM model is essentially identical to those obtained for full-membrane models, indicating the faithful representation of the membrane surface by the model. We demonstrate the efficiency of the model in capturing spontaneous binding and insertion of peripheral proteins by using the membrane anchor (γ-carboxyglutamic-acid-rich domain; GLA domain) of human coagulation factor VII as a test model. Achieving full insertion of the GLA domain consistently in 10 independent unbiased simulations within short simulation times clearly indicates the robustness of the HMMM model in capturing membrane association of peripheral proteins very efficiently and reproducibly. The HMMM model will provide significant improvements to the current all-atom models by accelerating lipid dynamics to examine protein-membrane interactions more efficiently.

Introduction

The cellular membrane plays an important role in signaling, transport, and metabolic processes in all living cells. In humans, nearly one third of the 34,000 identified proteins are estimated to function in membrane-associated forms (1). Though initially perceived as a passive environment, the central role of the membrane not only in proper function, but also in tight regulation of membrane-associated proteins and phenomena has been well established (2–4). Membrane-mediated effects on protein function can be generally attributed to two major mechanisms: the overall mechanical impact of the embedding lipid bilayer on protein structure and dynamics (5–7) and specific interactions between the membrane lipids (particularly the headgroups that form the membrane surface) and their respective binding sites in the protein (8–12). Furthermore, the overall membrane affinity of a given protein can also be modulated through variation of the lipid composition of the membrane (13–16). Indeed, this mechanism is widely used in biological systems to target and localize peripheral proteins to distinct areas of the membrane or toward specific cell types, and to regulate their activity in a lipid-dependent manner.

Despite the central role of the membrane in protein function and activity, due to the semifluid and highly dynamical nature of lipid bilayers, obtaining sufficiently detailed structural information on peripheral proteins in their membrane-bound form has proven extremely challenging. Limited information on the proximity of certain regions in membrane-binding proteins can be inferred from experimental methods such as small-angle x-ray scattering (17), electron paramagnetic resonance (18,19), Förster resonance energy transfer (18,20,21), and mutagenesis studies (22,23). Nevertheless, more details are needed to fully characterize the nature of protein-lipid interactions that are critical for binding and function of peripheral proteins. Another challenging aspect of studying peripheral proteins is that they often employ relatively small membrane-engaging parts (membrane anchors). Making predictions about such domains is far more difficult than for integral membrane proteins, whose orientation and depth of membrane insertion can be fairly reliably predicted by well-established protocols (24–26).

Molecular dynamics (MD) offers a promising method of gaining structural and dynamical information on such protein-lipid complexes and of characterizing the interactions therein that govern the membrane-controlled effects on protein function. The method combines high spatial (sub-Ångstrom) and temporal (femtosecond) resolutions with a dynamical description, thereby offering an ideal approach toward studying membrane-associated phenomena. Unfortunately, membrane lipids are known to exhibit slow dynamics on the timescales achievable by atomistic MD simulations of membrane proteins, which are currently performed routinely only for tens to hundreds of nanoseconds (27–29). The slow lateral diffusion of membrane lipids at ambient temperatures is typically on the order of 10⁻⁸ cm² s⁻¹, requiring simulations at least an order of magnitude longer to describe.

To fill this timescale gap, coarse-grained (CG) MD has been employed as an efficient method (30–37), in which the number of particles in the simulated system is reduced by representing groups of atoms (such as a moiety, a whole side chain, or even several residues) by a CG bead. CG models have successfully described various properties of lipid structures and associated phenomena, e.g., spontaneous formation of lipid bilayers (30), formation of the gramicidin A (gA) ion channel (38), formation of micelle (31) and disclike (39) structures, helix dimerization of glycophorin A (GpA) in a bilayer (32), and membrane sculpting (34) and liposome remodeling (35) induced by BAR domains. The efficiency of the CG method, however, is achieved by sacrificing the atomic resolution, which is indispensable for accurate description of specific protein-lipid interactions. In addition to CG methods, the generalized Born theory (40), based on Poisson-Boltzmann continuum electrostatics, has been utilized in the construction of implicit membranes (41) to probe the binding of peripheral proteins to the membrane. The method has been successfully used to describe the partitioning (42,43) and even oligomerization of peptides within the membrane (44). Similar to CG models, implicit representations do not take into account specific protein-lipid interactions that are key to binding and activation of peripheral proteins. Moreover, these models ignore the crucial headgroup region of the bilayer, treating the interface as an abrupt switch from a polar region to a nonpolar region.

As an alternative approach, we present what to our knowledge is a novel membrane representation for atomistic MD simulations, termed the highly mobile membrane-mimetic (HMMM) model, which is composed of a combination of a biphasic solvent system (45) and short-tailed lipids (st-lipids) at the aqueous-organic interface (Fig. 1). We demonstrate that the designed st-lipids spontaneously form bilayerlike structures and that the lipid diffusion has been accelerated by 1–2 orders of magnitude in the resulting bilayer. The results indicate that the HMMM model is ideal for studying membrane-associated phenomena via MD without compromising the atomic details necessary for accurate description of the interactions between the headgroups and the protein. Furthermore, we use the membrane-anchoring domain of a coagulation factor to demonstrate the efficiency of the HMMM model in capturing spontaneous membrane association and insertion of peripheral proteins without imposing any bias or external force. Coagulation proteins constitute a prominent class of peripheral membrane proteins whose function is highly dependent on, and indeed regulated by, their ability to bind to specific regions of biological membranes (46). Modulation of the lipid composition of the membrane, and thus the membrane affinity of the coagulation proteins, is one of the main physiological regulatory mechanisms in the clotting cascade (7,13). The lipid dependence of these processes makes coagulation factors an ideal case for testing the robustness of the HMMM model in capturing key lipid-protein interactions at an atomic level.

Figure 1.

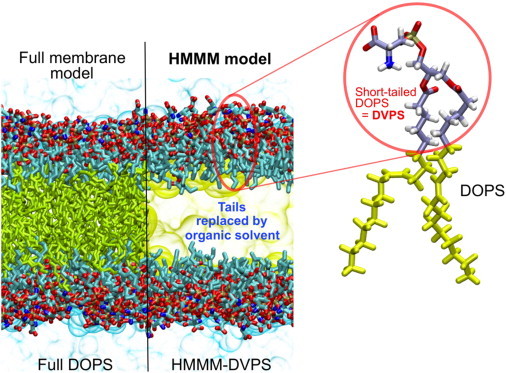
Contrasting the HMMM and conventional representations of a membrane. In an HMMM model, a large fraction of the acyl tails (left, yellow sticks) of the membrane-forming lipids is replaced by a liquid organic phase (right, yellow area). In this study, a full DOPS lipid molecule (inset) is represented by a short-tailed DVPS molecule (the circled fraction of the molecule), and the space vacated by the removal of the C₆–C₁₈ portion of the acyl tails is filled with an organic solvent (yellow). Oxygen atoms are red, nitrogen blue, phosphorus gold, and carbon ice blue, except the C₆–C₁₈, which are in yellow. Bulk water molecules are shown in light blue.

Materials and Methods

Here, we provide a brief description of the simulation systems and conditions used for this study. A detailed description of the methods is provided in the Supporting Material. Table 1 summarizes all the simulation systems described in this study.

Table 1.

System configurations

System	Lipid	n	Counterion	AL (Å2)	D (10−8cm2 s−1)
HMMM Simulations
HMMM-0	DVPS	5	Na+	133.0	—
HMMM-1	DVPS	5	Na+	294.0	314.0
HMMM-2	DVPS	5	Na+	144.0	171.0
HMMM-3	DVPS	5	Ca2+	144.0	134.0
HMMM-4	DVPS	5	Na+	100.0	97.7
HMMM-5	DVPS	5	Na+	68.6	26.4
GLA Domain Binding
HMMM-GLA (×10)	DVPS	5	Na+	127.0	—
Full Membrane Simulations
Full-1	DOPS	18	Na+	65.3	4.93
Full-2	DOPS	18	Ca2+	65.3	2.10

Systems simulated in this study for spontaneous membrane formation (HMMM-0), diffusion constant calculation (HMMM-1 to HMMM-5, Full-1, and Full-2), and GLA-domain binding (HMMM-GLA) are listed along with the membrane-forming lipid, the number of acyl tail carbons (n), the counterion, the area/lipid (A_L), and the measured lateral diffusion constant of the lipids (D). —, not measured. Simulation of system HMMM-GLA was repeated 10 times. An expanded version of this table including more details is provided as Supporting Material.

HMMM simulations

In the HMMM membrane used in this study, 1,1-dichloroethane (DCLE) is used to model the hydrophobic core, and divalerylphosphatidylserine (DVPS) molecules to represent the phosphatidylserine (PS) lipids. To investigate the efficiency and robustness of the HMMM model, its ability to form and maintain bilayers was tested in a simulation in which the st-lipids were initially distributed on a grid spanning the whole volume of the biphasic solvent box, with approximately half of the molecules in the organic phase and the other half in water (Fig. 2, upper left). Another set of five simulations were performed to calculate the lateral diffusion constant of the lipids in the HMMM model and its dependence on different configurations.

Figure 2.

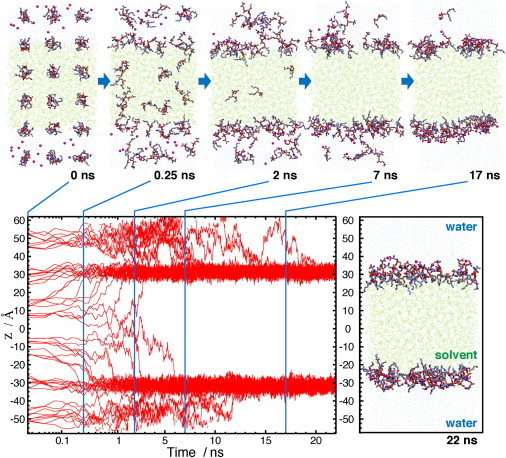
Spontaneous formation of the HMMM membrane. The formation of a bilayer-like structure is depicted using snapshots taken from the membrane-formation simulation at t = 0, 0.25, 2, 7, and 17 ns (upper, left to right). Short-tailed DVPS molecules were initially scattered over the simulation box on a grid to have an even distribution among different phases. The positions along the membrane normal, z, of individual phosphorus atoms of DVPS molecules as a function of the simulation time is shown with red lines (lower left). Also shown is a snapshot of the system (to scale) at t = 22 ns that depicts the fully formed bilayer (lower right). The z coordinate for individual lipids has been calculated in each frame in reference to the actual center of mass (COM) of the organic phase, i.e., in each frame, z = 0 is set to the COM of the DCLE layer. Note that the time axis is in the log scale for t = 0–2 ns and linear for the rest, to highlight fast movement of the lipids during the early phase of the simulation.

Full-membrane simulations

As a reference, a full membrane composed of 288 1,2-dioleoyl-sn-glycero-3-phospho-L-serine (DOPS) molecules was also simulated with either Na⁺ or Ca²⁺ as the counterion (we refer to these conventional membrane models as full membranes to contrast them with the HMMM model). The system was simulated for 20 ns as an NP_nAT (where P_n is the constant membrane-normal pressure and A is the membrane area) ensemble and using the conditions described elsewhere (47).

Insertion of the GLA domain into the HMMM model

Ten independent simulations were performed to test the ability and efficiency of the HMMM model in capturing membrane binding of a membrane anchor in unbiased simulations. The γ-carboxyglutamic-acid-rich (GLA) domain of hFVII with seven bound Ca²⁺ ions (48), preequilibrated in solution (49) was positioned in the bulk water at least 8 Å above the membrane (see Fig. 5). The system was then fully equilibrated for 50 ns.

Figure 5.

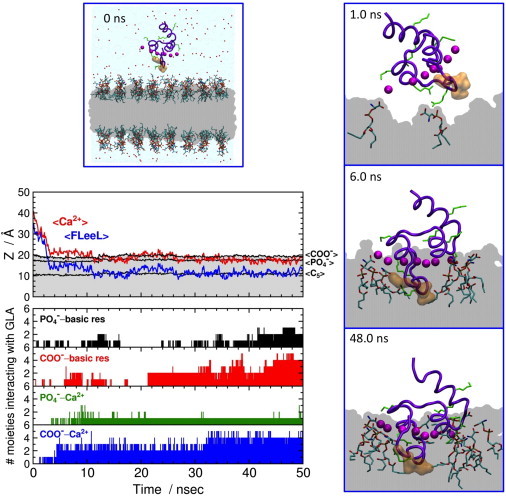
Spontaneous binding of the GLA domain to an HMMM membrane. (Left middle) Average heights (z) of the GLA-bound Ca²⁺ ions (red line; <Ca²⁺>), the C_α atoms of residues 4–8 (membrane anchor) in the ω-loop (blue; labeled <FLeeL>), the carboxy carbon atoms of DVPS lipids (black, <COO⁻>), the phosphate phosphorus atoms of DVPS lipids (black, <${\text{PO}}_4^{-}$>), and the C₅ atoms of DVPS acyl tails (black, <C₅>) as a function of simulation time. (Lower left) Time series for specific interactions between the GLA domain and the DVPS lipids in terms of the number of the contribution of various moieties of the lipid headgroups: first row, number of phosphate phosphorus atoms within 5.0 Å of any basic side chains of the GLA domain (black bars); second row, number of carboxy carbon atoms within 5.0 Å of any basic side chains of the GLA domain (red); third row, number of phosphate phosphorus atoms within 5.0 Å of any GLA-bound Ca²⁺ ions (green); fourth row, number of carboxy carbon atoms within 5.0 Å of any GLA-bound Ca²⁺ ions (blue). Molecular images depict, in side view, the whole simulation system at 0 ns (upper left) and close-up snapshots of the GLA domain interacting with DVPS lipids at 1.0 ns (upper right), 6.0 ns (middle right), and 48.0 ns (lower right). The backbone of the GLA domain is drawn in a thick violet tube representation with the hydrophobic side chains of Phe⁴, Leu⁵, and Leu⁸ in the ω-loop in an orange surface representation. The GLA-bound Ca²⁺ ions are drawn as purple spheres, basic side chains as thin green tubes, and the DCLE layer in gray.

Simulation protocols

All the simulations were performed using NAMD2 (50) with the CHARMM36 force field parameter set (51), the CMAP corrections (52) for proteins, and the TIP3P model for water (53) in the NP_nAT ensemble. Langevin dynamics with a damping coefficient, γ, of 0.5 ps⁻¹ and Langevin piston Nosé-Hoover methods (54,55) were employed to maintain the temperature at 310 K and the pressure at 1 atm, respectively. To evaluate long-range electrostatic forces without truncation, the particle mesh Ewald (PME) method (56), with a grid density of slightly finer than 1 Å⁻³, was used. The cut-off for van der Waals interaction was set at 12 Å. Integration time steps were set at 2, 2, and 4 fs for bonded, nonbonded, and PME calculations, respectively. For the simulations of full DOPS membranes, integration time steps of 1, 1, and 2 fs (for bonded, nonbonded, and PME) and CHARMM27 force field parameters were used; other conditions were the same as described above.

Results and Discussion

Spontaneous formation of stable bilayer by the HMMM model

To examine whether the employed st-lipids partition properly into the interfacial region of the biphasic solvent used in the HMMM model, and to test their robustness toward forming and sustaining a bilayer structure within affordable simulation time, a 40-ns-long MD simulation was performed in which the st-lipids (54 DVPS molecules) were scattered initially on a grid spanning the two solvent phases with approximately half of the lipids in the organic phase and the other half in the water phase (Fig. 2). The DVPS molecules rapidly partitioned to the organic-aqueous interface, with their headgroups optimally positioned in water and their acyl tails immersed in the organic phase. The st-lipids initially positioned in the organic phase exhibited faster partitioning; within <6 ns all of the lipids in this phase emerge from the organic layer, with 72% of them (13 lipids) doing so within only 1 ns and 83% (15 st-lipids) within 2 ns (Fig. 2). DVPS lipids in the aqueous phase remained in water longer, on average, before partitioning to the interface. Nevertheless, 83% of water-immersed DVPS lipids reached the interface within 10 ns, with the remaining three molecules completing their partitioning into the interface within 14, 16, and 20 ns. This behavior is fully expected from a surfactantlike molecule such as DVPS, whose charged headgroup establishes strong favorable interaction with water. Overall, the entire process of the formation of the bilayer is very fast and completed within 20 ns. Once partitioned into the interface, DVPS lipids remain there for the remainder of the 40-ns simulation (Fig. 2; data shown only for the first 22 ns). The results clearly indicate the efficiency of the model toward capturing the formation of a stable bilayerlike structure within short and affordable simulation times without compromising the atomic resolution of the system.

A key attribute of a membrane-mimetic model is its ability to reproduce the structure and atomic distribution of various chemical groups within the membrane, especially in the headgroup region, where specific interactions with coagulation proteins are formed. To examine this aspect of the HMMM model, atomic density profiles were calculated for the HMMM bilayer structure and compared with those of a full DOPS membrane (Fig. 3). Regarding interaction with a coagulation protein, the most important characteristics of these profiles are the positions and shapes of the density peaks for the headgroup moieties, which exhibit remarkable similarities in the two profiles (Fig. 3). The extent of hydration and the degree of counterion penetration are also similar for the two different membrane representations. The results clearly indicate that the HMMM model successfully captures the essential properties of a full membrane, despite the marked difference in acyl tail length (18 carbons for DOPS vs. 5 for DVPS) and lipid density. Minor differences include the relative distribution of the carboxy carbons, which indicates a more upright arrangement of the lipids in the DOPS membrane compared to the membrane composed of DVPS, an effect that is partially due to the lower lipid density of the latter model.

Figure 3.

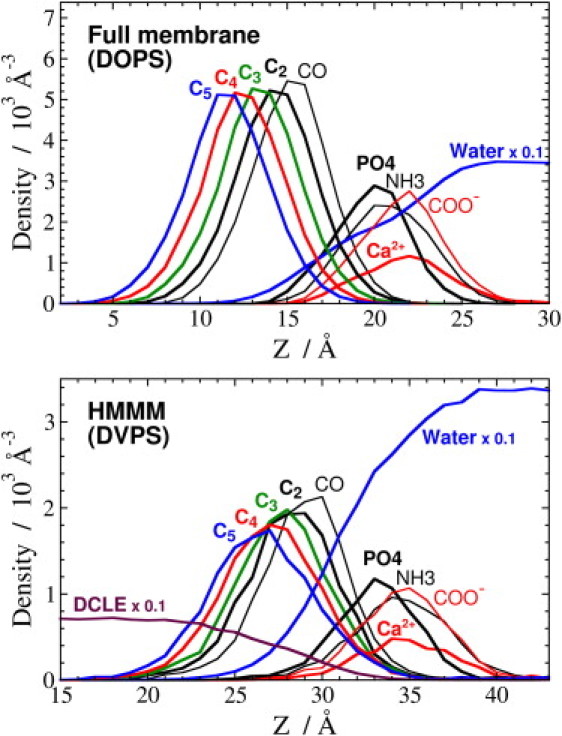
Structural comparison of full and HMMM membranes. The membrane profiles of a full DOPS membrane (upper) and an HMMM DVPS membrane (lower) aligned by the peak of the ${\text{PO}}_4^{-}$ groups. The atomic densities are plotted along the membrane normal, z, using a bin size of 1 Å for most of the heavy atoms: oxygen of bulk water (blue line, ×0.1), Ca²⁺ counterion (red), carboxy carbon (thin red), amine nitrogen (thin black), phosphate phosphorus (black), carbonyl carbon (thin black), C₂ (black), C₃ (green), C₄ (red), C₅ (blue), and C₁ of DCLE (maroon, ×0.1). Note that the distance between the COMs of the membrane and the ${\text{PO}}_4^{-}$ peak is different for the two membrane models (20.0 Å for DOPS and 33.0 Å for DVPS) due to different membrane thicknesses. The difference in the absolute heights of the density peaks are related to the different A_L of the two membranes (A_L of 65.3 Å² for DOPS vs. 133 Å² for DVPS). The lefthand-side y axes (atomic density) are scaled so that the ${\text{PO}}_4^{-}$ peaks are shown on the same scale.

Enhanced lipid mobility in the HMMM model

The main objective in constructing the HMMM model was to achieve enhanced mobility of the lipid molecules within the membrane without compromising atomic resolution of the headgroups. Fig. 4 A compares the lipid mobility of the HMMM and full-membrane models. The enhanced mobility of the lipids in the HMMM model is quite evident, even though the trajectory used for plotting full lipids is 10 times longer than the one used for the HMMM model (10 ns vs. 1 ns). Although DVPS lipids rapidly exchange positions within only 1 ns (average RMSD_xy of over 10 Å), DOPS lipids essentially retain their initial positions (average RMSD_xy of only ∼2 Å) within the 10-ns segment used to generate the plot (Fig. 4). The calculated lateral diffusion constant, D (Eq. S1 in the Supporting Material), for the HMMM and full-membrane models are 2.5 × 10⁻⁶ cm² s⁻¹ and 4.0 × 10⁻⁸ cm² s⁻¹, respectively, indicating the enhanced lateral lipid diffusion achieved by the HMMM model.

Figure 4.

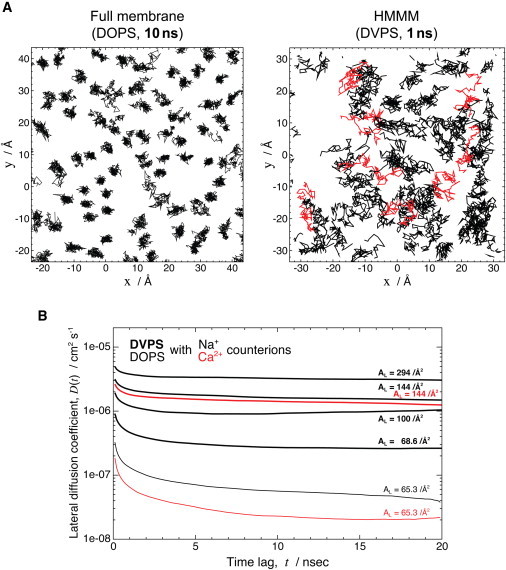
Enhanced lipid lateral diffusion in the HMMM membrane. (A) Comparison of the trajectory of phosphorus atoms within the membrane in a 10-ns-long segment of a simulation of a full DOPS membrane (left) with a 1-ns-long segment of a simulation of an HMMM DVPS membrane (right). In the DVPS membrane segment, some of the trajectory lines are depicted in red to make the distinction between different lipids more clear. Despite an order-of-magnitude-shorter simulation, the HMMM model exhibits clearly much larger lateral mobility for the lipids. (B) Lateral diffusion constants of DOPS and DVPS in different environments. The slope of the mean-square displacement of lipids (within the xy plane) as a function of time lag is plotted for membranes composed of pure DOPS (thin lines) or DVPS (thick lines) neutralized with either Na⁺ (black) or Ca²⁺ (red). The phosphate phosphorus atoms were used for the calculations. The area/lipid, A_L, of individual systems is also shown.

A more systematic comparison of the lateral diffusion constants for the HMMM models constructed and simulated using different configurations (different counterions and area/lipid values, A_L) is provided in Fig. 4 B. The average slopes of the mean-square displacement of the phosphorus atoms as a function of the time lag, D(t), defined in Eq. S1, are plotted for full DOPS membranes and different HMMM membranes. The lateral diffusion constant, D, was quantified as the asymptote of D(t) by averaging D(t) over larger t (10–20 ns), with the calculated values also summarized in the rightmost column of Table 1.

When simulated at an experimental area/lipid ratio, A_L, with Na⁺ as the counterion, D of PS lipids is enhanced by more than a factor of 5 for the HMMM model (2.64 × 10⁻⁷ cm² s⁻¹, compared to 4.93 × 10⁻⁸ cm² s⁻¹ for a full membrane composed of DOPS; Table 1), an effect mainly caused by shortening of the acyl tails. Around an order of magnitude further enhancement in lateral mobility is attained by reducing the lipid density, e.g., 1.71 × 10⁻⁶ cm² s⁻¹ and 3.14 × 10⁻⁶ cm² s⁻¹ for DVPS with A_L = 144 Å² and 294 Å², respectively.

In comparison with Na⁺ ions, divalent Ca²⁺ counterions interact with PS headgroups more strongly and form far longer-lived lipid-ion clusters, rigidifying the membrane lipids (57) and thus resulting in a smaller D for both the full DOPS membrane and HMMM models studied. The calculated D for the DOPS membrane is 4.93 × 10⁻⁸ cm² s⁻¹ when simulated with Na⁺, and 2.10 × 10⁻⁸ cm² s⁻¹ with Ca²⁺. This counterion effect is also clearly present in the HMMM simulations, although to a lesser degree, e.g., 1.71 × 10⁻⁶ cm² s⁻¹ with Na⁺ vs. 1.34 × 10⁻⁶ cm² s⁻¹ with Ca²⁺.

Spontaneous membrane insertion of coagulation factor VII

The main motivation for developing the HMMM model is to have an efficient model that allows for accelerated establishment of lipid-protein interactions and a membrane sufficiently mobile to allow the insertion of proteins to be captured without the need of additional forces or biased potential within affordable simulation times. To test the accuracy and efficiency of the HMMM model in this regard, the membrane-anchoring domain of a coagulation protein was used as an example. Binding to specific regions of the cellular membrane constitutes a pivotal step in the activation of almost all coagulation factors. Through largely unknown mechanisms, membrane binding and assembly of coagulation proteins result in an increase of several orders of magnitude in their catalytic activity, a process vital to the entire clotting cascade (58). The importance of membrane binding in the function of these proteins can be best highlighted by the presence of specialized membrane anchors in almost all coagulation factors, designed to bind to specific areas of the membrane that are rich in anionic lipids, particularly PS (58). Specifically, for the simulations presented here, we have used the GLA domain of hFVII. The GLA domain is a common membrane-anchoring domain in coagulation proteins and is known to bind to PS-rich regions of the cellular membrane. In one of our earlier reports (49), we constructed a membrane-bound model of the same anchoring domain by using steered MD (SMD) (59,60) simulations in which external forces were employed for insertion of the GLA domain of hFVII into a full DOPS membrane and the subsequent extended free equilibration. Although in that study the membrane-bound model was developed through biased simulations and computational cost permitted only one simulation (49), its comparison with the results obtained here will be helpful in further assessing the quality of the resulting structures from the HMMM simulations.

Given the efficiency of the HMMM model, the simulations of membrane insertion of the GLA domain were repeated 10 times, resulting in spontaneous insertion of the domain into the membrane in all cases. Here, we provide details of a typical scenario qualitatively describing the process for one of the simulations (Fig. 5; several additional examples are also provided in the Supporting Material). The GLA domain, initially placed in bulk water with the tip of the N-terminal ω-loop ∼8 Å away from the surface of the HMMM membrane (i.e., the headgroups of DVPS lipids; cf. Fig. 3), approaches the membrane within the first 1 ns, establishing direct interaction with the PS headgroups by its basic side chains (Arg⁹ and Lys¹⁸), leaning on the N-terminal helix side (Fig. 5, upper right). By t = 2.5 ns, the ω-loop has completely landed on, and is fully engaged with, the lipid surface (Fig. 5). The GLA domain continues its rapid insertion into the DVPS membrane, with the bound Ca²⁺ ions reaching the carboxy layer of PS lipids around 3 ns, at which point the GLA domain recovers a more upright configuration on the surface of the membrane. The structurally bound Ca²⁺ ions observed in the established membrane-bound model of the GLA domain by t = 6 ns (Fig. 5, middle right) shows a level of penetration into the membrane (converged to the level of the lipid phosphates) essentially identical to that obtained by >60 ns of SMD in a full DOPS membrane (Fig. 5 of Ohkubo and Tajkhorshid (49)).

The GLA domain completes its insertion into the membrane rather quickly during the first part of the simulation and does not further penetrate the membrane during the remainder of the simulation. Nevertheless, specific contacts between the PS headgroups and the GLA domain continue to form over a longer timescale (Fig. 5). The contact pattern between the GLA-bound Ca²⁺ ions and the PS headgroups (Fig. 6, upper) indicates that, similar to the results obtained from full-DOPS-membrane simulations (49), the HMMM model also captures two distinct roles for the GLA-bound Ca²⁺ ions. The Ca²⁺ ions located toward the periphery of the GLA domain participate primarily in direct interaction with the headgroups, whereas the ions in the middle remain buried inside the protein, thereby stabilizing the fold of the membrane anchor. The HMMM model, therefore, captures the essential features of membrane binding of the GLA domain, including the insertion depth and the orientation of the protein on the membrane as well as the specific patterns of lipid-Ca²⁺ interactions observed in full membrane systems (49). However, we also observe additional patterns of interaction between basic side chains and the headgroups in the HMMM model. For example, Lys³², which has been reported to affect membrane binding (61), forms contacts with both the phosphate and the carboxy groups in the HMMM model, whereas it did not do so in the full DOPS membrane simulation (49). We note that the above described patterns of interactions are observed in the resulting membrane-bound structures in repeated simulations, although the binding pathway and trajectory for the GLA domain are different among different simulations (Fig. S1). Consistent observation of specific interactions in different simulations using the HMMM model supports the notion that the HMMM model is effective in capturing lipid-protein interactions that were not identified using the full DOPS membrane simulation due to insufficient sampling.

Figure 6.

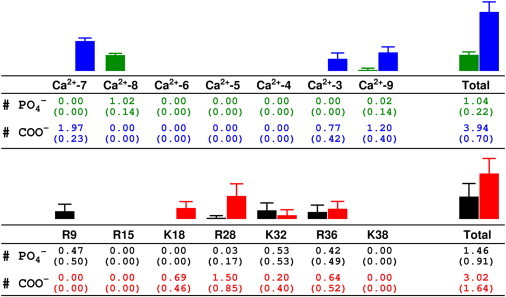
Interactions between the Ca²⁺ ions and basic residues of the GLA domain and lipid headgroups. The average number of phosphate or carboxy groups within 5.0 Å of each moiety (with the standard deviation below in parentheses) are calculated from the 30–50 ns portion of the MD simulation of hFVII-GLA and the HMMM membrane shown in Fig. 5. Color coding is the same as in Fig. 5.

Conclusions

A membrane representation for use in atomistic MD simulations of membrane-associated phenomena has been presented. This representation, termed the HMMM model, which to our knowledge is new, is based on the conceptually novel idea of “selective fragmentation”, i.e., replacing long acyl chains of lipids with an organic phase, in which the hydrophobic interactions are well represented. The atomistic details of the lipid headgroups are fully preserved by having st-lipids occupy the aqueous/organic interfacial region(s). We have demonstrated the unparalleled efficiency of this atomistic model in describing the self-assembly process of lipids into stable bilayerlike structures within several nanoseconds.

The lateral diffusion constant of the lipids in the studied HMMM membranes is in the range of 10⁻⁵–10⁻⁶ cm²s⁻¹, which exhibits an increase of one to two orders of magnitude in comparison to the conventional full-membrane representation. This improvement will allow for more efficient sampling of headgroup configurations, for example, during the binding and insertion of peripheral proteins. Using the membrane-binding domain of a coagulation protein (the GLA domain of hFVII) as an example, we have also demonstrated the robustness of the HMMM model in describing spontaneous membrane insertion of peripheral proteins and in capturing membrane-bound forms of these proteins at the all-atom level within routinely accessible simulation times. Given the efficiency of the model, we have been able to simulate the process of membrane insertion 10 times and achieved a converged picture and an unprecedented level of statistics on the lipid-protein interactions involved in this process.

The HMMM model can be readily used in MD simulations employing the standard and generalized (62,63) ensembles. The fully atomistic representation of the model makes it easy to use for any atomistic force field of choice, avoiding the need to develop a model-specific force field (64) or repeated transformation to different resolutions (65,66). Most important, the central concept of “selective fragmentation” (representing the membrane by smaller fragments) in the HMMM model may be further extended and used in other lipid structures, or even more generally in other molecular systems.

In addition to the large number of peripheral membrane proteins, the HMMM model can potentially be used for studying any membrane-associated phenomena in which atomistic details are desired but slow diffusion of the fully represented lipids is prohibitive of observing such phenomena. The immediate applications of the HMMM model include such membrane phenomena as diffusion and domain formation of lipids (67) and proteins (68,69), pore formation by (antimicrobial) peptides (65,66,70,71), hydrophobic matching of transmembrane helices (72), and membrane-associated assembly of coagulation factors (73–75). We note, however, that the HMMM model is by design not expected to reproduce all characteristics of a full membrane; in particular, mechanical properties such as volume/area compressibility and bending moduli can be only partially captured by the model (preliminary results not shown). The main purpose of the model is to provide a more flexible and mobile environment that allows for rapid rearrangement and displacement of the lipid headgroups, thereby facilitating any phenomenon that might be inaccessible with conventional membrane models due to the inherently slow dynamics of full lipids therein.

Finally, we note that the resulting membrane-bound models developed by the HMMM model can be readily converted into full-membrane representations using various molecular modeling techniques. For example, one might mutate the st-lipids into full lipids in one step or alternatively grow the lipid tails gradually (one carbon or two at a time) to their full length while subjecting the system to MD relaxations at each step. Our preliminary applications of such approaches have yielded promising results.