Geometry-Induced Bursting Dynamics in Gene Expression

Abstract

In prokaryotes and eukaryotes, genes are transcribed stochastically according to various temporal patterns that range from simple first-order kinetics to marked bursts, resulting in temporal and cell-to-cell variations of mRNA and protein levels. Here, we consider the effect of the transport of regulatory molecules on the noise in gene expression by taking into account explicitly the dynamics of a finite number of transcription factors confined in the cell. We calculate analytically time-dependent correlation functions of mRNA levels for a wide range of transport mechanisms and find that in the limit of small-transcription-factor copy number, the results differ significantly from standard approaches, which ignore confinement. It is shown how such dynamical quantities, which can now be obtained experimentally, can be used to identify the underlying mechanisms of transcription. Of particular importance, it is demonstrated that the geometry of transcription-factor trajectories in the cellular environment plays a key role in transcription kinetics, and can intrinsically generate the observed various transcription patterns ranging from simple first-order kinetics to bursts.

Introduction

Gene transcription is initiated by a series of intrinsically stochastic events of binding and unbinding of specific factors to their target sequence. These events, as well as others, such as cell division, result in fluctuations in time of messenger RNA (mRNA) and protein levels that play a key role in phenotypic variability, adaptation, and developmental transitions (1,2). Observations made possible over the last decade by new imaging techniques (3,4) show that mRNAs are produced in transcriptional patterns that depend strongly on both the gene and the cell type. For example, the transcription of constitutive genes in yeast was shown to occur in single uncorrelated events, i.e., to be well captured by simple first-order kinetics (5,6). In contrast to this simple scenario, in many cases it is found that the mRNA production occurs in bursts, which suggest more complicated kinetic schemes. In particular, transcriptional bursts seem extremely common in genes of higher eukaryotic cells (7–10). In prokaryotes, most of the data suggest that transcription is described well by first-order kinetics (3,11), although transcriptional bursts have also been observed in these cells (12).

Along with such increasing experimental evidence of variability in transcriptional patterns, it has been recognized theoretically that bursts give rise to a source of stochasticity in mRNA and protein levels that is much larger than that predicted by first-order stochastic chemical kinetics (13–16). These theoretical studies generally focus on the variance and distribution of mRNA and protein levels in the stationary state and reveal that such time-independent observables only poorly constrain transcriptional models (5,16). The microscopic origin of bursting is consequently largely undetermined, even though possible mechanisms, such as chromatin remodeling, have been proposed (2).

In this article, we discuss a prototypical model in which the limiting step in mRNA synthesis is given by the binding to the gene locus of a specific transcription factor (TF). Activation is then controlled by the distribution of the first-passage time of the TF to the target locus. It has been suggested that in many cases this transport step is a limiting factor of transcription (6), but so far, with the exception of the numerical results of van Zon et al. (17), theoretical approaches to quantify its impact on noise have been mostly restricted to classical Brownian motion (17–19) and have considered the case of a homogeneous concentration of transcription factors in infinite space.

The distribution of the first-passage time of a particle to a target in a confined volume was obtained recently for a wide range of transport processes (20) and was shown to strongly depend on the confinement and to involve a nontrivial range of timescales dependent on the geometry of the trajectories. Making use of these new tools, we quantify analytically the effect of the transport of regulatory molecules on noise in gene expression and find that in the regime of small copy numbers of TFs, the results differ significantly from those obtained by assuming a homogeneous concentration in infinite space (see Fig. 2 c). More precisely, our findings are as follows. 1), We quantify analytically the contribution of the transport step to the noise and show that, in contrast to the time-independent observables that have been the focus of most studies so far, time-dependent correlation functions, which can now be obtained experimentally (6,21), make it possible to identify microscopic mechanisms of transcription. 2), We distinguish between uncorrelated mRNA production events, which stem from an underlying Poisson process, and correlated bursts, which originate from nontrivial kinetics; we show that these two mechanisms are characterized by markedly different behaviors of correlation functions. 3), Of most importance, we show that within the framework of the model, the geometry of the TF trajectories in the cellular environment can intrinsically generate the various observed transcription patterns, ranging from simple first-order kinetics to marked correlated bursts.

Figure 2.

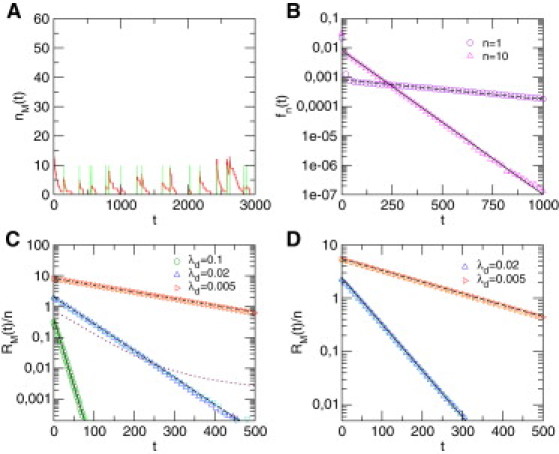
Fluctuations in mRNA level in the case of diffusion in a dilute environment, leading to noncompact exploration. The nucleus volume is $V={10}^3\mu m^3$, and we take $D=1\mu m^2/s$, and $\langle m\rangle =5$. (A) Typical evolution of the mRNA copy number, $n_M\left(t\right)$ (red line), obtained by numerical simulations of the model for n = 10, ${\lambda }_d=0.02{\text{min}}^{-1}$. Here, the nucleus is modeled as a 3-dimensional cubic lattice and $\langle T\rangle =648\text{min}$. Green bars mark the activation of the gene. (B) Waiting-time distribution, $f_n\left(T\right)$, between activation events for n = 1 (violet circles) and n = 10 (magenta triangles), compared to the theoretical prediction, derived in the Supporting Material (plain and dashed lines, respectively). (C) Normalized autocorrelation function $R_M\left(t\right)/n$ for diffusion on a 3-dimensional cubic lattice. Numerical simulations (symbols) for different values of ${\lambda }_d$ and n are compared to the theoretical prediction (plain and dashed lines). ${\lambda }_d=0.1{\text{min}}^{-1}$ (n = 1 (green circles) and n = 10 (light green crosses)); ${\lambda }_d=0.02{\text{min}}^{-1}$ (n = 1 (dark blue triangles) and n = 10 (light blue inverted triangles)); ${\lambda }_d=0.005{\text{min}}^{-1}$ (n = 1 (red triangles) and n = 10 (orange triangles)). The dotted line is obtained by assuming a homogeneous concentration $c_0=1/V$ of TFs in infinite space (case ${\lambda }_d=0.02{\text{min}}^{-1}$). (D) Normalized autocorrelation function $R_M\left(t\right)/n$ for diffusion with dilute obstacles (here modeled by a 3-dimensional supercritical percolation cluster with $p=0.8$). ${\lambda }_d=0.02{\text{min}}^{-1}$ (n = 1 (dark blue triangles) and n = 10 (light blue inverted triangles)); ${\lambda }_d=0.005{\text{min}}^{-1}$ (n = 1 (red triangles) and n = 10 (orange triangles)).

Model

We consider the basic reaction scheme in which a gene, G, when activated by a TF, produces mRNA molecules, M, at rate k (see Fig. 1). Note that strictly speaking, we consider pre-mRNA molecules and do not aim at describing the maturation process. The TFs are assumed to diffuse in a nucleus or cell of volume V, and we consider that their copy number, n, is regulated over long timescales and remains constant. The gene G is activated only when a TF is localized at the gene locus. The time, T, between successive production events of M is then a random variable (hereafter, time variables are discrete and expressed in the unit of a small elementary time step, ${\tau }_0$) whose distribution, $f_n\left(T\right)$, is governed by successive arrivals of TFs to the locus. The degradation process of a given mRNA molecule is generically described by the probability distribution, h(t), of its lifetime; in practice, we will assume a single-step reaction and write $h\left(t\right)={\lambda }_d{e}^{-{\lambda }_{d}t}$. The case of aging, where h(t) is not exponential (16), is discussed in the Supporting Material. Since the typical lifetime of mRNAs is smaller than a cell cycle, cell division can be ignored. We denote by τ the average residence time/visit at the locus, which is assumed to be much smaller than the mean waiting time between activation events, ${\langle T\rangle }_n$ (12); the number m of transcripts produced per visit is then Poisson-distributed with mean $\langle m\rangle =k\tau$. The case of larger binding times at the gene locus, which seems relevant to higher eukaryotes, can be treated in a similar manner and leads to increased noise levels. We focus on the random variable, $n_M\left(t\right)$, which gives the number of mRNA molecules in the cell at time t.

Figure 1.

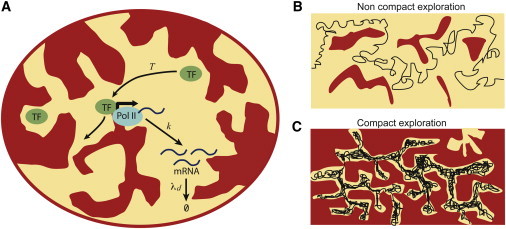
(A) Effect of the transport step on the noise in mRNA levels. A gene, G, is activated only when a TF is localized at the gene locus and produces mRNA molecules, M, at rate k. The TFs, of copy number n, are assumed to diffuse in a nucleus or cell of volume V. The space accessible to TFs is depicted in yellow and the space made inaccessible due to crowding effects in red. T denotes the random waiting time between successive production events of M, whose distribution, $f_n\left(T\right)$, is governed by successive returns of TFs to the locus. The mRNA molecules are degraded at rate ${\lambda }_d$. We will consider here both cases of eukaryotes (for which degradation generally occurs outside the nucleus) and prokaryotes. (B) Schematic TF trajectory when crowding effects are weak: the typical number of fast returns of a TF to a given site is small and the exploration of the cellular or nuclear environment is called noncompact. The production of mRNA is then shown to follow classical first-order kinetics. (C) Schematic TF trajectory when crowding effects are important, as in the case of a fractal organization of DNA: the typical number of fast returns of a TF to a given site is very large and the exploration is called compact. We show that the geometry of compact trajectories induces large correlated bursts of mRNA.

To analyze quantitatively the fluctuations of $n_M\left(t\right)$ in the stationary state, we go beyond the standard tools, which yield the variance, ${\sigma }_M^2$, of $n_M\left(t\right)$ (14,16), and focus on dynamical properties, which can be quantified by the autocorrelation function $R_M\left(t\right)=\langle n_M\left(t_0\right)n_M\left(t_0+t\right)\rangle -{\langle n_M\left(t_0\right)\rangle }^2$, where $\langle n_M\left(t_0\right)\rangle$ denotes the mean number of mRNAs in the stationary state. Denoting the Fourier transform of a given function, g, by $\hat{g}\left(\omega \right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{i\omega t}g\left(t\right)dt$, the autocorrelation function $R_M\left(t\right)$ can be derived analytically using queuing-statistics tools (22,23) and yields in Fourier space (see Supporting Material for details)

$${\hat{R}}_M\left(\omega \right)=\frac{\langle m\rangle }{{\langle T\rangle }_n}\left(1+\frac{\langle m\rangle }{2}\right)\frac{2}{{\lambda }_d^2+{\omega }^2}+\frac{{\langle m\rangle }^2}{{\langle T\rangle }_n}\left(\text{Re}\left(\frac{{\hat{f}}_n\left(\omega \right)}{1-{\hat{f}}_n\left(\omega \right)}\right)-\frac{\pi }{{\langle T\rangle }_n}\delta \left(\omega \right)\right)\frac{2}{{\lambda }_d^2+{\omega }^2}.$$ (1)

This equation elucidates the dynamics of fluctuations of the mRNA copy number, and in particular readily yields the usual static measure of noise, ${\sigma }_M^2=\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\hat{R}}_M\left(\omega \right)d\omega$. It has a clear interpretation: the first term accounts for random uncorrelated mRNA production events, whereas the second term accounts for memory effects generated by the waiting-time distribution, $f_n\left(T\right)$. In particular, it can be checked that the second term vanishes only if $f_n\left(T\right)$ is a single exponential. In that simple case, the autocorrelation function $R_M\left(t\right)$ is a single exponential and reads

$$R_M\left(t\right)=\frac{\langle m\rangle }{{\lambda }_d{\langle T\rangle }_n}\left(1+\frac{\langle m\rangle }{2}\right)e^{-{\lambda }_{d}t}.$$ (2)

This is reminiscent of the fact that the dynamics is in this case Markovian, as is generally assumed in the literature, with the notable exception of the article by Pedraza and Paulsson (16). One can then distinguish two cases. In the first case, each visit of a TF yields a small number of mRNAs, so that $\langle m\rangle \sim 1$, as observed in Zenklusen et al. (5), leading to first-order kinetics with no bursts. The second case $\langle m\rangle \gg 1$ corresponds to a standard mechanism for producing bursts (2): each visit of a transcription factor yields a large number of mRNA molecules. Note that the bursts, whose amplitude is directly controlled by $\langle m\rangle$, are then uncorrelated, since the waiting time distribution, $f_n\left(T\right)$, is exponential. This manifests itself in $R_M\left(t\right)$ decaying in time as a single exponential.

Results and Discussion

It is important to note that the assumption that the waiting-time distribution is exponential ignores the geometry of TF trajectories. Very recently, it was shown that depending on the geometry of the accessible space, the waiting-time distribution, $f_1\left(T\right)$, of a single diffusing particle to a given target site can significantly depart from a single exponential (20). Furthermore, this quantity is very different from the infinite volume limit implicitly used in works by Tkacik and colleagues (18,19) in the case of Brownian diffusion. As we now show, this results in markedly different dynamics for $n_M\left(t\right)$.

The so-called survival probability, $S_n\left(T\right)$, for n particles, i.e., the probability that the gene, activated at t = 0, remains unactivated until t = T, is readily obtained from the explicit expression of $f_1\left(T\right)$ derived in Bénichou et al. (20). One finds that $S_n\left(T\right)={\overline{S}}^{n-1}{S}_1$, where $\overline{S}$ is the survival probability of a TF averaged over all possible starting positions, which was derived in Bénichou et al. (24). The desired waiting-time distribution, $f_n\left(T\right)$, for n particles is then eventually given by $f_n=-d{S}_n/dT$. At this point, we stress that the derivation of Eq. 1 for the autocorrelation function relies on a renewal property (25). Renewal holds exactly in the case of a single TF but is approximate in the case of n TFs, as it does not account for events where several TFs are present simultaneously in the vicinity of the locus. This approximation is, however, accurate in the regime of a small TF copy number, as is checked in our numerical simulations (see Figs. 2 and 3).

Figure 3.

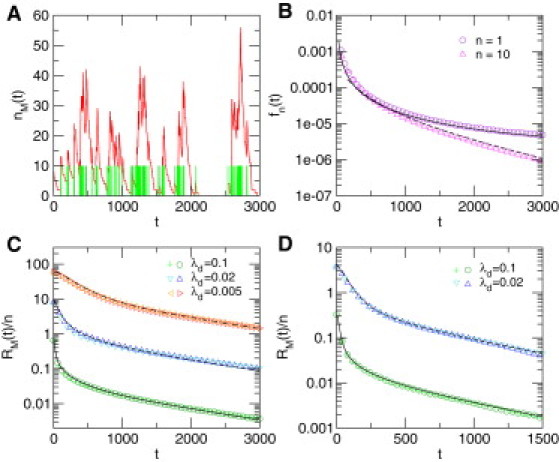
Fluctuations in mRNA levels in the case of diffusion with fractal crowding leading to compact exploration. (A) Typical evolution of the mRNA copy number, $n_M\left(t\right)$ (red line), obtained by numerical simulations of the model. The nucleus is modeled as a fractal environment (here, a 3-dimensional critical percolation cluster embedded in a 12³ cube) embedded in a volume $V=1.7{10}^3\mu {\text{m}}^3$, such that $\langle T\rangle =500\text{min}$. Other parameter values are $\langle m\rangle =5$, n = 10, ${\lambda }_d=0.02{\text{min}}^{-1}$. Green bars mark the activation of the gene. (B) Waiting time distribution, $f_n\left(T\right)$, between activation events for n = 1 (violet circles) and n = 10 (magenta triangles), compared to the theoretical prediction derived in the Supporting Material (plain and dashed lines, respectively) for the same critical percolation cluster. (C) Normalized autocorrelation function $R_M\left(t\right)/n$ for diffusion on the same 3-dimensional critical percolation cluster. Numerical simulations (symbols) for different values of ${\lambda }_d$ and n are compared to the theoretical prediction (plain and dashed lines, respectively). ${\lambda }_d=0.1{\text{min}}^{-1}$ (n = 1 (dark green circles) and n = 10 (light green crosses)), ${\lambda }_d=0.02{\text{min}}^{-1}$ (n = 1 (dark blue triangles) and n = 10 (light blue inverted triangles)), ${\lambda }_d=0.005{\text{min}}^{-1}$ (n = 1 (red triangles) and n = 10 (orange triangles)). (D) Normalized autocorrelation function $R_M\left(t\right)/n$ for diffusion on a Sierpinski gasket (example of deterministic fractal) such that $\langle T\rangle =729\text{min}$. ${\lambda }_d=0.1{\text{min}}^{-1}$ (n = 1 (dark green circles) and n = 10 (green crosses)), ${\lambda }_d=0.02{\text{min}}^{-1}$ (n = 1 (dark blue triangles) and n = 10 (light blue inverted triangles)).

As discussed in Bénichou et al. (20), on general grounds, the range of timescales involved in $f_1\left(T\right)$, and therefore in $f_n\left(T\right)$, crucially depends on the compact or noncompact nature of the transport process. This property is controlled by the geometry of the trajectories and therefore by the geometry of the accessible space. In dilute 3-dimensional environments, crowding effects are weak and the average number of visits of a diffusing particle to a given site is finite: exploration is then weakly redundant and said to be noncompact (26) (see Fig. 1). When crowding effects are important, as exemplified by diffusion in fractal environments, trajectories can become highly redundant due to multiple dead ends. The average number of visits to a given site can then be infinite, and exploration is called compact (26) (see Fig. 1). For concreteness, we will consider first the case where the accessible space has fractal properties and discuss more general cases later on. The transport process can then be parameterized by its walk dimension, d_w, defined by the scaling with time of the mean-squared displacement, $\langle r^2\rangle \propto t^{2/d_w}$ (strictly, for diffusion on a lattice, t should be taken as the number of steps), and the fractal dimension, d_f, of the medium defined by the scaling of the accessible volume with its linear dimension, $V\propto r^{d_f}$. Note that diffusion in a fractal medium is generally subdiffusive (i.e., $d_w\ge 2$). The compact case then corresponds to $d_w\ge d_f$, and the noncompact case to $d_f>d_w$ (26).

In the case of proteins in cellular and nuclear media, the existence of both compact and noncompact exploration seems to depend on protein types and their interactions with DNA. In particular, a fractal organization of the chromatin implying compact transport has been put forward by Bancaud et al. (27) and Lieberman-Aiden et al. (28). We give details of each scenario below and discuss the impact of each on the dynamics of fluctuations of the mRNA number.

Noncompact exploration

In the case of noncompact exploration, e.g., for regular diffusion in a 3-dimensional environment with weak crowding effects, the distribution of return times to the locus for n TFs can be written explicitly in the limit of large volume:

$$f_n\left(T\right)=\left(1-\text{Π}\right)\delta \left(T\right)+\text{Π}\frac{n}{\overline{\langle T\rangle }}{e}^{-nT/\overline{\langle T\rangle }},$$ (3)

where $\overline{\langle T\rangle }\sim V$ is the mean first-passage time for a single TF to the target averaged over all possible starting positions, the Diract delta function $\delta \left(T\right)$ accounts for trajectories returning to the gene locus within timescales much shorter than $\overline{\langle T\rangle }$, and $1-\text{Π}$ is the probability of such fast returns (see Supporting Material for explicit expressions of all quantities). Using Eq. 1, the following expression of the autocorrelation function is obtained:

$$R_M\left(t\right)\simeq \frac{n\langle m\rangle }{{\langle T\rangle }_1{\lambda }_d}\left(1+\frac{\langle m\rangle }{2}+\frac{\langle m\rangle \left(1-\text{Π}\right)}{\text{Π}}\right)e^{-{\lambda }_{d}t},$$ (4)

where ${\langle T\rangle }_1$ denotes the mean waiting time for a single TF. The analysis of the autocorrelation function, which differs significantly from the results obtained by assuming a homogeneous concentration of TFs in infinite space (see Fig. 2 c) therefore shows that the dynamics of mRNA is in this case very similar to the case where $f_n\left(T\right)$ is a single exponential, discussed above: it is governed only by the degradation rate, ${\lambda }_d$, of mRNA and the production events of mRNAs, of typical size $\langle m\rangle$, are fully uncorrelated (see Fig. 2).

This result has important consequences. 1), First-order kinetics with a Poisson distribution of the mRNA number is recovered in the regime of small $\langle m\rangle$, and the noise in the mRNA level is then quantified by ${\sigma }_M^2/{\langle n_M\rangle }^2=R_M\left(0\right)/{\langle n_M\rangle }^2\simeq {\langle T\rangle }_1{\lambda }_d/\left(n\langle m\rangle \right)\simeq 1/\langle n_M\rangle$. 2), The quantity ${\langle T\rangle }_1\sim V$ can be very large, which indicates that the transport step is a significant source of noise, especially in the regime of small TF copy number. For example, taking biologically relevant values for eukaryotes (see Fig. 2) indeed yields ${\langle T\rangle }_1$ of the order of hours and noise levels >1. 3), The scaling of the noise as the inverse of the mean mRNA number, here with a prefactor of order 1 (unless $\langle m\rangle$ is large), is consistent with experimental findings across various genes and even organisms (29–31). 4), Last, we note that the autocorrelation function depends linearly on the TF copy number, n, and that the dependence on $\langle m\rangle$ appears only in the amplitude of $R_M\left(t\right)$ but not in its time dependence.

Compact exploration

In the case of compact exploration, as exemplified by diffusion in fractal environments, the distribution of return times to the gene locus can be asymptotically written in the limit of large volume:

$$f_n\left(T\right)=\left(1-\text{Π}\right)\delta \left(T\right)+\text{Π}\sum _{i=1}^{\mathrm{\infty }}{\alpha }_i{e}^{-{\beta }_{i}nT/\overline{\langle T\rangle }},$$ (5)

where $\overline{\langle T\rangle }\sim V^{d_w/d_f}$ is again the mean first-passage time for a single TF to the target averaged over all possible starting positions (see Supporting Material for explicit expressions of Π and the constants ${\alpha }_i,{\beta }_i$). In this case the autocorrelation function can be written in Fourier space using Eq. 1. Due to the wide spectrum of timescales involved in $f_n\left(T\right)$, fluctuations are clearly non-Poissonian in this case and display large correlated bursts even for $\langle m\rangle$ small (see Fig. 3). The major difference from the noncompact case is that in the compact case the probability Π of long waiting times is extremely small (see Supporting Material) so that repeated fast returns to the gene locus are very likely and eventually collectively contribute to large bursts of mRNA. This amplification mechanism has a clear signature in the autocorrelation function, which is in marked contrast to the Poissonian case: it shows two different timescales, one of order $1/{\lambda }_d$, characterizing the burst duration, and one controlled by $\overline{\langle T\rangle }\sim V^{d_w/d_f}$, stemming from the waiting times between successive bursts. More precisely, in the long time regime the autocorrelation function decays as a series of exponentials whose characteristic times are all of the order of magnitude of $V^{d_w/d_f}$ (see Supporting Material). This shows finally that in the case of compact exploration, the very geometry of TF trajectories has a striking impact on mRNA dynamics and is at the origin of a mechanism generating large correlated bursts, which constitutes a central result of this study.

Several comments are in order. 1), The correlated bursts that we describe for compact transport are very different by nature from bursts that result only from the production of a large amount of mRNA at each visit of a TF. The latter case, which corresponds to $\langle m\rangle \gg 1$, leads to uncorrelated bursts that are characterized by an autocorrelation function with a single-exponential decay, as shown by Eq. 2. 2), The resulting noise in the mRNA level can be obtained and reads ${\sigma }_M^2/{\langle n_M\rangle }^2\sim {\langle T\rangle }_1/\left(n{\tau }_0\right)\sim {\left({\lambda }_d{\tau }_0\right)}^{-1}/\langle n_M\rangle$, where ${\langle T\rangle }_1\sim V$ can be very large. Taking biologically relevant values for eukaryotes (see Fig. 3) yields ${\langle T\rangle }_1$ of the order of hours and typical noise levels >10, which is much larger than in the noncompact case. 3), The scaling of the noise as the inverse of the mean mRNA number is recovered and is similar to the noncompact case. However, the prefactor ${\left({\lambda }_d{\tau }_0\right)}^{-1}$ can be large in the compact case and depends more strongly on the gene, as seems to be the case for eukaryotes (10). 4), The dependence of the autocorrelation function on n and $\langle m\rangle$ is similar to that in the noncompact case: it affects only the amplitude of the autocorrelation function but not its time dependence. In particular, it is linear in n, as illustrated in Fig. 3 (see Supporting Material for a derivation of this property).

The analysis above clearly illustrates the importance of the geometry of TF trajectories in the dynamics of mRNA levels. This result is in fact robust and remains unchanged for a broad class of transport processes. More precisely, the discussion above makes it clear that the mechanism of burst amplification relies on the occurrence with high probability of short timescales in the waiting-time distribution, $f_n\left(T\right)$, so that the hypothesis of a compact-scale invariant process made above can be relaxed and in fact only needs to hold over a given length or timescale, which only needs to be long enough to allow for multiple returns. In particular, our analysis shows that burst amplification can occur in environments that are fractal only over a finite range (as in the examples of Fig. 3), as is observed for the nuclear medium (27). This mechanism also applies to TFs whose trajectories, because of nonspecific interactions with DNA, are best described by a mechanism usually termed facilitated diffusion (32–34), that combines phases of compact sliding on the DNA and phases of noncompact bulk excursions (see, e.g., (35–39) for experimental evidence). The waiting-time distribution, $f_n\left(T\right)$, for facilitated diffusion can be obtained analytically according to the methods of others (34,40–42) and proves to be well approximated in the limit of long DNA length (compared to the average DNA length explored during a sliding phase) by the functional form described in Eq. 5. Π in this case denotes the weight of the long timescales, which is extremely small, since the compact property of sliding favors successive fast rebinding events to the gene locus (43). The dynamics of mRNA synthesis is then very similar to the compact case above: correlated bursts of mRNA of amplitude much larger than $\langle m\rangle$ emerge due to the repeated fast returns of the TFs to the gene locus, and the mRNA dynamics can be characterized by the emergence of two timescales in the autocorrelation function. We note also that the very nature of the nonspecific TF/DNA interaction was shown to yield in some cases a marked timescale separation leading to a waiting-time distribution, $f_n\left(T\right)$, similar to that in Eq. 5 (41,44).

Finally, our analysis underlines the importance of the geometry of TF trajectories and reveals the role of correlations induced by the statistics of returns. One could expect that in the case of multiple target genes regulated by the same TFs, correlations of expression levels could arise in the compact case due to a similar mechanism. This would be at work only if genes are close to each other, i.e., colocalized, which seems consistent with the available experimental data (45).

Conclusion

To conclude, autocorrelation functions of mRNA levels, which can now be obtained experimentally (6,21), carry clear signatures of the underlying mechanisms of transcription, as opposed to the classical static measures of noise. The geometry of TF trajectories, namely, their compact or noncompact nature, can generically generate markedly different transcription patterns ranging from first-order kinetics to correlated bursts, as observed in vivo. The compact or noncompact nature of transport strongly depends on the geometry of the cellular or nuclear environment as probed by TFs, and therefore on the nonspecific affinity for TFs with DNA, which we suggest could be used as a regulating parameter. Overall, our results highlight the importance of determining the geometry of in vivo TF trajectories, which was initiated recently (27).