Abstract
Modeling the transport of solutes through fluidic systems that have adsorbing surfaces is challenging due to the range of length and time scales involved. The components of such systems typically have dimensions from hundreds of nanometers to microns, whereas adsorption of solutes is sensitive to the atomic-scale structure of the solutes and surfaces. Here, we describe an atomic-resolution Brownian dynamics method for modeling the transport of solutes through sticky nanofluidic channels. Our method can fully recreate the results of all-atom molecular dynamics simulations at a fraction of the computational cost of the latter, which makes simulations of micron-size channels at a millisecond time scale possible without losing information about the atomic-scale features of the system. We demonstrate the capability of our method by simulating the rise and fall of solute concentration in sub-micron-long sticky nanochannels, showing that the atomic-scale features of the channels’ surfaces have a dramatic effect on the kinetics of solute transport in and out of the channel. We expect our method to find applications in design and optimization of micro and nanofluidic systems for solute-specific transport and to complement existing approaches to modeling lab-on-a-chip devices by providing atomic scale information at a low computational cost.
Introduction
Lab-on-a-chip technologies exploit miniaturization to create integrated systems that exceed their table-top predecessors in functionality by offering extreme parallelism while performing individual tasks more quickly and decreasing consumption of reagents and energy. Such integrated miniaturization of technology opens up a whole new range of applications1,2, including systems for epigenetic analysis3,4, protein crystallography5, low-cost DNA sequencing6,7, and direct, quantitative study of interfacial phenomena like adsorption8. By and large, development of lab-on-a-chip systems is enabled by advances in micro- and nanofluidic technologies. However, as the elements of microfluidic systems are miniaturized, the surface to volume ratio is increased until surface–solute interactions cannot be ignored. This offers opportunities for new functionality while also giving rise to new bottlenecks and failure mechanisms1. The new functionality can only be exploited with accurate models that assist in optimizing device design.9
Although the physics of micro and nanofluidic systems is well understood10–12, there is no one theoretical model that can accurately describe all parts of the system9. The variety of time and length scales of the pertinent physical phenomena calls for specialized techniques to model different parts of a lab-on-a-chip device9. For example, continuum appproaches can accurately describe pressure or electric field-driven fluid flow through micro and nanofluidic channels11–13, but break down in the regions of fluid near surfaces12 or macromolecules14, where the atomic-scale properties of the solvent, solutes and surfaces are important15,16.
One particular problem of interest is adsorption of solutes to the walls of a microfluidic system. As the surface-to-volume ratio of microfluidic channels increases, adsorption of analyte or reagent can degrade device performance. Adsorption limits the rates with which the concentration of solutes in microfluidic compartments can be increased or decreased without contamination, and, in extreme cases, can cause clogging of the channels and failure of the entire device1,17. In contrast, adsorption of specific solutes in designated areas of a device can be intentional and play a functional role in the device. A device possessing controllable sorptive regions can be used to precipitate particular solutes from a mixture, impose concentration gradients, catalyze chemical reactions, etc. Modeling such phenomena requires a method with exquisite sensitivity to atomic-scale details of the surface and the solute, such as classical all-atom molecular dynamics (MD).
The MD method has the advantage of being capable of explicitly evaluating inter-particle interactions accounting for contributions from every atom of the system18. This method has been extensively used to simulate biological macromolecules19–21, and conventional22 and hybrid materials23–25. Recent advancements in the development of inorganic force fields compatible with the all-atom MD description of biomolecules26–30 have made it possible to computationally model the interactions of biomolecules with inorganic substrates with atomic precision28,30–36. However, the accuracy of MD comes at a high computational cost, making this method impractical for simulations of up-to-scale models of micro and nanofluidic systems. Several methods have been proposed to increase the computational efficiency of particle-based simulations37–40, but improvements in computational efficiency usually require some loss of atomic-scale precision in the evaluation of inter-particle forces.
In this manuscript, we present an efficient computational method for modeling the transport of solutes through nanochannels with sticky surfaces. Building on previous work in this area41–43, we describe a microfluidic system using the Brownian dynamics (BD) method44 parameterized through all-atom MD simulations. Our method allows simulations of realistic nanofluidic systems to be performed while retaining atomic-scale precision in the description of solute-solute and solute-surface interactions. Below we demonstrate the accuracy of our method through comparison with the results of all-atom MD simulations and apply our method to simulate experimental-scale channels. We expect our method to be of immediate use for design and optimization of micro and nanofluidic systems for solute-specific transport and to complement existing methods of modeling lab-on-a-chip devices9 by providing atomic scale information at a low computational cost.
Results and Discussion
In this section, we describe our atomic-resolution BD method for modeling the transport of small solutes through sticky nanochannels and validate the method through comparison with the results of conventional all-atom MD simulations. Following that, we demonstrate the capability of our method by performing a sub-millisecond simulation in which a half-micron-long sticky nanochannel is filled with and then drained of solutes transported with the water flow. In this type of simulations, the channel always remains filled with the solution while the concentration of dissolved solutes vary. Furthermore, we show that the atomic-scale features of a nanochannel’s surface can have a dramatic effect on the rate the concentration of solute rises and falls in the channels. In all simulations, we use dimethyl methylphosphonate (DMMP) as a model solute.
Formulation of the BD method
Transport of a small solute through a micro or nanofluidic system combines the diffusion of the solute in the solvent, drift of the solute with the flow of the solvent and adsorption/desorption of the solute to/from the walls of the system. In our atomic resolution BD method, we describe these transport modalities with atomic-scale precision by extracting the essential parameters for the model from all-atom MD simulations. By eliminating the need to explicitly simulate the solvent and the nanochannel material, our method permits simulations of transport with atomic-scale resolution at a fraction of computational cost of all-atom MD, simultaneously expanding the spatial and temporal range of atomic-scale simulations from tens of nanometers and single-digit microseconds to microns and milliseconds. In our BD method, trajectories of individual solute particles are found by applying the following update rule:45
| (1) |
Here, ri(t) is the position of solute i at time t, Δt is the integration timestep, D is the diffusion coefficient, vflow(ri) is the local velocity of the solvent, F is the force on molecule i and R is a vector of independent normal deviates with a mean of zero and a standard deviation of one. The last term in Eq. 1 produces random displacements of the solute, mimicking the stochastic force of the solvent.
To capture atomic-scale information in our model, the diffusion coefficient D and force F are derived from all-atom MD simulations. The diffusion coefficient D can be calculated directly from MD simulations, as we have done previously for DMMP in water15. Here, we use the same diffusion coefficient everywhere in the system, but it is also possible to implement a position-dependent diffusion coefficient46,47 to better describe diffusion in close proximity to the walls of the channel.
For several simple geometries, the flow velocity in a nanochannel vflow(r) can be obtained analytically 48. For more complicated geometries, the flow profile can be computed numerically using a variety of methods9,49. It is also possible to obtain the flow velocity directly from all-atom MD simulations50 Thus, using the all-atom MD method, we have previously shown that pressure-driven flow of water through a silica nanochannel is accurately described by the Poiseuille formula50, excluding the region immediately adjacent to the silica surface (< 0.5 nm), where a boundary layer of liquid molecules is much less mobile than predicted by the Poiseuille expression16,51–54. Hence, we use the following analytic expression for vflow(r):
| (2) |
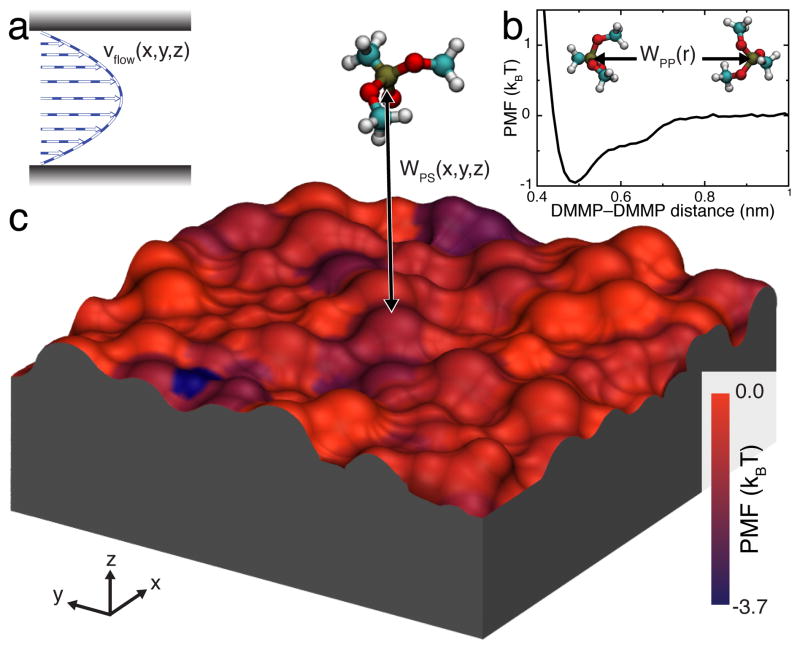
where v0 = (−∇p)h2/8η is the peak velocity (in the center of the channel), η is the viscosity, ∇p is the pressure gradient, h is the nanochannel height, and ẑ is the unit vector normal to the nanochannel’s surfaces. Here, the coordinate system is defined so that r · ẑ = 0 at the center of the nanochannel. The velocity profile of such flow is schematically shown in Figure 2a. In this work, we consider a pressure-driven flow but other flow patterns, such as plug flow13, can be easily incorporated into our model.
Fig. 2.
Elements of our BD approach to modeling solute transport through sticky nanochannels. a Representative profile of a pressure-driven flow through a nanochannel. b 1D-PMF between two DMMP solutes in water. c 3D-PMF of a DMMP solute in proximity to a silica surface. The silica slab is shown as a molecular surface colored by the local minimum value of the PMF in the direction normal to the slab. Both 1D and 3D PMFs were derived from all-atom MD simulations.
In our approach, the force on a solute F has two sources: the interaction with other solutes WPP; and the interaction with the channel’s surfaces WPS. Thus,
| (3) |
where WPP and WPS are solute-solute and solute-surface potentials of mean force (PMFs). The PMF between a solute and a surface (or a second solute) represents the change in free energy upon bringing the solute from a distant point to a particular position with respect to the surface (or the second solute), and includes all electrostatics, van der Waals, entropic, and solvation effects.
Figure 2b shows the PMF of the DMMP–DMMP interaction, computed from all-atom MD simulations using the umbrella-sampling55 and weighted histogram analysis56 methods. Details of all PMF calculations are given in the ESI†. WPP has a shallow (< 1 kBT), short-range attractive well and a steep excluded-volume repulsive part at short distances. The depth of the minima is in agreement with the results of our MD simulations, where no aggregation of DMMP was observed15.
Figure 2c illustrates the 3D-PMF of DMMP in proximity to a representative patch of a silica surface. The silica surface is colored by the local minimum value of the PMF for each (x,y) point, revealing the heterogeneous nature of the solute–surface interaction. The 3D solute–surface PMF was computed from all-atom MD simulations using a generalization of umbrella-sampling and weighted histogram analysis methods. The details of the calculations are described in the ESI† and in Carr et al.15
Note that in our all-atom calculations of both WPP and WPS, the rotational degrees of freedom of the solute are averaged out as the time scale of the solute rotation (trot < 100 ps for a full 2π spin of DMMP57) is much smaller than the length of a typical MD simulation in one of the umbrella-sampling windows (tsampl >3 ns). Solutes that satisfy trot ≪ tsampl condition are considered here as ”small”. In the form presented here, our atomic-resolution BD method is applicable only to those chemical compounds for which the above condition holds.
Validation of the BD method
We validate our BD method through comparison with the results of conventional all-atom MD simulations. Due to the time and length scale limitations of the latter method, the validation simulations were performed using relatively small nanochannel systems of 10 × 10 × 5.5 nm3. This system is small enough to be computationally tractable and large enough to exhibit bulk fluid velocities50, thus incorporating both near-surface and bulk effects.
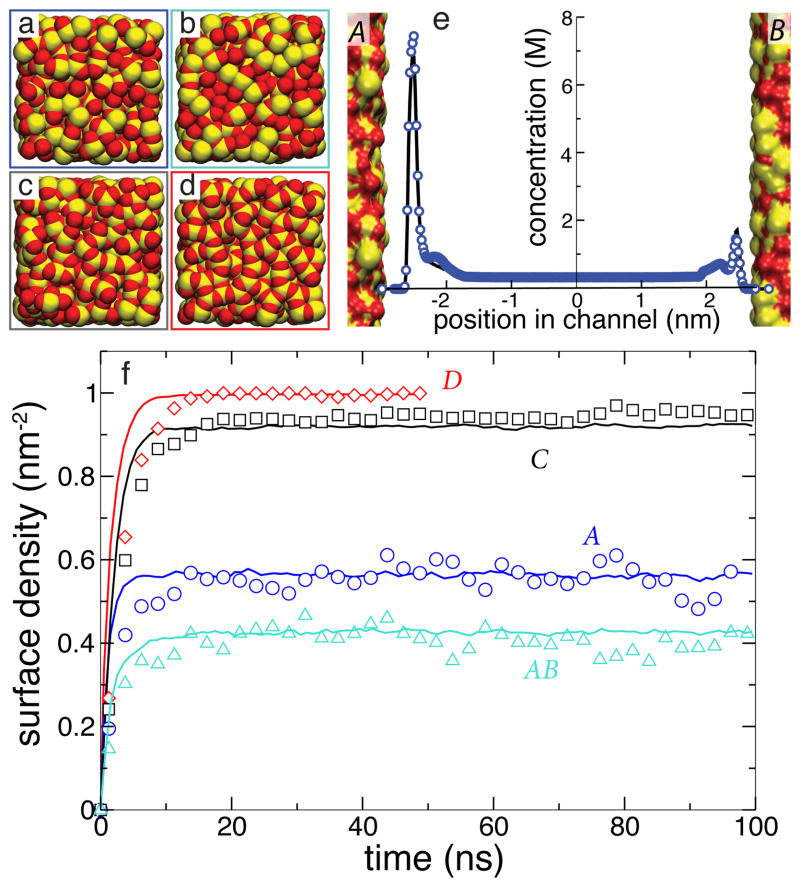
Each all-atom system contained an infinite-slit silica nanochannel filled with 0.6 M aqueous solution of DMMP, shown in the left part of Figure 1. Each surface of the nanochannel was built by tiling 16 identical slabs of amorphous silica 2.5 × 2.5 nm2 in area into a square. Figure 3 ad shows the four different silica tiles that we used to build nanochannels A, AB, C, and D. Each tile has different arrangement of its surface atoms, giving each surface a different overall affinity to DMMP 15. The nanochannels were created by placing two silica slabs 5.5-nm (surface to surface) apart and filling the gap with a pre-equilibrated solution of DMMP. Nanochannels A, C, and D were made using two identical surfaces A, C, or D, respectively; nanochannel AB was made using surfaces A and B, see Figure 3e. Under periodic boundary conditions, the nanochannels were effectively infinite in two dimensions. Flow of the DMMP solution was induced in the channel by imposing a pressure gradient across the system 50. The velocity of the flow was found to have a negligible effect on DMMP adsorption to the surface of the channel 15. A complete description of the protocols used to build and simulate our all-atom models is available in the ESI†.
Fig. 1.
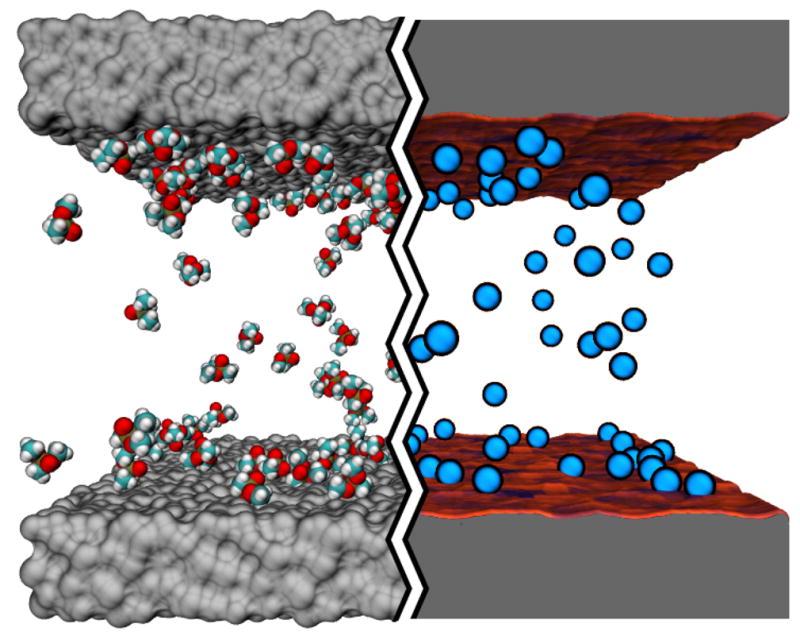
Atom-resolution models of small solute transport through a nanochannel. The left hand side of the image illustrates a conventional all-atom MD model: the silica walls of the nanochannel are shown as grey molecular surfaces, the solutes (DMMP) are shown in space-filling representation (C teal, O red, P tan and H white); water is not shown. The right hand side of the image illustrates our atomic-resolution BD model that describes the walls of the nanochannel by means of a three-dimensional potential of mean force (3D PMF) computed at atomic resolution. The walls of the nanochannel are shown as molecular surfaces colored according to the local values of the 3D-PMF (see also Figure 2). The solutes are shown as blue spheres.
Fig. 3.
Surface adsorption of DMMP solute simulated using our BD and all-atom MD models of the same nanochannels. a–d All-atom models of four silica surfaces (A–D) used in our simulations of DMMP adsorption. Oxygen and silicon atoms are shown as red and yellow vdW spheres, respectively. e Steady-state concentration profile of DMMP across the AB nanochannel. f Surface density of DMMP adsorbed at the walls of four nanochannels versus simulations time. The BD data (solid lines) were averaged over 25 unique trajectories that began having the same coordinates of DMMP as the corresponding MD simulation (symbols).
Figure 3f plots the average density of DMMP molecules adsorbed to the walls of the nanochannels as a function of time in the MD simulations of nanochannels A, AB, C and D (symbols). In less than 15 ns, each system reaches a steady state. Note that although all surfaces are made from the same material (silica), different arrangement of the surface atoms leads to different amounts of DMMP adsorbed in the steady state 15.
To use the results of the above simulations as a test of our BD method, a BD model of each all-atom nanochannel system was built by replacing each DMMP molecule by a BD particle and each nanochannel surface by the corresponding 3D-PMF potential. To make an unambiguous comparison possible, each BD system had exactly the same dimensions as the corresponding MD system and the same initial coordinates of the DMMP particles were used. The right part of Figure 1 shows one of the systems used for these BD simulations.
The average density of adsorbed DMMP particles observed in 25 BD simulations (using different seeds for the random number generator) of each of the four nanochannels is plotted versus time in Figure 3f. The plot indicates excellent quantitative agreement between BD and MD methods in predicting the steady-state surface density of adsorbed DMMP solute and good quantitative agreement in predicting the kinetics of the adsorption process. Figure 3e shows that the BD method can also quantitatively reproduce partitioning of DMMP in nanochannel AB that combined two surfaces of different affinities (A and B).
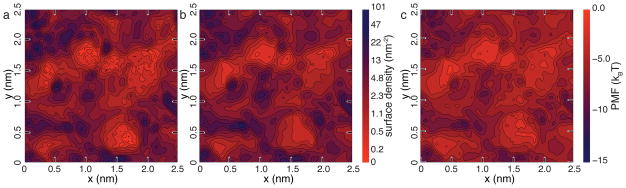
To determine if the BD model is capable of reproducing the atomic scale features of different silica surfaces, we computed the 2D density maps of adsorbed solutes for all four surfaces considered. Figure 4a and b shows the steady-state adsorption density maps for surface C; the plots for all four surfaces are available in the ESI†. Close inspection of the two maps reveals excellent quantitative agreement between the BD and MD methods. As the spatial resolution of the maps is 0.42 × 0.42 Å2, we can say with confidence that our BD method has truly achieved atomic resolution.
Fig. 4.
Atomic-scale features of DMMP adsorption. a, b Surface density maps of adsorbed DMMP in our MD (panel a) and BD (panel b) simulations of nanochannel C. The maps were computed by averaging over the steady-state parts of the corresponding trajectories and over the identical patches of the corresponding surfaces. The BD simulations quantitatively reproduce the results of the all-atom MD simulation. Note the use of logarithmic scale in coloring the surface density patterns. c Local minima of the solute-particle PMF near the surface of the nanochannel. The pattern of DMMP adsorption in both MD and BD models closely follows the pattern of the PMF minima. Similar plots for nanochannels A, B and D are available in the ESI†, Figure S1.
Figure 4c shows a 2D map of the local PMF minima near surface C, computed for each point on the surface along the line normal to the surface plane. As expected, the pattern of adsorption density, Figures 4a and b, closely matched the pattern of PMF minima, Figure 4c.
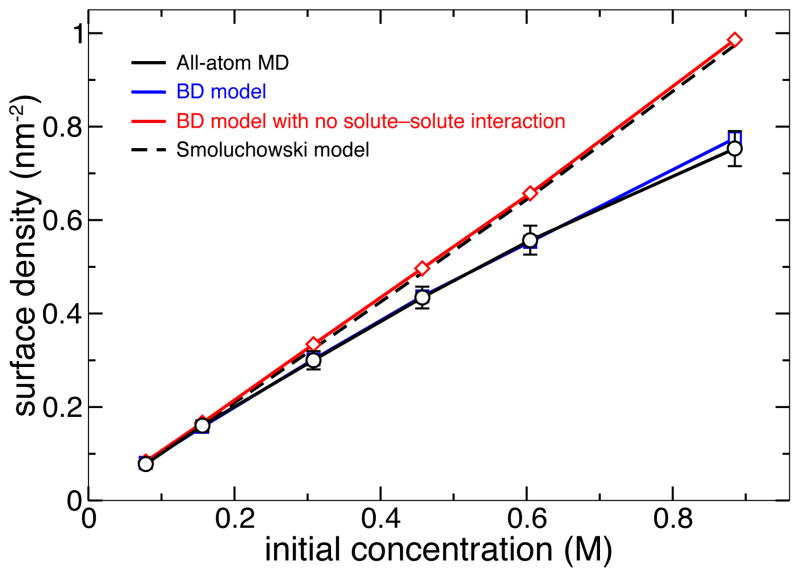
Figure 5 plots the dependence of the steady-state DMMP surface density on the initial concentration of DMMP particles in nanochannel A predicted using both the all-atom MD and atomic-resolution BD methods. Again, we find the predictions of both methods to be in quantitative agreement with each other. In general, the simulated adsorption isotherm of DMMP on silica was found to be in agreement with the Langmuir model of adsorption15. We note, however, that in the absence of the solute-solute interaction potential WPS, the BD model predicts a linear dependence between the average surface density of adsorbed solute and the bulk concentration of DMMP, which overestimates the amount of adsorbed DMMP at high concentrations.
Fig. 5.
Surface density of adsorbed DMMP versus its initial concentration in nanochannel A predicted using different simulation methods. Including the solute-solute interaction (Figure 2b) is essential for proper description of the adsorption isotherm using the BD model at high concentrations. Each BD data point represents the average of 25 independent trajectories; the error bars for the BD data are smaller than the symbols. The 1-D Smoluchowski model was based on the atomically precise 3D-PMF. Detailed description of the Smoluchowski model is provided in the ESI†.
Finally, we compare our BD method with the following two alternative approaches: numerical solution of the Smoluchowski equation58 and implicit solvent simulations37. The test of the Smoluchowski approach was performed using a one-dimensional projection of the 3D-PMF obtained by averaging out the latter (see the ESI†). The dependence of the steady-state adsorption density on the bulk concentration of DMMP is shown in Figure 5. The results of the Smoluchowski model quantitatively match the results of the BD and MD simulations at low solute concentrations, but deviate at higher concentrations as the Smoluchowski model neglects solute-solute interactions. We have also simulated adsorption of DMMP on silica using all-atom implicit-solvent MD. If compared to explicit-solvent MD, the use of implicit solvent did not cause a dramatic improvement in the computational efficiency of the simulations. Furthermore, the implicit solvent model of DMMP transport through nanochannel systems failed to reproduce the results of the all-atom MD simulations. A complete discussion of the implementation and results of the Smoluchowski and implicit-solvent MD models is provided in the ESI†.
Modeling transport at experimental spatial and temporal scales
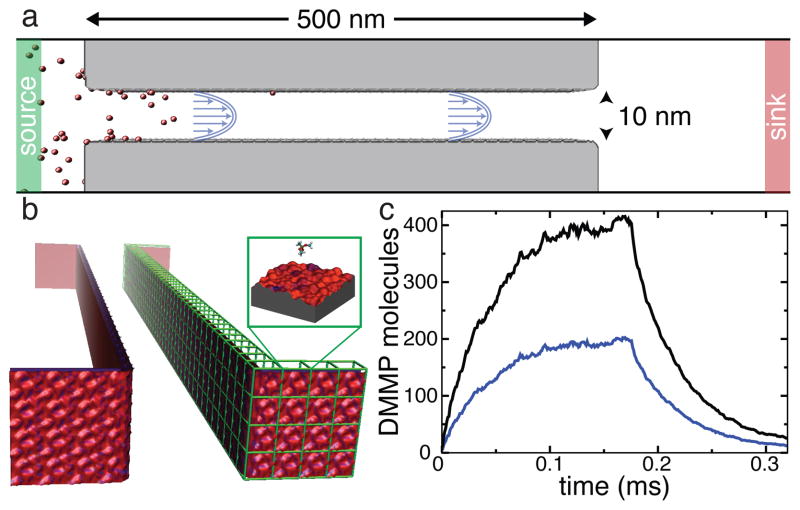
To demonstrate the ability of our method to bridge the angstrom and micron scales, we have constructed computational models of silica nanochannels 100- and 500-nm in length and simulated the process of filling the nanochannels with DMMP solutes and their subsequent removal by the flow of the solvent.
Figure 6a illustrates a typical setup of these simulations. The particular channel shown is 500 nm in length, 10 nm in width and is effectively infinite in the plane normal to the figure due to the use of periodic boundary conditions. In our BD simulations of the experimental-size channels, the total number of particles in the system can change as the simulation progresses. Two buffer regions away from the channel’s inlets (labeled source and drain) maintain the prescribed concentrations by an algorithm that can add or remove particles to the buffers if the number of particles in the buffer differs from the target. The latter is randomly selected from the Poisson distribution with the mean set at the prescribed number. Doing so not only maintains the desired average concentration of solutes in the buffer region but also introduces fluctuations in the buffer concentration consistent with the statistical mechanics of noninteracting particles in a uniform region. Systems that included constant concentration buffers were not periodic in the direction of the flow.
Fig. 6.
Atomic-resolution BD simulation of the rise and fall of DMMP concentration in a sticky 0.5 μm-long silica channel. a Diagram illustrating the setup of a BD simulation. The walls of the channel are shown in gray, the solute particles are shown in red. Green and red regions indicate the source and sink reservoirs where the concentration of solute is maintained constant. The channel is not drawn to scale. b 3D-PMF representation of the surface of the nanochannel, obtained by combining atomically precise 3D-PMF maps of a representative patch of the surface (such as the one shown in Figure 2c). c Sub-millisecond simulation of the rise and fall of solute concentration (see text for details). The total number of DMMP solutes in the nanochannel (black) and number of DMMP adsorbed to the nanochannel’s walls (blue) are plotted versus time.
Figure 6b illustrates our approach to modeling large nanochannels using atomic resolution 3D-PMF maps. For this particular simulation, a 2.5 × 2.5 nm2 patch of the 3D-PMF grid of surface A was used to tile the entire surface of the 500-nm-long nanochannel, including the surfaces that face the buffer regions (1664 tiles in total). It might also be possible to generate non-periodic statistical models of the channel’s surface using a 3D-PMF map of its representative patch.
In the initial state of the process considered, the channel is already filled with the solvent but no DMMP solute is present. To simulate the process of filling the channel with DMMP solute, at the beginning of the simulation the concentration in the source reservoir was set to 10 mM. The particles entered the nanochannel through a mix of diffusion and drift; the solvent flow was modeled implicitly as a Poiseuille flow, Eq. 2, with a peak velocity of v0 = 0.005 nm/ns in the center of the channel. Outside the channel, the solvent had a uniform velocity of 2v0/9, consistent with a constant mass current of solvent through the system. As DMMP molecules exited the nanochannel on the opposite side, they were absorbed by a second reservoir that maintained a zero concentration.
Figure 6c plots the total number of molecules in the channel along with the number of molecules adsorbed to its surface during the course of the simulation. The plot indicates gradual accumulation of the solutes in the nanochannel with roughly half of the molecules being adsorbed at its surface. At about 0.12 ms, the simulation reaches a steady state, where the rate of adsorption equals to the rate of desorption. After 0.176 ms from the beginning of the simulation, the concentration of DMMP in the source compartment was set to zero so that process of DMMP removal from the channel could be observed. At the end of the simulation, which spanned over 0.3 ms, the channel is almost devoid of solutes. Solutes attached to the front and back sides of the channel (the sides facing the buffer compartments) were not included in the above analysis.
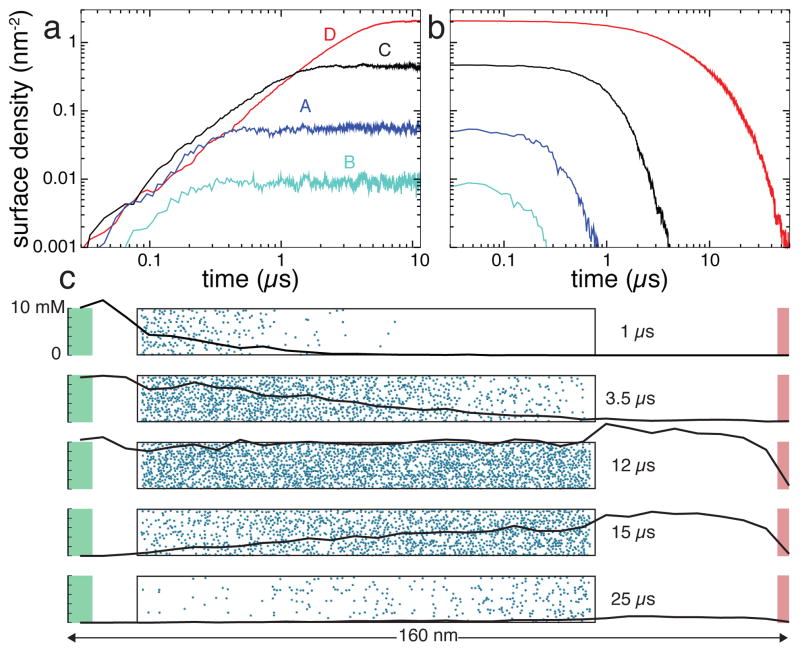
To demonstrate the effect of the atomic-scale features on the transport of solutes through sticky sub-micrometer channels, we built four BD models of a 100-nm-long channel, each tiled using one of the four 3D-PMF maps of the surfaces shown in Figure 3a–d. Following the same protocol as in the above simulation of the 500-nm channel, we simulated the rise and fall of DMMP concentration in the four channels, assuming the peak velocity of the Poiseuille flow in the channel v0 = 1 nm/ns.
Figure 7 presents the results of these simulations. Figure 7a and b show the number of solute molecules adsorbed to each channel’s surface as a function of time in the simulations of the filling the channels with DMMP solutes (a) and removal of the DMMP solutes from the channel (b). Each simulation shown in Figure 7a started with having no solutes in the channel and the concentration of DMMP in the source buffer set to 10 mM. At the beginning of the draining simulations, Figure 7a, the target concentration of the source compartment was set to zero. Prior to the beginning of the draining simulations, each system was simulated in a steady state for a period that varied between 2 to 10 μ s, in addition to first 10 μ s shown in Figure 7a.
Fig. 7.
The effect of the atomic-scale features on the transport of small solutes through experimental-scale nanochannels. a,b Atomic-resolution BD simulations of the filling (a) four 100-nm-long silica nanochannels with DMMP and subsequent removal (b) of DMMP from these channels. The four channels have different atomic-scale features of their surfaces (shown in Figure 3a–d). Note the logarithmic scale of the plots. c The rise and fall of DMMP concentration in nanochannel D. Each of the five snapshots characterizes the state of the system at a different instance of the BD simulation. The nanochannel is shown as a transparent box with adsorbed molecules in blue. The black line shows the profile of DMMP concentration through the system, from the particle source (shown in green) to the sink in red, not including solute bound to the nanochannel surface.
Figure 7a and b clearly show that the atomic-scale features of the channels’ surfaces determine not only the amount of DMMP adsorbed, but also the time it takes to both rise the concentration of DMMP to the steady-state levels and to remove DMMP from the channels. Thus, the amount of DMMP adsorbed in the steady state of the simulation differs by more than two orders of magnitude. Filling channel D with DMMP takes about 10 times longer than filling channel B. The time scale of the removal of DMMP from these channels differ by more than two orders of magnitude.
Figure 7c details the simulation of the channel lined with surface D, the surface that has the highest affinity to DMMP among the four considered here. The five plots characterize the state of the system at different instances of this simulation. As the channel begins to fill in with DMMP (t = 1 μs), the solute binds to the surface at the inlet of the channel. Halfway to reaching a steady state (t = 3.5 μs), the concentrations of DMMP in the bulk of the channel and at its surface exhibits a linear drop in the direction of the flow. In the steady state (t = 12 μs, not shown in Figures 7e or f), both bulk and surface concentrations of DMMP are uniform. Halfway in the process of DMMP removal (t = 15 μs), the concentration of DMMP linearly increases in the direction of the flow. Near the end of the simulation (t = 25 μs), no DMMP is left in the bulk of the channel, although some amount of DMMP appears to still be bound to the channel’s surface.
The computational efficiency of the BD simulations depends on the number of particles explicitly considered in the simulation. Thus, in our BD simulations of 100-nm channels B and D, which contained 420 and 5100 particles, respectively, we obtained 12,400 and 610 ns per day using 6 cores of a multicore workstation (AMD 2.1GHz ). This compares very favorably with the simulation speed of all-atom MD, which was 14 ns per day on 288 processors for a system 100 times smaller in volume than the 100-nm channels.
Conclusions
In this manuscript, we have presented a computational method for accurate description of small solute transport through nanofluidic channels that have surfaces of non-negligible affinity to the solutes. While no one theoretical model is capable of describing every aspect of transport in micro-and nanofluidic systems9, our model complements the existing techniques by bridging continuum hydrodynamics with atomic-scale structures of surfaces and solutes. If compared to conventional all-atom MD, our method offers orders of magnitude improvement in computational efficiency by eliminating the need to simulate atoms comprising the solvent and the walls of the nanochanel. Compared to conventional BD methods, our method preserves atomic scale resolution in evaluation of solute-solute and solute-surface interactions.
We believe that the accuracy and efficiency of the method presented here will open new possibilities for design and optimization of lab-on-a-chip systems. For example, one can envision fabrication of patterned surfaces that have differential affinity to specific solutes and using such surfaces in fluidic systems for high-throughput screening, drug design, combinatorial chemistry, catalysis, and purification. Furthermore, embedding electrodes in proximity to the channels’ surfaces can offer the means to electrically tune affinities of specific solutes to specific surfaces59,60 and thereby control the adsorption and desorption processes. Using the method described in this manuscript, such novel lab-on-a-chip systems can be designed and tested on a computer.
Methods
MD simulations
All MD simulations were performed using the program NAMD61, a 1 fs integration time step, particle mesh Ewald (PME) electrostatics62, and periodic boundary conditions. Simulations in the NPT ensemble (constant number of particles N, pressure P and temperature T) were performed using a Langevin thermostat63 and Nosé-Hoover Langevin piston pressure control64 set at 295 K and 1 atm, respectively. The damping coefficient of the Langevin thermostat was 1 ps−1 and was applied only to the atoms of the silica surfaces. A smooth (1.0–1.2 nm) cutoff was used to compute the Lennard-Jones forces. All simulations were performed using the TIP3P water model modified for the CHARMM65 force field and a CHARMM-compatible model for silica26. A complete description of the simulation setup and analysis was reported previously in Carr et al.15, and is available in the ESI†.
BD simulations
All BD simulations were performed using a custom multithreaded code developed in-house. The integration timestep Δt was 10−4 ns. A smooth (0.8–0.9 nm) cutoff was used for evaluation of solute–solute and solute–surface forces, as both forces are indistiguishable from zero at distances greater than the cutoff (see Figure 2). The concentration of particles in the constant-concentration reservoirs was checked every 0.05 ns, and particles were added or deleted to give the desired mean concentration and mean fluctuation of the concentration. The diffusion constant D of DMMP was 9.1 nm/ns2 15.
Supplementary Material
Acknowledgments
We would like to thank Ilia Solov’yov for his help with graphics design of the images. This work was supported by a grant from the National Science Foundation (DMR-0955959) and in part by the National Institutes of Health (PHS 5 P41-RR005969) and the Petroleum Research Fund (48352-G6), and through a cooperative research agreement with the Army Corps of Engineers Engineer Research and Development Center - Construction Engineering Research Laboratory (ERDC-CERL). The authors gladly acknowledge supercomputer time provided through TeraGrid Allocation grant MCA05S028 and by the Department of Defense High Performance Computing Modernization Program at the U.S. Army ERDC, DoD Supercomputing Resource Center, Information Technology Laboratory, Vicksburg, Mississippi.
Footnotes
Electronic Supplementary Information (ESI) available: [details of any supplementary information available should be included here]. See DOI: 10.1039/b000000x/
References
- 1.Tegenfeldt JO, Prinz C, Cao H, Huang RL, Austin RH, Chou SY, Cox EC, Sturm JC. Anal Bioanal Chem. 2004;378:1678–1692. doi: 10.1007/s00216-004-2526-0. [DOI] [PubMed] [Google Scholar]
- 2.Craighead H. Nature. 2006;442:387. doi: 10.1038/nature05061. [DOI] [PubMed] [Google Scholar]
- 3.Austin R, Tegenfeldt J, Cao H, Chou S, Cox E. IEEE Tran Nanotechnol. 2002;1:12–18. [Google Scholar]
- 4.Stavis S, Corgié S, Cipriany B, Craighead H, Walker L. Biomicrofluidics. 2007;1:034105. doi: 10.1063/1.2789565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hansen C, Classen S, Berger J, Quake S. J Am Chem Soc. 2006;128:3142–3143. doi: 10.1021/ja0576637. [DOI] [PubMed] [Google Scholar]
- 6.Rothberg JM, Hinz W, Rearick TM, Schultz J, Mileski W, Davey M, Leamon JH, Johnson K, Milgrew MJ, Edwards M, Hoon J, Simons JF, Marran D, Myers JW, Davidson JF, Branting A, Nobile JR, Puc BP, Light D, Clark TA, Huber M, Branciforte JT, Stoner IB, Cawley SE, Lyons M, Fu Y, Homer N, Sedova M, Miao X, Reed B, Sabina J, Feierstein E, Schorn M, Alanjary M, Dimalanta E, Dressman D, Kasinskas R, Sokolsky T, Fidanza JA, Namsaraev E, McKernan KJ, Williams A, Roth GT, Bustillo J. Nature. 2011;475:348–352. doi: 10.1038/nature10242. [DOI] [PubMed] [Google Scholar]
- 7.Pushkarev D, Neff N, Quake S. Nature Biotech. 2009;27:847–850. doi: 10.1038/nbt.1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lavén M, Velikyan I, Djodjic M, Ljung J, Berglund O, Markides K, Långström B, Wallenborg S. Lab Chip. 2005;5:756–763. doi: 10.1039/b418715f. [DOI] [PubMed] [Google Scholar]
- 9.Boy DA, Gibou F, Pennathur S. Lab Chip. 2008;8:1424–1431. doi: 10.1039/b812596c. [DOI] [PubMed] [Google Scholar]
- 10.Squires TM, Quake SR. Rev Mod Phys. 2005;77:977. [Google Scholar]
- 11.Schoch R, Han J, Renaud P. Rev Mod Phys. 2008;80:839. [Google Scholar]
- 12.Sparreboom W, Berg A, Eijkel J. New Journal of Physics. 2010;12:015004. [Google Scholar]
- 13.van der Heyden F, Bonthuis D, Stein D, Meyer C, Dekker C. Nano Lett. 2006;6:2232–2237. doi: 10.1021/nl061524l. [DOI] [PubMed] [Google Scholar]
- 14.Maffeo C, Schöflin R, Brutzer H, Stehr R, Aksimentiev A, Wedemann G, Seidel R. Phys Rev Lett. 2010;105:158101. doi: 10.1103/PhysRevLett.105.158101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Carr R, Comer J, Ginsberg MD, Aksimentiev A. J Phys Chem Lett. 2011;2:1804–1807. doi: 10.1021/jz200749d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sendner C, Horinek D, Bocquet L, Netz RR. Langmuir. 2009;25:10768–10781. doi: 10.1021/la901314b. [DOI] [PubMed] [Google Scholar]
- 17.Niedzwiecki DJ, Grazul J, Movileanu L. J Am Chem Soc. 2010;132:10816–10822. doi: 10.1021/ja1026858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Oxford University Press; New York: 1987. [Google Scholar]
- 19.Hsin J, Strümpfer J, Lee E, Schulten K. Annual review of biophysics. 2010;40:187–203. doi: 10.1146/annurev-biophys-072110-125325. [DOI] [PubMed] [Google Scholar]
- 20.Karplus M, McCammon J. Nature Struct Biol. 2002;265:654–652. doi: 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- 21.Lindahl E, Sansom MSP. Curr Op Struct Biol. 2008;18:425–431. doi: 10.1016/j.sbi.2008.02.003. [DOI] [PubMed] [Google Scholar]
- 22.Rountree C, Kalia R, Lidorikis E, Nakano A, Van Brutzel L, Vashishta P. Annu Rev Mater Res. 2002;32:377–400. [Google Scholar]
- 23.Johnson RR, Johnson aTC, Klein ML. Nano Lett. 2008;8:69–75. doi: 10.1021/nl071909j. [DOI] [PubMed] [Google Scholar]
- 24.Carr R, Weinstock IA, Sivaprasadarao A, Müller A, Aksimentiev A. Nano Lett. 2008;8:3916–3921. doi: 10.1021/nl802366k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tarek M, Tu K, Klein M, Tobias D. Biophys J. 1999;77:964–972. doi: 10.1016/S0006-3495(99)76947-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cruz-Chu ER, Aksimentiev A, Schulten K. J Phys Chem B. 2006;110:21497–21508. doi: 10.1021/jp063896o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hassanali AA, Singer SJ. J Phys Chem B. 2007;111:11181–11193. doi: 10.1021/jp062971s. [DOI] [PubMed] [Google Scholar]
- 28.Comer J, Dimitrov V, Zhao Q, Timp G, Aksimentiev A. Biophys J. 2009;96:593–608. doi: 10.1016/j.bpj.2008.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Park J, Aluru N. Mol Sim. 2009;35:31–37. [Google Scholar]
- 30.Schneider J, Ciacchi LC. J Chem Theory Comput. 2011;7:473–484. doi: 10.1021/ct1004388. [DOI] [PubMed] [Google Scholar]
- 31.Radadia AD, Stavis CJ, Carr R, Zeng H, King WP, Carlisle JA, Aksimentiev A, Hamers RJ, Bashir R. Adv Funct Mater. 2011;21:1040–1050. doi: 10.1002/adfm.201002251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Serr A, Horinek D, Netz R. J Am Chem Soc. 2008;130:12408–12413. doi: 10.1021/ja802234f. [DOI] [PubMed] [Google Scholar]
- 33.Ziemys A, Ferrari M, Cavasotto C. J Nanosci Nanotechnol. 2009;9:6349–6359. doi: 10.1166/jnn.2009.1822. [DOI] [PubMed] [Google Scholar]
- 34.Wong K-Y, Pettitt BM. Theor Chem Acc. 2010;106:233–235. [Google Scholar]
- 35.Wang Y, Cohen J, Boron WF, Schulten K, Tajkhorshid E. J Struct Biol. 2007;157:534–544. doi: 10.1016/j.jsb.2006.11.008. [DOI] [PubMed] [Google Scholar]
- 36.Aksimentiev A, Heng JB, Timp G, Schulten K. Biophys J. 2004;87:2086–2097. doi: 10.1529/biophysj.104.042960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Onufriev A, Bashford D, Case D. Proteins: Struct, Func, Bioinf. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 38.Knotts TA, Rathore N, Schwartz DC, de Pablo JJ. J Chem Phys. 2007;126:084901. doi: 10.1063/1.2431804. [DOI] [PubMed] [Google Scholar]
- 39.McGuffee SR, Elcock AH. J Am Chem Soc. 2006;128:12098–12110. doi: 10.1021/ja0614058. [DOI] [PubMed] [Google Scholar]
- 40.Noid WG, Chu J-W, Ayton GS, Krishna V, Izvekov S, Voth GA, Das A, Andersen HC. J Chem Phys. 2008;128:244114. doi: 10.1063/1.2938860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Im W, Seefeld S, Roux B. Biophys J. 2000;79:788–801. doi: 10.1016/S0006-3495(00)76336-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Fayad G, Hadjiconstantinou N. Microfluid Nanofluid. 2010;8:521–529. [Google Scholar]
- 43.Li Y, Xu J, Li D. Microfluid Nanofluid. 2010;9:1011–1031. [Google Scholar]
- 44.Ermak D, McCammon J. J Chem Phys. 1978;69:1352. [Google Scholar]
- 45.Potter M, Luty B, Zhou H, McCammons J. J Phys Chem. 1996;100:5149–5154. [Google Scholar]
- 46.Woolf T, Roux B. Proc Natl Acad Sci USA. 1994;91:11631. doi: 10.1073/pnas.91.24.11631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hummer G. New J Phys. 2005;7:34. [Google Scholar]
- 48.Landau LD, Lifshitz EM. Fluid Mechanics. 2. Vol. 6 Pergamon Press; Oxford, New York: 1999. [Google Scholar]
- 49.Zhang J. Microfluid Nanofluid. 2010:1–28. [Google Scholar]
- 50.Carr R, Comer J, Ginsberg MD, Aksimentiev A. IEEE Tran Nanotechnol. 2011;10:75–82. doi: 10.1109/tnano.2010.2062530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Horn RG, Smith DT, Haller W. Chemical Physics Letters. 1989;162:404–408. [Google Scholar]
- 52.Gruener S, Huber P. Phys Rev Lett. 2009;103:174501. doi: 10.1103/PhysRevLett.103.174501. [DOI] [PubMed] [Google Scholar]
- 53.Kusmin A, Gruener S, Henschel A, Holderer O, Allgaier J, Richter D, Huber P. The Journal of Physical Chemistry Letters. 2010;1:3116–3121. [Google Scholar]
- 54.Gruener S, Huber P. Journal of Physics: Condensed Matter. 2011;23:184109. doi: 10.1088/0953-8984/23/18/184109. [DOI] [PubMed] [Google Scholar]
- 55.Torrie G, Valleau J. Journal of Computational Physics. 1977;23:187–199. [Google Scholar]
- 56.Roux B. Computer Physics Communications. 1995;91:275–282. [Google Scholar]
- 57.Vishnyakov A, Neimark A. J Phys Chem A. 2004;108:1435–1439. [Google Scholar]
- 58.van Kampen NG. Stochastic Processes in Physics and Chemistry. North-Holland, Amsterdam, New York: 1992. [Google Scholar]
- 59.Vermesh U, Choi JW, Vermesh O, Fan R, Nagarah J, Heath JR. Nano Lett. 2009;9:1315–1319. doi: 10.1021/nl802931r. [DOI] [PubMed] [Google Scholar]
- 60.Gracheva ME, Vidal J, Leburton J-P. Nano Lett. 2007;7:1717–1722. doi: 10.1021/nl0707104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. J Comp Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Batcho PF, Case DA, Schlick T. J Chem Phys. 2001;115:4003–4018. [Google Scholar]
- 63.Brünger AT. X-PLOR, Version 3.1: A System for X-ray Crystallography and NMR. The Howard Hughes Medical Institute and Department of Molecular Biophysics and Biochemistry, Yale University; 1992. [Google Scholar]
- 64.Martyna GJ, Tobias DJ, Klein ML. J Chem Phys. 1994;101:4177–4189. [Google Scholar]
- 65.MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack RL, Jr, Evanseck J, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher IWE, Roux B, Schlenkrich M, Smith J, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.