Predicting the DNA sequence dependence of nanopore ion current using atomic-resolution Brownian dynamics

Abstract

It has become possible to distinguish DNA molecules of different nucleotide sequences by measuring ion current passing through a narrow pore containing DNA. To assist experimentalists in interpreting the results of such measurements and to improve the DNA sequence detection method, we have developed a computational approach that has both the atomic-scale accuracy and the computational efficiency required to predict DNA sequence-specific differences in the nanopore ion current. In our Brownian dynamics method, the interaction between the ions and DNA is described by three-dimensional potential of mean force maps determined to a 0.03 nm resolution from all-atom molecular dynamics simulations. While this atomic-resolution Brownian dynamics method produces results with orders of magnitude less computational effort than all-atom molecular dynamics requires, we show here that the ion distributions and ion currents predicted by the two methods agree. Finally, using our Brownian dynamics method, we find that a small change in the sequence of DNA within a pore can cause a large change in the ion current, and validate this result with all-atom molecular dynamics.

Introduction

Measurements of ion current have an illustrious history as a means to probe the state of nanoscale pores and molecules confined within them. In 1978, Neher, Sakmann, and Steinbach¹ described the patch clamp technique, which for the first time permitted the measurement of ion current through a single proteinaceaous nanopore. In a typical measurement, a thin insulating membrane splits a compartment containing electrolyte in two such that the nanopores within the membrane provide the only routes for ions to cross from one side of the membrane to the other. The ion current measured between the two volumes is therefore extremely sensitive to microscopic changes within the pore. Patch-clamp measurements of ion current were first used to identify the stochastic opening and closing of ion channel proteins.² Later, Bezrukov³ and Kasianowisz⁴ demonstrated that, in addition to indicating the state of the pore itself, ion current measurements could be used as a means to detect single molecules passing through the pore. Because the constriction of the pore represents a bottleneck for the flow of ions, the ion current is strongly affected by any molecules within the pore. Ion-current measurements can therefore reveal information about the identity and conformation of such molecules at nearly atomic resolution. Measurements of ion current have been used to determine the length⁴ and orientation of translocating nucleic acids,^5,6 discriminate nucleic acids of different sequences,^7–13 detect rupture of molecular bonds in force spectroscopy studies,^14–16 and distinguish between stereoisomers of drug molecules.¹⁷

Discriminating nucleic acid sequences has received particular attention due to the potential of using nanopores as a rapid low-cost means to sequence DNA^18,19 and the many benefits of genomic medicine^20–22 that might go along with it. The original proposal for nanopore sequencing called for identifying the DNA nucleotides by their unique current signatures as the DNA is electrophoretically driven through the pore.^7,18 However, this original proposal has not yet succeeded due to the difficulty of distinguishing DNA sequences with single-nucleotide resolution. As noted by Branton et al.,¹⁹ the ion current can not depend only on the identity of a single nucleotide but is necessarily the convolution of at least a handful of bases. Furthermore, the conformation of the DNA varies stochastically in time, and the distribution of conformations can depend on the DNA sequence. As of yet, systematic predictions of the effect of the sequences and conformation of a DNA molecule on the ion current through a nanopore are lacking.

Despite great successes in revealing behavior of single biomolecules, ion current measurements can be difficult to interpret because they effectively distill the interaction of the ions with the nanopore and biomolecules into a single value. For example, the same value of ion current may correspond to qualitatively different microscopic states.^23–25 As no experimental means currently exist to image the microscopic state of a nanopore system, computational methods have performed an essential role by linking observable values of current to microscopic events. The numerical methods that have been most widely used for simulations of ion current in nanopores can be categorized as molecular dynamics (MD), Brownian dynamics (BD), and continuum methods, such as Poisson-Nernst-Planck models. The latter have been shown to provide invaluable insights into the mechanisms of ion current modulation in nanopores.^26–30 However, for simulations that require atomic resolution, such as predicting the effect of a DNA sequence on the nanopore current, the discrete nature of ions and correlated ion motions, which are neglected in continuum methods, may be essential. Hence, we focus our attention below on the MD and BD approaches.

Molecular dynamics

All-atom MD simulations provide perhaps the greatest detail of methods that have been used to simulate ion current in pores.³¹ Until recently, the computational expense of all-atom MD simulation precluded direct calculation of ion currents.²⁷ Instead, the MD simulations were used to identify energy barriers and binding spots for ions within channels and infer mechanisms for channel selectivity^32,33 as well as providing some validation for computation of current by various levels of continuum theory^27,34 or BD simulations.²⁷

The MD method can now provide direct estimates of ion current in proteinaceous³¹ and synthetic^{23–25,35–38} nanopores. For some systems, the predicted values of ion current are in quantitative agreement with those measured in experiment.^39–41 For other systems, the lack of atomic-scale structures and imperfections in the molecular force fields^39,40,42 allow only for qualitative comparison between simulation and experiment.³¹ Due to explicit treatment of water, all-atom MD simulations can model phenomena often left out in coarser models, for example, electro-osmotic flow.⁴³

Despite spectacular developments in the field of high-performance computing, obtaining reliable current estimates remains expensive and time-consuming. For instance, ion currents through nanopores are typically on the order of 100 pA and sequence-dependent differences may be less than 10 pA.^10,11 100 pA represents the passage of only ~ 0.62 ions/ns. If we approximate the measurement of a current as counting the ions that pass through the pore, then the uncertainty in a measurement of the current scales as the square-root of the number of ion passages. Hence, to obtain a relative uncertainty of less than 1% for a mean current of 100 pA, we must observe the passage of 10⁴ ions, which requires a 16-μs MD simulation. We estimate that a 16-μs run of a 100,000-atom system would require at least 5 million CPU hours on a general-purpose supercomputer using an efficient parallel MD code such as NAMD.⁴⁴ While microsecond MD trajectories can be obtained in less than a day on specially designed computer systems,⁴⁵ such systems are not currently available for public use and may still not provide sufficient computational power.

Brownian dynamics

In the context of simulating ion current through nanopores, BD provides level of detail intermediate to MD and continuum methods. While discrete ions are included, water is usually not modeled explicitly. Compared to an MD model, dispensing with explicit water results in a large reduction of the number of degrees of freedom because water comprises a majority of the atoms in a typical MD simulation. Note that combining an explicit description of ions with an implicit description of water is possible in methods other than BD.⁴⁶ Explicit description of hydrogen motion limits the timestep that can be used in a typical all-atom MD simulation to ≤2.5 fs. In a BD simulation of ionic system, the choice of the timestep depends on the diffusivity of the ions and the magnitude of the forces applied to them, which allows for an additional speedup. For example, we use a 10 fs timestep for the BD simulations presented here.

In the limit of high friction, which is relevant for ions dissolved in water, inertia becomes insignificant and the motion of the ions is described by drift due to the explicit forces and stochastic displacement due to thermal fluctuations.^28,47,48

Here, we use the following first order BD update rule:²⁸

$${\mathbf{r}}_i(t+\mathrm{\Delta }t)={\mathbf{r}}_i(t)+\frac{D_i\mathrm{\Delta }t}{k_{\text{B}}T}({\mathbf{F}}_i^{\text{ext}}-{\nabla }_{i}W({\mathbf{r}}_1(t),{\mathbf{r}}_2(t),\dots ))+\sqrt{2D_i\mathrm{\Delta }t}\mathbf{R}(t)+\nabla D_i\mathrm{\Delta }t,$$ (1)

where Δt is the timestep, r_i(t + Δt) and r_i(t) are the positions of ion i at the next and current timestep, respectively, D_i = D_i(r_i(t)) is the position-dependent diffusivity of ion i, ${\mathbf{F}}_i^{\text{ext}}$ is the force of the external electric field on ion i, ∇_iW (r₁(t), r₂(t),…) is the gradient of the multi-ion potential of mean force (PMF) with respect to r_i(t), and R(t) is a vector of independent random numbers having a Gaussian distribution with a mean of zero and standard deviation of unity. The multi-ion PMF is a free energy surface which has the coordinates of all ions as independent variables. The multi-ion PMF is the sum of a spherically symmetric ion–ion PMF ( $W_{ij}^{\text{ion}-\text{ion}}$) and a PMF due to the pore, solution, and biomolecules ( $W_i^{\text{sys}-\text{ion}}$):

$$W({\mathbf{r}}_1,{\mathbf{r}}_2,\dots )=\sum _{ij}{W}_{ij}^{\text{ion}-\text{ion}}(\mid {\mathbf{r}}_i-{\mathbf{r}}_j\mid )+\sum _i{W}_i^{\text{sys}-\text{ion}}({\mathbf{r}}_i)$$ (2)

The BD method has been used with great success to study ion flow through protein nanopores,^27,28 including a modified α-hemolysin system that was used in experiment to identify DNA nucleotides.⁴⁹ This latter study of Egwolf et al.⁴⁹ demonstrates the ability of BD to predict the current–voltage relationships of nanopores.

However, in most BD models of ionic systems (see, for example, recent work by Cui⁵⁰), the interactions between ions and the biomolecules are described only by electrostatics and steric repulsion. Hydration effects due to the discrete nature of the solvent are usually neglected. We find here that hydration effects strongly modulate the interaction between ions and DNA nucleotides and may play a major part in the DNA sequence dependence of ion current. Gavryushov and coworkers^51,52 have also noted the need for detailed short-range PMFs for ion–ion and ion–macromolecule interactions, and calculated a number of detailed ion–ion PMFs in MD simulations using the SPC/E water model.

Atomic-resolution Brownian dynamics

What is needed is a method that has the accuracy of all-atom MD but the computational efficiency of BD. Here, we describe a method in which the ion–biomolecule and ion–ion interaction for BD simulations are derived using high-resolution explicit solvent all-atom MD. The result is a method, which we (for lack of a better name) refer to as atomic-resolution BD (ARBD). The ARBD method is 10⁴ to 10⁵ times more computationally efficient than the all-atom MD method and can predict ion distributions and ion currents in close agreement with the results of all-atom MD.

Using all-atom MD simulations to design and calibrate a coarser-scale model is not a new idea. For example, Im and Roux used all-atom MD simulations to determine the effective atomic radii⁵³ and a short-range solvation potential for BD simulations of ion transport.²⁷ Izvekov and Voth⁵⁴ used a force-matching method⁵⁵ to create a coarse-grain model of a lipid–water system.

Our ARBD method takes advantage of the size difference between ions and a DNA molecule and the fact that the conformational fluctuations of a DNA molecule are suppressed within nanopores.^35,56,57 We represent the entire DNA-nanopore system via static PMF maps that reproduce the mean force experienced by each ion in all-atom MD simulations. To this end, we derive the parameters of Eq. (1) and Eq. (2) from all-atom MD simulations.

While minimizing conformational fluctuations could be desirable in the design of a sequencing device as well as being optimal for the efficiency of the ARBD method, some conformational fluctuation of the DNA and pore is unavoidable and inherent to the nature of nanopore systems. Indeed, conformational fluctuations of nanopores are known to be responsible for certain types of noise in ion current measurements,⁵⁸ although many factors appear to contribute to this noise.^59–61 Thus, while for most of this work we restrict ourselves to static PMF maps, in the Conclusion we discuss extending the method to systems in which the DNA (or pore) undergoes appreciable conformational fluctuation.

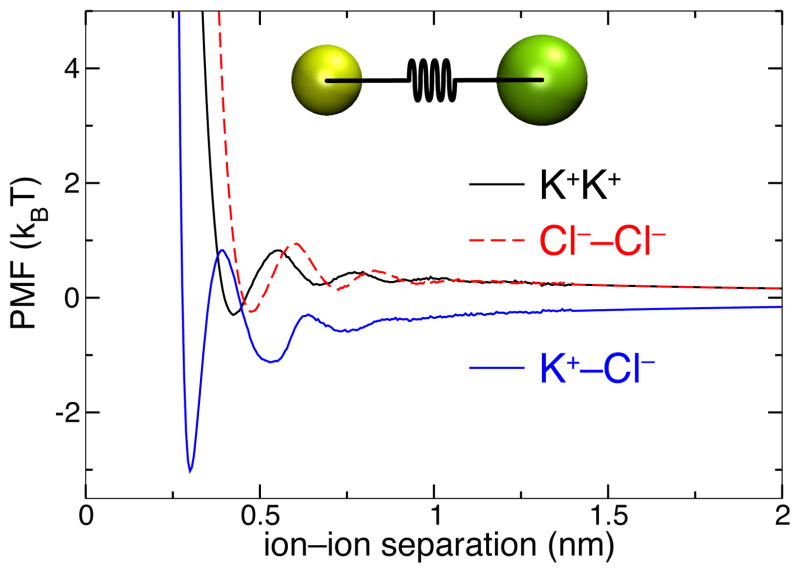
The ion–ion interaction potential $W_{ij}^{\text{ion}-\text{ion}}(\mid {\mathbf{r}}_i-{\mathbf{r}}_j\mid )$ is obtained by computing the PMF for each of the three ion pairs (K⁺–K⁺, Cl⁻–Cl⁻, and K⁺–Cl⁻) with a resolution of 0.01 nm (see Figure 1). For ion separations > 1.4 nm, a Coulomb form of the potential is used; however, the dielectric constant is computed using all-atom MD to give the best agreement with the results of the latter. This approach is similar to that of Villa et. al,⁶² who described the interaction between ions with a calculated PMF for separations < 1.2 nm and used a Coulomb form for larger separations.

Figure 1.

Potential of mean force for ion–ion interactions used in the ARBD simulations. The portions for separations ≤ 1.4 nm were determined (up to a constant) from all-atom MD simulations and incorporates the effect of discrete solvent, as is evident from the appearance of oscillations in the PMFs at small separations (see Methods). The inset image illustrates a setup of one such simulation, where the distance between two ions is restrained using a harmonic potential.

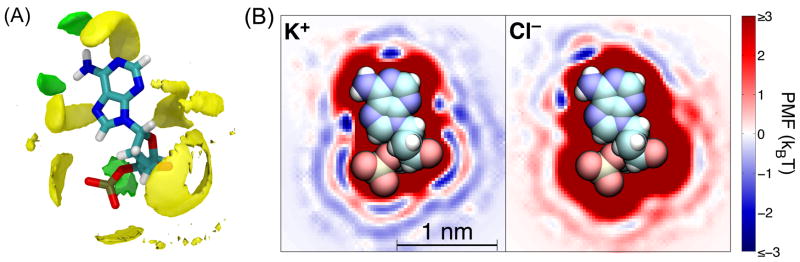
The interaction of the ions with the other components of the system $W_i^{\text{sys}-\text{ion}}({\mathbf{r}}_i)$ is determined by computing three-dimensional PMF maps with a 0.03 nm resolution in each spacial dimension. For example, Figure 2 shows the PMF maps of K⁺ and Cl⁻ ions near adenine. Such maps include the mean field contribution of explicit water molecules to the ion–biomolecule interactions, which can be easily seen in the oscillating hills and valleys in the PMF separated by distances near the size of a water molecule. Like for the ion–ion interactions, the interaction between the ions and biomolecules at large separations (approximately > 0.7 nm) is assumed to be purely electrostatic and is computed using the dielectric constant of water measured in MD. The inclusion of long-range electrostatics is particularly important for DNA, which is highly charged.

Figure 2.

Potential of mean force for ion–nucleotide interactions. (A) Three-dimensional rendering of regions near an adenine nucleotide that are attractive to K⁺ (yellow) and Cl⁻ (green). The rendered surfaces contain all points with PMF values < −1.4 k_BT. The location of the nucleotide is shown using a tube representation of the atomic bonds. (B) Cross sections of the PMF maps for K⁺ (left) and Cl⁻ (right) near an isolated adenine nucleotide. The location of the nucleotide is shown using a space-filling representation.

Our method employs a modular approach to constructing three-dimensional PMF maps. The PMF maps for a system’s components, such as individual nucleotides of a DNA strand, are calculated from MD simulations of relatively small systems containing just the pertinent component, water, and a single ion. Under some conditions, the PMF maps of the components can be combined, producing BD models of arbitrary size and complexity.

Finally, the position-dependent diffusivity D_i(r_i(t)) of K⁺ and Cl⁻ near biomolecules is computed from all-atom MD simulations using established methods.^63,64 Due to the fact that the ion currents are not extremely sensitive to the exact spatial distribution of D_i(r_i(t)), we do not compute high resolution diffusivity maps for each nucleotide system considered. Instead, we approximate the spatial dependence of the ion diffusivity by an empirical expression derived from calibration MD simulations.

The lack of explicit solvent makes ARBD a much more efficient computation method if compared with all-atom MD. However, this also implies that some explicit-solvent effects are lost in ARBD. The PMF maps incorporate the mean-field influence of the explicit solvent on the force between two ions or an ion and DNA, so that an ion approaching a DNA molecule in ARBD feels the same average force as in explicit solvent all-atom MD. However, the PMF interaction maps are valid, strictly speaking, only under the conditions they were determined. Thus, our application of the ARBD method assumes that the medium between two interacting objects remains unperturbed by the presence of other objects. So-called “three-body” effects may limit precision of ARBD simulations when applied to multi-ion systems and render inaccurate PMF maps of large biomolecules constructed using PMF maps of their constituents. Below, we quantitatively assess the influence of the three-body effects through extensive validation simulations. In the form presented here, the ARBD method does not describe hydrodynamic effects.

In the following, we assume that the MD model is sufficiently accurate to provide a basis for ARBD simulations. Future improvements to all-atom force field can be easily incorporated using the protocols described here.

The rest of the paper is organized as follows. In Methods, we describe in detail parametrization of the ARBD method using all-atom MD. In Results and Discussion, we first test the validity of our modular approach to building PMF maps of a large system using PMF maps of the system’s parts. Next, we validate the ion distributions of ARBD simulations against all-atom MD. Finally, we test our method for its ability to predict transport properties of ionic systems, including DNA sequence-specific ion current blockades in nanopores. Possible broader applications of our ARBD method and its limitations are discussed in the Conclusion.

Methods

In this section, we describe in detail our ARBD method. Because all-atom MD simulations were used for parametrization and validation of the ARBD method, we first describe methods and protocols used in our MD simulations. Next, we describe in detail the all-atom MD simulations used to determine the PMF functions $W_{ij}^{\text{ion}-\text{ion}}(\mid {\mathbf{r}}_i-{\mathbf{r}}_j\mid )$ and $W_i^{\text{sys}-\text{ion}}({\mathbf{r}}_i)$ defined in Eq. (2). For distances greater than about 1.0 nm between two ions or between an ion and DNA, these functions were Coulomb energies calculated using the dielectric constant of water measured in all-atom MD simulations. At shorter distances, the PMF functions were explicitly derived from umbrella sampling simulations in all-atom MD using the Weighted Histogram Analysis Method (WHAM).^65,66 At the end of the section, we describe the method we used to derive an empirical function that approximates the position-dependence of ion diffusivity near DNA.

General MD methods

The protocols used to perform all our MD simulations have been described in detail elsewhere.⁶⁷ Briefly, the all-atom MD simulations were performed using the program NAMD2, periodic boundary conditions, and multiple timestepping of 1, 2, 4 fs for calculation of bonded, explicit non-bonded, and long-range electrostatic interactions, respectively.⁴⁴ Non-bonded energies were calculated using particle-mesh Ewald full electrostatics⁶⁸ (grid spacing < 0.15 nm) and a smooth (1.0–1.2 nm or 0.7–0.8 nm) cutoff of the Lennard-Jones energy. The reduction of the cutoff of the Lennard-Jones energy from 1.2 to 0.8 nm was justified by simulations that showed no significant differences in ion distributions or ion currents using the two cutoff values.⁶⁹ A Langevin thermostat was applied to non-hydrogen atoms with a damping constant of 0.2 ps⁻¹ to maintain a temperature near 295 K. Interactions between all atoms of the systems, including water, ions, and nucleic acids, were calculated using the CHARMM force field.⁷⁰ Rigidity of water molecules and bonds to hydrogen was not enforced, i.e. algorithms such as SHAKE⁷¹ were not used. Repeating the PMF calculations using a rigid model of water and enforcing rigidity of the covalent bonds to hydrogens in the DNA model gave negligible corrections to the PMF maps.

After assembly, each all-atom system underwent 2000 steps of energy minimization using a conjugate gradient method.⁷² This was followed by > 500 ps of equilibration using a Langevin piston pressure control to obtain a pressure of 1 atm.⁷³ All production simulations were performed at constant volume, using the average volume measured in the constant pressure equilibration (neglecting the first 100 ps).

Phantom pore

Where indicated, we used an external potential energy U_phantom to define volumes of the system inaccessible to ions, such as a membrane separating two electrolyte compartments. This external potential served as a coarse model for various types of nanopores and is referred to as a phantom pore.³⁵

The pore and membrane surface were constructed as follows. The membrane was parallel to the xy plane, spanning the region of |z| < 1.95 nm; the center of the membrane was located at z = 0. The membrane contained a cylindrical pore with smooth corners whose radius was

$$s_{\text{pore}}(z)=\{\begin{array}{ll}{s}_0,\hfill & \mid z\mid \le L/2-c\hfill \\ s_0+c-{[c^2-{(\mid z\mid -c)}^2]}^{1/2},\hfill & L/2-c<\mid z\mid <L/2\hfill \end{array}$$ (3)

where L = 3.9 nm, c = 0.5 nm, and s₀ = 0.7 nm. The intersection of |z| < 2.0 nm and s > s_pore(z) (where s = (x² + y²)^1/2) defined the region inaccessible to the ions. The potential energy was modeled as a function of the minimum distance d between the surface of this region and each point:

$$u(d)=\{\begin{array}{ll}A{(d-w)}^2+B{(d-w)}^3+C{(d-w)}^4,\hfill & d<w\hfill \\ 0,\hfill & d\ge w\hfill \end{array}$$ (4)

where

$$\begin{array}{l}A=\frac{1}{w^2}(V_{max}+16V_{min}),\\ B=\frac{4}{w^3}(V_{max}+8V_{min}),\\ C=\frac{4}{w^4}(V_{max}+4V_{min}),\end{array}$$ (5)

and w = 0.25 nm, V_min = −2 k_BT, and V_max = 40 k_BT. U_phantom(r) = u(d(r)) was sampled on a discrete grid with dimensions of 4.0 × 4.0 × 7.2 nm³ and a resolution of 0.03 nm. We took the effective radius of the pore to be the maximum radial coordinate accessible to the center of mass of the ions plus the R_min/2 Lennard-Jones parameter of the ions, which should give a consistent pore radius for ions of different sizes as well as approximating the apparent pore radius in electron microscope images of an analogous synthetic pore.⁶⁷ Thus, the effective diameter of the pore was somewhat larger than 2s₀ and the membrane was somewhat thinner than L. The result was a pore with an effective diameter of 1.8 nm in a membrane with an effective thickness of 3.5 nm (see Figure 9A and Figure 15A).

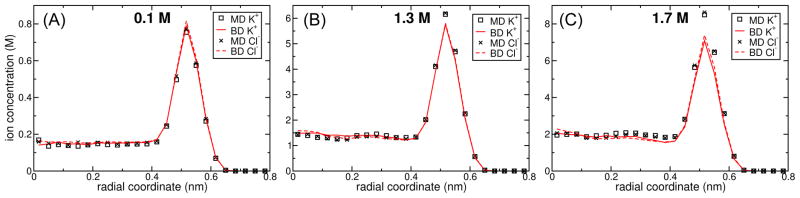
Figure 9.

Ion concentrations in a phantom pore shown as a function of distance from the pore axis. The ion concentrations are computed for the region −0.5 nm < z < 0.5 nm (the middle of the membrane). Due to the fact that the interaction with the pore walls is identical for both K⁺ and Cl⁻, little difference can be seen between the two distributions. The concentration is enhanced near the pore wall due to the −2k_BT potential well at the phantom pore’s surface. The ion concentration far from the pore is indicated on the top of each plot.

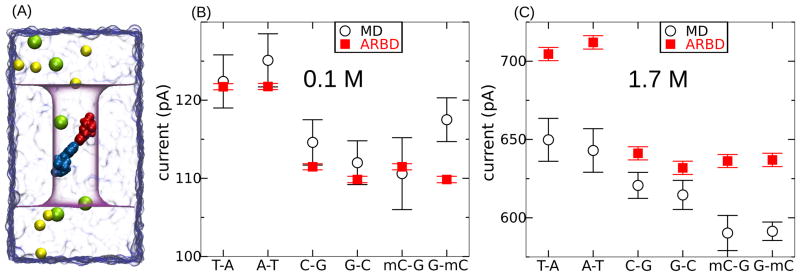
Figure 15.

Ion current through a nanopore blocked by a single DNA basepair. (A) All-atom model of the system. The K⁺ and Cl⁻ ions are shown by yellow and green spheres, while the A and T nucleotides of the A·T basepair are shown in blue and red, respectively. The atoms of water are not explicitly shown, but represented by a a blue translucent surface. The phantom pore is shown by a purple semitransparent surface. The electric field is applied such that K⁺ ions passing through the pore approach the A nucleotide before the T nucleotide. (B, C) Simulated dependence of the nanopore ion current on the sequence and orientation of the DNA basepair. The data shown in panels B and C are for bulk concentrations of 0.1 and 1.7 M. The tilting of the basepair makes it possible, in principle, to measure a different current for X·Y than for Y·X. The systematic deviation of the ARBD currents at 1.7 M is attributable to the higher conductivity of bulk electrolyte in the ARBD method if compared with all-atom MD. In the high-salt regime, ARBD is expected to be in a better agreement with experiment than MD in predicting the absolute nanopore currents, see Figure 13A.

Subject to potential U_phantom, an ion experienced an attractive energy well of −2 k_BT near the nanopore surface, similar to the change of free energy seen near graphite surfaces. In both MD and BD simulations, the potential energy representing the phantom pore was applied as described in Wells et al.⁷⁴

Calculation of the solvent dielectric constant

The dielectric constant of water was measured from an MD simulation of a 4.2 ×4.2 ×3.48 nm³ volume (after equilibration at 1 atm) containing 2130 water molecules. Interactions between water molecules were defined by the the TIPS3P water model⁷⁵ of the CHARMM force field. In accord with a method described by Xu et al.,⁷⁶ we applied an external electric field of 2.87 V/μm along the z axis (equivalent to a 0.01 V drop across the system along this axis³⁹). The mean dipole moment induced by the electric field was calculated from the last 50 ns of the simulation (the first 5 ns were discarded). Substituting the mean dipole moment into equations 12 and 13 of Ref.,⁷⁶ yielded the the dielectric constant ε_r = 176 ± 2. This value is significantly larger than the experimental value. Indeed, simulations using the same water model show significantly smaller dielectric constants⁷⁷ when SHAKE⁷¹ (or another algorithm) is used to impose a rigid internal geometry on the water molecules. In the simulation protocol used here, the H–O bond distances and H–O–H angles of the water molecules were not constrained, resulting in a more polarizable water molecule. Because our goal was to validate the ARBD simulations by comparison to all-atom MD simulations, we chose the dielectric constant of the long-range ARBD interactions to be consistent with our all-atom MD simulations.

Potential of mean force for ion–ion interactions

To obtain the first term of Eq. (2) (W^ion–ion), we performed three sets of all-atom MD simulations that determined the K⁺–K⁺, Cl⁻–Cl⁻, and K⁺–Cl⁻ PMF functions. Each set of simulations consisted of 80 individual simulations in which the distance between the two ions was harmonically resrained to a value between 0.26 and 1.445 nm. The restraint energy was given by $U_w({\mathbf{r}}_i,{\mathbf{r}}_j)=\frac{1}{2}{K}_W{(\mid {\mathbf{r}}_i-{\mathbf{r}}_j\mid -b_w)}^2$, where K_w and b_w were the force constant and equilibrium separation for umbrella sampling window w. The spring constant of K_w = 26 kcal/(mol Ų) allowed the position distributions of ions in the sampling windows to overlap for the 0.015 nm spacing of b_w. In each sampling window, the simulation was run for 12.7–13.1 ns. The first 1 ns of the data was discarded. The remaining data was analyzed using WHAM⁶⁶ with histogram bins with a spacing of 0.005 nm, yielding the ion–ion PMFs.

The long-range part of the PMF was computed using the analytical expression for the Coulomb energy: q_iq _j/(4πε₀ε_r), where q_k was the charge of ion k, ε₀ was the electric constant, ε_r = 176 was the dielectric constant of the water model used in MD, and r was the distance between the centers of the two ions.

To match the short- and long-range parts of the ion–ion PMFs, a least squares fit was performed between the MD-derived PMF and the Coulomb energy expression over the interval 1.0 nm < r ≤ 1.4 nm. Beyond the last sampling window (r = 1.445 nm), insufficient sampling results in noisy PMF. Thus, the PMF was truncated at r = 1.4 nm and the Coulomb energy was used for r > 1.4 nm. For r < 0.26, the PMF was extrapolated to approximate the large repulsive force for close encounters between the ions, reaching a maximum value of 800 k_BT/nm. The resulting PMFs are shown in Figure 1.

Potential of mean force for ion–nucleotide interactions

The 3D PMF maps representing the interaction between ions and different DNA structures were obtained using all-atom umbrella sampling simulations.^78,79 In these simulations, an ion was restrained to many different positions near the DNA. In the following, the harmonic potential used to restrain the ion is referred to as the umbrella sampling window and the position to which the ion is restrained is referred to as the center of the respective sampling window. In all cases, the centers of the umbrella sampling windows for the 3D PMF maps of the nucleotides were chosen from a hexagonal close-packed lattice with a distance of 0.25 nm between the nodes. Nodes that were farther than 0.68 nm from any atom of the DNA were discarded as well as those that were closer than 0.22 nm from any DNA atom. The ions were restrained to the window centers (r_w) by the bias energy $U_w(r)=\frac{1}{2}K{\mid \mathbf{r}-{\mathbf{r}}_w\mid }^2$, where the spring constant K = 0.0938 kcal/(mol Ų). These restraints provided good overlap of the position distributions between neighboring windows on the close-packed lattice. To provide a fixed reference structure for each PMF map, atoms of the DNA were restrained to their initial coordinates using spring constants of k = 2.0 kcal/(mol Ų). Ion positions were recorded every 200 fs.

Isolated nucleotides

Systems of ≈ 9440 atoms containing an approximately 4.5 nm × 5.0 nm × 4.0 nm periodic box of water, a single DNA nucleotide (adenine (A), thymine (T), cytosine (C), guanine (G) or 5-methylcytosine (mC)), and a single ion (K⁺ or Cl⁻) were prepared. Discrimination of a methylated variant of cytosine (mC) from cytosine (C) is one of the goals of high-throughput sequencing^10,80 due to the importance of cytosine methylation in epigenetics.⁸¹ The conformations of the single nucleotides were chosen from a canonical, B-form DNA double helix and did not contain the chemical modifications which are commonly present at the termini of a DNA molecule. The atoms of the nucleotides were restrained to their initial coordinates during equilibration. The above criteria for the choice of the window centers resulted in 342, 343, 350, 340, and 340 windows for A, T, C, G, and mC nucleotides, respsectively. Umbrella sampling simulations were performed for each of the five nucleotides and each of the two ions (K⁺ or Cl⁻), for a total of 3430 simulations. The simulation for each sampling window lasted 2.2–2.7 ns. Figure 2 shows the PMF maps for a single adenine nucleotide after all processing steps (see below).

Three-nucleotide DNA fragment

A three-nucleotide fragment of a single-stranded DNA molecule consisting of adenine nucleotides (referred to as AAA structure) was extracted from an MD simulation of DNA translocation through a biological nanopore MspA.⁸² A second structure (referred to as ATA) was produced by mutating the middle nucleotide to thymine. Both structures did not contain the chemical modifications which are commonly present at the termini of DNA molecules. Each structure was placed in a 4.5×5.0×4.1× nm³ volume of water and restrained to its initial coordinates during equilibration.

The K⁺ PMF map of the AAA structure was computed using 612 sampling windows. Only 296 of these windows were used to compute the K⁺ PMF for the ATA structure, as the PMF values at the nodes farther than 1.0 nm from the thymine substitution were nearly unchanged. The simulation for each window lasted 5.8–10.0 ns.

Effectively infinite DNA double helix

A double-stranded DNA (dsDNA) molecule consisting of 10 A·T basepairs was extracted from equilibrium MD simulations. The molecule spanned the periodic boundaries of the system and was therefore effectively infinite. Umbrella sampling simulations of 6.6–10.3 ns were performed for 1481 windows to produce a K⁺ PMF. For comparison, an incomplete K⁺ PMF was made for an effectively infinite G·C molecule in a representative volume containing 443 windows.

Generation and processing of the PMF maps for ARBD simulation

In the umbrella sampling MD simulations used to compute the PMFs, the position of the restrained ion was recorded every 200 fs. The data from the first 0.2 ns of each simulation were discarded, while what remained was used in the PMF calculation. As prescribed by WHAM,⁷⁸ the recorded ion positions for each window were placed in histogram bins, which here were cubic bins spaced with side lengths of 0.03 nm. The WHAM equations were then iterated using all three Cartesian coordinates as independent coordinates to produce estimates of the PMF at the center of each bin.⁷⁹

Further processing of the PMF maps was done for two reasons. First, the PMF was not sampled farther than approximately 0.7 nm from the DNA atoms or very close to the atoms of DNA; thus, it was necessary to assign the PMF map values in these regions using analytic expressions. Second, in many cases, we desired to create PMF maps of small components of the system that could later be combined and manipulated to create larger systems; thus, the PMF maps were processed to facilitate this combination and manipulation. Typically, we subtracted the electrostatic component of the PMF from the maps to produce the maps that had zero values in the volumes located more than ≈ 0.6 nm away from the DNA. Similarly, the values of the PMF in the unsampled regions very close to the DNA atoms were set to a uniform value. After this, the PMF maps were combined and manipulated using rigid transformations in space and addition and subtraction of the PMF fields. These manipulations are described in detail later in the text. After combining the PMF maps of the system’s components into a PMF map of the entire system, the long-range electrostatic energy and the repulsive portion of the Lennard-Jones energy were added in.

The first processing step applied to the raw PMF maps was the subtraction of the electrostatic energy. The atomic structure of the DNA was extracted from the all-atom model used in the umbrella sampling simulations. The PMEPot^39,68 module of VMD⁸³ was used to calculate the long-range portion of the electrostatic potential due to the DNA in vacuum on a periodic domain having the same dimensions as the MD system used for the umbrella sampling. The electrostatic energy map for each ion was computed by scaling this electrostatic potential by the charge of the ion and dividing by 176 to incorporate the effect of the solvent dielectric constant. This electrostatic energy map was then subtracted from the appropriate PMF map. Note that this procedure should not affect the forces experienced by ions near the DNA in the BD simulations because the electrostatic energy is later added back in.

With the long-range electrostatic energy removed, the PMF at the edge of the sampled domain (excluding the noisy undersampled regions) is nearly flat. For convenience, we consider the PMF values (that exclude the long-range electrostatic energy) far from the nucleotide to be zero. We define the zero-PMF volume by combining ion-position histograms from all sampling windows into a total histogram of ion positions. To exclude noisy PMF estimates, bins containing < 15 samples were discarded near the far edge of the sampled domain, creating a new domain edge closer to the nucleotide. The zero of the PMF map was computed by averaging the PMF values within 0.2 nm of the new domain edge. This average was subtracted from the PMF map and all points outside the domain were set to zero.

Undersampled bins also existed very near the atoms of the nucleotide, where a large steric force prevented sampling by the ions. To facilitate addition of the PMF maps, these regions were uniformly set to 4 k_BT. Subsequently, an approximation to the repulsive portion of the Lennard-Jones energy was added to the PMF map to faithfully describe steric energy barriers that exist near the atoms of DNA.

In many cases, PMF maps generated by all-atom MD were added and subtracted as described later to produce larger and more complex structures from smaller components. Before being used in BD simulations, all maps, whether derived directly from PMF calculations or constructed by combining PMF maps, had the long-range electrostatic energy and the short-range repulsive potential added in. The addition of the electrostatic energy was accomplished by creating an atomic model of the final system containing no ions or water. The long-range electrostatic energy was computed from this model using the particle-mesh Ewald algorithm on the periodic domain of the all-atom system and added, after scaling with the dielectric constant of the solvent, to the processed PMF map. Finally, a quadratic approximation of the Lennard-Jones steric energy barrier was added to prevent ions in a BD simulation from crossing the regions set to 4 k_BT. Such a choice of functional form prevented spurious effects during numerical integration of the equations of motion while having negligible effect on the agreement between BD and MD.

Ion diffusivity in bulk solution

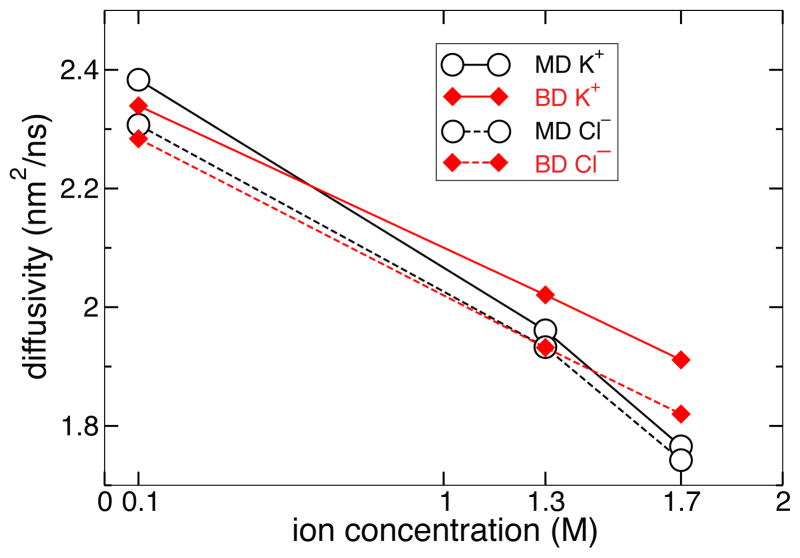
In an all-atom MD simulation, the diffusivity of an ion in bulk water is determined by its interactions with explicit water molecules. Adding ions to form a finite concentration of KCl solution changes the properties of this medium; thus, the diffusivity of a K⁺ or Cl⁻ ion in bulk KCl solution changes with the concentration of the solution. In BD, however, the diffusivity of an isolated ion is an input parameter as the water molecules are not explicitly present. Nevertheless, our test simulations have shown that the bulk diffusivity of ions in BD simulations change with the ion concentration, closely matching the dependence observed in all-atom MD simulations in the 0.1–1.3 M concentration range.

To calculate the bulk diffusivity of ions as a function of their concentration, we simulated a 4.0 × 4.0 × 7.2 nm³ periodic box of KCl solution at 0.1, 1.3, and 1.7 M concentrations, using analogous systems for all-atom MD and ARBD. Because the simulations were also used for other purposes, the center of the system contained a phantom membrane.³⁵ For this reason, the diffusivity was calculated using ion trajectories beginning > 1.5 nm from the membrane surface. The ion trajectories lasted 0.15 ns; therefore, it was unlikely that the ions reached the membrane during the trajectory. The diffusivity was calculated considering the ion motion parallel to the plane of the membrane (the xy plane): D = lim_Δt→0 〈(x(t) − x(0))² + (y(t) − y(0))²〉/(4Δt)⁸⁴.

In the BD simulations, the diffusivity of isolated (0 M limit) K⁺ and Cl⁻ ions was set to the value calculated from MD simulations at 0.1 M, which were 2.38 ±0.02 and 2.31 ±0.02 nm²/ns, respectively. The uncertainty in these values was calculated by randomly partitioning the data into three sets and recomputing the diffusivity from each of the three sets; the uncertainty was chosen to be the minimum interval that contained all four diffusivity estimates.

Figure 3 shows that, although the diffusivity parameters for the K⁺ and Cl⁻ ions were set to a fixed value, the effective diffusivity calculated from the BD trajectories changes with ion concentration. At small concentrations, such as 0.1 M, agreement is expected between MD and BD since the diffusivities are changed little from their values at infinite dilution. However, the diffusivities are in agreement even at 1.3 M.

Figure 3.

Concentration dependence of ion diffusivity in bulk KCl solution. For both all-atom MD and ARBD, the effective diffusivity decreases with concentration. Note that in ARBD, the diffusivity for an isolated ion is an input parameter set to a constant value. The uncertainty of the MD and ARBD values were approximately ±0.02 nm²/ns and ±0.01 nm²/ns, respectively.

It may be technically possible to modify the effective diffusivity of the BD ions as a function of their local concentration, so that the bulk diffusivity would exactly match the results of all-atom MD. However, the discrepancies between MD and BD in estimating the bulk diffusivity of the ions are small (< 10%) and are smaller than the discrepancies between the results of all-atom MD and experiment.³⁹ Hence we used 2.38 and 2.31 nm²/ns to descibe diffusivity of individual K⁺ and Cl⁻ ions in BD, producing the bulk diffusivity dependence shown in Figure 3.

Ion diffusivity near DNA

While the diffusivity of the ions has no effect on the equilibrium properties of ion–DNA systems, dynamic quantities, such as ion currents, do depend on the diffusivity field. However, even for these quantities, the accuracy and resolution of the diffusivity field D(r) is typically secondary in importance to those of the multi-ion PMF W(r₁(t), r₂(t),…). For instance, ion currents can more strongly depend on the multi-ion PMF than on the position-dependent diffusivity. As can be seen from Eq. (1), applying a small external electric force F^ext leads to a mean ion current density of J ∝ DcF^ext, where c is the mean ion concentration. If the force is small enough to not appreciably perturb the concentration from its equilibrium value c ∝ e^−W/(k_BT),⁶⁴ the mean current density is J ~ De^−W/(k_BT)F^ext. We find here that within a distance < 1 nm from DNA, e^−W/(k_BT) varies wildly over several orders of magnitude, while D does not change by more than a factor of 2 or 3 from its value far from the DNA. Likewise, Roux and coworkers⁸⁵ found e^−W/(k_BT) to vary by more than a factor of 1000 as the ion diffusivity varied by a factor of 10 in a narrow pore. Finally, Hummer⁶⁴ notes “…it is reassuring that the rates, while exponentially sensitive to the barrier height, are only linearly proportional to the diffusion coefficient in the Kramers theory.”

That said, there is a significant reduction in the diffusivity of K⁺ and Cl⁻ ions near DNA, which can have appreciable effects on ion current calculations. We sought to develop a model of position-dependent diffusivity that was simple to calculate but sufficiently accurate to yield quantitative agreement for the predictions of the ion current between ARBD and MD. To accomplish that, we first computed the ion diffusivity at many positions near a single basepair of DNA.

Several methods are available for computing position-dependent diffusivities from MD simulations.^64,84,86 Here, we use a method based on the Generalized Langevin Equation for a harmonic oscillator, first developed by Woolf and Roux⁶³ and reformulated by Hummer.⁶⁴ This method has also been used by Luo et al.⁸⁵ for studying the passage of ions through a modified α-hemolysin pore used in DNA sequencing experiments.

As with the PMF calculations, the ions were restrained to various points by a harmonic spring $(U(r)=\frac{1}{2}K{\mid \mathbf{r}-{\mathbf{r}}_0\mid }^2$, where K = 4.0 kcal/(mol Ų)). Obtaining accurate estimates of the ion diffusivity was found to require simulation trajectories substantially longer than those used to compute the PMF maps. Hence, the results of the umbrella sampling simulations were not reused to compute the ion diffusivity. Instead, we created a 4.0 × 4.0 × 7.2 nm³ periodic box of water containing a single A·T or G·C DNA basepair, 7 K⁺ ions, and 5 Cl⁻ ions. One ion (either K⁺ or Cl⁻) was restrained to an array of positions at various distances from the DNA. The DNA atoms were restrained as in the umbrella sampling simulations. Each simulation lasted 80–100 ns, with the position of the chosen ion recorded every 16 fs.

The first 9.6 ps of the trajectory were discarded, and the remaining portion was cut into 9.6 ps-long subtrajectories. These subtrajectories were used to compute the correlation time of the ion position for each simulation as $\tau ={\int }_0^{\infty }\text{d}t\langle \delta x(t)\delta x(0)\rangle /\langle \delta x^2\rangle$. The value of τ was seen to converge well for t = 9.6 ps, thus the infinite limit on the integral was replaced with the length of the subtrajectory t = 9.6 ps to enhance sampling. The diffusivity near the position to which the ion was restrained r is then D(r) = 〈δx²〉/τ.⁶⁴ Rigorously, the diffusivity near the DNA is not isotropic and should be represented by a tensor. However, for simplicity, we calculated the projection of the diffusivity along each axis (x, y, and z) and averaged the three values to obtain a scalar diffusivity.

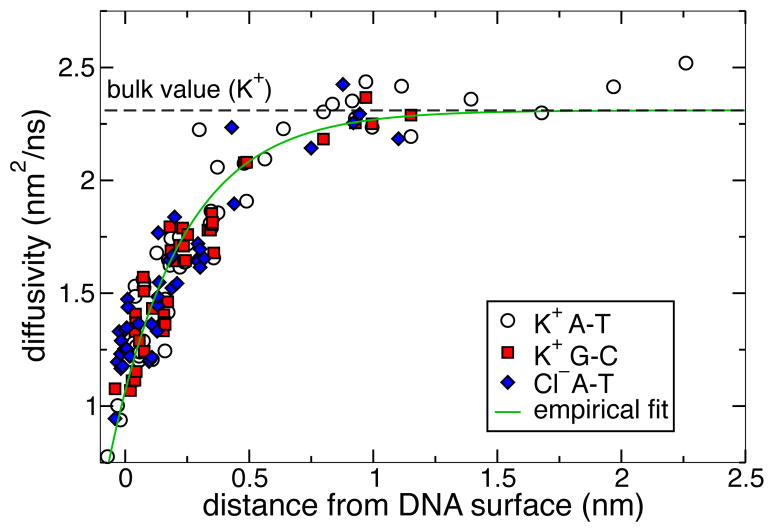
We then developed an easily computable approximation to the diffusivity of the ions near DNA. First, we assumed that the diffusivity depends only on the distance between the ion surface and the nearest surface of a DNA atom. The atomic surfaces were modeled as spheres with radii given by the CHARMM value of the Lennard-Jones parameter R_min/2. Figure 4 plots the ion diffusivity against the ion–DNA distance. We find the following function to accurately approximate the ion diffusivity data:

$$D(\mathbf{r})=D_{\text{bulk}}\left[1-(1-D_0/D_{\text{bulk}})e^{-d(\mathbf{r})/b}\right],$$ (6)

where D_bulk is the bulk diffusivity at 0.1 M calculated from MD, d(r) is the distance between the ion and DNA surfaces at position r, and D₀ is the diffusivity at d = 0, and b is a characteristic distance over which the diffusivity approaches its bulk value. Here, D₀ and b are parameters determined from the data shown in Figure 4.

Figure 4.

Local diffusivity of ions in proximity of DNA. The diffusivity values were computed as described in the text for a number of positions scattered around an A·T or a G·C basepair. The values are plotted against the distance between the atomic surfaces of the ion and DNA.

By performing a nonlinear fit of Eq. (6) to the data shown in Figure 4, we obtained D₀ = 1.01 nm²/ns and b = 0.293 nm for K⁺ ions. As the data for K⁺ and Cl⁻ ions were the same within the statistical accuracy of our calculations, we used the same values of D₀ and b for both K⁺ and Cl⁻ but a different D_bulk value for each ion type. BD simulations of ion current showed little sensitivity to the precise values of D₀ and b.

Results and Discussion

Here we validate the ARBD method by comparing the results of ARBD simulations with the results of all-atom MD. First, by comparing directly computed PMF maps with those constructed using smaller PMF fragments, we determine to what extent our modular approach to building PMF maps can be successful. Next, we compare the ion distributions resulting from ARBD and MD simulations. Finally, we show that the two methods make similar predictions for ion current. Of particular importance is that the ARBD method shows differences in the current through nanopores containing DNA molecules of different sequences, and that these differences agree well with those determined through conventional all-atom MD.

Validation of combining PMF maps

We first sought to determine to what extent it was possible to combine PMF maps of small systems into larger PMF maps. This portion of the validation of the method required no BD simulations at all, but instead relied on comparisons between PMF maps constructed by combining smaller maps and PMF maps directly calculated for larger systems. The water-mediated interaction included in the PMF maps should not be strictly additive; however, the sum of PMF maps can give approximately correct results in some cases.

Here, we show that systems consisting of a few nucleotides or basepairs can be constructed from PMF maps of isolated nucleotides with only minor artifacts. We also describe PMF map manipulations that emulate sequence substitutions in a DNA fragment. Finally, we find that constructing double-stranded DNA from the PMF maps of isolated nucleotides or basepairs fails to capture the strong attraction of K⁺ for the minor groove as shown in the PMF map for an effectively infinite molecule of double-stranded DNA. However, we find that it is possible to create maps for double-stranded DNA molecules of different sequences by substitution of the bases in the PMF map for an effectively infinite molecule.

Basepairs

Comparable PMF maps for a basepair of DNA were created in two ways. First, a PMF map of the basepairs was created directly by performing umbrella sampling simulations in all-atom MD using an A·T basepair. The second PMF map was made by combining independent PMF maps of isolated A and T nucleotides.

To produce the combined map, the isolated PMF maps were transformed to exactly fit the A·T basepair. Let T_A be the rigid transformation that maps each atom of the isolated nucleotide A to the corresponding atom of the nucleotide A in the A·T basepair structure: ${\mathbf{R}}_{\text{i}}^{\text{A}}=T_{\text{A}}{\mathbf{r}}_{\text{i}}^{\text{A}}$, where ${\mathbf{R}}_{\text{i}}^{\text{A}}$ is the position of atom i in the A·T basepair structure and ${\mathbf{r}}_{\text{i}}^{\text{A}}$ is the position of atom i in the isolated A nucleotide structure. Let T_T be likewise defined, so that the combined PMF map of an A·T basepair w_A·T(r) at an arbitrary position r is computed as

$$w_{\text{A}·\text{T}}(\mathbf{r})=W_{\text{A}}(T_{\text{A}}^{-1}\mathbf{r})+W_{\text{T}}(T_{\text{T}}^{-1}\mathbf{r}),$$ (7)

where W_A(r) and W_T(r) are the PMF maps directly computed from the isolated A and T nucleotides. In practice, the values of the PMF maps are only available on a discrete grid, so tricubic interpolation is used to obtain values at arbitary points.

We do not expect the combined PMF to exactly match the directly computed PMF. As noted earlier, the PMF maps of the isolated nucleotides include the effects of hydrating water molecules. The presence of a second nucleotide alters the structure of water in its vicinity, so that the hydration effects in the PMF of the combined system may not be a simple function of the PMF maps of the two isolated systems. However, we find map addition to be a rather accurate approximation in the case of systems comprising of few nucleotides.

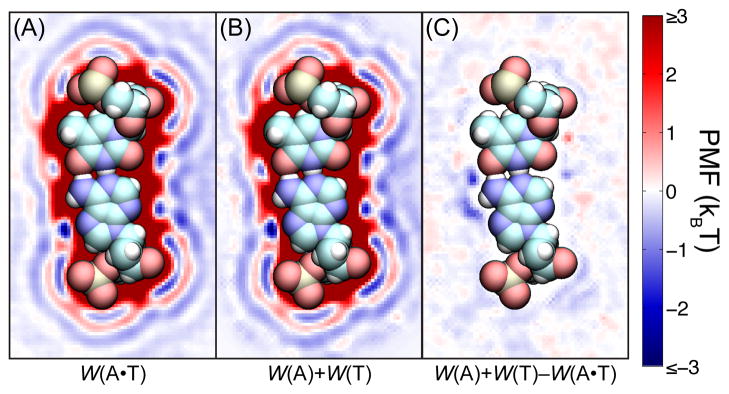
Thus, Figure 5 compares cross sections of the PMF map calculated directly for an A·T basepair (Figure 5A) and the PMF map constructed by combining the PMF maps for isolated A and T nucleotides (Figure 5B). Because the short range nature of the hydration effects, the combined PMF should be quite accurate for portions of the A nucleotide which are far from the T nucleotide and vice-versa. Indeed, the largest deviation between the combined and directly computed maps (Figure 5C) occurs where the amine group of the A nucleotide hydrogen bonds to the oxygen of the T nucleotide. However, this deviation occurs in the volume that is only 0.1 nm in diameter and the error introduced by it may be negligible for many purposes.

Figure 5.

Combining nucleotide PMF maps to form a PMF map for a basepair. (A) Cross section of a K⁺ PMF map directly computed from all-atom MD simulations of an A·T basepair. (B) Cross section of a K⁺ PMF generated by the addition of two PMF maps for isolated A and T nucleotides. (C) Difference between values shown in panels A and B. To indicate the location of the basepair, a space filling model of the atoms is overlaid on each cross section.

Sequence substitutions

A single-stranded DNA (ssDNA) molecule is very flexible in free solution and its nucleotides can adopt many different conformations. Thus, to accurately represent ssDNA in ARBD, it is necessary to generate PMF maps for many different conformations of DNA nucleotides. If we wish to study the sequence dependence of ion–DNA interaction, we might, in principle, need to generate PMF maps of each conformation for each possible sequence. The generation of these maps could easily consume all available computational resources. However, it may be possible to avoid such expensive computations.

DNA nucleotides have identical sugar-phosphate backbones and differ only by the structure of their nitrogen bases. Serendipitously, these bases consist mainly of ring structures which are relatively rigid, allowing each base to be accurately represented by a single rigid structure. Thus, it might be possible to construct approximate PMF maps for ssDNA molecules with identical backbones but different sequences.

Clearly, the sequence of the DNA affects which conformations of the backbones are likely and some structures with one sequence might be impossible with another sequence. For example, A and G bases may be sterically excluded from confomations accessible to the smaller T and C bases. However, it is of particular interest to determine how the DNA sequence can affect ion current directly; given two DNA molecules with nearly identical backbone conformations and similar base orientations, how do different DNA sequences produce different ion currents?

To answer this question, we developed the following scheme to substitute bases in the PMF maps of a multinucleotide DNA molecule. We began with having the maps of isolated nucleotides determined previously. Since each isolated nucleotide had the same backbone conformation, the maps can be formally represented as

$$\begin{array}{l}{W}_{\text{isolated}}(\text{A})=w({\text{backbone}}_0)+w({\text{base}}_{\text{A}}),\\ W_{\text{isolated}}(\text{T})=w({\text{backbone}}_0)+w({\text{base}}_{\text{T}})\end{array}$$ (8)

where an uppercase W represents PMF maps calculated from MD simulations and a lowercase w represents formal reconstitutions of these PMF maps. We calculated a PMF map for a three-nucleotide molecule of ssDNA with the sequence AAA, which can be represented as

$$w_{\text{mol}}(\text{AAA})=w({\text{backbone}}_1)+T_{1}w({\text{base}}_{\text{A}})+T_{2}w({\text{base}}_{\text{A}})+T_{3}w({\text{base}}_{\text{A}}),$$ (9)

where T_i is the rigid transformation of the base of the isolated nucleotide A that gives the best fit with the ith base of the three-nucleotide ssDNA molecule. In practice, T_i is the rigid transformation that minimizes the mass-weighted square-displacement between the atoms in the structure that was used to compute the isolated nucleotide PMF and the atoms in the ssDNA structure.

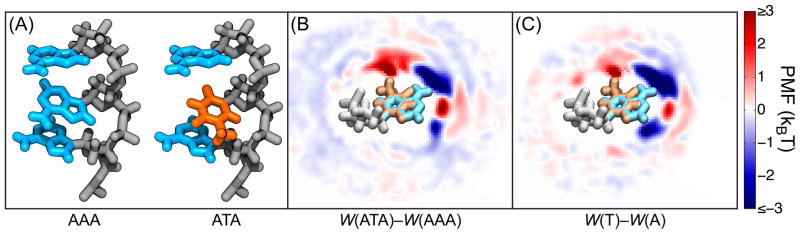
Figure 6 shows that a substitution of the base of an isolated nucleotide leads to approximately the same change in the PMF map as a substitution of a base in the ssDNA molecule. Thus, approximately,

Figure 6.

Sequence substitutions in the PMF map of an extended ssDNA molecule. (A) Atomic structures of three-nucleotide DNA molecules with similar conformations but different sequences. (B) The difference in the K⁺ PMF maps generated from the structures shown in panel A. A cross section of the map is shown with the position of the substituted nucleotide shown for reference. (C) The difference in the K⁺ PMF maps of isolated nucleotides transformed so that the bases match the structures in panel A. The changes in the PMF map upon the substitution from an A base to a T base are similar between the three-nucleotide DNA molecule and the isolated nucleotides, although there are some obvious differences.

$$W_{\text{mol}}(\text{ATA})-W_{\text{mol}}(\text{AAA})\approx T_2[W_{\text{isolated}}(\text{A})-W_{\text{isolated}}(\text{T})],$$ (10)

where W_mol and W_isolated are the calculated PMFs for the three-nucleotide molecules and the isolated nucleotides, respectively. To substitute the sequence, we subtract the transformed PMF maps for A and add the transformed PMF maps for the desired substitution.

For example, we approximated the change of sequence from AAA to ATA by

$$w(\text{ATA})=W(\text{AAA})-T_{2}W(\text{A})+T_{2}W(\text{T}),$$ (11)

We now show that this gives the desired formal result, that is, a PMF like Eq. (9), but with base 2 changed from A to T. By substituting Eq. (8) into Eq. (11), w(backbone₀) formally cancels:

$$w(\text{ATA})=W(\text{AAA})-T_2[w({\text{backone}}_0)+w({\text{base}}_{\text{A}})]+T_2[w({\text{backone}}_0)+w({\text{base}}_{\text{T}})].$$ (12)

Substituting W_mol(AAA) from Eq. (9) leaves us with

$$w(\text{ATA})=w({\text{backone}}_1)+T_{1}w({\text{base}}_{\text{A}})+T_{2}w({\text{base}}_{\text{T}})+T_{3}w({\text{base}}_{\text{A}}),$$ (13)

which is equivalent to Eq. (9) but with base 2 replaced by T.

Hence, beginning with a full PMF map for a multi-nucleotide ssDNA strand, it is possible to produce accurate PMF maps for its sequence variants by first subtracting the PMF map of the nucleotide to be replaced from the full PMF and then adding the PMF map of the substitution.

DNA double helix

Within living things, DNA is stored in the form of a stable double helix (often referred to as B-form DNA). An example of this structure is shown in Figure 7A. Our ARBD method for simulation of ion–DNA interaction would be incomplete if it could not describe this most common form of DNA. However, representing B-form DNA is particularly challenging because the nucleotides in the struture are packed very densely. As shown in Figure 7B, the PMF map of B-form DNA for K⁺ cannot be accurately constructed by adding the PMF maps of isolated nucleotides. Significant deviations are apparent between the directly computed PMF map and the combined PMF, especially within the minor groove that should exhibit strong attraction to K⁺ in B-form DNA. Attempting to construct a map for such a molecule from the maps of isolated nucleotides leads to a serious underestimation of this attraction. Water molecules within the tight confines of the minor groove show ordering and preferred orientations,⁸⁷ which affect K⁺ behavior but are not present for isolated nucleotides.

Figure 7.

PMF maps for a DNA double helix. (A) Ten basepairs of A·T DNA arranged in a B-form double helix. The atoms at the top of the molecule are linked to those at the bottom by the periodic boundary conditions, making the molecule effectively infinite. (B) Cross sections of the K⁺ PMF map for this molecule directly computed from MD simulations (left) and constructed by adding PMF maps of isolated nucleotides (right). Significant discrepancies exist, especially in the minor groove of the DNA. The locations of the minor and major grooves are indicated by “minor” and “major” in the left panel. An image of the basepair closest to the cross-section plane is overlays the cross sections. (C) Cross sections of the PMF difference between A·T and G·C basepairs for maps computed directly from MD simulations (left) and for maps constructed by adding PMF maps of isolated nucleotides (right).

To correctly describe ion interaction with the minor and major grooves of B-form DNA, it is necessary to generate the PMF map directly from an all-atom MD simulation of B-form DNA. The structure of DNA in the canonical B-form very nearly repeats itself over a step of 10 basepairs. Therefore, beginning with the PMF map of a 10 basepair-long molecule of DNA made effectively infinite by periodic boundary conditions, we can construct an arbitrarily long molecule. However, generating PMF maps for B-form DNA of arbitrary sequence might require an unfeasible number of umbrella sampling simulations. We found instead that it is possible to produce a PMF map for B-form DNA of an arbitrary sequence using the substitution method described above. Thus, Figure 7C compares the sequence-specific differences in the PMF maps obtained from direct PMF calculations and constructed using PMF maps of isolated nucleotides. The similarity of the difference maps suggests that the PMF maps for the isolated nucleotides can be combined with the PMF map of a duplex helix to produce approximate models for double-stranded DNA of arbitrary length and sequence.

Note that we have not considered the construction of PMF maps for Cl⁻ ions interacting with B-form DNA. Due to the high negative charge density of B-form DNA, the density of Cl⁻ ions is very low near the DNA under typical conditions. Thus, a PMF map constructed by adding the PMF maps of isolated nucleotides should suffice for Cl⁻.

Validation of ion distributions

Accurate description of the ion distribution near DNA is a prerequisite to accurate prediction of the ion current. Below we compare ion distributions obtained in ARBD and all-atom MD simulations of the following five types of systems: bulk KCl solution, a model nanopore with a surface attractive to ions, isolated nucleotides, DNA basepairs within a model nanopore, and an effectively infinite DNA double helix.

Radial distribution functions in bulk solution

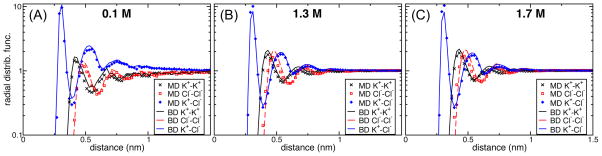
To ensure that the interaction between ions is properly accounted for in ARBD, we computed the radial distribution functions of each ion pair in both ARBD and MD simulations of the same system for several KCl concentrations. Both types of simulations were performed in a 4.0×4.0×7.2 nm³ unit cell. Figure 8 shows good agreement between MD and ARBD, although at 1.3 and 1.7 M the height of the first peak in the K⁺–Cl⁻ distribution is smaller in ARBD than in MD and decreases with concentration.

Figure 8.

Comparison of radial distribution functions for ions in MD and ARBD. (A), (B), and (C) show results for bulk KCl solution at 0.1, 1.3, 1.7 M concentrations. All-atom MD results are represented by symbols, while the ARBD results are shown by continuous or dashed lines. Note that the vertical axis has a logarithmic scale.

A model nanopore

Several types of nanopores have been used for performing DNA translocation experiments, including the protein nanopore α-hemolysin,⁷ α-hemolysin with an adaptor molecule,¹⁰ and MspA,¹¹ as well as synthetic nanopores made from silicon nitride⁸⁸ and graphene.^89–91 For the purpose of method validation, here we use a phantom pore, which is a featureless, frictionless potential energy surface that mimics the effect of a nanopore.³⁵ Specifically, we consider a 1.8 nm-diameter cylindrical pore in a 3.5 nm-thick membrane. In MD simulations, we have found that surfaces made of materials such as thin graphite sheets attract ions: the PMF of the ion near the surface is lower than that in bulk. As a model of such a surface, a −2 k_BT potential well was imposed near the surfaces of the pore and membrane as descibed in Methods.

All nanopore simulations were performed using a 4.0×4.0×7.2 nm³ unit cell in which the membrane filled the region −1.75 < z < 1.75 nm. Three systems having KCl concentrations of 0.1, 1.3, 1.7 M were used. Because these same simulations were also used for computing ion currents, an external bias of 180 mV was applied across the z axis. Several independent MD simulations were run in parallel for each KCl concentration. After discarding the first 0.5 ns of each simulation, the ion concentrations were calculated from 809, 523, and 214 ns of data for the 0.1, 1.3, and 1.7 M systems, respectively. Only two ARBD simulations were run for each concentration. Again, the first 0.5 ns of each were discarded, yielding 1990, 399, 199 ns of data for the 0.1, 1.3, and 1.7 M systems.

Figure 9 plots the ion concentration in a phantom pore as a function of the distance from the pore axis, obtained by averaging the corresponding BD and MD trajectories. At low and moderate concentrations (up to 5 M local concentration), both methods are in good quantitative agreement with each other. At very high ion concentrations (~7–8.5 M), small differences in the description of the ion–ion interaction between the two methods (possibly due to 3-body effects in the MD simulations) result in ion distributions that differ by up to 20% in the highest concentration regions, Figure 9C.

Isolated nucleotides

Next, we tested whether the ARBD method could reproduce the ion distribution near isolated nucleotides. For this purpose, we performed MD simulations similar to those used for producing the 3D PMF maps of the isolated nucleotides except that ion concentration was 1 M and no ions were restrained. The atoms of the DNA were restrained; a 4.5×5.0×4.1 nm³ unit cell was used. The ARBD systems were constructed to mimic the all-atom systems. Ten independent simulations (80 ns each) were performed for each system. To compute ion distribution, the first 0.5 ns of each simulation was discarded.

Cross sections of the ion distribution near isolated A and T nucleotides for all-atom MD and ARBD simulations are shown in Figure 10. The uncertainty in the averages is quite high due to the difficulty of obtaining long MD trajectories; however, the ARBD method seems to capture well the differences between the A and T nucleotides seen in the MD results.

Figure 10.

Comparison of the K⁺ ion distribution around isolated nucleotides. Shown is a 2D cross section of the K⁺ distribution in MD (A and B) and the ARBD (C and D) simulations of adenine (A and C) and thymine (B and D). In all simulations, bulk KCl concentration is 1 M. No (M) ions entered the area region nearest the nucleotides shown in white.

Pore containing DNA basepairs

To create an all-atom representation of a very simple DNA nanopore system, we placed sets of two nucleotides in the form of a basepair within the phantom nanopore. PMF maps of the isolated nucleotides were transformed and added to the potential energy map of the phantom pore to create 3D PMF maps that mimicked the all-atom systems. In all simulations, external electric field was applied along the z axis (parallel to the pore axis) to produce a voltage drop of 180 mV across the entire system.

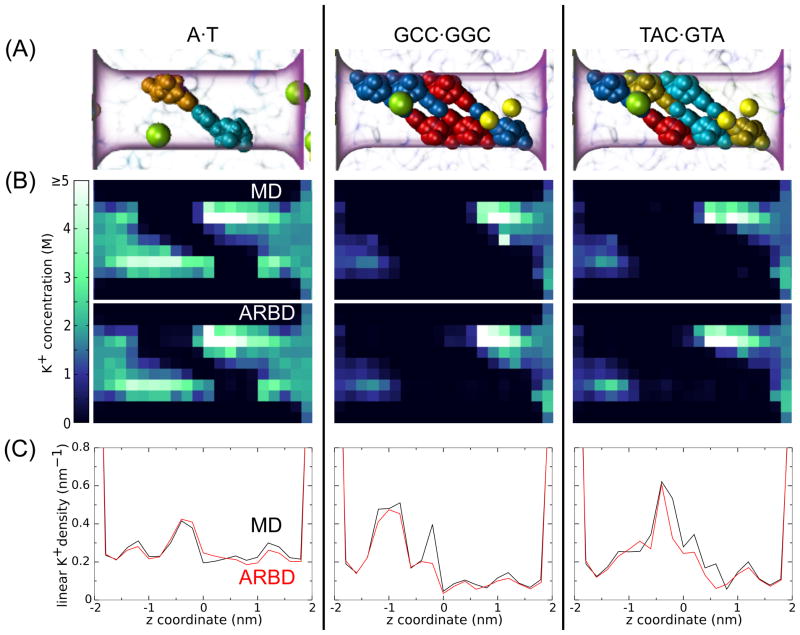
As a measure of the success of the ARBD method for reproducing MD results, we calculated the density of K⁺ ions (which interact most strongly with DNA). Figure 11A illustrates the conformations of DNA in the following three test systems. One system contains a single A·T basepair, tilted with respect to the pore axis. The other two systems contain the basepair triplets GCC and TAC (see Figure 16B for the naming convention). In Figure 11B, we compare cross sections of the K⁺ concentration between all-atom MD and ARBD. Note that the concentration within the pore is much larger than the bulk concentration, which was 1.7 M for the single basepair system and 1.3 M for the triplet systems.

Figure 11.

K⁺ distribution in a pore containing DNA basepairs. (A) Atomic structures of DNA molecules in a nanopore, including a single A·T basepair, and basepair triplets with GCC and TAC sequences. The semi-transparent purple surface shows the location of the pore. The DNA nucleotides A, T, G, and C are shown in cyan, orange, blue, and red, respectively. K⁺ and Cl⁻ ions are shown as yellow and green spheres. For clarity, fewer ions are shown than the typical numbers in the pore at 1.3 and 1.7 M. Water is not shown. (B) Cross sections of the K⁺ concentrations for each system. All-atom MD results are shown above the ARBD results. The cross section plane passes through the center of the pore and contains the pore axis. (C) Number density (number/nm) of K⁺ and Cl⁻ along the pore axis. The all-atom MD and ARBD results are shown in black and red, respectively.

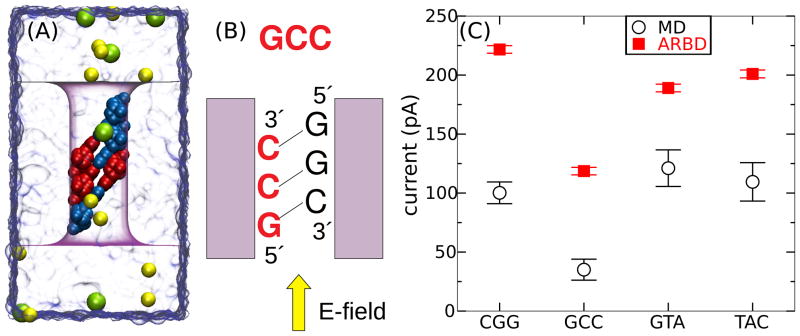
Figure 16.

Ion current through a nanopore blocked by DNA basepair triplets. (A) All-atom MD model of the simulation system. The system is drawn using the same representations as Figure 15A (B) Diagram showing the convention used for naming the sequences. The system shown here is referred to as GCC. (C) Calculated ion current through the pore containing basepair triplets of four different sequences. The MD simulations for CGG and GCC lasted 0.4 μs, while those for GTA and TAC lasted 0.14 μs. The ARBD simulations lasted 16 μs in all four cases. The systematic deviation of the ARBD results is attributable to the higher bulk conductivity of the ARBD solution, Figure 13A, and the high (>2 M) ion concentration in the pore, Figure 11B. The ARBD method qualitatively reproduces large sequence-dependent differences in the currents.

A close correspondence between the results of all-atom MD and ARBD can be clearly seen from the plot of the K⁺ density along the pore axis, shown in Figure 11C. Most strikingly, ARBD reproduces many of the sequence-dependent features of the all-atom MD simulations.

DNA double helix

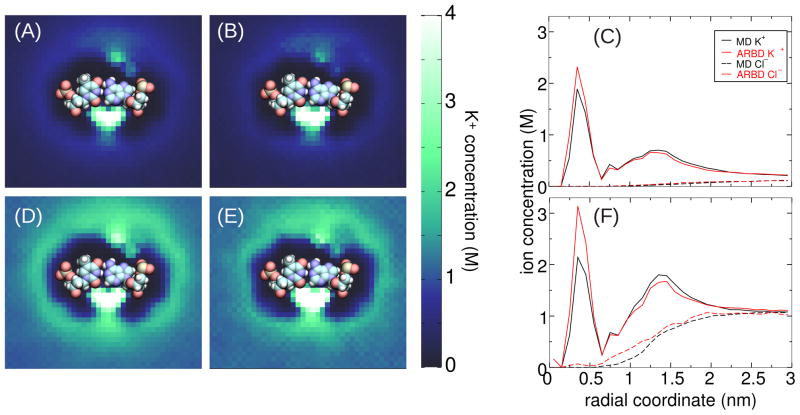
In the last two sets of simulations, the positions of the atoms of the DNA nucleotides were restrained in the MD simulations to facilitate the comparisons between the ARBD and MD methods. Double helical DNA is sufficiently rigid that we can easily compare the ion distribution in ARBD simulations to that in all-atom MD simulations with no artificial restraints. In the MD simulations, the effectively infinite dsDNA (20 basepairs in the length) was free to diffuse laterally and undergo conformational fluctuations. In the ARBD simulations, we used the PMF map for an effectively infinite dsDNA 10 basepairs in length. This map was duplicated to produce a PMF map of a 20 basepair dsDNA. Despite the fact that conformational fluctuations were present in the MD simulations, we found that ARBD was able to approximately reproduce the local ion distribution near the DNA.

To permit comparisons between the all-atom MD, in which the DNA was unrestrained, and the ARBD simulations, which used a static 3D PMF map for each ion type, we computed the local ion distribution around each basepair. The basis of each basepair was defined by the vectors e_x, e_y, and e_z. Vector e_z was the average normal of the bases; specifically, e_z = U(n_T − n_A), where U(v) scales v to unit length and n_B is the unit vector orthogonal to the plane of the pyrimidine or purine rings of base B and pointing in the 5′ to 3′ direction of the backbone. Vector e_x ran along the vector connecting the C1′ atom of the T nucleotide to the C1′ atom of the A nucleotide, with the projection along e_z removed. Letting r_TA = r_A(C1′) − r_T(C1′), we calculate e_x = U(r_TA − (r_TA · e_z)e_z). The final basis vector was chosen to produce an orthonormal right-handed basis: e_y = e_z × e_x.

The ion positions were histogrammed every 5 ps in the local basis of each basepair using cubic bins with 0.1 nm side lengths. The results were averaged over all 20 basepairs and over 55 ns in the MD simulations and over 100 ns of ARBD simulations. The results are shown in Figure 12. The MD simulations show a very high concentration of K⁺ in the minor groove for both 0.1 and 1.0 M concentrations of KCl (Figure 12A, D). Smaller but prominent concentration maxima are visible in the major groove as well. The ARBD method seems to reproduce well the shape and location these high concentration regions (Figure 12B, E), although the occupancy of the major groove at all concentrations and the occupancy of the minor groove at 1.0 M KCl is somewhat smaller in ARBD than in MD. The radial averages of the ion concentration cross sections (Figure 12C, F) clearly show that the ARBD simulations reproduce the K⁺ distributions in the volume that extends beyond the grooves of dsDNA (radial coordinates > 0.5 nm), which is the region contributing the most of the nanopore ionic current.⁴³

Figure 12.

Ion distribution near a DNA double helix (A) Cross section of the K⁺ distribution near A·T in a 0.1 M KCl solution computed from an all-atom MD simulation. (B) The same as panel A except computed from an ARBD simulation. (C) Radial average of the cross sections for K⁺ and Cl⁻ from the center of mass of the basepair (0.1 M bulk KCl). (D) Cross section of the K⁺ distribution near A·T in a 1.0 M KCl solution computed from an all-atom MD simulation. (E) The same as panel D except computed from an ARBD simulation. (F) Radial average of the the cross sections for K⁺ and Cl⁻(1 M bulk KCl). An image of the basepair nearest to the cross section plane is faithfully overlaid on the cross section plots. The minor groove of the DNA molecule lies just beneath the bases; the major groove lies above.

Validation of transport properties

Our motivation for the development of the ARBD method was to enable computationally efficient but accurate estimates of ion current through nanopores containing DNA. Thus, the final test is to show that our method is capable of predicting current values that agree with the results of all-atom MD. Most importantly, we wish to see that the ARBD method makes the same predictions as all-atom MD with regard to the relative values of ion current for DNA systems of similar conformations, but different sequences.

To induce current flow, we applied a uniform electric field E_z to the each system described below, corresponding to an additional force in both the MD and BD formalisms given by ${\mathbf{F}}_i^{\text{ext}}=q_i{E}_z{\mathbf{e}}_z$, where q_i is the charge of ion i and e_z is a unit vector along the z axis. For nanopore systems, we report the external bias voltage V, which was calculated by V = −E_zL_z, where L_z is the length of the system along the z axis.⁶⁷ Due to the geometry of systems and the presence of free ions, this external bias voltage is approximately equal to the voltage drop across the membrane. In systems with KCl concentrations of 0.1 M, however, the small number of free ions makes this approximation less accurate and the voltage drop across the pore is appreciably less than V.

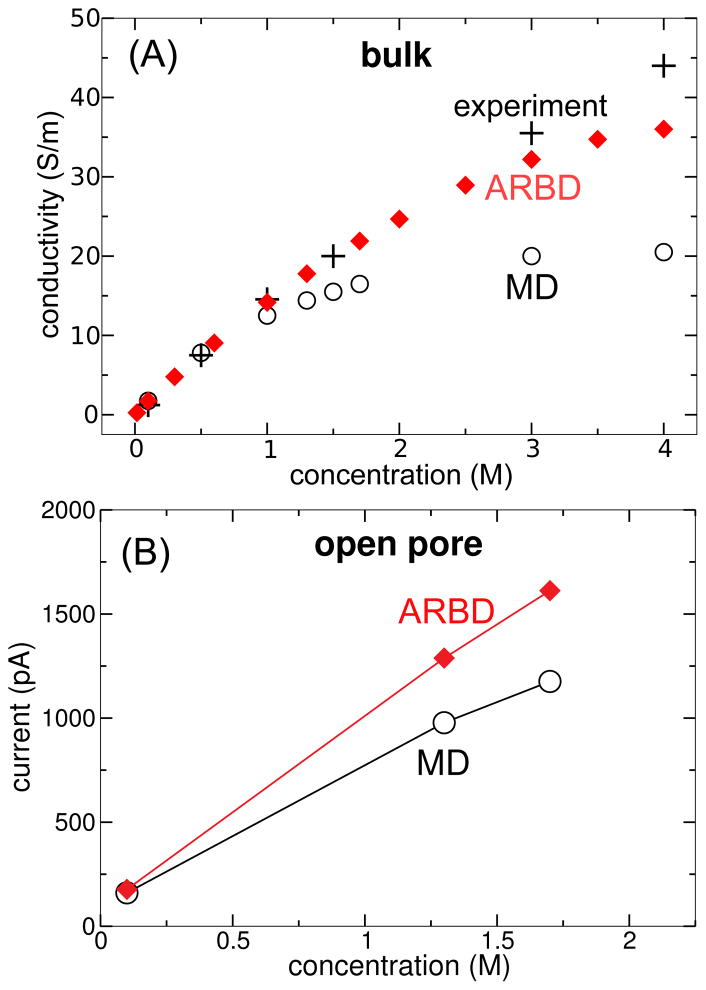
Conductivity of bulk electolytes

First, we compared the conductivity of bulk KCl solutions simulated using the all-atom MD and ARBD methods. A periodic box having dimensions of 4.0×4.0×7.2 nm³ was filled with KCl solutions of several concentrations. In all-atom MD, these solutions consisted of ions and water molecules, while in ARBD they consisted solely of ions. An electric field of 2.5×10⁷ V/m was applied in the z direction to induce a current of ions.

Figure 13A plots the current as a function of the ion concentration for all-atom MD and ARBD, along with experimental values.⁴⁰ At 0.1 M, the three current values agree within the uncertainty of the measurements. However, despite the fact that the bulk diffusivities of the ions differ by <4% at 1.3 M (see Figure 4) there is a difference in the conductivity of about 30%. The reason for this is that while the ions in the BD simulations closely obeyed the Einstein relation (the diffusivity is related to the electrical mobility μ_elec by D = k_BT μ_elec/q, where q is the ion’s charge), the ions in the all-atom MD simulations did not, presumably due to formation of ion pairs.⁹² Indeed, at bulk concentrations of 1.3 and 1.7 M the number of ion pairs was about 14% larger in the MD trajectories than in the ARBD trajectories. The MD simulations show an electrical mobility significantly less than qD/(k_BT), where D is the diffusivity calculated from the mean-square displacement of the ions orthogonal to the electric field.

Figure 13.

Bulk and open-pore ion currents predicted by all-atom MD and ARBD. (A) Conductivity of bulk KCl solution plotted against the KCl concentration. Experimental values (shown as black crosses) from⁴⁰ are included. (B) Current through a phantom nanopore plotted against the KCl concentration.

At a KCl concentration of 1.3 M, the conductivity predicted by ARBD is 23% larger than that predicted by all-atom MD. The deviation increases with concentration; however, ARBD closely follows the experimental dependence⁴⁰ for KCl concentrations <3.0 M. Although our goal for ARBD was to reproduce the results of all-atom MD, it appears that the currents predicted by ARBD are closer to experiment than those predicted by all-atom MD at ion concentrations > 1 M. While bulk ion concentrations > 1 M are only occasionally used in experiments, the accuracy of the model at these concentrations remains relevant due to the enhanced ion concentrations near DNA (see Figure 11B).

Open-pore current

The current through a 1.8 nm-diameter cylindrical phantom pore in a 3.5 nm-thick membrane was calculated in both ARBD and all-atom MD. A voltage drop of 180 mV was applied along the z axis of the system. Figure 13B indicates good agreement between the results of all-atom MD and ARBD at 0.1 M, but a systematic overestimation of the current by ARBD at the larger KCl concentrations, which is similar to the trend observed in the simulations of bulk conductance (Figure 13A). Not only does the total current agree well between MD and ARBD, but the two methods also give similar spatial distributions of the currents within the pore, as shown in Figure 14. An interesting observation is that although the ion concentration 0.5 nm away from the center of the pore (shown in Figure 9) is systematically lower in ARBD than in MD at 1.3 and 1.7 M concentrations, the ion current there (in Figure 14) does not follow the same trend, likely due to the difference in conductivity between the two methods at high concentrations.

Figure 14.

Distribution of K⁺ and Cl⁻ currents in a phantom pore. The density of the current in an annular regions centered on the pore axis is plotted against the mean distance from the pore axis to the annulus for bulk KCl concentrations of (A) 0.1 M, (B) 1.3 M, and 1.7 M (C). Note that the current maximum near a radial coordinate of 0.75 nm coincides with the maximum of the ion concentration (see Figure 9), which is due to the −2k_BT attractive potential energy at the pore wall.

Blockade current: single DNA basepairs

Next, we analyze the ion current through a nanopore containing a single basepair of DNA, using a model shown in Figure 15A. Again, a voltage drop of 180 mV was applied along the z axis. Because of the tilting of the basepairs, we formally distinguish the configuration A·T from T·A. Here, X·Y means that a positive ion moving along the direction of the electric field will first encounter the X nucleotide before encountering the Y nucleotide. Such tilted conformations of DNA nucleotides are common in stretched dsDNA molecules.^93,94

Figure 15B,C compares the predictions of the MD and ARBD methods at KCl concentrations of 0.1 and 1.7 M. For each basepair system, MD simulations had durations between 0.7 and 2.1 μs at 0.1 M and between 0.4 and 2.1 μs at 1.7 M. The ARBD simulations lasted 100 and 8 μs for the 0.1 and 1.7 M simulations, respectively. The uncertainty of the MD values are such that A·T and T·A or G·C and C·G cannot be unequivocally distinguished. However, the MD simulations reveal significantly higher currents on average for basepairs containing As and Ts than for basepairs containing Gs and Cs. Likewise, the ARBD method also predicts larger nanopore currents for A·T and T·A than for G·C and C·G. Due to the computational efficiency of ARBD, it is possible to obtain current estimates with a much higher accuracy. For the DNA conformation considered in these test simulations, G·C could be differentiated from C·G by an ion current measurement. Methylation of the cytosines had negligible effect on the blockade current.

At a KCl concentration of 0.1 M, the currents predicted by the ARBD and MD methods are in excellent quantitative agreement. At 1.7 M bulk concentration of KCl, the currents predicted by ARBD and all-atom MD exhibit similar qualitative dependences on the sequence and orientation of the DNA basepair. However, the ARBD currents are systematically larger than those predicted by all-atom MD. This should not be surprising given the high K⁺ concentration within the pore (see Figure 11B) and the fact that ARBD shows significantly larger currents at high ion concentrations than all-atom MD (see Figure 13). Taking into consideration that the ARBD method describes the concentration dependence of bulk conductance better than all-atom MD (Figure 13A), one might expect the BD method to provide more accurate estimates of the nanopore ionic current in the high-salt concentration regime than MD.

Blockade current: triplets of DNA basepairs

The current through a small nanopore containing DNA can depend dramatically on the conformation of the DNA and its sequence. To demonstrate the feasibility of using the ARBD method to predict the effect of sequence substitutions on nanopore ion current, we performed both ARBD and MD simulations of tilted triplets of DNA basepairs placed in the phantom pore. These models were constructed by replicating and translating by −0.65 or 0.65 nm single-nucleotide PMFs along the z axis. An all-atom model of this system is illustrated in Figure 16A. The bulk ion concentration in these simualations was 1.3 M; a voltage drop of 180 mV was applied across the entire system along the z axis. Figure 16B illustrates our convention for naming the basepair triplets.

In the ARBD simulations, we found the current through a nanopore blocked by a CGG DNA basepair triplet to differ from that of a GCC triplet by about a factor of two. This result was rather surprising because both structures consist of the same set of nucleotides. To determine whether this result was an artifact of the ARBD method or truly a consequence of the spatial arrangements of the DNA atoms, we simulated the ion current using the all-atom MD method for these two sequences along with another two sequences (GTA and TAC). Figure 16C shows that, indeed, all-atom MD predicts that the current for CGG is about twice the current for GCC. The relative values of the other triplets appear to be in agreement with the results of ARBD as well. We would like to stress that the MD results were not known prior to performing the ARBD simulations of the DNA basepair triplets. Thus, the ARBD method has been demonstrated to have predictive power, at least, in comparison with the all-atom MD method.

Conclusion

We have presented a BD method (referred to here as ARBD) capable of computing the ion current with accuracy similar to that of all-atom MD but at a substantially reduced (3–5 orders of magnitude) computational cost. Using contemporary commodity computers, such as single-core laptops or desktops, the ARBD method yields ion current trajectories tens of microseconds in length in a single day. Using many such commodity computers, one can obtain reliable estimates of the ion current through nanopores containing DNA of different sequences. The atomic-scale accuracy of our BD method originates from 3D PMF maps derived from all-atom MD simulations. By combining such PMF maps, it may also be possible to obtain current estimates for DNA molecules adopting many different conformations, with a minimum of expensive all-atom MD simulations. This method will find uses in interpreting data from nanopore sequencing experiments¹⁹ and designing nanopores for better DNA sequence discrimination.

That said, the ARBD method has a number of limitations that may need to be remedied in the future or may limit its applicability to particular problems. One major limitation of the method is that it requires computationally expensive all-atom MD simulations to derive the 3D PMF maps. While this procedure is essential to its accuracy, no computational resources would be saved if a new PMF map has to be generated for each new system. The efficiency of the method, therefore, is reliant on our ability to combine PMF maps to simulate many variants of similar systems. We have described our procedures for combining the maps, such as addition and subraction of the PMF maps to produce sequence variants of a DNA strand. Due to three-body interactions involving water molecules, these manipulations are approximations and may not succeed in all situations. For instance, we found that adding isolated PMF maps to form a DNA double helix did not result in an accurate map. However, it did appear to be possible to modify the sequence of the DNA in a map computed directly from a DNA double helix. Further improvements to the PMF map manipulation procedures, perhaps employing a model of the water-mediated effects that lead to non-additivity of the PMF maps, could extend the usefulness of the method.

While we have demonstrated that changing the DNA sequence represented in the PMF maps can be possible, changes to the conformation of the DNA are more difficult. In some cases, it may be possible to perform geometric transformations to the maps, such as adding a gentle bend to double helical DNA. However, smaller scale manipulations are likely to result inaccurate maps due to water-mediated effects. Thus, it may be necessary to generate PMF maps for each conformation of interest. Also, large external electric fields can stretch or distort the DNA²³ and smaller fields could change its distribution of conformations; therefore, the use of different DNA PMF maps for different values of the external electric field could be necessary.

Modeling different conformations is particularly important for flexible molecules, such as unfolded single-stranded DNA, whose conformation may change drastically on timescales as short as a few nanoseconds. In this work, we use only one static PMF map to represent the interaction between each ion and a given biomolecule, which worked well even for unrestrained double helical DNA. However, single-stranded DNA in the absence of tight confinement of a nanopore pore or other structure, may require multiple PMF maps to model the representative conformations that appear on the relevant timescales. These PMF maps could be dynamically alternated (perhaps in a smooth fashion) during the ARBD simulations to produce a current distribution similar to that measured in experiment. When and how to perform the alternations could be determined from a few long all-atom MD simulations, free-energy calculations, or perhaps by another coarser method. However, if long all-atom simulations are necessary to obtain conformational transitions on the micro- to millisecond timescale, it might in the end be more efficient to calculate the current directly from all-atom models.

As discussed in the introduction, three-body effects due to the exclusion of explicit solvent may cause a loss of accuracy. For example, the force acting between K⁺ and Cl⁻ ions is computed assuming only water between the two ions, unperturbed by any other bodies. Placing a nucleotide between the two ions should cause a considerable change in the force between the ions due to the lower dielectric constant of the DNA relative to the medium.⁹⁵ Such effects might be particularly important for incorporating various pore components used in nanopore experiments, such as proteins, lipid bilayers, and silicon-based materials, which typically have much lower dielectric constants than water. However, methods have already been developed to describe ionic systems in contact with dielectric materials.^96,97

Another limitation is the lack hydrodynamics in the ARBD method as presented. Including hydrodynamics interactions into models of Brownian motion by means of a diffusivity tensor is well developed⁹⁸ and could be applied to ARBD as well.

The model for position-dependent diffusivity used for production ARBD simulations is fairly simple. Whereas position-dependent diffusivity maps could be directly calculated from all-atom MD simulations, there appears to be no straightforward way to combine such maps. Thus, using such maps might require expensive computation of the map for each system of interest.

Clearly, the accuracy of the predictions of the ARBD method can only be as good as the accuracy of the PMF maps from which they were derived. Thus, our method is entirely reliant on the accuracy of the all-atom MD. It is quite reasonable to expect that any improvements to the all-atom MD method, such as the use of polarizable force fields,⁹⁹ can be incorporated into ARBD by recalculation of the PMF maps.

As a final note, we stress that the method presented here is not only applicable to ions interacting with DNA. For many applications where the interaction between a small ion or molecule and a larger body is important, and where reliable but costly atomistic models exist, similar approaches could be successful. For instance, we have recently applied a similar approach to simulate transport of a small solute through sticky submicron-long nanochannels.¹⁰⁰ The same approach can be used to describe competitive binding of ligands to an ensemble of proteins or the search of a DNA binding protein for its cognate site on dsDNA.¹⁰¹ Some of the ideas described here could also be applied to ion transport through protein channels; however, a proper description of the dielectric environment would be essential, and feedback between ion positions and the protein’s conformation could make the implementation much more difficult.