Solute Transport Across a Contact Interface in Deformable Porous Media

Abstract

A finite element formulation of neutral solute transport across a contact interface between deformable porous media is implemented and validated against analytical solutions. By reducing the integral statements of external virtual work on the two contacting surfaces into a single contact integral, the algorithm automatically enforces continuity of solute molar flux across the contact interface, whereas continuity of the effective solute concentration (a measure of the solute mechano-chemical potential) is achieved using a penalty method. This novel formulation facilitates the analysis of problems in biomechanics where the transport of metabolites across contact interfaces of deformable tissues may be of interest. This contact algorithm is the first to address solute transport across deformable interfaces, and is made available in the public domain, open-source finite element code FEBio (http://mrl.sci.utah.edu/software).

1. Introduction

Biological soft tissues may be modeled as deformable porous media to describe the deformation of their solid matrix as well as the transport of their interstitial fluid (Mow et al., 1980; Lai et al., 1991). The interstitial fluid typically consists of a solvent and multiple solutes, which play an important role in tissue metabolism. Finite element modeling of solid deformation and fluid transport in porous media has been an active topic of research over the last two decades (Simon et al., 1996; Frijns et al., 1997; Sun et al., 1999; Kaasschieter et al., 2003; Steck et al., 2003; Sengers et al., 2004; Yao and Gu, 2007). Modeling of contact interfaces in solid-fluid mixtures under finite deformation has been of particular interest in certain areas of biomechanics, such as diarthrodial joint mechanics (Donzelli et al., 1999; Un and Spilker, 2006; Yang and Spilker, 2007; Ateshian et al., 2010). However, an algorithm for modeling a deformable contact interface that allows solute transport has not yet been proposed. The objective of this article is to present a formulation of solute transport across a contact interface that builds upon our recent algorithm for contact of biphasic (solid-fluid) mixtures under finite deformation (Ateshian et al., 2010), and our recent implementation of neutral solute transport in a biphasic medium (Ateshian et al., 2011). Sample contact problems are presented, which demonstrate the application of this algorithm to problems involving large solid deformation and solvent and solute transport.

2. Contact Algorithm

A biphasic-solute mixture consists of a mixture of a solid matrix, a solvent and a solute (Mauck et al., 2003). Each of these constituents is idealized as intrinsincally incompressible, but the mixture can change in volume as a result of fluid exchanges with the solid matrix pore space (Bowen, 1980; Mow et al., 1980; Lai et al., 1991). The volume fraction of the solute is negligible in comparison to that of the solid (ϕ^s) and solvent (ϕ^w), so that ϕ^s + ϕ^w ≈ 1.

The solute concentration (moles per volume of interstitial fluid) is denoted by c. From principles of physical chemistry, c is not necessarily continuous across a boundary or contact interface, therefore it is not suitable as a nodal variable in a finite element analysis. As shown previously (Sun et al., 1999; Ateshian et al., 2011), based on the continuity of the solute mechano-chemical potential across non-dissipative interfaces (Ateshian, 2007), a suitable nodal variable is the effective concentration c̃ = c/κ̃, where κ̃ is the effective solubility (representing the fraction of the pore space actually occupied by the solute).

The fluid pressure, denoted by p, represents a combination of osmotic and mechanical effects. In the presence of solutes, the fluid pressure is not necessarily continuous across a boundary or contact interface. Therefore, based on the continuity of the solvent mechano-chemical potential across non-dissipative interfaces (Ateshian, 2007), a more suitable nodal variable in a finite element implementation is the effective fluid pressure p̃ = p − RθΦc, where p̃ represents the mechanical contribution to the pressure. The term RθΦc is the osmotic contribution to the pressure, where R is the universal gas constant, θ is the absolute temperature (assumed uniform), and Φ is the osmotic coefficient that describes the deviation of the osmotic pressure from ideal physico-chemical behavior.

The governing equations for a biphasic-solute mixture (Mauck et al., 2003; Ateshian et al., 2011) consist of the balance of linear momentum for the mixture,

$$\text{div}\mathbf{T}=\mathbf{0},$$ (2.1)

where T is the mixture Cauchy stress; the balance of mass for the mixture,

$$\text{div}({\mathbf{v}}^s+\mathbf{w})=0,$$ (2.2)

where v^s is the solid matrix velocity and w is the volumetric flux of solvent relative to the solid; and the balance of mass for the solute,

$$\frac{1}{J}\frac{D^s(J{\varphi }^w\stackrel{\sim }{\kappa }\stackrel{\sim }{c})}{Dt}+\text{div}\mathbf{j}=0$$ (2.3)

where J = det F, F is the deformation gradient of the solid matrix, D^s/Dt is the material time derivative in the spatial frame, following the solid, and j is the molar flux of solute relative to the solid. The dependence of w and j on gradients of fluid pressure and solute concentration may be derived from the balance of linear momentum for the solvent and solute (Mauck et al., 2003; Ateshian et al., 2011) (see Supplementary Data). These explicit relations are not needed for the presentation of the biphasic-solute contact formulation.

These governing equations may be solved in a finite element framework by applying the principle of virtual work and separating the virtual work δW into internal and external parts using the divergence theorem, as described previously (Bonet and Wood, 1997). For contact analyses (Laursen and Simo, 1993; Yang and Spilker, 2007; Ateshian et al., 2010), only the external virtual work is needed, which is given by

$$\delta W_{\text{ext}}={\int }_{\partial b}(\delta \mathbf{v}·\mathbf{t}+\delta \stackrel{\sim }{p}{w}_n+\delta \stackrel{\sim }{c}{j}_n)da,$$ (2.4)

where δv is the virtual velocity of the solid, δp̃ is the virtual effective fluid pressure, and δc̃ is the virtual molar energy of the solute; b represents the mixture domain in the spatial frame and ∂b is the boundary of b; da is an elemental mixture area on ∂b. Here, t = T · n is the mixture traction, with n representing the unit outward normal on ∂b; w_n = w · n is the normal component of the relative solvent flux; and j_n = j·n is the normal component of the relative solute flux. According to axioms of mass and momentum balance across surfaces (Eringen and Ingram, 1965), t, w_n and j_n must be continuous across boundaries and contact interfaces.

Because of the close similarity between the terms δp̃w_n and δc̃j_n, the finite element treatment of contact of biphasic-solute media is a natural extension to that of contacting biphasic media as presented in our earlier study (Ateshian et al., 2010). Therefore we forgo the detailed derivation and summarize the salient equations. A contact interface is defined between two surfaces, ∂b⁽¹⁾ and ∂b⁽²⁾. The portions of these surfaces which are in contact are respectively denoted by γ⁽¹⁾ and γ ⁽²⁾. The external virtual work produced at the contact interface is the sum of two expressions of the form given in (2.4), evaluated on γ⁽¹⁾ and γ⁽²⁾. Accounting for the continuity conditions t⁽¹⁾ + t⁽²⁾ = 0, $w_n^{(1)}+w_n^{(2)}=0$, and $j_n^{(1)}+j_n^{(2)}=0$, the contact virtual work, denoted by δG_c, may be reduced to an evaluation on the first of the two surfaces,

$$\delta G_c={\int }_{{\gamma }^{(1)}}(\delta {\mathbf{v}}^{(1)}-\delta {\mathbf{v}}^{(2)})·{\mathbf{t}}^{(1)}{da}^{(1)}+{\int }_{{\gamma }^{(1)}}(\delta {\stackrel{\sim }{p}}^{(1)}-\delta {\stackrel{\sim }{p}}^{(2)})w_n^{(1)}{da}^{(1)}+{\int }_{{\gamma }^{(1)}}(\delta {\stackrel{\sim }{c}}^{(1)}-\delta {\stackrel{\sim }{c}}^{(2)})j_n^{(1)}{da}^{(1)}.$$ (2.5)

By substituting these traction and normal flux continuity conditions in the formulation of a single contact integral, these conditions become enforced automatically, since equal and opposite values become prescribed on opposing contact surfaces.

In a finite element implementation the solution for the displacement of the solid matrix, u, effective fluid pressure p̃, and effective solute concentration c̃ is obtained at the nodes of the finite element mesh by letting δW = 0. Since δW is a nonlinear function of these variables, the solution is obtained iteratively using the linearization of δW along incremental changes Δu, Δp̃, and Δc̃. When applied to δG_c, this linearization has the general form

$$D\delta G_c=\sum _{i=1}^{2}D\delta G_c[\mathrm{\Delta }{\mathbf{u}}^{(i)}]+D\delta G_c[\mathrm{\Delta }{\stackrel{\sim }{p}}^{(i)}]+D\delta G_c[\mathrm{\Delta }{\stackrel{\sim }{c}}^{(i)}],$$ (2.6)

where Df [Δq] represents the directional derivative of the function f along Δq (Bonet and Wood, 1997). Clearly, the linearization needs to be performed by accounting for deformation, pressure and concentration on both of the contacting surfaces.

The linearization process involves the evaluation of Dt⁽¹⁾, Dw_n ⁽¹⁾ and j_n ⁽¹⁾, since they appear in (2.5). A standard approach for evaluating these directional derivatives is to employ the penalty method for relating the traction (Laursen and Simo, 1993) and fluxes (Ateshian et al., 2010) to the deformation, pressure and concentration, in a manner that helps enforce continuity requirements on these nodal variables. For a frictionless contact interface, as considered here, let t⁽¹⁾ = t_nn⁽¹⁾. Then the penalty method provides that

$$t_n=\{\begin{array}{ll}{\epsilon }_{n}g\hfill & g<0\hfill \\ 0\hfill & g\ge 0\hfill \end{array},$$ (2.7)

where the gap function g measures the distance between γ⁽¹⁾ and γ⁽²⁾. ε_n is a parameter that penalizes large values of g to prevent unacceptable overlap (g < 0) of the contacting surfaces. By choosing ε_n to be sufficiently large, the gap function g will tend toward zero, enforcing the continuity of the normal component of solid velocity across the contact interface (Laursen and Simo, 1993).

Similarly, the penalty method may be used to help enforce continuity of the effective fluid pressure and effective solute concentration, by letting

$$\{\begin{array}{ll}{w}_n\hfill & ={\epsilon }_p({\stackrel{\sim }{p}}^{(1)}-{\stackrel{\sim }{p}}^{(2)}),t_n<0\hfill \\ {\stackrel{\sim }{p}}^{(i)}\hfill & ={\stackrel{\sim }{p}}^{\ast },t_n=0\hfill \end{array},$$ (2.8)

and

$$\{\begin{array}{ll}{j}_n\hfill & ={\epsilon }_c({\stackrel{\sim }{c}}^{(1)}-{\stackrel{\sim }{c}}^{(2)}),t_n<0\hfill \\ {\stackrel{\sim }{c}}^{(i)}\hfill & ={\stackrel{\sim }{c}}^{\ast },t_n=0\hfill \end{array},$$ (2.9)

where w_n = w⁽¹⁾ ·n⁽¹⁾, j_n = j⁽¹⁾ ·n⁽¹⁾; ε_p and ε_c are penalty parameters for the solvent and solute flux, respectively; and p̃^* and c̃^* are the ambient pressure and concentration outside the contact interface. By choosing sufficiently large values for ε_p and ε_c, the continuity requirements p̃⁽¹⁾ = p̃⁽²⁾ and c̃⁽¹⁾ = c̃⁽²⁾ are enforced to within an acceptable tolerance. The units of ε_c and ε_p are those of diffusivity per unit length (e.g., m/s) and hydraulic permeability per unit length (e.g., m³/N · s), respectively. For contact interfaces where one of the contacting surfaces is impermeable to the solute (or solvent), it suffices to let j_n = 0 (or w_n = 0) on γ⁽¹⁾; this is done simply by not enforcing any boundary condition explicitly, since j_n = 0 (w_n = 0) is a natural boundary condition for the solute (solvent). Therefore this algorithm may also be adapted for contact of a biphasic-solute material against a biphasic material (j_n = 0), and against an impermeable elastic or rigid solid (w_n = 0 and j_n = 0).

This penalty method may also be incorporated within an augmented Lagrangian algorithm (Laursen and Simo, 1993; Yang and Spilker, 2007) to provide a more stable numerical scheme for enforcing these continuity requirements, when the choice of large penalty parameters compromises the convergence of iterative solution schemes. Since the derivation of DδG_c and the formulation of the matrix form of the discretized contact equations is a natural extension of the biphasic contact algorithm (Ateshian et al., 2010), only salient equations are provided in the Supplementary Data section.

3. Validations and Examples

Classical diffusion problems can be recovered in the framework of solute transport in deformable porous media when assuming that there is no solid deformation, that κ̃ = 1 and Φ = 1, and that solute diffusivity in the porous medium is the same as in free solution (see Supplementary Data). Analytical solutions are readily available for various canonical diffusion problems, such as the one-dimensional transient diffusion and steady-state convection problems considered here.

3.1. 1-D Transient Diffusion

The canonical problem of one-dimensional diffusion through a porous medium, exposed to a well-stirred bathing solution on one face and an impermeable wall on the opposite face, has a closed-form solution for the concentration c (Crank, 1979),

$$\frac{c(z,t)}{c^{\ast }}=1+\frac{4}{\pi }\sum _{n=1}^{\infty }\frac{{(-1)}^n}{2n-1}cos\left[\left(n-\frac{1}{2}\right)\pi \left(\frac{1}{2}-\frac{z}{h}\right)\right]\times exp\left[-{\left(n-\frac{1}{2}\right)}^2{\pi }^2\frac{d}{h^2}t\right],-\frac{h}{2}\le z\le \frac{h}{2}$$ (3.1)

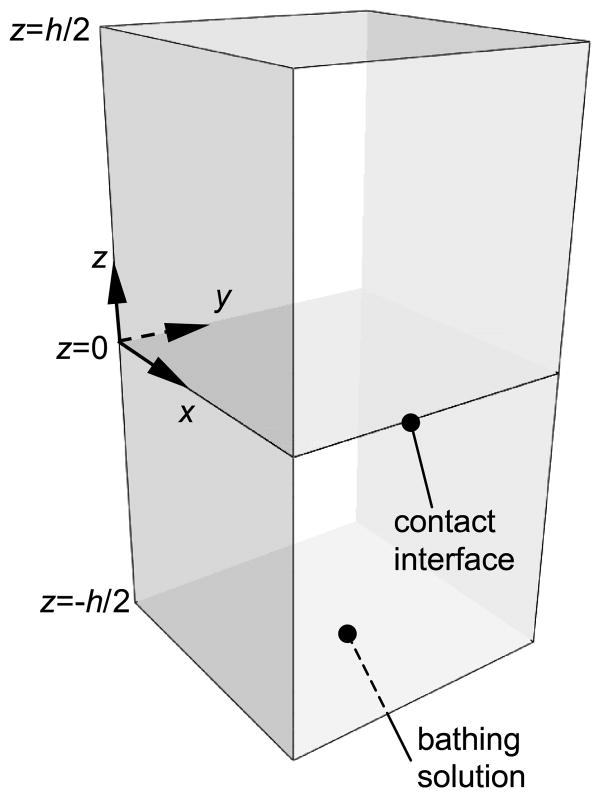
where t is the time, z is the spatial dimension, h is the height, c^* is the bath concentration and d is the diffusivity. If the medium is split in half at z = 0 to produce a contact interface (Fig. 3.1), the analytical solution for diffusion through the entire medium, including the contact interface, remains unchanged. Therefore this canonical problem may be used toward the validation of the finite element contact algorithm.

Figure 3.1.

1-D transient diffusion across a contact interface. All faces are impermeable to the solvent and solute, except where facing the bathing solution (z = −h/2).

Consider that the two contacting porous media are cubical in geometry, with each cube being 1 mm on the side (h = 2 mm). Let the external solute concentration on the exposed face of the bottom cube (z = −1 mm) be c^* = 1 mM. Assume that the effective solubility is κ̃ = 1 (thus c̃ = c), the osmotic coefficient is Φ = 1, and the fluid volume fraction is ϕ^w = 0.8. The ambient pressure is p = 0 and ambient temperature is θ = 298 K. Therefore, in the finite element analysis, the boundary conditions on the face exposed to the bathing solution are t = 0, p̃ = −Rθc^* = −2.5 kPa, and c̃ = c^*. The stress-strain response of the solid matrix is neo-Hookean, with a Young’s modulus of 10 MPa and Poisson’s ratio of 0. Since the osmotic pressure difference between the external bath and the porous medium prior to solute uptake is much smaller than the solid matrix modulus, negligible solid deformation occurs in this problem. The hydraulic permeability of the solid matrix to the solvent is k = 10⁻⁴ mm⁴/N · s. The solute diffusivity in the porous medium is d = 5 × 10⁻⁴ mm²/s. The contact penalty parameters for this analysis are ε_n = 1400 N/mm, ε_p = 10⁻³ mm³/N · s, and ε_c = 4 × 10⁻⁴ mm/s. Since the contact interface needs to be engaged to enforce interface conditions in the finite element analysis, a small displacement of 10⁻³ mm is prescribed at z = h/2 to push the two blocks together and produce nominal contact.

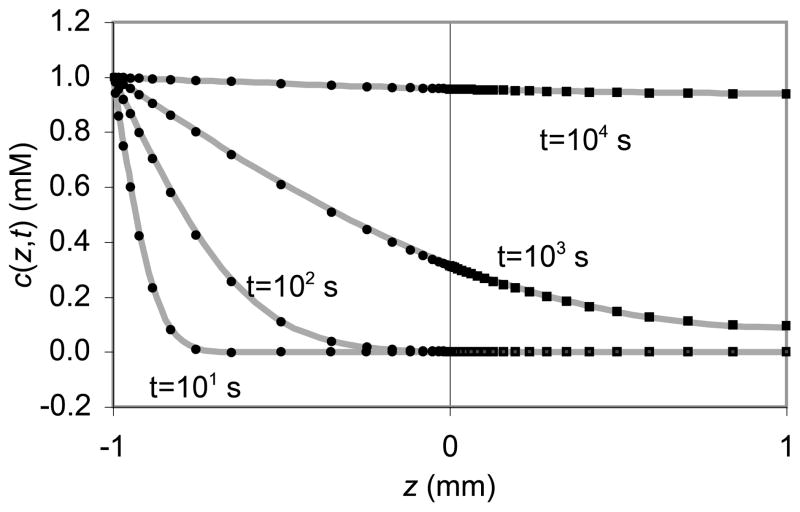
The transient response of the concentration is shown in Fig. 3.2. The spatial distribution of the concentration c (z, t) at four representative time points provides evidence of continuity of the concentration across the contact interface at z = 0. A comparison of the concentration profiles from the analytical and finite element solutions also demonstrates agreement between the two methods.

Figure 3.2.

Analytical (solid curves) and finite element (symbols) solutions to the 1-D transient diffusion problem across a contact interface, at four representative time points. Solid circles represent nodal values of the concentration in the range −h/2 ≤ z ≤ 0 and solid squares represent corresponding values in the range 0 ≤ z ≤ h/2. Continuity of the concentration across the contact interface, z = 0, is enforced by the contact interface algorithm. Agreement with the analytical solution serves to further validate the finite element implementation.

3.2. 1-D Steady-State Convection

Consider one-dimensional steady-state convection of solute and solvent through a porous medium of thickness h and porosity ϕ^w. The fluid pressure and solute concentration are prescribed upstream (p_u and c_u, respectively) and downstream (p_d and c_d). For the given conditions, the uniform solvent flux, w₀, is related to the pressure gradient according to Darcy’s law,

$$w_0=k\frac{p_u-p_d}{h}.$$ (3.2)

The steady-state concentration distribution over the range −h/2 ≤ z ≤ h/2 is given by

$$c(z)=\frac{c_d\left(e^{Pe\left(\frac{z}{h}+\frac{1}{2}\right)}-1\right)+c_u{e}^{Pe}\left(1-e^{Pe\left(\frac{z}{h}-\frac{1}{2}\right)}\right)}{e^{Pe}-1},$$ (3.3)

where Pe = hw₀/dϕ^w is the Peclet number, representing the ratio of convective solvent velocity to diffusive solute velocity. Also note that

$$\underset{Pe\to 0}{lim}c(z)=c_d\left(\frac{1}{2}+\frac{z}{h}\right)+c_u\left(\frac{1}{2}-\frac{z}{h}\right).$$ (3.4)

The finite element model consists of two cubes, 1 mm on the side (h = 2 mm), with the contact interface located at z = 0. The solid matrix of each cube is described by a neo-Hookean constitutive model, with Young’s modulus= 100 MPa and Poisson’s ratio= 0. The porosity is ϕ^w = 0.8, the solute diffusivity is d = 5 × 10⁻⁴ mm²/s and the hydraulic permeability is k = 10⁻³ mm⁴/N · s. The fluid pressure downstram is p_d = 0 MPa. The solute concentrations are c_u = 1 mM and c_d = 0 mM. For these values, the Peclet number is given by Pe = 2.5 p_u and may be varied by changing the value of the upstream pressure. The values of p_u = 0, 0.4 and 4 MPa are used to produce Pe = 0, 1 and 10. As done in the diffusion problem, a small displacement of 10⁻³ mm is prescribed at z = h/2 to push the two blocks together and produce nominal contact.

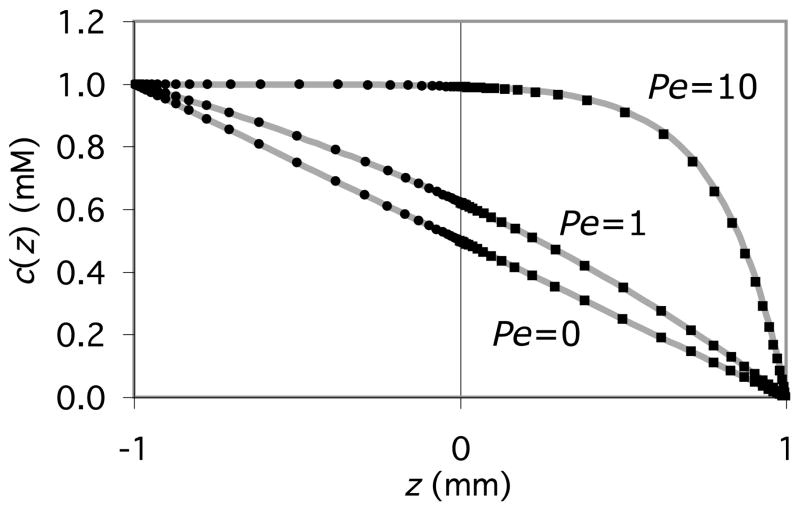
Results for the steady-state response (Fig. 3.3) demonstrate continuity of the concentration across the contact interface and agreement with the analytical solutions in (3.3) and (3.4).

Figure 3.3.

Analytical (solid curves) and finite element (symbols) solutions to the 1-D steady-state convection problem across a contact interface, at three representative values of the Peclet number. Solid circles represent nodal values of the concentration in the range −h/2 ≤ z ≤ 0 and solid squares represent corresponding values in the range 0 ≤ z ≤ h/2. Continuity of the concentration across the contact interface, z = 0, is enforced by the contact interface algorithm. Agreement with the analytical solution serves to further validate the finite element implementation.

3.3. 2-D Transient Contact

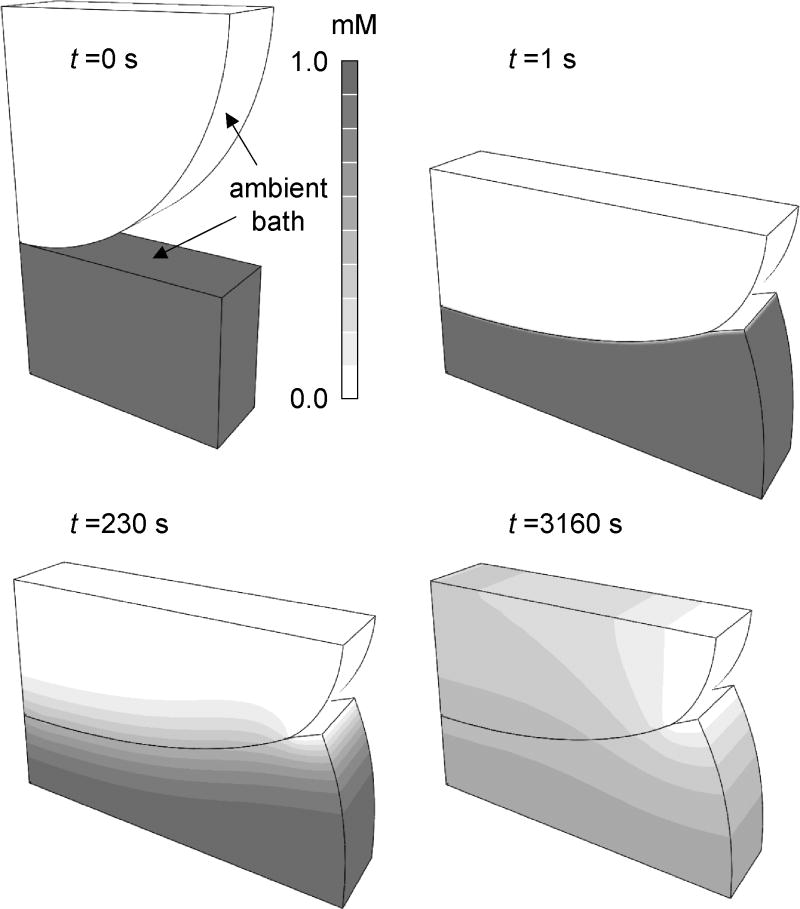
Consider the two-dimensional contact of a semi-cylindrical deformable porous slab (radius= 3 mm) displaced against a rectangular slab (3 mm wide × 2 mm high) (Fig. 3.4). The solute concentration is initially 1 mM in the rectangular slab, and zero in the semi-cylinder. The ambient bath, whose concentration is 0 mM, wets the exposed portions of the contact surfaces as shown in Fig. 3.4. The solute solubility is κ̃ = 1; the osmotic coefficient is Φ = 1; the diffusivity inside the porous medium is 5 × 10⁻⁴ mm²/s and the diffusivity in free solution is 10⁻³ mm²/s. The hydraulic permeability is 10⁻³ mm⁴/N · s. The solid matrix is neo-Hookean with a Young’s modulus of 1 MPa and a Poisson’s ratio of 0.3. The semi-cylindrical slab is displaced downward by 2 mm over a ramp time of 1 s, then maintained there for 6000 s.

Figure 3.4.

Two-dimensional contact with solute transport. The semi-cylindrical slab has a radius of 3 mm and an initial solute concentration of 0 mM (t = 0). The bottom rectangular slab dimensions are 3 mm × 2 mm and the initial solute concentration is 1 mM. The top slab is displaced downward by 2 mm in 1 s, then allowed to relax. Solute transports from the bottom slab to the top slab, while also diffusing out into the ambient bath. In the early time response (t = 1 s), solute transport occurs over a thin boundary layer across the contact interface. Over time, the solute concentration decreases in both slabs, eventually reducing to zero. Contour plots demonstrate continuity of the (effective) concentration across the contact interface.

In the early time response, there is only limited solute transport out of the rectangular slab, in a narrow boundary layer near its top surface (Fig. 3.4). Over time, substantial solute transport from the rectangular slab into the semi-cylindrical slab takes place, progressively evening the solute distribution between the two contacting bodies. This solute transport occurs at the same time as solvent transports out of the two bodies, producing a stress-relaxation and recoiling behavior of the solid matrixes. Eventually all of the solute diffuses out of both contacting bodies, producing a steady-state concentration of zero. Contour plots of the concentration exhibit continuity across the contact interface throughout the large range of deformation of the solid.

4. Discussion

This study provides what appears to be the first finite element implementation of solute transport across contact interfaces in deformable porous media. It is shown that this novel implementation is a natural extension of our recently formulated biphasic contact algorithm (Ateshian et al., 2010). A validation of the finite element code is achieved by comparing results against available analytical solutions for solute diffusion (Fig. 3.2) and convection (Fig. 3.3), using canonical problems where solid deformation is negligible. In addition, an illustration is provided for a two-dimensional contact problem where large deformations occur (Fig. 3.4).

Biological soft tissues often interact closely in crowded environments in situ, such as cartilage contacting cartilage, or cartilage contacting synovium, fat pads or ligaments in diarthrodial joints. Various metabolites may be exchanged between these tissues as a result of contact interactions. Therefore the ability to model solute transport across contact interfaces enhances the tool set available for bioengineers in their investigation of problems that combine mechanics and transport. This contact algorithm is made available in the open-source FEBio code (http://mrl.sci.utah.edu/software/febio), available in the public domain, to enhance its dissemination.