Identifying sources of variation and the flow of information in biochemical networks

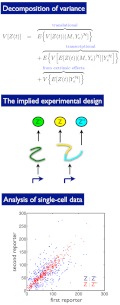
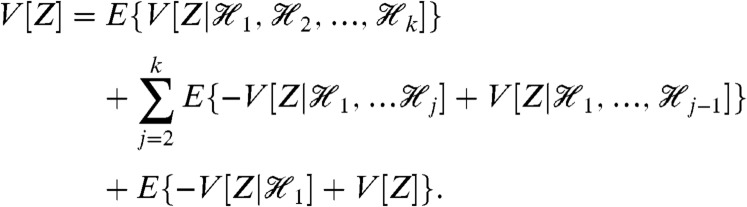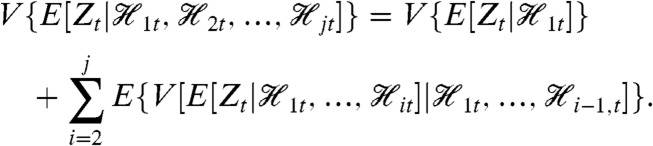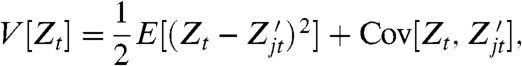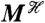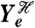Abstract

To understand how cells control and exploit biochemical fluctuations, we must identify the sources of stochasticity, quantify their effects, and distinguish informative variation from confounding “noise.” We present an analysis that allows fluctuations of biochemical networks to be decomposed into multiple components, gives conditions for the design of experimental reporters to measure all components, and provides a technique to predict the magnitude of these components from models. Further, we identify a particular component of variation that can be used to quantify the efficacy of information flow through a biochemical network. By applying our approach to osmosensing in yeast, we can predict the probability of the different osmotic conditions experienced by wild-type yeast and show that the majority of variation can be informational if we include variation generated in response to the cellular environment. Our results are fundamental to quantifying sources of variation and thus are a means to understand biological “design.”

Cells must make decisions in fluctuating environments using stochastic biochemistry. Such effects create variation between isogenic cells, which despite sometimes being disadvantageous for individuals may be advantageous for populations (1). Although the random occurrence and timing of chemical reactions are the primary intracellular source, we do not know how much different biochemical processes contribute to the observed heterogeneity (2). It is neither clear how fluctuations in one cellular process will affect variation in another nor how an experimental assay could be designed to quantify this effect. Further, we cannot distinguish variation that is extraneous “noise” from that generated by the flow of information within and between biochemical networks. We will show that a general technique to decompose fluctuations into their constituent parts provides a solution to these problems.

Previous work divided variation in gene expression in isogenic populations into two components (3, 4): intrinsic and extrinsic variation. Both components necessarily include a variety of biochemical processes yet dissecting the effects of these processes has previously not been possible. Intrinsic variation should be understood as the average “variability” in gene expression between two copies of the same gene under identical intracellular conditions (4); extrinsic variation is the additional variation generated by interaction with other stochastic systems in the cell and the cell’s environment. Single-cell experiments established that stochasticity generated during gene expression can be substantial in both bacteria (3, 5) and eukaryotes (6, 7), but did not identify the biochemical processes that generate this variation, regardless of whether the variation is intrinsic or extrinsic.

Decomposing Variation in Biochemical Systems

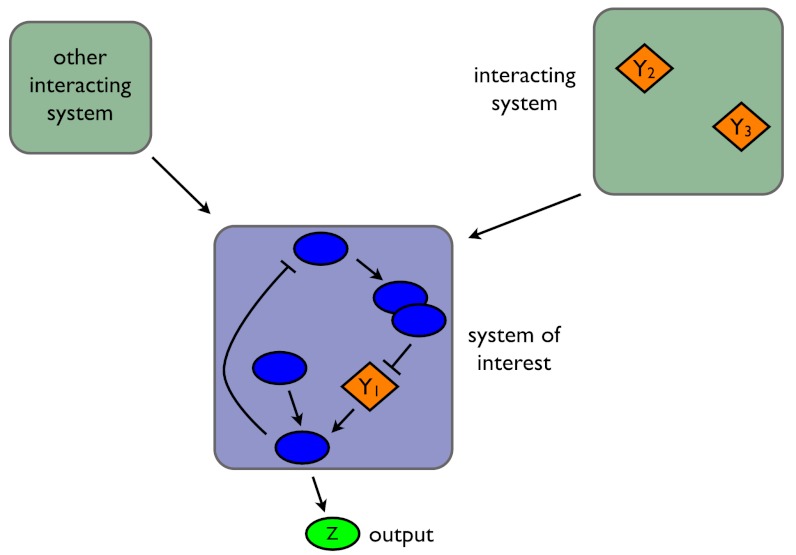
Consider a fluctuating molecular species in a biochemical system and let the random variable Z be the number of molecules of that species, for example a transcription factor in a gene regulatory network or the number of active molecules of a protein in a signaling network. Suppose we are interested in how variation in Z is determined by three stochastic variables, labeled Y₁, Y₂, and Y₃ (Fig. 1). Each Y could be, for example, the number of molecules of another biochemical species, a property of the intra- or extracellular environment, a characteristic of cell morphology (8), a reaction rate that depends on the concentration of a cellular component such as ATP, or even the number of times a particular type of reaction has occurred. We emphasize that the Y variables are the stochastic variables whose effects are of interest: They are not all possible sources of stochasticity.

Fig. 1.

Decomposing fluctuations in the output of a biochemical system. In this example, we consider how fluctuations in three variables, denoted Y_i, affect fluctuations in Z, the system’s output. Y₁ is a biochemical species within the system being studied; Y₂ and Y₃ are variables in other stochastic systems that interact with the system of interest, but whose dynamics are principally generated independently of that system. We show Y₂ and Y₃ in the same system, but they need not be.

We wish to determine how fluctuations in Y₁, Y₂, and Y₃ affect fluctuations in Z, the output of the network. Intuitively, we can measure the contribution of, say, Y₁ to Z by comparing the size of fluctuations in Z when Y₁ is free to fluctuate with the size of these fluctuations when Y₁ is “fixed” in some way. Mathematically, we can fix Y₁ by conditioning probabilities on the history of Y₁: the value of Y₁ at the present time and at all previous times. By using histories, we capture the influence of the past behavior of the system on its current behavior (9, 10). For example, fluctuations in protein numbers depend on the history of mRNA levels because proteins typically do not finish responding to a change in the level of mRNA before mRNA levels change again. If 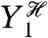then is the history of Y₁ up to time t, the expected contribution of fluctuations in Y₁ to the variation of Z at time t is

[1]

where E denotes expectation (here, taken over all possible histories of Y₁) and V denotes variance. The notation 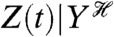is read as Z(t) conditioned on, or given, the history at time t of the stochastic variable Y. We use E, as for example in 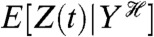, to denote averaging over all random variables except those given in the conditioning. Therefore, 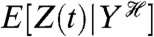is itself a random variable: it is a function of the random variables generating 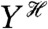(we give a summary of the properties of conditional expectations in the SI Text). Eq. 1 can be shown to be equal to .

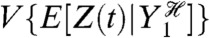General Decomposition of Variation.

To determine the effects of fluctuations in multiple Y variables on the variation in Z, we must successively condition on groups of Y variables. We prove (Appendix) that

[2]

Each of the middle terms can be understood as a mean difference between two conditional variances. For example, the third term, generated by fluctuations in Y₂, is equal to the average difference in the variance of Z when Y₁ is fixed and when Y₁ and Y₂ are fixed: 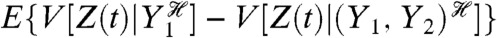. This term therefore quantifies the additional variation generated by fluctuations in Y₂ when the history of Y₁ is given. It requires first averaging Z(t) over all other stochastic variables given a particular history of Y₁ and Y₂ (the resulting expectation is a function of and ), then the calculation of the variance of this conditional expectation given the particular history of Y₁ (the variance is taken over all ), and finally the average of the resulting conditional variance over all .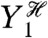

Our decomposition of variance holds at any point in time for any stochastic dynamic system and can be generalized to any number of groups of Y variables (Appendix, Eq. 13). It is unchanged if some of the stochastic Y variables are constant over time, with conditioning on their histories then being equivalent to conditioning on the values of the variables. As indicated, Eq. 2 has one term for each of the Y variables. This term becomes zero if the corresponding Y variable is deterministic or if the history of that Y variable is independent of Z(t) given the history of the other Y variables involved in the conditioning of that term. The remaining variance in Z after conditioning on the joint history of all the Y variables is measured by the first term. It requires the variance of Z(t) given the history of Y₁, Y₂ and Y₃ (the variance is taken over all other stochastic variables in the system) and then the average of this variance over all possible histories of Y₁, Y₂, and Y₃.

Eq. 2 is only unique given a particular choice of the conditioning: we could, for example, have decided to condition on the history of Y₂ in the last term. Mathematically, there is no unique way to decompose the variance if we wish to determine the effects of fluctuations of more than one Y variable on variation in Z. Rather the decomposition is sequential, with all Y variables appearing in multiple components. Biological systems, however, often suggest a natural order of conditioning that follows their flow of control. The hierarchy described by the central dogma is one example. Nevertheless, freedom in choosing the order of conditioning can be an advantage because different decompositions give different insights and may be more or less amenable to experimental analysis.

Defining Transcriptional and Translational Variation.

We can identify the contribution of a subsystem to downstream fluctuations by conditioning on the history of that subsystem. As an example, to investigate whether transcription or translation is more “noisy” during gene expression, we should condition on the history of the mRNA levels of the gene of interest, 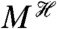, and on the history of all stochastic processes extrinsic to gene expression. Examples of such processes include the synthesis and turnover of ribosomes and the rate of cellular growth. We will denote the collection of extrinsic processes as Y_e. If Z is the number of molecules of the expressed protein, then

[3]

Variation from translation is the extra variation generated on average once the history of fluctuations in mRNA and Y_e is given (the first term in Eq. 3); variation from transcription is the extra variation generated by fluctuating levels of mRNA given the history of fluctuations in Y_e.

Measuring the Components of Variation

Using Conjugate Reporters.

Our general decomposition of variance for a biochemical system (Appendix, Eq. 13) allows us also to determine exact conditions that reporter systems should satisfy in order to quantify the different sources of variation. Such conditions establish a basis for experimental design. First, we need a reporter for the biochemical output of interest, Z. This reporter could be a fluorescently tagged protein for a genetic network or the nucleo-cytoplasmic ratio for a fluorescently tagged transcription factor that translocates in response to a signaling input. Second, given a variable of interest, Y, we use a conjugate reporter, Z^′, that by definition must obey two conditions:

1. Z^′(t) is conditionally independent of Z(t) given the history of Y;

2. Z^′(t) and Z(t) have the same conditional means and the same conditional variances given the history of Y.

The first, conditional independence, implies that given the history of fluctuations in Y, no other fluctuations result in the level of the first reporter correlating (in the most general sense) with the level of the second (10, 11). The second condition says that 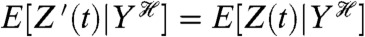and , and in practice often means that the reporter system generating Z^′ is as close a copy as possible of the relevant subsystem generating Z.

The reporter system is thus designed so that it is only fluctuations in Y that “cause” a covariance between the level of Z and the level of Z^′. Consequently, measuring this covariance quantifies the effects of fluctuations in Y on the variance of Z. Mathematically, 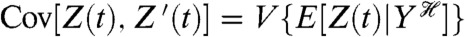, from the conjugacy of the reporters and the law of total covariance. Depending on the choice of Y, this covariance gives either the last term or the sum of the last terms in Eq. 2. The mean squared difference between the reporters, E[(Z(t) - Z^′(t))²]/2, complements the covariance measurement and gives the sum of the remaining terms in Eq. 2 (Appendix).

We need a reporter for each component of Eq. 2 and so four in total: a reporter for Z from which we can measure V[Z], the variance of Z across a population of isogenic cells; a reporter conjugate to Z given the history of Y₁ whose covariance with Z, again across an isogenic population, gives the last term of Eq. 2; a reporter conjugate to Z given the history of Y₁ and Y₂ whose covariance with Z gives the sum of the last two terms of Eq. 2; and a reporter conjugate to Z given the history of Y₁, Y₂, and Y₃ whose covariance with Z gives the sum of the last three terms (Appendix). These reporters can in principle be constructed in the same cell or, if simultaneously distinguishing four reporters is technically challenging, in pairs in different cells (with the reporter for Z and one of its conjugate reporters comprising a pair).

Measuring Transcriptional and Translational Variation.

Returning to the example of measuring transcriptional and translational contributions to variation in gene expression (Eq. 3), we can construct the appropriate conjugate reporters by having a reporter for the level of the protein and a bicistronic mRNA coding for two other reporters of the protein—each with a distinct fluorescent tag—in the same cell (Fig. 2A). Only fluctuations in mRNA levels and extrinsic variables generate correlations between the two bicistronic reporters Z and Z^′′ (12), and their covariance therefore equals the sum of the last two terms in Eq. 3 provided the conditions for conjugate reporters are met. Their mean squared difference (halved) then measures translational variation, the first term in Eq. 3. We should therefore construct the mRNA for all reporters to have identical rates of transcription, translation, and turnover. The reporters Z and Z^′ are conditionally independent given the history of the extrinsic fluctuations, and their covariance measures the last term in Eq. 3 (Fig. 2B).

Fig. 2.

Designs of conjugate reporters to measure the effects of different cellular subsystems on variation in output. (A) To distinguish transcriptional from translational effects, three reporters are needed including a bicistronic mRNA with two independent ribosome binding sites. (B) Simulated results for the reporters in A assuming that extrinsic fluctuations affect only the rate of transcription, which fluctuates between three different levels (reactions and parameter values are given in SI Text). Blue dots show Z plotted against Z^′: The average spread along the Z = Z^′ diagonal equals the sum of V[Z] and the extrinsic variance; the average spread perpendicular to the diagonal equals the sum of the transcriptional and translational variation (SI Text). Red dots show Z plotted against Z^′′: the average spread along the diagonal equals the sum of V[Z], extrinsic, and transcriptional variation; the average spread perpendicular to the diagonal equals translational variation. For the parameters chosen (SI Text), the translational noise (coefficient of variation) is 0.12; the transcriptional noise is 0.39; and the extrinsic noise is 0.41. These numbers agree with Eqs. 9 through 11 to two decimal places. (C) Four reporters are needed to distinguish transductional variation from variation generated by gene expression. Here, a signaling network activates a transcription factor, T, in response to extracellular inputs. To measure variation in the output Z arising from gene expression, we require two conjugate reporters, Z and Z^′, whose expression is controlled by this transcription factor. To find a bound on transductional variation, we use two further conjugate and constitutively expressed reporters, Z_c and .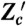

Such bicistronic mRNAs have been constructed in Escherichia coli, but for distinguishable fluorescent proteins tagged to two different rather than identical proteins (13). We can show that these measurements give an upper bound on the translational variance: for CheY and CheZ from E. coli’s chemotaxis network, we show that the average translational variance for the two proteins, normalized by the product of the means of their fluorescence, is less than 0.2² (SI Text). As we will show later (Eq. 9 and SI Text), transcriptional variation usually dominates translational variation for typical parameters appropriate for E. coli.

Identifying Sources of Variation in Cell Signaling

Much gene expression is initiated by signaling networks (14), and we will study examples of such expression to illustrate how to apply our decomposition (Fig. 2C). The variation observed may be determined predominantly by stochasticity in upstream signal transduction rather than by gene expression itself (15) and will not only be a consequence of biochemical noise but also a signature of information flowing through the network (16, 17). Fluctuations in gene expression can carry information on environmental changes because new rates of transcription are often caused by such changes (18). By having a general decomposition of variance, we can distinguish both signaling from expression effects and information flow from noise.

Informational Variation.

We begin by considering variation generated in response to the extracellular environment. We will condition on the extracellular input signals, X, sensed by the signaling network. This input could be a collection of ligands or, for example, light intensity for a circadian system. In nature, different levels of input would correspond to different states of the environment. If Z is the number of protein molecules expressed from a downstream gene at a particular time, then

[4]

We write Eq. 4 assuming that the biochemical system responds sufficiently quickly to reach steady state before the input changes (otherwise the system would still be responding to a previous environmental change when the next change happens). Therefore, X in Eq. 4 is not a history but takes a unique, constant value for each state of the environment. If X is dynamic, then Eq. 4 can be rewritten replacing X with its history .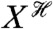

The variance on the left-hand side of Eq. 4, V[Z], is generated by both variation in the extracellular input X and by variation in the output Z given a particular value of that input. If we were to measure cellular variation with the cell in its natural environment (and could not simultaneously detect the value of X), we would see variation in the output because of X taking different values for different measurements of the output. In the laboratory, however, we can measure the distribution of output holding the level of X fixed. For example, with a fluorescent reporter for Z, we can use either microscopy (15) or fluorescence activated cell sorting (19) to measure the mean, E[Z|X], and variance, V[Z|X], of the response conditional on the level of the input. We can then determine V[Z] as follows: by calculating the variance of E[Z|X] for a given distribution of the input, we find V{E[Z|X]}, the last component in Eq. 4; by calculating the expectation of V[Z|X] over the distribution of the input, we find E{V[Z|X]}, the first component. We will discuss subsequently different choices of the input distribution.

We interpret the last term of Eq. 4 as the “informational” component of the variance of Z. When the means, E[Z|X], are not the same for any two values of X, the size of this component compared to V[Z] typically indicates how difficult it is for the cell to decide the state of the environment X from the output of the sensing network. Because E[Z|X] gives the mean output for a given input, the magnitude of the variance of E[Z|X] reflects the extent to which the system can respond to a change of input. The first term of Eq. 4 describes stochasticity generated by the system during the process of sensing. The larger this term relative to V[Z], typically the greater the deterioration in transfer of information about the environmental state to the output.

Unambiguous identification of the environmental state usually becomes easier as the fraction of the output variance that is informational increases because the distributions of output for each environmental state then typically overlap less. From information theory (20), identifying the environmental state is undermined by such overlap because different environmental states can then generate the same output (although some states are typically more likely to generate that output than others). Increased transductional variation, for example, usually leads to broader and overlapping output distributions. If the mean output when X is in state s is μ_s and the variance of the output is then 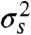, we define the informational fraction of output variance as

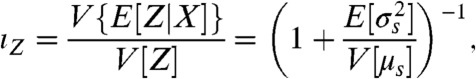[5]

where the expectation and variance are over the probability distribution for the states of X. As the informational fraction tends to its maximum value of one, then 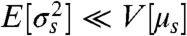: the average “width” of a conditional output distribution typically becomes much less than the average distance between the means of two of these output distributions (SI Text). Heuristically, each output distribution is less likely to overlap with another and the system should become more efficient at transmitting information.

We can make these ideas more precise by relating the informational fraction to mutual information, the standard measure of information transfer (20). When the joint distribution of the input and output is Gaussian, the mutual information between X and Z equals 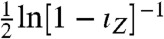(SI Text): an increasing function of ι_Z. As the informational fraction increases so too must the mutual information between X and Z, and Z becomes more informative about the environmental state. We consider 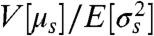as a generalized signal-to-noise ratio that increases whenever ι_Z increases. Indeed, this signal-to-noise ratio simplifies to give the one familiar from information theory for the jointly Gaussian case (21). The information capacity is the maximum possible mutual information over all potential input distributions (20). In general, we can show that the capacity is bounded below by the same increasing function, 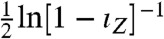, evaluated using a suitable choice of the distribution of X (SI Text), and provided the conditional means μ_s are not exactly the same for different states of X. Further, under mild conditions on the joint distribution of the input and output we can prove that the mutual information between X and Z becomes maximal as the informational fraction becomes close to one (SI Text). Such a convergence of ι_Z occurs, for example, in the limit of large numbers of molecules. Nevertheless, the informational fraction is not an exact proxy for mutual information because mutual information, unlike ι_Z, accounts for the entire joint distribution of input and output. As a consequence, though, reliably estimating the mutual information can require substantially more data than reliably estimating the informational fraction.

Using Informational Variation to Analyze Osmosensing in Budding Yeast.

We can apply these ideas to measurements of the transcriptional response of budding yeast to hyperosmotic stress (Fig. 3A). Pelet et al. made single-cell measurements of a Yellow Fluorescent Protein (YFP) expressed from the promoter of STL1 under different conditions of osmotic stress by using various concentrations of extracellular salt (Fig. 3B) (19). STL1 is the typical reporter for the response to a hyperosmotic change (22). Using this data and Eq. 5, we can determine the informational fraction for any particular probability distribution of extracellular salt (the input X). The distribution of osmotic stress encountered by yeast in the wild is unknown. We can, however, find distributions of salt concentration that give high informational fractions, an example of “inverse ecology” (23–26).

Fig. 3.

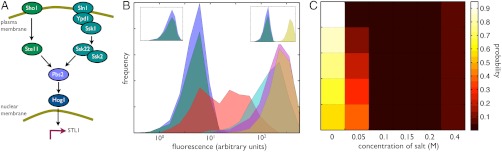
Determining informational variation for osmosensing in budding yeast allows us to predict the probability of the different osmotic conditions experienced by yeast. (A) Hyperosmotic stress is sensed by two pathways in budding yeast, which activate the MAP kinase kinase kinases Ste11 and Ssk2/22 (22). Both these kinases activate the MAP kinase kinase Pbs2, which in turn activates the MAP kinase Hog1. Activated Hog1 translocates from the cytosol to the nucleus and initiates new gene expression. (B) Histograms of fluorescence data from a YFP reporter expressed from the promoter for STL1 and measured by Pelet et al. (19). Fluorescence levels typically increase with increasing extracellular salt: Blue corresponds to zero extracellular salt; dark green to 0.05 M salt; red to 0.1 M; cyan to 0.15 M; magenta to 0.2 M; and brown to 0.4 M. Approximately 1,000 data points were measured for each concentration (19) and are shown using 20 bins for the fluorescence level (calculated in log-space). The left inset shows the same histograms but weighted by the probability of the different salt concentrations for an input distribution that has a low informational fraction of output variance; the right inset is analogous but for an input distribution that has a high informational fraction of output variance. (C) The five probability distributions for extracellular salt that give the five highest informational fractions (each approximately equal to 0.8 because of the high degree of overlap of the fluorescence distributions for zero and 0.05 M salt). Each distribution is read horizontally. We calculated the informational fraction for all possible probability distributions of the six concentrations of extracellular salt that were chosen experimentally. The informational fraction decreases continuously from around 0.8 to zero. A uniform probability distribution of salt gives an informational fraction of approximately 0.6.

From the Pelet et al. data for the STL1 promoter, we find the highest informational fraction (of around 0.8) for distributions that have a high probability of low osmotic stress, zero probability for intermediate stresses, and a low probability for high stress (Fig. 3C). Intermediate levels of stress have zero probability in these distributions because the corresponding expression from STL1 covers a broad range and extends into the levels of expression typical of both high and low stress (Fig. 3B). If expression from STL1 is “read” by the cell to determine the level of osmotic stress, then this readout is most unambiguous for distributions of salt concentrations that have these properties (Fig. 3B, Insets). If we believe that the network has been selected to have an ability to distinguish different environmental states (27), then we can go further and suggest that the natural distribution of osmotic stress experienced by yeast is of the same form. The osmosensing network then “expects” frequent low level osmotic stress interspersed with rare, high level stress. An alternative distribution with frequent high and infrequent low level stress has a substantially lower informational fraction (of around 0.15) and does not lead to distinct responses from STL1 in different environmental states. Low levels of expression are now ambiguous about the environmental state. The joint probability of a low level of expression and a particular state of the environment is a product of the probability of the state and the probability of low expression given that state. These joint (and the posterior) probabilities are now similar for the states of low and high stress when expression is low. In the high stress environment, low levels of expression are quite rare (lying in the long left-hand tail of the output distribution in Fig. 3B), but the high stress environment itself occurs with a high probability. Similarly, although the low stress environment occurs rarely, when it does so, low levels of expression are highly probable.

We emphasize that this example is intended to be illustrative, and there are numerous caveats (17): considering expression of several genes as the output could change the predicted input distribution; expression of YFP is itself a “noisy” measure of levels of protein; and inputs in yeast’s natural environment other than osmotic shock may affect the output response.

Quantifying Components of Variation in Yeast’s Osmosensing.

We can decompose the first, noninformational term in Eq. 4 into a component generated by gene expression and a component generated by fluctuations in processes extrinsic to the expression of Z. Most experiments are carried out for given levels of input X, and therefore we will consider the decomposition of V[Z|X]. Any decomposition of V[Z|X] can be inserted into Eq. 4 to give the decomposition of V[Z]. The transcription factors, T, activated by upstream signaling (Fig. 3A) are extrinsic to gene expression, and we will define all other extrinsic processes by Y_e∖T. The decomposition of V[Z|X] is then (Appendix, Eq. 15)

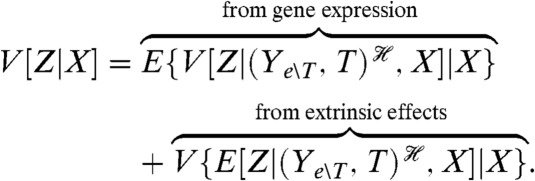[6]

To measure these components, we introduce a reporter Z^′ conjugate to Z given both X and the joint history of the transcription factors and the other extrinsic variables. Measuring the covariance of Z with this reporter for a given X will determine the extrinsic variance for that level of input; measuring half of the mean squared difference between Z and Z^′ will determine the intrinsic variation arising from gene expression. We can construct the appropriate conjugate reporter using a second copy of the promoter and gene for Z but with the corresponding protein marked with a different fluorescent tag (Fig. 2C).

Combining Eqs. 4 and 6, we can show that informational variation can be the dominant source of heterogeneity. In their study of osmosensing, Pelet et al. expressed a Cyan Fluorescent Protein from a second copy of the STL1 promoter in the same cells (19). This reporter is conjugate to the original YFP reporter (measuring output Z) given the salt concentration, X, and the history of the extrinsic variables. Its covariance with Z for a given X therefore gives the extrinsic variation in Z for that level of X. Using this data (SI Text) and defining the extrinsic fraction of variance as the ratio of the extrinsic variance to V[Z|X], we can show that the extrinsic fraction is typically about 45% for each fixed concentration of salt (noting that V{E[Z|X]} is then zero). When we allow for a probability distribution over osmotic conditions that generates a high informational fraction for expression of STL1, we find that the extrinsic fraction becomes about 90%, of which almost 90% is generated by informational variation. In contrast, salt distributions that generate a low, positive informational fraction (such as Fig. 3B, Left Inset) give an extrinsic fraction of around 45%, with almost no contribution from informational variation. Our results thus imply that it is important to include the effects of the natural distributions of environmental states when considering cellular heterogeneity.

Distinguishing Variation due to Gene Expression from Variation due to Upstream Signaling.

We can further decompose the variation of Z for a given X to distinguish the variation generated by the signaling network from that generated by gene expression:

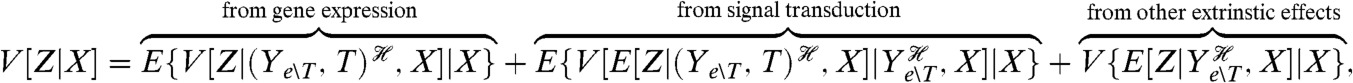[7]

where the last two terms sum to give the last term of Eq. 6. Transductional variation at a given X is therefore the extra variation generating by fluctuating levels of the transcription factor given the history of the other extrinsic processes and the level of X. To directly measure the third component of Eq. 7, which arises from those processes extrinsic to gene expression other than T, would require a reporter conjugate to Z given the input and the history of only those extrinsic processes. It is difficult to see how to construct such a reporter without having to create a copy of the upstream signaling network and have transduction in that copy insulated from transduction in the original network.

We can, however, find a lower bound on this extrinsic component, and consequently an upper bound on the transductional component, by introducing a reporter that is conditionally independent of Z given the history of all extrinsic variables except the transcription factor T (and given the input X). An example is a constitutively expressed reporter, which is conditionally independent of Z given the input X and the history of Y_e∖T. This reporter, denoted Z_c, need not have the same conditional mean as Z (Fig. 2C). Introducing a further reporter conjugate to Z_c given X and 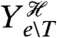, we can prove that (SI Text)

[8]

where 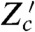is the conjugate reporter to Z_c and Cov denotes covariance. This inequality reflects the intuition that an observed covariance between expression of genes from different networks, here Z and Z_c, is determined by the strength of the extrinsic fluctuations common to both (15, 28). The prefactor corrects for the different conditional means (given 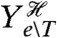and X) of the two processes. Eq. 8 becomes an equality if transduction through the signaling network makes this conditional mean of Z a linear function of the conditional mean of Z_c (SI Text). Eq. 8 implies an upper bound on the variation generated by signal transduction because we have already measured the sum of the last two terms of Eq. 7, the extrinsic variance, using Cov[Z,Z^′|X]. To measure a component of Eq. 7 and to find bounds on the others, four reporters are therefore needed in one cell or three pairs of reporters in different cells: Z and Z^′; Z and Z_c; and Z_c and 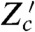(Fig. 2C).

Decomposing Variation in Yeast’s Pheromone Response.

Such reporters have already been constructed by Colman-Lerner et al., who studied the pheromone pathway in budding yeast (15). In the presence of extracellular pheromone, this pathway activates a MAP kinase cascade and a transcription factor, Ste12 (29). Colman-Lerner et al. analyzed variation by equating the output of the pathway to the product of the downstream gene expression measured per unit of the upstream signaling response and the response from upstream signaling itself. They constructed, among others, three strains: one expressing two fluorescent proteins from two copies of the pheromone-responsive promoter PRM1 (equivalent to Z and Z^′); one expressing two fluorescent proteins from two copies of the promoter for actin (equivalent to Z_c and 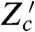); and another expressing fluorescent proteins from the promoters of PRM1 and actin (equivalent to Z and Z_c). We can therefore reanalyze their data using Eq. 7 (SI Text). We find that the fraction of variance in Z generated by gene expression is low and approximately 0.1; that the fraction generated by processes extrinsic to gene expression (other than fluctuations in the transcription factor Ste12) is greater than approximately 0.5 (from Eq. 8); and that the fraction generated by signal transduction is therefore less than approximately 0.4 for cells exposed to 1.25 nM of pheromone. We can conclude that signal transduction is a less substantial source of variation than other processes extrinsic to gene expression for these data.

Analyzing Variation in Models of Biochemical Systems

Given that we now have a general method for decomposing variance, can we make predictions of how the components of variance will behave as properties of the system change? Indeed, our method of conjugate reporters can also be used to compute the components of the variance for a given model. We can either use the chemical master equation to model both reporters and to calculate their covariance (30) or use Monte Carlo simulations to numerically estimate the covariances of the reporters (31).

Calculating Transcriptional and Translational Variation.

For example, we calculated the three components of Eq. 3 for a standard model of gene expression (32) and with the assumption that the extrinsic variables Y_e are dominated by fluctuations in the rate of transcription (33). At steady state, with Z being the number of proteins, we find that the translational and the transcriptional components are (SI Text)

[9]

and

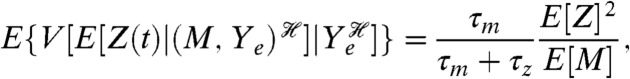[10]

where τ_m denotes the lifetime of the mRNA and τ_z denotes the lifetime of the protein. If τ_e is the lifetime of fluctuations in the rate of transcription, then the extrinsic component is

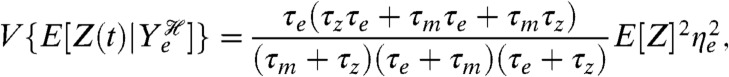[11]

where η_e is the coefficient of variation of the fluctuations in the rate of transcription (their standard deviation over their mean). For this model, the translational component is equal to the mean number of proteins and the transcriptional component is determined partly by the coefficient of variation of fluctuations in mRNA levels (the square of which is the reciprocal of E[M]) scaled by a function of the ratio of the mRNA to protein lifetimes.

Intrinsic and Extrinsic Variation.

Throughout, we condition on the histories of stochastic variables (9–11, 34), and such conditioning is needed for a general definition of intrinsic and extrinsic variation because it allows for extrinsic variables that fluctuate on any timescale. It we let Y_e denote all extrinsic variables, then by conditioning on the history of Y_e we have

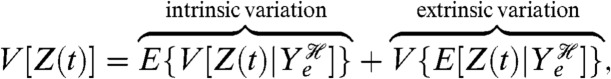[12]

for expression of a protein Z. This decomposition is mathematically analogous to that given originally (4), except that the conditioning is on the history of the extrinsic variables rather than on just a single value of each extrinsic variable. The original conditioning is only valid if the extrinsic variables change substantially more slowly than the dynamics of the system of interest (34, 35). This change in definition alters neither the interpretation of intrinsic variation as the average variability in gene expression between two identical copies of the gene subject to the same extrinsic fluctuations (empirically, the mean squared difference in levels of expression from the two genes) nor the measurements needed for experimental assays (34). These measurements are the covariance between a reporter for Z and another reporter conjugate given the history of the extrinsic variables (3), as required by our general decomposition.

Intrinsic variation is often heuristically understood as the “variation generated inherently” by the biochemical reactions that comprise the system (36, 37). However, intrinsic variation also depends on the environment in which the system is embedded, that is on the extrinsic processes themselves (4, 34, 35). This dependence is made explicit in Eq. 12: 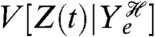is unambiguously the variance due to processes that are not extrinsic, but its magnitude depends on the realized history of Y_e. We must therefore take its expectation over all such histories to obtain a useful numerical measure. We can also write the intrinsic variation as equal to the expectation of 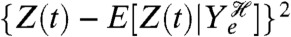, that is the average squared deviation of Z(t) away from its mean given the history of the extrinsic variables.

An implication is that attempting to validate a model by comparing its variance components with experimental measurements can be problematic because the model must include the extrinsic processes appropriately. Detailed models of these processes, however, may not always be necessary. For example, a model specifying a mean, variance, and autocorrelation function for an extrinsic process could potentially give informative comparisons with data. Importantly, once a model has been selected and parametrized statistically, we can use conjugate reporters to evaluate its different components of variation in silico, some of which may not be easily measured experimentally. As an illustration, we considered constitutive gene expression for four different models each of which has a single source of extrinsic fluctuations, in either degradation or synthesis of mRNA or protein (SI Text). Calculating the intrinsic variation using the master equation augmented with a conjugate reporter, we found that extrinsic fluctuations in some processes increased the measurement of intrinsic noise in protein levels (the variability between two conjugate reporters normalized by the product of their means), and extrinsic fluctuations in others decreased it, relative to a model with no extrinsic fluctuations. Therefore, predictions from a model with only intrinsic fluctuations cannot even act as an upper or lower bound on the intrinsic noise measured experimentally. Once a model has been validated statistically, perhaps using time-series data, then results such as Eqs. 9–11 can be used to understand and predict the importance of different sources of variation. For example, Eq. 9 predicts that transcriptional variation usually dominates translational variation for typical parameters appropriate for E. coli (SI Text).

Finally, we point out that we have chosen an “operational” definition of intrinsic variation—the average variability in gene expression between two copies of the same gene under identical cellular conditions—in part because of the ease of constructing reporters by copying the promoter and other control regions of a gene of interest. If desired, this definition can be made more inclusive: the average variability of the output between two copies of the same subsystem under identical cellular conditions. Such a definition, for example, could include fluctuations in signal transduction in the example of Fig. 2C as “intrinsic,” with the first component in Eq. 4 then constituting the intrinsic variation.

Discussion

A challenge when investigating variation in any biochemical network is the influence of the wider stochastic system in which the network is embedded. The general decomposition of variance we have introduced allows the variance to be decomposed into as many components as there are potential sources of variation and provides exact mathematical expressions for each component. Further, we show that all components can be measured using reporters that are conjugate to the reporter for the original system. For each component, we give two conditions that these reporters must satisfy.

Through its use of conjugate reporters, our approach provides both a means to compute the magnitude of different components of variance for mathematical models and a framework for thinking about experimental approaches to quantifying sources of variation. Although we have described experimental realizations of conjugate reporters for two different types of decomposition (Fig. 2), the design of conjugate reporters to measure some components of variation may be challenging. For example, fluctuations in the numbers of mitochondria have been proposed to generate much of the variation in the rates of transcription seen in mammalian cells (33). To measure the contribution of such fluctuations to variation in gene expression, our decomposition requires a reporter conjugate to the output given only the history of the levels of mitochondria. Currently, constructing such a reporter is difficult, but this prediction in itself is important. Knowing the exact conditions required for a reporter is the first step in experimental design. If those conditions are challenging to establish, the experimenter can consider different decompositions of variance or alternative approaches. Using our techniques for quantifying sources of variation to analyze models whose parameters have been fitted to experimental data, for example, provides such an alternative approach. More generally, advances in synthetic biology that aim to create biochemistry “orthogonal” to the endogenous biochemistry may make suitably conjugate reporters commonplace (38).

Using our decomposition, we can identify a component of the variance determined by environmental signals or inputs—the informational variance—and as such can disentangle fluctuations that carry information from those that disrupt it. For given input distributions, measuring the fraction of the variance in the output that is informational allows quantitative comparison of the efficacy of different biochemical networks for information transfer and so addresses why one network architecture might be selected over another (39). The informational component can also be used for “inverse ecology”: to determine the distribution of inputs from which the network is best able to unambiguously transduce an input signal given the network’s structure (Fig. 3). Our analysis of data for osmosensing in budding yeast implies that the majority of variation can be generated by the response of the network to extracellular signals (we find that such environmental stochasticity can generate 80% of the variation in the response of the osmosensing network in yeast).

Stochasticity is now believed to pervade molecular and cellular biology, but the principal biochemical processes that generate stochasticity are mostly unknown. Our general decomposition of variance, each component of which can be evaluated with suitably constructed conjugate reporters, provides a means to quantify the effect of fluctuations in one biochemical process on the variation in the constituents of another. It provides a measure of the contribution of information flow to biochemical variation: a contribution that can be the dominant source of variation, at least for some distributions of input. Our approach thus provides a mathematical foundation for studies investigating the biological role of stochasticity and variation in cellular decision-making.

Appendix

General Decomposition of Variance for Stochastic Dynamic Systems.

We denote a stochastic dynamic system with n variables in all by Y = {Y_1t,…,Y_n-1,t,Z_t}_t≥0 and write, for example, Y_1t in place of Y₁(t). We will use 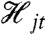to denote the history at time t of Y_j, where Y_j is some subset of the n variables of the full system. (The subscript j will index the different subsets or collections of variables; the subsets may overlap.) We note for those familiar with stochastic process theory that 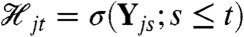. Intuitively, knowledge of 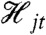is equivalent to knowing the trajectory of all of the variables in the vector Y_j for times s up to and including time t.

Our general theorem for decomposition of variance is as follows. Let Y be a stochastic dynamic system with a variable of interest Z_t whose variance exists (is finite). Suppose we have the histories 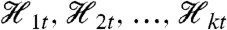, k≥2, each one for a different collection of variables of the system. Then,

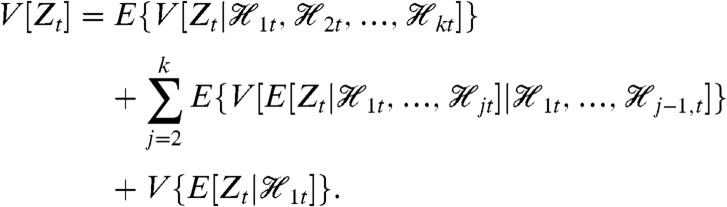[13]

Proof:

We now derive Eq. 13 (omitting the subscripts t in order to give the proof in its most general form where each is any σ field). To see that Eq. 14 below holds, notice that terms cancel to give the identity V[Z] = E{V[Z]}:

[14]

For any two σ fields , a conditional version of the law of total variance is seen to hold:

[15]

and hence on taking (unconditional) expectations of both sides and rearranging,

because . Therefore, the summation in Eq. 14 simplifies to give , [by setting and for j = 2,…,k]. Using the law of total variance to simplify the last two terms of Eq. 14 completes the proof. When k = 1 Eq. 13 simplifies to give a two-way decomposition: a measure theoretic version of the law of total variance. The two-way decomposition applied to the internal history is It then follows from Eq. 13 that for any j≥2,

[16]

Conjugate Reporters Identify all Components of the Variance Decomposition.

We define a reporter 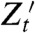to be first-moment conjugate to Z_t for the history 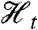if (i) Z_t and 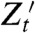are conditionally independent given 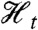and (ii) 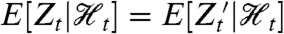. (It is implicit in our definition that neither the history 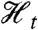nor the process Z_t is “affected” by introducing the reporter 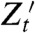into the system.) The following derivation shows that the measurement of variance components using the (contemporaneous) covariance of conjugate reporters at time t remains valid despite the “dependence” of Z_t on the histories of the relevant fluctuations as well as on the value of those variables at time t [see also Hilfinger and Paulsson (34)].

We wish to measure each of the variance components in the decomposition given by Eq. 13. These measurements require a reporter 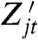that is first-moment conjugate to Z_t for the history for each j = 1,…,k, which gives (k + 1) reporters in all including the original one for Z_t. Measurement of each of their covariances with Z_t, denoted , identifies all of the (k + 1) terms in the decomposition.

Proof:

That follows directly from the law of total covariance after noting that condition (i) for the conjugacy of the reporter (conditional independence) implies that the conditional covariance equals zero. Alternatively, the property may be derived as follows. Condition (ii) for the conjugacy of the reporter implies that , and thus

where we have again used the conditional independence of condition (i). It follows from Eq. 16 that identifies the sum of the last j terms in the decomposition in Eq. 13. Therefore, equals the jth term from the end of the equation, for j = 1,…,k. The first term of Eq. 13 is obtained as .

Furthermore, suppose that, for j = 1,…,k, has the same second conditional moment as . We then say that is conjugate to Z_t for the history . The variance now decomposes as

[17]

because . Eq. 17 formally justifies the empirical measure of intrinsic noise proposed by Elowitz et al. (3).