Tipping Points in the Arctic: Eyeballing or Statistical Significance?

Abstract

Arctic ecosystems have experienced and are projected to experience continued large increases in temperature and declines in sea ice cover. It has been hypothesized that small changes in ecosystem drivers can fundamentally alter ecosystem functioning, and that this might be particularly pronounced for Arctic ecosystems. We present a suite of simple statistical analyses to identify changes in the statistical properties of data, emphasizing that changes in the standard error should be considered in addition to changes in mean properties. The methods are exemplified using sea ice extent, and suggest that the loss rate of sea ice accelerated by factor of ~5 in 1996, as reported in other studies, but increases in random fluctuations, as an early warning signal, were observed already in 1990. We recommend to employ the proposed methods more systematically for analyzing tipping points to document effects of climate change in the Arctic.

Electronic supplementary material

The online version of this article (doi:10.1007/s13280-011-0223-8) contains supplementary material, which is available to authorized users.

Introduction

Increasing concentrations of greenhouse gasses in the atmosphere, mainly from human combustion of fossil fuels during the anthropocene, have resulted in a global warming (IPCC 2007). Whereas the global sea surface temperature (SST) has increased by 0.135°C per decade from 1979 to 2005, temperature trends were three to four times larger in many areas of the Arctic Sea (1965–1995, Steele et al. 2008). Warming impacts the physiology of species present (e.g., Roleda et al. 2008) and promotes the invasion of lower-latitude species into the Arctic (Carmack and Wassmann 2006). Furthermore, the temperature increase has led to a rapid decline in Arctic sea ice cover (Stroeve et al. 2007; Comiso et al. 2008) and reduced habitats for marine mammals and polar bears, in addition to changing the light conditions and mixing processes and consequently primary production (Gradinger 1995; Arrigo et al. 2008). Thus, all trophic levels, from the base of the food-web to the top predators, are potentially affected by global change. Model projections suggest a continued accelerated warming with a potential ice-free Arctic in late summer within 25–30 years (Wang and Overland 2009). Such scenarios have severe repercussions for the Arctic ecosystems and the people living of the resources they provide (ACIA 2004).

It is evident from long-term monitoring and experiments that Arctic ecosystems will undergo drastic changes in response to warming, but it is less clear how and when these changes will actually occur. Whereas responses to smooth changes in the ecosystem services only involve a gradual adaptation for humans, an abrupt change such as sudden loss of valuable fisheries can have more fatal consequences for people living in the Arctic. Over the last decades there is mounting evidence that ecosystem responses to extrinsic pressure such as climate can be nonlinear and abrupt (May 1977; Groffman et al. 2006). Occasionally ecosystem responses display hysteresis behavior with multiple stable states, also known as regime shifts (Scheffer et al. 2001). Thus, large changes in the ecosystem functioning may result, even from small changes in the climate. The term ‘‘tipping point’’ commonly refers to a critical threshold at which minor perturbations can qualitatively alter the state or development of a system (Lenton et al. 2008). Polar, and especially Arctic, ecosystems are particularly likely to show regime shifts in response to climate change, because temperature increases have been and will be larger than elsewhere and because the structure of the food-web is relatively simple, implying that loss of key species and invasion of new species can fundamentally alter the flow of organic matter and nutrients through the system (Frank et al. 2005).

A large and diverse range of climate-induced changes in Arctic ecosystems resulting from warming, reduced sea ice cover, altered circulation patterns, and increasing freshwater discharge have been reported (Greene and Pershing 2007; Wassmann et al. 2011), however, the nature of these changes (gradual or abrupt) is not known. The existence of ecological tipping points has mostly been investigated by means of theoretical modeling studies and experiments, whereas studies examining long-term monitoring data sets for abrupt changes are few. In fact, there is an apparent mismatch between studies reporting regime shifts and threshold response, and the application of statistical methods to actually document their existence. However, over the last two decades, methods and software have become available for analyzing nonlinear and step change responses (Andersen et al. 2009).

Here, we will review the scientific literature for studies suggesting regime shifts in Arctic ecosystems and carefully determine the statistical basis for the reported tipping points. We will present a range of simple and flexible statistical tests for identifying tipping points, which can be customized to the hypothesis in question. Our objective is to demonstrate, by means of examples, the usefulness of such statistical methods for exploring Arctic data sets.

Recent Ecological Tipping Points in the Arctic Literature

The Arctic has, so far, passed a few documented tipping points resulting in ecological regime shifts. Although ecological regime shifts in marine environments are usually associated with climate change and/or overfishing (Lees et al. 2006), it has been suggested that biological variables could provide a more diagnostic or earlier signal of regime shifts than climate indices (Hare and Mantua 2000; Wooster and Zhang 2004).

Probably the best described Arctic regime shifts are those observed in the Bering Sea and a subarctic Gulf of Alaska, and connected with the Pacific Decadal Oscillation (PDO). The PDO is a pan-Pacific phenomenon that includes inter-decadal climate variability and is correlated with temperature anomalies and precipitation patterns around the Pacific Ocean. It has a great impact on marine ecosystems, including the Pacific sector of the Arctic Ocean (Mantua et al. 1997; Mantua and Hare 2002). Hare and Mantua (2000) applied a principal component analysis (PCA) to 100 time series from the North Pacific and Bering Sea and identified two shifts (1977 and 1989) in climate and fish community structure. Overland et al. (2004) also applied a PCA to an even more complex set of time series, mostly from the Arctic Sea, and identified step changes in the first two principal components coinciding with those identified by Hare and Mantua (2000). Although the shifts in the principal components for both these studies are rather convincing, the significance of the changes was not tested. In a more recent study, Rodionov and Overland (2005) identified an additional step change in 1998 using the method of Sequential T-test Analysis of Regime Shifts (STARS). Finally, it has also been postulated that regime shifts could have happened in 1925 and 1945 (Benson and Trites 2002).

The climatic regime shift in the North Pacific Ocean that took place in the winter of 1976–1977 was fully recognized no sooner than 10–15 years afterwards (Hare and Mantua 2000) although some symptoms of the event, like changes in SSTs and zooplankton abundance, were apparent within a few years of the shift (Wooster and Zhang 2004). In the Bering Sea and the subarctic Gulf of Alaska ecosystems, it resulted in a reorganization of community structure and a change from a highly productive benthic community of commercially important crab and pandalid shrimp populations as well as capelin population to a similarly productive gadid and other groundfish populations. The main changes were distinguished based on changes in the catch biomass. The observed reorganization in a trophic chain was reported to have negative effects on piscivorous sea birds and marine mammals (Anderson and Piatt 1999).

According to Hare and Mantua (2000) the shift in 1989 was not as pervasive as the previous one and was not just a simple reversal of the climatic and ecosystem conditions established by the 1977 shift. The biological features of this shift were clear, although the indices of Pacific climate were not so significantly changed. The most notable ecosystem changes beginning in 1989 involved reduced groundfish recruitment and large increase in jellyfish biomass in the Bering Sea (Mantua 2004). Brodeur et al. (2008) reported a steep increase in jellyfish biomass, primarily over the eastern Bering Sea shelf over the 1990s. Also a positive response to the 1989 shift of pelagic fish species was observed in the Gulf of Alaska and Bering Sea (Benson and Trites 2002).

The last observed climate regime shift occurred in the North Pacific in 1998–1999, but there is lack of evidence of community reorganization following this climate event. Warmer conditions that came to the eastern Bering Sea after 2000 resulted in declining jellyfish biomass, but the response to temperature was not unequivocal for the two regions examined (Brodeur et al. 2008). Also mesozooplankton biomass and species composition of the subarctic Gulf of Alaska and Alaskan shelf show significant changes between years before and after this regime shift in a non-parametric test for sample means (Batten and Welch 2004).

According to Benson and Trites (2002), the timing of the anomalous environmental events in the North Pacific Ocean appears to be linked to physical and biological responses in other oceanic regions of the world. However, regime shifts in the Arctic and subarctic region of the North Atlantic have not been described in such details so far. Coincident with the above-mentioned regime shift in the North Pacific, the upper ocean circulation in the Arctic Ocean changed substantially after an atmospheric regime shift between the late 1980s and early 1990s, and resulted in freshening and stratification of the shelf waters (Greene and Pershing 2007). Lindsay and Zhang (2005) used the model results from a regional coupled ice-ocean model covering the Arctic Ocean, the Barents and Kara Seas, and the Greenland–Iceland–Norwegian seas. They stated that the late 1980s and early 1990s could be considered a tipping point during which the ice–ocean system began to enter a new era of thinning ice and increasing summer open water because of positive feedbacks.

Increased phytoplankton production in autumn caused by increasing area of open water and enhanced stratification, coincided with the increase of smaller, shelf-associated copepods. PCA applied by Frank et al. (2005) to time series of biotic, abiotic and human variables provided statistical evidence and a concise assessment of the change in the structure of the ecosystem. A dramatic shift from benthic fish to a pelagic fish/macroinvertebrate-dominated system in the Northwest Atlantic was described. Another ecological response connected with the changes in Arctic Ocean circulation patterns is the observation of biogeographic range expansions by boreal plankton, including renewal of the trans-Arctic exchanges of Pacific and Atlantic species (Greene et al. 2008). However, Drinkwater (2006) argued that the largest and most significant climate-induced regime shift in the North Atlantic and the high Arctic over the last century had occurred in 1920 s and 1930 s. Among the observed biological changes were an increased abundance of Atlantic cod off West Greenland, Iceland, and Svalbard, migrations of capelin over the Barents Sea, as well as the northward expansion of the boreal invertebrates. Other “tipping elements” in the Arctic, according to Lenton et al. (2008), are associated with the Arctic sea ice, Greenland ice sheet and Atlantic thermohaline circulation.

Statistical Analysis of Tipping Points

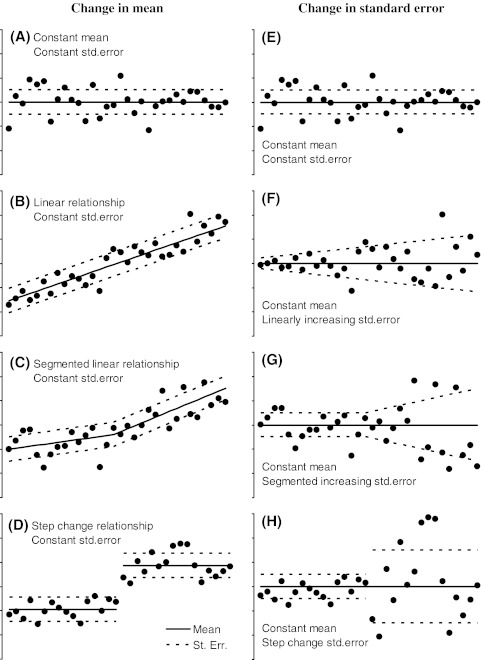
The definition of a “tipping point” as “a critical threshold at which minor perturbations can qualitatively alter the state or development of a system” (cf. Lenton et al. 2008) cannot be readily assessed in a statistical hypothesis framework. In order to formulate a testable hypothesis it is necessary to define how “an altered state or development of a system” manifests itself in the statistical properties of the data describing the system. For example, can a small change in temperature lead to the disappearance of the Arctic copepod Calanusglacialis, i.e., is there a temperature threshold beyond which the mean biomass of C. glacialis quickly drops below expected values (Fig. 1). The change in mean biomass is just one of many potential symptoms of a fundamentally altered state. In fact, there are many ways in which the statistical properties of data may change in response to various perturbations, and it is generally advisable to thoroughly explore the data before formulating the statistical hypothesis. We will here outline some potential ways for tipping points to manifest themselves using the two basic statistical properties of all distributions, the mean μ and variance σ² (Carpenter and Brock 2006). Other statistical properties, such as increasing skewness (Guttal and Jayaprakash 2008) and spectrum reddening (Kleinen et al. 2003), have been proposed as an early warning signal for regime shifts and can be tested within the same principal framework outlined below.

Fig. 1.

Will increasing sea surface temperatures and loss of sea ice lead to sudden disappearence of key species such as Calanus glacialis in the Arctic marine ecosystems? Photos: Slawek Kwasniewski and Agata Weydmann

We will formulate our hypothesis testing framework using parametric statistics, assuming that we can describe the observed ecosystem state (given by observations Y = y₁, y₂, …, y_n) with a known distribution (given by parameters θ) such that the likelihood function L(Y; θ) can be computed. All statistical testing is based on the formulation of a null-hypothesis, which is basically a model without a tipping point, and an alternative hypothesis that includes the tipping point. The likelihood ratio (LR) test is a general statistical test, which compares the likelihood function for the null-hypothesis, L₀(Y; θ₀), with that for the alternative hypothesis, L₁(Y; θ₁), where θ₀ and θ₁ denote the parameters of the models under the null-hypothesis and alternative hypothesis, respectively. The test statistic is calculated as the ratio between the two likelihood functions, such that ratios close to 1 suggests the two alternative models to be equally good and smaller values suggest the alternative model to describe the observations better than the null-hypothesis.

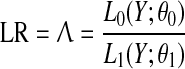1

This general test statistic can be applied to many different hypotheses, provided that a parametric distributional function for the observations is proposed. However, the problem with the LR-statistic is that the distribution of Λ under the null-hypothesis is known only for a few special cases, but if the model proposed under the null-hypothesis constitute a sub-model (i.e., by fixing parameter values) of the alternative hypothesis model then −2 log(Λ) is asymptotically (n → ∞) χ² distributed with degrees of freedom equal to the reduction of free parameters between the models under the two hypotheses (dim (θ₁) − dim (θ₀)). In the special case of normal distributed observations with a known standard error, the χ² approximation is exact.

We will consider four different types of responses in both mean and variance (Fig. 2) to a perturbation (X =x₁, x₂,…,x_n). The case with constant mean and variance constitute the most basic null-hypothesis (Fig. 2a, e), that can be expanded to the hypotheses of a linearly increasing relationship (Fig. 2b) or linearly increasing heteroscedasticity (Fig. 2f). These two models can be further expanded to include a change point that changes the slope of the relationship (Fig. 2c) or changes the variance (Fig. 2g). Finally, alternatives to the basic null-hypothesis model having a constant mean and variance are step changes in the mean (Fig. 2d) and variance (Fig. 2h). Hence, the basic null-hypothesis model constitutes a sub-model to the linear models (Fig. 2b, f) by setting the slope equal to zero, and the linear models constitute sub-models to the segmented models (Fig. 2c, g, respectively), which can be seen from the model formulation of the segmented linear model (Fig. 2c) below,

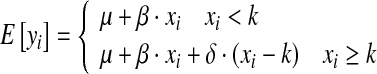2

where μ is the intercept, β is the initial slope, and δ is the change in slope at the change point k. The segmented linear model includes two additional free parameters to the strictly linear model (δ and k), and additional change points can be added to the model at the expense of two degrees of freedom for each change point, sometimes also referred to as knot. The segmented linear model is actually a special case of the widely used smooth polynomial splines with the condition of continuity in the change points only. Since the location of the change point is not known and should be estimated, the model (2) and its maximum likelihood should be estimated by means of nonlinear regression (Gallant and Fuller 1973). A similar model for the standard error can be formulated and estimated.

Fig. 2.

Simulated relationships to illustrate simple models for testing the significance of tipping points. Solid and dashed lines mark the mean and standard errors of the simulated distributions

The step change model differs from the segmented linear model since it includes an unknown discontinuity point (k) that cannot be estimated as a continuously varying parameter by nonlinear regression, because the likelihood function can be evaluated for the n discrete observations only, given values for (μ and δ). The step change model is

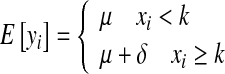3

This means that the likelihood function will be computed for all n – 1 potential location of the step change, and the model is chosen for that specific location of the change point that maximizes the likelihood. Similarly, a LR-type statistic can be computed for assessing the significance of the model (3) relative to the constant mean and variance model.

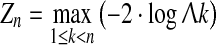4

However, since this implies calculating several test statistics for the same basic hypothesis, the χ² approximation does not apply. Calculated test statistics for Z_n can be compared with tabularized critical values on a given significance level (e.g., 5%) for various numbers of observations, derived either from theoretical approximations or from percentiles of Z_n calculated from multiple repeated simulations under the null-hypothesis (typically at least 10 000). A summary of critical values under different distributional assumptions and test types is found in Gombay and Horváth (1996). Moreover, these critical values of Z_n will be larger than for −2log(Λ) in (1), since the analysis involves the calculation of many test statistics to find the maximum. For comparison the critical value at the 5% significance level with n = 30 is 9.30 for Z_n, whereas the critical value for −2log(Λ) is approximated by χ²(1) = 3.84.

The step change model cannot be tested against the linear models (both strictly and segmented) by means of LR-type statistics, because they are alternative models and do not form a nested hierarchy of models and sub-models. In such cases, alternative models can be compared by various goodness-of-fit criteria such as Akaike’s Information Criterion (AIC) or Bayesian Information Criterion (BIC) that are both calculated from the likelihood function with a penalty for the number of parameters used in the model formulation. AIC (−2log(Λ) + 2n_parameters) penalizes the number of parameters less strongly than BIC (−2log(Λ) + log(n)n_parameters) and is therefore claimed to over-parameterize models for larger data sets (n is the number of observations) (Madsen 2008). A more detailed discussion on model building and statistical inference can be found in, e.g., Stephens et al. (2007).

The methods outlined above assume observations to be independent but they can be expanded to also incorporate various correlation patterns across the observations. The LR test for the segmented linear model remains valid, whereas the critical values for Z_n increase with correlation (see Tang and MacNeill 1993 for more details). However, if correlation patterns between predictors and residuals still persist after developing models like in Fig. 2, this could suggest for improving the model describing the mean rather than choosing a complex covariance structure for the data. This subject is rather extensive and will not be covered any further here (see, e.g., Madsen 2008 for an introduction).

Analysis of the models described above can be carried out using statistical software for nonlinear regression (e.g., PROC MODEL in SAS or nls in R). The models in the example given below were estimated using SAS and the code can be found in the Supplementary material.

Example: Identification of Tipping Points

The most drastic change for Arctic ecosystems is probably the loss of sea ice (Stroeve et al. 2007; Comiso et al. 2008) that even during the extreme negative phase of the Arctic Oscillation in 2009/2010 had a record year low ice extent (Stroeve et al. 2011). An abrupt change in the sea ice extent has been reported to have occurred in 1996 (Comiso et al. 2008), suggesting that the loss rate of sea ice increased by factor of four, although the exact timing of the change was not identified and tested by means of statistical methods. Moreover, the two regressions in the analysis by Comiso et al. (2008) were not connected and implicitly included a discontinuity in 1996 suggesting an abrupt increase in sea ice extent by 0.2–0.3 × 10⁶ km² in addition to the slope change. Here, we will revisit a subset of these data and examine the existence of tipping points with an improved statistical approach. We will exemplify the application of the statistical methods described above for detecting tipping points using data on the Arctic sea ice extent downloaded from the National Snow and Ice Data Center (NSIDC, www.nsidc.org) (Cavalieri et al. 1999). We used the annual extent in September (n = 22, 1979–2010), which is the month with the minimum extent.

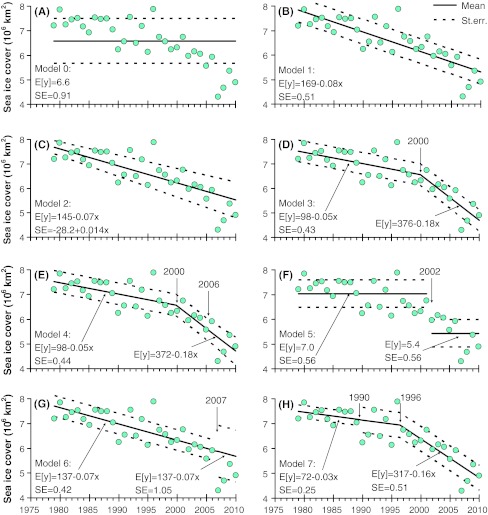
During the 22 years with data there was a mean sea ice extent of 6.6 × 10⁶ km² with a standard error of 0.91 × 10⁶ km² (Fig. 3a), but it was also apparent that the sea ice extent was above the average in the beginning and less than average for the more recent years (Fig. 3a). Therefore, as the next step we analyzed if a model with a linear trend in the mean would give a better description of the data (Fig. 3b). The likelihood significantly improved (Table 1) according to the LR test statistic (−2log(Λ) = 37.02; p < 0.0001), and the residual variation was reduced to 0.51 × 10⁶ km². The linear model suggested a mean loss rate of sea ice extent of 0.08 × 10⁶ km² year⁻¹ for the entire period.

Fig. 3.

Time series models describing the extent of Arctic sea ice (1979–2010) with statistics in Table 1. Solid line shows the estimated model and dashed lines the standard error around the mean model

Table 1.

Likelihood statistics, AIC, and BIC for different time series models (cf., Fig. 3) describing the sea ice extent (1979–2010)

Model	Mean	Std. Error	No. of parameters	−2log(L)	AIC	BIC
0	Constant	Constant	2	84.54	88.54	90.73
1	Linear	Constant	3	47.52	53.52	56.79
2	Linear	Linear	4	44.59	52.59	56.96
3	Segmented	Constant	5	37.21	47.21	52.67
4	Segmented	Segmented	7	35.72	49.72	57.36
5	Step change	Constant	4*	53.30	61.30	65.67
6	Linear	Step change	5*	42.34	52.34	57.80
7	Segmented	Step change	7*	31.76	45.76	53.39

The number of parameters in the step change models (Models 5, 6 and 7, marked with asterisk) included one parameter degrees of freedom for the year of the step change, although this year was not estimated as a free-floating parameter in the same manner as other parameters

An extension to this model was to examine if the residual variation also changed linearly over time (Fig. 3c). Indeed, there was an almost threefold increase in the residual standard error with time from 0.28 × 10⁶ km² at the beginning of the time series to 0.73 × 106 km² at the end of the time series. Due to increasing uncertainty with time, recent years had less weight than earlier years and the slope was therefore less (0.07 × 10⁶ km² year⁻¹) than for the model with constant standard error. There was a slight improvement in the likelihood function only (Table 1), but this gradual increase of the residual variation was not significant according to the LR test statistics (−2log(Λ) = 2.93; p = 0.0871). Nevertheless, the fact that this extension was at the borderline of the significance level (p = 0.05) was also reflected in improvements for AIC, but not BIC. However, we will discard the hypothesis of a linearly increasing residual standard error on the basis of the likelihood statistics.

It has been suggested that there was a change in the loss of sea ice extent around 1996 (Comiso et al. 2008), so to investigate this hypothesis we proposed that the mean sea ice extent was composed of two joined line segments with the time location of the joint unknown (Fig. 3d). Estimating this model resulted in a loss rate of sea ice extent by 0.05 × 10⁶ km² year⁻¹ before 2000 (uncertainty of the estimated change point was ±2.3 years), followed by more than a three-doubling (0.18 × 10⁶ km² year⁻¹). The residual standard error was further reduced to 0.43 10⁶ km². The likelihood function, AIC and BIC all improved and the LR test statistic also documented the significance of the change of slope in 2000 (−2log(Λ) = 10.31; p = 0.0058).

In addition to the segmented linear model we hypothesized that the standard error could be described by a segmented model (cf., Fig. 2g). Estimating this model yielded almost the same slopes and change point for the mean (Fig. 3e), whereas the standard error was constant (0.44 × 10⁶ km²) before 2006 (±3.8 years), and then increased linearly to (0.57 × 10⁶ km²) by the end of the time series. The change in the likelihood function, relative to the model with a constant standard error, was marginal and neither AIC nor BIC improved (Table 1). Moreover, the LR test statistics also clearly suggested that this proposed model extension was not significant (−2log(Λ) = 1.49; p = 0.4748).

As an alternative to the segmented linear model we estimated the step change model with an unknown change point (cf., Fig. 2d) assuming the standard error to be constant. The most probable time of the step change was in 2002 with a mean sea ice extent of 7.0 × 10⁶ km² before and 5.4 × 10⁶ km² after, both periods having a standard error of 0.56 × 10⁶ km² (Fig. 3f). Although the test statistics Z_n = 31.24 was clearly above the critical value, even at the 1% significance level (~12.60; Gombay and Horváth 1996) and the model constituted a significant improvement to the constant mean model, the AIC and BIC also indicated that the step change model was less adequate than both the linear and segmented linear models (Table 1). Therefore, we investigated a potential step change in the standard error as an extension to the linear and segmented linear mean model (models 1 and 3 in Table 1).

For the linear mean model, the optimal step change in the standard error was 2007, suggesting an increase in the standard error from 0.42 × 10⁶ to 1.05 × 10⁶ km² (Fig. 3g). The loss rate of sea ice extent over the entire period was estimated at 0.07 × 10⁶ km² year⁻¹. However, the improvement in the likelihood function was relatively small and only AIC suggested a model improvement, whereas BIC did not (Table 1). The test statistics (Z_n = 5.18) was also somewhat below the critical value at the 5% significance level (~9.30). Thus, there was no significant change point for the standard error in addition to the linear mean model.

Finally, we tested a step change in the standard error in addition to the segmented linear mean model and found that there was an optimal step change for the standard error in 1990 and a change in the slope of ice extent in 1996 (Fig. 3h). This model suggested a loss rate of ice extent of 0.03 × 10⁶ km² year⁻¹ increasing more than five-fold after 1996 (±2.8) to a staggering rate of 0.16 × 10⁶ km² year⁻¹. The period before 1990 had relatively small random fluctuations (standard error of 0.25 × 10⁶ km²) that doubled afterwards. This model improved the AIC relative to model 3, whereas BIC favored model 3 to model 7 (Table 1). The test statistics (Z_n = 5.45) was also somewhat below the critical value at the 5% significance level (~9.30), corresponding to a significance level of p = 0.22. Although this change in fluctuations did not significantly improve the model with constant standard error, it does indicate that there could be increases in the random fluctuations before the change in mean occurred. It is visually appealing that the period 1990–1996 could have stronger random fluctuations than other periods, and such a model actually resulted in optimal values for both AIC (44.76) and BIC (52.40), but nevertheless the model was not strong enough to provide sufficient statistical evidence relative to the simpler model 3 (Z_n = 6.45, p = 0.15). It is, however, likely that if more data were included in the analyses, provided that they showed similar patterns, the significance of this model would improve.

Conclusions

The potential existence of thresholds or tipping points in ecosystem responses to changing climate and human disturbances has gained more popularity in the scientific literature as reflected in the growing number of publications on this subject, but studies reporting statistical evidence for such nonlinear responses are remarkably few (Andersen et al. 2009). Therefore, we have outlined some basic statistical methods that can be further expanded and customized to analyze data sets for abrupt changes in the mean and standard error of the distributions. As illustrated with the example, the statistical analysis of tipping points is an iterative model selection process more than a rigid framework for hypothesis testing, where model extensions are proposed and tested consecutively. The amount of data naturally imposes constraints on the complexity of the model, particularly pronounced for Arctic data sets, but this constraint will gradually be alleviated with a continued monitoring effort aiming at documenting climate change effects.

In fact, tipping points can manifest themselves in various types of responses and consequently, it is important in the statistical analysis to examine potential changes in different properties of the data. Although changes in the mean probably are the most important property of such analyses, it is also important not to neglect other properties such as the magnitude of random fluctuations. We have outlined statistical methods to examine changes in the standard error of the distribution, and applying this method to sea ice extent suggested a potential tipping point, not reported previously, in the random fluctuations 6 years prior to changes in the mean. This observation is consistent with the conceptual theory for regime shifts, where a continued erosion of the sea ice resilience may amplify perturbations of the system before critical thresholds are exceeded and the system enters a new regime. Although the change in random fluctuations was not significant relative to a simpler model, the other months, that were not included, showed similar patterns (www.nsidc.org) and would, most likely, lend sufficient power to identify this proposed early warning signal. Such analyses could be derived from the general statistical approaches outlined in this study, taking seasonality into account, however, the main objective here was to introduce the methods.

Biographies

Jacob Carstensen

is a professor at the department of Bioscience at Aarhus University. His research interests include statistical analysis and modeling of anthropogenic impacts on marine ecosystems.

Agata Weydmann

is a post-doc at the Marine Ecology Department at the Institute of Oceanology of the Polish Academy of Sciences. Her research interests include Arctic zooplankton ecology and genetics.