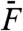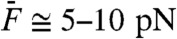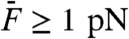Phantom tones and suppressive masking by active nonlinear oscillation of the hair-cell bundle

Abstract

Processing of two-tone stimuli by the auditory system introduces prominent masking of one frequency component by the other as well as additional “phantom” tones that are absent in the sound input. Mechanical correlates of these psychophysical phenomena have been observed in sound-evoked mechanical vibrations of the mammalian cochlea and are thought to originate in sensory hair cells from the intrinsic nonlinearity associated with mechano-electrical transduction by ion channels. However, nonlinearity of the transducer is not sufficient to explain the rich phenomenology of two-tone interferences in hearing. Here we show that active oscillatory movements of single hair-cell bundles elicit two-tone suppression and distortions that are shaped by nonlinear amplification of periodic stimuli near the characteristic frequency of spontaneous oscillations. When both stimulus frequencies enter the bandwidth of the hair-bundle amplifier, two-tone interferences display level functions that are characteristic both of human psychoacoustics and of in vivo mechanical measurements in auditory organs. Our work distinguishes the frequency-dependent nonlinearity that emerges from the active process that drives the hair bundle into spontaneous oscillations from the passive nonlinear compliance associated with the direct gating of transduction channels by mechanical force. Numerical simulations based on a generic description of an active dynamical system poised near an oscillatory instability—a Hopf bifurcation—account quantitatively for our experimental observations. In return, we conclude that the properties of two-tone interferences in hearing betray the workings of self-sustained “critical” oscillators, which function as nonlinear amplifying elements in the inner ear.

The human ear does not work as a high-fidelity sound receiver. First, the perceived loudness of a tone diminishes in the presence of a second tone at a nearby frequency, a phenomenon called masking (1). Second, a person listening simultaneously to two pure tones f₁ and f₂ can hear not only these frequencies but also additional tones that are not present in the acoustic stimulus (2, 3). These “phantom” tones have been recognized as distortion products of the input; they are produced at linear combinations of f₁ and f₂. Any device evinces nonlinearity when the stimulus becomes too intense to elicit a proportional response. In the inner ear, mechano-electrical transduction by sensory hair cells is usually accepted as the dominant source of two-tone interferences, for the sigmoidal relation between hair-bundle deflections and transduction currents provides a saturating nonlinearity that distorts receptor potentials (4, 5). Because gating of transduction channels is directly coupled to tip-link tension, the hair-cell bundle also acts as a nonlinear spring (6) that produces mechanical distortions of sound-evoked vibrations (7). If the transduction process only displayed a static nonlinearity, for which the output can be expressed as a power-series expansion of the input (see section 1 in SI Text), the distortion would vanish for weak stimuli and become more and more pronounced as the magnitude of stimulation increases. For a two-tone stimulus, the level of distortion relative to that of the primaries at f₁ and f₂ would in turn grow superlinearly.

The behavior of the auditory nonlinearity is in striking contrast to that expected from a static nonlinearity (3, 8). First, the most prominent “phantom tone” in the auditory percept, which occurs at 2f₁ - f₂ when the frequency ratio f₂/f₁ is near 1.2, is detected even at low levels of stimulation. Second, its magnitude increases at about the same rate as the stimulus, so that its relative level remains practically constant at 15–20% over a broad range of sound levels. In addition, both masking and phantom tones display a sharp dependence on the frequency separation between the two components of the stimulus, indicating that the auditory nonlinearity must be coupled to a filter that allows interaction of neighboring frequency components only.

Two-tone suppression and distortions have been observed in vivo on the basilar membrane that supports the organ of Corti of the mammalian cochlea (9, 10). These phenomena appear to be intimately related to the nonlinear, frequency-selective active process that enhances sensitivity, sharpens frequency tuning and compresses six orders of magnitudes of sound-pressure levels into a much narrower range of vibration amplitudes (11). Distorted cochlear vibrations are strong enough to be reemitted in the ear canal as distortion-product oto-acoustic emissions (DPOAEs) that contain the cubic difference tone 2f₁ - f₂ (12, 13). Notably, the ears of nonmammalian vertebrates produce similar distortion-product oto-acoustic emissions (14–16). Like in mammals, this manifestation of nonlinear inner-ear mechanics is associated with high sensitivity and sharp frequency selectivity (17), which are key specifications of active hearing.

Two forms of motility by mechanosensory hair cells have been implicated in the active process (18). The hair cell can power active movements of its mechanosensory hair bundle, including spontaneous oscillations that have been shown in nonmammalian vertebrates to provide nonlinear and frequency-selective amplification of sinusoidal stimuli (19–22). In mammals, active hair-bundle motility coexists with membrane-based somatic motility (23, 24), a biological form of piezoelectricity by which the soma of an outer hair cell changes length in response to variations of its membrane potential (25). Although electromotility appears to be necessary for cochlear amplification (26, 27), this process is by itself linear over the physiological range of receptor potentials. It is likely that hair-bundle and somatic motility cooperate to mediate the active process in the mammalian cochlea (28–30), with the hair bundle bringing the nonlinearity that is associated with both cochlear amplification and two-tone interferences (31, 32).

In this work, we evaluate the effects of active hair-bundle oscillations on two-tone suppression and distortions by a single hair cell. For stimulation near the characteristic frequency of spontaneous oscillations, we show that a hair bundle produces two-tone interferences with level functions that are characteristic of both human psychoacoustics and in vivo measurements of inner-ear mechanics. We interpret our observations within the general theoretical framework of “critical oscillators,” which are active dynamical systems poised near an oscillatory instability called a Hopf bifurcation.

Results

Two-Tone Suppression.

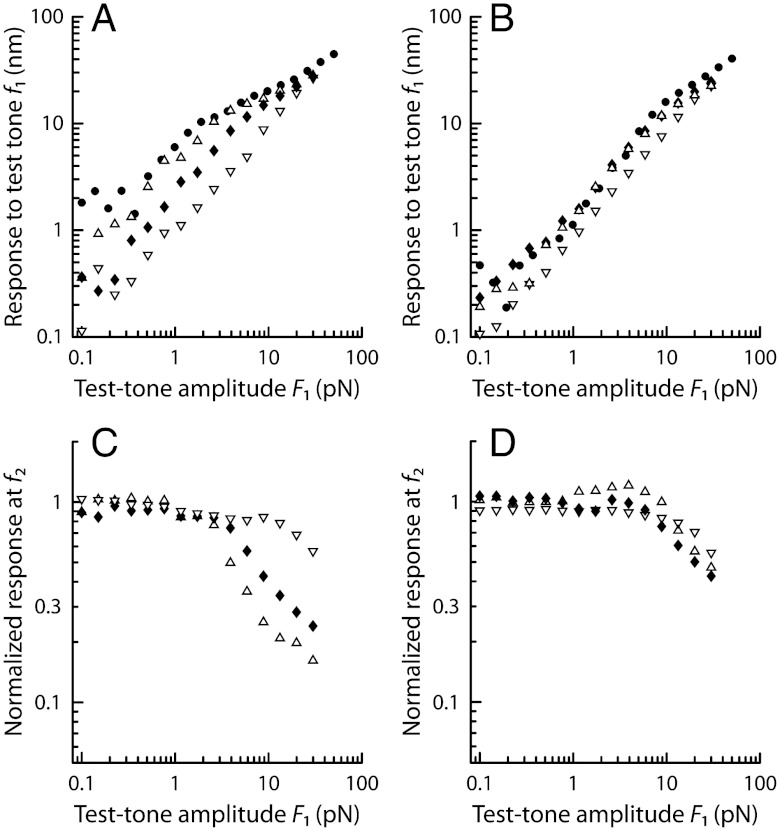
We took advantage of a two-compartment preparation of the bullfrog’s sacculus (33) in which hair cells routinely power spontaneous oscillations of their hair bundle at a characteristic frequency f_C = 5–80 Hz. Using a flexible glass fiber, we applied periodic forces F to the top of a hair bundle. Previous work indicates that oscillatory hair bundles actively resonate with pure tones F(t) = F₁ sin(2πf₁t) and amplify their responsiveness at the frequency f₁ of stimulation (20, 34). Significant amplification happens only when stimulus frequencies fall within a limited bandwidth that is centered at the characteristic frequency of oscillation f_C. Accordingly, for small stimulus amplitudes F₁ of a test tone, a hair bundle displayed a larger response near its frequency of spontaneous oscillation (f₁ ≅ f_C; Fig. 1A, black disks) than at a higher frequency (f₁ ≅ 10 × f_C; Fig. 1B, black disks). Amplification at resonance (f₁ ≅ f_C) was associated with a compressive nonlinearity that accommodated a large range of stimulus amplitudes (0.5–50 pN) into a narrower range of hair-bundle movements (3–40 nm). In contrast, stimulation off-resonance (f₁ ≅ 10 × f_C) elicited passive hair-bundle movements that grew almost in proportion to the stimulus, although a small, but noticeable, deviation from linearity was observed for forces near 10 pN (Fig. 1B, black disks).

Fig. 1.

Two-tone suppression. (A) The magnitude of the bundle motion’s Fourier component at the frequency f₁ = 13 Hz of a test tone is plotted as a function of the amplitude F₁ of this component of the two-tone stimulus. The various symbols correspond to different amplitudes F₂ (•, 0 pN; △, 2 pN; ⧫, 5 pN; ▿, 10 pN) of the masker tone that was added to the test tone at a nearby frequency f₂ = 12 Hz. Stimulation was here delivered at resonance—i.e., near the bundle’s characteristic frequency f_C = 11 Hz of spontaneous oscillation. (B) Same as in A but for stimulation off-resonance, with f₁ = 130 Hz and f₂ = 120 Hz that are both one order of magnitude larger than f_C. (C) Using the same data as in A, the response at f₂, normalized to its value when F₁ = 0, is here plotted as a function of the amplitude F₁ for different amplitudes F₂. (D) Same as in C but for stimulation at f₁ = 130 Hz and f₂ = 120 Hz. All data from same cell.

By applying two-tone stimuli F(t) = F₁ sin(2πf₁t) + F₂ sin(2πf₂t), we studied how the hair-bundle response to a test tone (frequency f₁) was affected by the addition of a second tone (frequency f₂) at a nearby frequency. For stimuli at resonance (f₁ and f₂ near f_C), we observed that the response to the test tone was partially suppressed by the additional tone (Fig. 1A). For intense masker levels, the test tone displayed a level function that was nearly linear, resembling that obtained off-resonance in response to the test tone only (Fig. 1B). Amplification of the test tone thus appeared to be turned off by the masker tone. As expected from a complete loss of gain from active hair-bundle motility, the amplitude of stimulation that was required to elicit a response beyond a given threshold was increased by as much as 10-fold. The response at f₂ was also suppressed by the stimulus at f₁ (Fig. 1C). When the amplitudes of the two tones were dissimilar (e.g., F₂/F₁ ≅ 10 with F₁ = 1 pN in Fig. 1A), the response to the stronger tone was almost unaffected whereas the response to the weaker tone was largely suppressed, decreasing by about 90%. The contrast between the frequency components of the two-tone stimulus was thus enhanced. Remarkably, the phenomenon of two-tone suppression, which was so compelling at resonance, was barely observed when the hair bundle was stimulated off-resonance (Fig. 1B and D).

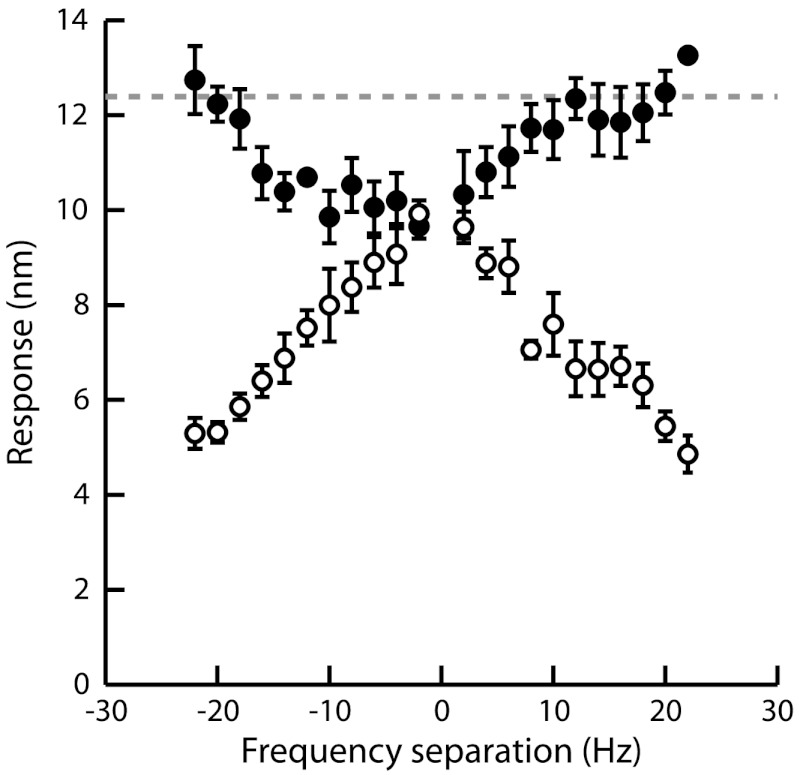
To further characterize the frequency specificity of two-tone suppression, we measured how the amplified response to a test tone at resonance was affected by an additional tone with the same amplitude but varying frequency (Fig. 2). We used low stimulation levels, for which amplification was maximal (Fig. 1). When the frequency difference between the two tones was large enough, the response to the test tone was the same as when this tone was presented alone. As the frequency mismatch was reduced, we observed that the response to the test tone was increasingly suppressed. This response reached a minimum, and two-tone suppression was thus maximal, when both stimuli had about the same frequency. Correspondingly, the response to the masker tone increased as its frequency approached the characteristic frequency of the hair-bundle oscillator but, as the result of mutual suppression of the two tones, never rose to the maximal amplified value that would have been reached, had this tone been presented alone.

Fig. 2.

Frequency specificity of two-tone suppression. The two components of the stimulus had here the same amplitude F₁ = F₂ = 2 pN. The frequency f₁ = 24 Hz of the test tone was fixed near the bundle’s characteristic frequency of oscillation f_C = 23 Hz, while the frequency f₂ of the masker tone was varied. The magnitude of bundle motion, at frequencies f₁ (●) and f₂ (○), is plotted as a function of the frequency separation Δf = f₂ - f₁. The dashed line represents the response level when the test tone was presented alone.

Two-Tone Distortions.

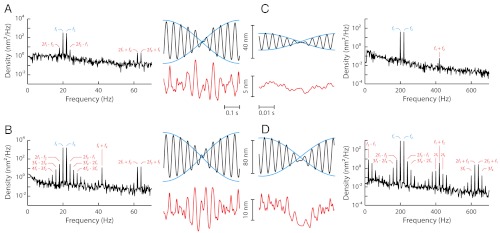
A two-tone stimulus constructed from the sum of two sinusoids with equal amplitudes 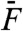and nearby frequencies produces a beating pattern. Although this pattern dominated the waveform of hair-bundle movement, filtering the primary frequencies of motion at f₁ and f₂ revealed that the hair bundle distorted its response to the stimulus (Fig. 3). The distortion was significantly larger in magnitude for stimulation at resonance than off-resonance and its waveform was qualitatively different in the two cases. The spectral density of hair-bundle motion disclosed the presence of discrete frequency components that were not present in the stimulus. In particular, for moderate to intense stimuli (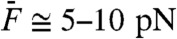), the hair bundle produced a series of odd distortion products at frequencies f₁ - kΔf and f₂ + kΔf, where k is a positive integer (k < 6) and Δf = f₂ - f₁. Distortion products of increasing order k displayed a hierarchy of magnitude X_k that was well described by an exponential decay X_k+1/X_k = exp(-λ), where λ is a fit parameter.

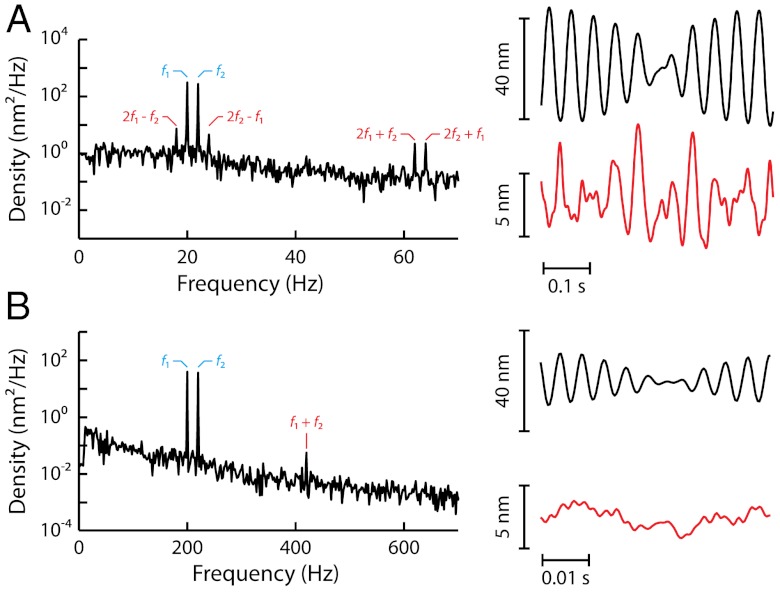
Fig. 3.

Two-tone distortions. Hair-bundle response to the sum 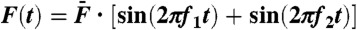of two sinusoidal forces with equal amplitudes 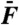(2 pN, A and C; 10.1 pN, B and D). Two-tone stimulation was delivered at resonance (A and B), with f₁ = 20 Hz and f₂ = 22 Hz near the bundle’s characteristic frequency of spontaneous oscillations f_C = 20 Hz, or off-resonance (C and D; f₁ = 200 Hz and f₂ = 220 Hz). The hair-bundle motion displayed a periodic beating pattern of magnitude; the ensemble average of 40 (A and B) or 400 (C and D) beats is plotted here (black line). The spectral density of bundle movement is shown on the side of each temporal trace for 20 s of recording. The frequencies of the distortion products are labeled in red. Keeping only the Fourier components f₁ and f₂ of the primaries resulted in a beating pattern of motion with an envelope (blue line) that is superimposed on the bundle’s global response. Conversely, filtering the primaries disclosed, in the temporal domain, the waveform of distortion (red line) that the hair bundle introduced into its response to the stimulus.

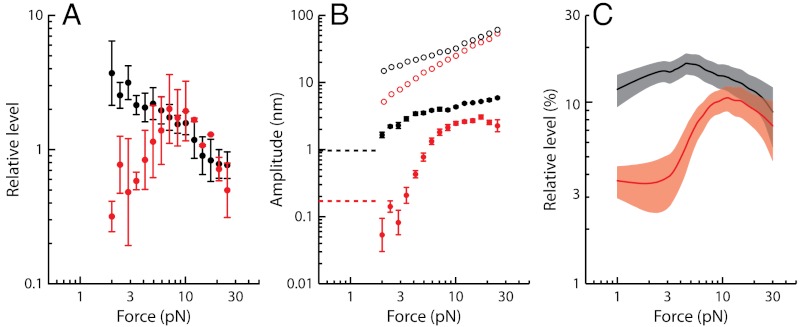
At resonance (f₁ and f₂ near f_C), a condition that maximizes amplification by active hair-bundle motility (34), stimulation of increasing magnitude enriched the spectrum of hair-bundle movements almost exclusively near the primaries (Fig. 3 A and B). The most prominent components of distortion were the cubic difference products at frequencies 2f₁ - f₂ and 2f₂ - f₁. These products, which had nearly the same magnitude, could be as much as fourfold more intense than the quadratic summation tone f₁ + f₂ for weak stimuli, but cubic and quadratic products reached similar levels for intense stimuli (Fig. 4A). In addition, the cubic products appeared at low level of stimulation (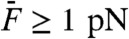), showed a linear growth for weak stimuli and a compressive growth for intermediate stimuli (Fig. 4B) that was well described by a power law 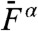with α = 0.26 ± 0.08 (mean ± SD, n = 11). This level function resembled that of the primaries (α = 0.41 ± 0.07, n = 11) or of the response to a pure tone (α = 0.38 ± 0.07, n = 43). Correspondingly, the level of the cubic difference products relative to that of the primaries showed little variation over the range of stimulus amplitudes that we explored, remaining approximately constant at 10–20% (Fig. 4C).

Fig. 4.

Level function of cubic difference products. (A) The level of the cubic-difference products at 2f₁ - f₂ and 2f₂ - f₁, for which we computed the arithmetic mean, is here compared to that of the quadratic-summation product f₁ + f₂. The ratio of these two quantities is plotted as a function of the magnitude 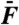of the external force for stimulation at resonance (black) and off-resonance (red). (B) Arithmetic-mean level of the two cubic difference products 2f₁ - f₂ and 2f₂ - f₁ (filled circles) and of the two primaries f₁ and f₂ (open circles) at resonance (black) and off-resonance (red) as a function of the stimulus amplitude 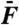. Dashed horizontal lines mark noise-floor levels when distortion products first appeared. Data in A and B from the same dataset as that used to plot Fig. 3. (C) For n = 11 cells with f₂/f₁ = 1.08 - 1.15, the arithmetic-mean level of the two cubic difference products was divided by that of the primaries at resonance (black) and off-resonance (red). This relative level is plotted as a function of the stimulus amplitude 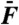. The continuous lines correspond to a moving average over a window comprising seven data points. The shaded areas represent 95% confidence intervals.

These properties are in stark contrast with those elicited by off-resonance stimuli (f₁ and f₂ near 10 × f_C), which probe passive hair-bundle mechanics (34). In this case, the stimulus elicited distortion products that were uniformly distributed across the spectrum (Fig. 3 C and D). In particular, harmonic distortions were clearly visible as well as even distortion products at f₁ + f₂ ± mΔf (m < 3). The quadratic summation product f₁ + f₂ often emerged first (Fig. 3C). The cubic difference products at 2f₁ - f₂ and 2f₂ - f₁ surfaced from the noise floor for relatively intense stimuli (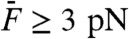). These cubic products grew more rapidly than the quadratic summation product, resulting in a relative level that increased (Fig. 4A). For 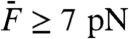, the relative levels of distortion at and off-resonance were similar, suggesting that two-tone distortions no longer depended on the frequency of stimulation. The cubic products showed a steep increase with the stimulus amplitude that followed a power law 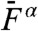(α = 2.74 ± 0.34, n = 11), until saturation afforded no further increase of distortion magnitude (Fig. 4 B and C). At any given stimulation level, these products were fainter than those observed at resonance, with a difference that was more pronounced for smaller stimuli. Notably, in four of the 11 cells that we analyzed, the level function was nonmonotonic and displayed a notch.

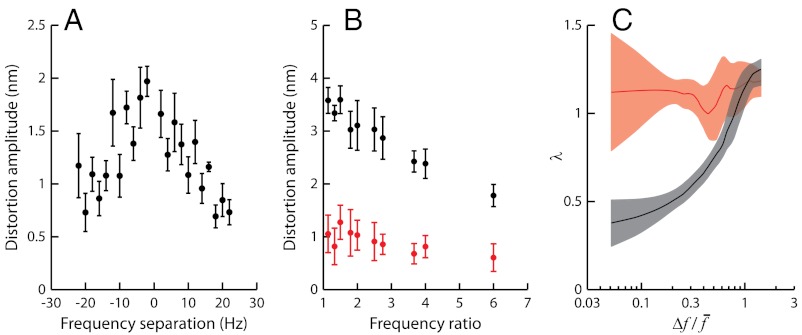
We then measured how distortion products depended on the frequency separation between the two components of the stimulus. When a test tone was applied at resonance, the addition of a second tone with the same amplitude produced cubic difference products with a magnitude that displayed a maximum when the frequency mismatch approached zero (Fig. 5A). The bell-shaped behavior mirrored that observed for two-tone suppression (Fig. 2, black disks), indicating a reciprocal relation between the two nonlinear phenomena. In a second set of experiments, we kept 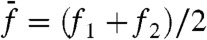constant. For stimulation about resonance (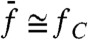), the magnitude of the cubic difference products decreased by 50% when f₂/f₁ was raised from 1.05 to 6 (Fig. 5B). In addition, higher-order odd products near the primaries became much less prominent: The parameter λ, which characterizes the exponential decay rate of the relation between a product’s magnitude X_k and its order k, increased from 0.4 to 1.2 (Fig. 5C). Correspondingly, the relative magnitude X_k+1/X_k decreased from 67% to 30%. Off-resonance (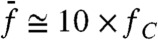), the cubic difference products as well as higher-order products were instead insensitive to variations of the frequency separation between the two components of the stimulus (Fig. 5 B and C).

Fig. 5.

Frequency specificity of odd distortion products near the primaries. (A) Arithmetic-mean level of the two cubic difference products 2f₁ - f₂ and 2f₂ - f₁ as a function of the frequency separation Δf = f₂ - f₁. Same cell and stimulus series as in Fig. 2. (B) Level of the cubic difference products as a function of the frequency ratio f₂/f₁. We varied f₁ and f₂ in a way that kept 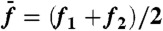constant and stimulated the hair bundle about resonance (black; 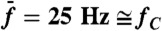), or off-resonance (red; 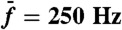). (C) In this semilogarithmic plot, the parameter λ that characterizes the exponential hierarchy of distortion products is represented as a function of the relative frequency separation 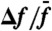, where Δf = f₂ - f₁. The continuous lines result from moving averages over a window of five data points obtained from five hair bundles; 95% confidence intervals are shown as shaded areas. Black and red plots are for stimulation about resonance (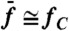) and off-resonance (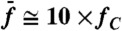), respectively. In B and C, the stimulus amplitude was .

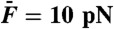The endolymphatic Ca²⁺ concentration acts as a control parameter of active hair-bundle motility (33, 35, 36). Because raising this concentration in the millimolar range brings spontaneous oscillations to a halt, we could compare, with the same hair bundle, two-tone distortions in oscillatory and quiescent regimes of hair-bundle mechanics (Fig. 6). In agreement with a previous study (7), we found that a quiescent hair bundle still produced distortion products. However, the cubic difference products were much weaker than in the oscillatory regime and the spectrum of distortion was in this case dominated by quadratic products (Fig. 6 A and B). In addition, the level function of cubic products had lost frequency specificity and displayed a superlinear growth (Fig. 6C). This behavior was similar to that observed off-resonance with oscillatory hair bundles.

Fig. 6.

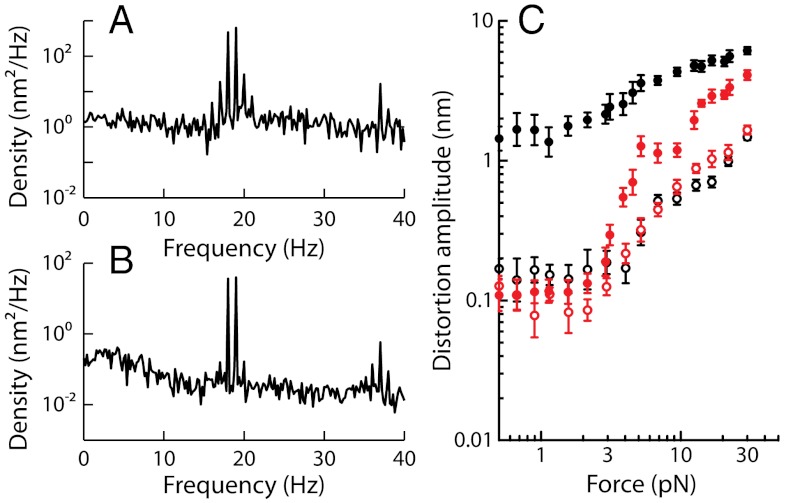
Effects of Ca²⁺ on cubic difference products. This hair bundle was subjected to the sum of two sinusoidal forces with equal amplitudes 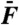. (A) At an endolymphatic Ca²⁺ concentration of 250 μM, the hair bundle displayed spontaneous oscillations at a characteristic frequency f_C = 19 Hz. The spectral density of hair-bundle movement is plotted for stimulation at resonance (f₁ = 18 Hz and f₂ = 19 Hz) with a stimulus amplitude 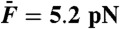. (B) When the Ca²⁺ concentration was raised to a value of 1 mM, the hair bundle became quiescent. The spectral density of motion resulted from the same stimulus as in A. (C) The arithmetic-mean level of the two cubic difference products is plotted as a function of the stimulus amplitude 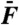for f₁ = 18 Hz and f₂ = 19 Hz (black) and f₁ = 180 Hz and f₂ = 190 Hz (red). Close and open symbols correspond to oscillatory and quiescent conditions, respectively. Note the notch in the level function depicted by red disks. Data in A–C from the same cell.

Discussion

Static and Passive Nonlinearity from Gating Compliance.

What is the mechanical nonlinearity that underlies the production of two-tone interferences? The nonlinear compliance that ensues from direct gating of the transduction channels by tip-link tension is a well-recognized source of mechanical distortion by the hair bundle (7). Gating compliance is clearly sufficient to explain two-tone suppression and distortions under ionic conditions for which the hair bundle does not oscillate, or for off-resonance stimulation of an oscillatory hair bundle (see section 2 in SI Text and Figs. S1 and S2). In particular, this nonlinearity produces distortion products at 2f₁ - f₂ and 2f₂ - f₁ that grow superlinearly, until saturation of mechano-electrical transduction affords no further increase of their magnitude. Simulations also indicate that when gating compliance is strong enough to elicit negative stiffness, a condition associated with the production of spontaneous hair-bundle oscillations (37), the level function of these cubic products displays a pronounced notch. Interestingly, in the example shown in Fig. 6C, the notch that was apparent for stimulation off resonance in the regime of spontaneous oscillation was lost in the quiescent regime, suggesting that the property of negative stiffness had vanished at higher Ca²⁺ concentrations.

Near the characteristic frequency of spontaneous hair-bundle oscillations, two-tone interferences acquire three main features that, together, are inconsistent with static nonlinearities such as that provided by gating compliance. First, the cubic difference products, as well as the other odd distortion products near the primaries, appear at lower levels of stimulation and become prominent in the spectral density of hair-bundle movements (Figs. 3 and 4). Second, both cubic difference products and primaries show a compressive growth over a large range of stimulus magnitudes, yielding a relative level that is nearly constant (Fig. 4). Finally, the level of these cubic products (Figs. 4 and 5), the exponential hierarchy of odd distortion products near the primaries (Fig. 5C), as well as the phenomenon of two-tone suppression (Figs. 1 and 2) display pronounced frequency specificity.

Dynamic and Active Nonlinearity from Critical Oscillation.

Clearly, the oscillatory activity of the hair bundle harnesses the intrinsic nonlinearity associated with mechano-electrical transduction to produce a dynamic nonlinearity with new properties. This makes sense because active hair-bundle motility introduces an extended compressive nonlinearity of responsiveness for frequency components of the stimulus that fall near the characteristic frequency of oscillation (20) (Fig. 1 A and B, black disks). This behavior is characteristic of “critical” oscillators, which are active dynamical systems that operate in the vicinity of a Hopf bifurcation (38–41). A Hopf bifurcation corresponds to an oscillatory instability by which the system changes abruptly from quiescence to a regime of spontaneous oscillations as a control parameter is varied continuously (42). At the characteristic frequency of the instability, an energy-transducing mechanism cancels the impedance of the system to sinusoidal stimuli. The system’s response is in turn amplified and under the control of an essential nonlinearity, for which there is no stimulus weak enough to evoke a linear response. Evidently, an active system of this sort should produce conspicuous two-tone interferences for stimulation near the characteristic frequency of the oscillator (43, 44). Simulations (Fig. 7) that are based on a generic description of a critical oscillator (Eq. 1; see Methods) demonstrate that these interferences are in qualitative agreement with those elicited by an oscillatory hair bundle (Fig. 1, 2, 4 and 5). In particular, the frequency specificity of two-tone suppression and distortions as well as the parallel compressive growth of the cubic difference products and of the primaries for stimulation at resonance emerge as properties that should be shared by all dynamical systems that operate near a Hopf bifurcation.

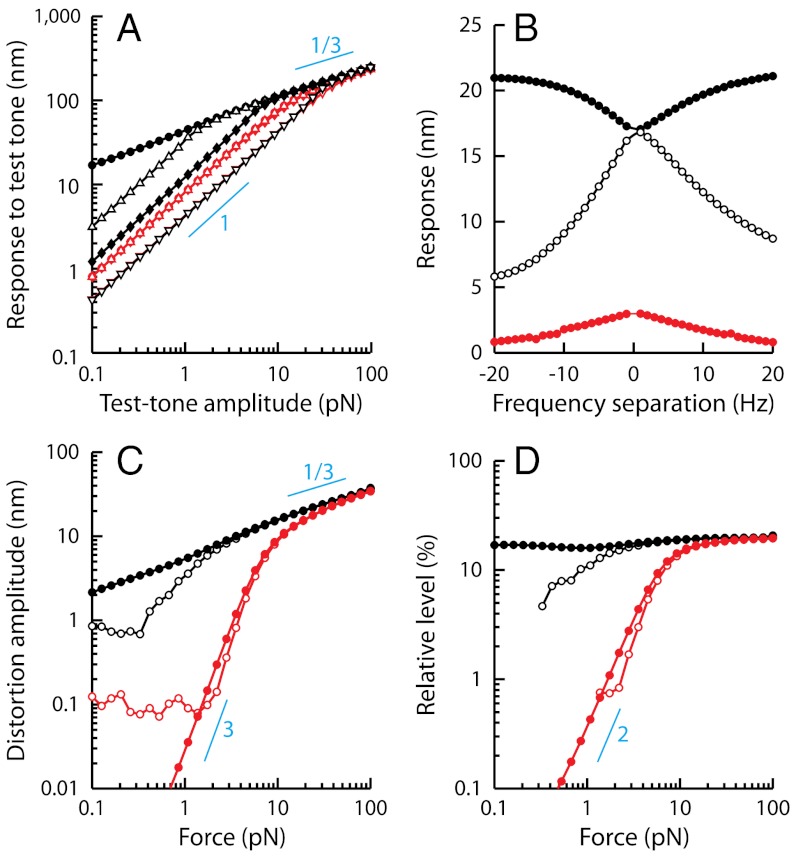
Fig. 7.

Simulations of two-tone interferences by a critical oscillator. (A) Two-tone suppression. The response at the frequency f₁ = 20 Hz (black) or f₁ = 200 Hz (red) of a test tone is plotted as a function of the amplitude F₁ of this component of the two-tone stimulus for various amplitudes F₂ (•, 0 pN; △, 1 pN; ⧫, 5 pN; ▿, 25 pN) of a masker tone at f₂ = 22 Hz (black) or f₂ = 220 Hz (red). The oscillator displayed a characteristic frequency of spontaneous oscillation f_C = 20.9 Hz. (B) Here F₁ = F₂ = 0.2 pN, the test-tone frequency f₁ = 21 Hz ≅ f_C was fixed while the masker-tone frequency f₂ was varied. The responses at frequencies f₁ (black disks) and f₂ (white disks), as well as the arithmetic-mean level of the cubic difference products at frequencies 2f₁ - f₂ and 2f₂ - f₁ (red disks), are plotted as a function of the frequency separation Δf = f₂ - f₁. (C) Two-tone distortions. The arithmetic-mean level of the cubic difference products is plotted as a function of the stimulus amplitude 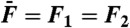at resonance (black; f₁ = 20 Hz and f₂ = 22 Hz) and off-resonance (red; f₁ = 200 Hz and f₂ = 220 Hz). (D) The arithmetic-mean level of the two cubic difference products was divided by that of the primaries and plotted as a function of the stimulus amplitude 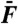. The system was deterministic, except in C and D (open symbols) where the oscillator was subjected to random noise. Thin blue lines represent power laws (power indicated next to the line). Parameter values: μ = 0, b = 10¹⁷ m^-2·s^-1, Λ = 1·10^-7 N·s·m^-1.

The theoretical framework provided by the generic behavior of a critical oscillator explains why the cubic difference tones dominate the spectrum of distortion products. If both components of a two-tone stimulus approximate the characteristic frequency of the oscillator, a condition that requires a small frequency separation, so will the cubic difference tones. Because they enter the active bandwidth of the oscillator, these distortion products are amplified and in turn contribute significantly to the hair-bundle motion. Moreover, the amplified response to a test tone by the active oscillator is readily extinguished by adding a masker tone at a nearby frequency, because the masker tone increases the impedance to the test tone by effectively detuning the oscillator away from the bifurcation point (44).

Some features of the experimental recordings, however, are not reproduced by the simulations of a critical oscillator. These include the notch that was observed in the level function of distortion products at 2f₁ - f₂ and 2f₂ - f₁ for stimulation off-resonance (Fig. 6C), as well as the saturation that was measured in response to intense stimuli both for the suppression of the response to a test tone by a masker tone (Fig. 1A) and in the level functions of distortion products (Fig. 4). These two properties can be interpreted as consequences of negative hair-bundle stiffness and of the saturation of mechano-electrical transduction, respectively (Figs. S1 and S2). Off-resonance or intense stimuli thus provide specific information about passive hair-bundle mechanics. In addition, active oscillations by a single hair bundle are noisy. By limiting the phase coherence of active force production, intrinsic fluctuations conceal the bifurcation at which a deterministic dynamical system might operate and restore a linear regime of responsiveness to weak stimuli (45, 46). In contrast to a truly critical oscillator, which can distort arbitrarily small inputs for stimulation at resonance, a noisy system thus evinces nonlinearities only for stimuli with magnitudes beyond some threshold under the control of the noise strength (Fig. 7 C and D). If noise is weak enough, however, the signatures of critical oscillation remain (46). Notably, when the noise strength matches that expected for a hair bundle (see Methods), cubic difference products by a critical oscillator can arise at stimulus magnitudes that accord with those observed experimentally (Fig. 7 C and D, open disks).

Active and Passive Distortions in Vivo.

The unusual properties of the phantom tones that are heard in the human percept in response to two-tone stimulation had early been recognized as indirect evidence for the existence of an essential nonlinearity in hearing (3, 8). Yet, the physical origin of this nonlinearity remained elusive. The compressive and frequency-specific nonlinearity evinced by an oscillatory hair bundle (Fig. 1 A and B, black disks), or more generally by any self-sustained oscillator operating near a Hopf bifurcation (47), is ideally suited to account for the auditory nonlinearity. In response to two-tone stimuli of increasing magnitudes, this dynamic nonlinearity produces distorted vibrations at 2f₁ - f₂ that appear at low levels and grow nearly in parallel with vibrations at the primary frequencies f₁ and f₂ (Figs. 4 and 7). In agreement with psychoacoustical studies (3), the subjective intensity of the corresponding phantom tone would thus be expected to remain practically proportional to that of the stimulus over the extended range of stimulation for which the oscillator’s response remains compressive. In addition, because this compressive nonlinearity holds only near the condition of resonance (f₁ and f₂ near f_C), two-tone interferences by the active oscillator are inherently dependent on the frequency separation between the primary frequencies.

Signatures of critical oscillators can also be found in vivo on the basilar membrane of the mammalian cochlea. First, for two-tone stimuli at nearby frequencies, the cubic difference product 2f₁ - f₂ appears at its characteristic place for stimulation levels as low as 30 dB and displays a compressive growth that parallels that observed in response to a pure tone at the same frequency over a 50-dB variation of sound-pressure levels (10). Assuming that the pure tone response provides a fair estimate for the level function of the primaries, this behavior conforms to that shown in Figs. 4 and 7. Second, the cubic-difference product displays a power-law relation to the stimulus level that is similar to that anticipated for an active oscillator near a Hopf bifurcation (Fig. 7). Third, moderate to intense sound stimuli produce an exponential hierarchy of distortion products, as measured with a single hair bundle (Fig. 3) and expected for a critical oscillator (44). Finally, these properties strongly depend on the frequency separation between the primary frequencies.

Distortion-product oto-acoustic emissions afford another noninvasive means to assay the properties of the mechanical nonlinearity that underlies two-tone distortions in vivo. The spectrum of DPOAEs in the bobtail lizard shows prominent cubic difference tones in live animals, whereas passive mechanics instead favors quadratic products postmortem (16). This change in spectral content agrees with that reported here for a single oscillatory hair bundle for stimulation at and off resonance, respectively (Fig. 3), and in response to an increase in Ca²⁺ concentration that stops spontaneous oscillations (Fig. 6). In mammals, furosemide or anoxia, which both depress cochlear amplification, evoke a progressive loss of the cubic difference tones at low levels of stimulation and a transition from a compressive to a superlinear level function for these distortion products (48). Similarly, prestin knockout mice lacking electromotility still display DPOAEs, but the cubic difference tone at 2f₁ - f₂ appears at higher sound levels than in wild-type animals and displays a superlinear level function (49) that is characteristic of passive nonlinear mechanics. The qualitative resemblance between the two-tone distortions that are measured in vivo as oto-acoustic emissions in the ear canal and those evoked in vitro by a single oscillatory hair bundle is remarkable considering that the former are not evaluated at the site of production but after propagation through the hearing organ.

Integration of the Hair-Bundle Oscillator in Hearing Organs.

We have demonstrated here that a single oscillatory hair bundle qualitatively recapitulates the most salient features of phantom tones and suppressive masking in the field of psychoacoustics as well as of two-tone distortions and suppression that characterize active inner-ear mechanics. Being observed over a relatively narrow range of stimulus amplitudes, two-tone interferences from active oscillations of a single hair bundle are significantly weaker than those observed in intact organs. Understandably, intrinsic noise limits the nonlinear amplification that a single hair bundle can achieve for weak stimuli (45, 46). Mechanical coupling of noisy hair-bundle oscillators by overlying membranous structures, however, has been shown to enlarge the compressive nonlinearity produced by the hair-bundle amplifier (50, 51). An oscillatory module comprising a few tens of hair cells is predicted to produce similar amplificatory gains as those measured in vivo in the mammalian cochlea and in turn to elicit two-tone suppression and distortions over a much wider range of stimulus amplitudes than that reported here with a single hair bundle.

Our results do not pinpoint active hair-bundle motility as the only player in the active process that both boosts the ear’s technical specifications as a sound detector and fosters nonlinear interference in hearing. In the mammalian cochlea, a complex interplay between active hair-bundle and somatic motility of outer hair cells with the micromechanical environment may bring the cochlear partition on the brink of a Hopf bifurcation (32, 47). Any critical oscillator must show the same generic behavior as that observed here experimentally with a single oscillatory hair bundle. In return, we argue that the properties of two-tone interferences in hearing betray the workings of active mechanical oscillators that provide nonlinear amplification of sound-evoked vibrations in the inner ear.

Methods

Experimental Preparation.

Details of the experimental procedure have been published elsewhere (35). An excised preparation of the bullfrog’s (Rana catesbeiana) saccule was mounted on a two-compartment chamber. The basal bodies of hair cells were bathed in standard saline containing (in mM): 110 NaCl, 2 KCl, 4 CaCl₂, 3 D-glucose, 2 Na₂-creatine phosphate, 2 Na-pyruvate and 5 Na-HEPES. Hair bundles instead projected into an artificial endolymph of composition (in mM): 2 NaCl, 118 KCl, 0.25 CaCl₂, 3 D-glucose and 5 Na-HEPES. To disconnect the hair bundles from the overlying otolithic membrane, the apical surface of the preparation was exposed for 20 min to endolymph supplemented with 67 mg·mL^-1 of the protease subtilisin (type XXIV, Sigma). The otolithic membrane was then peeled off to obtain access to individual hair bundles.

Microscopic Apparatus and Mechanical Stimulation.

The preparation was viewed through a × 60 water-immersion objective of an upright microscope (BX51WI, Olympus). The tip of a stimulus fiber attached to the hair bundle was imaged at a magnification of × 1,000 onto a displacement monitor that included a dual photodiode. For movements that did not exceed ± 150 nm, this photometric system reported the fiber motion with no detectable distortion and was thus linear. Calibration was performed by measuring the output voltages of the photometric system in response to a series of offset displacements.

Flexible glass fibers were fabricated from borosilicate capillaries and coated with a thin layer of gold-palladium to enhance contrast. The stiffness K_F and drag coefficient λ_F of the fibers were, respectively, 0.1–0.15 pN·nm^-1 and 40–200 nN·s·m^-1, as determined by power spectral analysis of Brownian motion of the fiber’s tip in water. The fiber was secured by its base to a stack type piezoelectric actuator (PA-4/12, Piezosystem Jena) driven by a custom-made power supply (Elbatech). The fiber’s tip was affixed to the kinociliary bulb of an individual hair bundle. Neglecting viscous components, the force F_HB = K_F·(Δ - X) exerted by the stimulus fiber at the bundle’s top was proportional to the deflection of the fiber, in which X and Δ are the positions of the hair bundle and of the fiber’s base, respectively.

We define here the stimulus as F = K_F·Δ = F_HB + K_F·X, which corresponds to the force effectively applied to the top of the hair bundle when this organelle is loaded by a fiber. The mechanical system under study is therefore composed of the parallel arrangement of the hair bundle with the elastic fiber; this system is slightly stiffer than the hair bundle alone. Using flexible fibers ensured that spontaneous hair-bundle oscillations were only weakly disturbed by the elastic load (33).

To study two-tone interferences, the hair bundle was subjected to the time-dependent sum F(t) = F₁ sin(2πf₁t) + F₂ sin(2πf₂t) of two sinusoidal forces at frequencies f₁ and f₂, with a ratio f₂/f₁ = 1.08–1.15, unless explicitly stated (Figs. 2 and 5). Here, F₁ and F₂ are the amplitudes of the two tones. To make sure that the frequency components of the stimulus, as well as their linear combinations, were precisely represented by a single data point in the Fourier domain, we used only stimulus frequencies and recording durations that were integer numbers of hertz and seconds, respectively. A typical recording lasted 10–30 s.

Signal Generation, Acquisition.

All signals were generated and acquired under the control of a computer running a user interface programmed with LabVIEW software (version 8.6; National Instruments). The command signal controlling the external force F applied to the hair bundle was produced by a 16-bit interface card at a sampling rate of 2.5 kHz (PCI-6733, National Instruments). A second interface card (PCI-6250, National Instruments) conducted signal acquisition with a precision of 16 bits and a sampling rate of 2.5 kHz. Signals coming from the displacement monitor or going to the stimulation apparatus were conditioned with an eight-pole Bessel antialiasing filter adjusted to a low-pass half-power frequency of 1 kHz.

Data Analysis.

We defined the characteristic frequency f_C of spontaneous oscillations as the peak frequency of the bundle’s power spectrum of spontaneous motion or of the bundle’s frequency-dependent linear response function to small (1–2 pN) sinusoidal forces (34).

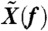In response to two-tone stimulation, the hair bundle elicited distortion products at linear combinations nf₁ + mf₂ of the stimulus frequencies f₁ and f₂, where n and m are integers. The amplitude X_nf1+mf2 of the bundle’s motion Fourier component at frequency nf₁ + mf₂ was calculated as , where is the Fourier component at frequency f of the time-varying hair-bundle motion X(t) and T_exp is the duration of the recording. The minimal distortion amplitude that could be measured was limited by the noise-floor level at the frequency of the distortion product. This noise level was estimated by computing the average power of bundle motion in a frequency window of 2·(f₂ - f₁) centered at the frequency of the distortion product, with a stimulus magnitude just below the threshold value for which a clear peak of distortion emerged in the power spectrum. Because the cubic difference products 2f₁ - f₂ and 2f₂ - f₁ were not significantly different, we considered only their arithmetic-mean level (X_2f1-f2 + X_2f2-f1)/2. The amplitude X_nf1+mf2 of each product was averaged over 4–6 realizations of the stimulation procedure. Error bars in Figs. 2 and 4–6 represent standard errors to the mean value.

At intermediate-to-large stimulus intensities, a hierarchy of odd distortion products was observed on either side of the primaries at frequencies f₁ - kΔf and f₂ + kΔf, respectively, where k is a positive integer. For each side, the decrease in distortion amplitude with increasing order k was described by an exponential decay X_k = X₀· exp(-λ·k), where X₀ and λ are fit parameters. In the main text, we consider the arithmetic mean of the two decay coefficients λ that resulted from this fitting procedure.

Simulations of Two-Tone Interferences by a Critical Oscillator.

An active dynamical system undergoes a Hopf bifurcation when its behavior exhibits an abrupt change from quiescence to spontaneous oscillations upon continuous variation of a parameter μ describing some component of the system (42). When this control parameter is poised near the critical value μ = μ_C where spontaneous oscillations just emerge, the system is called a critical oscillator. The generic behavior of a critical oscillator is described by a dynamic equation of a complex variable Z:

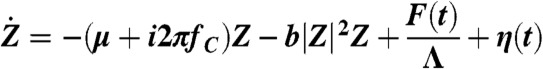[1]

where 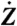is the time derivative of Z, f_C is the characteristic frequency of the oscillator, b is the magnitude of the cubic nonlinear term that stabilizes the amplitude of spontaneous oscillations when μ < 0, and i² = -1. In simulations, we took μ_C = 0 and b was a real number of positive sign. The real part of Z represents the hair-bundle displacement X(t), F(t) = F₁ sin(2πf₁t) + F₂ sin(2πf₂t) describes the two-tone stimulus applied to the system, and Λ is a friction coefficient. In some cases, a complex noise term η(t) = η₁(t) + iη₂(t) was added to account for fluctuations. We considered Gaussian white noise with zero mean 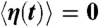and with a strength characterized by correlations 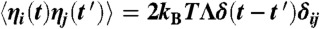, where δ(t) is the Dirac distribution and δ_ij denotes the Kronecker delta (i = 1, 2). We chose Λ = 1·10^-7 N·s·m^-1 to accord with measured values of a hair bundle’s friction coefficient (52). Note that by imposing the value of the parameter Λ, we also set the magnitude of the noise terms η_i(t). The value b = 10¹⁷ m^-2·s^-1 ensured that the oscillator entered the nonlinear regime of responsiveness to sinusoidal stimuli at a vibration magnitude that agreed with those measured experimentally with oscillatory hair bundles, typically 10 nm (20). The two coupled first-order differential equations describing the time evolution of the real and imaginary part of Z were integrated by the Euler method.