Longitudinal Penalized Functional Regression for Cognitive Outcomes on Neuronal Tract Measurements

Abstract

We describe and analyze a longitudinal diffusion tensor imaging (DTI) study relating changes in the microstructure of intracranial white matter tracts to cognitive disability in multiple sclerosis patients. In this application the scalar outcome and the functional exposure are measured longitudinally. This data structure is new and raises challenges that cannot be addressed with current methods and software. To analyze the data, we introduce a penalized functional regression model and inferential tools designed specifically for these emerging types of data. Our proposed model extends the Generalized Linear Mixed Model by adding functional predictors; this method is computationally feasible and is applicable when the functional predictors are measured densely, sparsely or with error. An online appendix compares two implementations, one likelihood-based and the other Bayesian, and provides the software used in simulations; the likelihood-based implementation is included as the lpfr() function in the R package refund available on CRAN.

1 Introduction

Traditionally, longitudinal studies have collected scalar measurement on subjects over time. As technologies for the collection and storage of larger measurements have become widely available, longitudinal studies have begun to collect functional or imaging observations on subjects over several visits. One example is our current dataset, in which diffusion tensor imaging (DTI) brain scans are recorded for many multiple sclerosis patients over several visits with the goal of assessing the impact of neurodegeneration on disability. Adequately relating functional predictors to accompanying scalar outcomes requires longitudinal functional regression models, which are not currently available. We address this problem by introducing a generally applicable regression model that adds subject-specific random effects to the well-studied cross-sectional functional regression model. We also develop inferential techniques for all parameters in this new model, and implement these methods in computationally efficient and publicly available software available in the refund R package.

1.1 Data Description

Our application explores the relationship between cerebral white matter tracts in multiple sclerosis (MS) patients and cognitive impairment over time. White matter tracts are made up of myelinated axons: axons are the long projections of a neuron that transmit electrical signals and myelin is a fatty substance that surrounds the axons in white matter, enabling the electrical signals to be carried very quickly. Multiple sclerosis, an autoimmune disease which results in axon demyelination and lesions in white matter tracts, leads to significant disability in patients.

DTI is a magnetic resonance imaging (MRI) based modality that traces the diffusion of water in the brain. Because water diffuses anisotropically in the white matter and isotropically elsewhere, DTI is used to generate images of the white matter specifically (Basser et al., 1994, 2000; LeBihan et al., 2001; Mori and Barker, 1999). Several measurements of water diffusion are provided by DTI, including fractional anisotropy and mean diffusivity. Continuous summaries of white matter tracts, parameterized by distance along the tract and called tract profiles, can be derived from diffusion tensor images.

By collecting longitudinal information about patient cognitive function and about disease progression via DTI, researchers hope to better understand the relationship between MS and disability. From this study, we have densely sampled mean and parallel diffusivity measurements from several white matter tracts. Our dataset consists of 100 subjects, 66 women and 34 men, aged between 21 and 70 years at first visit. The number of visits per subject ranged from 2 to 8, with a median of 3, and were approximately annual; a total of 340 visits were recorded. At each visit full DTI scans were obtained and used to create tract profiles, accompanied by several tests of cognitive and motor function with scalar outcomes.

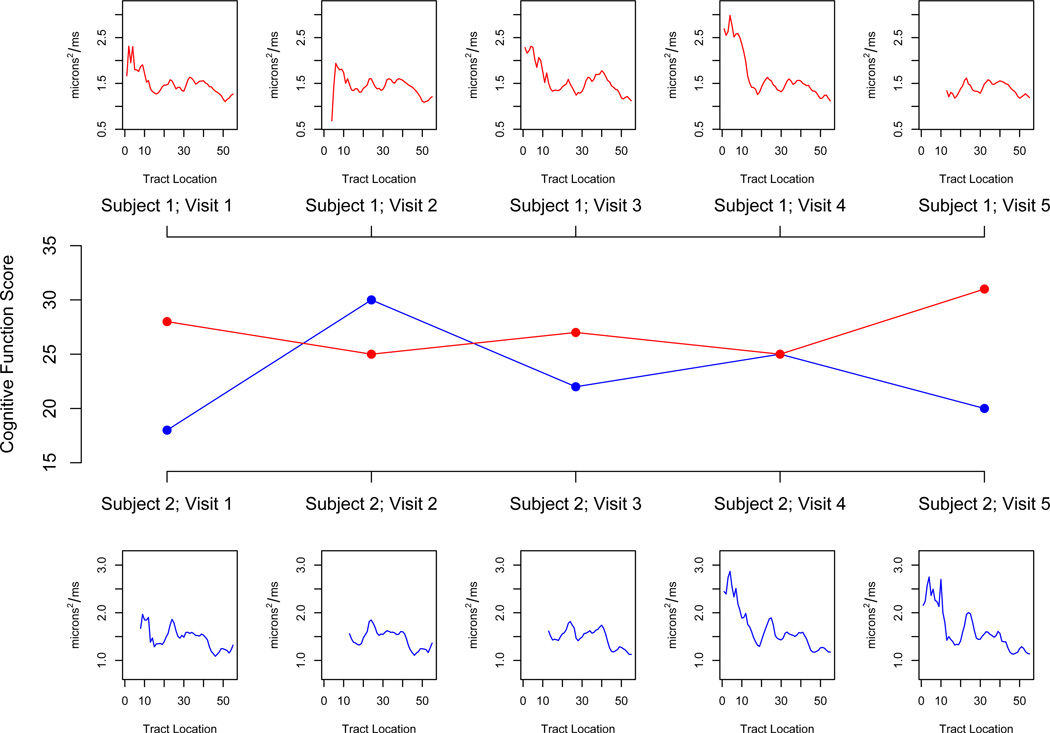
In Figure 1 we display a functional predictor and cognitive disability outcome for two subjects over time. We stress that this data structure, with high-dimensional predictors and scalar outcomes observed longitudinally, is increasingly common. Moreover, we emphasize that our methods are motivated by this study, but are generally applicable. A single-level analysis of these data was presented in Goldsmith et al. (2011).

Figure 1.

Structure of the data. The center panel displays the scalar PASAT-3 cognitive disability measure for two subjects over five visits (measured as the number of questions answered correctly out of sixty); above and below are the parallel diffusivity tract profiles of the right corticospinal tract corresponding to each subject-visit outcome, which we use as a functional regressor.

1.2 Proposed Model

More formally, we consider the setting in which we observe for each subject 1 ≤ i ≤ I at each visit 1 ≤ j ≤ J_i data of the form [Y_ij, W_ij1(s), …, W_ijK(s), X_ij], where Y_ij is a scalar outcome, W_ijk(s) ∈ ℒ²[0, 1], 1 ≤ k ≤ K, are functional covariates, and X_ij is a row vector of scalar covariates. We propose the longitudinal functional regression outcome model

$$\begin{array}{cc}\hfill Y_{\mathit{\text{ij}}}& ~\text{EF}({\mu }_{\mathit{\text{ij}}},\eta )\hfill \\ \hfill g({\mu }_{\mathit{\text{ij}}})& =X_{\mathit{\text{ij}}}\beta +Z_{\mathit{\text{ij}}}{b}_i+{\displaystyle \sum _{k=1}^K}{\displaystyle {\int }_0^1}{W}_{\mathit{\text{ijk}}}(s)\gamma k(s)\mathit{\text{ds}}\hfill \end{array}$$ (1)

where “EF(μ_ij, η)” denotes an exponential family distribution with mean μ_ij and dispersion parameter η. Here X_ijβ is the standard fixed effects component, Z_ijb_i is the standard random effects component, $b_i~\text{Normal}(0,{\sigma }_{\mathit{b}}^2{\mathit{I}}_I)$ are subject-specific random effects, and the ${\displaystyle {\int }_0^1}{W}_{\mathit{\text{ijk}}}(s){\gamma }_k(s)\mathit{\text{ds}}$ are the functional effects. Both the functional coefficients γ_k(s) and the scalar coefficients β are population-level parameters, rather than subject-specific effects, and do not vary across visits.

Model (1) is novel in that it adds subject-specific random effects to the standard cross-sectional functional regression model; from another point of view, this model adds functional predictors to generalized linear mixed models. The latter viewpoint is particularly instructive in that ideas familiar from traditional longitudinal data analysis can be transferred seamlessly to longitudinal functional data analysis. As an example, many different structures of random effects b_i, including random intercepts and slopes, will be needed in practice and can be implemented by appropriately specifying the random effect design matrices and covariance structures. For expositional clarity we use a single vector of subject-specific random effects and assume that these random effects are independent, but more complex structures can be included. In practice the W_ijk(s) are not truly functional but are observed on a dense (or sparse) grid and often with error; moreover, the predictors are not necessarily observed over the same domain. In fact, while the measurement error is negligible in our application, there are some missing values in the functional predictor in Figure 1, and the mean and parallel diffusivity functional predictors have different domains. We point out that solutions to these problems are well known (Di et al., 2009; Ramsay and Silverman, 2005; Staniswalis and Lee, 1998; Yao et al., 2003), and do not discuss them here.

Our proposed approach is based on the single-level functional regression model developed in Goldsmith et al. (To Appear) but is extended to the scientifically important longitudinal setting. Strengths of this approach are that: 1) it extends functional regression to model the association between outcomes and functional predictors when observations are clusted into groups or subjects; 2) it casts a novel functional model in terms of well-understood mixed models; 3) it is applicable in any situation in which the W_ijk(s) are observed or can be estimated, including when they are observed sparsely or with error; 4) it can be fit using standard, well-developed statistical software available as the lpfr() function in the refund R package; 5) from a Bayesian perspective, it allows the joint modeling of longitudinal outcomes and predictors; and 6) it provides confidence or credible intervals for all the parameters of the model, including the functional ones. We emphasize this final point, as confidence intervals are rarely discussed in the functional regression literature, and in penalized approaches to functional regression they are typically bootstrap or empirical intervals. The connection to mixed models provides a simple, statistically principled approach for constructing confidence or credible intervals.

1.3 Existing Methods for Functional Regression

We contrast the setting of this paper with the large body of existing functional regression work. Foremost, existing functional regression work (Cardot et al., 1999, 2003; Cardot and Sarda, 2005; Cardot et al., 2007; C et al., 2009; Ferraty and Vieu, 2006; James, 2002; James et al., 2009; Marx and Eilers, 1999; Müller and Stadtmüller, 2005; Ramsay and Silverman, 2005; Reiss and Ogden, 2007) deals only with cross sectional regression. Here, we are focused on longitudinally observed functional predictors and outcomes, which necessitates the addition of random effects to the standard functional regression model. To the best of our knowledge, this setting has not been considered previously. Moreover, the addition of random effects increases the complexity of the functional regression model, requiring new methodology implemented in efficient software.

Additionally, we point out that several alternative penalized approaches to single-level functional regression exist (Cardot et al., 2003; Cardot and Sarda, 2005; Reiss and Ogden, 2007), but that each of these incorporates a computationally expensive cross-validation procedure. How and whether such methods would extend to fitting longitudinal models of type (1) remains to be elucidated. The additional complexity of a longitudinal model may increase the computational burden, perhaps prohibitively. Low-dimension approaches to single-level functional regression (Müller and Stadtmüller, 2005), in which the smoothness of γ_k(s) depends on the dimension of its basis, are less automated than penalized approaches but are, notably, generalizable to the longitudinal setting. In fact, such models are a special case of the method we propose in Section 2.

It is also important to distinguish the proposed longitudinal functional regression model from the well developed Functional ANOVA models (Brumback and Rice, 1998; Guo, 2002). Here, one observes functions organized into groups; the goal is to express the functions as a combination of a group mean, a subject-specific deviation from the group mean, and possibly a subject-visit-specific deviation. Much of this work has focused on the estimation of and inference for the group means, and has employed penalized splines in expressing these functions. A scalar-on-function regression that incorporates random effects to account for group effects, as proposed in this paper, is not considered; we however point out that the work in FANOVA suggests that numerous datasets necessitating such a model exist and are under investigation. Others (Di et al., 2009; Greven et al., 2010) have extended functional principal components analysis to the multilevel and longitudinal settings, emphasizing parsimonious and computationally efficient methods for the expression of subject-visit specific curves. While these methods are the state of the art in describing the variability in observed multilevel and longitudinal functions, they do not consider accompanying longitudinal outcomes.

Finally, we highlight the distinction between the treatment of scalars observed longitudinally as sparse functional covariates (Hall et al., 2006; Müller, 2005; Yao et al., 2005) and the current setting, in which functions are observed longitudinally.

The introduction of a longitudinal functional regression model, therefore, fills a gap in the functional data analysis literature. While the proposed approach is based on the framework described in Goldsmith et al. (To Appear) and arises naturally therein, the longitudinal extension developed here defines a broadly useful class of functional regression models. Moreover, computationally feasible software for the estimation and inference related to longitudinal functional regression models is freely available online.

The remainder of this manuscript is organized in the following way. Section 2 describes the proposed general method for longitudinal functional regression. In Section 3 we pursue a simulation study to examine the viability of the proposed method and in Section 4 we apply our method to the DTI data. We end with a discussion in Section 5. Implementations of the method proposed in Section 2, provided in both likelihood-based and Bayesian frameworks and accompanied by a discussion of the the advantages and disadvantages of each, are available in an online appendix which also contains all software used in the simulation exercise.

2 Longitudinal Penalized Functional Regression

The longitudinal penalized functional regression (LPFR) method builds on an approach to single-level functional regression in which the penalization is achieved via a mixed model (Goldsmith et al., To Appear). Briefly, the two steps in this method are: 1) to express the predictors using a large number of functional principal components obtained from a smooth estimator of the covariance matrix estimator; and 2) to express the function coefficient using a penalized spline basis. The addition of random effects to this model arises naturally and with a minimal increase in complexity. In the following, we will use i to index subject, j to index visit, k to index functional predictor, l to index objects associated with PC bases, and m to index objects associated with spline bases.

Specifically, given data of the form [Y_ij, W_ij1(s), …, W_ijK(s), X_ij] for subjects 1 ≤ i ≤ I over visits 1 ≤ j ≤ J_i, we model the functional effect in the following way. First, express the W_ijk(s) in terms of a truncated Karhunen-Loève decomposition. That is, let Σ^W_k (s, t) = Cov[W_ijk(s), W_ijk(t)] be the covariance operator on the kth observed functional predictor; thus Σ^W_k (s, t) is a bivariate function providing the covariance between two locations of the functional predictor. Further, let ${\displaystyle {\sum }_{l=1}^{\mathrm{\infty }}}{\lambda }_{\mathit{\text{kl}}}{\psi }_{\mathit{\text{kl}}}(s){\psi }_{\mathit{\text{kl}}}(t)$ be the spectral decomposition of Σ^W_k (s, t), where λ_k1 ≥ λ_k2 ≥ … are the non-increasing eigenvalues and ψ_k(·) = {ψ_kl(·) : l ∈ ℤ⁺} are the corresponding orthonormal eigenfunctions. In practice, functional predictors are observed over finite grids, and often with error. Thus we estimate Σ^W_k (s, t) using a method-of-moments approach, and then smooth the off-diagonal elements of this observed covariance matrix to remove the “nugget effect” caused by measurement error (Staniswalis and Lee, 1998; Yao et al., 2003). Moreover, in the case that the W_ijk(s) are sampled sparsely or over different grids, one can construct an estimate of the covariance matrix using the following two-stage procedure (Di et al., 2009). First, use a fine grid to bin each subject’s observations to construct a rough estimate of the covariance matrix based on these under-smoothed functions; second, smooth the rough covariance matrix estimated in the previous step.

A truncated Karhunen-Loève approximation for W_ijk(s) is given by $W_{\mathit{\text{ijk}}}(s)={\mu }_k(s)+{\displaystyle {\sum }_{l=1}^{K_w}}{c}_{\mathit{\text{ijkl}}}{\psi }_{\mathit{\text{kl}}}(s)$, where K_w is the truncation lag, the $c_{\mathit{\text{ijkl}}}={\displaystyle {\int }_0^1}\{W_{\mathit{\text{ijk}}}(s)-{\mu }_k(s)\}{\psi }_{\mathit{\text{kl}}}(s)\mathit{\text{ds}}$ are uncorrelated random variables with variance λ_kl, and μ_k(s) is the mean of the kth functional predictor, taken over all subjects and visits. Unbiased estimators of c_ijkl can be obtained either as the Riemann sum approximation to the integral ${\displaystyle {\int }_0^1}\{W_{\mathit{\text{ijk}}}(s)-{\mu }_k(s)\}{\psi }_{\mathit{\text{kl}}}(s)\mathit{\text{ds}}$ or via the mixed effects model (Crainiceanu et al., 2009; Di et al., 2009)

$$\begin{array}{cc}{W}_{\mathit{\text{ijk}}}(s)\hfill & ={\mathit{\mu }}_k(s)+{\displaystyle {\sum }_{k=1}^{K_w}}{c}_{\mathit{\text{ijkl}}}{\psi }_{\mathit{\text{kl}}}(s)+{\epsilon }_{\mathit{\text{ijk}}}(s)\hfill \\ {\mathit{c}}_{\mathit{\text{ijk}}}\hfill & ~\mathrm{N}(0,{\mathrm{\Lambda }}_k),{\epsilon }_{\mathit{\text{ijk}}}(s)~\mathrm{N}(0,{\sigma }_{{\mathit{W}}_k}^2),\hfill \end{array}$$ (2)

where ${\mathit{c}}_{\mathit{\text{ijk}}}^{\prime }=(c_{\mathit{\text{ijk}}1},\dots ,c_{{\mathit{\text{ijkK}}}_w})$ is the vector of subject-visit specific loadings for the kth functional predictor, Λ_k is a K_w × K_w matrix with (l, l)^th entry λ_kl and 0 elsewhere, and the c_ijk, ε_ijk(s) are mutually independent for every i, j, k. Note we have expressed the W_ijk(s) without taking the repeated subject-level observations into account; alternatively, one could use longitudinal functional principal components analysis for a decomposition that borrows strength across visits (Greven et al., 2010).

The second step in LPFR is to model the coefficient functions γ_k(s) using a large spline basis with smoothness induced explicitly via a mixed effects model. For example, let ϕ_k(s) = {ϕ_k1(s), ϕ_k2(s), …, ϕ_kKg (s)} be a truncated power series spline basis, so that ${\gamma }_k(s)={\mathit{\varphi }}_k(s){\mathit{g}}_k=g_{k1}+g_{k2}t+{\displaystyle {\sum }_{m=3}^{K_g}}{g}_{\mathit{\text{km}}}{(t-{\kappa }_{\mathit{\text{km}}})}_{+}\text{ where }{\mathit{g}}_k={\{g_{k1},\dots ,g_{{\mathit{\text{kK}}}_g}\}}^T\text{ and }{\{{\kappa }_{\mathit{\text{km}}}\}}_{m=3}^{K_g}$ are knots (note that the index on the knots begins at 3 to match the index of the spline terms in g_k). Thus,

$${\displaystyle {\int }_0^1}{W}_{\mathit{\text{ijk}}}(s){\gamma }_k(s)\mathit{\text{ds}}=a_k+{\displaystyle {\int }_0^1}{\mathit{c}}_{\mathit{\text{ijk}}}^{\prime }{\mathit{\psi }}_k^T(s){\mathit{\varphi }}_k(s){\mathit{g}}_k\mathit{\text{ds}}=a_k+{\mathit{c}}_{\mathit{\text{ijk}}}^{\prime }{\mathit{M}}_k{\mathit{g}}_k,$$

where M_k is a K_w × K_g dimensional matrix with the (l, m)^th entry equal to ${\displaystyle {\int }_0^1}{\psi }_{\mathit{\text{kl}}}(s){\varphi }_{\mathit{\text{km}}}(s)\mathit{\text{ds}}\text{and }{a}_k={\displaystyle {\int }_0^1}{\mu }_k(s){\gamma }_k(s)\mathit{\text{ds}}$. Then, letting C_k be the $\left({\displaystyle {\sum }_{i=1}^I}{J}_i\right)\times K_w$ matrix of PC loadings with rows ${\mathit{c}}_{\mathit{\text{ijk}}}^{\prime }$, X be the design matrix of fixed effects, and Z₁ be the random effect design matrix used to account for repeated observations, the outcome model (1) is posed as

$$\begin{array}{cc}\hfill \mathit{Y}|\mathit{W}(s)& ~\mathit{\text{EF}}(\mathit{\mu },\eta )\hfill \\ \hfill g(\mathit{\mu })& =\mathit{X}\mathit{\beta }+\mathit{\text{Zu}}\hfill \\ \hfill \mathit{u}& ~\mathrm{N}\left[\right[\begin{array}{c}\hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill \\ \hfill ⋮\hfill \\ \hfill \mathbf{0}\hfill \end{array}],[\begin{array}{cccc}\hfill {\sigma }_{\mathit{b}}^2{\mathit{I}}_I\hfill & \hfill \mathbf{0}\hfill & \hfill \dots \hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\sigma }_{{\mathit{g}}_1}^2{\mathit{I}}_{K_g-2}\hfill & \hfill \hfill & \hfill \mathbf{0}\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill {\sigma }_{{\mathit{g}}_L}^2{\mathit{I}}_{K_g-2}\hfill \end{array}\left]\right].\hfill \end{array}$$ (3)

where X = [1 X (C₁M₁)^[,1:2] … (C_KM_K)^[,1:2]] is the design matrix consisting of scalar covariates and fixed effects used to model the γ_k(s), Z = [Z₁ (C₁M₁)^[,3:K_g] … (C_KM_K)^[,3:K_g]] is the design matrix consisting of subject-specific random effects and random effects used to model the coefficient functions; β = [α, β, g₁₀, g₁₁, …, g_K0, g_K1] is the vector of fixed effect parameters; and $\mathit{u}=[{\{b_i\}}_{i=1}^I,{\{g_{1m}\}}_{m=3}^{K_g},\dots ,{\{g_{\mathit{\text{Km}}}\}}_{m=3}^{K_g}]$ is the vector of subject-specific random effects and the random effects used to model the γ_k(s). The terms $a_k={\displaystyle {\int }_0^1}{\mu }_k(s){\gamma }_k(s)\mathit{\text{ds}}$ are incorporated into the overall model intercept α.

In this way longitudinal functional regression models can be flexibly estimated using standard, yet carefully constructed, mixed effects models. Once again, we note that the random effect structure is simple for expositional purposes only; complex combinations of random effects and covariance structures can be implemented just as in standard generalized mixed models. Similarly to Crainiceanu and Goldsmith (2010), it is possible to model jointly the principal component loadings c_ijk and the outcome. This is important if there is substantial variability in the estimates of the c_ijk, but may not be necessary if good estimates are available. We have assumed the same truncation lags K_w, K_g for each functional predictor and coefficient, but this assumption is easily relaxed. For the choice of truncation lags, we refer to Goldsmith et al. (To Appear) and Ruppert (2002) and choose them large, subject to the identifiability constraint K_w ≥ K_g; typically K_w = K_g = 30 will suffice. Spline bases other than the truncated power series basis can (and, in the Bayesian software implementation, will) be used with appropriate changes to the specification of the random effects u used to model the γ_k(s).

A related approach, which can be advantageous when the shape of γ_k(_s) is known, takes ϕ_k(·) as a collection of parametric functions, i.e. ϕ_k(s) = {1, t} if γ_k(s) is a linear function, and uses random effects to model the longitudinal structure of the data but not to induce smoothness on γ_k(s). However, absent setting-specific knowledge of the shape of γ_k(s) we typically advocate the more flexible penalized approach described above.

3 Simulations

We pursue a simulation study to test the effectiveness of our proposed method in estimating one or more functional coefficients in longitudinal regression models. We use two implementations, a likelihood-based approach and a Bayesian approach, and briefly note a few differences between the two. First, the likelihood based approach estimates the matrix of PC loadings C using a Riemann sum approximation and then treats this matrix as fixed, while the Bayesian approach estimates C as in equation (2). Second, the Bayesian implementation uses a b-spline basis for the γ_k(s) to improve mixing of the MCMC chains. A more detailed discussion of the two implementations is available in an online appendix. To ensure reproducibility, full code for the simulation exercise is also available online.

3.1 Single Functional Predictor

We first generate samples from the model

$$\begin{array}{cc}\hfill Y_{\mathit{\text{ij}}}& =b_i+{\displaystyle {\int }_0^{10}}{W}_{\mathit{\text{ij}}}(s)\gamma (s)\mathit{\text{ds}}+{\epsilon }_{\mathit{\text{ij}}},i=1,\dots ,100\hfill \\ \hfill W_{\mathit{\text{ij}}}^{\prime }(s)& =W_{\mathit{\text{ij}}}(s)+{\delta }_{\mathit{\text{ij}}}(s)\hfill \\ \hfill W_{\mathit{\text{ij}}}(s)& =u_{\mathit{\text{ij}}1}+u_{\mathit{\text{ij}}2}s+{\displaystyle \sum _{t=1}^{10}}\left\{{\upsilon }_{\mathit{\text{ijt}}1}\text{sin}\right(\frac{\pi t}{5}s)+{\upsilon }_{\mathit{\text{ijt}}2}\text{cos}(\frac{\pi t}{5}s)\}\hfill \end{array}$$

where ${\epsilon }_{\mathit{\text{ij}}}~\mathrm{N}[0,{\sigma }_{\mathit{Y}}^2],{\delta }_{\mathit{\text{ij}}}(s)~\mathrm{N}[0,{\sigma }_{\mathit{W}}^2],b_i~\mathrm{N}[0,{\sigma }_b^2]$, u_ij1 ~ Unif[0, 5], u_ij2 ~ N[1, 0.2], υ_ijt1, υ_ijt2 ~ N[0, 1/t²] and $W_{\mathit{\text{ij}}}^{\prime }(s)$ denotes the observed functional predictor for subject i at visit j. By construction the W_ij(s) are a combination of a vertical shift, a slope, and sine and cosine terms of various periods. The W_ij(s) are observed on the dense grid $[s_g=\frac{g}{10}:g=0,\dots ,100]$. We assume I = 100 subjects, and use two true coefficient functions in separate simulations: γ₁(s) = 2 sin(πs/5) and ${\gamma }_2(s)=\sqrt{s}$. Note that the first true coefficient function is selected to be an early principal component of the observed functions, and the second is an arbitrary smooth function. We take J ∈ {3, 10}, ${\sigma }_{\mathit{Y}}^2\in \{5,10\},{\sigma }_{\mathit{W}}^2\in \{0,.5\}\text{ and }{\sigma }_{\mathit{b}}^2\in \{5,50\}$, which gives a total of 16 possible parameter combinations and two coefficient functions. For each of these combinations, we generate 100 datasets and fit model 1 using both likelihood-based and Bayesian approaches. For the Bayesian implementation, we used chains of length 500 with the first 100 as burn-in; the estimated parameters are taken to be the posterior mean of the generated samples.

We calculate the mean squared error of the estimated coefficient function γ̂(s) as

$$\text{MSE}={\displaystyle \sum _{g=0}^{100}}{\{\hat{\gamma }(s_g)-\gamma (s_g)\}}^2.$$

Table 1 provides the average mean squared error (AMSE) using the both implementations taken over the 100 simulated datasets for ${\sigma }_{\mathit{W}}^2=0.5,{\sigma }_{\mathit{b}}^2=50$, and all possible combinations of J, ${\sigma }_{\mathit{Y}}^2$, and coefficient function; results for other values of ${\sigma }_{\mathit{W}}^2{\sigma }_{\mathit{b}}^2$ are quite similar to those presented and are omitted. Thus, we see that the estimation of γ(s) is very accurate regardless of the magnitude of the random effect variance or, notably, the presence or absence of measurement error. As expected, there is a substantial decrease in AMSE when one observes 10 visits per subject compared to 3 visits per subject. Doubling the error variance on the outcome has the largest impact on the AMSE, but in many situations this impact is small. To provide context for Table 1, in Figure 2, we show the estimates resulting in the median MSE for J = 3, ${\sigma }_{\mathit{W}}^2=0,{\sigma }_{\mathit{Y}}^2=5,{\sigma }_{\mathit{b}}^2=5$ under both coefficient functions.

Table 1.

Average MSE for the likelihood-based and Bayesian implementations in with single functional predictors over 100 repetitions for ${\sigma }_{\mathit{W}}^2=0.5,{\sigma }_{\mathit{b}}^2=50$, and all other possible parameter combinations and true coefficient functions. Results are similar for other levels of ${\sigma }_{\mathit{W}}^2,{\sigma }_{\mathit{b}}^2$.

		γ1(·)		γ2(·)
		${\sigma }_{\mathit{Y}}^2=5$	10	5	10
J=3	Likelihood	0.021	0.031	0.009	0.010
	Bayesian	0.017	0.036	0.014	0.019
J=10	Likelihood	0.009	0.013	0.006	0.007
	Bayesian	0.008	0.009	0.006	0.008

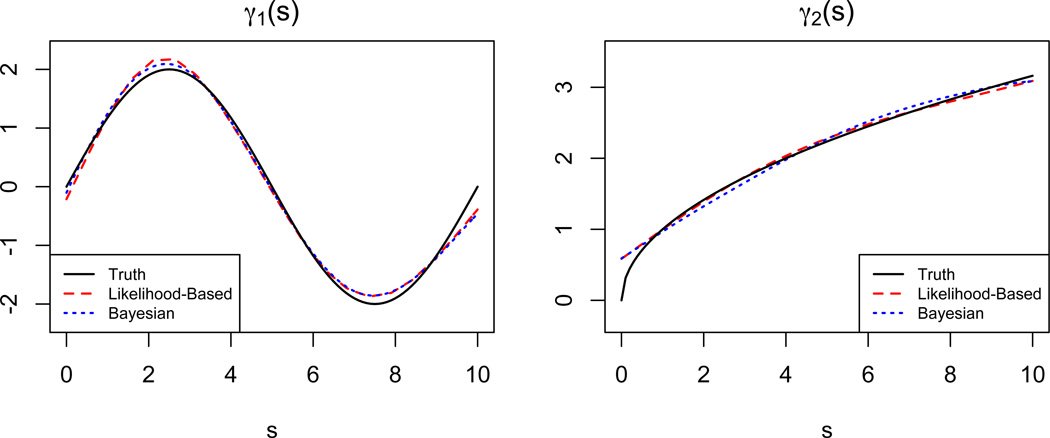
Figure 2.

For both true coefficient functions and both implementations, we show the estimate γ̂(s) with median MSE. Median MSEs for likelihood-based and Bayesian approaches are, respectively, 0.016 and 0.012 for γ₁(s) and 0.006 and 0.009 for γ₂(s).

We note that several differences between the results for the likelihood-based and Bayesian implementations are apparent for J = 3. Particularly, notice that the likelihood-based implementation generally has better performance for γ₂(s). A possible reason for this is that the Bayesian implementation uses a smaller basis for both the functional predictors and the coefficient function and uses a b-spline basis for γ(s), rather than a truncated power series. With fewer observations, the smaller b-spline basis may lack the flexibility to adequately represent γ₂(s). Though not shown, a second difference in the results for the different implementations is the slightly larger impact of measurement error on AMSE for the Bayesian implementation. Recall that this approach jointly estimates the model parameters and the matrix of PC loadings C. The added variability in estimating C in the presence of measurement error may lead to more variable estimation of the functional coefficient γ(s). However, for J = 10 these differences largely disappear.

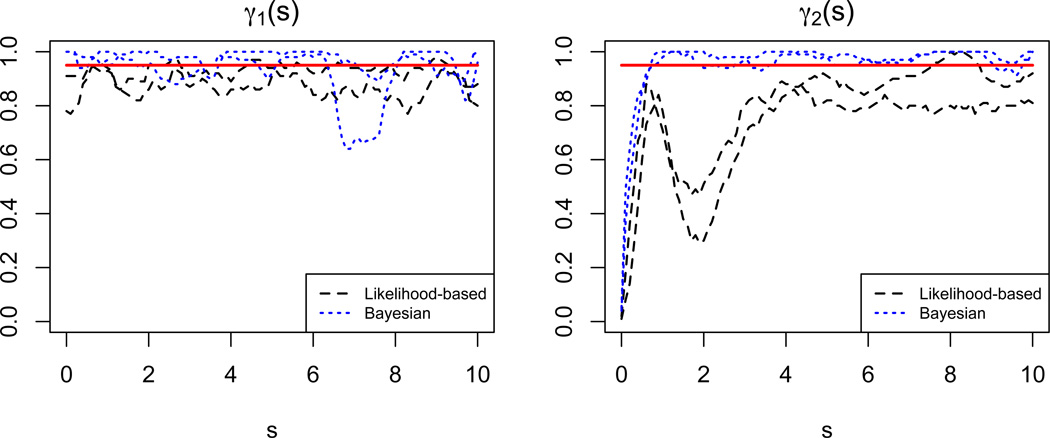
Finally, in Figure 3 we show the coverage probabilities for the 95% confidence and credible intervals produced by a subset of the simulations described above. We show the two extreme situations: first, we let J = 3, ${\sigma }_{\mathit{W}}^2=0,{\sigma }_{\mathit{Y}}^2=5,{\sigma }_{\mathit{b}}^2=5$; second, we let J = 10, ${\sigma }_{\mathit{W}}^2=.5,{\sigma }_{\mathit{Y}}^2=10,{\sigma }_{\mathit{b}}^2=50$. For γ₁(s), we generally see that the confidence intervals have coverage probabilities somewhat lower than the nominal level, while the credible intervals are slightly conservative with the exception of one region. A more interesting situation is apparent for γ₂(s). We note from Figure 2 that both implementations tend to oversmooth the leftmost tail of the coefficient function; this is reflected in the very low coverage probabilities there. The Bayesian implementation recovers from this initial oversmoothing and has conservative credible intervals over the remainder of the domain, but the likelihood-based implementation has a second dip corresponding to a second region of oversmoothing before achieving coverage probabilities more similar to those for γ₁(s). The oversmoothing of γ₂(s) is most likely related to the use of a single parameter ${\sigma }_{\mathit{g}}^2$ to control smoothness across the domain of the coefficient function. In the case of γ₂(s), the leftmost tail exhibits much more curvature than the remainder of the function, meaning that the single parameter may induce more smoothness than is accurate.

Figure 3.

Coverage probabilities for 95% confidence and credible intervals for both true coefficient functions in simulations with single functional predictors.

3.2 Multiple Functional Predictors

Next, we generate samples from the model

$$\begin{array}{cc}\hfill Y_{\mathit{\text{ij}}}& =b_i+{\displaystyle {\int }_0^{10}}{W}_{\mathit{\text{ij}}1}(s){\gamma }_1(s)\mathit{\text{ds}}+{\displaystyle {\int }_0^{10}}{W}_{\mathit{\text{ij}}2}(s){\gamma }_2(s)\mathit{\text{ds}}+{\epsilon }_{\mathit{\text{ij}}},i=1,\dots ,100\hfill \\ \hfill W_{\mathit{\text{ijk}}}^{\prime }(s)& =W_{\mathit{\text{ijk}}}(s)+{\delta }_{\mathit{\text{ijk}}}(s)\hfill \\ \hfill W_{\mathit{\text{ijk}}}(s)& =u_{\mathit{\text{ijk}}1}+u_{\mathit{\text{ijk}}2}s+{\displaystyle \sum _{t=1}^{10}}\left\{{\upsilon }_{\mathit{\text{ijtl}}1}\text{sin}\right(\frac{\pi t}{5}s)+{\upsilon }_{\mathit{\text{ijtl}}2}\text{cos}(\frac{\pi t}{5}s\left)\right\}\hfill \end{array}$$

where ${\epsilon }_{\mathit{\text{ijk}}}~\mathrm{N}[0,{\sigma }_{\mathit{Y}}^2],{\delta }_{\mathit{\text{ijk}}}(s)~\mathrm{N}[0,{\sigma }_{{\mathit{W}}_k}^2],b_i~\mathrm{N}[0,{\sigma }_b^2]$, u_ijl1 ~ Unif[0, 5], u_ijl2 ~ N[1, 0.2], υ_ijtl1, υ_ijtl2 ~ N[0, 1/t²] and $W_{\mathit{\text{ijk}}}^{\prime }(s)$ denotes the k^th observed functional predictor for subject i at visit j. Thus the W_ijk(s) are independent functions constructed in the same manner as in Section 3.1. The W_ijk(s) are observed on the dense grid $[s_g=\frac{g}{10}:g=0,\dots ,100]$ and we set I = 100. Again we choose γ₁(s) = 2 sin(πs/5) and ${\gamma }_2(s)=\sqrt{s}$ and we take J ∈ {3, 10}, ${\sigma }_{\mathit{Y}}^2\in \{5,10\},{\sigma }_{{\mathit{W}}_k}^2\in \{0,.5\}\text{ and }{\sigma }_{\mathit{b}}^2\in \{5,50\}$. For each of these combinations, we generate 100 datasets and fit model 1 using both of the implementations described in Section A. Due to the added complexity of the model, we used chains of length 1000 with the first 500 as burn-in.

Table 2 provides the AMSEs resulting from both likelihood-based and Bayesian implementations of the longitudinal functional regression model with multiple functional predictors taken over the 100 simulated data sets; again, results for various combinations of ${\sigma }_{{\mathit{W}}_k}^2,{\sigma }_{\mathit{b}}^2$ are similar and have been omitted. We see that the results in this setting are remarkably similar to those considered in Section 3.1, despite the additional complexity of the model. Specifically, the AMSEs are negligibly affected and the comparisons between the likelihood-based and Bayesian implementations remain valid. Though not presented, figures examining the coverage probabilities of confidence and credible intervals are also largely unchanged.

Table 2.

Average MSE for the likelihood-based and Bayesian implementations with multiple functional predictors over 100 repetitions for ${\sigma }_{{\mathit{W}}_k}^2=0.5,{\sigma }_{\mathit{b}}^2=50$, and all other possible parameter combinations and true coefficient functions. Results are similar for other levels of ${\sigma }_{{\mathit{W}}_k}^2,{\sigma }_{\mathit{b}}^2$.

		γ1(·)		γ2(·)
		${\sigma }_{\mathit{Y}}^2=5$	=10	=5	=10
J=3	Likelihood	0.019	0.028	0.008	0.011
	Bayesian	0.015	0.029	0.010	0.016
J=10	Likelihood	0.009	0.013	0.004	0.006
	Bayesian	0.008	0.009	0.004	0.006

4 Application to Longitudinal DTI Regression

Recall that in this study, 100 patients are scanned approximately once per year and undergo a collection of tests to assess cognitive and motor function; patients are seen between 2 and 8 times, with a median of 3 visits per subject. Here we focus on the mean diffusivity profile of the corpus callosum tract and the parallel diffusivity profile of the right corticospinal tract as our functional predictors and the Paced Auditory Serial Addition Test (PASAT), a commonly used examination of cognitive function affected by MS with scores ranging between 0 and 60, as our scalar outcome.

We begin by fitting models of the form

$$\begin{array}{cc}\hfill Y_{\mathit{\text{ij}}}& =\alpha +X_{\mathit{\text{ij}}}\beta +b_i+{\displaystyle {\int }_0^1}{W}_{\mathit{\text{ij}}}(s)\gamma (s)\mathit{\text{ds}}+{\epsilon }_{\mathit{\text{ij}}}\hfill \\ \hfill b_i& ~\mathrm{N}[0,{\sigma }_{\mathit{b}}^2],{\epsilon }_{\mathit{\text{ij}}}~\mathrm{N}[0,{\sigma }_{\mathit{Y}}^2]\hfill \end{array}$$ (4)

where Y_ij is the PASAT score for subject i at visit j, W_ij(s) is functional predictor for subject i at visit j, and the variable X_ij = I(j > 1) is used to account for a learning effect that causes PASAT scores to generally rise between the first and second visit. Two such models are fit, one using the mean diffusivity profile of the corpus callosum and another using the parallel diffusivity profile of the right corticospinal tract. Next, we fit additional models that include the subject-specific time since first visit as a fixed effect and random slopes on this variable. These models illustrate that more complex random effect structures are possible within our proposed framework with a minimal increase in computation time and allow the treatment of irregularly timed observations. However, these models gave results indistinguishable from the random intercept only model, and are not discussed further. The random intercept models are fit using both likelihood-based and Bayesian implementations of the method describe in Section 2. Because our model uses a continuous outcome and identity link, the coefficient function has a marginal interpretation; that is, the effect of the predictor function on the outcome (as mediated by the coefficient function) does not depend on a subject’s random effect.

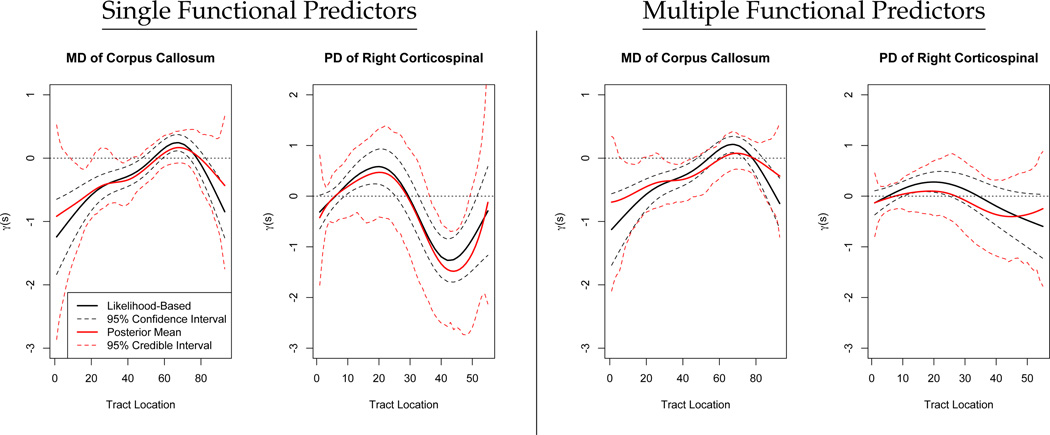
Estimates of the functional coefficient γ(s), along with credible and confidence intervals, are presented in the left panels of Figure 4. Note that in both cases the credible and confidence intervals are quite different; we recall from our simulations that the credible intervals were conservative, while the confidence intervals were slightly below the nominal coverage. However, for the corpus callosum both intervals indicate that the first half of the tract has a significant impact on the PASAT outcome, although only the confidence intervals indicate significance for the region from 60 to 80. For the corticospinal tract, the region from 40–50 is indicated as having a significant impact on the outcome.

Figure 4.

Results of analyses with single and multiple functional predictors. On the left, we show the estimated coefficient function the mean diffusivity (MD) profile of the corpus callosum and the parallel diffusivity (PD) profile of the right corticospinal tract treated separately as single functional predictors. On the right we show the results of an analysis including both profiles as functional predictors. In all panels, solid lines depict estimated coefficient functions and dashed lines represent confidence intervals, while black curves are likelihood-based and red are Bayesian.

In Table 3 we show the percent of the outcome variance explained, defined as $\text{PVE}=100\times \left(1-\frac{{\widehat{\sigma }}_{\mathit{Y}}^2}{\text{Var}(Y_{\mathit{\text{ij}}})}\right)\text{ where }{\widehat{\sigma }}_{\mathit{Y}}^2$ is the estimated residual variance and Var(Y_ij) is the overall outcome variance, in each of several models. Included in this Table are the longitudinal functional models described above, as well as a random intercept only model and a standard linear mixed model with visit indicator and the average mean diffusivity in the corpus callosum as a scalar predictor (rather than the functional tract profile). We note that the largest source of variation in the outcome is the subject-specific random effect, and that the functional regression models substantially outperform the standard linear mixed model. Further, the two functional predictors explain a similar amount of variability beyond the random intercept only model.

Table 3.

Percent of the variance in the PASAT outcome explained by a random intercept only model, a model without functional effects (labeled the “Non-functional Model”), two models with single functional predictors (labeled “Single: MD” and “Single: PD” for the models using the mean diffusivity and parallel diffusivity tract profiles, respectively), and a model with multiple functional predictors (labeled “Multiple”).

	Random Int. Only	Non-functional Model	Single: MD	Single: PD	Multiple
PVE	81.2 %	83.8%	88.6%	88.7	88.8%

Next, we carry out an analysis that includes both the corpus callosum mean diffusivity profile and the corticospinal tract parallel diffusivity profile in a single model. The estimated functional coefficients in this model are given in the right panels of Figure 4. The estimated coefficient function for the corpus callosum and accompanying confidence intervals are largely unchanged from regression using this profile as a single functional predictor, but the estimate for the corticospinal tract is quite different. Rather than a peak from 10–20 and a dip from 40–50, the coefficient for the corticospinal tract is near zero over its entire range, and no regions appear particularly important in predicting the outcome. The model with multiple functional predictors explains only slightly more of the outcome variance than either model with a single predictor, indicating that the information contained in the two predictors is similar.

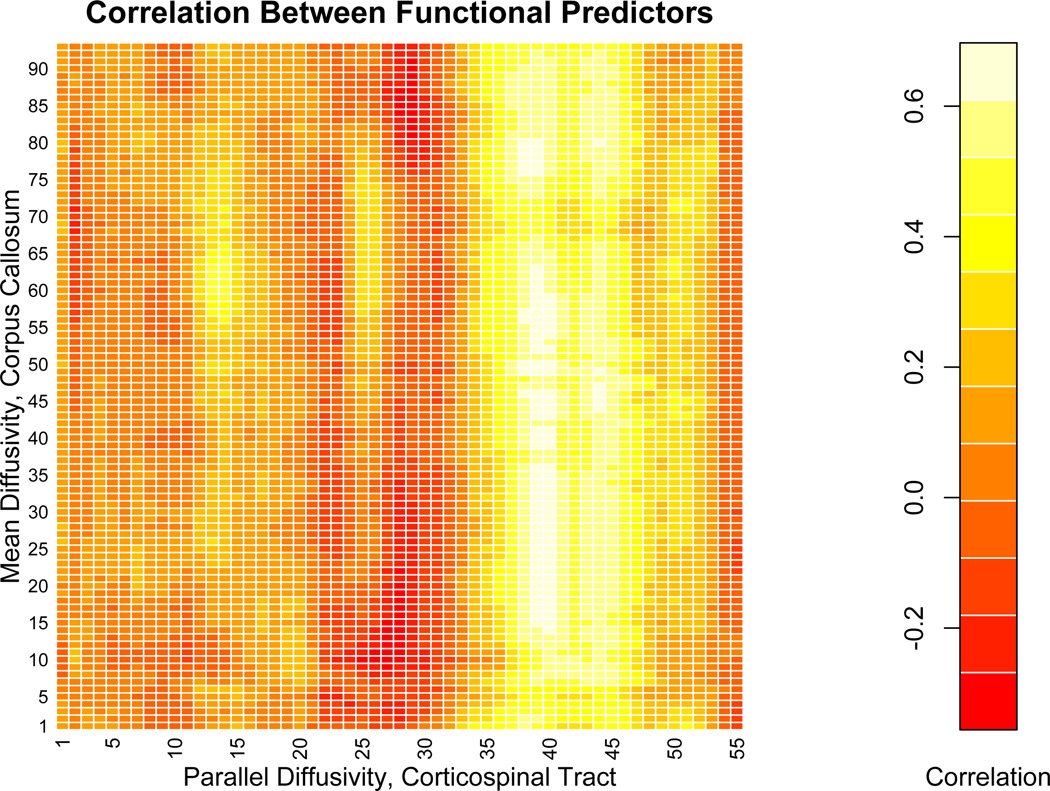
The collection of results from the regression models displayed in Table 3 is reminiscent of confounding in standard regression models: the effect of one variable largely disappears in the presence of a second variable. A heatmap of the correlation matrix between the corpus callosum and corticospinal tract profiles, shown in 5, indicates that the region spanning locations 40–50 of the corticospinal tract are have correlations between .5 and .6 with the corpus callosum. This region is similar to the region of interest when the corticospinal tract is used as a single predictor. The high correlations likely occur due to the anatomical proximity of the corpus callosum and corticospinal tracts in this region. Finally, the PASAT score is a measure of cognitive function, and has been linked to degradation of the corpus callosum (Ozturk et al., 2010). However, the corticospinal tract mediates movement and strength, not cognition, and therefore should not have a direct impact on the PASAT score. Based on these findings, it is therefore scientifically plausible that the corticospinal tract is not directly linked to cognitive function, but is correlated through its correlation with the corpus callosum. On the other had, the direct relationship between the corpus callosum and the PASAT score appears scientifically and statistically plausible.

5 Discussion

In this paper we are posed with a scientifically interesting and clinically important data set exploring the relationship between intracranial white matter tracts and cognitive disability in multiple sclerosis patients. Data of this type, in which functional predictors and scalar outcomes are observed longitudinally, will soon be regularly observed in the statistical community. To properly analyze these data, we proposed a longitudinal functional regression model which is broadly applicable. The results of our analysis indicate that the combination of functional data techniques with more traditional longitudinal regression models is a powerful tool to enhance our understanding of basic scientific questions.

The approach we propose is appealing in that in casts difficult longitudinal functional regression problems in terms of the popular and well-known mixed model framework. The methods developed are: 1) very general, allowing for the functional coefficient to be fit using a flexible penalized approach or modeled parametrically; 2) applicable whether the functional covariates are sparsely or densely sampled, or measured with error; and 3) computationally efficient and tractable. To the last point, we developed two implementations for this approach using common statistical software and demonstrated their effectiveness in a detailed simulation study; code for these implementations, as well as a discussion of their relative merits, is available in an online appendix.

Future work may take several directions. Most broadly, there is a need for rigorous model selection techniques in the context of functional regression. In our analysis, we chose the model based on the scientifically plausible appearance of confounding, but the development of hypothesis tests suitable for this setting is necessary. Because in our model the flexibility in the coefficient function is based on a random effect distribution, testing for a zero variance component can examine the null hypothesis that the effect of the functional predictor is constant over its domain. Methods exist to conduct this test, but their performance should be carefully studied in this setting. Alternatively, the use of LASSO-based methods in similar settings allow penalized approaches to variable selection, although their feasibility in the longitudinal functional regression setting must be evaluated (Fan and James, Under Review; Yi et al., To Appear). Related to the issue of variable selection, it is common for scientific applications to produce many correlated predictors for each subject. The inclusion of such predictors in a single model raises the issue of “concurvity”, a functional analog of collinearity, and may result in unstable estimates or computational errors. Concurvity has been studied in the generalized additive model literature, but additional work is needed to address the problems caused by correlation in functional predictors (Ramsay et al., 2003).

Other directions for future work include the possibility of basing longitudinal functional regression on functional decomposition techniques tailored to the structure of the data, which may give results that are simpler to implement or interpret. Penalized approaches that use cross validation to impose smoothness, though computationally expensive, could provide a useful alternative to the mixed model approach presented here. Borrowing from the smoothing literature, the use of adaptive smoothing methods for the estimation of coefficient functions could alleviate the issue of localized over- or undersmoothing demonstrated in our simulations. Finally, functional regression techniques for data sets in which the predictor contains tens or hundreds of thousands of elements, either from extremely dense observation or because the predictor is a 2- or 3-dimensional image, will be needed as such data sets are collected and analyzed.

Figure 5.

Heatmap of the correlation matrix between the mean diffusivity of the corpus callosum and the parallel diffusivity of the right corticospinal tract, the tract profiles used as functional predictors in the analyses with single and multiple functional predictors. Tract locations are provided on the axes of the heatmap.