Double inverse-weighted estimation of cumulative treatment effects under non-proportional hazards and dependent censoring

Summary

In medical studies of time to event data, non-proportional hazards and dependent censoring are very common issues when estimating the treatment effect. A traditional method for dealing with time-dependent treatment effects is to model the time-dependence parametrically. Limitations of this approach include the difficulty to verify the correctness of the specified functional form and the fact that, in the presence of a treatment effect that varies over time, investigators are usually interested in the cumulative as opposed to instantaneous treatment effect. In many applications, censoring time is not independent of event time. Therefore, we propose methods for estimating the cumulative treatment effect in the presence of non-proportional hazards and dependent censoring. Three measures are proposed, including the ratio of cumulative hazards, relative risk and difference in restricted mean lifetime. For each measure, we propose a double-inverse-weighted estimator, constructed by first using inverse probability of treatment weighting (IPTW) to balance the treatment-specific covariate distributions, then using inverse probability of censoring weighting (IPCW) to overcome the dependent censoring. The proposed estimators are shown to be consistent and asymptotically normal. We study their finite-sample properties through simulation. The proposed methods are used to compare kidney wait list mortality by race.

1. Introduction

In clinical and epidemiologic studies of survival data, it is very common that the treatment effect is not constant over time. In the presence of non-proportional hazards, the Cox (1972) model is often modified such that the treatment effect is assumed to vary as a specified function of time. However, the functional form chosen may not be correct. Moreover, researchers are usually more interested in the cumulative treatment effect in settings where the treatment effect is time-dependent. Without specifying the functional form of the treatment effect, one can compare survival or cumulative hazard curves using the Nelson-Aalen (Nelson, 1972; Aalen, 1978) estimator or Kaplan-Meier (Kaplan and Meier, 1958) estimator. These estimators may lead to biased results when confounders for treatment exist, as is often the case in observational studies. When censoring time depends on factors predictive of the event, the event and censoring time are correlated through these factors. If these prognostic factors are time-dependent and if they are not only risk factors for the event but also affected by treatment, standard methods of covariate adjustment may produce biased treatment effects. If adjustment is made for baseline values instead of time-dependent factors, standard regression methods are still invalid since the event and censoring times will be dependent through their mutual correlation with the time-dependent factors.

The investigation which motivated our proposed research involves comparing wait-list survival for patients with end-stage renal disease. The effect of race (Caucasian vs African American) on survival is of interest and may vary over time. There exist time-constant covariates (e.g., age, renal diagnosis) for which adjustment is necessary. Moreover, a patient's hospitalization history is a predictor of wait-list mortality and also affects transplantation probability, since patients with more hospitalizations are less likely to receive a kidney transplant. Although a patient's death may be observed following kidney transplantation, receipt of a transplant does censor wait-list mortality. Therefore, the mortality and censoring will be correlated unless the model adjusts for hospitalization history. However, one would generally not want to adjust for hospitalization history (e.g., through a time-dependent Cox model), since the race effect obtained through such an approach does not have a good interpretation and may be much closer to the null than the marginal race effect of interest. It is therefore necessary to handle dependent censoring in this analysis. Note that, alternatively, one could obtain marginal effects through time-dependent approaches via the G-computation algorithm (Robins, 1986, 1987).

Current methods usually focus on the survival or cumulative hazard function when estimating cumulative treatment effects in the presence of censored data. However, mean lifetime is often the most relevant quantity, particularly since clinicians often describe a patient's prognosis in terms of how long the patient is expected to live. Zucker (1998) and Chen and Tsiatis (2001) compared restricted mean lifetime between two treatment groups using Cox proportional hazard models. The survival function for each group was estimated by averaging over all subjects in the sample. These methods require that proportionality hold for each of the adjustment covariates.

Without specifying the functional form for the effects of adjustment covariates, inverse probability of treatment weighting (IPTW) can be applied to balance the distribution of adjustment covariates across treatment groups. Hernan, Brumback and Robins (2000, 2001) and Robins, Hernan and Brumback (2000) used marginal structural models to estimate the causal effect of a time-dependent exposure. Inverse weighting was applied to adjust for time-dependent confounders that are affected by previous treatment. In the context of survival analysis, the authors assumed that hazards were proportional across treatments. With respect to the related nonparametric methods, Xie and Liu (2005) developed an adjusted Kaplan-Meier curve using inverse weighting to handle potential confounders, assuming that the event time and censoring time are independent.

Inverse probability of censoring weighting (IPCW), proposed by Robins and Rotnitzky (1992) and Robins (1993), has been utilized in many applications to overcome dependent censoring. A Cox proportional hazard model is assumed for the event time, while an inverse probability of censoring weight is applied to the Cox model score equation. The weight can be thought of as the inverse of the probability of remaining uncensored, which can be estimated non- or semi-parametrically. Robins and Finkelstein (2000) described the use of IPCW to handle dependent censoring induced by considering patients who switch therapy as censored, not unlike the data set which motivated our current work. The IPCW method has been applied in various other settings (Matsuyama and Yamaguchi, 2008; Yoshida, Matsuyama and Ohashi, 2007).

We propose methods for quantifying the cumulative effect of a treatment in the absence of randomization and presence of dependent censoring. Three cumulative treatment effect measures are developed: ratio of cumulative hazards, relative risk, and difference in restricted mean lifetime. The proposed estimators are computed by double inverse weighting, wherein inverse probability of treatment weighting is used to balance the treatment-specific baseline adjustment covariate distributions and IPCW is concurrently applied to handle the dependent censoring due to time-varying factors for which no adjustment is made. After applying the double inverse weight to the observed data, estimation of the cumulative treatment effects proceeds nonparametrically, negating the need to specify functional forms for the effect of either the treatment or the adjustment covariates.

The remainder of this article is organized as follows. We describe our proposed methods in the next section. In Section 3, we derive asymptotic properties of our proposed estimators; proofs of which are provided in the Web Appendix. We evaluate the performance of our estimators in finite samples in Section 4. In Section 5, we apply the methods to kidney wait list data obtained from a national organ failure registry. Discussion is provided in Section 6.

2. Proposed methods

Suppose that n subjects are included in the data set. Let D_i be the event time and C_i be the censoring time for subject i. Let X_i = min{D_i, C_i} and δ_i = I(D_i ≤ C_i) where I(A) is an indicator function taking the value 1 when condition A holds and 0 otherwise. The observed event and censoring counting processes are defined as $N_i^D(t)={\delta }_{i}I(X_i\le t)\text{ and }{N}_i^C(t)=(1-{\delta }_i)I(X_i\le t)$, respectively. The at risk indicator is denoted by Y_i(t) = I(X_i ≥t). Let j be the index for treatment group (j = 0, 1, …, J), with group j = 0 representing the reference category to which the remaining treatment groups are compared. Let G_i denote the treatment group for subject i and set G_ij = I(G_i = j). Correspondingly, we set Y_ij(t) = Y_i(t)G_ij, ${\mathit{\text{dN}}}_{\mathit{\text{ij}}}^D(t)={\mathit{\text{dN}}}_i^D(t)G_{\mathit{\text{ij}}}\text{ and }{\mathit{\text{dN}}}_{\mathit{\text{ij}}}^C(t)={\mathit{\text{dN}}}_i^C(t)G_{\mathit{\text{ij}}}$. The observed data consist of n independent and identically distributed vectors, ${[X_i,{\delta }_i,G_i,{\mathbf{Z̃}}_i^T(X_i)]}^T$, where Z̃_i(t) = {Z_i(s); s ∈ [0, t]} and Z_i(t) is a p × 1 vector of covariates which will typically contain some time-dependent elements. We let Z_i(0) denote the covariate values at baseline. We

We assume that there are no unmeasured baseline (t = 0) predictors of both group membership and death, conditional on Z_i(0). We also assume that the death and censoring processes are conditionally independent given group membership and Z̃_i(t). More specifically, with the death and censoring hazard functions for subject i defined as

$$\begin{array}{c}{\lambda }_i^D(t)=\underset{\delta \to 0}{\text{lim}}\frac{1}{\delta }P\{t\le D_i<t+\delta |D_i\ge t\}\hfill \\ {\lambda }_i^C(t)=\underset{\delta \to 0}{\text{lim}}\frac{1}{\delta }P\{t\le C_i<t+\delta |C_i\ge t\},\hfill \end{array}$$

respectively, we are assuming that

$${\lambda }_i^D\{t|G_i,{\tilde{\mathbf{Z}}}_i(t),C_i\ge t\}={\lambda }_i^D\{t|G_i,{\tilde{\mathbf{Z}}}_i(t)\}$$ (1)

$${\lambda }_i^C\{t|G_i,{\tilde{\mathbf{Z}}}_i(t),D_i\ge t\}={\lambda }_i^C\{t|G_i,{\tilde{\mathbf{Z}}}_i(t)\}.$$ (2)

Further, we assume that there are no unmeasured confounders for censoring,

$${\lambda }_i^C\{t|G_i,{\tilde{\mathbf{Z}}}_i(t),D_i\ge t,D_i\}={\lambda }_i^C\{t|G_i,{\tilde{\mathbf{Z}}}_i(t),D_i\ge t\};$$ (3)

i.e., that the cause-specific hazard for censoring does not further depend on the possibly unobserved death time. In a standard survival analysis featuring time-dependent covariates, a condition analogous to (1) would typically be assumed. We require condition (3) since our proposed methods require modeling ${\lambda }_i^C(t)$, as will be described shortly.

The plausibility of such no-unmeasured-confounders assumptions depends on the nature of the data at hand. In settings where treatment is not randomized, the conditions will likely never hold exactly. However, if the covariate Z̃_i(t) is sufficiently rich (e.g., the important risk factors have been collected), then the assumptions may hold approximately; at least to the extent that meaningful inference can be achieved.

Note that we use the term ‘treatment’ here rather generically. In practice, G_i could represent any baseline categorical factor of interest, including one which is not explicitly assigned. For instance, in the example which motivated our work, the factor of interest is race. The fact that race is not a factor which is randomized (or even assigned) introduces issues which we discuss in Section 6. For now, note that our objective is to obtain valid associational (as opposed to causal) inference.

In the case where Z_i(t) not only affects the event time but also affects censoring, event and censoring are dependent unless the effect of Z_i(t) on the event is modeled explicitly. However, one would usually prefer to adjust for Z_i(0), instead of Z_i(t) when Z_i(t) is, at least in part, a consequence of treatment. A frequently employed manner of describing the treatment effect is to compare the average survival resulting from treatment j (as opposed to the reference treatment) being assigned to the entire population. In the setting where treatment j is assigned to all subjects, the average survival function is given by S_j(t) = E{S(t|G_i = j, Z_i(0))}. The expectation is with respect to the marginal distribution of Z_i(0), such that the same averaging is done across all J + 1 treatment groups.

To compare the cumulative effect of treatment j to the reference treatment, three measures are proposed. The first proposed measure is the ratio of cumulative hazards,

$${\varphi }_j(t)=\frac{{\mathrm{\Lambda }}_j(t)}{{\mathrm{\Lambda }}_0(t)},$$ (4)

where Λ_j(t) = −log{S_j(t)} is the cumulative hazard at time t. When treatment-specific hazards are proportional, ϕ_j(t) is equal to the familiar hazard ratio. The second proposed measure is the ratio of cumulative distribution functions,

$${\mathit{\text{RR}}}_j(t)=\frac{F_j(t)}{F_0(t)},$$ (5)

where F_j(t) = 1 − S_j(t) is the average probability of death by time t, when treatment j is assigned. The measure RR_j(t) is a process version of relative risk, a quantity which is frequently estimated in epidemiologic studies. The third proposed measure is the difference in restricted mean lifetime,

$${\mathrm{\Delta }}_j(t)=e_j(t)-e_0(t),$$ (6)

where $e_j(t)={\displaystyle {\int }_0^t}{S}_j(u)\mathit{\text{du}}$ is the area under the survival curve (restricted mean lifetime) over (0, t]. The Δ_j(t) measure equals the area between the survival curves that would result if treatment j (versus treatment 0) was assigned to all subjects in the population.

Let ${\mathbf{X}}_{\mathit{\text{ij}}}={[{\mathbf{0}}_{1\times (j-1)(p+1)},1,{\mathbf{Z}}_i^T(0),{\mathbf{0}}_{1\times (J-j)(p+1)}]}^T$ where 0_{1×(j−1)(p+1)} is a 1 by (j−1)(p+1) matrix with elements 0, for j = 1, …, J. We assume that treatment assignment follows a generalized logits model,

$$\text{log }\left\{\frac{p_{\mathit{\text{ij}}}({\beta }_0)}{p_{i0}({\beta }_0)}\right\}={\beta }_0^T{\mathbf{X}}_{\mathit{\text{ij}}},$$

where p_ij(β₀) = Pr{G_i = j|Z_i(0)}. The model could be extended to include interaction terms. The maximum likelihood estimator of β₀, denoted by β̂, is the root of U_G(β) = 0, where

$${\mathrm{U}}_G(\beta )={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^J}{\mathbf{X}}_{\mathit{\text{ij}}}[G_{\mathit{\text{ij}}}-p_{\mathit{\text{ij}}}(\beta )].$$ (7)

Since it is preferred to adjust for Z_i(0) instead of Z_i(t), the event and censoring processes are dependent through their mutual association with {Z_i(t): t > 0}. We apply an inverse probability of censoring weight to handle the dependent censoring. We assume that C_i follows a Cox model with hazard function

$${\lambda }_i^C(t)={\lambda }_0^C(t)\text{exp}\{{\mathit{\theta }}_0^T{\mathbf{Z}}_i^C(t)\},$$ (8)

where ${\mathbf{Z}}_i^C(t)$ contains terms representing G_i and Z_i(t). The inverse censoring weight at time t is denoted by $w_i^C(t,{\mathit{\theta }}_0)=Y_i(t)\text{ exp}\{{\mathrm{\Lambda }}_i^C(t)\},\text{where }{\mathrm{\Lambda }}_i^C(t)={\displaystyle {\int }_0^t}{\lambda }_i^C(s)\mathit{\text{ds}}$. The quantity $w_i^C(t,{\mathit{\theta }}_0)$ is estimated by ${\widehat{w}}_i^C(t,\widehat{\mathit{\theta }})=Y_i(t)\text{ exp}\{{\widehat{\mathrm{\Lambda }}}_i^C(t,\widehat{\mathit{\theta }})\}$, where

$$\begin{array}{cc}\hfill {\widehat{\mathrm{\Lambda }}}_i^C(t,\mathit{\theta })& ={\displaystyle {\int }_0^t}\text{exp}\{{\mathit{\theta }}^T{\mathbf{Z}}_i^C(s)\}d{\widehat{\mathrm{\Lambda }}}_0^C(s,\mathit{\theta }),\hfill \\ \hfill {\widehat{\mathrm{\Lambda }}}_0^C(t,\mathit{\theta })& =\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\displaystyle {\int }_0^t}\frac{{\mathit{\text{dN}}}_i^C(s)}{R_C^{(0)}(s,\mathit{\theta })},\hfill \end{array}$$

and ${\mathbf{R}}_C^{(d)}(t,\mathit{\theta })=n^{-1}{\displaystyle {\sum }_{i=1}^n}{Y}_i(t){\mathbf{Z}}_i^C{(t)}^{\otimes d}\text{exp}\{{\mathit{\theta }}^T{\mathbf{Z}}_i^C(t)\}$ for d = 0, 1, 2 with a^⊗0 = 1, a^⊗1 = a and a^⊗2 = aa^T for a vector a. The quantity ${\widehat{\mathrm{\Lambda }}}_0^C(t,\widehat{\mathit{\theta }})$ is the Breslow-Aalen estimator for ${\mathrm{\Lambda }}_0^C(t)$. The parameter θ₀ is estimated through partial likelihood (Cox, 1975) by θ̂, the solution of the score equation, U_C(θ) = 0, where

$$\begin{array}{cc}\hfill {\mathrm{U}}_C(\mathit{\theta })& ={\displaystyle \sum _{i=1}^n}{\displaystyle {\int }_0^{\tau }}\{{\mathbf{Z}}_i^C(t)-{\overline{\mathbf{Z}}}_C(t,\mathit{\theta })\}{\mathit{\text{ dN}}}_i^C(t),\hfill \\ \hfill {\overline{\mathbf{Z}}}_C(t,\mathit{\theta })& =\frac{{\mathbf{R}}_C^{(1)}(t,\mathit{\theta })}{R_C^{(0)}(t,\mathit{\theta })}.\hfill \end{array}$$ (9)

Note that if the treatment-specific censoring hazards are not proportional, a treatment-stratified version of model (8) could be applied.

The measure ϕ_j(t) is estimated by

$${\widehat{\varphi }}_j(t)=\frac{{\widehat{\mathrm{\Lambda }}}_j(t,\widehat{\beta },\widehat{\mathit{\theta }})}{{\widehat{\mathrm{\Lambda }}}_0(t,\widehat{\beta },\widehat{\mathit{\theta }})},$$

where

$$\begin{array}{cc}\hfill {\widehat{\mathrm{\Lambda }}}_j(t,\beta ,\mathit{\theta })& \hfill =\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\displaystyle {\int }_0^t}\frac{{\widehat{w}}_i^C(s,\mathit{\theta })w_{\mathit{\text{ij}}}^G(\beta )}{R_j^{(0)}(s,\beta ,\mathit{\theta })}{\mathit{\text{dN}}}_{\mathit{\text{ij}}}^D(s),\\ \hfill R_j^{(0)}(s,\beta ,\mathit{\theta })& =\frac{1}{n}{\displaystyle \sum _{i=1}^n}{Y}_{\mathit{\text{ij}}}(s){\widehat{w}}_i^C(s,\mathit{\theta })w_{\mathit{\text{ij}}}^G(\beta ),\hfill \end{array}$$

with $w_{\mathit{\text{ij}}}^G(\beta )=G_{\mathit{\text{ij}}}/p_{\mathit{\text{ij}}}(\beta )$. The relative risk measure, RR_j(t), is estimated by

$${\widehat{\mathit{\text{RR}}}}_j(t)=\frac{{\widehat{F}}_j(t,\widehat{\beta },\widehat{\mathit{\theta }})}{{\widehat{F}}_0(t,\widehat{\beta },\widehat{\mathit{\theta }})},$$

where F̂_j(t, β, θ) = 1 − Ŝ_j(t, β, θ) and Ŝ_j(t, β, θ) = exp{−Λ̂_j(t, β, θ). The estimator for the difference in restricted mean lifetime, Δ_j(t), is given by

$${\widehat{\mathrm{\Delta }}}_j(t)={\widehat{e}}_j(t,\widehat{\beta },\widehat{\mathit{\theta }})-{\widehat{e}}_0(t,\widehat{\beta },\widehat{\mathit{\theta }}),$$

where ${\widehat{e}}_j(t,\beta ,\mathit{\theta })={\displaystyle {\int }_0^t}{\widehat{S}}_j(s,\beta ,\mathit{\theta })\mathit{\text{ds}}$.

The measures ϕ_j(t) and RR_j(t) are considered on a time interval [t_L, t_U], while Δ_j(t) is considered in a time interval [0, t_U], where t_L is chosen to avoid division by 0 and t_U is chosen to avoid the well recognized instability in the tail of the observation time distribution.

The IPTW weight, $w_{\mathit{\text{ij}}}^G({\beta }_0)$, is used for balancing the covariate distribution among the treatment groups. After applying $w_{\mathit{\text{ij}}}^G({\beta }_0)$ to our estimators, J + 1 pseudo-populations are created with treatment-specific Z_i(0) distribution equal to that of the entire population. For example, for the restricted mean lifetime $e_j(t)={\displaystyle {\int }_0^t}E[S(s|G_i=j,{\mathbf{Z}}_i(0))]\mathit{\text{ds}}$, the expectation is with respect to the marginal distribution of Z_i(0), such that same averaging is done across all J + 1 treatment groups. The IPCW weight, $w_i^C(t,{\mathit{\theta }}_0)$, is applied to handle the dependent censoring. After applying the proposed double inverse weighting, each of the proposed measures converges to the value which would apply to a population in which treatment was randomized and no censoring occurred.

3. Asymptotic properties

We summarize the asymptotic properties of the proposed estimators in the following theorems. The set of assumed regularity conditions is listed in the Appendix, while proofs of the theorems are provided in the Web Appendix.

THEOREM 1. Under conditions (a) to (f) listed in the Appendix, Λ̂_j(t) = Λ̂_j(t;β̂θ̂) converges almost surely and uniformly to Λ_j(t) for t ∈ [0, t_U], and n^1/2{Λ̂_j(t) − Λ_j(t)] converges asymptotically to a zero-mean Gaussian process with covariance function σ_j(s, t) = E{Φ_ij(s)Φ_ij(t)}, where

$$\begin{array}{cc}\hfill {\mathbf{\Phi }}_{\mathit{\text{ij}}}(t)& ={\mathbf{\Phi }}_{\mathit{\text{ij}}1}(t)+{\mathbf{\Phi }}_{\mathit{\text{ij}}2}(t)+{\mathbf{\Phi }}_{\mathit{\text{ij}}3}(t)+{\mathbf{\Phi }}_{\mathit{\text{ij}}4}(t)\hfill \\ \hfill {\mathbf{\Phi }}_{\mathit{\text{ij}}1}(t)& ={\{{\mathbf{h}}_j(t)+{\mathbf{d}}_j(t)\}}^T{\mathbf{\Omega }}_G^{-1}({\beta }_0)n^{-1/2}{\psi }_i^G({\beta }_0)\hfill \\ \hfill {\mathbf{\Phi }}_{\mathit{\text{ij}}2}(t)& {=\{{\mathbf{g}}_j(t)+{\mathbf{f}}_j(t)\}}^T{\mathbf{\Omega }}_C^{-1}({\mathit{\theta }}_0)n^{-1/2}{\psi }_i^C({\mathit{\theta }}_0)\hfill \\ \hfill {\mathbf{\Phi }}_{\mathit{\text{ij}}3}(t)& ={\displaystyle {\int }_0^t}{q}_j(s,t)r_j^{(0)}{(s;{\beta }_0,{\mathit{\theta }}_0)}^{-1}{\mathit{\text{dM}}}_i^C(s)\hfill \\ \hfill {\mathbf{\Phi }}_{\mathit{\text{ij}}4}(t)& {\displaystyle ={\int }_0^t}\frac{w_{\mathit{\text{ij}}}^G({\beta }_0)w_i^C(s,{\mathit{\theta }}_0)}{r_j(s,{\beta }_0,{\mathit{\theta }}_0)}{\mathit{\text{dM}}}_{\mathit{\text{ij}}}^D(s),\hfill \end{array}$$

where ${\mathbf{\Omega }}_G{({\beta }_0)}^{-1}{\psi }_i^G({\beta }_0)\text{ and }{\mathbf{\Omega }}_C{({\mathit{\theta }}_0)}^{\mathit{-}1}{\psi }_i^C({\mathit{\theta }}_0)$ are the influence functions for the Cox and logistic models, respectively (for which explicit expressions given in the Appendix); ${\mathit{\text{dM}}}_i^C(t)-{\mathit{\text{dN}}}_i^C(t)-Y_i(t)d{\mathrm{\Lambda }}_i^C(t),{\mathit{\text{dM}}}_{\mathit{\text{ij}}}^D(s)={\mathit{\text{dN}}}_{\mathit{\text{ij}}}^D(s)-Y_{\mathit{\text{ij}}}(s)d{\mathrm{\Lambda }}_j(s)$, and with h_j(t), d_ij(t), g_j(t) and f_j(t) defined in the Appendix.

The consistency of Λ̂_j(t) is proved through the consistency of β̂ and θ̂, the continuous mapping theorem, and the Uniform Strong Law of Large Numbers (USLLN). The proof of asymptotic normality involves decomposing n^1/2{Λ̂_j(t, β̂, θ̂) − Λ_j(t)} into α̂_j1(t) + α̂_j2(t) + α̂_j3(t) + α̂_j4(t), where

$$\begin{array}{cc}{\widehat{\alpha }}_{j1}(t)\hfill & =n^{1/2}\{{\widehat{\mathrm{\Lambda }}}_j(t,\widehat{\beta },\widehat{\mathit{\theta }},{\widehat{\mathrm{\Lambda }}}_0^C)-{\widehat{\mathrm{\Lambda }}}_j(t,{\beta }_0,\widehat{\mathit{\theta }},{\widehat{\mathrm{\Lambda }}}_0^C)\}\hfill \\ {\widehat{\alpha }}_{j2}(t)\hfill & =n^{1/2}\{{\widehat{\mathrm{\Lambda }}}_j(t,{\beta }_0,\widehat{\mathbf{\theta }},{\widehat{\mathrm{\Lambda }}}_0^C)-{\widehat{\mathrm{\Lambda }}}_j(t,{\beta }_0,{\mathit{\theta }}_0,{\widehat{\mathrm{\Lambda }}}_0^C)\}\hfill \\ {\widehat{\alpha }}_{j3}(t)\hfill & =n^{1/2}\{{\widehat{\mathrm{\Lambda }}}_j(t,{\beta }_0,{\mathit{\theta }}_0,{\widehat{\mathrm{\Lambda }}}_0^C)-{\widehat{\mathrm{\Lambda }}}_j(t,{\beta }_0,{\mathit{\theta }}_0,{\mathrm{\Lambda }}_0^C)\}\hfill \\ {\widehat{\alpha }}_{j4}(t)\hfill & =n^{1/2}\{{\widehat{\mathrm{\Lambda }}}_j(t,{\beta }_0,{\mathit{\theta }}_0,{\mathrm{\Lambda }}_0^C)-{\mathrm{\Lambda }}_j(t)\}.\hfill \end{array}$$

The quantity n^1/2{Λ̂_j(t, β̂, θ̂) − Λ_j(t)} can then be written as, asymptotically, a sum of independent and identically distributed mean 0 variates. The Multivariate Central Limit Theorem can then be used to demonstrate asymptotic normality, while convergence to a Gaussian process follows from various results from the theory of empirical processes (Pollard, 1990; Bilias, Gu and Ying, 1997). A proof of Theorem 1 is provided in the Web Appendix.

THEOREM 2. Under conditions (a) to (f), ϕ̂_j(t) = ϕ̂(t; β̂, θ̂) converges almost surely to ϕ_j(t) for t ∈ [t_L, t_U], and n^1/2{ϕ̂_j(t) − ϕ_j(t)} converges asymptotically to a zero-mean Gaussian process with covariance function ${\sigma }_j^{\varphi }(s,t)=E\{{\xi }_{\mathit{\text{ij}}}^{\varphi }(s){\xi }_{\mathit{\text{ij}}}^{\varphi }(t)\}$, where

$${\xi }_{\mathit{\text{ij}}}^{\varphi }(t)={\mathrm{\Lambda }}_0{(t)}^{-1}{\mathbf{\Phi }}_{\mathit{\text{ij}}}(t)-{\mathrm{\Lambda }}_j(t){\mathrm{\Lambda }}_0{(t)}^{-2}{\mathbf{\Phi }}_{i0}(t),$$

with Φ_ij(t) as given in Theorem 1.

The proof of Theorem 2 (provided in the Web Appendix) involves combining Theorem 1 and the Functional Delta Method. The covariance function can be consistently estimated by replacing all limiting values with their empirical counterparts.

THEOREM 3. Under the assumed regularity conditions, ${\widehat{\mathit{\text{RR}}}}_j(t)=\widehat{\mathit{\text{RR}}}(t;\widehat{\mathit{\beta }},\widehat{\mathit{\theta }})$ converges almost surely and uniformly to RR_j(t) for t ∈ [t_L, t_U], and $n^{1/2}\{{\widehat{\mathit{\text{RR}}}}_j(t)-{\mathit{\text{RR}}}_j(t)\}$ converges asymptotically to a zero-mean Gaussian process with covariance function ${\sigma }_j^R(s,t)=E\{{\xi }_{\mathit{\text{ij}}}^R(s){\xi }_{\mathit{\text{ij}}}^R(t)\}$, where

$${\xi }_{\mathit{\text{ij}}}^R(t)=\frac{S_j(t)}{F_0(t)}{\mathbf{\Phi }}_{\mathit{\text{ij}}}(t)-\frac{F_j(t)S_0(t)}{F_0{(t)}^2}{\mathbf{\Phi }}_{i0}(t),$$ (10)

with Φ_ij(t) defined as in Theorem 1.

The proof of Theorem 3 (Web Appendix) is quite similar in structure to that of Theorem 2.

THEOREM 4. Under the assumed regularity conditions, Δ̂_j(t) = Δ̂(t β̂, θ̂ converges almost surely and uniformly to Δ_j(t) for t ∈ [0, t_U], while n^1/2{Δ̂_j(t)−Δ_j(t)}, converges asymptotically to a zero-mean Gaussian process with covariance function ${\sigma }_j^{\mathrm{\Delta }}(s,t)=E\{{\xi }_{\mathit{\text{ij}}}^{\mathrm{\Delta }}(s){\xi }_{\mathit{\text{ij}}}^{\mathrm{\Delta }}(t)\}$, where

$${\xi }_{\mathit{\text{ij}}}^{\mathrm{\Delta }}(t)=-{\displaystyle {\int }_0^t}\{S_j(t)-S_j(u)\}d{\mathbf{\Phi }}_{\mathit{\text{ij}}}(u)+{\displaystyle {\int }_0^t}\{S_0(t)-S_0(u)\}d{\mathbf{\Phi }}_{i0}(u),$$ (11)

with Φ_ij(t) as defined as in Theorem 1.

The proof begins by expressing n^1/2{ê_j(t)−e_j(t)} as a sum of independent and identically distributed zero-mean variates, as n → ∞ (Andersen et al, 1993). The Functional Delta Method is then combined with Theorem 1.

For large data sets, variance estimation can be computationally intense, in which case the bootstrap is a useful alternative. Although the bootstrap is not typically suggested in the interests of reducing computing time, it can achieve such an objective in settings where the point estimator can be computed quickly but computation of the asymptotic variance is slow. In cases where the size of the data set precludes the standard bootstrap, the m of n bootstrap may be applied, such that resamples of size m(< n) are drawn and the estimated variance is then multiplied by m/n.

4. Simulation study

We evaluated the finite sample properties of the proposed estimators through a series of simulation studies. For each of the n subjects, a covariate Z_i1 was generated as a binary variable with values 0 or 1 and Pr(Z_i1 = 1) = 0.5. The treatment indicator, G_i, was generated from a Bernoulli distribution with parameter p_i1(β) = exp(β₀+β₁Z_i1)/[1 + exp(β₀ + β₁ Z_i1)]. We chose β₀ = log(1/3) and β₁ = log(9) such that Pr(Z_i1 = 1|G_i = 1) = 0:75 and Pr(Z_i1 = 1|G_i = 0) = 0:25. When G_i = 1, we generated a variable Z_i2 as piece-wise constant with probabilities P(Z_i2 = k) = P(Z_i2 = k + 1) = 0.5 across time interval (k, k + 1], for k = 0, …, 4. When G_i = 0, Z_i2 was generated as a binary variable (0 or 1) with Pr(Z_i2 = 1) = 0.5. Event times were generated from a Cox model with hazard function

$${\lambda }_i(t)={\lambda }_0(t)\text{ exp}\{{\eta }_1{G}_i+{\eta }_2{Z}_{i1}+{\eta }_3{Z}_{i2}(t)\},$$

while censoring times were generated from a Cox model with hazard function

$${\lambda }_i^C(t)={\lambda }_0^C(t)\text{ exp}\{\theta Z_{i2}(t)\}.$$

Various values of (η₁, η₂, η₃), and µ were employed for the Cox models. For each set of parameters, several percentages of censoring were investigated by varying the baseline death and censoring hazards. Censoring times were truncated at t = 5.

Sample sizes of n = 500 and n = 200 were examined, and a total of 1000 simulations were used for each simulation setting. For the first two measures, we employed the log transform to ensure that the confidence interval bounds were in a valid range. To assess the finite-sample performance of our proposed method, the bias of each of the three estimators was evaluated at time points t = 1, t = 2 and t = 3. The bootstrap standard errors were evaluated at t = 2 with sample size n = 200, and 100 bootstrap resamples per simulation.

For n = 200, our estimators appear to be approximately unbiased in general (Table 1).

Table 1.

Simulation results: Examination of bias at different time points (n=200)

			t=1		t=2		t=3
	Setting	C%	log ϕ1(t)	BIAS	log ϕ1(t)	BIAS	log ϕ1(t)	BIAS
	I	23%	0	0.004	0.283	0.017	0.584	0.008
		40%	0	0.019	0.283	0.022	0.584	−0.007
log ϕ̂1(t)	II	13%	0.496	0.013	0.778	0.004	1.076	0.009
		33%	0.496	0.037	0.778	0.022	1.076	0.017
	III	28%	0.496	0.038	0.778	0.018	1.076	0.012
		46%	0.496	0.058	0.778	0.024	1.076	0.006
	Setting	C%	log RR1(t)	BIAS	log RR1(t)	BIAS	log RR1(t)	BIAS
	I	23%	0	0.004	0.238	0.015	0.429	0.008
		40%	0	0.019	0.238	0.019	0.429	−0.004
$\text{log }{\widehat{\mathit{\text{RR}}}}_1(t)$	II	13%	0.451	0.014	0.619	0.007	0.715	0.011
		33%	0.451	0.036	0.619	0.021	0.715	0.016
	III	28%	0.451	0.037	0.619	0.017	0.715	0.011
		46%	0.451	0.056	0.619	0.024	0.715	0.011
	Setting	C%	Δ1(t)	BIAS	Δ1(t)	BIAS	Δ1(t)	BIAS
	I	23%	0	0.001	−0.036	−0.002	−0.171	−0.002
		40%	0	−0.001	−0.036	−0.004	−0.171	−0.003
Δ̂1(t)	II	13%	−0.042	0.001	−0.197	0.005	−0.502	0.009
		33%	−0.042	−0.001	−0.197	−0.002	−0.502	0.001
	III	28%	−0.042	−0.001	−0.197	−0.002	−0.502	0.001
		46%	−0.042	−0.001	−0.197	−0.001	−0.502	0.005

Setting I: η₁ = 0, η₂ = 0.2, η₃ = 0.5, θ = 1

Setting II: η₁ = 0.5, η₂ = 0.2, η₃ = 0.5, θ = 1

Setting III:η₁ = 0.5, η₂ = 0.2, η₃ = 0.5, θ = 0.25

The bias is reduced when sample size increases to n = 500 (Web Table 1). The average bootstrap standard errors (ASE) are generally close to the empirical standard deviations (ESD) for sample size n = 200 (Table 2) and, correspondingly, the empirical coverage probabilities (CP) are fairly close to the nominal value of 0.95.

Table 2.

Simulation results: Examination of bootstrap standard errors (t=2, n=200)

	Setting	C%	log ϕ 1(t)	BIAS	ASE	ESD	CP
	I	23%	0.283	0.017	0.331	0.317	0.96
		40%		0.022	0.344	0.337	0.96
log ϕ̂1(t)	II	13%	0.778	0.004	0.309	0.320	0.94
		33%		0.022	0.323	0.332	0.95
	III	28%	0.778	0.017	0.321	0.326	0.95
		46%		0.024	0.347	0.356	0.95
	Setting	C%	log RR1(t)	BIAS	ASE	ESD	CP
	I	23%	0.238	0.015	0.283	0.270	0.96
		40%		0.019	0.293	0.286	0.96
$\text{log }{\widehat{\mathit{\text{RR}}}}_1(t)$	II	13%	0.619	0.007	0.255	0.264	0.94
		33%		0.021	0.267	0.274	0.95
	III	28%	0.619	0.017	0.265	0.269	0.96
		46%		0.024	0.288	0.297	0.95
	Setting	C%	Δ1(t)	BIAS	ASE	ESD	CP
	I	23%	−0.036	−0.002	0.087	0.087	0.95
		40%		−0.004	0.089	0.090	0.94
Δ̂1(t)	II	13%	−0.196	0.005	0.095	0.100	0.93
		33%		−0.002	0.096	0.099	0.93
	III	28%	−0.196	−0.002	0.096	0.099	0.94
		46%		−0.001	0.099	0.102	0.94

Setting I: η₁ = 0, η₂ = 0.2, η₃ = 0.5, θ = 1

Setting II: η₁ = 0.5, η₂ = 0.2, η₃ = 0.5, θ = 1

Setting III: η₁ = 0.5, η₂ = 0.2, η₃ = 0.5, θ = 0.25

5. Data analysis

We applied the proposed methods to analyze wait-list survival for patients with end-stage renal disease, where the effect of race (Caucasian vs. African American) was of interest. Data were obtained from the Scientific Registry of Transplant Recipients (SRTR) and collected by the Organ Procurement and Transplant Network (OPTN). Hospitalization data were obtained from the Centers for Medicare and Medicaid Services (CMS). Only patients whose primary payer was Medicare were included in the analysis. The data included n=7110 Caucasian and African American patients who were placed on the kidney transplant waiting list in calender year 2000. Patients were followed from the time of placement on the kidney transplant waiting list to the earliest of death, transplantation, loss to follow-up or end of study (Dec 31, 2005). Among the 2975 African Americans, 27% died and 45% received a kidney transplant. Among the 4135 Caucasians, 27% died and 54% got transplanted.

It has previously been reported that African Americans have lower kidney wait list mortality rate than Caucasians. However, Caucasians also have a higher kidney transplant rate than African Americans. Unlike liver, lung and heart transplantation, poor patient health is a contra-indication for kidney transplantation. Although donor kidneys are not specifically directed towards healthier patients, it is generally felt that patients in poorer health are less likely to receive a kidney transplant. It is quite possible that the healthiest patients are transplanted off the wait list at a greater rate for Caucasians than for African Americans. Therefore, we suspect that dependent censoring of kidney wait list mortality occurs via patient health. We use time-dependent hospitalization history as a surrogate for patient health. Note that hospitalization history is inappropriate as an adjustment covariate for patient wait list survival. Patients with a greater number of previous hospitalizations have a greater mortality hazard and hospital admissions can be viewed as intermediate end points along the path from wait listing to death. Previous comparisons of wait list mortality by race did not adjust for dependent censoring. Moreover, most previous comparisons of Caucasians and African Americans assumed that effect of race is constant over time.

Logistic regression was used to model the probability that a patient is Caucasian given age, gender, diagnosis (diabetes, hypertension, glomerulonephritis, polycystic kidney disease and other), body mass index and chronic obstructive lung disease (yes or no). A Cox model, stratified by race, was fitted to estimate the inverse probability censoring weight adjusting for the covariates listed above, as well as time-dependent number of previous hospitalizations. The transplant hazard is significantly decreased by 8% for each additional hospitalization (Web Table 2). The IPTW weight ranged from 1.04 to 21.39 and the IPCW weight ranged from 1.04 to 33.07.

Due to the size of the data set, standard error estimators were based on the m of n bootstrap to reduce computation time. Specifically, we repeatedly sampled with replacement m = 1000 patients from the n = 7110 patients in the study population, then multiplied the bootstrap standard error by $\sqrt{1000/7110}$. A total of 5000 bootstrap resamples were drawn.

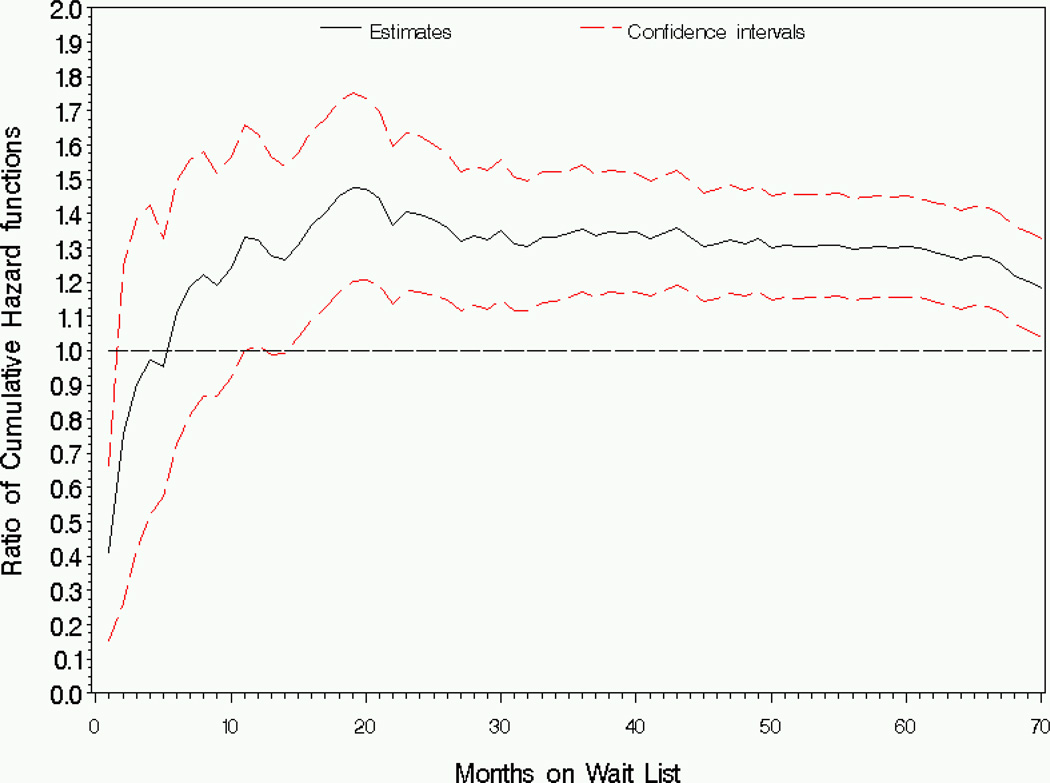
We evaluated the race effect over the [0,70] month interval. Within approximately one month after wait listing, Caucasians had significantly lower cumulative hazard of death than African Americans (Figure 1).

Figure 1.

Analysis of wait list mortality by race: Estimator and 95% pointwise confidence intervals for the ratio of cumulative hazard functions (Caucasian/African American), ϕ₁(t).

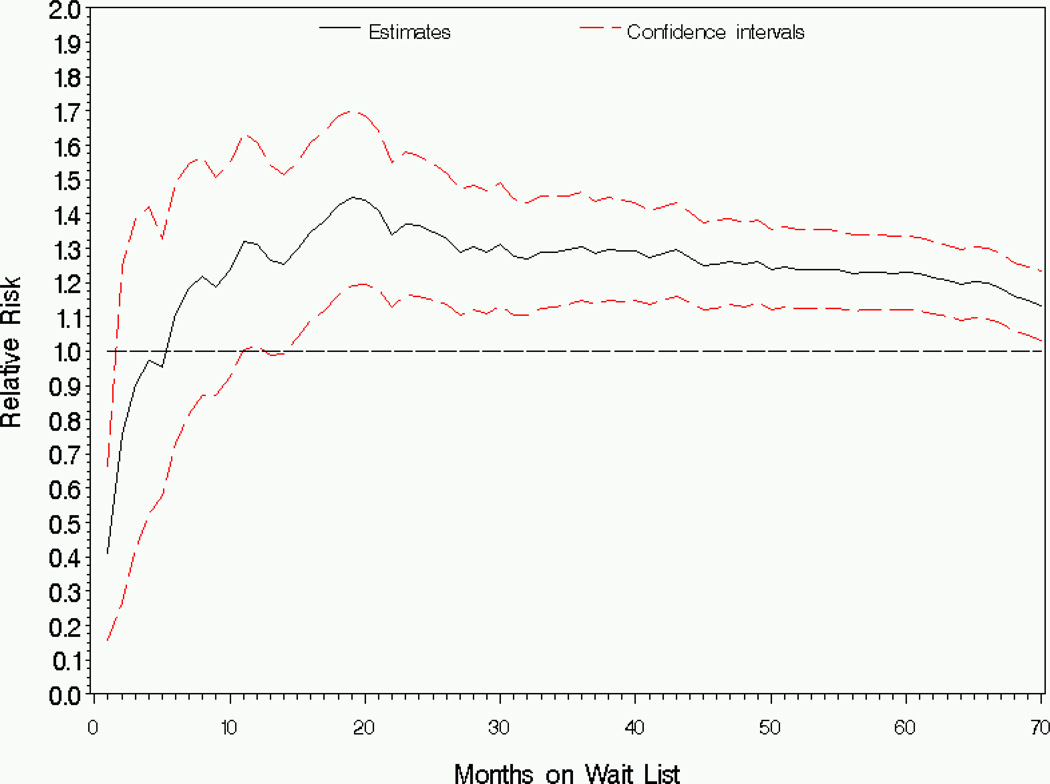
Compared to African Americans, the cumulative hazard for Caucasians is lower at the very beginning of follow-up, but is significantly higher comparing after approximately 11 months with ratio of cumulative hazards ranging from ϕ̂₁(t) = 1:18 to ϕ̂₁(t) = 1:47. The pattern of the estimated relative risk is similar to the ratio of cumulative hazards (Figure 2).

Figure 2.

Analysis of wait list mortality by race: Estimator and 95% pointwise confidence intervals for the risk ratio (Caucasian/African American), RR₁(t).

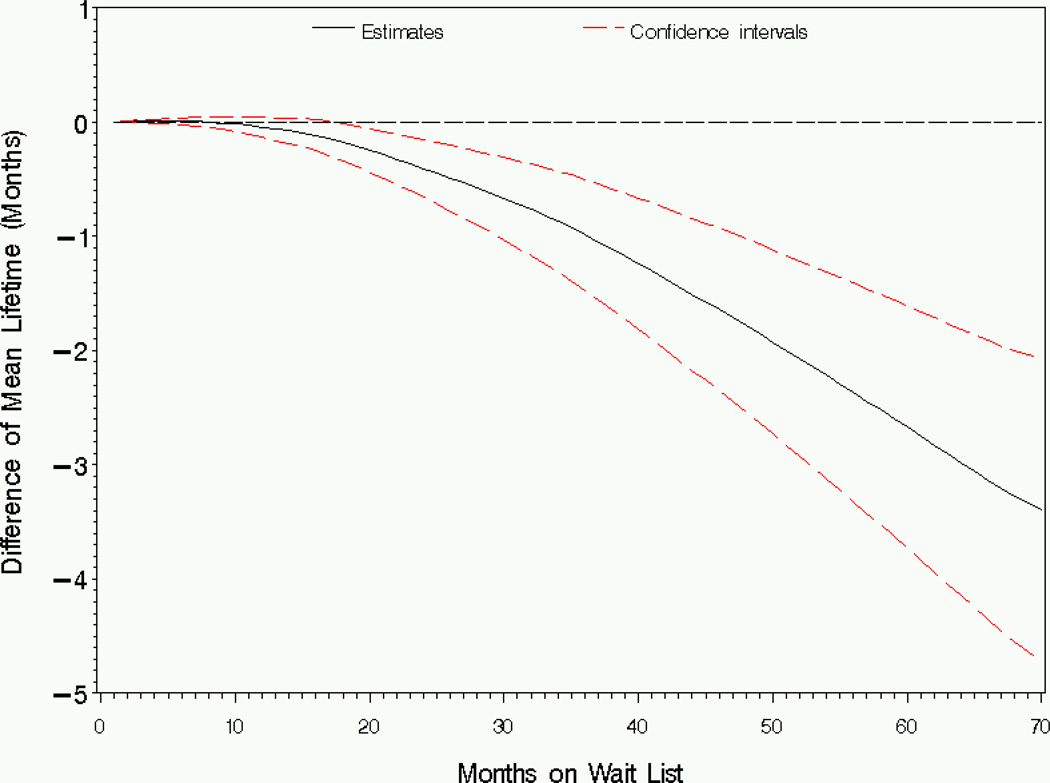
Figure 3 shows that Caucasians have shorter restricted mean lifetime than African Americans based on the first 8 months after wait-listing. The difference in restricted mean lifetime is significant after 18 months of wait-listing, with the estimated difference ranging from Δ̂₁(t) = −0:17 months to Δ̂₁(t) = −3:39 months comparing Caucasians to African Americans.

Figure 3.

Analysis of wait list mortality by race: Estimator and 95% pointwise confidence intervals for the difference in restricted mean lifetime (Caucasian-African American), Δ₁(t).

Supplementary analysis is provided in the Web Appendix. We examine 4 different estimators of each of ϕ₁(t) (Web Figure 1), RR₁(t) (Web Figure 2) and Δ₁(1) (Web Figure 3): the proposed IPTW/IPCW estimator (denoted by the solid line); an IPTW estimator (long dashes); an IPTW estimator adjusted for age only (short dashes); and an unadjusted estimator (dotted line). There is not much difference between IPTW/IPCW and IPTW estimators, implying that the dependent censoring was not strong. There was a considerable difference between the unadjusted and IPTW estimator, indicating that substantial confounding was controlled by the baseline adjustment covariate, Z_i(0). There was only a slight discrepancy between the Z_i(0)- and age-adjusted IPTW estimators, indicating that the majority of the covariate adjustment due to Z_i(0) was actually through age alone. Comparing Web Figures 1–3, the discrepancy between the four estimators was most pronounced for Δ̂₁(t). This makes sense in that, although both ϕ₁(t) and RR₁(t) are cumulative in nature, Δ₁(t) involves an integration of quantities from each.

6. Discussion

In this article, we propose methods for estimating the cumulative treatment effect when the proportional hazards assumption does not hold. Through double inverse weighting, the proposed estimators adjust for discrepancies in treatment-specific baseline covariate distributions and overcome dependent censoring. Simulation studies show that the proposed estimators are approximately unbiased and that the bootstrap standard errors perform well in finite samples.

An alternative to the methods we propose is the G-computation method (Robins, 1986, 1987). The fact that this method requires specification of a model for the longitudinal covariate process may be considered a disadvantage in settings where the longitudinal covariate is of no inherent interest, or is difficult to model. A parallel disadvantage of our proposed methods is the requirement to model the dependent censoring process. Since methods for such modeling are well-established, such modeling will typically be straightforward. However, the dependent censoring process may be of little interest. Moreover, the inverse weighting may lead to instability, a phenomenon which has no analog in the G-computation method. Note that, in many practical applications, models for the both the longitudinal and dependent censoring processes will in fact be of clinical relevance. For instance, with respect to the end-stage renal disease data analyzed in Section 5, hospitalization history represents an important outcome which, arguably, has received insufficient attention in the nephrology literature. Further, the time-until-transplant model is of interest since there are relatively few published rigorous analyses of the factors affecting transplant rates.

Applying our methods to kidney wait list survival data, we found that the effect of race (Caucasian vs. African American) is time dependent. The cumulative hazard and risk of death are significantly higher for Caucasians relative to African Americans 11 months after wait listing, while Caucasians have significantly shorter (3.39 months shorter) restricted mean lifetime based on the first 70 months after wait listing. The difference in restricted mean lifetime is statistically significant in the long term, although not of clinical importance.

It is likely that race is associated with unmeasured factors which predict kidney wait list death and that, as a result, our estimates of the race effect may be subject to residual bias. However, a few points are important in this regard. First, we are not trying to separate the biological/genetic factors associated with race from the socioeconomic. The proposed methods are designed to elicit valid (and perhaps associational as opposed to causal) estimators of group-specific contrasts. Second, the threat of unmeasured confounders is likely less than if race groups from the general population were being compared. Since all members of the study population have end-stage renal disease, the variability of mortality risk factors is likely less variable than in the general population. Third, although the SRTR database does not have information on every mortality risk factor, it has the most important factors (e.g., age, diabetes status). The nature of the information collected by patients is not decided haphazardly, since the SRTR database is used to build models to compare center-specific mortality to the national average. Fourth, the degree of association between any missing mortality predictors and race (i.e., after adjusting for the measured baseline covariate) is questionable; as is the degree to which such factors predict mortality after adjusting for race and Z_i(0). Fifth, supplementary analysis revealed that most of the confounding adjusted by Z_i(0) was via age alone. Although far from proving its absence, the hypothesis of meaningful bias due to unmeasured confounders is weakened by the fact that confounding due to the “usual suspects” was adjusted away by age alone.

As implied in the preceding paragraph, our supplementary analysis pertaining to residual confounding was predicated on measured covariates being at least as strong confounders as the unmeasured covariates. More formal methods exist for evaluating unmeasured confounding, and the sensitivity analysis area has received considerable attention in the last decade. For example, Lin et al (1998) developed methods for both logistic and Cox regression, through which bias-corrected regression parameter estimators are computed from the uncorrected counterparts. Robins, Rotnitzky and Scharfstein (1999) proposed sensitivity analysis methods for marginal structural models (see also Brumback at et, 2004). Such methods involve removing the impact of the unmeasured confounder through bias-corrected versions of the response variates. Chiba (2010) proposes that different techniques are appropriate for bias-correction if the causal risk ratio (as opposed to risk difference) is being estimated. Klungsor et al (2009) developed sensitivity analysis method for the causal hazard ratio estimated through marginal structural Cox models; the methods involve bias correction that is incorporated as a treatment-specific offset. It is possible that the methods of Klungsor et al (2009) could be applied to our setting, in which case the bias-correction offsets would be used to compute corrected weighted Nelson-Aalen estimators. Several other forms of sensitivity analyses are available. Brumback et al (2004) describe the use of methods such as those described above as perhaps preliminary steps on the way to a full Bayesian analysis (e.g., Greenland, 2005). Further, McCandless, Gustafson and Levy (2007) described yet another layer of sensitivity analysis by formally incorporating uncertainty in the assumed prior distributions.

The consistency of the estimators proposed in this article requires the consistency of the double inverse weight. Therefore, misspecification of the logistic model for treatment or the proportional hazards model for censoring may result in bias for the treatment effect estimators. It has been suggested that models used for IPTW and IPCW contain a rich set of covariates, comparing the pitfalls of omitting important covariates with those of including non-significant covariates. The magnitude of the bias introduced by model misspecification would depend on number of covariates mis-modeled, the strength of their association with both the treatment and failure time, and their variability in the study population. The impact of misspecifying the IPCW model would also depend on the percentage of subjects censored. In practice, when very few subjects are censored in the sample, it may not be worthwhile to use IPCW, since the weight estimator will have little precision, and since little bias would result from dependent but infrequent censoring. Diagnostic methods are well-established for the logistic model (Hosmer and Lemeshow, 1989) and the Cox model (Klein and Moeschberger, 2003).

In the proposed inverse weight, the IPTW and IPCW components are the unstabilized versions. Stabilization in its usual form (e.g., Hernan et al, 2000; Robins et al, 2000) may not be feasible in our setting since the estimators do not condition on the baseline covariate, Z_i(0) of which the stabilization factor is typically a function. However, it may be possible to develop augmented estimators along the lines of Robins, Rotnitzsky and Zhao (1994) which could offer improved efficiency and robustness.

Inference at some specific time point, or small set of time points, can be based on the point-wise confidence intervals we propose. The rationale for our presenting each estimator as a process is to satisfy different investigators who may have different opinions on the appropriate truncation time. If simultaneous inference is desired, confidence bands can be constructed as in several previous articles, including Wei and Schaubel (2008).

Appendix

Functions listed in Theorem 1

Definitions for the functions used in Theorem 1 are as follows.

$$\begin{array}{cc}\hfill {\psi }_i^G(\beta )& ={\displaystyle \sum _{j=1}^J}{\mathbf{X}}_{\mathit{\text{ij}}}[G_{\mathit{\text{ij}}}-p_{\mathit{\text{ij}}}(\beta )]\hfill \\ \hfill {\psi }_i^C({\mathit{\theta }}_0)& ={\displaystyle {\int }_0^{\tau }}\{{\mathbf{Z}}_i^C(t)-{\overline{\mathbf{z}}}_C(t,{\mathit{\theta }}_0)\}{\mathit{\text{dM}}}_i^C(t)\hfill \\ \hfill {\mathbf{h}}_j(t)& =E[{\displaystyle {\int }_0^t}\frac{w_i^C(s,{\mathit{\theta }}_0){\mathbf{a}}_{\mathit{\text{ij}}}({\beta }_0)}{r_j^{(0)}(s,{\beta }_0,{\mathit{\theta }}_0)}{\mathit{\text{dN}}}_{\mathit{\text{ij}}}^D(s)]\hfill \\ \hfill {\mathbf{a}}_{\mathit{\text{ij}}}(\beta )& =I(G_i>0)[\frac{{\displaystyle {\sum }_{k=1}^J}\text{ exp}\{{\beta }^T{\mathbf{X}}_{\mathit{\text{ik}}}\}{\mathbf{X}}_{\mathit{\text{ik}}}}{\text{exp}\{{\beta }^T{\mathbf{X}}_{\mathit{\text{ij}}}\}}-{\mathbf{X}}_{\mathit{\text{ij}}}{p}_{\mathit{\text{ij}}}^{-1}(\beta )]+G_{i0}{\displaystyle \sum _{k=1}^J}\text{exp}\{{\beta }^T{\mathbf{X}}_{\mathit{\text{ik}}}\}{\mathbf{X}}_{\mathit{\text{ik}}}\hfill \\ \hfill {\mathbf{d}}_j(t)& =E[{\displaystyle {\int }_0^t}\frac{{\mathbf{r}}_j^{(\beta )}(s;\beta ,\mathit{\theta })}{r_j^{(0)}(s;\beta ,\mathit{\theta })}d{\mathrm{\Lambda }}_j(s)]\hfill \\ \hfill {\mathbf{r}}_j^{(\beta )}(s;\beta ,\mathit{\theta })& =E[Y_{\mathit{\text{ij}}}(t)w_{\mathit{\text{ij}}}^G(\beta )w_i^C(s;\mathit{\theta }){\mathbf{a}}_{\mathit{\text{ij}}}(\beta )]\hfill \\ \hfill {\mathbf{g}}_j(t)& =E[{\displaystyle {\int }_0^t}{w}_{\mathit{\text{ij}}}^G({\beta }_0)w_i^C(s;{\mathit{\theta }}_0)r_j^{(0)}{(s;{\beta }_0,{\mathit{\theta }}_0)}^{-1}{\mathbf{b}}_i(s){\mathit{\text{dN}}}_{\mathit{\text{ij}}}^D(s)]\hfill \\ \hfill {\mathbf{b}}_i(s,{\mathit{\theta }}_0)& ={\displaystyle {\int }_0^s}\text{exp}\{{\mathit{\theta }}_0^T{\mathbf{Z}}_i^C(u)\}\{{\mathbf{Z}}_i^C(u)-{\overline{\mathbf{z}}}_C(u)\}d{\mathrm{\Lambda }}_0^C(u)\hfill \\ \hfill {\mathbf{f}}_j(t)& ={\displaystyle {\int }_0^t}\frac{{\mathbf{r}}_j^{(\theta )}(s;{\beta }_0,{\mathit{\theta }}_0)}{r_j^{(0)}(s;{\beta }_0,{\mathit{\theta }}_0)}d{\mathrm{\Lambda }}_j(s)\hfill \\ \hfill {\mathbf{r}}_j^{(\theta )}(s;\beta ,\mathit{\theta })& =E[Y_{\mathit{\text{ij}}}(s)w_{\mathit{\text{ij}}}^G(\beta )w_i^C(s;\mathit{\theta }){\mathbf{b}}_i(s)]\hfill \\ \hfill q_j(s,t)& =E[\text{exp}\{{\mathit{\theta }}_0^T{\mathbf{Z}}_i^C(u)\}{\displaystyle {\int }_u^t}\frac{w_{\mathit{\text{ij}}}^G({\beta }_0)w_i^C(s;{\mathit{\theta }}_0)}{r_j^{(0)}(s;{\beta }_0,{\mathit{\theta }}_0)}{\mathit{\text{dN}}}_{\mathit{\text{ij}}}^D(s)].\hfill \end{array}$$