Population Growth Enhances the Mean Fixation Time of Neutral Mutations and the Persistence of Neutral Variation

Abstract

A fundamental result of population genetics states that a new mutation, at an unlinked neutral locus in a randomly mating diploid population, has a mean time of fixation of ∼4N_e generations, where N_e is the effective population size. This result is based on an assumption of fixed population size, which does not universally hold in natural populations. Here, we analyze such neutral fixations in populations of changing size within the framework of the diffusion approximation. General expressions are derived for the mean and variance of the fixation time in changing populations. Some explicit results are given for two cases: (i) the effective population size undergoes a sudden change, representing a sudden population expansion or a sudden bottleneck; (ii) the effective population changes linearly for a limited period of time and then remains constant. Additionally, a lower bound for the mean time of fixation is obtained for an effective population size that increases with time, and this is applied to exponentially growing populations. The results obtained in this work show, among other things, that for populations that increase in size, the mean time of fixation can be enhanced, sometimes substantially so, over 4N_e,0 generations, where N_e,0 is the effective population size at the time the mutation arises. Such an enhancement is associated with (i) an increased probability of neutral polymorphism in a population and (ii) an enhanced persistence of high-frequency neutral variation, which is the variation most likely to be observed.

HOW are properties of mutations at neutral loci, such as the mean time of fixation, modified when population size is not constant? The answer to this question directly influences the persistence of neutral variation in a population and the probability of neutral polymorphism. To put the question in context, we note that the genomes of many organisms contain loci and sites that can be described as neutral, with most substitutions seeming to have a neutral effect on the fitness of the host organism (see, e.g., Kimura 1983; Gillespie 1994, Chap. 6; Nei et al. 2010).

When mutation produces a new allele, its long-term outcome (neglecting additional mutations) is either loss or fixation. Henceforth, we restrict attention to mutations at unlinked neutral loci in randomly mating diploid populations. Typically, a new allele at such a locus does not achieve high relative frequencies and becomes lost in a short time (Kimura and Ohta 1969; Crow and Kimura 1970). A rarer outcome is fixation, which typically takes a relatively long time to occur. With N_e the (variance) effective population size, alleles that start at low relative frequencies take a mean time to fix of ∼4N_e generations (Kimura and Ohta 1969), under the implicit assumption that the effective population size is constant. An allele that fixes generally achieves intermediate and high relative frequencies on the way to fixation and hence contributes to the neutral variation of the population for a time of the order of the mean fixation time. Related to this is neutral polymorphism, which arises from recurrent neutral mutation and random genetic drift. The likelihood of observing neutral polymorphism in a population is governed by the size of the product of mean fixation time and neutral genomic mutation rate (Kimura 1983). Thus there are direct ways the mean fixation time affects a population.

The above ideas form a standard part of our understanding of neutral mutations and connect with a larger body of work describing the effects of random genetic drift at the gene and molecular levels (Crow and Kimura 1970; Kimura 1983). Here we present an analysis of random genetic drift in situations involving neutral fixation in populations of changing size. Such an analysis is required to establish how fundamental results, such as the “4N_e” result for the mean time to fixation, become modified when population size is not constant and whether such results have an impact on neutral effects in a population.

Background

Fixation is a process that takes a random time to occur. For an unlinked neutral locus, the distribution of fixation times is approximately known when population size is constant (Kimura and Ohta 1969). It is recognized, however, that the assumption of fixed population size does not universally hold. Many natural populations have a size that significantly changes over time. In a study of the effects of changing population size on the fixation of nonneutral mutations, Otto and Whitlock (1997) listed the following as possible reasons for changing population numbers in the wild: (i) varying physical conditions, (ii) resource availability, (iii) habit availability, (iv) predator density, and (v) human disturbance. Human beings constitute an example of a population whose size is changing at a varying rate of growth.

To illustrate some of the issues associated with changing population size, let us consider examples involving fixation of a neutral allele.

Examples

Assume first that a single mutant allele arises in a population of fixed size N and that the allele ultimately fixes. From the first appearance of the allele to its fixation, which we assume takes T generations, all 2N resident alleles of the population are lost (strictly, the number lost is 2N − 1, given one initial mutant allele) and are replaced by mutant alleles. The disappearance of resident alleles thus occurs at an average rate of 2N/T alleles per generation. Using the estimate T = 4N_e generations leads to an average rate of loss of resident alleles of N/(2N_e) alleles per generation. This simple picture becomes complicated if the mutant allele arises and goes to fixation in a population of changing size. To see this, consider a population whose size always remains close to its carrying capacity, which, for reasons external to the population, changes with time. We assume the carrying capacity exhibits the simplest nontrivial behavior, namely a linear change for a limited period of time. During this limited period, the population size is given by N(t) = N₀ + γt, where γ is the constant rate of change of population size. We consider the implications of population sizes that either decrease (γ < 0) or increase (γ > 0).

Generally, the effective population size at any time t, written N_e(t), will change over time. For the purposes of this example, we assume the simplest relation between the actual and effective population sizes and take N_e(t) = constant × N(t). Such an assumption is consistent with results from static populations. For example, in a population with a biased sex ratio, the quantity N/N_e depends solely on the sex ratio (see, e.g., Gillespie 2004, p. 49).

Let us now consider a mutant allele that arises at time t = 0 and that ultimately fixes in a population of linearly changing size. Fixation of the mutant allele occurs when all resident alleles are lost. We thus focus on the overall rate of loss of resident alleles, which arises from a sum of two terms: (i) a contribution caused by population size changes and (ii) a contribution arising from loss of the alleles due to random genetic drift.

In the early stages of the fixation process, residents comprise the vast majority of individuals in the population, and a rate of change of population size of γ (which may be positive or negative) closely corresponds to resident alleles changing at the rate of 2γ alleles per generation and hence of resident alleles being lost at the rate of −2γ alleles per generation. Thus we take −2γ as the contribution of population size change to the overall rate of loss of resident alleles; it may be positive or negative, depending on the sign of γ.

In a population of constant size, the rate of loss of resident alleles, due to random genetic drift, was estimated above to be N/(2N_e) alleles per generation. In a changing population, the corresponding rate of loss of resident alleles will generally differ from this result, but we use N/(2N_e) as an estimate of this rate.

Under population decrease (γ < 0) the contributions to the overall rate of loss of resident alleles, from random genetic drift and population size change, are N/(2N_e) and −2γ ≡ 2|γ|, respectively, and are both positive. As a consequence the instantaneous rate of loss of resident alleles, when the population size is N, will typically be faster than that of a population of fixed size N.

Under population increase (γ > 0), the overall rate of loss of resident alleles has a negative contribution from population size change (estimated above to be −2γ) and a positive contribution from random genetic drift [estimated above to be N/(2N_e)]. Thus when the population size is N, the total rate of loss of resident alleles is ∼N/(2N_e) − 2γ, i.e., slower than that of a population of fixed size N. A particularly interesting regime is where the rate of loss of resident alleles due to random genetic drift can be overcome by the effect of population size increase, which increases the number of resident alleles. This will occur when γ is sufficiently large compared with N/N_e that the number of resident alleles does not decrease but typically changes at a net positive rate, i.e., increases. We should then expect that fixation could take much longer to occur. Indeed if the population growth persisted at such a rate indefinitely, the mean time to fixation could, plausibly, become infinite.

From the above examples it is reasonable to infer that the mean time to fixation is generally sensitive to a changing population size.

Methods

To address the issue of neutral fixation in a changing population, we separate the problem into two components:

• i. The first component is a statistic, associated with fixation, which has the properties that its distribution is independent of the pattern of population-size changes over time. The statistic introduced has a distribution that depends on a single parameter (the initial frequency of the mutant allele).

• ii. The second component is a function that encapsulates the way that population size changes over time. This function is independent of the fixation time.

In this way we cleanly separate a common feature of fixation (the distribution of the statistic introduced here) from the pattern of size changes of the particular population under consideration.

Model

Consider an unlinked neutral locus within the genome of a randomly mating diploid population with discrete generations. We assume the population-size changes over time, such that in generation t there are N(t) adults. The processes that lead from the adults of one generation to the adults of the next generation are taken to be (i) reproduction, shortly followed by the death of all adults; (ii) viability selection; and (iii) nonselective ecological thinning (which is required, on the assumption that more individuals survive selection than can be supported by the environment). The thinning process reduces the number of individuals in the population to the N(t + 1) adults of the next generation. It is step iii where random genetic drift can be identified as occurring. Alternative assumptions about step iii may alter the way random genetic drift affects the population.

Associated with random genetic drift is the variance effective population size (Ewens 2004), which we assume also changes with time. The variance effective population size in generation t is denoted by N_e(t). This is determined from an averaging over processes that occur in a single generation. Throughout this work we use N_e(t) to refer only to such a local quantity, that is, one associated with generation t. In particular, we do not make use of averages of the effective population size (such as the harmonic mean) that summarize properties of the effective population size over multiple generations and hence reflect population-size information that is nonlocal in time. For generality, we leave the relation between the actual population size, N(t), and the effective population size, N_e(t), arbitrary. It is very natural, however, to regard the effective population size as a proxy for the actual population size and hence assume that changes in N(t) are accompanied by closely related changes in N_e(t).

The question we address concerns features of the fixation process when the actual and effective population sizes have known historical variation over time. Thus we view N(t) and N_e(t) as being completely determined and not having any stochasticity. Accordingly, it would be inappropriate to carry out any averaging over these functions. Addressing questions of a different nature may require population-size averaging (see, e.g., Parsons and Quince 2007; Engen et al. 2009; Parsons et al. 2010; Uecker and Hermisson 2011; Waxman 2011c).

Let the locus in question have two alleles, denoted A and a, with a the wild-type allele and Α a mutant allele that is the focus of interest.

In the adults of generation t, the proportion of all genes at the locus that are allele A, written X(t), is the relative frequency of the A allele (henceforth termed the frequency). The frequency X(t) generally exhibits random variation over time, due to the uncertainties of individuals contributing their genes to the following generation. The statistical properties of X(t) can be obtained by considering many different replicates of a population with identical population-size behaviors. Initially, all replicates start with the same frequency of the A allele, but after the initial time different replicates may, due to stochasticity of the dynamics, have different values of the frequency. An extension of the Wright–Fisher model (Fisher 1930; Wright 1931), which takes into account changes in population size over time, can be used to calculate statistical results for X(t), but this is mathematically complicated and normally leads only to numerical results. To make theoretical progress we perform an analysis on the basis of the diffusion approximation, where time t and frequency X(t) are both treated as continuous quantities. The frequency X(t) becomes a continuous random variable and is described by a probability density whose value at frequency x and time t is f(x, t). The diffusion approximation derives its name from the diffusion equation governing f(x, t). For an unlinked neutral locus in a randomly mating diploid population this reads −∂f(x, t)/∂t = −[4N_e(t)]⁻¹ ∂²[x(1−x)f(x,t)]/∂x² (Crow and Kimura 1970), where, as stated above, N_e(t) is the effective population size that is appropriate for generation t.

Let the A allele have a frequency of y at the time of its initial appearance, which we take throughout this work to be t = 0. Thus if n copies of the A allele are present in a population at the initial time, then the initial frequency is given by y = n/(2N(0)). At large times the A allele will have either fixed, with probability y, or been lost, with probability 1 − y. These probabilities hold irrespective of the way that the effective population size changes after appearance of the mutation (see Appendix A).

Statistic

More complex information about the evolutionary process is contained in the description of the random time it takes for fixation or loss of the A allele to occur. If fixation ultimately occurs, the random time to fixation, denoted T_fix, has a probability distribution that depends on the behavior of the effective population size over time. We have found it advantageous to work with a statistic that is associated with the fixation time, but whose distribution is independent of the behavior of N_e(t), and hence has an invariant form. The statistic, denoted R, is defined by

$$R={\displaystyle {\int }_0^{T_{\text{fix}}}\frac{dv}{4N_{\text{e}}\left(v\right)}}$$ (1)

and explicitly involves T_fix. In Appendix B we establish that under the diffusion approximation, the statistic R has the property that its distribution depends upon just one parameter, namely the frequency of the A allele at its time of appearance (t = 0). Let us briefly note the implications of this property for two populations where the A allele starts with the same initial frequency and ultimately fixes, but the two populations have different effective sizes over time. Despite differences in N_e(t), all statistical properties of the two populations that do not explicitly depend on N_e(t) and involve only R (for example, the mean or variance of R) will be identical for both populations. The independence of the distribution of R on the behavior of N_e(t) contrasts sharply with statistical properties of fixation times, which will generally be different for the two populations. Before we illustrate the different statistical properties of the fixation time in populations with different N_e(t), it is necessary to fully characterize R.

Generally, all statistical properties of R are summarized by its cumulative distribution function, F_y(r), which depends on the initial frequency (y) as a parameter. The cumulative distribution function is defined as the probability

$$F_y\left(r\right)=\text{Prob}\left(R\hspace{0.17em}\le \hspace{0.17em}r|X\left(0\right)=y\right)$$ (2)

with 0 ≤ r < ∞. In Appendix B we establish that the diffusion approximation yields

$$F_y\left(r\right)\hspace{0.17em}\mathrm{\simeq }\hspace{0.17em}1-2\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{n=0}}\frac{\left(1-y\right)\left(2n+3\right)}{\left(n+1\right)\left(n+2\right)}{\left(-1\right)}^n{C}_n^{\left(3/2\right)}\left(1-2y\right)e^{-\left(n+1\right)\left(n+2\right)r},$$ (3)

where $C_n^{\left(3/2\right)}\left(y\right)$ is a particular polynomial of y [a Gegenbauer polynomial of order 3/2 and degree n (Abramowitz and Stegun 1964)]. In the practically important case of low initial frequencies (y → 0) we write the cumulative distribution as F₀(r) and this has the simple approximation

$$F_0\left(r\right)\hspace{0.17em}\mathrm{\simeq }\hspace{0.17em}\{\begin{array}{l}{\left(\frac{\pi }{r}\right)}^{3/2}{e}^{r/4-{\pi }^2/4r},\hspace{1em}\hspace{0.5em}0\hspace{0.17em}\le \hspace{0.17em}r\hspace{0.17em}\le \hspace{0.17em}2\\ 1-3\hspace{0.17em}{e}^{-2\hspace{0.17em}r},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}r>2\end{array}$$ (4)

(see Appendix B). The expressions in Equations 3 and 4 follow from existing results in the literature (Kimura 1955; Waxman 2011b).

For an initial frequency of y, the mean and variance of R are written as E_y[R] and Var_y(R). These have simple forms under the diffusion approximation (see Appendix C for details):

$$E_y\left[R\right]={\displaystyle {\int }_0^{\mathrm{\infty }}\left[1-F_y\left(r\right)\right]}dr\hspace{0.17em}\mathrm{\simeq }-\frac{\left(1-y\right)\text{ln}\left(1-y\right)}{y}$$ (5)

and

$$\begin{array}{l}{\text{Var}}_y\left(R\right)\hspace{0.17em}\mathrm{\simeq }\hspace{0.17em}\frac{2\left(1-y\right)\text{ln}\left(1-y\right)}{y}-{\left(\frac{\left(1-y\right)\text{ln}\left(1-y\right)}{y}\right)}^2\\ \hspace{1em}+\hspace{0.5em}\frac{{\pi }^2}{3}-2\hspace{0.17em}\text{dilog}\left(1-y\right),\end{array}$$ (6)

where $\text{dilog}\left(x\right)={\displaystyle {\int }_1^x\text{(ln}\left(u\right)/(1-u))} du$ denotes the dilogarithm function (Abramowitz and Stegun 1964).

The results of Equations 5 and 6 reduce, in the limit of small y (y → 0), to E₀[R] = 1 and Var₀(R) ≃ (π²/3 − 3).

In Appendix D we use simulations and the results of Equations 5 and 6 to illustrate the prediction of the diffusion approximation, that statistical properties of R depend only on the initial frequency of the A allele and not on the behavior of the effective population size.

Results

Statistical properties of the time to fixation

Equation 1 relates the statistic R to another random quantity—the fixation time, T_fix. Equation 1 can always be solved (by either analytical or numerical methods) to yield T_fix as a function of R and we write this relation as

$$T_{\text{fix}}=h\hspace{0.17em}\left(R\right).$$ (7)

Expectations involving the fixation time follow from knowledge of h(r) and F_y(r). For example, with a an arbitrary positive number, the mean of (T_fix)^a, namely E_y[(T_fix)^a], can be written as $E_y\left[{\left(T_{\text{fix}}\right)}^a\right]\mathrm{\simeq }{{\displaystyle {\int }_0^{\mathrm{\infty }}\left[h\left(r\right)\right]}}^{\mathit{a}}\left[\partial F_y\left(r\right)/\partial r\right]dr$. This result can be used to derive expressions for statistical properties of T_fix such as its mean and variance (see Appendix E for details). In particular, the mean and the variance of the time to fixation are given by

$$E_y\left[T_{\text{fix}}\right]\hspace{0.17em}\mathrm{\simeq }{\displaystyle {\int }_0^{\mathrm{\infty }}h\left(r\right)}\frac{\partial F_y\hspace{0.17em}\left(r\right)}{\partial r}\hspace{0.17em}dr={\displaystyle {\int }_0^{\mathrm{\infty }}4N_{\text{e}}\left(h\left(r\right)\right)\left[1-F_y\left(r\right)\right]dr}$$ (8)

$$\begin{array}{l}{\text{Var}}_y\left(T_{\text{fix}}\right)=2{\displaystyle {\int }_0^{\mathrm{\infty }}h}\left(r\right)\frac{dh\left(r\right)}{dr}\hspace{0.17em}\left[1-F_y\left(r\right)\right]dr\\ \hspace{1em}-{\left({\displaystyle {\int }_0^{\mathrm{\infty }}\frac{dh\left(r\right)}{dr}}\hspace{0.17em}\left[1-F_y\left(r\right)\right]dr\right)}^2.\end{array}$$ (9)

Equation 8 is the generalization of the constant population result to effective population sizes that are time dependent.

When the effective population size is constant, Equation 8 leads to E_y[T_fix] ≃ −4N_e × (1 − y)ln(1 − y)/y and for a small initial frequency (y → 0) this result reduces to the standard result E₀[T_fix] ≃ 4N_e (Kimura and Ohta 1969). Furthermore, for a constant population size and y → 0, the variance reduces to the known result Var₀(T_fix) ≃ (π²/3 − 3) × (4N_e)² (Kimura 1970).

The form of the function h(r), which appears in Equations 7–9 and relates T_fix to R, depends specifically on the history of N_e(t), from the time the mutant allele appears (at t = 0) onward. We next provide details of two examples, following from known forms of N_e(t), to illustrate the behavior of the mean and variance of T_fix. We also present two different inequalities for E_y[T_fix] that do not require knowledge of the full history of N_e(t). One inequality applies when N_e(t) is known to lie within a finite range of values for all times, and the other inequality provides a lower bound on E_y[T_fix] when the population size increases over time.

Examples

Example 1:

For the first example, consider the situation where N_e(t) has a discontinuous jump in size at time τ (see curve b in Figure D1, Appendix D):

$$N_{\text{e}}\left(t\right)=\{\begin{array}{l}{N}_{\text{e,0}},\hspace{1em}t\hspace{0.17em}\le \hspace{0.17em}\tau ,\\ N_{\text{e,1}},\hspace{1em}t\hspace{0.17em}>\hspace{0.17em}\tau .\end{array}$$ (10)

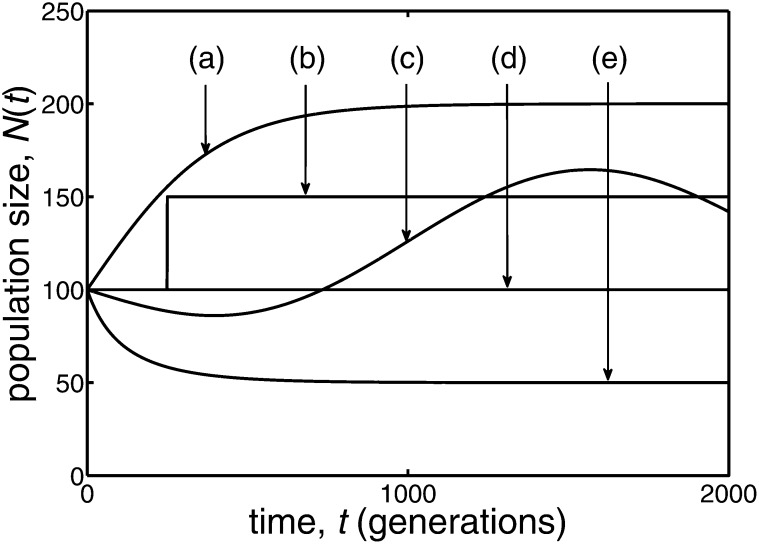
Figure D1 .

Five quite different examples of population size behavior, N(t), are illustrated. In all cases the initial population size was 100. Case a corresponds to logistic growth, with an intrinsic growth rate of 1/200 and the population size eventually doubling to 200. In case b the population discontinuously jumps to 150 individuals at generation 250, while case c has a variable population size that was derived from the sum of a constant and several different sine functions. In case d the population size remains constant, while in case e the population undergoes logistic decay, with an intrinsic decay rate of 1/200 and the population size eventually halving to 50.

In Appendix F it is shown that Equations 1, 7, and 8 lead to a mean fixation time of

$$E_y\left[T_{\text{fix}}\right]\hspace{0.17em}\mathrm{\simeq }\hspace{0.17em}4N_{\text{e,0}}{\displaystyle {\int }_0^{\rho }\left[1-F_y\left(r\right)\right]}dr+4N_{\text{e,1}}{\displaystyle {\int }_{\rho }^{\mathrm{\infty }}\left[1-F_y\left(r\right)\right]} dr,$$ (11)

where ρ is a measure of the time of population-size jump:

$$\rho =\frac{\tau }{4N_{\text{e,0}}}.$$ (12)

Note that because N_e,0 and N_e,1 are arbitrary, Equation 11 can apply to a population experiencing a sudden expansion (N_e,1 > N_e,0) or a sudden bottleneck (N_e,1 < N_e,0).

In Appendix F we also derive an expression for the variance of T_fix, which has a more complex form than that of Equation 11. To gain intuition about Equation 11, let us consider some informative extreme limits.

If N_e,0 → ∞ with N_e,1 held constant, Equation 11 reduces to E_y[T_fix] = τ + 4N_e,1E_y[R] and corresponds to fixation occurring only after time τ and, then, only from a frequency of y. This has the explanation that an effectively infinite effective population size up to time τ prevents any change of the allele frequency from its initial value; hence fixation occurs only after the population size has become finite. Alternatively, if N_e,1 → ∞ with N_e,0 held constant, then the mean time to fixation diverges. This arises because there is a finite probability that a mutant allele does not fix before time τ; the allele then finds itself in an effectively infinite population and will not fix in any finite time. In the methods presented in this work, this result arises because 4N_e,1, in Equation 11, is multiplied by the finite probability that R will be larger than ρ.

In the limit of low initial frequencies (y → 0), the mean and variance of T_fix become E₀[T_fix] and Var₀(T_fix), respectively, and we can obtain approximations for these quantities. For small, intermediate, and relatively large values of ρ we find that

$$E_0\left[T_{\text{fix}}\right]\mathrm{\simeq }\{\begin{array}{l}\rho \hspace{0.17em}\times \hspace{0.17em}4N_{\text{e,0}}+\left(1-\rho \right)\times 4N_{\text{e,1}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\rho \mathrm{\ll }1,\\ 0.50\hspace{0.17em}\times \hspace{0.17em}4N_{\text{e,0}}+0.50\times 4N_{\text{e,1}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\rho \hspace{0.17em}\mathrm{\simeq }\hspace{0.17em}0.51,\\ 0.80\hspace{0.17em}\times \hspace{0.17em}4N_{\text{e,0}}+0.20\times 4N_{\text{e,1}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.5em}\hspace{0.17em}\rho =1,\\ \left(1-\frac{3e^{-2\rho }}{2}\right)\hspace{0.17em}\times \hspace{0.17em}4N_{\text{e,0}}+\frac{3e^{-2\rho }}{2}\times 4\hspace{0.17em}{N}_{\text{e,1}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\rho \hspace{0.17em}\ge \hspace{0.17em}2\end{array}$$ (13)

(see Appendix F for details.) An inspection of Equation 13 indicates that when the scaled time of population-size jump, ρ, is small (ρ ≪ 1, corresponding to τ ≪ N_e,0), the mean fixation time approximately equals 4N_e,1 and hence is largely determined by the population size achieved at later times. This is naturally attributed to most replicate populations not having fixed the A allele by the time of the population-size jump. The intermediate value of ρ used in Equation 13, namely ρ ≃ 0.51, was chosen so that 4N_e,0 and 4N_e,1 make equal contributions to E₀[T_fix]. The result obtained is very similar to the result obtained by using this value of ρ in the small ρ result in the preceding line. For relatively large values of ρ (ρ ≥ 2, corresponding to τ ≥ 8N_e,0) the mean fixation time approximately equals 4N_e,0 and hence is largely determined by the population size achieved at early times; this is naturally attributed to most replicate populations having fixed the A allele by the time of the population-size jump.

The variance of T_fix can also be approximated for low initial frequencies (y → 0). We find (see Appendix F for details)

$$\begin{array}{l}{\text{Var}}_0\left(T_{\text{fix}}\right)\\ \hspace{1em}\mathrm{\simeq }\{\begin{array}{l}\left(\frac{{\pi }^2}{3}-3\right)\times {\left(4N_{\text{e,1}}\right)}^2,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{1em}\rho \mathrm{\ll }1,\\ 0.27\times {\left(4N_{\text{e,1}}\right)}^2+0.01\times \left(4N_{\text{e,0}}\right)\left(4N_{\text{e,1}}\right),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.5em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\rho \hspace{0.5em}\mathrm{\simeq }\hspace{0.5em}0.51,\\ 0.05\times {\left(4N_{\text{e,0}}\right)}^2+0.08\times \left(4N_{\text{e,0}}\right)\left(4N_{\text{e,1}}\right)+0.16\times {\left(4N_{\text{e,1}}\right)}^2,\hspace{0.17em}\rho =1,\\ \left(\frac{{\pi }^2}{3}-3+\frac{3}{2}\left(1-2\rho \right)e^{-2\rho }\right)\times {\left(4N_{\text{e,0}}\right)}^2+\frac{3}{2}{e}^{-2\rho }\times {\left(4N_{\text{e,1}}\right)}^2,\hspace{0.17em}\rho \hspace{0.5em}\ge \hspace{0.5em}2.\end{array}\end{array}$$ (14)

The variance obtained for ρ ≃ 0.51 is close to the result obtained using this value in the small ρ result (since π²/3 − 3 ≃ 0.29 is close to 0.27). It is somewhat surprising that the variance, when ρ = 1, has the largest weighting given to the later population size (N_e,1), given that the mean of T_fix for this value of ρ (see Equation 13) has the largest weighting given to the contribution of the earlier population size (N_e,0).

Example 2:

For the second example, consider the situation outlined at the start of this article, where the effective population size was assumed to change linearly, for a finite period of time, and then maintain a constant value. We present only the details of an analysis for an increasing population. A formal solution is justified in this case since the issues involved are potentially complex (see Background).

We write

$$N_{\text{e}}\left(t\right)=\{\begin{array}{l}{N}_{\text{e,0}}+{\gamma }_{\text{e}}t,\hspace{1em}t\le \tau ,\\ N_{\text{e,0}}+{\gamma }_{\text{e}}\tau ,\hspace{1em}t>\tau ,\end{array}$$ (15)

where the rate of change, γ_e, is taken to be positive. We find (see Appendix G for details)

$$\begin{array}{l}{E}_y\left[T_{\text{fix}}\right]\hspace{0.5em}\mathrm{\simeq }\hspace{0.5em}4N_{\text{e,0}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{1em}\times \left({\displaystyle {\int }_0^{r_0}{e}^{4{\gamma }_{\text{e}}r}}\left[1-F_y\left(r\right)\right] dr+e^{4{\gamma }_{\text{e}}{\mathit{r}}_0}{\displaystyle {\int }_0^{\mathrm{\infty }}\left[1-F_y\left(r\right)\right]}dr\right),\end{array}$$ (16)

where r₀ = (4γ_e)⁻¹log(1 + γ_eτ/N_e,0). Appendix G contains an expression for the variance of T_fix, which again has a more complex form than that of the mean.

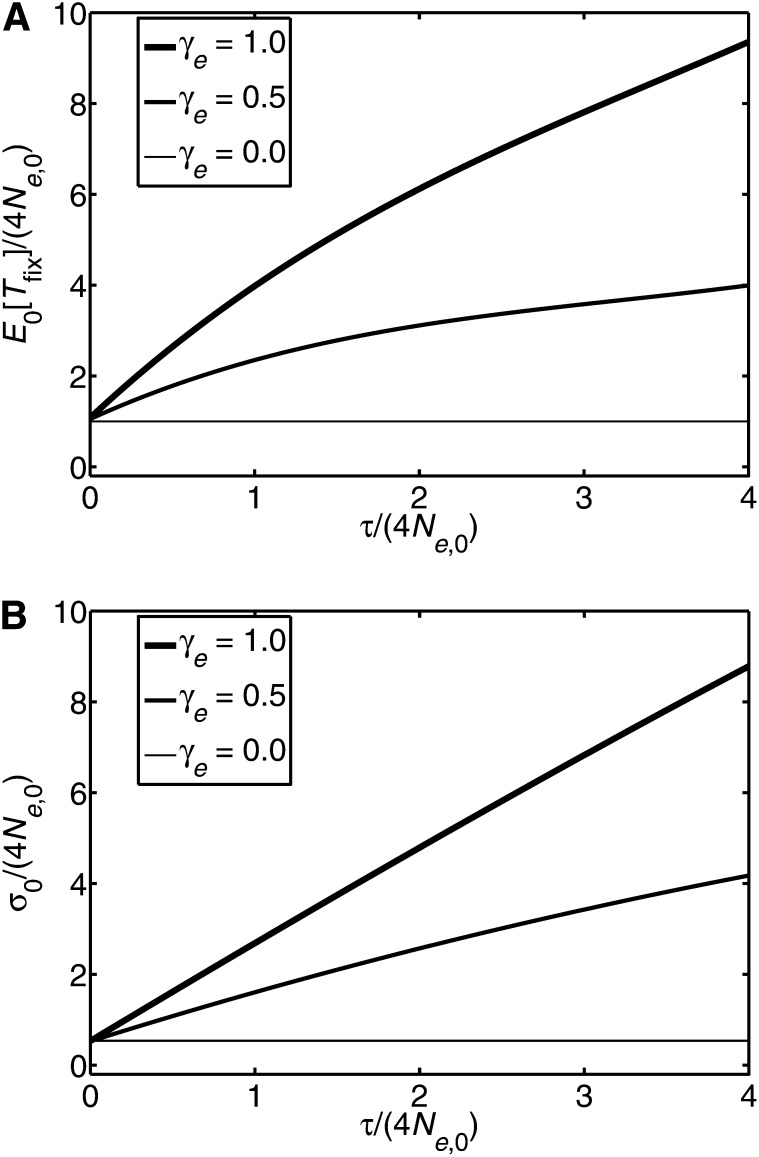
Restricting considerations to low initial frequencies, where the mean and variance of T_fix become E₀[T_fix] and Var₀(T_fix), respectively, the results for these can, using Equation 4, be numerically evaluated. The dependence of E₀[T_fix] on the duration of linear change, τ, is affected by the rate of change of the effective population size, γ_e, as illustrated in Figure 1A. The dependence of the variance on τ is also affected by γ_e, and to facilitate direct comparison with E₀[T_fix], the square root of the variance is plotted as a function of τ in Figure 1B.

Figure 1 .

The case where the effective population size has a period of linear growth of duration τ before remaining constant (Equation 15). (A) Illustration of the behavior of the mean time to fixation, as a function of τ, for mutant alleles with low initial frequency. It follows from Equation 16 that if both γ_eτ/N_e,0 and τ/N_e,0 are small (≪ 1), then E₀[T_fix] ≃ 4N_e(τ) ≡ 4(N_e,0 + γ_eτ); i.e., E₀[T_fix] increases linearly with τ. For larger τ it is apparent from A that E₀[T_fix] increases with τ, but more slowly than linearly. (B) Illustration of the behavior of the square root of the variance, ${\sigma }_0=\sqrt{{\text{Var}}_0\left(T_{\text{fix}}\right)}$, as a function of τ, for mutant alleles with low initial frequency.

Approximate results can also be obtained for the dependence of E₀[T_fix] and Var₀(T_fix) on τ. When γ_e has a fixed value and τ is sufficiently large that it satisfies both ${\gamma }_{\text{e}}\tau /\left(4N_{\text{e,0}}\right)>e^{8{\gamma }_{\text{e}}}-1$ and γ_eτ/(4N_e,0) ≫ 1, we find the following approximate τ dependences:

$$E_0\left[T_{\text{fix}}\right]\hspace{0.5em}\mathrm{\simeq }\hspace{0.5em}{k}_1+k_2{\left(\frac{{\gamma }_{\text{e}}\tau }{N_{\text{e,0}}}\right)}^p$$ (17)

$${\text{Var}}_0\left(T_{\text{fix}}\right)\hspace{0.5em}\mathrm{\simeq }\hspace{0.5em}{k}_3+k_4{\left(\frac{{\gamma }_{\text{e}}\tau }{N_{\text{e,0}}}\right)}^p+k_5{\left(\frac{{\gamma }_{\text{e}}\tau }{N_{\text{e,0}}}\right)}^{2p}+k_6{\left(\frac{{\gamma }_{\text{e}}\tau }{N_{\text{e,0}}}\right)}^{1+p},$$ (18)

where k₁,k₂, … , k₆ are independent of τ and p is the parameter

$$p=\frac{{\gamma }_{\text{e}}-1/2}{{\gamma }_{\text{e}}}$$ (19)

(see Appendix G for details). The three powers of τ appearing in Equations 17 and 18, namely p, 2p, and 1 + p, are all negative for γ_e < 1/4, but for 1/4 < γ_e < 1/2, p and 2p are negative while 1 + p is positive, and for γ_e > 1/2 all three powers are positive. This leads to E₀[T_fix] and Var₀(T_fix) having dependences on τ (when τ is large), which is sensitive to the value of γ_e. When γ_e < 1/4, both E₀[T_fix] and Var₀(T_fix) vary as τ to a negative power, indicating a weak dependence on τ. However, when 1/4 < γ_e < 1/2, it follows that E₀[T_fix] varies as τ to a negative power while Var₀[T_fix] has a term varying as τ to a positive power. Thus the variance has a potentially strong dependence on τ in this regime. Finally, when γ_e > 1/2, both E₀[T_fix] and Var₀(T_fix) vary as positive powers of τ, indicating that both have potentially a strong dependence on τ.

Bounds on the mean

The above results are based on explicit forms for N_e(t). To make use of Equation 8, for the mean time to fixation, requires full knowledge of N_e(t), so that the function h(r) can be determined. We can circumvent the requirement of full knowledge of N_e(t) at the cost of obtaining bounds, not precise values. The bounds obtained are based on the diffusion approximation and hence are not rigorous inequalities for E_y[T_fix]:

1. For the first bound, note that Equation 8 can be written in the alternative form $E_y\hspace{0.17em}\left[T_{\text{fix}}\right]\mathrm{\simeq }4{\overline{N}}_{\text{e}}\times E_y\hspace{0.17em}\left[R\right],$ where E_y[R] is given in Equation 5, and ${\overline{N}}_{\text{e}}$ represents a particular sort of average of N_e(t), namely ${\overline{N}}_{\text{e}}={{\displaystyle \int }}_0^{\mathrm{\infty }}{N}_{\text{e}}\left(h\left(r\right)\right)\left[1-F_y\left(r\right)\right]dr/{{\displaystyle \int }}_0^{\mathrm{\infty }}\left[1-F_y\left(r\right)\right]dr$. If N_e(t) is known to always lie within the range N_e,min to N_e,max it immediately follows that ${\overline{N}}_{\text{e}}$, by virtue of being an average, must lie in the range $N_{\text{e,min}}<{\overline{N}}_{\text{e}}<N_{\text{e,max}}$. It follows that the mean time of fixation satisfies

   $$4N_{\text{e,min}}\hspace{0.17em}\times \hspace{0.17em}{E}_y\left[R\right]\hspace{0.17em}<\hspace{0.17em}{E}_y\left[T_{\text{fix}}\right]\hspace{0.17em}<\hspace{0.17em}4N_{\text{e,max}}\hspace{0.17em}\times \hspace{0.17em}{E}_y\left[R\right].$$
2. A different bound can be obtained for an increasing population. A mutation that appears at time t = 0 has a mean time of fixation that satisfies

   $$E_y\left[T_{\text{fix}}\right]\hspace{0.17em}>\hspace{0.17em}\left(\frac{1}{L}{\displaystyle {\int }_0^{L}4N_{\text{e}}}\left(v\right)dv\right)\times \hspace{0.17em}{E}_y\left[R\right],$$ (20)

   • where L = 4N_e(0) × E_y[R] (see Appendix H for details). Since E_y[R] ≤ 1, the maximum value of L is 4N_e(0). In the case of small initial frequencies we have E_y[R] ≃ E₀[R] = 1 and hence L ≃ 4N_e(0).

The inequality in Equation 20 involves the average $L^{-1}{\displaystyle {\int }_0^{L}4}{N}_{\text{e}}\left(v\right)dv$, which requires knowledge of N_e(t) only over times t = 0 to t = L. If, for example, the effective population size exhibits exponential growth over this time interval, with N_e(t) = N_e(0)e^at, then Equation 20 leads to $E_y\left[T_{\text{fix}}\right]/4N_{\text{e}}\left(0\right)>\left(e^{aL}-1\right)\hspace{0.17em}{E}_y\left[R\right]/aL$. If a × L is appreciable, then neutral mutations should have a mean time to fixation that is large relative to 4N_e(0).

Discussion

In this work we have considered statistical properties of the time it takes mutations at unlinked neutral loci to fix in populations of changing effective size. Such alleles contribute to the neutral variation of a population during the random time they are segregating. Even in populations of constant size, neutral alleles constitute a special case since they take longer (on average) to fix than beneficial or equally deleterious alleles under genic selection (Maruyama 1977, pp. 80 and 81). In the present work we show that the mean and variance of the time to fixation of neutral alleles are sensitive to the behavior of the effective population size. In particular, the mean time to fixation can be significantly increased beyond the constant population result when the effective size increases over time. In a population that increases over time, alleles that start with a low initial frequency have a mean time to fixation that is predicted to be >4N_e(0), where N_e(0) is the effective population size at the time the mutation arises. We use two of the results obtained in this work to illustrate this:

• i. Equation 17 indicates how long-term linear growth of the effective population size affects the mean time of fixation. If linear population growth continues for a very long time (τ→∞), then Equation 17 shows that γ_e = 1/2 is a critical value of the growth rate, which separates small and potentially large values of E₀[T_fix]. When actual and effective population sizes coincide, the critical value of the growth rate (i.e., γ_e = 1/2) corresponds to an increase by one new individual every two generations. This is a modest rate of growth. The variability of the fixation time also depends on the value of γ_e. When population growth continues for a very long time (τ→∞), the variance, Var₀[T_fix], exhibits different behavior from the mean. The variance changes character at γ_e=1/4 from small to potentially large values [due to the term (γ_eτ/N_e,0)^1+p in Equation 18]. This last feature, which corresponds to an increase of the population by one new individual every four generations, when actual and effective population sizes coincide, also illustrates that the mean and variance of T_fix can depend on parameters in quite different ways.

• ii. Equation 20 shows that a large mean time of fixation results if the population grows an appreciable amount in the first 4N_e(0) generations. For example, with exponential growth at rate a we obtained $E_y\left[T_{\text{fix}}\right]/4N_{\text{e}}\left(0\right)>\left(e^{aL}-1\right)E_y\left[R\right]/ aL$, where L = 4N_e(0)E_y[R]. Thus if the growth rate has the value a = 0.05 per generation, then an initial effective size as small as N_e(0) = 20 leads, for small initial frequencies, to E₀[T_fix] > 10³ generations, which is >4N_e(0) by more than a factor of 10.

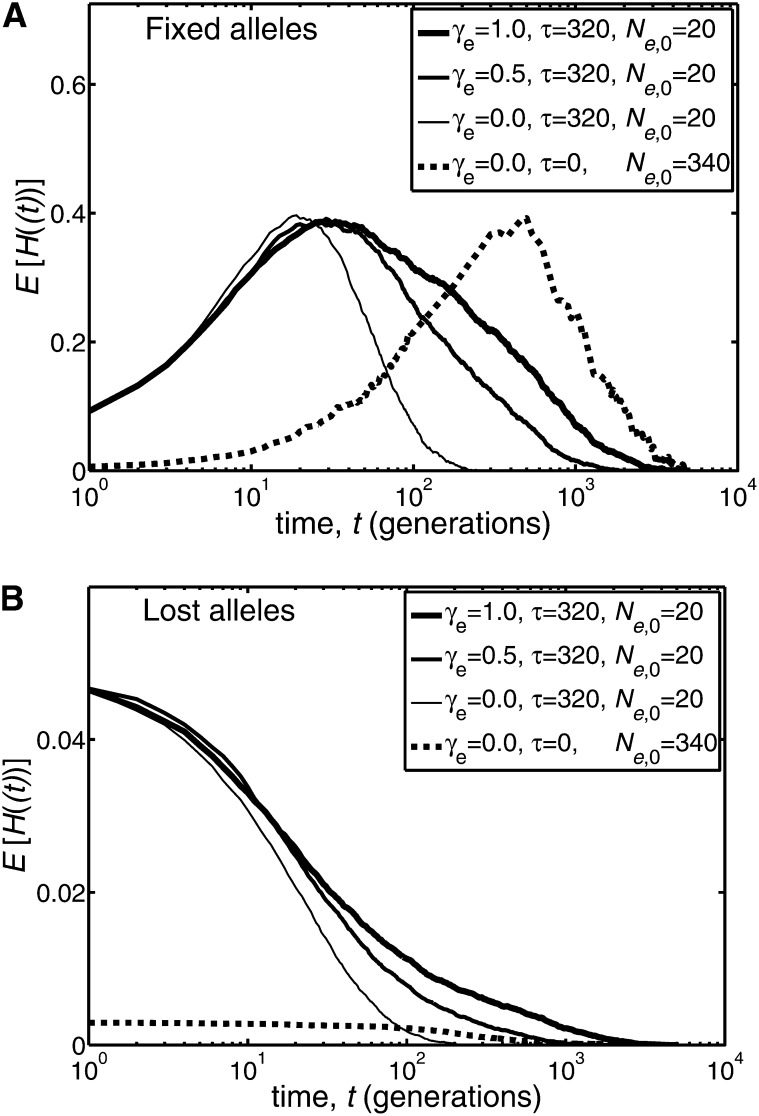
The time a mutation takes to fix in a population is closely related to the persistence of variation in that population. A measure of variation in a population (which in the present work arises from the segregation of neutral alleles) is given by the mean heterozygosity, E[H(t)], where H(t) = 2X(t)(1 − X(t)). To illustrate the relation between fixation and the persistence of variation consider a population with a period of linear growth as in Equation 15, with γ_e positive. Simulations of the heterozygosity are plotted as a function of time in Figure 2, for the case where a single A allele is initially present in the population.

Figure 2 .

Illustration of the behavior of the mean heterozygosity E[H(t)] [where H(t) = 2X(t)(1−X(t))] as a function of the time, t, when the effective population size has a period of linear growth, as in Equation 15. The results presented were derived from simulations of 2 × 10⁴ replicate populations, which were run until either fixation or loss occurred. Binomial sampling was used, and hence actual and effective population sizes coincided. A single copy of a mutant allele was assumed present at time t = 0. The heterozygosities plotted are conditional on the mutant alleles either fixing (A) or being lost (B). The solid lines correspond to an initial effective population size of N_e,0 = 20 and a duration of linear growth of τ = 16 × N_e,0 = 320 generations. For comparison, the dashed line corresponds to a population of constant effective size, whose value is the largest size achieved by a population with γ_e = 1 and N_e,0 = 20; namely, N_e,0 = 20 + 320 = 340.

For a fixed duration of linear change, τ, different values of the linear growth rate, γ_e, were used in Figure 2. The mean heterozygosity is very different for mutant alleles that fix compared with those that are lost. Mutant alleles that fix lead to a relatively high level of mean heterozygosity (∼0.4), which has a persistence that increases with γ_e. Mutant alleles that are lost lead to a mean heterozygosity that is relatively small and that persists for substantially less time than that of alleles that fix. For comparison, Figure 2 also contains a curve showing the heterozygosity of a population of constant effective size, whose value is the largest size achieved by the population with γ_e=1 and N_e,0=20, namely N_e,0 = 340 (dashed curve). The comparison is partially confounded because the initial frequency used in this constant population corresponds to a single copy of a mutant allele and hence has the value 1/(2 × 340), while the initial frequency in all of the populations that changed size (solid curves) was 1/(2 × 20). Figure 2A suggests that the maximum value that the mean heterozygosity achieves, for a mutant allele that ultimately fixes, is insensitive to the population size; however, the time the heterozygosity persists, and the actual pattern realized, is sensitive to the behavior of the effective population size. The evidence from Figure 2A is that an increasing population enhances the persistence of the neutral variation associated with the most observable mutant alleles, that is to say those that achieve intermediate and high frequencies and proceed to fix. No such phenomenon is strongly apparent in the variation associated with alleles that typically remain at low frequencies and are ultimately lost (Figure 2B).

To establish the connection between the persistence of variation from mutant alleles that proceed to fix and the mean fixation time, consider the mean heterozygosity, given that fixation ultimately occurs. We write this as E[H(t)|Fix]. The only mutant alleles contributing to E[H(t)|Fix] are those that fix after time t (i.e., that have T_fix > t). Accordingly, we have E[H(t)|Fix] = E[H(t)|Fix, T_fix > t] × Prob(T_fix > t), and from the simulations for Figure 2A, we find that Prob(T_fix > t) is the factor in this expression that is largely responsible for the observed decrease of E[H(t)|Fix] with t. That is, for the range of t where E[H(t)|Fix] decreases, we find that E[H(t)|Fix] ≃ constant × Prob(T_fix > t). It follows that the persistence of E[H(t) | Fix] is largely determined by the behavior of Prob(T_fix > t). Additionally, E[T_fix] is fully determined from knowledge of Prob(T_fix > t). Thus a changing population size can be viewed as most fundamentally affecting Prob(T_fix > t), which then affects other quantities such as E[H(t)|Fix] and E[T_fix]. From the simulations, an increasing population size is found to shift the decay of Prob(T_fix > t) to larger values of t, and this explains why an increased mean time of fixation is accompanied by an enhanced persistence of variation.

This work has concerned itself with neutral mutations. The degree to which alleles affect the fitness of their carriers is determined by the environment. Selective neutrality may be a transient property, because under environmental changes, originally neutral loci may become selected. The associated variation then becomes converted to nonneutral variation that becomes a target for selection, as has been discussed in the literature for, e.g., alleles associated with 6PG allozymes (Dykehuizen and Hartl 1980). Such nonneutral variation will generally be significant for the continued survival of a population. It could allow rapid adaptation to a changed environment or, perhaps, result in a very high load that leads to extinction. Either way, the potential to evolve and the direction of evolution are closely associated with the presence of neutral alleles in a population and hence on the time they take to achieve fixation.

Appendix A: Preliminaries and Probability of Fixation

To obtain analytical results for the Wright–Fisher model of an unlinked neutral locus, as described in the main text, we use the diffusion approximation. Under this approximation time and allele frequencies are approximated as continuous quantities. The probability density of the frequency of the A allele at time t and frequency x, written f(x, t), obeys the diffusion equation

$$-\frac{\partial }{\partial t}\hspace{0.5em}f\left(x,t\right)=-\frac{1}{4N_{\text{e}}\left(t\right)}\frac{{\partial }^2}{\partial x^2}\left[x\left(1-x\right)f\left(x,t\right)\right]$$ (A1)

(Crow and Kimura 1970), where N_e(t) is the variance effective population size at time t. We solve Equation A1 subject to the condition that at time t = 0 all replicate populations start with the A allele at a frequency of y. This corresponds to the initial probability density

$$f\hspace{0.17em}\left(x,0\right)=\delta \hspace{0.17em}\left(x-y\right),$$ (A2)

where δ(x) denotes a Dirac delta function of argument x.

To make the solution f(x, t) of Equation A1 mathematically well defined, it is necessary to impose conditions at the boundaries x = 0 and x = 1. We require that probability is conserved for all times $\left({\displaystyle {\int }_0^{1}f\left(x,t\right)\hspace{0.17em}dx=1}\right)$ and this leads us to impose the condition that the probability current, defined by $j\left(x,t\right)=-(1/ 4N_{\text{e}}\left(t\right))(\partial / \partial x)\left[x\left(1-x\right)f\left(x,t\right)\right]$, vanishes at the boundaries (McKane and Waxman 2007):

$$j\left(0,t\right)=0,j\left(1,t\right)=0.$$ (A3)

A consequence of Equation A3 is that fixation and loss are included in the solution of Equation A1 in the form of Dirac delta functions located at x = 0 and x = 1 (McKane and Waxman 2007; Waxman 2011a). The total integrated probability density, which includes contributions of the delta functions at the boundaries, then has the value of unity for all times. This property of the solution of the diffusion equation is in accordgance with the probability distribution of the Wright–Fisher model, which has a sum over all frequency states of unity.

Proof

We now prove that the probability of the ultimate fixation or loss of a neutral allele is independent of the way that the effective population size, N_e(t), changes over time, subject to a mild restriction on N_e(t).

Proceeding, we write $\overline{x^n}\hspace{0.17em}\left(t\right)$ for the expected value $E_y\left[X^n\left(t\right)\right]\stackrel{\text{def}}{\equiv }E\left[X^n\left(t\right)|X\left(0\right)=y\right]$ and have $E_y\left[X^n\left(t\right)\right]={\displaystyle {\int }_0^1{x}^{n}f\left(x,t\right)dx}$. Multiplying Equation A1 by x or x², integrating over all x, and using Equation A3 yields

$$\frac{d\overline{x}\left(t\right)}{dt}=0$$ (A1)

and

$$\frac{d\overline{x^2}\left(t\right)}{dt}=\frac{\overline{x}\left(t\right)-\overline{x^2}\left(t\right)}{2N_{\text{e}}\left(t\right)}.$$ (A5)

The initial frequency, X(0), has the precise value of y since f(x, t) satisfies Equation A2. Defining

$$Q\left(t\right)={\displaystyle {\int }_0^t\frac{1}{2N_{\text{e}}\left(v\right)}}dv,$$ (A6)

the solutions of Equations A4 and A5 are $\overline{x}\left(t\right)=y$ and $\overline{x^2}\left(t\right)=y-y\left(1-y\right)e^{-Q\left(t\right)}$. If

$$\underset{t\to \mathrm{\infty }}{\text{lim}}Q\left(t\right)=\mathrm{\infty },$$ (A7)

then ${\text{lim}}_{t\to \mathrm{\infty }}\overline{x^2}\left(t\right)=y$. That is, at large t, $\overline{x^2}\left(t\right)$ converges to $\overline{x}\left(t\right)=y$. The only way this dispersionless convergence can come about is if lim_t→∞f(x, t) = (1 − y)δ(x) + yδ(1 − x). The coefficient of δ(1 − x) in this expression is the long time fixation probability (McKane and Waxman 2007) and equals the initial frequency, y, of the A allele. Similarly, the long time probability of loss is 1 − y. These long time results for the probabilities of fixation and loss are independent of N_e(t) and hence apply for static or time-dependent N_e, providing only that the condition of Equation A7 holds. This condition is fairly mild: for example, any N_e(t) that is bounded from above [N_e(t) < ∞ for all t] will lead to Equation A7 holding. Populations that grow too rapidly at large t, such as exponentially growing populations, will violate Equation A7, but this should not be problematic since such indefinite growth is not biologically feasible.

Appendix B: Establishing Properties of the R Statistic

In this Appendix we establish that under the diffusion approximation, the statistic

$$R={\displaystyle {\int }_0^{T_{\text{fix}}}\frac{dv}{4N_{\text{e}}\left(v\right)}}$$ (B1)

has a probability distribution that depends upon only a single parameter, namely the frequency of the A allele at time t = 0. In particular, the probability density of R is independent of the form of N_e(t).

To establish the claimed property of R, let A(t | y, u) denote the probability that X(t) = 1, given that X(u) = y. The probability A(t | y, u) appears within part of the solution of the forward diffusion equation and therefore also obeys the backward diffusion equation

$$\frac{\partial }{\partial u}A(t|y,u)=-\frac{y\left(1-y\right)}{4N_{\text{e}}\left(u\right)}\frac{{\partial }^2}{\partial y^2}\hspace{0.5em}A(t|y,u)$$ (B2)

and is subject to the initial and boundary conditions A(t | y, t) = 0 for 0 < y < 1, A(t | 0, u) = 0 for u ≤ t, and A(t | 1, u) = 1 for u ≤ t.

By changing the time variable in the backward diffusion equation, Equation B2, from u to the quantity ${\displaystyle {\int }_u^t(dv/ 4N_{\text{e}}\left(v\right))}$, it may be verified that the initial and boundary conditions depend only on y and ${\displaystyle {\int }_u^t(dv/ 4N_{\text{e}}\left(v\right))}$ and do not depend on t. Accordingly, A(t | y, u) depends only on y and ${\displaystyle {\int }_u^t(dv/4N_{\text{e}}\left(v\right))}$ and we can therefore write

$$A\left(t|y,u\right)=G_y\left({\displaystyle {\int }_u^t\frac{dv}{4N_{\text{e}}\left(v\right)}}\right)$$ (B3)

for some function G_y(r). Properties of G_y(r) follow from properties of A(t | y, u). From Equations B2 and B3 it follows that G_y(r) obeys

$$-\frac{\partial }{\partial r}{G}_y\left(r\right)=-y\left(1-y\right)\frac{{\partial }^2}{\partial y^2}{G}_y\left(r\right).$$ (B4)

Furthermore, G_y(r) is subject to the initial condition

$$G_y\left(0\right)=0\hspace{1em}\text{for}\hspace{1em}0<y<1$$ (B5)

and the boundary conditions

$$\begin{array}{l}{G}_0\left(r\right)=0\hspace{1em}\text{for}\hspace{1em}r\ge 0\\ G_1\left(r\right)=1\hspace{1em}\text{for}\hspace{1em}r\ge 0.\end{array}$$ (B6)

Additionally, G_y(r) also satisfies

$$G_y\hspace{0.17em}\left(\mathrm{\infty }\right)=y$$ (B7)

since G_y(∞) ≡ A(∞| y, u) = y is the probability of ultimate fixation of a neutral allele (see Appendix A).

We can determine G_y(r) by solving Equation B4 subject to Equations B5 and B6. However, this is not necessary since we can infer the form of G_y(r) from an existing result in the literature. We note that the probability A(t | y, u), when u = 0 and for a population of fixed size, has been found by Kimura (1955) and depends only on t and N_e in the combination t/(4N_e). Because of Equation B3, we can take Kimura’s solution and replace t/(4N_e) by r to obtain the form for G_y(r). It is often convenient to work with the quantity G_y(r)/y. Accordingly, we define

$$F_y\hspace{0.17em}\left(r\right)=\frac{G_y\hspace{0.17em}\left(r\right)}{y}$$ (B8)

and then find from Kimura’s form for A(t | y u) that

$$F_y\left(r\right)=1-\stackrel{\mathrm{\infty }}{{\displaystyle \sum }_{n=0}}\frac{2\left(1-y\right)\left(2n+3\right)}{{\lambda }_n}{\left(-1\right)}^n{C}_n^{\left(3/2\right)}\left(1-2y\right)\text{exp}\left(-{\lambda }_{n}r\right),$$ (B9)

where λn = (n + 1)(n + 2) and $C_n^{\left(3/2\right)}\left(y\right)$ denotes a Gegenbauer polynomial in y of order 3/2 and degree n (Abramowitz and Stegun 1964). In the limit of small y we write F_y(r) as F₀(r). In this regime a simple approximate form for A(t | y, u) is known (Waxman 2011b) and hence we have the simple approximation for F₀(r):

$$F_0\left(r\right)\mathrm{\simeq }\{\begin{array}{l}{\left(\frac{\pi }{r}\right)}^{3/2}{e}^{r/4-{\pi }^2/\left(4\hspace{0.17em}r\right)},\hspace{1em}0\hspace{0.17em}\le \hspace{0.17em}r\hspace{0.17em}\le \hspace{0.17em}2,\\ 1-3e^{-2\hspace{0.17em}r},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}r\hspace{0.17em}>\hspace{0.17em}2.\end{array}$$ (B10)

Since the process of fixation among replicate populations is irreversible (once a replicate population has fixed, it remains fixed), the quantity A(t | y, u) is the probability that fixation has actually occurred within the time interval u to t. That is, A(t | y, u) is the probability that fixation has occurred by time t. It follows that for populations where fixation ultimately occurs, the random time at which fixation occurs, written T_fix, obeys

$$\text{Prob}\left(T_{\text{fix}}\hspace{0.17em}\le \hspace{0.17em}t|X\left(u\right)=y\right)=\frac{A\left(t|y,u\right)}{A\left(\mathrm{\infty }|y,u\right)}.$$ (B11)

Strictly, the probability on the left-hand side should indicate that it is conditional on fixation ultimately occurring. Given, however, that T_fix is not defined unless fixation will ultimately occur, we adopt the simpler notation where this conditioning is left implicit.

Equation B11 can be written for any u ≤ t as $\text{Prob}\left(T_{\text{fix}}\le t|X\hspace{0.17em}\left(u\right)=y\right)=G_y\left({\displaystyle {\int }_u^t(dv/4N_{\text{e}}\left(v\right))}\right)/y=F_y\left({\displaystyle {\int }_u^t(dv/4N_{\text{e}}\left(v\right))}\right)$ and completely equivalently, we have

$$\text{Prob}\left({\displaystyle {\int }_u^{T_{\text{fix}}}\frac{dv}{4N_{\text{e}}\left(v\right)}}\hspace{0.17em}\le {\displaystyle {\int }_u^t\frac{dv}{4N_{\text{e}}\left(v\right)}}|X\left(u\right)=y\right)=F_y\left({\displaystyle {\int }_u^t\frac{dv}{4N_{\text{e}}\left(v\right)}}\right).$$ (B12)

Restricting ourselves to the special case of u = 0, so T_fix is the amount of time that elapses before the mutant allele fixes (if u ≠ 0, the amount of time that elapses before fixation is T_fix − u), we can write Equation B12 as

$$\text{Prob}\left(R\hspace{0.17em}\le \hspace{0.17em}r|X\left(0\right)=y\right)=F_y\left(r\right),$$ (B13)

where R is the random variable given in Equation B1.

We thus have established that the function of r given by F_y(r) is, by virtue of Equation B13, the cumulative distribution function of the random variable R, and this depends on only one parameter, namely y, the initial frequency of the A allele. Differentiating F_y(r) with respect to r yields the probability density of r, and this also depends on the single parameter y.

Appendix C: Deriving Expressions for the Mean and Variance of R

In this Appendix we determine expressions for the mean and variance of the statistic R defined in Equation 1 of the main text.

Moments of R are expectations of the form E[Rⁿ | X(0) = y] with n = 1, 2, … , which we write in the shorter form E_y[Rⁿ]. The probability density of R is the derivative, with respect to r, of the cumulative distribution function of R. Here, following Appendix B, we write the cumulative distribution function of R as G(r, y)/y. Accordingly,

$$\begin{array}{c}{E}_y\left[R^n\right]={\displaystyle {\int }_0^{\mathrm{\infty }}{r}^n\frac{\partial }{\partial r}\left(\frac{G_y\left(r\right)}{y}\right)={\displaystyle {\int }_0^{\mathrm{\infty }}{r}^n\frac{\partial }{\partial r}\left(\frac{G_y\left(r\right)}{y}-1\right)dr}}\\ =\frac{n}{y}{\displaystyle {\int }_0^{\mathrm{\infty }}{r}^{n-1}\left[y-G_y\left(r\right)\right]dr.}\end{array}$$ (C1)

We write

$$E_y\left[R^n\right]=\frac{n}{y}{J}_{n-1}\left(y\right),$$ (C2)

where

$$J_n\left(y\right)\stackrel{\text{def}}{\equiv }{\displaystyle {\int }_0^{\mathrm{\infty }}{r}^n\left[y-G_y\left(r\right)\right]dr}.$$ (C3)

Because of Equation B6, we take

$$J_n\hspace{0.17em}\left(0\right)=0,\hspace{0.17em}{J}_n\hspace{0.17em}\left(1\right)=0.$$ (C4)

From Equation B4 we can establish equations that the J_n(y) obey. We write Equation B4 as $-y\left(1-y\right)({\partial }^2 / \partial y^2)\left[y-G_y\left(r\right)\right]=-(\partial / \partial r)\left[y-G_y\left(r\right)\right]$. Multiplying this equation by rⁿ and integrating from r = 0 to r = ∞ yields $-y\left(1-y\right)(d^2 / d{y}^2)J_n\left(y\right)=-{\displaystyle {\int }_0^{\mathrm{\infty }}{r}^n(\partial /\partial r)\left[y-G_y\left(r\right)\right]dr}$. An integration by parts yields

$$-y\left(1-y\right)\frac{d^2}{d{y}^2}{J}_n\left(y\right)={\left[-\underset{}{\stackrel{}{r^n\left[y-G_y\left(r\right)\right]}}\right]}_{r\hspace{0.17em}=\hspace{0.17em}0}^{r\hspace{0.17em}=\hspace{0.17em}\mathrm{\infty }}+n{J}_{n-1}\left(y\right).$$ (C5)

When n = 0, there is a contribution from the boundary term on the right-hand side at r = 0, while for n > 0 there is no such contribution. It follows that

$$-y\left(1-y\right)\frac{d^2}{d{y}^2}{J}_0\left(y\right)=y$$ (C6)

and

$$-y\left(1-y\right)\frac{d^2}{d{y}^2}{J}_n\left(y\right)=n{J}_{n-1}\left(y\right),\hspace{1em}n=1,\hspace{0.5em}2,\hspace{0.5em}3,\hspace{0.5em}\mathrm{...}\hspace{0.5em}.$$ (C7) (C7)

The solution to Equation C6, subject to Equation C4, is J₀(y)=−(1 − y)ln(1 − y). The corresponding solution to Equation C7 for n = 1 is $J_1\left(y\right)=\left(1-y\right)\text{ln}\left(1-y\right)+y\left[{\pi }^2 / 6-\text{dilog}\left(1-y\right)\right]$, where dilog(x) denotes the dilogarithm function: $\text{dilog}\left(x\right)={\displaystyle {\int }_1^x\text{(ln}\left(t\right)/(1-t)) }dt$ (Abramowitz and Stegun 1964). We have not found a particularly simple expression for J₂(y); however, a small y expansion can be determined if required.

We can now determine E_y[R], which equals J₀(y)/y:

$$E_y\left[R\right]={\displaystyle {\int }_0^{\mathrm{\infty }}\left[1-F_y\left(r\right)\right]}dr=-\frac{\left(1-y\right)\text{ln}\left(1-y\right)}{y}.$$ (C8)

Also, we have E_y[R²] = 2J₁(y)/y, i.e.,

$$E_y\left[R^2\right]=2\frac{\left(1-y\right)\text{ln}\left(1-y\right)}{y}+\frac{{\pi }^2}{3}-2\text{dilog}\left(1-y\right),$$ (C9)

where $\text{dilog}\left(x\right)={\displaystyle {\int }_1^x\text{(ln}\left(u\right)/(1-u))}du$ denotes the dilogarithm function (Abramowitz and Stegun 1964). The result for the variance in the main text follows directly by combining the results of Equations C8 and C9:

$$\begin{array}{c}{\text{Var}}_y\left(R\right)=E_y\left[R^2\right]-{\left(E_y\left[R\right]\right)}^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{\simeq }\frac{2\left(1-y\right)\text{ln}\left(1-y\right)}{y}-{\left(\frac{\left(1-y\right)\text{ln}\left(1-y\right)}{y}\right)}^2+\frac{{\pi }^2}{3}-2\text{dilog}\left(1-y\right).\end{array}$$ (C10)

Appendix D: Illustrating the Independence of the Distribution of R on Population Behavior

In this Appendix we present a set of results for the statistic R of Equation 1 to illustrate the independence of its distribution on the way population size changes over time, as predicted by the diffusion approximation. To obtain data we carried out individually based simulations of a neutral population that evolves in discrete time. These simulations used binomial sampling of individuals in discrete time, which results in the effective and actual population sizes coinciding: N_e(t) = N(t). In Figure D1, five quite different forms of N(t) have been adopted, ranging from logistic growth to logistic decay.

For each case of N(t) shown in Figure D1, the fate of the mutants was followed in 10⁶ replicate populations. As expected, a fraction very close to y of these replicate populations underwent fixation. For a given population behavior, the times of fixation were recorded in the different replicate populations where fixation occurred. If fixation occurred in a replicate population at time t_fix, then the statistic corresponding to R of Equation 1 was taken to be the discrete analogue of the integral, namely ${\displaystyle {\sum }_{t=0}^{t_{\text{fix}}-1}(1/ 4N_e\left(t\right))}$. With a single copy of a mutant allele initially present, the mean times to fixation for the population behaviors a–e in Figure D1 differed among themselves by considerable amounts, >200% (see Table D1). The mean values of the R statistic for the different population behaviors were all within 2% of the value predicted by Equation 5. We also used Equation 6 to predict the variance of R for Figure 1. The variances of R determined from cases a–e in Figure D1 were all within 7% of the predicted value—see Table D1.

Table D1 . Results from individually based simulations for the fixation of a neutral mutant allele are given for the population behaviors illustrated in Figure D1.

	Ey[R] (% error)	Vary[R] (% error)	Ey[T]
a: Logistic growth	1.001 (−0.338)	0.294 (−1.268)	625.6
b: Discontinuous jump	0.995 (0.248)	0.291 (−0.294)	479.2
c: Variable	0.978 (2.027)	0.272 (6.658)	361.1
d: Constant	0.993 (0.453)	0.280 (3.348)	397.2
e: Logistic decay	0.990 (0.770)	0.292 (−0.593)	268.8

The initial population size was 100 in all cases, and other parameters are given in the Figure D1 legend. The initial frequency of the mutant allele was y = 1/200 and 10⁶ replicate populations were simulated for each of the five behaviors illustrated in Figure D1. The expectations and variances given are estimates from the simulations. For the mean and variance of R, the percentage errors, given in parentheses, are the errors of the diffusion results (given in Equations C8 and C10), relative to the simulation results.

To test the quality of the diffusion results for the mean time for fixation, we calculated the percentage error in this quantity, relative to the simulation results, for two cases. For the standard case of a constant population (curve d in Figure D1) we used the diffusion result E[T_fix] = 4N_eE_y[R]. For a discontinuous jump in the population size (curve b in Figure D1) we used the diffusion result Equation E5, employing Equation 4 of the main text, thereby approximating the initial frequency by zero. For both cases, the errors in the calculated mean times of fixation were found to be <1%.

Appendix E: Deriving Expressions for the Mean and Variance of the Time to Fixation

In this Appendix we establish expressions for the mean and the variance of the time to fixation.

Equation 7 of the main text reads T_fix = h(R) and we first determine E_y[(T_fix)^a] with a an arbitrary positive number. With F_y(r) the cumulative probability distribution of R at value r (see Equation 2), we have

$$\begin{array}{c}{E}_y\left[{\left(T_{\text{fix}}\right)}^a\right]\mathrm{\simeq }\hspace{0.17em}{E}_y\left[h^a\left(R\right)\right]={\displaystyle {\int }_0^{\mathrm{\infty }}{h}^a}\left(r\right)\frac{\partial F_y\left(r\right)}{\partial r}dr=-{\displaystyle {\int }_0^{\mathrm{\infty }}{h}^a}\left(r\right)\frac{\partial }{\partial r}\hspace{0.17em}\left[1-F_y\left(r\right)\right]dr\\ =a{\displaystyle {\int }_0^{\mathrm{\infty }}{h}^{a-1}}\left(r\right)\frac{dh\left(r\right)}{dr}\hspace{0.17em}\left[1-F_y\left(r\right)\right]dr.\end{array}$$ (E1)

Taking a = 1 in Equation E1 leads to the following expression for the mean time to fixation:

$$E_y\left[T_{\text{fix}}\right]\hspace{0.17em}\mathrm{\simeq }{\displaystyle {\int }_0^{\mathrm{\infty }}h\left(r\right)\frac{\partial F_y\left(r\right)}{\partial r}dr}={\displaystyle {\int }_0^{\mathrm{\infty }}\frac{dh\left(r\right)}{dr}}\left[1-F_y\left(r\right)\right]dr.$$ (E2)

There is an alternative way of writing the second form of this expression. We note that the function h(r) is formally defined by

$$r={\displaystyle {\int }_0^{h\hspace{0.17em}\left(r\right)}\frac{dv}{4N_{\text{e}}\left(v\right)}}.$$ (E3)

Differentiating Equation E3 with respect to r leads to

$$\frac{dh\left(r\right)}{dr}=4N_{\text{e}}\left(h\left(r\right)\right)$$ (E4)

and using this result in Equation E2 yields an alternative expression for the mean:

$$E_y\left[T_{\text{fix}}\right]\hspace{0.17em}\mathrm{\simeq }{\displaystyle {\int }_0^{\mathrm{\infty }}4N_{\text{e}}\left(h\left(r\right)\right)\left[1-F_y\left(r\right)\right]dr}.$$ (E5)

To determine an expression for the variance we use Var_y(T_fix) = E_y[(T_fix)²]−(E_y[T_fix])² and set a = 1 and a = 2 in Equation E1 to obtain Equation 9 of the main text.

Appendix F: Derivation of the Results for a Population-Size Jump Given in Equations 13 and 14 of the Main Text

In this Appendix we determine exact and approximate results for the mean time of fixation and its variance when the effective population size discontinuously jumps at time τ from N_e,0 to N_e,1, as given in Equation 10 of the main text.

To begin, we note that the function h(r), which relates T_fix to R, is formally defined by Equation E3. It may be verified that with N_e(t) given by Equation 10, h(r) is given by

$$h\left(r\right)=\{\begin{array}{l}4N_{\text{e,0}}r,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}r\le \rho ,\\ 4N_{\text{e,0}}\rho +4N_{\text{e,1}}\left(r-\rho \right),\hspace{1em}r>\rho ,\end{array}$$ (F1)

where ρ = τ/(4N_e,0) is a scaled measure of the time of the population-size jump.

The mean of T_fix can be obtained from Equations E2 and F1 and takes the form

$$E_y\left[T_{\text{fix}}\right]=A_0\times 4N_{\text{e,0}}+A_1\times 4N_{\text{e,1,}}$$ (F2)

where

$$A_0={\displaystyle {\int }_0^{\rho }\left[1-F_y\left(r\right)\right]}dr,\hspace{1em}{A}_1={\displaystyle {\int }_{\rho }^{\mathrm{\infty }}\left[1-F_y\left(r\right)\right]}dr\equiv 1-A_0.$$ (F3)

The variance of T_fix follows from Equations 9 and F1 and takes the form

$$\begin{array}{c}{\text{Var}}_y\left(T_{\text{fix}}\right)=\left(B_{00}-A_0^2\right)\times {\left(4N_{\text{e,0}}\right)}^2+\left(B_{01}-2A_0{A}_1\right)\times \left(4N_{\text{e,0}}\right)\left(4N_{\text{e,1}}\right)\\ \hspace{1em}+\left(B_{11}-A_1^2\right)\times {\left(4N_{\text{e,1}}\right)}^2,\end{array}$$ (F4)

where

$$\begin{array}{l}{B}_{00}=2{\displaystyle {\int }_0^{\rho }r\left[1-F_y\left(r\right)\right]dr,\hspace{1em}{B}_{01}=2\rho {\displaystyle {\int }_{\rho }^{\mathrm{\infty }}\left[1-F_y\left(r\right)\right]}dr\equiv 2\rho A_1},\\ B_{11}=2{\displaystyle {\int }_{\rho }^{\mathrm{\infty }}\left(r-\rho \right)}\left[1-F_y\left(r\right)\right]dr.\end{array}$$ (F5)

We derive results for the case of vanishingly small initial frequencies (y → 0) and make extensive use of the following y → 0 forms of Equations C8 and C9:

$${\displaystyle {\int }_0^{\mathrm{\infty }}\left[1-F_0\hspace{0.17em}\left(r\right)\right]}dr=1,\hspace{1em}{\displaystyle {\int }_0^{\mathrm{\infty }}r\hspace{0.17em}\left[1-F_0\hspace{0.17em}\left(r\right)\right]}\hspace{0.17em}dr\hspace{0.17em}\equiv \hspace{0.17em}\frac{1}{2}{E}_0\left[R^2\right]=\frac{1}{2}\left(\frac{{\pi }^2}{3}-2\right).$$ (F6)

Derivation of results for y → 0 and ρ ≪ 1

We used Equation 4 of the main text and obtained the following approximate results, which all have corrections of $O\left(e^{-{\pi }^2/\left(4\rho \right)}\right)$: A₀≃ρ, A₁≃1−ρ, B₀₀ ≃ ρ², B₀₁ ≃ 2ρ(1 − ρ). For B₁₁ we write $B_{11}=2\left({\displaystyle {\int }_0^{\mathrm{\infty }}r\left[1-F_0\left(r\right)\right]}dr-{\displaystyle {\int }_0^{\rho }r\left[1-F_0\left(r\right)\right]dr}\hspace{0.17em}\right)-2\rho A_1$, which leads to $B_{11}={\pi }^2 / 3-2-2\rho +{\rho }^2+O\left(e^{-{\pi }^2/\left(4\rho \right)}\right)$. Combining these results leads to E₀[T_fix] ≃ ρ × 4N_e,0 + (1 − ρ) × 4N_e,1 and ${\text{Var}}_0\left(T_{\text{fix}}\right)\mathrm{\simeq }\left({\pi }^2 / 3-3\right)\times {\left(4N_{\text{e,1}}\right)}^2$.

Derivation of results for y → 0 and ρ ≃ 0.51 or ρ = 1

Results for these cases were obtained using Equation 4 of the main text and numerically determining the coefficients in Equations F3 and F5.

Derivation of results for y → 0 and ρ ≥ 2

We used Equation 4 of the main text and obtained the following results: $A_0={\displaystyle {\int }_0^{\mathrm{\infty }}\left[1-F_0\left(r\right)\right]}\hspace{0.17em}dr-{\displaystyle {\int }_{\rho }^{\mathrm{\infty }}\left[1-F_0\hspace{0.17em}\left(r\right)\right]}\hspace{0.17em}dr\mathrm{\simeq }1-(3/2)\hspace{0.17em}{e}^{-2\rho }$, $A_1=1-A_0\mathrm{\simeq }(3/2)e^{-2\rho }$, $B_{00}=2{\displaystyle {\int }_0^{\mathrm{\infty }}r\left[1-F_0\left(r\right)\right]}\hspace{0.17em}dr-2\hspace{0.17em}{\displaystyle {\int }_{\rho }^{\mathrm{\infty }}r\left[1-F_0\left(r\right)\right]}dr\mathrm{\simeq }{\pi }^2 / 3-2-(3/2)\left(1+2\rho \right)e^{-2\rho }$, B₀₁≃3ρe^−2ρ, and $B_{11}\mathrm{\simeq }(3/2)e^{-2\rho }$. Combining these results gives $E_0\left[T_{\text{fix}}\right]=\left(1-(3/2)e^{-2\rho }\right)\times 4N_{\text{e,0}}+(3/2)e^{-2\rho }\times 4N_{\text{e,1}}$ and on neglecting terms of O(e^−4ρ) gives ${\text{Var}}_0\left(T_{\text{fix}}\right)\mathrm{\simeq }\left({\pi }^2 / 3-3+(3/2)\left(1-2\rho \right)e^{-2\rho }\right)\times {\left(4N_{\text{e,0}}\right)}^2+(3/2)e^{-2\rho }\times {\left(4N_{\text{e,1}}\right)}^2$.

Appendix G: Mean and Variance of the Time to Fixation When N_e Has a Period of Linear Growth

In this Appendix we consider a situation outlined in the main text, where population size increases linearly, for a finite period of time, and then remains constant, as given in Equation 15 of the main text. We give results only for the case of vanishingly small initial frequencies (y → 0).

In terms of the quantity r₀ defined by

$$r_0=\frac{1}{4{\gamma }_{\text{e}}}\hspace{0.17em}\text{log}\left(1+\frac{{\gamma }_{\text{e}}\tau }{N_{\text{e,0}}}\right)$$ (G1)

the function h(r) defined by Equation E3 can be verified to be given by

$$h\hspace{0.17em}\left(r\right)=\{\begin{array}{l}\frac{N_{\text{e,0}}}{{\gamma }_{\text{e}}}\left(e^{4{\gamma }_{\text{e}}r}-1\right),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.17em}r\hspace{0.17em}\le \hspace{0.17em}{r}_0,\\ \frac{N_{\text{e,0}}}{{\gamma }_{\text{e}}}\left(e^{4{\gamma }_{\text{e}}{r}_0}-1\right)+4N_{\text{e,0}}{e}^{4{\gamma }_{\text{e}}{r}_0}\left(r-r_0\right),\hspace{1em}r\hspace{0.17em}>\hspace{0.17em}{r}_0.\end{array}$$ (G2)

To determine the mean time to fixation, we use Equations G2 and E2 to obtain

$$E_0\left[T_{\text{fix}}\right]=4N_{\text{e,0}}\times \left(A_0+A_1\right),$$ (G3)

where

$$A_0={\displaystyle {\int }_0^{r_0}{e}^{4{\gamma }_{\text{e}}r}}\left[1-F_0\left(r\right)\right]dr,\hspace{1em}{A}_1=e^{4{\gamma }_{\text{e}}{r}_0}{\displaystyle {\int }_{r_0}^{\mathrm{\infty }}\left[1-F_0\hspace{0.17em}\left(r\right)\right]}dr.$$ (G4)

The variance follows from Equations G2 and 9 and takes the form

$${\text{Var}}_0\left(T_{\text{fix}}\right)={\left(4N_{\text{e,0}}\right)}^2\times \left[B_0+B_1-{\left(A_0+A_1\right)}^2\right],$$ (G5)

where

$$\begin{array}{l}{B}_0=2{\displaystyle {\int }_0^{r_0}{e}^{4{\gamma }_{\text{e}}r}\frac{e^{4{\gamma }_{\text{e}}r}-1}{4{\gamma }_{\text{e}}}\left[1-F_0\left(r\right)\right]}dr\\ B_1=2e^{4{\gamma }_{\text{e}}{r}_0}{\displaystyle {\int }_{r_0}^{\mathrm{\infty }}\left[\frac{e^{4{\gamma }_{\text{e}}{r}_0}-1}{4{\gamma }_{\text{e}}}+e^{4{\gamma }_{\text{e}}{r}_0}\left(r-r_0\right)\right]}\left[1-F_0\left(r\right)\right]dr.\end{array}$$ (G6)

We derive results for just the τ dependence of E₀[T_fix] and Var₀(T_fix). The results obtained are restricted to large τ, such that r₀ (given in Equation G1) > 2.

We make extensive use of Equation 4 of the main text.

With c₁ and c₂ constants with respect to τ we can write

$$\begin{array}{l}{A}_0={\displaystyle {\int }_0^2{e}^{4{\gamma }_{\text{e}}r}\left[1-F_0\left(r\right)\right]}dr+{\displaystyle {\int }_2^{r_0}{e}^{4{\gamma }_{\text{e}}r}\left[1-F_0\left(r\right)\right]}dr=c_1+\frac{3e^{\left(4{\gamma }_{\text{e}}-2\right)r_0}}{4{\gamma }_{\text{e}}-2};\\ A_1=\frac{3}{2}{e}^{\left(4{\gamma }_{\text{e}}-2\right)r_0};\\ B_0=2{\displaystyle {\int }_0^2{e}^{4{\gamma }_{\text{e}}r}}\frac{e^{4{\gamma }_{\text{e}}r}-1}{4{\gamma }_{\text{e}}}\left[1-F_0\left(r\right)\right]dr+2{\displaystyle {\int }_2^{r_0}{e}^{4{\gamma }_{\text{e}}r}}\frac{e^{4{\gamma }_{\text{e}}r}-1}{4{\gamma }_{\text{e}}}\left[1-F_0\left(r\right)\right]dr=c_2+\frac{3}{2{\gamma }_{\text{e}}}\left(\frac{e^{\left(8{\gamma }_{\text{e}}-2\right)r_0}}{8{\gamma }_{\text{e}}-2}-\frac{e^{\left(4{\gamma }_{\text{e}}-2\right)r_0}}{4{\gamma }_{\text{e}}-2}\right);\\ B_1=2e^{4{\gamma }_{\text{e}}{r}_0}{\displaystyle {\int }_{r_0}^{\mathrm{\infty }}\left[\frac{e^{4{\gamma }_{\text{e}}{r}_0}-1}{4{\gamma }_{\text{e}}}+e^{4{\gamma }_{\text{e}}{r}_0}\left(r-r_0\right)\right]}3e^{-2r}dr=\frac{3}{4{\gamma }_{\text{e}}}{e}^{\left(4{\gamma }_{\text{e}}-2\right)r_0}\left[{\left(1+2\gamma \right)}_{\text{e}}{e}^{4{\gamma }_{\text{e}}{r}_0}-1\right].\end{array}$$

These lead to

$$\frac{E_0\left[T_{\text{fix}}\right]}{4N_{\text{e,0}}}\hspace{0.17em}\mathrm{\simeq }\hspace{0.17em}{c}_1+\frac{3{\gamma }_{\text{e}}{e}^{\left(4{\gamma }_{\text{e}}-2\right)r_0}}{2{\gamma }_{\text{e}}-1}$$ (G7)

$$\frac{{\text{Var}}_0\left(T_{\text{fix}}\right)}{{\left(4N_{\text{e,0}}\right)}^2}\hspace{0.17em}\mathrm{\simeq }\hspace{0.17em}{c}_2+\frac{3}{2{\gamma }_{\text{e}}}\hspace{0.17em}\left(\frac{e^{\left(8{\gamma }_{\text{e}}-2\right)\hspace{0.17em}{r}_0}}{8{\gamma }_{\text{e}}-2}-\frac{e^{\left(4{\gamma }_{\text{e}}-2\right)\hspace{0.17em}{r}_0}}{4{\gamma }_{\text{e}}-2}\right)+\frac{3}{4{\gamma }_{\text{e}}}\hspace{0.17em}\left[{\left(1+2\gamma \right)}_{\text{e}}{e}^{\left(8{\gamma }_{\text{e}}-2\right)\hspace{0.17em}{r}_0}-e^{\left(4{\gamma }_{\text{e}}-2\right)\hspace{0.17em}{r}_0}\right]-{\left(c_1+\frac{3{\gamma }_{\text{e}}{e}^{\left(4{\gamma }_{\text{e}}-2\right)\hspace{0.17em}{r}_0}}{2{\gamma }_{\text{e}}-1}\right)}^2.$$ (G8)

Assuming that τ is sufficiently large that γ_eτ ≫ N_e,0, Equation G1 allows us to write $e^{4{\gamma }_{\text{e}}{r}_0}\mathrm{\simeq }{\gamma }_{\text{e}}\tau / N_{\text{e,0}}$. Using this result, and the parameter p defined by $p=(2{\gamma }_{\text{e}}-1)/2{\gamma }_{\text{e}}\equiv \left({\gamma }_{\text{e}}-1/2\right)/{\gamma }_{\text{e}}$, we find that the τ dependence in Equations G7 and G8 takes the form given in Equations 17 and 18 of the main text.

Appendix H: Derivation of an Inequality for E_y[T_fix]

In this Appendix we establish an inequality for E_y[T_fix] that applies when N_e(t) increases with t.

We write the condition that N_e(t) increases with t as

$$d{N}_{\text{e}}\left(t\right)/dt\hspace{0.17em}>\hspace{0.17em}0.$$ (H1)

We note that because of Equations E4 and H1, the function h(r) is convex (d²h(r)/dr² > 0). We can thus employ Jensen’s inequality, which for φ(r) convex reads E[φ(R)] > φ(E[R]) (Gradsteyn and Ryzhik 1980), and hence obtain E_y[h(R)] > h(E_y[R]). Since E_y[T_fix] = E_y[h(R)] (using Equation 7 of the main text), we have

$$E_y\left[T_{\text{fix}}\right]>h\left(E_y\left[R\right]\right).$$ (H2)

We write this inequality in a different way that allows additional development. From Equation E4 we obtain $h\left(r\right)={\displaystyle {\int }_0^{r}4N_{\text{e}}\left(h\left(v\right)\right)dv}$ and hence Equation H2 is equivalent to

$$E_y\left[T_{\text{fix}}\right]>{\displaystyle {\int }_0^{E_y\left[R\right]}4}{N}_{\text{e}}\left(h\left(v\right)\right)dv.$$ (H3)

Because of Equation H1, we have N_e(v) > N_e(0) for v > 0 and using Equation E3 gives $r={\displaystyle {\int }_0^{h\left(r\right)}(dv/4N_{\text{e}}\left(v\right))}\hspace{0.17em}<\hspace{0.17em}{\displaystyle {\int }_0^{h\left(r\right)}(dv/4N_{\text{e}}\left(0\right))}$; i.e., h(r) > 4N_e(0)r. Using Equation H1 again then yields 4N_e(h(v)) >4N_e(4N_e(0)v), which can be used in Equation H3 to yield $E_y\left[T_{\text{fix}}\right]>{\displaystyle {\int }_0^{E_y\left[R\right]}4}{N}_{\text{e}}\left(4N_{\text{e}}\left(0\right)v\right)dv$. The change of variable 4N_e(0)v → v gives $E_y\left[T_{\text{fix}}\right]\hspace{0.17em}>\hspace{0.17em}(1/4N_{\text{e}}\left(0\right)){\displaystyle {\int }_0^{4N_{\text{e}}\left(0\right)E_y\left[R\right]}4}{N}_{\text{e}}\left(v\right)dv$, which is equivalent Equation 20 of the main text.