Comparing the Predictions of the Nonlinear Poisson-Boltzmann Equation and the Ion Size-Modified Poisson-Boltzmann Equation for a Low-Dielectric Charged Spherical Cavity in an Aqueous Salt Solution

Abstract

The ion size-modified Poisson Boltzmann equation (SMPBE) is applied to the simple model problem of a low-dielectric spherical cavity containing a central charge, in an aqueous salt solution to investigate the finite ion size effect upon the electrostatic free energy and its sensitivity to changes in salt concentration. The SMPBE is shown to predict a very different electrostatic free energy than the nonlinear Poisson-Boltzmann equation (NLPBE) due to the additional entropic cost of placing ions in solution. Although the energy predictions of the SMPBE can be reproduced by fitting an appropriatelysized Stern layer, or ion-exclusion layer to the NLPBE calculations, the size of the Stern layer is difficult to estimate a priori. The SMPBE also produces a saturation layer when the central charge becomes sufficiently large. Ion-competition effects on various integrated quantities such the total number of ions predicted by the SMPBE are qualitatively similar to those given by the NLPBE and those found in available experimental results.

INTRODUCTION

Numerous processes involving the folding, bending, melting and binding of highly charged biopolyelectrolytes, which are vital for biological function, are strongly influenced by changes in the ionic solvent environment. Non-specific salt-mediated electrostatic interactions play an important role in these biomolecular processes because of their long-range influence, and such interactions largely govern the complex salt dependent behavior of the above mentioned processes. Therefore, physically realistic models of these long-range and salt-mediated electrostatic interactions are essential to predict the physiochemical behavior of charged biomacromolecules in ionic solutions.

Because of its simplicity and ability to accurately predict many thermodynamic properties, the nonlinear Poisson-Boltzmann equation, NLPBE,^1-4 has been extensively used to model the ionic solvent environment of biomolecules. Despite this success, it is subject to well known approximations, such as omitting finite ion size and ion-ion correlation effects, which prohibit its application to systems where such effects become pronounced such as ionic layering, overcharging or charge inversion, like-charge attraction, and ion selectivity inversion, all of which are associated with highly charged macroions, usually under high salt conditions or in the presence of multivalent ions.^5-11

Addressing these approximations within the Poisson-Boltzmann approach while retaining its simplicity is therefore desirable. As a result, several investigators have formulated various corrections to the NLPBE in order to include the effects of ion-ion correlations¹², a dipolar solvent with variable density¹³ and other effects¹⁴ in an effort to account for the above mentioned intriguing experimentally observed phenomena.

Experimental studies have shown that even for small inorganic ions at intermediate to high salt concentrations, ion size effects cannot be ignored in quantitative predictions of nanopore selectivity at high surface charge densities¹⁵. In light of such experimental observations, several methods have been developed to address the effects of finite ion size one of the first being the use of an ion exclusion region or “Stern layer” surrounding the charged biomolecule where ions are not permitted to penetrate.¹⁶ Others include using a cutoff on the maximum local salt concentration,¹⁷ Coulomb gas with finite size,¹⁸ modified Poisson-Boltzmann based on the generalized-Poisson Fermi formalism,¹⁹ lattice statistics models^20-22, equation of state coupled to a function integral representation for a hard sphere fluid mixture approach,²³ and Bogoliubov-Bom-Green-Yvon hierarchy by Outhwaite and co-workers.^24,25

In this paper, we chose to investigate the lattice-gas based method because it provides a physically realistic model that can be extended to the case of nonuniform ion sizes, without increasing the computational complexity of the original Poisson-Boltzmann solution. The predictions of one such theory, the uniform ion-size modified Poisson-Boltzmann equation, SMPBE,^20,21,26 are compared with those of the traditional NLPBE with and without an ion-exclusion region. The uniform ion-size MPBE is implemented for a low-dielectric spherical cavity with a central charge embedded in an aqueous salt solution. The mathematical details of this uniform ion SMPBE model are described in the Appendix, and its numerical implementation discussed in the Methods section.

The most popular method of accounting phenomenologically for the excluded volume or steric effects in the NLPBE relies on using a Stern layer, or ion-exclusion region. Its use is motivated by reasoning that ions will not come within their van der Waal’s radius of the biomolecule, an observation that has been confirmed by different Monte Carlo simulations^27,28 of ionic distributions around biomolecules. However, this approximate model provides a limited representation of finite ion size effects, and, as will be shown later, does not reproduce the predictions of the SMPBE. Some investigators²⁹ have used a Stern layer in conjunction with the SMPBE, but doing so is an effective overcounting of the observed lack of ion centers within their atomic radius of the molecular surface because in the SMPBE an ion with its atomic center at that distance would still contribute charge density at the molecular surface because of the ion’s finite size.

Unfortunately, as will be discussed below, current experimental data^29-32 is insufficient to conduct a decisive validation of these models since they have generally measured global or integrated (over the entire space) properties, such as the number of bound counterions, which are essentially identical for all of the candidate models. To determine which of these competing methods is best, experimental probes of local properties must be devised to measure, say, the forces between charged biomolecules at short separation distances, whose predictions would be sensitive to modeling choice

METHODS

Nonlinear Poisson-Boltzmann Equation

In the NLPBE, the normalized electrostatic potential ϕ = eφ / k_bT of a biomolecule immersed in an ionic solvent obeys:

$$\nabla \cdot \epsilon \left(r\right)\nabla \varphi +\frac{4\pi e}{k_{b}T}\rho \left(r\right)=0$$ (1)

where ε(r) is the dielectric constant, e is the protonic charge, k_b is the Boltzmann constant and T is the absolute temperature of the ionic solution. The charge density ρ^NLPBE (r) in the solute, ion-exclusion, and solvent regions (respectively, Ω₁, Ω₂, and Ω₃) is given by:

$${\rho }^{\mathit{NLPBE}}\left(r\right)=\{\begin{array}{cc}{\rho }^f=\sum _i{Q}_i\delta (r-r_i),\hfill & r\in {\Omega }_1\hfill \\ 0,\hfill & r\in {\Omega }_2\hfill \\ {\rho }^{\text{ion}}=e\sum _{k=1}^{\mathit{n}\text{salt}}\left(z_k^{+}{c}_{bk}^{+}\exp \right(-z_k^{+}\varphi )-z_k^{-}{c}_{bk}^{-}\exp (+z_k^{-}\varphi \left)\right),\hfill & r\in {\Omega }_3\hfill \end{array}\phantom{\}}$$ (2)

In eq 2 Q_i is the discrete charge of the solute at position r_i, and $z_k^{\pm }$ and $c_{bk}^{\pm }$ are the valence and the bulk concentration for both the coion and the counterion, respectively. The region Ω₂ is frequently modified by setting ρ_ion to 0 in the vicinity of the molecular surface, creating the Stern layer or ion-exclusion region.

In the case of small electrostatic potentials, ϕ≪ 1, eq 1 in region Ω₃, reverts to the well known linearized PBE:

$${\nabla }^2\varphi ={\kappa }^2\varphi$$ (3)

where the Debye-Hückel screening parameter, κ, is given by ${\kappa }^2=(4\pi e^2∕k_{b}T{\epsilon }_{\mathit{ext}}){\sum }_{k=1}^{\mathit{nsalt}}\{c_{bk}^{+}{\left(z_k^{+}\right)}^2+c_{bk}^{-}{\left(z_k^{-}\right)}^2\}$ and ε_ext is the dielectric constant of the solvent.

The Uniform Ion Size Modified Poisson-Boltzmann Equation

To account for the uniform finite size of ions, the NLPBE can be modified as in the lattice gas model.²⁰ In this model, each ion is assumed to occupy a cube of volume a³ where a is twice the radius of the ion, r_ion, and all of the ions in the solution have equal radii. The mobile ion density in the exterior region Ω₃ is therefore modified to²⁰:

$${\rho }^{\mathit{SMPBE}}\left(r\right)=\frac{{\rho }^{\mathit{NLPBE}}\left(r\right)}{1+\xi \left(r\right)}$$ (4)

where $\xi \left(r\right)=\sum _k{\xi }_k\left(r\right)$, and the volume exclusion factor of the i’th ion is given by:

$${\xi }_i\left(r\right)=a^3\left\{c_{\mathit{bi}}^{+}\exp \right(-z_i^{+}\varphi \left(r\right))+c_{\mathit{bi}}^{-}\exp (z_i^{-}\varphi \left(r\right))-(c_{\mathit{bi}}^{+}+c_{\mathit{bi}}^{-}\left)\right\}$$ (5)

In both the NLPBE and the SMPBE, the electrostatic free energy F^elec can be expressed as the sum of three terms. In the SMPBE, this can be written as:

$$F^{\mathit{SMPBE}}={\int }_V{d}^{3}r(-\frac{\epsilon {\mid \nabla \phi \left(r\right)\mid }^2}{8\pi }+{\rho }^f\phi (r)-\frac{k_{b}T}{a^3}\ln \left(1+\xi \left(r\right)\right))$$ (6)

where the first term is the electrostatic stress, and the third term, denoted by ΔΠ^SMPBE, is the osmotic pressure whose NLPBE counterpart is,

$$\Delta {\Pi }^{\mathit{NLPBE}}=k_{b}T{\int }_V{d}^{3}r\sum _k{c}_{bk}\left\{z_k^{-}\exp \right(-z_k^{+}\varphi \left(r\right))+z_k^{+}\exp (-z_k^{-}\varphi \left(r\right))-(z_k^{+}+z_k^{-}\left)\right\}$$ (7)

which is readily obtained in the limit a→0. Note that ΔΠ^SMPBE, unlike ΔΠ^NLPBE, is not separable into contributions from individual ions because these contributions combine nonlinearly in the logarithm. This means that the well-known relationship between ΔΠ and the derivative of the electrostatic free energy with respect to log(c_b) available for the NLPBE,

$$\frac{d{F}^{\mathit{NLPBE}}}{d\log \left(c_{bk}\right)}=-\Delta {\Pi }_k^{\mathit{NLPBE}}$$ (8)

does not hold in the SMPBE. However, an expression for this derivative is nevertheless available and is given by (see Appendix):

$$\frac{d{F}^{\mathit{SMPBE}}}{d\log \left(c_{bk}\right)}=-\frac{k_{b}T}{a^3}{\int }_V{d}^{3}r\frac{{\xi }_k\left(r\right)}{(1+\xi (r\left)\right)}$$ (9)

A simple relationship can be found between F^SMPBE and F^NLPBE in the limit of small ξ by writing:

$$\frac{d{F}^{\mathit{SMPBE}}}{da}=\frac{3}{a}\left(\sum _k{c}_{bk}\frac{d{F}^{\mathit{SMPBE}}}{d{c}_{bk}}+\Delta {\Pi }^{\mathit{SMPBE}}\right)$$ (10)

In the limit of ξ(r) << 1 eq 10 simplifies to:

$$\log (F^{\mathit{SMPBE}}-F^{\mathit{NLPBE}})=3\log \left(a\right)+\log \left(\frac{1}{2}{k}_{b}T{\int }_V{f}^2\left(r\right)d^{3}r\right)$$ (11)

where this integral is taken over Ω₃, and it is assumed that ξ(r) = a³f(r), where f(r) is independent of a to first order (see Appendix). This approximation does not hold when a saturation layer of counterions forms near the surface of the sphere, so eq 11 will not apply in these cases.

In ionic solutions, a charged biomolecule alters the distribution of counter- and co- ions by attracting a cloud of counterions and repelling coions. The number of excess counterions attracted to the biomolecule, ν_k, is experimentally accessible^29,30. Given a solution to either the NLPBE or the SMPBE, this number can be obtained from the following expression:

$${\upsilon }_k^{\pm }={\int }_V{c}_{bk}^{\pm }\left(\frac{\exp \left(\overline{+}{z}_k^{\pm }\varphi \right)}{1+\xi }-1\right)d^{3}r$$ (12)

Numerical Implementation of the 1D Uniform Ion SMPBE

Here the case of a low-dielectric spherical cavity containing a central charge and surrounded by ionic solution is considered. This simple spherical configuration is directionally invariant, with the solution depending solely on the radial coordinate r and with origin at the center of the low-dielectric spherical cavity. Therefore, eq 1 reduces to the 1D NLPBE equation:

$$\frac{d}{dr}\left(\epsilon \left(r\right)r^2\frac{d\varphi }{dr}\right)+\frac{4\pi e}{k_{b}T}{r}^2\rho \left(r\right)=0$$ (13)

A discrete approximation to this equation is easily developed using either finite difference or finite element methods and results in high resolution solutions. The following results use an approximation¹ previously developed for solving the NLPBE, extended here by modifying the source term to account for uniform finite ion size as in eq 4 and by incorporating the boundary treatment described in Boschitsch and Fenley,³³ which applies to both the linear and the nonlinear PBE and requires only that the potential at the outer boundary be small, ∣ϕ∣<<1. Correction terms are also added to the calculated electrostatic energies and salt gradients to account for contributions from outside the computational domain. These terms can become important, especially at lower salt concentrations.

The calculations presented here used 5000 nodes and an outer boundary placed at 200 Å from the surface of the sphere of radius 20 Å. The solution was considered to have converged when the maximum change in potential at a grid node was less than 10⁻⁵*min{1, ∣ϕ_s∣} where ϕ_s is the surface potential. To verify that results were both converged and accurate, additional calculations were conducted for randomly selected cases to ensure that no significant changes occurred when: (i) the mesh resolution was halved and (ii) when a smaller convergence criterion was used. The derivatives of the electrostatic free energy with respect to bulk concentration and with respect to ion size were also verified by using finite difference method.

RESULTS

Unless specified otherwise all results were generated for a spherical cavity of radius 20 Å containing a central charge of −50e. The ion radius is equal to one half of the size of the lattice spacing (a) used in the SMPBE. It is set to values between approximately 1 to 8 Å. The Stern layer is not invoked for the the SMPBE calculations. However, as noted in the text below for some NLPBE calculations a Stern layer is employed. The dielectric constant was set to 78.5 in the exterior region (Ω₂⋃Ω₃) and 4 inside the molecule (Ω₁). All calculations were performed at 298.15 K.

Ion Competition Effects on Global Thermodynamic Properties

The behavior of many highly charged biomolecules such as nucleic acids is highly influenced by changes in ionic conditions due to the presence of neutralizing counterions that form a characteristic ionic cloud surrounding the charged biomolecule. Moreover, many vital biological processes occur in salt mixtures and involve changes in competition effects between monovalent and multivalent ions.^34,35

Because the SMPBE models ions differently than the NLPBE, its predictions of competition effects between different ion species may differ from those of the classical NLPBE. This is investigated in Figure 1 which plots F^SMPBE against [NaCl] for different values of [MgCl₂]. For increasing [MgCl₂], the resulting curves exhibit gradual flattening with decreased slopes. This reflects the Mg⁺² counterions competing the Na⁺ ions away from near the surface of the molecule. These curves have the same qualitative form as similar curves for the NLPBE, as shown by Shen and Honig,² Boschitsch and Fenley,¹ and Figure A.1. in the Supporting Information, and therefore there is no clear difference between the ion competition effects predicted by the NLPBE with or without the Stern layer and those predicted by the SMPBE at least for the integrated quantities considered here.

Figure 1.

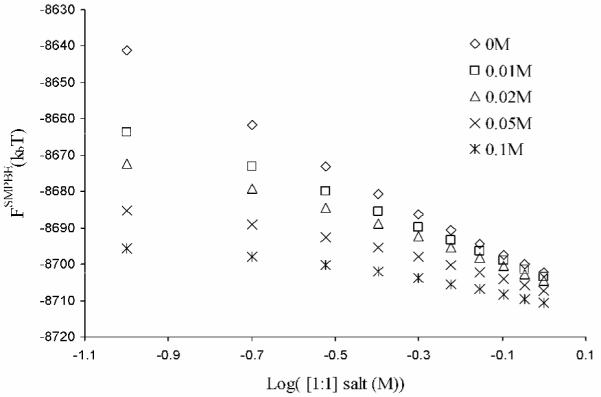
The electrostatic free energy (in k_bT) computed with the uniform ion size-modified Poisson-Boltzmann equation, F^SMPBE, of a low-dielectric spherical cavity of radius 20 Å and a central charge of −50e at concentrations of 2:1 salt, [MgCl₂], of 0, 0.01, 0.02, 0.05, and 0.1 M and an ion radius of 1.5 Å is plotted against the logarithm of the concentration of 1:1 salt, [NaCl].

That the SMPBE produces similar predictions for ion competition effects on global thermodynamic properties of the low-dielectric spherical cavity to those of the NLPBE can be further demonstrated by examining Figure 2, where υ_Mg, υ_Na, and υ_Cl are plotted against log([MgCl₂]) for NaCl = 0.1 M. These curves are qualitatively similar to the comparable curves generated by Lipfert and co-workers^26,30, which included the three-dimensional structure of actual biomolecules. This behavior indicates that, as they discussed, the inclusion of accurate three-dimensional structures does not significantly change the predictions of ion competition effects for such integrated quantities. Once again, the ion competition effects of thermodynamic parameters predicted by the SMPBE are in close agreement with the NLPBE’s predictions. In these calculations and others we have carried out (though by no means exhaustive), we have generally found that both the NLPBE’s and SMPBE’s predictions of global or integrated quantities are in good agreement. However, the ion sizes considered here (sodium and magnesium), are comparatively small (radii are on the order of 1 Å), whereas, as was pointed out by Chu and co-workers²⁹, if a much larger ion radius is considered (on the order of 10 Å), the equivalent ion competition curves of global properties predicted by the SMPBE are found to differ significantly from those of the NLPBE. Exploring the validity of the SMPBE may therefore be possible by conducting experiments with much larger ions such as polyamines (spermine and spermidine).¹⁹ Note that increasing the charge on the biomolecule does not seem to increase the difference between the predictions of the traditional NLPBE and those of the SMPBE, as is evident from the Figure A.2. in the Supporting Information Materials. Increasing the charge of the biomolecule therefore does not appear to be a viable experimental method for investigating the effects of the SMPBE. Although the NLPBE results in this figure use a Stern layer, the figure appears nearly identical when a Stern layer is not used, so the presence or absence of a Stern layer does not alter these conclusions.

Figure 2.

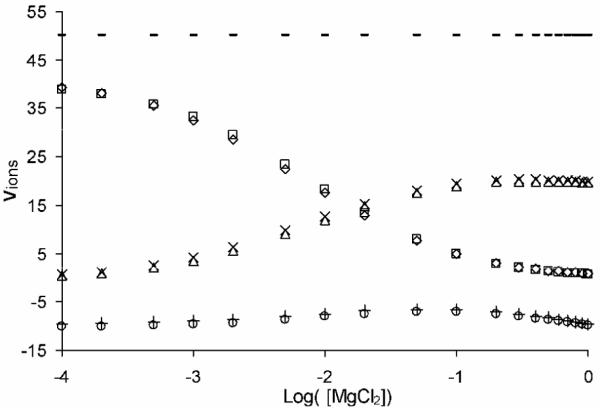
The number of bound Mg²⁺, Na⁺, and Cl⁻ ions (ν_Mg, ν_Na, and ν_Cl ) for a mixed salt solution, with an ion radius of 1.4 Å and1:1 NaCl salt concentration fixed at 0.1 M, calculated with both the nonlinear Poisson-Boltzmann equation (Δ,□,o), and the size-modified Poisson-Boltzmann equation (×, ◇, +) are plotted as a function of MgCl₂salt concentration ([MgCl₂]). The NLPBE calculations were performed with a Stern layer of 1.4 Å thickness.

Electrostatic Free Energy and its Salt Sensitivity

As mentioned before, any processe (e.g., folding, stability, binding) involving highly charged biopolyelectrolytes, are affected by changes in salt concentration³⁶. Here we examine how the electrostatic free energy and its salt sensitivity obtained with the SMPBE differs from that of the standard NLPBE.

The electrostatic free energy, F^SMPBE differs from F^NLPBE due to the additional entropic energy cost of displacing solvent when placing ions in solution and the different electrostatic potentials predicted by the SMPBE. Eq 11 indicates that to first order the difference, F^SMPBE−F^NLPBE is proportional to a³ under conditions where no saturation layer forms. This is illustrated in Figure 3 where log(F^SMPBE−F^NLPBE) for the low dielectric spherical cavity in a 1:1 salt solution is plotted against log(r_ion) (a=2r_ion) for different concentrations of [NaCl]. The curves in this plot are linear, and their slopes are very close to the expected value of 3. Interestingly, although F^SMPBE depends upon [NaCl], F^SMPBE−F^NLPBE is essentially independent of [NaCl] in the absence of a saturation layer. Despite the high charge of the sphere, the difference between the electrostatic energies predicted by the SMPBE and NLPBE is less than k_bT. This indicates that distinguishing between the SMPBE and NLPBE predictions on the basis of experimental solvation free energies is unlikely.

Figure 3.

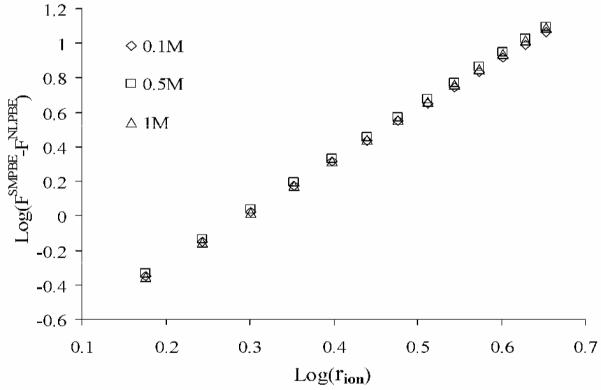
The logarithm of the difference between the electrostatic free energy (in units of k_bT) given by the uniform ion size-modified Poisson-Boltzmann equation and that given by the standard nonlinear Poisson-Boltzmann equation without a Stern layer, log(F^SMPBE−F^NLPBE), is plotted against log(r_ion) for 3 different values of NaCl concentration. The slopes of the curves are 3 to within 0.67%.

One important difference between the NLPBE and the SMPBE can be seen in the osmotic pressure term, ΔΠ. In the NLPBE, ΔΠ is equal to −dF^NLPBE / d log(c_b) as shown by Sharp and co-workers.³⁷ This relationship does not hold in the SMPBE because adding an ion to the solvent displaces solvent molecules, introducing an additional entropic cost to ΔΠ. This additional entropic cost of placing an ion in solution explains the result, discussed by Chu and co-workers²⁹, that the NLPBE underestimates the preference that biomolecules have for magnesium counterions over sodium counterions. Because the magnesium ions have roughly the same size as the sodium ions, placing one magnesium ion costs less entropy than placing two sodium ions, thereby increasing the predicted affinity of biomolecules for magnesium in the SMPBE. The additional entropic cost of placing ions introduced in the SMPBE means that, although dF^SMPBE / d log(c_b) depends only weakly on r_ion, ΔΠ is very sensitive to changes in this parameter. This is clear from Figure 4, where ΔΠ^SMPBE and −dF^SMPBE / d log(c_b) are plotted against ion size r_ion. ΔΠ^SMPBE = −dF^SMPBE / d log(c_b) when r_ion = 0, but quickly diverges for larger values of r_ion, while dF^SMPBE / d log(c_b) remains relatively constant.

Figure 4.

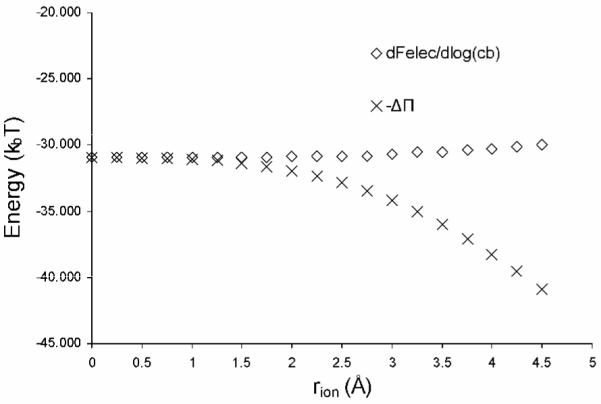
The excess osmotic pressure, ΔΠ^SMPBE computed using the uniform ion size-modified Poisson-Boltzmann equation, SMPBE, and its derivative with respect to the logarithm of the bulk 1:1 salt concentration, −dF^SMPBE / d log(c_b), are plotted against ion size r_ion, where r_ion, is equal to one half of a, the size of the lattice spacing used in the SMPBE theory.

Traditionally, a Stern layer has been added to the NLPBE to approximate ion size effects by reasoning that the main effect of a finite ion size is to exclude ions from the immediate vicinity of the charged biomolecule. To test this assertion, both F^SMPBE as a function of r_ion and F^NLPBE as a function of the thickness of the Stern layer are plotted in Figure 5. The two electrostatic energies diverge with increasing r_ion, because the NLPBE with a Stern layer overestimates the change in electrostatic free energy with ion size. The predictions of the salt dependence of the free energy by the two models are also different, as is clear from Figure 6, where the dependence −dF^SMPBE / d log(c_b) on ion size is given with the same parameters as in Figure 5. While it may be possible to adjust the Stern layer size to match the SMPBE’s predictions, how to perform this adjustment in an a priori manner for general bimolecular configurations and ionic conditions is not obvious. Note further that the disparities in the slopes of the curves in Figures 5 and 6 at a=0 point to a fundamental physical modeling discrepancy in how finite ion size is accounted for. Specifically, the SMPBE model indicates an O(a³) dependence on F near a=0 whereas the NLPBE model with a Stern layer reflects an O(a) behavior. The former variation is expected on the basis of a volume-based exclusion effect whereas the latter behavior reflects the distance-based exclusion characteristic of the Stern layer.

Figure 5.

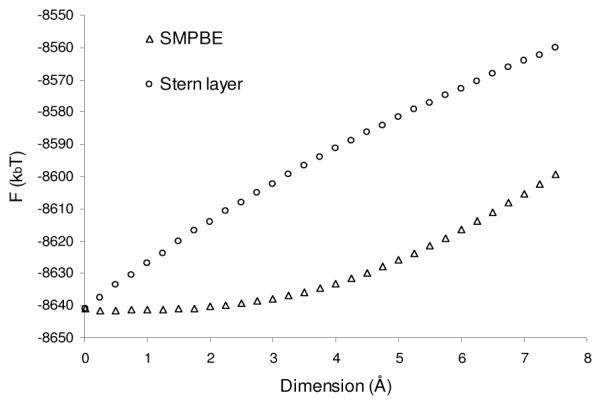
The electrostatic free energy predicted by the uniform ion size-modified Poisson-Boltzmann equation, F^SMPBE, as a function of the ion radius, r_ion, and the electrostatic free energy predicted by the standard nonlinear Poisson-Boltzmann equation, F^NLPBE, as a function of the thickness of the Stern layer.

Figure 6.

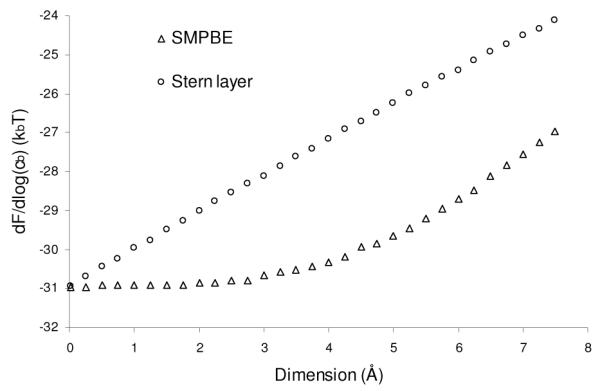
The derivative of the electrostatic free energy predicted by the uniform ion size-modified Poisson-Boltzmann equation with respect to the logarithm of the bulk concentration of 1:1 salt, −dF^SMPBE / d log(c_b), as a function of the ion radius, r_ion, and the equivalent quantity predicted by the classical nonlinear Poisson-Boltzmann equation, −dF^NLPBE / d log(c_b), as a function of the thickness of the Stern layer.

It will be important to examine if the salt dependence of various thermodynamic properties of biopolyelectrolytes in salt mixtures can be better explained or predicted using the more accurate SMPBE, with non-uniform ion size, as opposed to using the NLPE with the Stern layer. Future studies should address this point for realistic biopolyelectrolytes for which thermodynamic salt dependent data is available in the literature.

Saturation Layer

One feature that the SMPBE is able to capture is the presence of a saturation layer around the biomolecule. Essentially, as the local potential increases, the density of ions reaches a nonzero saturation concentration, which it cannot exceed because of the finite size of the ions. This contrasts with the standard NLPBE, with or without the use of Stern layer, which allows the concentration of ions to increase without bound and reach physically implausible values in the vicinity of the charged interface. This behavior is illustrated in Figure 7, where the local concentration of counterions is plotted as a function of the distance from the surface of the low-dielectric spherical cavity. In this case the 1:1 salt solution has concentration [NaCl] = 0.01 M. The ion radius is 3.5 Å and the central charge of the spherical cavity is varied. For a sufficiently large central charge, the counterions form a layer with a saturated ion density before falling off monotonically and rapidly to the bulk ion concentration. This same behavior was captured by Outhwaite and co-workers using a more sophisticated theory.³⁸ Interestingly, this figure indicates that the saturation layer will form even at very low salt concentrations (0.01M) provided the charge of the sphere is sufficiently large, and indeed, a saturation layer will develop at all nonzero salt concentrations for sufficiently high central charges. This behavior agrees with observations that have been made in other studies for other geometries, including charged cylinders and parallel plates.^21,22,39 Future experimental, simulation and theoretical studies should confirm the existence of this saturation layer and examine its implications to other physical properties of arbitrary shaped biopolyelectrolytes under varying ionic conditions, including salt mixtures.

Figure 7.

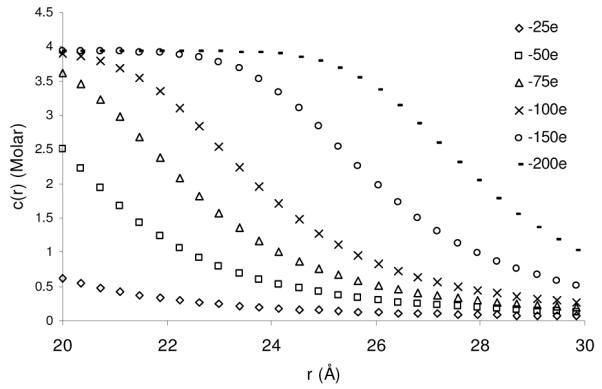
The local concentration of Na⁺, c(r), outside a low dielectric spherical cavity in a 1:1 salt solution with [NaCl] = 0.01 M and an ion radius of 3.75 Å for different central charge values.

CONCLUSIONS

The influence of finite ion size was assessed on the basis of the SMPBE applied to a low-dielectric spherical cavity containing a central charge and compared against the standard NLPBE in the context of competition effects between ion species and the salt-dependence of the electrostatic free energy. It is found that the predictions of ion competition effects given by the SMPBE do not differ significantly from those of the NLPBE for the global quantities here considered. However, the SMPBE predictions may differ from those of the NLPB for ion distribution profiles of highly charged 3D biomolecules in salt mixtures, especially at and near to the highly charged 3D biomolecular surface.

Although the SMPBE does not yield significantly different ion competition effects than the NLPBE, it does produce different electrostatic free energy predictions. In particular, although dF^SMPBE / d log(c_b) closely matches the predictions of the classical NLPBE, ΔΠ gains an additional entropic energy term from the displacement of solvent upon the placement of ions in solution that is very sensitive to changes in the ion radius. This means that, unlike in NLPBE, ΔΠ predicted by the SMPBE is not equal to −dF^SMPBE / d log(c_b) as shown in the appendix. Unfortunately, the electrostatic free energy is not directly accessible to experiment, making it impossible to examine the difference between the SMPBE’s predictions of the free energy and those of the NLPBE.

The SMPBE predicts the formation of a saturation layer. When the central charge on the biomolecule is large enough to create a field that would normally cause the local ion concentration predicted by the NLPBE to exceed the saturation concentration, the SMPBE instead shows the presence of a saturation layer for various geometries including the charged sphere, cylinder and infinite plate.^20,22,39,40

We also sought to determine whether these effects of the SMPBE could be approximated by the NLPBE with a Stern layer, but, as we demonstrated, these two models predict very different behaviors. Although the SMPBE does not include such effects as ion-ion correlations, it has a more rigorous foundation in statistical mechanics than the NLPBE with and without a Stern layer, and it therefore appears to be a preferable method for including the effects of ion size. The ion distributions can be different to that of the uniform SMPBE when ions with different charges and radii are present in the ionic solution. By using a non-uniform ion SMPBE based on the generalized Poisson-Fermi approach, Tresset and co-workers⁴¹ predicted ion stratification around a uniformly charged plane. The proper modeling of biopoelectrolytes in salt mixtures will require non-uniform ion size modified PB solvers. In order to verify the robustness of such non-uniform SMPB solvers will require the availability of pertinent experimental and simulation data. Unfortunately, comparing the predictions of the SMPBE to experimental findings was impossible in the present paper because the code used could not use a realistic three-dimensional molecular surface. This capability will be implemented shortly, and the results will be presented in a future publication. However, the results presented in this paper should also pertain to calculations performed on realistic molecular surfaces.

APPENDIX

Electrostatic Free Energy

The electrostatic free energy, F^SMPBE, of the SMPBE model can be expressed as the integral over the entire domain:

$$F^{\mathit{SMPBE}}={\int }_V{d}^{3}r(-\frac{\epsilon {\mid \nabla \phi \mid }^2}{8\pi }+{\rho }^f\phi )-\Delta \Pi$$ (14)

where the first term is the electrostatic stress, the third term is the excess osmotic pressure term, ΔΠ, ε is the dielectric constant, φ is the electrostatic potential, ρ^f is the biomolecule charge distribution, and ΔΠ is the excess osmotic pressure of the mobile ion cloud. In the SMPBE, ΔΠ is given by²⁰:

$$\Delta {\Pi }^{\mathit{SMPBE}}=-{\int }_{{\Omega }_3}\frac{k_{b}T}{a^3}\ln \left(\frac{1-C}{1-C_0}\right)d^{3}r$$ (15)

where the domain of integration in eq 15 is the region Ω₃. C is the fraction of the local volume taken up by ions in the presence of the biomolecule, and C₀ is the same quantity in the absence of the biomolecule:

$$C=a^3\sum _{k=1}^{N\text{salt}}(c_k^{+}+c_k^{-})$$ (16)

$$C_0=C(\varphi =0)=a^3\sum _{k=1}^{N\text{salt}}(c_{bk}^{+}+c_{bk}^{-})$$ (17)

Here $c_k^{+}$ and $c_k^{-}$ are the local concentrations of the k’th ion species in the presence of the biomolecule, and $c_{bk}^{+}$ and $c_{bk}^{-}$ are the local concentrations in the absence of the biomolecule.

In the SMPBE, $c_k^{\pm }$ is given by²⁰:

$$c_k^{\pm }=c_{bk}^{\pm }\frac{\exp \left(\overline{+}{z}_k^{\pm }\varphi \right)}{1+\xi \left(r\right)}$$ (18)

where $\xi \left(r\right)=\sum _k{\xi }_k\left(r\right)$ and

$${\xi }_k\left(r\right)=a^3\left\{c_{bk}^{+}\exp \right(-z_k^{+}\varphi )+c_{bk}^{-}\exp (z_k^{-}\varphi )-(c_{bk}^{+}+c_{bk}^{-}\left)\right\},$$ (19)

where $z_k^{+}$ and $z_k^{-}$ are the valences of ions A and B.

Salt Gradient of the Electrostatic Free Energy

The salt gradient of the electrostatic free energy, $\frac{d{F}^{\mathit{SMPBE}}}{d{c}_{\mathit{bi}}}$ is defined as the derivative of the free energy with respect to the bulk concentration of salt. To compute this quantity, first take the variation of the electrostatic free energy term in eq 14.

$$\begin{array}{cc}\hfill \delta F^{\mathit{SMPBE}}& ={\int }_V-\nabla \left(\delta \phi \right)\cdot \frac{\epsilon }{4\pi }\nabla \phi +{\rho }^f\delta \phi +\frac{k_{b}T}{a^3}\delta \ln \left(\frac{1-C}{1-C_0}\right)d^{3}r\hfill \\ \hfill & ={\int }_V-\nabla \cdot (\frac{\epsilon }{4\pi }\delta \phi \nabla \phi )+\delta \phi \nabla \cdot (\frac{\epsilon }{4\pi }\nabla \phi )+{\rho }^f\delta \phi +\frac{k_{b}T}{a^3}\delta \ln \left(\frac{1-C}{1-C_0}\right)d^{3}r\hfill \end{array}$$ (20)

From this equation, the salt gradient of the electrostatic free energy is:

$$\frac{d{F}^{\mathit{SMPBE}}}{d{c}_{bi}}=S_i+{\int }_V\frac{d\phi }{d{c}_{bi}}\left(\nabla \cdot \frac{\epsilon }{4\pi }\nabla \phi +{\rho }^f+{\rho }^{\text{ion}}\right)-{\rho }^{\text{ion}}\frac{d\phi }{d{c}_{bi}}+\frac{k_{b}T}{a^3}\frac{d}{d{c}_{bi}}\ln \left(\frac{1-C}{1-C_0}\right)d^{3}r$$ (21)

where the ion distribution ρ^ion is given by:

$${\rho }^{\text{ion}}=e\sum _{k=1}^{N\text{salt}}{c}_k^{+}{z}_k^{+}\exp (-z_k^{+}\varphi )-c_k^{-}{z}_k^{-}\exp \left(z_k^{-}\varphi \right)$$ (22)

and the surface integral term is given by:

$$S_i=-{\int }_{S_{\infty }}\frac{\epsilon }{4\pi }\frac{d\phi }{dn}\frac{d\phi }{d{c}_{bi}}dS$$ (23)

The second term of eq 21 is zero because it is a restatement of the PBE. The fourth term can be rewritten by combining eqs 16-19 as:

$$\ln \left(\frac{1-C}{1-C_0}\right)=-\ln \left(1+\xi \left(r\right)\right)$$ (24)

Therefore the salt gradient of the electrostatic free energy for the i-th ion species is given by:

$$\frac{d{F}^{\mathit{SMPBE}}}{d{c}_{bi}}=S_i+{\int }_V-{\rho }^{\text{ion}}\frac{d\phi }{d{c}_{bi}}-\frac{k_{b}T}{a^3(1+\xi (r\left)\right)}\frac{d\xi \left(r\right)}{d{c}_{bi}}{d}^{3}r$$ (25)

By assuming that the charge neutrality condition for salt A_xB_y requires that $c_{\mathit{bi}}^{+}{z}_i^{+}=c_{\mathit{bi}}^{-}{z}_i^{-}$, and that the salt completely dissociates in the solvent, we get $c_{\mathit{bi}}:c_{\mathit{bi}}^{+}:c_{\mathit{bi}}^{-}=1:x:y$.

By calculating the derivative of ξ(r) with respect to c_bi and using eq 22, further simplification is possible:

$$\begin{array}{cc}\hfill \frac{d{F}^{\mathit{SMPBE}}}{d{c}_{bi}}& =S_i+{\int }_V{d}^{3}r\left(-{\rho }^{\text{ion}}\frac{d\phi }{d{c}_{bi}}-\frac{k_{b}T}{a^3(1+\xi (r\left)\right)}\frac{d\xi \left(r\right)}{d{c}_{bi}}\right)\hfill \\ \hfill & =S_i+{\int }_V{d}^{3}r\left(-{\rho }^{\text{ion}}\frac{d\phi }{d{c}_{bi}}-\frac{k_{b}T}{a^3(1+\xi (r\left)\right)}\frac{d\xi \left(r\right)}{d{c}_{bi}}\right)\hfill \\ \hfill & =S_i+{\int }_V{d}^{3}r\left(\begin{array}{c}-{\rho }^{\text{ion}}\frac{d\phi }{d{c}_{bi}}-\frac{k_{b}T}{a^3(1+\xi (r\left)\right)}\left\{x{z}_i^{+}\exp \right(-z_i^{+}\varphi )+y{z}_i^{-}\exp (z_i^{-}\varphi )-(z_i^{+}+z_i^{-}\left)\right\}\hfill \\ +{\rho }^{\text{ion}}\frac{d\phi }{d{c}_{bi}}\hfill \end{array}\right)\hfill \\ \hfill & =S_i-{\int }_V{d}^{3}r\left(\frac{k_{b}T}{a^3(1+\xi (r\left)\right)}\left\{x{z}_i^{+}\exp \right(-z_i^{+}\varphi )+y{z}_i^{-}\exp (z_i^{-}\varphi )-(z_i^{+}+z_i^{-}\left)\right\}\right)\hfill \\ \hfill & =S_i-\frac{k_{b}T}{a^3{c}_{bi}}{\int }_V{d}^{3}r\frac{{\xi }_i\left(r\right)}{(1+\xi (r\left)\right)}\hfill \end{array}$$ (26)

where the salt gradient of the electrostatic free energy contains a normalization constant 1+ξ(r).

At finite salt concentrations, the surface integral term, S_i, is zero because the exponential decay in the potential guarantees that the integrand is zero at infinity, but in the limit of zero salt concentration, this is not true and S_i diverges. This difficulty is avoided by considering instead the derivative of the electrostatic free energy with respect to log(c_b) (c_b^½ is another useful choice yielding finite derivatives) to obtain:

$$\frac{d{F}^{\mathit{SMPBE}}}{d\log \left(c_{bi}\right)}=c_{bi}{S}_i-\frac{k_{b}T}{a^3}{\int }_V{d}^{3}r\frac{{\xi }_i\left(r\right)}{(1+\xi (r\left)\right)}$$ (27)

The product c_biS_i now vanishes as c_bi→0. To prove this, note that at a large distance, R, the potential is sufficiently small that the local behavior in the region r>R is governed by the linear PBE. Thus the potential solution behaves as:

$$\phi \left(r\right)\sim \frac{B\exp (-\kappa r)}{r},\mathrm{r}>\mathrm{R}$$ (28)

where B is a constant and

$$\begin{array}{cc}\hfill {\kappa }^2& =\frac{8\pi e^2}{k_{b}T\epsilon }\sum _k\frac{1}{2}\{c_{bk}^{+}{\left(z_k^{+}\right)}^2+c_{bk}^{-}{\left(z_k^{-}\right)}^2\}\hfill \\ \hfill & =\frac{4\pi e^2}{k_{b}T\epsilon }\sum _k{c}_{bk}{z}_k^{-}{z}_k^{+}\{z_k^{+}+z_k^{-}\}\hfill \end{array}$$ (29)

The derivative of φ with respect to κ is given by:

$$\frac{d\phi }{d\kappa }=-B\exp (-\kappa r)$$ (30)

and its derivative with respect to r is given by:

$$\frac{d\phi }{dr}=-\frac{B(\kappa r+1)\exp (-\kappa r)}{r^2}$$ (31)

Inserting into eq 23:

$$\begin{array}{cc}\hfill S_i& =-\underset{R\to \infty }{\lim }\frac{\epsilon }{4\pi }\left(-\frac{B(\kappa R+1)\exp (-\kappa R)}{R^2}\right)\left(-B\exp (-\kappa R)\frac{d\kappa }{d{c}_{bi}}\right)4\pi R^2\hfill \\ \hfill & =-\epsilon B^2\left(\frac{d\kappa }{d{c}_{bi}}\right)\underset{R\to \infty }{\lim }\left\{(\kappa R+1)\exp (-2\kappa R)\right\}\hfill \end{array}$$ (32)

The last term in braces is bounded by 1 so that:

$$c_{bi}\mid S_i\mid \le \epsilon B^2\left(c_{bi}\frac{d\kappa }{d{c}_{bi}}\right)$$ (33)

The derivative of κ with respect to c_bi is:

$$\frac{d\kappa }{d{c}_{bi}}=\frac{2\pi e^2}{\kappa k_{b}T\epsilon }{z}_i^{-}{z}_i^{+}\{z_i^{+}+z_i^{-}\}$$ (34)

so that

$$c_{bi}\frac{d\kappa }{d{c}_{bi}}\le \sqrt{c_{bi}}D$$ (35)

, where $D=\sqrt{\frac{\pi e^2{z}_i^{+}{z}_i^{-}(z_i^{+}+z_i^{-})}{k_{b}T\epsilon }}.$ Substituting into the result for c_bi∣S_i∣ confirms the convergence with zero concentration, c_bi.

Dependence of the Electrostatatic Free Energy on Ion Size

At small salt concentrations, the difference between the free energy predictions of the SMPBE and those of the NLPBE are dominated by the additional entropic cost of placing an ion in solution in the SMPBE model. By considering the derivative of electrostatic free energy with respect to a, $\frac{d{F}^{\mathit{SMPBE}}}{da}$, a formula relating F^SMPBE to F^NLPBE in the limit of small salt concentrations can be derived as follows:

$$\frac{d{F}^{\mathit{SMPBE}}}{da}=M+{\int }_V{d}^{3}r(\frac{d\phi }{da}\left(\nabla \cdot \frac{\epsilon }{4\pi }\nabla \phi +{\rho }^f+{\rho }^{\text{ion}}\right)-{\rho }^{\text{ion}}\frac{d\phi }{da}-k_{b}T\frac{d}{da}\frac{\ln (1+\xi (r\left)\right)}{a^3})$$ (36)

where $M=-\underset{S_{\infty }}{\int }\frac{\epsilon }{4\pi }\frac{d\phi }{dn}\frac{d\phi }{da}dS$.

Because the electrostatic potential has the asymptotic form $\frac{\exp (-\kappa r)}{r}$, M=0 and the second term on the right side of eq 36 is zero because it is the SMPBE equation. By calculating the derivative of ξ(r) with respect to a and using eq 15, eq 36 can be further simplified to:

$$\begin{array}{cc}\hfill \frac{d{F}^{\mathit{SMPBE}}}{da}& =\left(\frac{3}{a}\right)\frac{k_{b}T}{a^3}{\int }_V{d}^{3}r(\ln \left(1+\xi \left(r\right)\right)-\frac{\xi \left(r\right)}{1+\xi \left(r\right)})\hfill \\ \hfill & =\left(\frac{3}{a}\right)(\sum _k\frac{d{F}^{\mathit{SMPBE}}}{d\log \left(c_{bk}\right)}+\Delta {\Pi }^{\mathit{SMPBE}})\hfill \end{array}$$ (37)

By considering the limit of small ξ(r), we can derive a relationship between F^SMPBE and F^NLPBE. The Taylor series expansion of eq 37 for small ξ is:

$$\frac{d{F}^{\mathit{SMPBE}}}{da}=\frac{3k_{b}T}{a^4}{\int }_V{d}^{3}r\left(\frac{1}{2}{\xi }^2\right(r)+O({\xi }^3\left(r\right)\left)\right)$$ (38)

Expanding ξ(r) to lowest order gives ξ(r) = a³f(r), where f(r) does not depend on a (see Supplementary Information Materials). By retaining only the ξ²(r) term, this equation becomes

$$\frac{d{F}^{\mathit{SMPBE}}}{da}=\frac{3a^2}{2}{k}_{b}T{\int }_V{d}^{3}r\left(f^2\right(r\left)\right)$$ (39)

Integrating:

$$F^{\mathit{SMPBE}}\left(a\right)=F^{\mathit{SMPBE}}\left(0\right)+\left(\frac{1}{2}{k}_{b}T{\int }_V{f}^2\left(r\right)d^{3}r\right)a^3$$ (40)

demonstrating that (F^SMPBE−F^NLPBE) is proportional to a³.